SAS学习系列38.时间序列分析报告Ⅱ—非平稳时间序列地确定性分析报告
时间序列分析实验报告

时间序列分析实验报告P185#1、某股票连续若干天的收盘价如表5-4(行数据)所示。
表5-4304 303 307 299 296 293 301 293 301 295 284 286 286 287 284 282 278 281 278 277 279 278 270 268 272 273 279 279 280 275 271 277 278 279 283 284 282 283 279 280 280 279 278 283 278 270 275 273 273 272 275 273 273 272 273 272 273 271 272 271 273 277 274 274 272 280 282 292 295 295 294 290 291 288 288 290 293 288 289 291 293 293 290 288 287 289 292 288 288 285 282 286 286 287 284 283 286 282 287 286 287 292 292 294 291 288 289选择适当模型拟合该序列的发展,并估计下一天的收盘价。
解:(1)通过SAS软件画出上述序列的时序图如下:程序:data example5_1;input x@@;time=_n_;cards;304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290 288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292 294 291288 289;proc gplot data=example5_1;plot x*time=1;symbol1c=black v=star i=join;run;上述程序所得时序图如下:上述时序图显示,该序列具有长期趋势又含有一定的周期性,为典型的非平稳序列。
时间序列分析中的非平稳信号分析方法研究

时间序列分析中的非平稳信号分析方法研究时间序列分析是统计学中的领域,用来研究一组与时间有关的数据。
时间序列分析非常重要,因为它可以帮助研究者预测机器人,股市和其他急于观察的数据。
但是,有时候我们会遇到一些非平稳的信号,导致预测分析非常困难。
在这种情况下,对非平稳信号的分析方法成为了非常重要的研究领域。
I. 什么是非平稳信号?平稳信号是指时间序列中平均值和方差都不随时间而变化的信号。
在这种情况下,我们可以使用平稳信号的统计模型进行分析和预测。
但是,在现实生活中,出现非平稳信号的情况是普遍存在的。
例如,物价、股票价格等往往都呈现出随时间变化的趋势性和季节性。
II. 非平稳信号的特点非平稳信号是指时间序列中均值,方差或者两者都在变化的信号。
与平稳信号不同,非平稳信号的各种统计量都会随时间的推移而变化,因此在真实的数据应用过程中非常常见。
1. 缺乏稳定性:不同时间点的数据存在着不同的特征,可以说非平稳序列在统计特征上表现出的一种不稳定性。
2. 时间相关性:非平稳时间序列中的不同时间点可能不是独立的,也就是说以前的一个时间点可能会对后续的时间点产生影响,这种影响通常以趋势的形式呈现。
3. 不存在平稳的统计模型:由于非平稳信号缺乏稳定性,所以不存在平稳的统计模型,要研究非平稳信号需要寻找其他方法。
III. 非平稳信号分析方法在研究非平稳信号的过程中,最常用的方法包括:时间序列分解、差分方法、ARIMA和ARCH模型等。
1. 时间序列分解时间序列分解是将非平稳信号分解为一些成分,例如趋势、周期和随机元素。
这种方法可以使我们更好地理解信号的变化过程和对不同成分的影响。
时间序列分解同时也对信号的去除趋势和季节成分非常有用。
2. 差分方法差分方法是通过对时间序列之间差异的计算,将其转化为平稳时间序列,从而避免非平稳信号带来的影响,使得时间序列分析得以进行。
这种方法适用于不太具有周期性的时序数据。
3. ARIMA模型ARIMA模型是最常用的时间序列分析方法之一。
非平稳序列的确定性分析
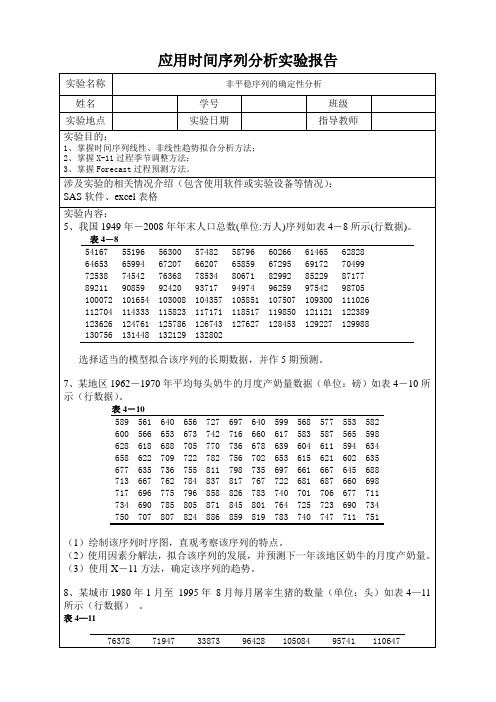
应用时间序列分析实验报告27708281449,1,2,3,,60t t X t l t =-++=⎧⎪SAS程序如下:data example1;input x@@;time=1949+_n_-1;cards;54167 55196 56300 57482 58796 60266 61465 6282864653 65994 67207 66207 65859 67295 69172 7049972538 74542 76368 78534 80671 82992 85229 8717789211 90859 92420 93717 94974 96259 97542 98705100072 101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 118517 119850 121121 122389 123626 124761 125786 126743 127627 128453 129227 129988 130756 131448 132129 132802;proc gplot data=example1;plot x*time=1;symbol1c=black v=star i=join;run;proc autoreg data=example1;model x=time;output out=out p=example1_cup;run;proc gplot data=out;plot x*time=1 example1_cup*time=2/overlaysymbol2 c=red v=none i-join w=21=3;run;7、(1)时序图如下:—11拟合序列图:剔除季节效应后的时序图有非常显著的线性递增趋势。
SAS程序如下:(1)symbol c=black i=join v=star; run;(2)data example2;input x@@;time=intnx ('month','01jan1962'd,_n_-1);format time date;cards;589 561 640 656 727 697 640 599 568 577 553 582600 566 653 673 742 716 660 617 583 587 565 598628 618 688 705 770 736 678 639 604 611 594 634658 622 709 722 782 756 702 653 615 621 602 635677 635 736 755 811 798 735 697 661 667 645 688713 667 762 784 837 817 767 722 681 687 660 698717 696 775 796 858 826 783 740 701 706 677 711734 690 785 805 871 845 801 764 725 723 690 734750 707 807 824 886 859 819 783 740 747 711 751;proc gplot data=example2;plot x*time=1;symbol1c=red I=join v=star;run;(3)data example2;input x@@;t=intnx ('monthly','1jan1962'd,_n_-1);cards;589 561 640 656 727 697 640 599 568 577 553 582600 566 653 673 742 716 660 617 583 587 565 598628 618 688 705 770 736 678 639 604 611 594 634658 622 709 722 782 756 702 653 615 621 602 635677 635 736 755 811 798 735 697 661 667 645 688713 667 762 784 837 817 767 722 681 687 660 698717 696 775 796 858 826 783 740 701 706 677 711734 690 785 805 871 845 801 764 725 723 690 734750 707 807 824 886 859 819 783 740 747 711 751;proc x11 data=example2;monthly date=t;var x;output out=out b1=x d10=season d11=adiusted d12=trend d13=irr;data out;set out;estimate=trend*season/100;proc gplot data=out;plot x*t=1 estimate*t=2/overlay;plot adjusted*t=1trend*t=1irr*t=1;symbol1c=black i=join v=star;symbol2c=red i=join v=none w=2l=3;run;(4)data example4_7;input x @@;t=intnx ('quarter','1jan1962'd,_n_-1);format t aa4.;cards;589 561 640 656 727 697 640 599 568 577 553 582600 566 653 673 742 716 660 617 583 587 565 598628 618 688 705 770 736 678 639 604 611 594 634658 622 709 722 782 756 702 653 615 621 602 635677 635 736 755 811 798 735 697 661 667 645 688713 667 762 784 837 817 767 722 681 687 660 698717 696 775 796 858 826 783 740 701 706 677 711734 690 785 805 871 845 801 764 725 723 690 734750 707 807 824 886 859 819 783 740 747 711 751;proc x11 data=example4_7;quarterly date=t;var x;output out=out b1=x d10=season d11=adjusted d12=trend d13=irr;data out;set out;estimate=trend*sesson/100;proc gplot data=out;plot season*t=2 adjusted*t=2 trend*t=2 irr*t=2;plot x*t=1 estimate*t=2/overlay;symbol1i=spline v=star h=1cv=blue ci=red;symbol2i=spline v=star h=1cv=red ci=green;run;8、时序图如下:从图中曲线可以看出,数据并没有周期性或者趋向性规律,并且每月的生猪的屠宰量大约在80000上下波动。
时间序列分析实验报告

《时间序列分析》课程实验报告一、上机练习(P124)1.拟合线性趋势程序:data xiti1;input x@@;t=_n_;cards;;proc gplot data=xiti1;plot x*t;symbol c=red v=star i=join;run;proc autoreg data=xiti1;model x=t;output predicted=xhat out=out;run;proc gplot data=out;plot x*t=1 xhat*t=2/overlay;symbol2c=green v=star i=join;run;运行结果:分析:上图为该序列的时序图,可以看出其具有明显的线性递增趋势,故使用线性模型进行拟合:x t=a+bt+I t,t=1,2,3,…,12分析:上图为拟合模型的参数估计值,其中a=,b=,它们的检验P值均小于,即小于显著性水平,拒绝原假设,故其参数均显著。
从而所拟合模型为:x t=+.分析:上图中绿色的线段为线性趋势拟合线,可以看出其与原数据基本吻合。
2.拟合非线性趋势程序:data xiti2;input x@@;t=_n_;cards;;proc gplot data=xiti2;plot x*t;symbol c=red v=star i=none;run;proc nlin method=gauss;model x=a*b**t;parameters a= b=;=b**t;=a*t*b**(t-1);output predicted=xh out=out;run;proc gplot data=out;plot x*t=1 xh*t=2/overlay;symbol2c=green v=none i=join;run;运行结果:分析:上图为该时间序列的时序图,可以很明显的看出其基本是呈指数函数趋势慢慢递增的,故我们可以选择指数型模型进行非线性拟合:x t=ab t+I t,t=1,2,3,…,12分析:由上图可得该拟合模型为:x t=*+I t分析:图中的红色星号为原序列值,绿色的曲线为拟合后的拟合曲线,可以看出原序列值与拟合值基本上是重合的,故该拟合效果是很好的。
SAS分析非平稳时间序列

运用SAS对谷物产量进行分析—、摘要利用SAS软件(程序见附录)判断谷物产量数据为平稳序列且为非白噪声序列,然后先后通过模型的识别、参数的估计、模型的优化、残差白噪声检验,确定AR(1)模型拟合时间序列显著有效。
由于时间序列之间的相关关系,且历史数据对未来数据有一定的影响,对未来5期的谷物生产量进行预测。
二、理论准备首先判断序列的随机性和平稳性。
通过随机性检验,判断该序列是否为白噪声序列,如果是白噪声序列,就认为该随机事件没有包含任何值得提取的有用信息,我们就应该终止分析。
通过平稳性检验,序列可以分为平稳序列和非平稳序列。
如果序列平稳,通过相关计算进行模型拟合,并利用过去行为对将来行为进行预测,达到预测效果。
如果序列为非平稳,再确定模型为非平稳序列中四大类模型中的哪种种模型或者几种模型对序列的综合影响,通过把序列转化为平稳序列,再进一步分析。
三、数据选取本实验采用某地区连续74年的谷物产量(单位:千吨),如下所示:0.97 0.45 1.61 1.26 1.371.43 1.321.23 0.84 0.89 1.18 1.33 1.21 0.98 0.91 0.61 1.23 0.97 1.10 0.74 0.80 0.810.80 0.600.59 0.63 0.87 0.36 0.81 0.91 0.77 0.96 0.93 0.95 0.65 0.98 0.70 0.86 1.320.88 0.680.78 1.25 0.79 1.19 0.69 0.92 0.86 0.86 0.85 0.90 0.54 0.32 1.40 1.14 0.690.91 0.680.57 0.94 0.35 0.39 0.45 0.99 0.84 0.62 0.85 0.730.66 0.76 0.63 0.32 0.170.46四、数据进行平稳性与纯随机性的检验与判别(一)序列的纯随机性检验tutocorrelation Check for Uhite NoiseTo Chi-Fr)Lag Square OF ChiSq ........ ......... ........... A utocorrelations ....................629川 6 t.lltl 0.3630.26t 0.227 9.21! 0.20?图1序列延迟6阶LB检验结果序列纯随机性检验结果显示延迟6阶LB检验统计量的P值小于1%勺显著性水平0.0001,说明序列之间蕴含着很强的相关信息,即该序列是非随机性序列,为非白噪声。
平稳性和非平稳时间序列分析

“单积”(Integrated)的,并记I为(d) 。
14
四、时间序列的协积性 (一)定义 如果一组时间序列都 X1, , X n 是同阶单积
的(I (d) ),并且存在向量 (1, , n )
使加权组合1X1 n X n 为平稳序列 (I (0)),则称这组时间序列为“协积的”
(Cointegrated),其中 (1, , n ) 称为
“协积向量”。
15
具有协积性的非平稳序列各自的非平稳 趋势和波动有相互抵消的作用,因此虽 然非平稳本身有导致回归分析失效的影 响,但如果模型中的几个非平稳时间序 列具有协积性,回归分析仍然可以是有 效的,不需要担心非平稳性会造成问题。
16
11
不少非平稳时间序列作差分变换得到的差分序 列都是平稳序列。对于这种非平稳时间序列的 差分序列,基于平稳数据的计量分析就是有效 的。
由于时间序列的差分序列与时间序列本身包含 许多一致的信息,差分与原变量之间常常可以 相互转换,因此利用差分数据进行计量分析也 是有意义的。
并不是所有非平稳时间序列的差分序列都是平 稳的。利用差分数据进行分析之前,必须对差 分序列进行平稳性检验。检验的方法是把单位 根检验用于时间序列的差分序列。
Yt Yt1 t ,其中 t 为白噪声过程。
(2)检验思路 首先 Yt 服从如下的自回归模型
Yt Yt 1 t
6
如果其中 1 ,或者变换成如下的回归 模型 Yt Yt 1 t
中的 0 ,那么时间序列{Yt }就是最基
本的单位根过程 Yt Yt1 t ,肯定是非平 稳的。 对上述差分模型中的显著性检验,就是 检验时间序列是否存在上述单位根问题。
非平稳序列的确定性分析
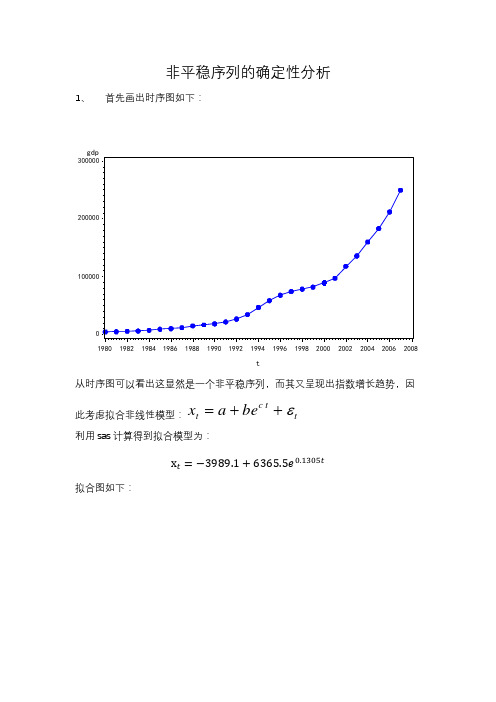
非平稳序列的确定性分析1、 首先画出时序图如下:从时序图可以看出这显然是一个非平稳序列,而其又呈现出指数增长趋势,因此考虑拟合非线性模型:t tc t be a x ε++= 利用sas 计算得到拟合模型为:拟合图如下:检验:Sum of Mean ApproxSource DF Squares Square F Value Pr > FModel 2 1.26E11 6.3E10 1778.88 <.0001Error 25 8.8539E8 35415408Corrected Total 27 1.269E11ApproxParameter Estimate Std Error Approximate 95% Confidence Limitsa -3989.1 3179.5 -10537.3 2559.1b 6365.5 1085.9 4129.0 8602.0c 0.1305 0.00606 0.1180 0.1430可以看到各项检验都通过。
接下来对残差进行白噪声检验:残差计算为:检验:Autocorrelation Check for White NoiseToLag ChiSquare DF Pr > ChiSq --------------------Autocorrelations--------------------6 57.36 6 <.0001 0.779 0.437 0.009 -0.370 -0.574 -0.637 12 72.31 12 <.0001 -0.474 -0.264 -0.057 0.090 0.155 0.157可以看出p值都小于0.05,没有通过检验,考虑到其指数趋势,因对序列取对数,得到时序图:取对数后的序列呈现线性增长趋势,对取对数后的数据进行一阶差分,时序图:再进行平稳性检验:AutocorrelationsLag Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 Std Error0 0.0039491 1.00000 | |********************| 01 0.0024154 0.61164 | . |************ | 0.1924502 0.00070015 0.17730 | . |**** . | 0.2544573 -0.0005546 -.14045 | . ***| . | 0.2589924 -0.0014108 -.35726 | . *******| . | 0.2617985 -0.0015622 -.39558 | . ********| . | 0.2792726 -0.0011031 -.27934 | . ******| . |可以看出序列已经平稳。
SAS讲义-第四十一课非平稳序列的确定性分析

第四十一课 非平稳序列的确定性分析在实际情况中,绝大部分序列都是非平稳的,因而对非平稳序列的分析更普遍、更重要,相应地各种分析方法也更多。
通常,把非平稳时间序列的分析方法分为:确定性时间序列分析和随机性时间序列分析两大类。
所谓非平稳确定性时间序列是指在自然界中由确定性因素导致的非平稳时间序列,通常这种非平稳的时间序列显示出非常明显的规律性,比如有显著的趋势或有固定的变化周期,这种规律性信息一般比较容易提取。
所谓非平稳随机性时间序列是指由随机因素导致的的非平稳时间序列,通常这种随机波动非常难以确定和分析。
传统的时间序列分析方法通常都把分析的重点放在确定性信息的提取上,而忽视对随机信息的提取。
通常将序列简单地假定为t t t x εμ+=,如果t ε是均值为零的白噪声序列,那么就可以采用确定性分析方法。
一、 时间序列的平滑技术有些时间序列具有非常显著的趋势,有时我们分析的目的就是要找到序列中的这种趋势,并利用这种趋势对序列的发展作出合理的预测。
对趋势进行分析和预测常用方法有:● 趋势拟合法——把时间作为自变量,相应的序列观察值作为因变量,建立序列值随时间变化的回归模型的方法。
根据序列所表现出的线性或非线性特征,我们的拟合方法又可以具体分为线性拟合和曲线拟合。
● 平滑法——利用修匀技术,消弱短期随机波动对序列的影响,使序列平滑化,从而显示出变化的规律。
根据所用的平滑技术的不同,又可具体分为移动平均法和指数平滑法。
1. 滑动平均与加权滑动平均法一般说来,已知序列值为t x x x x ,,,,321 ,欲预测1+t x 的值,则其预测值为:Nx x x xN t t t t 111ˆ+--++++=(41.1)这种均值随t 的变化而变化,称它为滑动平均值。
这里N 称为滑动平均的时段长。
滑动平均的目的主要是平滑数据,消除一些干扰,使趋势变化显示出来,从而可以用于趋势预测。
在计算滑动平均值时,若对各序列值不作同等看待,而是对每个序列值乘上一个加权因子,然后再作平均,则称此为加权滑动平均,称下述预测值Nx x x xNt N t t tw ---+++=ααα 2211ˆ(41.2)为加权滑动平均拟合值,α1,α2,…,αN 为加权因子,满足11=∑=NNi iα例如,当N =3时,α1 =1.5, α2 =1,α3 =0.5,有35.05.1ˆ321---++=t t t tw x x x x滑动平均值与所选的时段长短有关,时段长时的滑动平均值比时段短时的滑动平均值的反应速度慢,这是对于干扰的敏感性降低的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
38. 非平稳时间序列的确定性分析实际中大多数时间序列是非平稳的,对非平稳时间序列的分析方法主要有两类:确定性分析和随机性分析。
确定性分析——提取非平稳时间序列明显的规律性(长期趋势、季节性变化、周期性),目的是:①克服其它因素影响,单纯测度出单一确定因素对序列的影响;②推断各种确定性因素彼此之间相互作用关系及它们对序列的综合影响。
随机性分析——分析非平稳时间序列由随机因素导致的随机波动性。
(一)趋势分析有的时间序列具有明显的长期趋势,趋势分析就是要找出并利用这种趋势对序列发展做出合理预测。
1. 趋势拟合法即把时间作为自变量,相应的序列观察值作为因变量,建立序列值随时间变化的回归模型。
分为线性拟合和非线性拟合。
2. 平滑法利用修匀技术,消弱短期随机波动对序列的影响,使序列平滑化,从而显示出长期趋势变化的规律。
(1)移动平均、加权移动平均已知序列值x1, …, x t-1, 预测x t的值为12ˆt t t nt x x x xn---+++=L称为n 期移动平均值,n 的选取带有一定的经验性,n 过长或过短,各有利弊,也可以根据均方误差来选取。
一般最新数据更能反映序列变化的趋势。
因此,要突出新数据的作用,可采用加权移动平均法:1122ˆt t n t ntw x x x xnωωω---+++=L其中,111ni i n ω==∑.(2)二次移动平均对应线性趋势,移动平均拟合值有滞后性,可以采用二次移动平均加以改进:对移动平均值再做一次移动平均。
(3)指数平滑法指数平滑法是一种对过去观察值加权平均的特殊形式,观测值时间越远,其权数呈指数下降。
一次指数平滑法可用于对时间序列进行修匀,以消除随机波动。
预测公式为:1ˆˆ(1)t t t sx s αα-=+- 其中α∈(0, 1)为平滑常数,ˆt s为第t 期平滑预测值,初始预测值0ˆs (通常取最初几个实测数据的均值)。
一般来说,时间序列有较大的随机波动时,宜选择较大的α值,以便能较快跟上近期的变化;也可以利用预测误差选择。
(4)二次、三次指数平滑法即对一次指数平滑后的序列再做一次指数平滑,但不是直接将二次指数平滑值作为预测值,而是利用其来求出方程参数,利用滞后偏差的规律来建立直线趋势模型。
计算公式:(1)(1)1ˆˆ(1)t t t s x s αα-=+- (2)(1)(2)1ˆˆˆ(1)t t t s s s αα-=+-(1)(2)ˆˆ2t tta ss =-, (1)(2)ˆˆ()1t t t b s s αα=-- ˆt m t t xa b m +=+ 其中,m 为预测超前期数,取(2)(1)00ˆˆs s=. (5)霍尔特双参数线性指数平滑法设α, β∈(0, 1)为参数,ˆtb 为趋势增量。
用趋势增量来修正,消除了滞后性,对数据进行平滑:11ˆˆˆ(1)()t t t t s x s b αα--=+-+ 用指数平滑法估计趋势增量,对相邻两次平滑之差做修正,再加上前期趋势增量,对趋势进行平滑:11ˆˆˆˆ()(1)t t t t b s s b ββ--=-+- 计算超前m 期的预测值:ˆˆˆt m t tx s b m +=+ 初值的选取:11ˆs x =, 121ˆb x x =-.(二)时间序列的分解一、Gramer 分解定理1963年,Gramer 在Wald 分解定理的基础上,得到了Gramer 分解定理:任一时间序列{X t }都可以分解为叠加的两部分:由多项式决定的确定性趋势成分,平稳的零均值误差成分,即0()dj t t t j t j X u t B νβε==+=+Θ∑其中,t ε为0均值白噪声序列,B 为延迟算子,且()(())()()0t t t E E B B E ξεε=Θ=Θ= 0()()()ddjj t t j j j j E X E u E t t ββ=====∑∑即均值序列0dj j j t β=∑反映了{X t }受到的确定性影响,而{:()}t t t B ξξε=Θ反映了{X t }受到的随机影响。
Gramer 定理说明任何一个序列的波动都可以视为同时受到了确定性影响和随机性影响的综合作用。
平稳时间序列要求这两方面的影响都是稳定的,而非平稳时间序列产生的机理就在于它所受到的这两方面的影响至少有一方面是不稳定的。
二、时间序列的结构形式非平稳时间序列(x t )的确定性因素分为4种:(1)趋势变化因素(T t )——表现出某种倾向,上升或下降或水平;(2)季节变化因素(S t )——周期固定的波动变化; (3)循环变化因素(C t )——周期不固定的波动变化; (4)不规则因素(εt )——随机波动,由许多不可控的因素影响而引起的变化。
时间序列{X t}的结构形式有三种:(1)加法模式:x t = T t+ S t+ C t+εt(2)乘法模式:x t = T t S t C tεt(3)混合模式:x t = T t S t C t+εt上述模式中,趋势变化T t是基础,其它变化与趋势变化结合,构成序列{ x t }. 在加法模式中,各变化因素均与x t的单位相同;在乘法模式中,T t与x t有相同的单位,其它因素的变化均数比例值;在混合模型中,T t、εt与x t有相同的单位,S t和C t是比例值。
各式中的随机因素εt,均假定为独立的、方差不变的、均值为0的白噪声序列。
在这些假定下,对时间序列进行分解。
三、时间序列的传统分解法步骤1. 分解出长期趋势因素与循环因素设序列的季节长度为4(一年分为4季)。
由假定E(εt)=0,故只要对序列x t作移动长度为4的移动平均,就可消除季节和随机波动的影响(因为随机波动有正波动和负波动,一做平均,正负波动就相互抵消,随机波动影响就接近于零)。
记移动平均值为:则移动平均后的序列,即为序列的趋势因素和循环因素。
类似地,若序列按月份周期,则取12。
2. 分解季节因素与随机因素x得考虑乘法模式x t= T t S t C tεt,则两边同除以MAt只含季节因素与随机因素。
因此,它含有确定季节因素所必须的信息。
若它的比值大于100%,就意味着序列的实际值x t比滑动平均值T t C t 要大(该季度的季节性与随机性高于平均数,反之低于平均数),反之要小。
3. 从S tεt中分解季节因素S t即保留季节性,消除随机性,可以采取了按季节平均的方法,将前面得到的序列S tεt逐年逐季排列起来,然后将各年的相同季节的S tεt相加起来,再进行平均。
4. 从T t C t序列中分解出C t序列T t C t包含了趋势因素与循环因素,要把这两者分离出来,首先要确定一种能最好地描述数据的长期趋势变化的曲线类型。
趋势变化曲线,可能有以下几种类型:(1)线性趋势:T t=a+bt(2)指数曲线:T t=αeβt(3)S型曲线:属于何种趋势曲线,要根据序列的数值进行判断,并运用最小二乘法,估计出有关参数。
确定了趋势因素T t后,可以用下式计算出循环指数C t:C t也围绕100%波动,若C t低(高)于100%,则意味着第t年的经济活动水平低(高)于所有年份的平均水平。
四、温特线性和季节性指数平滑既含有线性趋势和季节性的数据进行处理和预测,使用温特(Winter)线性和季节性指数平滑方法,模型形式为:x t=S t(T t+εt)判断数据是否有季节性,粗略判断可以直接观察时序图,更好的方法是解析法,即通过研究数据序列的自相关性判断。
温特方法由三个基础的平滑公式和一个预测方程组成,每个平滑公式都含有一个平滑系数:总体平滑公式:趋势平滑公式:季节的平滑公式:预测公式:其中,α, β, γ是三个不同的平滑系数,T t 是消除季节因素后的趋势平滑值,x t 是序列的实际值,h t 是趋势增加或减少量序列,S t 是季节调整因子,τ是季节的长度(如一年中的月数12或季度数4),l是向前预测期数,ˆt l x是向前l 期的预测值。
总体平滑和趋势平滑公式是序列x t 消除季节因素S t 后,霍尔特双参数α和β线性指数平滑法。
季节平滑公式是序列x t 消除趋势因素T t 后,季节指数的加权平均修匀值。
以当前观察的季节指数x t / T t 和上期季节指数S t-τ进行γ加权平均。
对于乘法模型来说,季节指数围绕1波动,可能大于1,也可能小于1。
在拟合模型时可以通过求解最小的均方误差MSE 得到三个平滑系数的具体值。
预测公式是利用拟合模型短期向前预测l期的预测值公式。
(三)季节调整——PROC X11过程X11过程是根据美国国情调查局编制的时间序列季节调整过程X-11改编的,可以对月度或季度时间序列进行季节调整。
其基本原理就是时间序列的确定性因素分解方法。
X11过程是基于这样的假定:任何时间序列都可以拆分成长期趋势波动T t、季节波动S t、不规则波动εt的影响。
又有经济学家发现在经济时间序列中交易日D t也是一个很重要的影响因素(日历天数的组成不同而引起的变动)。
因此,任一时间序列可以分解乘法模型x t=T t S t D tεt或加法模型x t=T t +S t+D t+εt。
由于宏观调控部门主要关注的是序列的长期趋势波动T t的规律,所以X11过程主要目的是要从原序列中剔除季节影响、交易日影响和不规则波动影响,得到尽可能准确的长期趋势规律。
而采取的方法就是前文的因素剔除法和平滑技术。
X11过程不依赖任何模型,普遍采用移动平均法:用多次短期中心移动平均法消除不规则波动,用周期移动平均消除趋势,用交易周期移动平均消除交易日的影响。
在整个过程中总共要用到11次移动平均,所以得名为X11过程。
基本语法:proc x11 data=数据集 </可选项> ;monthly 选项列表;quarterlly选项列表;arima 选项列表;macurves 选项;output out=数据集 </选项列表>;pdweights 变量tables表名列表;var变量列表;by 变量;id变量列表;说明:(1)monthly或quarterly语句是必不可少的,用来说明数据集是月度序列还是季度序列;(2)pdweights和macurves语句只能与monthly语句一起用,分别用来指定星期几的权重和月份的滑动平均长度;(3)tables语句控制各种表格的输出。
output语句语句控制生成out=后指定的数据集;(4)proc x11语句的可选项:outtdr=数据集名——输出交易日回归的结果(B15表和C15表中的内容)到数据集;outstb=数据集名——输出稳定季节性检验的结果(表D8中的内容)到数据集;outex——把在arima处理过程中预测的观察加到out=输出数据集中;(5)arima语句及可选项X-11方法用一系列中心化滑动平均来估计季节成分,但在起始和结尾处只能用非对称权重。
