第2章 拉伸与压缩
合集下载
材料力学(机械类)第二章 轴向拉伸与压缩

第
二
章
拉伸压缩与剪切
1
பைடு நூலகம்
§2-1
轴向拉伸与压缩的概念和实例
轴向拉伸——轴力作用下,杆件伸长 (简称拉伸) 轴向压缩——轴力作用下,杆件缩短 (简称压缩)
2
拉、压的特点:
1.两端受力——沿轴线,大小相等,方向相反 2. 变形—— 沿轴线
3
§2-2 轴向拉伸或压缩时横截面上的内力和应力
1 、横截面上的内力
A3
2
l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
40
目录
例 2—5 截面积为 76.36mm² 的钢索绕过无摩擦的定滑轮 F=20kN,求刚索的应力和 C点的垂直位移。 (刚索的 E =177GPa,设横梁ABCD为刚梁)
16
§2-4
材料在拉伸时的力学性能
材料的力学性能是指材料在外力的作用下表现出的变 形和破坏等方面的特性。
现在要研究材料的整个力学性能(应力 —— 应变):
从受力很小
破坏
理论上——用简单描述复杂
工程上——为(材料组成的)构件当好医生
17
一、 低碳钢拉伸时的力学性能 (含碳量<0.3%的碳素钢)
力均匀分布于横截面上,σ等于常量。于是有:
N d A d A A
A A
得应力:
N A
F
FN
σ
10
例题2-2
A 1
45°
C
2
二
章
拉伸压缩与剪切
1
பைடு நூலகம்
§2-1
轴向拉伸与压缩的概念和实例
轴向拉伸——轴力作用下,杆件伸长 (简称拉伸) 轴向压缩——轴力作用下,杆件缩短 (简称压缩)
2
拉、压的特点:
1.两端受力——沿轴线,大小相等,方向相反 2. 变形—— 沿轴线
3
§2-2 轴向拉伸或压缩时横截面上的内力和应力
1 、横截面上的内力
A3
2
l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
40
目录
例 2—5 截面积为 76.36mm² 的钢索绕过无摩擦的定滑轮 F=20kN,求刚索的应力和 C点的垂直位移。 (刚索的 E =177GPa,设横梁ABCD为刚梁)
16
§2-4
材料在拉伸时的力学性能
材料的力学性能是指材料在外力的作用下表现出的变 形和破坏等方面的特性。
现在要研究材料的整个力学性能(应力 —— 应变):
从受力很小
破坏
理论上——用简单描述复杂
工程上——为(材料组成的)构件当好医生
17
一、 低碳钢拉伸时的力学性能 (含碳量<0.3%的碳素钢)
力均匀分布于横截面上,σ等于常量。于是有:
N d A d A A
A A
得应力:
N A
F
FN
σ
10
例题2-2
A 1
45°
C
2
第二章_直杆的拉伸和压缩

F
1
FN1 A1
28.3103 202 106
4
90106 Pa 90MPa
2
FN2 A2
20103 152 106
89106Pa 89MPa
2.1.3 应变的概念
绝对变形ΔL, 相对变形或线应变:
L
L
伸长时ε为正,缩短时ε为负
2.2 拉伸和压缩时材料的力学性能
2.2.1 拉伸和压缩试验及材料的力学性能
1、强度校核:
max
N A
2、设计截面:
A
N
3、确定许可载荷: NA
目录
塑性材料 :以材料的屈服极限作为确定许用应力的基础。 变形特征:当杆内的最大工作应力达到材料的屈服极限时,沿 整个杆的横截面将同时发生塑性变形,影响杆的正常工作。 许 用内力的表示为:
对于一般构件的设计,ns规定为1.5到2.0 脆性材料 :以材料的断裂极限作为确定许用应力的基础。 变形特征:直到拉断也不发生明显的塑性变形,而且只有断裂 时才丧失工作能力。许用内力的表示为:
OA
BC
D
PA
PB
PC
PD
N1 A
BC
D
PA
PB
PC
PD
解: 求OA段内力N1:设置截面如图
X 0 N 1 P A P B P C P D 0
N 1 5 P 8 P 4 P P 0N1 2P
N2
BC
D
PB 同理,求得AB、BC、 CD段内力分别为:
N2= –3P N3= 5P N4= P
2.1.3 拉伸和压缩时横截面上的应力
FN F
AA
应力集中:在截面突变处应力局部增大的 现象
应力集中系数:k=σmax/σ
5 材料力学第二章 轴向拉伸和压缩

μ
16锰钢
合金钢 铸铁 混凝土 石灰岩 木材(顺纹)
196-216
186-216 59-162 15-35 41 10-12
0.25-0.30
0.25-0.30 0.23-0.27 0.16-0.18 0.16-0.34
橡胶
0.0078
0.47
25
材料力学
§2-5
轴向拉伸时材料的机械性能
一、试验条件及试验仪器
P BC段:N 2 3 P
1
3P + P
AB段:N
3
2 P
+
–
12
2P
三、横截面上的应力
问题提出: P P (一)应力的概念 P P
度量横截面 上分布内力 的集度
1.定义:作用在单位面积上的内力值。 2.应力的单位是: Pa KPa MPa GPa
3.应力:a:垂直截面的应力--正应力σ 拉应力为正,压应力为负。
※E为弹性模量,是衡量材料抵抗弹 性变形能力的一个指标。“EA”称 为杆的抗拉压刚度。
l E Sl S E E l l EA A
胡克定律:
=Eε
23
四、横向变形
d d 1 d 0
泊松比(或横向变形系数)
d d 1 d 0 相对变形: ' d0 d0
e
DE段:颈缩阶段。
• 材料的分类:根据试件断裂时的残余相对变形率将材料分类: 延伸率(δ )>5% 塑性变形:低碳钢,铜,塑料,纤维。 延伸率(δ )<5% 脆性变形:混凝土,石块,玻璃钢,陶瓷, 玻璃,铸铁。 • 冷作硬化:材料经过屈服而进入强化阶段后卸载,再加载时,弹 性极限明显增加,弹性范围明显扩大,承载能力增大的现象。 • 强度指标:对塑性材料,在拉断之前在残余变形0.2 %(产生 0.2%塑性应变)时对应的应力为这种材料的名义屈服应力,用 0.2表示 ,即此类材料的失效应力。 锰钢、镍钢、铜等 • 脆性材料拉伸的机械性能特点: 1.断裂残余相对变形率δ <5% 0.2 or s max b 2.弹性变形基本延伸到破坏 3.拉伸强度极限比塑性材料小的多 4.b是脆性材料唯一的强度指标
16锰钢
合金钢 铸铁 混凝土 石灰岩 木材(顺纹)
196-216
186-216 59-162 15-35 41 10-12
0.25-0.30
0.25-0.30 0.23-0.27 0.16-0.18 0.16-0.34
橡胶
0.0078
0.47
25
材料力学
§2-5
轴向拉伸时材料的机械性能
一、试验条件及试验仪器
P BC段:N 2 3 P
1
3P + P
AB段:N
3
2 P
+
–
12
2P
三、横截面上的应力
问题提出: P P (一)应力的概念 P P
度量横截面 上分布内力 的集度
1.定义:作用在单位面积上的内力值。 2.应力的单位是: Pa KPa MPa GPa
3.应力:a:垂直截面的应力--正应力σ 拉应力为正,压应力为负。
※E为弹性模量,是衡量材料抵抗弹 性变形能力的一个指标。“EA”称 为杆的抗拉压刚度。
l E Sl S E E l l EA A
胡克定律:
=Eε
23
四、横向变形
d d 1 d 0
泊松比(或横向变形系数)
d d 1 d 0 相对变形: ' d0 d0
e
DE段:颈缩阶段。
• 材料的分类:根据试件断裂时的残余相对变形率将材料分类: 延伸率(δ )>5% 塑性变形:低碳钢,铜,塑料,纤维。 延伸率(δ )<5% 脆性变形:混凝土,石块,玻璃钢,陶瓷, 玻璃,铸铁。 • 冷作硬化:材料经过屈服而进入强化阶段后卸载,再加载时,弹 性极限明显增加,弹性范围明显扩大,承载能力增大的现象。 • 强度指标:对塑性材料,在拉断之前在残余变形0.2 %(产生 0.2%塑性应变)时对应的应力为这种材料的名义屈服应力,用 0.2表示 ,即此类材料的失效应力。 锰钢、镍钢、铜等 • 脆性材料拉伸的机械性能特点: 1.断裂残余相对变形率δ <5% 0.2 or s max b 2.弹性变形基本延伸到破坏 3.拉伸强度极限比塑性材料小的多 4.b是脆性材料唯一的强度指标
材料力学 第二章 轴向拉伸和压缩

明德行远 交通天下
材料力学
2. 轴力的正负规定 FN 与外法线同向,为正轴力(拉力)
FN
FN F N > 0
FN与外法线反向,为负轴力(压力)
FN
FN
二、轴力图--表明构件不同截面轴力的变化规律
意 ①反映出轴力与截面位置变化关系,较直观; 义 ②确定最大轴力的数值及其所在横截面的位置,
即确定危险截面位置,为强度计算提供依据。
斜截面外法线方向为正,反之为负。
明德行远 交通天下
材料力学
a pa cosa cos2 a
pa
a
pa
sin a
cosa sin a
1
2
sin 2a
讨 论:
当a = 0°时, (a )max (横截面上正应力最大)
当a = 90°时,
( a )min 0
当a
=
±
45°时,| a
|max
2
结果表明,杆件的最大工作应力在BC段,其值为0.75MPa。
明德行远 交通天下
材料力学
二、斜截面上的应力
k
F
F
设有一等直杆受拉力F作用,横截面面积为A。
求:斜截面k-k上的应力。
F
αk
Fα
解:截面法求内力。由平衡方程:
Fa=F
F
则:pa
Fa Aa
Aa:斜截面面积;Fa:斜截面上内力。
由几何关系:
A
材料力学
第二章 轴向拉伸和压缩
明德行远 交通天下
材料力学
主要内容
• §2-1 轴向拉伸与压缩的概念 • §2-2 轴力及轴力图 • §2-3 应力 • §2-4 轴向拉伸或压缩杆件的变形及节点位移 • §2-5 材料拉伸和压缩时的力学性能 • §2-6 轴向拉伸和压缩杆件的强度计算 • §2-7 轴向拉(压)杆的超静定问题
材料力学 第2章轴向拉伸与压缩

15mm×15mm的方截面杆。
A
FN128.3kN FN220kN
1
(2)计算各杆件的应力。
C
45°
2
B
s AB
FN 1 A1
28.3103
202
M
Pa90MPa
4
F
FN 1
F N 2 45°
y
Bx
s BC
FN 2 A2
21052103MPa89MPa
F
§2.4 材料在拉伸和压缩时的力学性能
22
5 圣维南原理
s FN A
(2-1)
(1)问题的提出
公式(2-1)的适用范围表明:公式不适用于集中力作
用点附近的区域。因为作用点附近横截面上的应力分布是非
均匀的。随着加载方式的不同。这点附近的应力分布方式就
会发生变化。 理论和实践研究表明:
不同的加力方式,只对力作
用点附近区域的应力分布有
显著影响,而在距力作用点
力学性能:指材料从开始受力至断裂的全部过程中,所表 现出的有关变形和破坏的特性和规律。
材料力学性能一般由试验测定,以数据的形式表达。 一、试验条件及试验仪器 1、试验条件:常温(20℃);静载(缓慢地加载);
2、标准试件:常用d=10mm,l=100 mm的试件
d
l
l =10d 或 l = 5d
36
b点是弹性阶段的最高点.
σe—
oa段为直线段,材料满足 胡克定律
sE
sp
E
se sp
s
f ab
Etana s
O
f′h
反映材料抵抗弹
性变形的能力.
40
A
FN128.3kN FN220kN
1
(2)计算各杆件的应力。
C
45°
2
B
s AB
FN 1 A1
28.3103
202
M
Pa90MPa
4
F
FN 1
F N 2 45°
y
Bx
s BC
FN 2 A2
21052103MPa89MPa
F
§2.4 材料在拉伸和压缩时的力学性能
22
5 圣维南原理
s FN A
(2-1)
(1)问题的提出
公式(2-1)的适用范围表明:公式不适用于集中力作
用点附近的区域。因为作用点附近横截面上的应力分布是非
均匀的。随着加载方式的不同。这点附近的应力分布方式就
会发生变化。 理论和实践研究表明:
不同的加力方式,只对力作
用点附近区域的应力分布有
显著影响,而在距力作用点
力学性能:指材料从开始受力至断裂的全部过程中,所表 现出的有关变形和破坏的特性和规律。
材料力学性能一般由试验测定,以数据的形式表达。 一、试验条件及试验仪器 1、试验条件:常温(20℃);静载(缓慢地加载);
2、标准试件:常用d=10mm,l=100 mm的试件
d
l
l =10d 或 l = 5d
36
b点是弹性阶段的最高点.
σe—
oa段为直线段,材料满足 胡克定律
sE
sp
E
se sp
s
f ab
Etana s
O
f′h
反映材料抵抗弹
性变形的能力.
40
材料力学--轴向拉伸和压缩

2、轴力图的作法:以平行于杆轴线的横坐标(称为基
线)表示横截面的位置;以垂直于杆轴线方向的纵坐
标表示相应横截面上的轴力值,绘制各横截面上的轴 FN
力变化曲线。
x
§2-2 轴力、轴力图
三、轴力图
FN
3、轴力图的作图步骤:
x
①先画基线(横坐标x轴),基线‖轴线;
②画纵坐标,正、负轴力各绘在基线的一侧;
③标注正负号、各控制截面处 、单位及图形名称。
FN
4、作轴力图的注意事项: ①基线一定平行于杆的轴线,轴力图与原图上下截面对齐; ②正负分绘两侧, “拉在上,压在下”,封闭图形; ③正负号标注在图形内,图形上下方相应的地方只标注轴力绝对值,不带正负号; ④整个轴力图比例一致。
50kN 50kN 50kN
第二章 轴向拉伸和压缩
第二章
轴向拉伸和压缩
第二章 轴向拉伸和压缩
§2 — 1 概述
§2 — 2 轴力 轴力图
目
§2 — 3 拉(压)杆截面上的应力
§2 — 4 拉(压)杆的变形 胡克定律 泊松比
录
§2 — 5 材料在拉伸与压缩时的力学性质
§2 — 6 拉(压)杆的强度计算
§2 — 7 拉(压)杆超静定问题
FN
作轴力图的注意事项: ①多力作用时要分段求解,一律先假定为正方向,优先考虑直接法; ②基线‖轴线,正负分绘两侧, “拉在上,压在下”,比例一致,封闭图形; ③正负号标注在图形内,图形上下方相应的地方只标注轴力绝对值,不带正负号; ④阴影线一定垂直于基线,阴影线可画可不画。
§ 2-3拉(压)杆截面上的应力
§2 — 8 连接件的实用计算
§2-1 概述 §2-1 概述
——轴向拉伸或压缩,简称为拉伸或压缩,是最简单也是做基本的变形。
拉伸和压缩
解 (1)计算AB杆和BC杆的轴力
d
A
B
30
取结点B为研究对象,其受力如图所示。由 平衡方程
Fx 0, FNBC cos 30 FNAB 0
Fy 0, FNBC sin 30 F 0
C aa FNAB
F
B AB
FNAB
3F,FNBC
2F
(2)校核AB杆和BC杆的强度
FNAB AAB
3F d2 /4
3
二、内力与应力
1、内力
杆件在外力作用下产生变形,其内部相互间的 作用力称为内力。这种内力将随外力增加而增 大。当内力增大到一定限度时,杆件就会发生 破坏。内力是与构件的强度密切相关的,拉压
杆上的内力又称为轴力。
F
FN
2、求内力的方法—截面法
将受外力作用的杆件假想地 切开,用以显示内力的大 小,并以平衡条件确定其 合力的方法,称为截面法。 它是分析杆件内力的唯一 方法。具体求法如下:
例 图示支架中,杆①的许用应力[]1=100MPa,杆②的许用 应力[]2=160MPa,两杆的面积均为A=200mm2,求结构的许
可载荷[F]。
解 (1)计算AC杆和BC杆的轴力
B 取C铰为研究对象,受力如图所示。列平衡
方程
A ① 45 30 ②
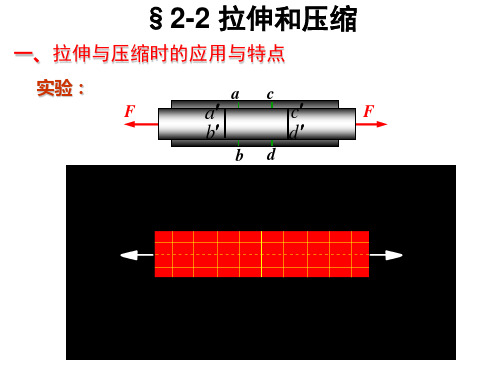
§2-2 拉伸和压缩
一、拉伸与压缩时的应用与特点
实验:
F
ac
a
c
F
b
d
bd
1.变形现象
横向线ab和cd仍为直线,且仍然垂直于轴线;
结论:各纤维的伸长相同,所以它们所受的力 也相同。 2.平面假设
变形前原为平面的横截面,在变形后仍保
持为平面,且仍垂直于轴线。
材料力学第二章-轴向拉伸与压缩

FN 3 P
1
2
P
P
1
2
FN1
3 P
3
P FN2
PP FN3
FN 1 P FN 2 0 FN 3 P
1
2
4、作内力图
P
P
P
3 P
1 FN
P
2
3
P x
[例2] 图示杆旳A、B、C、D点分别作用着大小为5P、8P、 4P、 P 旳力,方向如图,试画出杆旳轴力图。
OA PA
B PB
C PC
D PD
q
u 正应力旳正负号要求:
sx
sx sx
s
x
P
u 对变截面杆, 当截面变化缓慢时,横截面上旳 正应力也近似为均匀分布,可有:
s (x) FN (x)
A( x)
合力作用线必须与杆件轴线重叠;
圣维南原理
若用与外力系静力等 效旳合力替代原力系, 则这种替代对构件内应 力与应变旳影响只限于 原力系作用区域附近很 小旳范围内。 对于杆件,此范围相当 于横向尺寸旳1~1.5倍。
h
解: 1) BD杆内力N
取AC为研究对象,受力分析如图
mA 0 , (FNsinq ) (hctgq) Px 0
FN
Px
hcosq
2) BD杆旳最大应力: s max FN max PL A hAcosq
突变规律: 1、从左边开始,向左旳力产生正旳轴力,轴力图向上突变。 2、从右边开始,向右旳力产生正旳轴力,轴力图向上突变。 3、突变旳数值等于集中力旳大小。
即:离端面不远处,应力分布就成为均匀旳。
§2–3 直杆轴向拉压时斜截面上旳应力
一、斜截面上旳内力
n
1
2
P
P
1
2
FN1
3 P
3
P FN2
PP FN3
FN 1 P FN 2 0 FN 3 P
1
2
4、作内力图
P
P
P
3 P
1 FN
P
2
3
P x
[例2] 图示杆旳A、B、C、D点分别作用着大小为5P、8P、 4P、 P 旳力,方向如图,试画出杆旳轴力图。
OA PA
B PB
C PC
D PD
q
u 正应力旳正负号要求:
sx
sx sx
s
x
P
u 对变截面杆, 当截面变化缓慢时,横截面上旳 正应力也近似为均匀分布,可有:
s (x) FN (x)
A( x)
合力作用线必须与杆件轴线重叠;
圣维南原理
若用与外力系静力等 效旳合力替代原力系, 则这种替代对构件内应 力与应变旳影响只限于 原力系作用区域附近很 小旳范围内。 对于杆件,此范围相当 于横向尺寸旳1~1.5倍。
h
解: 1) BD杆内力N
取AC为研究对象,受力分析如图
mA 0 , (FNsinq ) (hctgq) Px 0
FN
Px
hcosq
2) BD杆旳最大应力: s max FN max PL A hAcosq
突变规律: 1、从左边开始,向左旳力产生正旳轴力,轴力图向上突变。 2、从右边开始,向右旳力产生正旳轴力,轴力图向上突变。 3、突变旳数值等于集中力旳大小。
即:离端面不远处,应力分布就成为均匀旳。
§2–3 直杆轴向拉压时斜截面上旳应力
一、斜截面上旳内力
n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五、例题讲解
例2-4 旋臂起重机的结构如图所示,通过小车起吊重物,小车工作时能沿着横梁 AB 移动。已知小车自重G= 5kN,拉杆BC 的直径d = 20mm,材料为低碳钢, 许用应力[ζ] = 120MPa, 试由拉杆BC 确定此起重机的许可起吊重[Q]。
六、纵向变形
F F
l
l1
l l1 l
一、金属材料拉伸时的强度与塑性
拉伸试验的测量方法:《金属拉力实验法》GB228-87。
圆截面:l=10d(10倍构件),或l=5d(5倍构件) 矩形截面:l=11.3√A,或l=5.65√A
一、金属材料拉伸时的强度与塑性
Q235的F-Δl
Q235的ζ-ε
一、金属材料拉伸时的强度与塑性
1、弹性阶段( Oa 段)
4、颈缩断裂阶段(ek 段)
伸长率(延伸率):
σ
e k c a ζb
l1 - l δ= × 100% l
δ> 5% 的材料称为塑 性材料; δ< 5% 的材料称为脆 性材料。;
ζp
ζs
o o1 δ
Q235的ζ-ε
ε/%
一、金属材料拉伸时的强度与塑性
其它塑性材料
一、金属材料拉伸时的强度与塑性
其它塑性材料
第二章 拉伸与压缩
本章主要讨论的四个问题:
(1) 内力与截面法; (2)应力与强度条件; (3)材料的变形与虎克定律; (4)材料的力学性能。
2.1材料力学的基本概念
一、任务和研究对象
什么叫刚体? 刚体是实际固体的理想化模型,即在受力后其大小、形 状和内部各点相对位置都保持不变的物体。
什么叫弹性形变?什么叫非弹性形变? 弹性形变是指固体受外力作用而使各点间相对位置的改 变,当外力撤消后,固体又恢复原状谓之“弹性形变”。 当外力撤消后,无法回到原来的形状称为非弹性形变。
σmax
N [ σ] A
此式是保证直杆有足够强度, 能够安全可靠地使用的条件, 叫做强度条件。
四、直杆受轴向拉伸或压缩时的强度条件
3、根据强度条件可以解决杆件三个方面的问题:
A 强度校核:
σmax [ σ]
N A [ σ]
B 截面设计:
C 确定许用载荷: N A[ σ]
五、例题讲解
一、应力的基本概念
1、定义:我们把横截面上各点所承受的内力数值称为应力。 2、公式: ζ=N/A 3、单位: N/m2 Pa; N/mm2 MPa;
4、规定:拉应力为正,压应力为负。 5、杆件受外力拉压时是否破坏, 决定于它的横截面上各点的 应力大小。
二、直杆受轴向拉伸或压缩时横截面上的应力
1、平面截面假设:
Ny
α
F
N
F
Nx
三、直杆受轴向拉伸或压缩时斜截面上的应力
Ny
F
α
N
F
Nx
N x = N sin
N y = N cos
斜截面的面积: Aα =
A cosα
斜截面法向应力:σ = α (正应力) 斜截面切向应力: τ α= (剪应力)
Ny N σ = cos 2α= σ0cos 2α= 0 (1+ cos2α) Aα A 2
σ
e k
ζp
ζs
o o1 δ
Q235的ζ-ε
ε/%
一、金属材料拉伸时的强度与塑性
3、强化阶段(ce段) σ
材料的强化; 颈缩; a ζb ζb 称为材料的强度极 限(抗拉强度);ζb 是 危险应力ζ0 的最明显 标志; c e k
ζp
ζs
o o1 δ
Q235的ζ-ε
ε/%
一、金属材料拉伸时的强度与塑性
根据化工专业的需要和本课程的特点, 我们首先着重讨论
直ቤተ መጻሕፍቲ ባይዱ的基本变形与稳定性问题, 然后结合化工容器讨论壳
体的强度和稳定性问题。
三、构件及杆件变形的基本形式
杆件产生变形的基本形式: A 轴向拉伸及压缩;——拉压变形 B 弯曲;——弯曲变形 C 剪切;——剪切变形 D 扭转;——扭转变形
2.2 拉伸和压缩
2.1材料力学的基本概念
一、任务和研究对象
为了保证整个机器设备在外力作用下安全可靠地工作,它们的每一个构 件都必须满足以下三个基本要求: (1)具有足够的强度;(强度的概念:构件抵抗破坏的能力) (2)具有一定的刚度;(刚度的概念:构件抵抗弹性变形的能力) (3)具有足够的稳定性;(稳定性的概念:构件受力后保持原有平衡状态 的能力) 在研究构件的强度、刚度和稳定性时,构件的变形虽然很小,却是一 个重要的因素, 必须加以考虑而不能忽略。因此,在材料力学中所研究 的一切物体都是变形固体。 材料力学的主要任务是分析、计算构件的强度、刚度和稳定性,为 正确解决安全与经济之间的矛盾提供必要的理论基础。
这些材料与低碳钢相比,其共同点是, 都具有良好的塑性;不同点是,这些 材料没有明显的屈服极限。对于这些材料,工程上规定:取对应于试件卸载 后产生0.2%的残余应变时的应力值作为材料的名义屈服极限,以σ0.2 表示, 也 可用σs 表示。
一、金属材料拉伸时的强度与塑性
脆性材料
有些材料在拉伸时,一直到断裂,变 形都不显著,而且没有屈服阶段,也 没有颈缩现象,只有断裂时的强度极 限ζb 。这些材料的特点是伸长率很小, 一般δ< 5% ,因此称它们为脆性材料。
二、内力与截面法
截面法:假想将杆件切开,使内力转化为外力,运用静
力平衡条件求出截面上内力的方法。 轴力图:若选取一个坐标系,其横坐标表示横截面位置,
纵坐标表示相应截面上的轴力,便可用图形表示出轴力 沿杆件轴线的变化情况,这种图形称为轴力图。
在轴力图中,将拉力绘在X轴的上侧, 压力绘在X轴的下侧。这样, 轴力图不但可显示出杆件各段内轴力的大小,而且还可表示出各 段内的变形是拉伸或是压缩。
四、直杆受轴向拉伸或压缩时的强度条件
1、危险应力:杆件横截面上的应力达到某一数值时,杆件就开始破坏,这一 应力称为危险应力,用ζ0 表示。
为了使杆件能安全工作, 杆件横截面上的正应力———最大工作应力σmax 不应 超过危险应力ζ0 , 即
σmax < σ0
2、许用应力:①为了补偿构件实际工作情况与设计计算时所设想的条件不一致。 ②为了有必要的强度储备。故应选取危险应力ζ0 的若干分之一作为构件工作时 允许应力的最大值, 这种最大的允许应力称为许用应力,用符号[ζ]来表示。为 了保证受轴向拉伸或压缩时的杆件安全可靠地工作,必须使
μ称为横向变形系数或泊松比。因为 ε′与ε的符号总是相反, 所以又可写为
=
=
μ也是无因次的量, 它和弹性模量E 一样, 也是表示材料力学性质的一个弹性常数, 其数值可由实验求出, 在一般情况下, 碳钢的横向变形系数μ约为0 .27。
2.3 材料的机械性质
1、工程上所用的构件一般都是由一定几何形状和尺寸的金 属材料制成。要保证构件的正常工作, 不仅要知道应力的计 算, 还必须了解构件材料抵抗破坏的能力和它的受力和变形 过程中所具有的特性, 也即材料的机械性质。 2、材料的机械性质是材料本身固有的特性,它能反映出材 料的机械方面的特点, 它包括强度、塑性、韧性和硬度四个 方面的指标,它们都是通过科学实验的方法测定出来的。 3、金属材料大致可以分成塑性材料和脆性材料两大类。
例2-2 立式容器重20kN,用4 根88 .5×4mm 钢管作为容器的支脚,其总高H = 200mm, 已知钢管许用应力[ζ] = 108MPa,试校核钢管的强度。
五、例题讲解
例2-3 管架由横梁AB,拉杆AC组成。横梁AB承受管道的重力分别为G1 = 8kN, G2 = G3 = 5kN。横梁AB的长度l = 6m,B 端由支座支承,A 端由直径 为d 的两根拉杆(圆钢) 吊挂着。圆钢的许用应力[ζ] = 100MPa,试确定圆钢 截面尺寸。
二、金属材料压缩时的强度与塑性
塑性材料
当应力小于比例极限σp 或屈服极限σs 时, 它所表现的性质与拉伸时相同,而 且比例极限与弹性模量的数值,与受拉 伸时数值大致相等。对于钢来说,甚至 屈服极限σs 也基本相同。 应力超过屈服极限后, 材料产生明显的 残余变形,圆柱形试件高度显著缩短, 而直径则增大,试件由鼓形逐渐变成圆 饼形。塑性材料在压缩下不会发生断裂, 所以测不出强度极限。 对于塑性材料,拉伸试验是主要的,塑性材料的机械性质主要是用拉伸试验 来测定。
2.1材料力学的基本概念
材料力学的基本假设: (1)连续性假设(数学假设) 组成固体的物质不留空隙的充满整个固体的体积。 (2)均匀性假设(力学假设)
固体内各点处具有相同的力学性能。
(3)各向同性假设(物理学假设) 各向同性材料:固体材料内沿各个不同方向的力学性能相同;
各向异性材料:固体材料内沿各个不同方向的力学性能不同。
2、若其他条件相同,则E 值愈大,杆件的伸长或缩短就愈 小;EA称为杆件的抗拉刚度或抗压刚度。
八、横向变形
纵向伸长: l l1 l 横向收缩: 纵向应变: a1 横向应变: a 实验指出, 在弹性范围内, 横向应变 与纵向应变之比的绝对值为一常数, 即
a=a1 -a
l = l a = a
(4)小变形假设(几何假设) 固体受力后的变形比固体的原始尺寸小的多。
二、内力与截面法
外力:物体对构件的作用,如约束反力、主动力;
内力:构件一部分与相邻部分之间的相互作用力;
材料力学所注意的就是这种内力。对于具有一定横截面积、 由一定材料制成的构件,其内力的增大具有一定的限度, 若超过这个限度, 构件就发生破坏。不同的材料制成的构 件,各有其不同的限度,这个限度就是材料的强度。
弹性;弹性形变; 虎克定律σ= Eε; 斜直线的斜率就是弹 性模量E; ζp 称为材料的比例极 限, 它是应变ε与应力 ζ成正比的应力最高 限。 c a ζb
