6-晶体结构详解
晶体材料基础---第六、七讲 晶体结构及对称性(5) 单形和聚形
复三方双锥:12
中级晶族各晶系的单形
①柱类：三方柱、复三方柱、四方 柱、复四方柱、六方柱、复六方柱
注意：晶面和交棱都平行于高次轴。
中级晶族各晶系的单形
②单锥类：三方单锥、复三方单锥、 四方单锥、复四方单锥、六方单锥、复 六方单锥
注意：出现在没有对称中心和其它水平对称要素 的对称型中。所有晶面交高次轴于一点。
实例⑴
正交晶系以L22P（mm2）为例：
将L2为Z轴，对称面的法线分别为X、Y轴，进行极射 赤平投影。
在1/4的扇形区域内，原始晶面与对称要素之间的相 对位置关系有7种： 3个角顶（1、2、3号晶面） 3条边上（4、5、6号晶面） 中部（7号晶面）
六 单形的推导
Z Y Y X X
位置1：单面{001} 位置2：平行双面{100} 位置3：平行双面{010} 位置4：双面{h0l} 位置5：双面{0kl} 位置 6：斜方柱{hk0} 位置 7：斜方单锥{hkl}
称型逐一进行推导，能导出146种不同的单
形，称为结晶单形。
实际晶体单形的对称型判断
实际晶体的单形都是结晶单形．可根据晶 面花纹、蚀像、物性等特点判断。 如黄铁矿立方体晶面 上常发育有相互垂直的不是3L44L36L29PC
四 47种几何单形的形态特点
五角十二面体的三个变形
有关单形的几个概念：
⒋左形（left-hand form）和右 形（right-hand form） ：形状完全 相同而在空间的取向正好彼此相反 的两个形体，若相互间不能借助于 旋转、但可借助于反映而使两者的 取向达到一致，此二同形反向体即 构成左形和右形。
三方偏方面体 的左形和右形
六四面体：
高中化学新教材同步选择性必修第二册第3章微专题6：晶体结构的分析与计算
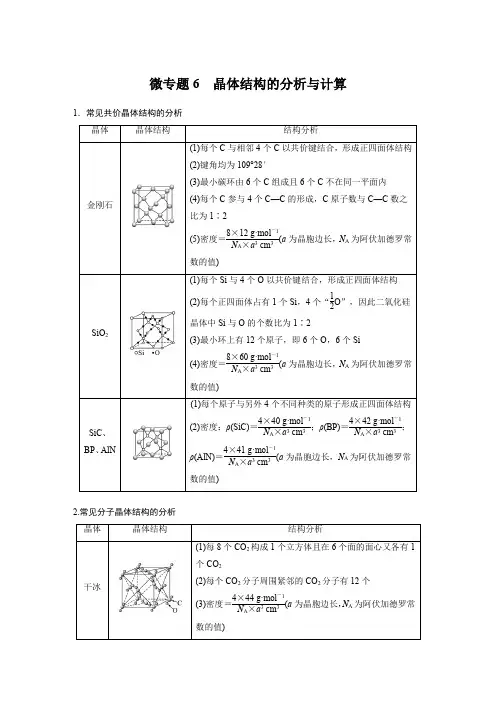
微专题6晶体结构的分析与计算1．常见共价晶体结构的分析晶体晶体结构结构分析金刚石(1)每个C与相邻4个C以共价键结合，形成正四面体结构(2)键角均为109°28′(3)最小碳环由6个C组成且6个C不在同一平面内(4)每个C参与4个C—C的形成，C原子数与C—C数之比为1∶2(5)密度＝8×12 g·mol－1N A×a3 cm3(a为晶胞边长，N A为阿伏加德罗常数的值)SiO2(1)每个Si与4个O以共价键结合，形成正四面体结构(2)每个正四面体占有1个Si，4个“12O”，因此二氧化硅晶体中Si与O的个数比为1∶2(3)最小环上有12个原子，即6个O，6个Si(4)密度＝8×60 g·mol－1N A×a3 cm3(a为晶胞边长，N A为阿伏加德罗常数的值)SiC、BP、AlN (1)每个原子与另外4个不同种类的原子形成正四面体结构(2)密度：ρ(SiC)＝4×40 g·mol－1N A×a3 cm3；ρ(BP)＝4×42 g·mol－1N A×a3 cm3；ρ(AlN)＝4×41 g·mol－1N A×a3 cm3(a为晶胞边长，N A为阿伏加德罗常数的值)2.常见分子晶体结构的分析晶体晶体结构结构分析干冰(1)每8个CO2构成1个立方体且在6个面的面心又各有1个CO2(2)每个CO2分子周围紧邻的CO2分子有12个(3)密度＝4×44 g·mol－1N A×a3 cm3(a为晶胞边长，N A为阿伏加德罗常数的值)白磷密度＝4×124 g·mol－1N A×a 3 cm 3(a为晶胞边长，N A为阿伏加德罗常数的值)3.常见离子晶体结构的分析NaCl型CsCl型ZnS型CaF2型晶胞配位数684F－：8；Ca2＋：4密度的计算(a为晶胞边长，N A为阿伏加德罗常数的值)4×58.5 g·mol－1N A×a3 cm3168.5 g·mol－1N A×a3 cm34×97 g·mol－1N A×a3 cm34×78 g·mol－1N A×a3 cm31．AB型化合物形成的晶体结构多种多样。
晶体结构的类型分类
晶体结构的类型分类晶体是由原子、离子或分子按照一定的规律排列而成的固体物质，其结构具有高度的有序性和周期性。
根据晶体内部原子、离子或分子的排列方式和结构特征，可以将晶体结构分为几种不同的类型。
下面将介绍几种常见的晶体结构类型分类。
1. 根据晶体的周期性分为：- 长程有序晶体：具有长程有序性，即晶体中原子、离子或分子的排列呈现出明显的周期性，如立方晶系、四方晶系、六方晶系等。
- 短程有序晶体：具有短程有序性，即晶体中只有一部分原子、离子或分子的排列呈现出周期性，而整体结构并不呈现规则的周期性。
2. 根据晶体的原子、离子或分子排列方式分为：- 离子晶体：由正负离子按照一定比例排列而成，如氯化钠晶体。
- 共价晶体：由共价键连接的原子或分子构成，如金刚石晶体。
- 金属晶体：由金属原子通过金属键连接而成，如铜晶体。
- 分子晶体：由分子之间通过范德华力或氢键等相互作用力连接而成，如冰晶体。
3. 根据晶体的结构特征分为：- 离子晶体：具有高度的电荷平衡，通常硬度较大，熔点较高，易溶于水。
- 共价晶体：具有坚硬的结构，通常硬度很大，熔点也很高。
- 金属晶体：具有电子云海结构，通常具有良好的导电性和热导性。
- 分子晶体：分子之间的相互作用力较弱，通常易溶于有机溶剂，熔点较低。
4. 根据晶体的晶体系统分类：- 立方晶系：包括立方晶体、体心立方晶体、面心立方晶体。
- 四方晶系：包括四方晶体。
- 六方晶系：包括六方晶体。
- 斜方晶系：包括斜方晶体。
- 单斜晶系：包括单斜晶体。
- 单轴晶系：包括单轴晶体。
总的来说，晶体结构的类型分类是根据晶体内部原子、离子或分子的排列方式、结构特征以及晶体系统等因素进行划分的。
不同类型的晶体结构具有不同的性质和特点，对于研究物质的性质和应用具有重要意义。
通过对晶体结构的分类和研究，可以更深入地了解物质的结构和性质，为材料科学和化学领域的发展提供重要参考。
6-晶体结构详解
等价原子有完全相同的化学环境。
平移对称性
在某给定方向上，相距最近的两个等价原子之间的距离为a， 则将晶体沿该方向平行移动距离na(n为整数)晶体就复原， 这种性质就是晶体的平移对称性。 连接晶体中任意两个等价原子得一矢量a，将晶体沿着该矢量 平移a或a的整数倍na，晶体复原。
NaCl 晶胞： 面心立方 复晶胞(4)
c
b a
石墨 晶胞：平行六面体 素晶胞
原子坐标
将晶胞的晶轴a, b, c的方向取作三个坐标轴x, y, z的方向(按右手 定则) ，从晶胞的坐标原点指向原子的位置矢量 r 可以表示为： r = x a + yb + zc (x, y, z)称为该原子的坐标。
(1). 金属Na (2). 金属铜
a c b b
a
b
c
平移对称性：晶体沿a方向平移na复原，沿b方向平移mb复原, 沿c方向平移lc复原。 平移矢量： na + mb + lc
(3). NaCl
(4). 金刚石
c
b c a a
b
(5). 石墨
c
b
a
2. 点阵和结构单元
重复单位: 晶体内部原子、离子或分子, 在三维空间作周期性重 复排列。每个重复单位的化学组成相同，空间结构相同，若 忽略晶体的表面效应，重复单位周围的环境也相同。 重复单位: 单个原子或分子，离子团或多个分子。
点阵点位于立方体的顶点
Na
点阵点：黑点 ，位于立方体的顶点与体心
结构单元= 1个Na = 1个平行六面体 = ½立方体
Cu
点阵点：黑点，位于立方体的顶点与面心
结构单元 = 1个Cu = 斜平行六面体
上海交大材基-第二章晶体结构--复习提纲讲解
第2章晶体结构提纲：2.1 晶体学基础2.2 金属的晶体结构2.3 合金相结构2.4 离子晶体结构2.5 共价晶体结构2.6 聚合物的晶态结构2.7 非晶态结构学习要求：掌握晶体学基础及典型晶体的晶体结构，了解复杂晶体(包括合金相结构、离子晶体结构，共价晶体的结构，聚合物的晶态结构特点)、准晶态结构、液晶结构和非晶态结构。
1．晶体学基础（包括空间点阵概念、分类以及它与晶体结构的关系；晶胞的划分，晶向指数、晶面指数、六方晶系指数、晶带和晶带定律、晶面间距的确定、极射投影）；2．三种典型金属晶体结构（晶胞中的原子数、点阵常数与原子半径、配位数与致密度、堆垛方式、间隙类型与大小）；3．合金相结构（固溶体、中间相的概念、分类与特征）；4．离子晶体的结构规则及典型晶体结构（AB、AB2、硅酸盐）；5、共价晶的结构规则及典型晶体结构体（金刚石）6、聚合物的晶态结构、准晶态结构、液晶结构和非晶态结构。
重点内容1.选取晶胞的原则；Ⅰ) 选取的平行六面体应与宏观晶体具有同样的对称性；Ⅱ）平行六面体内的棱和角相等的数目应最多；Ⅲ）当平行六面体的棱角存在直角时，直角的数目应最多；Ⅳ）在满足上条件，晶胞应具有最小的体积。
2.7个晶系，14种布拉菲空间点阵的特征；（1）简单三斜（2）简单单斜底心单斜（3）简单正交底心正交体心正交面心正交（4）简单六方（5）简单四方体心四方（6）简单菱方（7）简单立方体心立方面心立方3.晶向指数与晶面指数的标注，包括六方体系，重要晶向和晶面需要记忆。
4.晶向指数，晶面指数，晶向族，晶面族，晶带轴，共带面，晶面间距5.8种,即1，2，3，4，6，i，m，。
或C1，C2，C3，C4，C6 ，C i，C s，S4。
微观对称元素6.极射投影与Wulff网；标hkl直角坐系d4⎧⎨⎩微观11213215243滑动面 a，b，c，n，d螺旋轴 2；3，3；4，4，4；6，6，6，6，67.三种典型金属晶体结构的晶体学特点；在金属晶体结构中，最常见的是面心立方(fcc)、体心立方（bcc）和密排六方(hcp)三种典型结构，其中fcc和hcp系密排结构，具有最高的致密度和配位数。
无机材料科学基础第二章-晶体结构-第6节(3)
CaO静电键强度与MgO相同，但晶体结构疏松，不稳定，易水 化。因为Ca2+离子半径大，使O2-离子的立方密堆积紧密程度变 松。 CaO 的晶格能为3469KJ/mol ，熔点2560 ℃。
6
2、CsCl型
r+/r- = 0.93（大于0.732）
CsCl晶体为Pm3m空间群（立方原始格子）； a0=0.411nm； Cl-按简立方形式堆积，位于立方体的8个角顶上；Cs+填充在立方体 中心。 Cl-、Cs+的配位数均为8；单位晶胞中的分子数Z=1；
r+/r- = 0.102/0.181=0.56 （0.414～0.732）
3
②球体紧密堆积方法：Cl-按面心立方紧密堆积，Na+填入 全部八面体空隙（Na︰Cl=1︰1）； ③配位多面体及其连接方式：[NaCl6]八面体以共棱方式 连接，该描述方法适宜于复杂晶体结构。
NaCl中的正八面体结构
4
属于NaCl型结构的晶体很多，表2-7所示。
按离子堆积分析， O2-按变 形的六方密堆积， Ti4+只填 充了O2-所形成的八面体空隙 的一半（Ti︰O=1 ︰2）。
16
晶胞中质点的坐标为：Ti4+（000），（1/2 1/2 1/2）；
O2-（uu0），（(1-u) (1-u) 0），（(1/2+u)(1/2-u)1/2），
1号点 2号点 4号点 3号点
单位晶胞中质点的坐标如图所示。 属于CsCl结构的晶体有CsBr、CsI、NH4Cl 等。
7
3、闪锌矿（立方ZnS）型结构（共价晶体）
闪锌矿为Fm3m 空间群， a0=0.540nm。面心立方格子，S=按立方 紧密堆积，Zn2+交错处于八分之一小立方体中心，占据四面体空 隙的一半； 质点坐标及投影图如图所示。
6-13双极晶体管的单管结构及工作原理
V1
(e VT
V2
(e VT
V3
(e VT
1) 1)
1)
理想本征集成双极晶体管的 EM模型
2020/6/15
理想本征集成双极晶体管的EM1模5 型
§2.3 集成双极晶体管的有源寄生效应
双极晶体管的四种工作状态
S
IS
E(n+)
VBC
p I3 n I2
IB p n I1
V3 B(p)
IC C pnp
N沟MOSFET的输出特性曲线
ID 非饱和区
饱和区
VG
VD
2020/6/15
34
§2.6 MOS集成电路中的有源寄生效应
• 场区寄生MOSFET • 寄生双极晶体管 • 寄生PNPN效应（闩锁（Latch up）
效应）
2020/6/15
35
场区寄生MOSFET
n+
n+
L
p substrate
n+
2020/6/15
集成双极晶体管的有源寄生2效3 应
§2.4 集成双极晶体管的无源寄生效应
C
BE
N+
P+
N+
P+ P
N-epi
N+-BL
2020/6/15
24
发射极串联电阻rES
rES=rE,c+ rE,b
接触电阻
体电阻
E rrEE,,bc
发射区为N+扩散,杂质浓度在1020cm-3以上, 所以发射区的体电阻很小,串联电阻主要由 金属与硅的接触电阻决定
VBC<0 正向工作区和截止区
npn管
2020/6/15
6-晶体结构优化收敛测试
操作步骤
pwd
查看当前目录路径，确保在~/20191010/xxx目录下
cp -r siopt siopte300
通过复制创建siopte300目录
cd siopte300 进入siopte300
vi INCAR 将ENCUT修改为300，并退出保存
bash JOB 提交任务
INCAR
ISTART=0 ICHARG=2 PREC=N
ALGO=V NELM=80 EDIFF=1E-5 ENCUT=300
IBRION=2 NSW=100 ISIF=3 EDIFFG=-0.05
ISMEAR=-5
练习：根据ENCUT=300的操作步骤，完成ENCUT=350、400的计算
vi KPOINTS 将k点网格修改为11x11x11，并退出保存
bash JOB 提交任务
比较不同k点网格体系的总能量
操作步骤
pwd
查看当前目录路径，确保在~/20191010/xxx/sioptk11目录下
cd ..
tail -n 1 siopt/OSZICAR sioptk7/OSZICAR sioptk9/OSZICAR sioptk11/OSZICAR 当不同k点计算得到的体系能量相差0.001eV/atom，即可采用此k点网格。
vi KPOINTS 将k点网格修改为9x9x9，并退出保存
bash JOB 提交任务
pwd
查看当前目录路径，确保在~/20191010/xxx/sioptk9目录下
cd ..
后退至xxx目录
cp -r sioptk9 sioptk11
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
晶体的基本特性：周期性
周期性：是指在任意方向上，晶体中的原子每隔一定的距
离就重复出现的性质。(忽略晶体的表面效应) 周期性是晶体结构最基本的特征。 周期：某方向上原子重复出现的最小距离。
例1. 一维周期性
(1). 伸展的聚乙烯(CH2CH2)n
a (2). NaCl晶体的一条晶棱
a
周期为a
例2. 二维周期性
b a
(2). NaCl 结构单元= 虚线的正方形= 1Na+ + 1Cl-
(3). Cu(黑点代表点阵点) 结构单元 = 虚线的平行四边 形 = 1个Cu原子
等价原子: 晶体中每隔相等的距离就重复出现的原子。
等价原子有完全相同的化学环境。
平移对称性
在某给定方向上，相距最近的两个等价原子之间的距离为a， 则将晶体沿该方向平行移动距离na(n为整数)晶体就复原， 这种性质就是晶体的平移对称性。 连接晶体中任意两个等价原子得一矢量a，将晶体沿着该矢量 平移a或a的整数倍na，晶体复原。
a
(d). NaCl: 点阵点 结构单元 = 1Na+ + 1Cl-
a
(e).伸展的聚乙烯(CH2CH2)n: 点阵点结构单元 = CH2CH2
a
例8. 二维平面点阵
(1). 石墨片层
点阵点: 黑点, 放在某一类等价原子, 或者其他等价位置 结构单元 = 两个不等价碳原子 = 虚线的平行四边形
Se
点阵点 = 结构单元
如果在晶体的点阵中的各个点阵点上，按照同一种方式安置 结构单元，则得到整个晶体结构。
晶体结构 = 点阵 + 结构单元
例7. 一维直线点阵
(a). Cu: 点阵点=结构单元= 1个铜原子
a
(b). 石墨:
点阵点 = 结构单元 = 两个C原子
a
(c). Se:
点阵点 结构单元 = 3个Se原子
例4. 一维 平移对称性
(1). 石墨
(2). Se
平移对称性：晶体平移na而复原。
例5. 二维
(1). 石墨烯
平移对称性
(2). NaCl 的一个晶面
T
T
b
b
a a
平移对称性：晶体沿a方向平移na复原，沿b方向平移mb复原
平移矢量： na + mb
T = 2a + b
例6. 三维 平移对称性
(1). 金属Na (2). 金属铜
a c b b
a
b
c
平移对称性：晶体沿a方向平移na复原，沿b方向平移mb复原, 沿c方向平移lc复原。 平移矢量： na + mb + lc
(3). NaCl
(4). 金刚石
c
b c a a
b
(5). 石墨
c
b
a
2. 点阵和结构单元
重复单位: 晶体内部原子、离子或分子, 在三维空间作周期性重 复排列。每个重复单位的化学组成相同，空间结构相同，若 忽略晶体的表面效应，重复单位周围的环境也相同。 重复单位: 单个原子或分子，离子团或多个分子。
3.点阵与平面间距离 介绍点阵点、直线点阵与平面点阵的数学表示方法，用晶面 指标计算晶面间距的公式。 4.空间群及晶体结构的表达* 5.晶体的结构和晶体的性质* 6.晶体的X射线衍射原理 介绍晶体 X射线衍射的基本原理，主要是确定衍射方向的布 拉格方程与劳埃方程。
教学要求
理解晶体结构的周期性特征，掌握点阵与晶体结构的关系以 及点阵的平移对称性，掌握晶胞的概念与晶胞内原子的分 数坐标，了解晶体结构的对称性，掌握根据晶体对称性划 分的七大晶系、六种正当晶胞与十四种空间点阵型式，了 解晶面指标与晶面间距。了解晶体衍射方向的两个基本方 程布拉格方程与劳埃方程。
重点难点
• 1．重点：晶体的周期性结构，点阵和晶胞，晶胞内原子 的分数坐标，晶体的对称性，七大晶系、六种正当晶胞与 十四种空间点阵型式。 • 2．难点：晶体结构的对称性和晶面指标，确定衍射方向 的两个方程。
ห้องสมุดไป่ตู้
晶体周期性, 点阵与晶胞
固态物质分为二类
一类是晶体。自然界存在大量的晶体物质，如高山岩石、地 下矿藏、海边砂粒、两极冰川,金属、合金,水泥制品,食 盐和糖等。 晶体有确定的熔点 ，有均匀性，各向异性，能自发地形成凸 多面体外形，有特定的对称性，能使X射线、电子流与中 子流产生衍射。 晶体中的原子、分子都按一定的规律周期性地重复排列。
(1). 金属铜 (2). B(OH)3
a a a
周期为 2asin(/3) = 31/2a
b
两个方向的周期分别为a, b
例3. 三维周期性
(1). 金属Po (2). CsCl
a
a
边长方向的周期为a, 面对角线方向的周期为21/2a, 体对角线方向的周期为31/3a。
周期性 平移对称性，或平移不变性
结构单元 = 重复单位
结构单元是晶体中所有不等价原子构成的最小集合体。
Se
点阵点
将每个结构单元用一个点来表示，这样的点称为点阵点。
点阵
将表示结构单元的点阵点放置在空间等价的位置，如一组等价 原子的位置，则得到一个点的空间序列，称为点阵。
点阵的基本特性
平移对称性或平移不变性：连结任意两个点阵点得一矢量，按 此矢量平移, 点阵能够复原。 (1) 所有点阵点都是等价的 (2) 每个点阵点都具有完全相同的周围环境
晶体结构
教学内容
1. 晶体结构的周期性，点阵与晶胞 讲授晶体微观结构的周期性或平移不变性或平移对称性；根据 周期性如何从晶体结构中抽象出点阵，什么是结构单元， 如何提取结构单元；进一步如何从点阵划分晶体的晶胞，如 何给出原子分数坐标。本节内容主要就是如何根据晶体对 称性抽象出简单的几何体---晶胞来描述晶体的结构。 2. 晶体结构的对称性，晶族晶系与空间点阵型式, 晶体的点 群和群符号 本节讲授晶体中所可能拥有的各种对称元素与对称操作，包括 点操作及其与平移操作的组合。进一步，根据晶体的对称性 将自然界中的所有晶体进行分类描述，包括7大晶系，32个 晶体学点群，然后根据对称性对各大晶系选取合适的标准 晶胞以形成国际通用标准；同一晶系中点阵点在空间的分布 方式也可以不同，从而将晶体划分为14种空间点阵形式。
人工宝石
另一类是非晶态或叫玻璃体或叫无定形态。如玻璃、明胶、 碳粉、塑料制品等。 晶体拥有的特性非晶体都没有，如没有确定的熔点，没有对 称性，不能产生衍射等。 非晶体内部的原子、分子排列杂乱无章，没有周期性规律。
1. 晶体的结构特征
晶体是原子、离子或分子在空间按照一定的规律周期性地重复
排列所构成的固体物质。