拱桥计算
拱桥浇筑长度计算公式

拱桥浇筑长度计算公式拱桥是一种古老而又美丽的建筑形式,它不仅能够承载重量,还能够美化环境,成为一道风景线。
在建造拱桥的过程中,浇筑长度是一个非常重要的参数,它直接影响着拱桥的稳定性和耐久性。
因此,我们需要通过一定的公式来计算拱桥的浇筑长度,以保证拱桥的质量和安全性。
拱桥浇筑长度的计算公式可以通过以下步骤来推导:首先,我们需要确定拱桥的设计要求,包括跨度、高度、拱度等参数。
这些参数将直接影响到拱桥的浇筑长度。
其次,我们需要根据拱桥的设计要求来确定混凝土的配合比和强度等参数。
这些参数将决定混凝土的质量和性能。
接下来,我们需要根据拱桥的设计要求和混凝土的配合比来确定拱桥的截面形状和尺寸。
这些参数将直接影响到拱桥的受力性能和稳定性。
然后,我们需要根据拱桥的截面形状和尺寸来确定拱桥的受力分布和受力大小。
这些参数将决定拱桥的浇筑长度。
最后,我们可以通过一定的理论模型和计算方法来确定拱桥的浇筑长度。
一般来说,拱桥的浇筑长度可以通过以下公式来计算:L = 2πR + 2H。
其中,L表示拱桥的浇筑长度,π表示圆周率,R表示拱桥的拱度,H表示拱桥的高度。
通过这个公式,我们可以很方便地计算出拱桥的浇筑长度,从而保证拱桥的质量和安全性。
在实际的工程中,拱桥的浇筑长度计算是一个非常复杂的问题,需要考虑到很多因素,包括材料的性能、结构的受力特点、施工的工艺要求等。
因此,在进行拱桥的浇筑长度计算时,我们需要充分考虑到这些因素,进行合理的假设和简化,以保证计算的准确性和可靠性。
除了上述的公式计算方法,我们还可以通过有限元分析、结构力学分析等方法来确定拱桥的浇筑长度。
这些方法可以更加精确地考虑到材料的非线性特性、结构的非均匀性等因素,从而得到更加准确的结果。
总之,拱桥的浇筑长度计算是一个非常重要的问题,它直接关系到拱桥的质量和安全性。
通过合理的公式计算方法和结构分析方法,我们可以确定拱桥的浇筑长度,从而保证拱桥的稳定性和耐久性。
桥梁工程-拱桥计算1 - 其它内力计算分享

在软土地基上修建拱桥和桥墩较柔的多孔拱桥,拱 踋变位是难以避免的。
(一)拱脚相对水平位移
采用悬臂曲梁作为基本结构
X222+2=0
拱脚相对水平位移内力计算公式
H HB HA
HA HB 为左右拱脚水平位移,右移为正,左移为负。
两拱脚发生相对水平位移在弹性中心产生的赘余力:
X 2
H
22
转角外,还引起相对水平位移和相对垂直位移,因此,在弹性中心会产
生三个赘余力:
X1
B 11
X 2
B
f ys y 2 ds
s EI
X 3
2
Bl
x2ds
s EI
11
s
M
2 1
ds
EI
s
ds EI
l EI
1
1
1 1
查《拱桥(上)》第607页表(III)-8;
y 2ds 可查《拱桥(上)》第581页表(III)-5。
(3)目前通用的有限元软件较多,如SAP2000, NASTRAN,ANSYS,ADINA等,专用于桥梁计算的软件也 不少,例如GQJS、桥梁博士、Midas/Civil等。
(二)有限元方法计算拱桥简介
2、数据准备及计算分析 (1)结构离散或单元划分 (2)组织数据文件:节点信息(节点编号和节点坐
(1)温度内力计算
例题:某钢筋混凝土拱桥,计算跨径l=90m, 计算矢高f=18m,拱轴系数=2.24,合拢温度为 20℃,现温度为10℃,试计算由此温度差在拱 顶和拱脚截面产生的附加内力。公式中可以用 δ11,δ22,δ33表示,弹性中心YS=0.32f。
(1)温度内力计算
解:根据公式:
Ht
lt
拱桥设计实用计算表2

重力
底梁重力
P1=号[0立.5柱*0重.5
力2号:立P=柱3*重(
力3号:立P=柱3*重(
4号腹拱座 力: P=3*(
重(力3):腹P孔=(
集中力
P13 =
P14 =
P15 =
5.拱上实 P16 =( 腹段(1()如拱顶 填料及桥 P17=Lxhd
(2)悬链 γB =
线曲边三 f1=f+y上
(1-1/cosφ
m^2
0.6512 0.6508
0.79641
m m
0.60476 0.79641
y1/f
主拱圈几何特性表
1 0.821783 0.665442 0.52911 0.411164 0.310395
6.000 7.000 8.000 9.000 10.000 11.000 12.000
2.拱上腹 孔布置
y
3.824
△M
36.435
20.458
Mp
1331.124 1353.853
考虑弹 性压缩的
项目 cos 与Ms相in应的 与M相H1应的 V N △H △N Np M y △M Mp
拱顶截面
Mmax
Mmin
1.000
0.000
105.952
97.384
105.952
97.384
1.855
1.705
公路1级
相应的H1 公路1级
拱脚截面 相应的V1 公路1级
不计弹性 压缩的人
截面
拱顶截面
l/4截面
考拱虑脚弹截性面 压缩的汽
项目 cos 与Ms相in应的 与M相H1应的 V N △H △N
项目 Mmax 相应的H1 Mmin 相应的H1 Mmax 相应的H1 Mmin 相应的H1 Mmax 相应的H1 相应的V1 Mmin 相应的H1 相应的V1
(完整版)14米景观板拱桥计算书

景观桥结构设计计算书设计阶段施工图部位拱圈、基础审核人校核人计算人2010年2月目录一、工程概况 (1)二、计算内容 (1)三、基本设计资料 (1)四、地质、水文资料 (2)1、地形地貌 (2)2、地基岩土的构成 (2)3、地下水 (3)4、场地及地基条件综合评价 (3)5、建议 (4)五、计算程序 (4)六、说明 (4)1、拱圈结构验算 (4)2、地基承载力、基础稳定性验算 (10)一、工程概况本桥为小区内的一座景观桥,是小区工程的一部分,主要用于小区内日常通行和消防通行。
桥梁基本尺寸和外观由景观设计人员结合小区总体情况进行拟定后,我们对此桥进行了桥梁结构设计.本桥为一座一跨14米的钢筋混凝土板拱桥。
桥梁横断面布置则为:2x0。
4m栏杆+2x1。
5m人行道+2x4.5m 车行道=12.8m。
桥梁拱圈采用等截面钢筋混凝土圆弧拱,拱圈外半径为9.1m,内半径为8.7m,拱圈夹角为105。
29°。
拱圈中心线矢高3。
5m,跨径14。
15m,矢跨比为1/4。
04。
拱圈采用等截面,截面高0。
4m,宽12。
8m。
桥台采用重力式桥台,桥台台身长12.8m。
基础为浅基础,基础长13。
8m。
桥梁轴线按道路线型近似取值进行设计,桥梁正交.二、计算内容拱圈结构验算,地基承载力、基础稳定性验算,按极限状态法设计.三、基本设计资料1、设计荷载:(1) 永久荷载:●恒载:片石混凝土容重25KN/m3,钢筋混凝土容重26KN/m3,人行道石栏杆2。
6KN/m,沥青混凝土铺装24KN/m3。
●基础变位作用:不均匀沉降0。
01m。
(2)可变荷载:●车道荷载:按双向二车道加载,荷载采用:公路-Ⅱ级,车道荷载见规范.●人群荷载: 3。
0kN/m².●温度荷载:根据《公路桥涵设计通用规范》(JTG D60—2004)取值。
(3)偶然荷载:地震动峰值加速度为0。
10g,建筑场地为稳定的建筑场地。
2、材料性能:1) 拱圈、拱座采用C35混凝土。
第4篇第3章 拱桥的计算
5
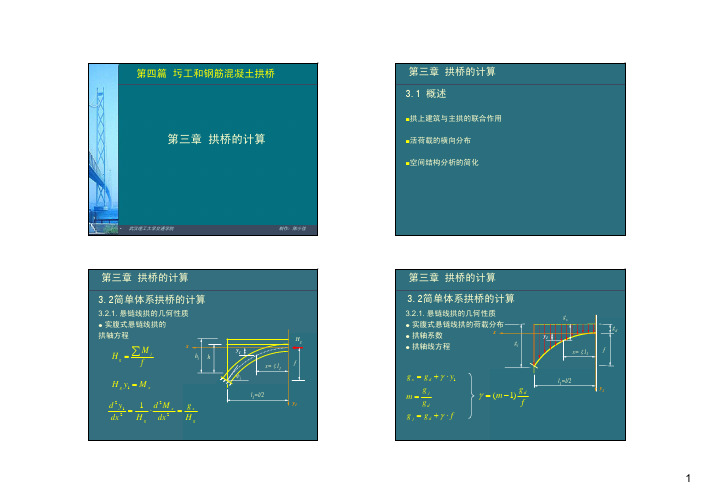
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.2. 考虑弹性压缩引起的内力 在恒载产生的压力作用下,拱沿轴线方向会产生弹性压 缩。由此将在超静定结构上产生内力。水平赘余力为:
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.3.恒载作用下拱圈各截面的总内力 符号规定
x
φj
Q N M
g x = g d + γ ⋅ y1
y1
m=
gj gd
g γ = (m − 1) d f
l1=l/2
y1
g j = gd + γ ⋅ f
1
第三章 拱桥的计算 3.2简单体系拱桥的计算
3.2.1. 悬链线拱的几何性质 z 实腹式悬链线拱的荷载分布 x z 拱轴系数 z 拱轴线方程
gx y1 x=ξl1 f gd
s
弹性中心
y1
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.1. 不考虑弹性压缩的恒载内力 实腹式悬链线拱的恒载内力
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.1. 不考虑弹性压缩的恒载内力 空腹式悬链线无铰拱的恒载内力: 直接根据静力平衡条 件写出:
g l2 H g = kg d f
( H g + ∆X 2 ) sin ϕ ± ∆X 2 sin ϕ
6
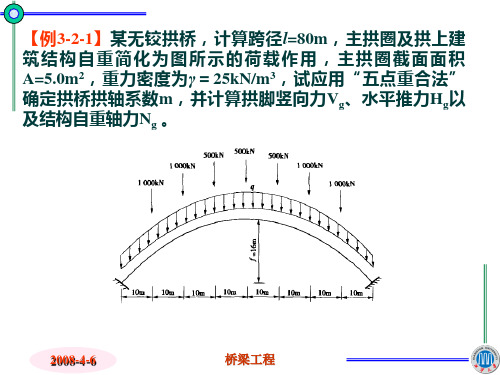
第三章 拱桥的计算 3.3 恒载作用下拱的内力计算
3.3.4. 计算实例
如图所示无铰拱, 计算跨径l=80m,主拱圈及拱上建筑恒载见图,主 拱圈截面面积A=5.0m2,截面惯性矩I=1.0m4,容重γ=25kN/m3 。试应用 “五点重合法”,
②
确定拱桥拱轴系数m 计算
拱桥的计算例题
2008-4-6
桥梁工程
解:
y1/4
2008-4-6
桥梁工程
【例3-2-2】某无铰拱桥,计算跨径l=80m,主拱圈及拱上建 筑结构自重简化为图所示的荷载作用,主拱圈截面面积 A=5.0m2,重力密度为γ=25kN/m3,由“五点重合法”确定 拱桥拱轴系数m=2.24,截面抗弯惯矩I=1.0m4,计算考虑弹性 压缩后,拱脚竖向力Vg、水平推力Hg以及结构自重轴力Ng, 以及弹性压缩引起的拱脚截面弯矩。
V KVV 216.8790.1662250 280.6kN N H1 cos j V sin j 819.2 0.7357 280.6 0.68284 790.1kN
2、拱脚最大负弯矩及相应轴力
1)根据
l 50m
拱脚最大负M及汽车-20查《基本资料》第79页的等代荷载:
KM 23.547kN / m, KH 10.932, KV 16.724kN / m
M1/4
1
f M j 2(m 1) 2
半拱悬臂集中力荷载作用时:
1)假定拱轴系数m=2.514, f/l=16/80 =1/5,查 表(III)-19得:
所有荷载: 所以
2008-4-6
桥梁工程
需重新计算
2)假定拱轴系数m=2.24
所有荷载:
所以 小于半级,因此取拱轴系数m=2.24
3)查表(III)-19得半拱悬臂自重对拱脚截面的竖向剪力为 半拱悬臂集中力对拱脚截面的竖向剪力为:
拱桥内力计算51
Hg
Mj f
半拱恒载对拱脚的弯矩
Vg P (半拱恒载重力)
N Hg
cos
三、拱桥内力计算
偏离的影响可按式计算出的 X1, X 2 然后根据静力平
衡条件计算任意截面的轴力N,弯矩M和剪力Q。
N X 2 cos M X1 X 2 ( y1 ys ) H g y Q X 2 sin
向缩短l(右图所示)。由于在实际
结构中,拱顶没有相对水平位移,其 变形受到约束,则在弹性中心处必有
一水平拉力Hg
三、拱桥内力计算
Hg的计算
由变形相容方程有:
其中:
H
g
' 22
l
0
H g
l '
22
l
l
0
dx
sds cos
s
Nds EA
cos
N Hg
N H1
c os
拱顶:数值很小,可不考虑
拱脚: Q H1 sin j V cos j 拱顶:数值较小,可不考虑
三、拱桥内力计算
由于活载弹性压缩产生的内力
活载弹性压缩与恒载弹性压缩计算相似,也在弹性中心产生赘余水平 力H,其大小为:
H
l '
22
Nds cos
s EA
' 22
取脱离体如下图,将各力投影到水平方向有:
N H1 Q sin H1 (1 Q sin )
cos
cos H1
Q sin 相对较小,可近似忽略,则有:
H1
N H1 cos
三、拱桥内力计算
拱桥工程量计算
拱桥工程量
净跨径L0 拱矢比(f0/L0)
f0
内半径r
5.00
0.25
1.25
3.13
2 拱上侧墙
①
1/2拱
②
1/3拱
净跨径L0
拱角x
参数l
侧墙体积
5.00
0.28
5.56
6.13
③
1/4拱
5.00
0.28
5.56
6.13
④
1/5拱
8.50
0.24
8.98
16.46
3 U型桥台
①
台身
涵长
桥台顶宽W 桥台底宽a1 拱角x
11.00
1.50
1.98
0.28
8.00
1.20
2.47
0.46
②
侧墙 桥台底宽a1 桥台顶宽W
拱角x
拱角y
1.98
1.50
0.28
0.21
侧墙底宽C1
襟边dd
基础侧边长A 基础厚度D
1.69
0.10
2.29
0.60
4 桥台护拱
护拱尖角至拱圈 顶部水平距离S’
外半径R
拱圈厚度d 0.35
外半径R 拱半内角φ0
3.48
0.93
拱角x 0.28
拱角y 0.21
拱轴长度S 6.12
拱角y 0.21 0.19 侧墙高H 4.35 基础宽度 1.89
桥台高h 1.90 4.88
桥台高h 1.90
基础体积 5.19372
台身体积V 40.00 74.08
侧墙边坡m' 4.00
1.50
3.70
混凝土拱桥的设计与计算方法
混凝土拱桥的设计与计算方法一、绪论混凝土拱桥是一种常见的桥梁结构形式,其独特的造型、强大的承载能力和良好的经济性受到了广泛的认可和应用。
混凝土拱桥的设计与计算方法是建造这种桥梁的重要前提,本文将详细介绍混凝土拱桥的设计与计算方法。
二、混凝土拱桥的基本结构混凝土拱桥主要由桥墩、拱肋、桥面、支座和伸缩缝等部分组成。
其中,桥墩是承载拱肋和桥面荷载的主要构件,通常采用钢筋混凝土或预应力混凝土制成。
拱肋是拱桥的主要承载构件,其形状和尺寸直接影响着拱桥的力学性能。
桥面是承载行车荷载和行人重量的部分,通常采用钢筋混凝土制成。
支座用于支承拱肋和桥面,使其能够自由伸缩和旋转。
伸缩缝则用于补偿温度变形和桥梁的变形。
三、混凝土拱桥的设计方法混凝土拱桥的设计方法通常包括以下几个步骤:1、确定桥梁跨径和净空高度桥梁跨径和净空高度是拱桥设计的最基本参数,其确定需要考虑到拱桥所处的地理环境、交通流量、车辆类型和荷载等。
一般情况下,桥梁跨径和净空高度的设计应满足规范的要求和实际使用的需要。
2、确定拱肋形状和尺寸拱肋的形状和尺寸是决定拱桥力学性能的主要因素,其设计需要考虑到拱桥的荷载和几何形状。
一般情况下,拱肋的形状可以采用圆弧形、椭圆形、抛物线形等,其尺寸则需要根据实际情况进行计算和确定。
3、确定桥墩和支座桥墩和支座的设计需要考虑到拱桥的荷载、几何形状和地基条件等。
一般情况下,桥墩的形状可以采用圆柱形、矩形、T形等,其尺寸则需要根据实际情况进行计算和确定。
支座的设计需要考虑到拱桥的伸缩和旋转,一般采用橡胶支座或滑动支座。
4、确定桥面结构桥面结构是承载行车荷载和行人重量的主要构件,其设计需要考虑到拱桥的荷载、几何形状和使用要求等。
一般情况下,桥面结构可以采用钢筋混凝土梁板、钢箱梁、钢桁架等形式。
四、混凝土拱桥的计算方法混凝土拱桥的计算方法通常包括以下几个方面:1、拱肋的内力计算拱肋的内力计算是拱桥设计的重要环节,其结果直接影响着拱桥的力学性能。
8 拱式桥梁的计算
拱式桥梁的计算拱桥计算包括成桥状态受力分析和强度、刚度、稳定验算以及必要的动力分析,施工阶段结构受力分析和验算。
拱轴线的选择与确定拱轴线的形状直接影响主拱截面内力大小与分布。
压力线:荷载作用下拱截面上弯矩为零(全截面受压)的截面合内力作用点的连线;恒载压力线:恒载作用下截面弯矩为零的截面合内力作用点的连线;各种荷载压力线:各种荷载作用下截面弯矩为零的截面合内力作用点的连线;合内力作用点的连线理想拱轴线:与各种荷载压力线重合的拱轴线;拱截面上各点为受压应力尽量趋均 合理拱轴线:拱截面上各点为受压应力,尽量趋于均匀分布,能充分发挥圬工材料良好的抗压性能;选择拱轴线的原则:尽量降低荷载弯矩值;考虑拱轴线外形与施工简便等因素拱轴线的选择¾选择原则:尽可能降低荷载弯矩值三种拱轴线形¾种拱轴线形:()线、(1)圆弧线----15m-20m石拱桥、拱上腹拱(),(2)抛物线----轻型拱桥,或中承式拱桥(3)悬链线----最常用的拱轴线1、圆弧线(1)圆弧线拱轴线线形简单,全拱曲率相同,施工方便:拱轴线的选择与确定2、抛物线拱轴线的选择与确定3、悬链线¾实腹式拱桥的恒载集度是由拱顶到拱脚连续分布、逐渐增大的,其恒载压力线是一条悬线。
链线。
¾空腹式拱桥恒载的变化不是连续的函数,如果要与压力线重合,则拱轴线非常复杂。
拱轴线的选择与确定3、悬链线悬链线拱的拱轴方程及几何性质基本微分方程式悬链线拱的拱轴方程及几何性质悬链线拱的拱轴方程及几何性质代入基本微分方程悬链线拱的拱轴方程及几何性质悬链线拱的拱轴方程及几何性质拱轴形状与拱轴系数的关系一般的拱桥中:故m>1(悬链线拱的拱轴系数,宜采用2.814~1.167,随跨径的增大或矢跨比的减小而减小)当m=1时,表示恒载压力均布,压力线为二次抛物线,空腹式悬链线拱空腹式拱桥恒载及其压力线的特点¾拱轴线变化:空腹式拱中桥跨结构恒载分为两部分:分布恒载和集中恒载。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 拱桥计算第一节 拱轴方程的建立教学内容:1、实腹式悬链线拱拱轴方程的建立2、空腹式悬链线拱拱轴方程的建立3、悬链线无铰拱的弹性中心重点:空腹式悬链线拱拱轴方程的建立、悬链线无铰拱的弹性中心 难点:1、逐次逼近法 2、五点重合法 3、弹性中心(一)实腹式悬链线拱拱轴方程的建立1、拱轴线方程的得出:实腹式悬链线拱采用恒载压力线作为拱轴线在恒载作用下,拱顶截面:0=d M ,由于对称性,剪力0=d Q ,仅有恒载推力g H 。
对拱脚截面取矩,则有:fMH jg ∑=式中 ∑jM——半拱恒载对拱脚截面的弯矩;g H ——拱的恒载水平推力(不考虑弹性压缩);f ——拱的计算矢高。
对任意截面取矩,可得:gxH M y =1 式中 x M ——任意截面以右的全部恒载对该截面的弯矩值;1y ——以拱顶为坐标原点,拱轴上任意点的纵坐标。
将上式两边对x 求二阶导数得:g x xg H g dx M d .H dxy d ==222121 解此方程,则得拱轴线方程为:)1(11--=ξchk m fy 2 拱轴系数m : 拱轴系数:为拱脚与拱顶的恒载集度比拱脚截面:ξ=1,y 1=f , )1m m ln(m ch k 21-+==- 当1=m 时,均布荷载。
压力线方程为:21ξf y = (二次抛物线) 当拱的矢跨比确定后,拱轴线各点的纵坐标(拱轴形状)将取决于m 。
(表3-3-1)供设计时根据拱轴系数确定拱轴坐标。
3.实腹式悬链线拱拱轴系数m 的确定方法:dj g g m =, d h g d d γγ+=1, γϕγγjd j dh h g cos 21++=式中 d h ——拱顶填料厚度,一般为0.30~0.50m ;d ——拱圈厚度;γ——拱圈材料容重1γ——拱顶填料及路面的平均容重; 2γ——拱腹填料平均容重j ϕ——拱脚处拱轴线的水平倾角。
jd d f h ϕcos 22-+= 由于j ϕ为未知,故不能直接算出m 值,需用逐次逼近法确定;逐次逼近法:(1)根据跨径和矢高假定m 值,(2)由表3-3-4查得拱脚处的ϕtg ,求得ϕcos 值; (3)代入求得j g 后,再连同d g 一起代入算得m 值。
(4)与假定的m 值比较,如相符,则假定的m 值即为真实值;如两者不符,则以算得的m 值作为假定值,重新进行计算,直至两者接近为止。
当拱的跨径和矢高确定之后,悬链线的形状取决于拱轴系数m ,其线型特征可用4/l 点纵坐标4/1y 的大小表示。
)12k ch (1m 1f y 4l --=∵21212+=+=m chk kch∴2)1m (211m 121m fy 4l ++=--+=拱跨4L点纵坐标与m的关系j g 、d g 、m 与拱轴线坐标的关系由上式可见,4l y 随m 的增大而减小,随m 的减小而增大。
当m 增大时,拱轴线抬高;反之当m 减小时,拱轴线降低。
(二)空腹式悬链线拱1、特点:集中力的存在,恒载压力线是一条在集中力下有转折的曲线,不是悬链线,不是光滑的曲线。
2.M 值求解思路:五点重合法:要求拱轴线在全拱有五点(拱顶、两点4/l 和两拱脚)与其相应三铰拱恒载压力线重合,根据上述五点弯矩为零的条件确定m 值。
条件:(1)拱顶弯矩为零(2)恒载对称拱顶:弯矩0=d M ,剪力0=d Q 。
由∑=0A M ,得 fM H jg∑=由∑=0B M ,得 ∑=-04/4/l l g M y H 和4/4/l l g y MH ∑=将H g 代入上式,可得:∑∑=j4/l 4/l MM fy式中∑jΜ——半拱恒载对拱脚截面的弯矩;∑4/l M——拱顶至拱跨4/l 点区域的恒载对4/l 截面的弯矩。
4/l M 、j M 可由表3-3-3查得。
1)2(2124/--=l y f m 求得m 值。
3.M 值求解方法:(逐次逼近法)(1)先假定一个m 值,定出拱轴线,作图布置拱上建筑, (2)计算拱圈和拱上建筑的恒载对4/l 和拱脚截面的力矩∑4/l M和∑jM,根据式(3-3-18)求出f y l /4/(3)利用1)2(2124/--=l y fm 算出m 值,如与假定的m 值不符,则应以求得的m 值作为新假定值,重新计算,直至两者接近为止。
4.偏离影响的计算:(1)除五点重合,其它截面都有不同程度的偏离。
计算证明,从拱顶到4/l 点,一般压力线在拱轴线之上; 而从4/l 点到拱脚,压力线则大多在拱轴线之下拱轴线与相应三铰拱恒载压力线的偏离类似于一个正弦波。
(2)偏离附加内力计算对于静定三铰拱: y H M p p ∆⋅=;对于无铰拱:以y H M p p ∆⋅=作为荷载,算出无铰拱的偏离弯矩值。
由结构力学知,荷载作用在基本结构上引起弹性中心的赘余力为:⎰⎰⎰⎰⎰⎰∆-=-=-=∆-=∆Ids ds I y H Ids dsI M EIds M ds EI M M X s s gs psspsp2111111δ⎰⎰⎰⎰∆==∆-=∆Ids y ds I y y H EIds M dsEI M M X s s g spsp22222222δ 1X ∆数值较小。
若Iydss∆⎰=0,则1X ∆=0。
2X ∆恒为正值(压力)。
任意截面之偏离弯矩:21X X M ∆-∆=∆·p M y +式中 y ——以弹性中心为原点(向上为正)的拱轴纵坐标。
对于拱顶、拱脚截面,0=p M ,偏离弯矩为:⎭⎬⎫>-∆+∆=∆<⋅∆-∆=∆0)(0y 21s 21s j d y f X X M X X M式中 s y ——弹性中心至拱顶之距离.(3)结论:空腹式无铰拱桥,采用“五点重合法”确定的拱轴线,而与无铰拱的恒载压力线实际上并不存在五点重合的关系。
由于拱轴线与恒载压力线有偏离,在拱顶、拱脚都产生了偏离弯矩。
拱顶的偏离弯矩d M ∆为负,而拱脚的偏离弯矩j M ∆为正,恰好与这两截面控制弯矩的符号相反。
偏离弯矩对拱顶、拱脚都是有利的。
因而,空腹式无铰拱的拱轴线,用悬链线比用恒载压力线更加合理。
(三)悬链线无铰拱的弹性中心 利用拱的弹性中心的概念目的:是将求解三个赘余力的联立方程的问题解耦,从而变为解三个独立的一元一次方程的问题。
在荷载作用下,以半拱悬臂为基本结构,在拱顶处会产生三个赘余力X 1、X 2、X 3,典型方程为:⎪⎭⎪⎬⎫=∆+++=∆+++=∆+++000333323213123232221211313212111p p p X X X X X X X X X δδδδδδδδδ赘余力中弯矩1X 和轴力2X 是正对称的,剪力3X 是反对称的,故知副系数:⎭⎬⎫====0032233113δδδδ如果能设法使2112δδ=也等于零,则典型方程中的全部副系数都为零,解三个独立的一元一次方程的问题,从而简化计算。
我们讨论的是对称拱,弹性中心在对称轴上。
以悬臂曲梁为基本结构,由计算得知,作用于弹性中心的三个赘余力以单位力分别作用时引起的内力为⎪⎭⎪⎬⎫ϕ=ϕ==ϕ=ϕ-=====sin N ,cos Q ,x M cos N ,sin Q ,y M 0N ,0Q ,1M 333222111(x 轴向左为正,y 轴向下为正,弯矩以使拱下缘受拉为正,剪力以绕隔离体逆时针方向转动为正,轴力以压力为正,上式中ϕ在右半拱取正,左半拱取负),因此:00212121212112++⋅=⋅+⋅+⋅==⎰⎰⎰⎰EIds M M GA ds Q Q k EA ds N N EI ds M M s s s sδδ=EIdsy EI ds y EI ds y y EI ds yss s s s s⎰⎰⎰⎰-=-=11)( 令02112==δδ,便可得到弹性中心距拱顶之距离为:EIds EIdsy y s s s ⎰⎰=1式中 ζϕϕξd l dx ds chk m fy cos 12cos )1(11⋅==--=其中 ξηϕϕk sh tg 2221111cos +=+=则 ξξηd k sh ds 22121+=以1y 及ds 代入式(3-3-28),并注意到等截面拱中I 为常数,则:f d k sh d k sh chk m fds dsy y s ss⋅=++-⋅-==⎰⎰⎰⎰1222211011)1(011αξξηξξηξ (由表3-3-5查得)第三章 拱桥计算教学内容:1、不考虑弹性压缩的恒载内力2、弹性压缩引起的内力3、结构总内力重点:1、不考虑弹性压缩的恒载内力 2、弹性压缩引起的内力 难点:1、弹性压缩引起的内力第二节 恒载作用下拱的内力计算一、计算内容:不考虑弹性压缩影响的内力+仅因弹性压缩引起的内力=恒载作用下的总内力。
(一)、不考虑弹性压缩的恒载内力 1.实腹拱恒载内力实腹式悬链线拱的拱轴线与恒载压力线完全吻合,可按纯压拱的公式计算。
由公式(3-3-9))1(212-⋅=m fH g l k g df lg k f l g km H d g d g 22241=⨯-= 式中 241km k g -=。
⎰⎰==ξd l g dx g l V x x g 1101将公式(3-3-8)、式(3-3-11)代入上式积分得:l g k l g m m m V d g d g '22)]1[ln(21=-+-=式中 )]1[ln(2122'-+-=m m m k g系数gk、gk'可自表3-3-6查得。
结构重力产生的水平推力系数g k 和垂直反力系数gk' m1.347 1.543 1.756 1.9882.240 2.514 2.8143.1423.500g k0.13200 0.13577 0.13974 0.14392 0.14834 0.15300 0.15793 0.16315 0.16869 g k '0.55663 0.58762 0.62060 0.65574 0.69323 0.73327 0.77611 0.82201 0.87126因为恒载弯矩和剪力均为零,拱圈各截面的轴向力N 按下式计算:ϕ=cos H N g2.空腹拱恒载内力(1)考虑拱轴线与恒载压力线偏离弯矩空腹式无铰拱桥的恒载内力=不考虑偏离的影响+偏离引起的恒内力。
(2)不考虑偏离的影响时,空腹拱的恒载内力亦按纯压拱计算 fMH jg ∑=,∑=P V g (半拱恒载重)弯矩和剪力均为零,所以轴力ϕcos g H N =注:(1)设计中、小跨径的空腹式拱桥时,可偏安全地不考虑偏离弯矩的影响。
(2)大跨径空腹式拱桥,偏离一般比中、小跨径大,恒载偏离弯矩是一种可供利用的有利因素,应当计入偏离弯矩的影响。
(二) 、弹性压缩引起的内力拱轴长度的缩短,会在拱中产生相应的内力。
