青岛版七年级数学下册期中试题
2020-2021学年青岛版数学七年级下册期中测试题及答案解析(共3套)
青岛版数学七年级下册期中测试题（一）一、选择题1．下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）A．B．C．D．2．已知，∠α与∠β互补，且∠α﹣∠β=30°，则∠α与∠β的大小关系依次为（）A．110°，70°B．105°，75°C．100°，70°D．110°，80°3．下列计算正确的是（）A．a2+a2=2a4B．（﹣a2b）3=﹣a6b3C．a2•a3=a6D．a8÷a2=a44．若A，B，C是直线l上的三点，P是直线l外一点，且PA=5cm，PB=4cm，PC=3cm，则点P到直线L的距离（）A．等于3cm B．大于3cm而小于4cmC．不大于3cm D．小于3cm5．要使（y2﹣ky+2y）（﹣y）的展开式中不含y2项，则k的值为（）A．﹣2B．0C．2D．36．如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=32°，则∠2的度数为（）A．25°B．28°C．30°D．32°7．用加减法解方程组时，要使方程中同一个未知数的系数相等或互为相反数，必须适当变形，以下四种变形正确的是（）（1）（2）（3）（4）A．（1）（2）B．（2）（3）C．（3）（4）D．（4）（1）8．如图，直线AB、CD交于点O，OT⊥AB于O，CE∥AB交CD于点C，若∠ECO=30°，则∠DOT等于（）A．30°B．45°C．60°D．120°9．古代有这样一个寓言故事：驴子和骡子一同走，它们驮着不同袋数的货物，每袋货物都是一样重的．驴子抱怨负担太重，骡子说：“你抱怨干吗如果你给我一袋，那我所负担的就是你的两倍；如果我给你一袋，我们才恰好驮的一样多！”那么驴子原来所托货物的袋数是（）A．5B．6C．7D．810．若a=240，b=332，c=424，则下列关系正确的是（）A．a＞b＞c B．b＞c＞a C．c＞a＞b D．c＞b＞a二、填空题11．若（m﹣3）x+2y|m﹣2|+8=0是关于x，y的二元一次方程，m=．12．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.000000076克，用科学记数法表示是克．13．若x n﹣1•x n+5=x10，则n﹣2=．14．如图，在三角形ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B=35°，∠C=65°，则∠EFD=．15．若实数m，m满足|m﹣2|+（n﹣2015）2=0，则m﹣1+n0=．16．已知关于x，y的二元一次方程组的解互为相反数，则k的值是．17．若（2x+5）（4x﹣10）=8x2+px+q，则p=，q=．18．五一前夕，某超市促销，由顾客抽奖决定折扣，某顾客购买甲乙两种商品，分别抽到七折（按售价70%）和九折销售，共付款386元，这两种商品原销售之和为500元，则甲乙两种商品原销售价分别为、．三、解答题19．化简求值：（1）a3•a3+（﹣2a3）2+（﹣a2）3，其中a=﹣1．（2）4x（x﹣1）﹣（2x+1）（2x﹣1），其中x=﹣5．20．解方程组（1）（2）．21．（1）一个角的余角与这个角的补角的和比平角的多1°，求这个角的度数．（2）已知5m=2，5n=3，求53m﹣2n．22．如图，直线EF，CD相交于点O，OA⊥OB，且OC平分∠AOF．（1）若∠AOE=40°，求∠BOD的度数；（2）若∠AOE=α，求∠BOD的度数．（用含α的代数式表示）23．某开发区去年出口创汇额为25亿美元，今年达到30.55亿美元，已知今年上半年出口创汇额比去年同期增长18%，下半年比去年同期增长25%，求去年上半年和下半年的出口创汇额各是多少亿美元？24．已知如图，在三角形ABC中，AC⊥AB，DG⊥BC，EF⊥AB，∠1=∠2，试判断CD与AB的位置关系？并说明理由．25．小亮在做“化简（2x+k）（3x+2）﹣6x（x+3）+5x+16并求x=2时的值”一题时，错将x=2看成x=﹣2，但结果却和正确答案一样，由此，你能推算出k 值吗？26．如图，长青化工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨1 000元的原料运回工厂，制成每吨8 000元的产品运到B地．已知公路运价为1.5元/（t•km），铁路运价为1.2元/（t•km），且这两次运输共支出公路运输费15000元，铁路运输费97200元．求：（1）该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？（2）这批产品的销售款比原料费与运输费的和多多少元？参考答案一、选择题1．【解答】解：A、图中的∠AOB不能用∠O表示，故本选项错误；B、图中的∠1和∠AOB不是表示同一个角，故本选项错误；C、图中的∠1和∠AOB不是表示同一个角，故本选项错误；D、图中∠1、∠AOB、∠O表示同一个角，故本选项正确；故选：D．2．【解答】解：∵∠α与∠β互为补角，∴∠α+∠β=180°，又∵∠α﹣∠β=30°，∴，解得：，故选：B．3．【解答】解：A、a2+a2=2a2B，故A错误；B、（﹣a2b）3=﹣a6b3，故B正确；C、a2•a3=a5，故C错误；D、a8÷a2=a6，故D错误；故选：B．4．【解答】解：根据点到直线的距离的定义，点P到直线L的距离即为点P到直线L的垂线段的长度，垂线段的长度不能超过PC的长．故选C．5．【解答】解：∵（y2﹣ky+2y）（﹣y）的展开式中不含y2项，∴﹣y3+ky2﹣2y2中不含y2项，∴k﹣2=0，解得：k=2．故选：C．6．【解答】解：过A作AE∥NM，∵NM∥GH，∴AE∥GH，∴∠3=∠1=32°，∵∠BAC=60°，∴∠4=60°﹣32°=28°，∵NM∥AE，∴∠2=∠4=28°，故选：B．7．【解答】解：把y的系数变为相等时，①×3，②×2得，，把x的系数变为相等时，①×2，②×3得，．故选：C．8．【解答】解：∵CE∥AB，∴∠DOB=∠ECO=30°，∵OT⊥AB，∴∠BOT=90°，∴∠DOT=∠BOT﹣∠DOB=90°﹣30°=60°．故选：C．9．【解答】解：设驴子原来驮x袋，根据题意，得到方程：2（x﹣1）﹣1﹣1=x+1，解得：x=5，答：驴子原来所托货物的袋数是5．故选：A．10．【解答】解：∵a=240=328，b=332=818，c=424=648，∴b＞c＞a，故选：B．二、填空题11．【解答】解：根据题意，得|m﹣2|=1且m﹣3≠0，解得m=1．故答案为：1．12．【解答】解：0.000000076=7.6×10﹣8．故答案为：7.6×10﹣8．13．【解答】解：由x n﹣1•x n+5=x10，得x2n+4=x10，即2n+4=10，解得n=3．n﹣2=3﹣2=，故答案为：．14．【解答】解：∵EF∥AC，∴∠EFB=∠C=65°，∵DF∥AB，∴∠DFC=∠B=35°，∴∠EFD=180°﹣65°﹣35°=80°，故答案为：80°．15．【解答】解：由m，m满足|m﹣2|+（n﹣2015）2=0，得m﹣2=0，n﹣2015=0．解得m=2，n=2015．m﹣1+n0=+1=，故答案为：．16．【解答】解：解方程组得：，因为关于x，y的二元一次方程组的解互为相反数，可得：2k+3﹣2﹣k=0，解得：k=﹣1．故答案为：﹣1．17．【解答】解：已知等式整理得：8x2﹣50=8x2+px+q，则p=0，q=﹣50，故答案为：0，﹣5018．【解答】解：设甲、乙两商品的原价分别是x元，y元，则，解得．故答案为：320元；180元三、解答题19．【解答】解：（1）原式=a6+4a6﹣a6=4a6，当a=﹣1时，原式=4；（2）原式=4x2﹣4x﹣4x2+1=﹣4x+1，当x=﹣5时，原式=20+1=21．20．【解答】解：（1），①+②×4得：23x=23，即x=1，把x=1代入①得：y=2，则方程组的解为；（2），①×3+②得：14x=﹣14，即x=﹣1，把x=﹣1代入①得：y=3，则方程组的解为．21．【解答】解：（1）设这个角为x，根据题意得：90°﹣x+180°﹣x=180°×+1°，解得：x=67°，则这个角的度数为67°；（2）∵5m=2，5n=3，∴原式=（5m）3÷（5n）2=．22．【解答】解：（1）∵∠AOE+∠AOF=180°（互为补角），∠AOE=40°，∴∠AOF=140°；又∵OC平分∠AOF，∴∠FOC=∠AOF=70°，∴∠EOD=∠FOC=70°（对顶角相等）；∵∠BOE=∠AOB﹣∠AOE=50°，∴∠BOD=∠EOD﹣∠BOE=20°；（2）∵∠AOE+∠AOF=180°（互为补角），∠AOE=α，∴∠AOF=180°﹣α；又∵OC平分∠AOF，∴∠FOC=∠AOF=90°﹣α，∴∠EOD=∠FOC=90°﹣α（对顶角相等）；∵∠BOE=∠AOB﹣∠AOE=90°﹣α，∴∠BOD=∠EOD﹣∠BOE=α．23．【解答】解：设去年上半年出口创汇额为x亿美元，去年下半年的出口创汇额为y亿美元，则今年上半年出口创汇额为（1+18%）x=1.18x（亿美元），今年下半年的出口创汇额为（1+25%）y=1.25（亿美元），根据题意可列方程组，解得，答：去年上半年出口创汇额为10亿美元，去年下半年的出口创汇额为15亿美元．24．【解答】解：垂直．理由：∵AC⊥BC，DG⊥BC，∴AC∥DG，∴∠2=∠3，∵∠1=∠2，∴∠1=∠3，∴EF∥CD，∵EF⊥AB，∴CD⊥AB．25．【解答】解：原式=6x2+4x+3kx+2k﹣6x2﹣18x+5x+16=（3k﹣9）x+2k+16，由结果与x取值无关，得到3k﹣9=0，解得：k=3．26．【解答】解：（1）设工厂从A地购买了x吨原料，制成运往B地的产品y 吨，根据题意得：，解得：．答：工厂从A地购买了400吨原料，制成运往B地的产品300吨．（2）300×8000﹣400×1000﹣15000﹣97200=1887800（元）．答：这批产品的销售款比原料费与运输费的和多1887800元．青岛版数学七年级下册期中测试题（二）一、选择题（每题3分）1．16的算术平方根是（）A．16 B．4 C．﹣4 D．±4【考点】22：算术平方根．【分析】根据算术平方根的概念即可求出答案．【解答】解：∵42=16，∴16的算术平方根是4，故选（B）【点评】本题考查算术平方根的概念，解题的关键是正确理解算术平方根的概念，本题属于基础题型．2．如图，∠1和∠2是对顶角的图形个数有（）A．1个B．2个C．3个D．4个【考点】J2：对顶角、邻补角．【专题】12 ：应用题．【分析】一个角的两边分别是另一个角两边的反向延长线，那么这两个角是对顶角．据此作答即可．【解答】解：只有丙图中的两个角是对顶角，故选：A．【点评】本题考查了对顶角的概念，解题的关键是掌握对顶角的概念．3．下列说法中，不正确的是（）A．10的立方根是B．﹣2是4的一个平方根C．的平方根是D．0.01的算术平方根是0.1【考点】24：立方根；21：平方根；22：算术平方根．【分析】根据立方根，平方根的定义，即可解答．【解答】解：A．10的立方根是，正确；B．﹣2是4的一个平方根，正确；C.的平方根是±，故错误；D． 0.01的算术平方根是0.1，正确；故选C．【点评】本题考查了平方根，立方根，解决本题的关键是熟记立方根，平方根的定义．4．如图，下列条件：①∠1=∠3，②∠2=∠3，③∠4=∠5，④∠2+∠4=180°中，能判断直线l1∥l2的有（）A．1个B．2个C．3个D．4个【考点】J9：平行线的判定．【专题】11 ：计算题．【分析】利用平行线的判定方法判断即可得到结果．【解答】解：∵∠1=∠3，∴l1∥l2；∵∠4=∠5，∴l1∥l2；∵∠2+∠4=180°，∴l1∥l2，则能判断直线l1∥l2的有3个．故选C【点评】此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．5．如图，直线a∥b，射线DC与直线a相交于点C，过点D作DE⊥b于点E，已知∠1=25°，则∠2的度数为（）A．115°B．125°C．155°D．165°【考点】JA：平行线的性质．【专题】11 ：计算题．【分析】如图，过点D作c∥a．由平行线的性质进行解题．【解答】解：如图，过点D作c∥a．则∠1=∠CDB=25°．又a∥b，DE⊥b，∴b∥c，DE⊥c，∴∠2=∠CDB+90°=115°．故选：A．【点评】本题考查了平行线的性质．此题利用了“两直线平行，同位角相等”来解题的．6．如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数等于（）A．20°B．30°C．35° D．40°【考点】J2：对顶角、邻补角；IJ：角平分线的定义．【分析】根据角平分线定义求出∠AOC=∠EOC=35°，根据对顶角的定义即可求出∠BOD的度数．【解答】解：∵OA平分∠EOC，∠EOC=70°，∴∠AOC=∠EOC=35°，∴∠BOD=∠AOC=35°．故选：C．【点评】本题考查了对顶角、角平分线定义的应用，关键是求出∠AOC的度数．7．若a2=4，b3=27且ab＜0，则a﹣b的值为（）A．﹣2 B．±5 C．5 D．﹣5【考点】1E：有理数的乘方．【分析】根据有理数的乘方求出a、b，再根据异号得负判断出a的值，然后代入代数式进行计算即可得解．【解答】解：∵a2=4，b3=27，∴a=±2，b=3，∵ab＜0，∴a=﹣2，∴a﹣b=﹣2﹣3=﹣5．故选D．【点评】本题考查了有理数的乘方，有理数的乘方，有理数的减法运算，熟记运算法则并确定出a=﹣2是解题的关键．8．如果点A（a、b）在第三象限，则点B（﹣a+1，3b﹣5）关于原点的对称点是（）A．第一象限B．第二象限C．第三象限D．第四象限【考点】R6：关于原点对称的点的坐标．【分析】此题首先明确两个点关于原点对称，则横、纵坐标都是互为相反数；然后能够根据点所在的位置判断点的坐标符号，根据坐标符号得到字母的取值范围．【解答】解：∵点B（﹣a+1，3b﹣5）关于原点的对称点是（a﹣1，5﹣3b）．又∵点A在第三象限即a＜0，b＜0．∴a﹣1＜0，5﹣3b＞0，∴（a﹣1，5﹣3b）是第三象限的点．故选B．【点评】本题考查了坐标平面内的点坐标的符号，同时考查了关于原点对称的两点坐标之间的关系．9．在实数：3.14159，，1.010010001，4.21，π，中，无理数有（）A．1个B．2个C．3个D．4个【考点】26：无理数．【分析】根据无理数的定义，可得答案．【解答】解：π是无理数，故选：A．【点评】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．10．一个长方形在平面直角坐标系中三个顶点的坐标为（﹣1，﹣1），（﹣1，2），（3，﹣1），则第四个顶点的坐标为（）A．（2，2）B．（3，2）C．（3，3）D．（2，3）【考点】D5：坐标与图形性质；LB：矩形的性质．【分析】本题可在画出图后，根据矩形的性质，得知第四个顶点的横坐标应为3，纵坐标应为2．【解答】解：如图可知第四个顶点为：即：（3，2）．故选：B．【点评】本题考查学生的动手能力，画出图后可很快得到答案．11．如图，在下列四组条件中，能得到AB∥CD的是（）A．∠ABD=∠BDC B．∠3=∠4C．∠BAD+∠ABC=180°D．∠1=∠2【考点】J9：平行线的判定．【分析】根据平行线的判定定理对各选项进行逐一判断即可．【解答】解：A、若∠ABD=∠BDC，则AB∥CD，故本选项正确；B、若∠3=∠4，则AD∥BC，故本选项错误；C、若∠BAD+∠ABC=180°，则AD∥BC，故本选项错误；D、若∠1=∠2，则AD∥BC，故本选项错误；故选A．【点评】本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．12．如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C的方向平移到△DEF的位置，AB=10，DO=4，平移距离为6，则阴影部分面积为（）A．48 B．96 C．84 D．42【考点】Q2：平移的性质．【分析】根据平移的性质得出BE=6，DE=AB=10，则OE=6，则阴影部分面积=S四边形ODFC =S梯形ABEO，根据梯形的面积公式即可求解．【解答】解：由平移的性质知，BE=6，DE=AB=10，∴OE=DE﹣DO=10﹣4=6，∴S四边形ODFC =S梯形ABEO=（AB+OE）•BE=（10+6）×6=48．故选：A．【点评】本题主要考查了平移的性质及梯形的面积公式，得出阴影部分和梯形ABEO的面积相等是解题的关键．二、填空（每题3分）13．如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是连接直线外一点与直线上所有点的连线中，垂线段最短．【考点】J4：垂线段最短．【专题】12 ：应用题．【分析】过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．【解答】解：根据垂线段定理，连接直线外一点与直线上所有点的连线中，垂线段最短，∴沿AB开渠，能使所开的渠道最短．故答案为：连接直线外一点与直线上所有点的连线中，垂线段最短．【点评】本题是垂线段最短在实际生活中的应用，体现了数学的实际运用价值．14．直线l1∥l2，一块含45°角的直角三角板如图放置，∠1=85°，则∠2= 40°．【考点】JA：平行线的性质；K7：三角形内角和定理．【专题】11 ：计算题．【分析】根据两直线平行，同位角相等可得∠3=∠1，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠4，然后根据对顶角相等解答．【解答】解：∵l1∥l2，∴∠3=∠1=85°，∴∠4=∠3﹣45°=85°﹣45°=40°，∴∠2=∠4=40°．故答案为：40°．【点评】本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质是解题的关键．15．已知a，b为两个连续的整数，且a＜b，则a+b=9．【考点】2B：估算无理数的大小．【分析】根据无理数的性质，得出接近无理数的整数，即可得出a，b的值，即可得出答案．【解答】解：∵a＜b，a、b为两个连续的整数，∴＜＜，∴a=4，b=5，∴a+b=9．故答案为：9．【点评】此题主要考查了无理数的大小，得出比较无理数的方法是解决问题的关键．16．已知点P在第二象限，且横坐标与纵坐标的和为1，试写出一个符合条件的点P（3，﹣2）．【考点】D1：点的坐标．【专题】26 ：开放型．【分析】根据第二象限内点的横坐标是负数，纵坐标是正数写出即可．【解答】解：点P（3，﹣2）．故答案为：（3，﹣2）答案不唯一．【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．17．如果P（a+b，ab）在第二象限，那么点Q（a，﹣b）在第二象限．【考点】D1：点的坐标．【分析】应先判断出所求的点的横纵坐标的符号，进而判断其所在的象限．【解答】解：∵P（a+b，ab）在第二象限，∴a+b＜0，ab＞0，∴a，b都是负号，∴a＜0，﹣b＞0，∴点Q（a，﹣b）在第二象限．故填：二．【点评】解决本题的关键是记住平面直角坐标系中各个象限内点的符号．18．把一张纸各按图中那样折叠后，若得到∠AOB′=70°，则∠B′OG=55度．【考点】IK：角的计算．【专题】11 ：计算题．【分析】根据题意∠B′OG=∠BOG，根据平角和角平分线的定义即可求得．【解答】解：由题意可得∠B′OG=∠BOG，则∠B′OG=（180﹣∠AOB′）÷2=55°．故答案为55．【点评】已知折叠问题就是已知图形全等，因而得到相等的角．三、解答题：19．（6分）求下列等式中x的值：（1）2x2﹣=0（2）（x+4）3=125．【考点】24：立方根；21：平方根．【分析】（1）直接开平方法解方程即可；（2）直接开立方解方程即可．【解答】解：（1）2x2﹣=0x=±0.5（2）（x+4）3=125x=1【点评】此题主要考查了利用立方根和平方根的性质解方程．要灵活运用使计算简便．20．（6分）已知2a﹣1的平方根是±3，11a+b﹣1的立方根是4，求a+2b的平方根．【考点】21：平方根；24：立方根．【分析】根据已知得出2a﹣1=9，11a+b﹣1=64，求出a=5，b=10，求出a+2b的值，最后求出a+2b的平方根即可．【解答】解：∵2a﹣1的平方根是±3，11a+b﹣1的立方根是4，∴2a﹣1=9，11a+b﹣1=64，∴a=5，b=10，∴a+2b=25，即a+2b的平方根是±5．【点评】本题考查了平方根，解二元一次方程组，立方根的应用，关键是得出关于a、b的方程组．21．（7分）如图是小明所在学校的平面示意图，请你以教学楼为坐标原点建立平面直角坐标系，描述学校其它建筑物的位置．【考点】D3：坐标确定位置．【分析】根据题意建立平面直角坐标系进而得出各点坐标即可．【解答】解：如图所示：实验楼（﹣2，2），行政楼（﹣2，﹣2），大门（0，﹣4），食堂（3，4），图书馆（4，﹣2）．【点评】此题主要考查了坐标确定位置，正确建立平面直角坐标系是解题关键．22．（6分）如图，直线AB、CD相交于点O，OE把∠BOD分成两部分．（1）直接写出图中∠AOC的对顶角：∠BOD，∠EOB的邻补角：∠AOE （2）若∠AOC=70°且∠BOE：∠EOD=2：3，求∠AOE的度数．【考点】J2：对顶角、邻补角．【分析】（1）根据对顶角和邻补角的定义直接写出即可；（2）根据对顶角相等求出∠BOD的度数，再根据∠BOE：∠EOD=2：3求出∠BOE的度数，然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数．【解答】解：（1）∠AOC的对顶角是∠BOD，∠EOB的邻补角是∠AOE，故答案为：∠BOD，∠AOE；（2）∵∠AOC=70°，∴∠BOD=∠AOC=70°，∵∠BOE：∠EOD=2：3，∴∠BOE=×70°=28°，∴∠AOE=180°﹣28°=152°．∴∠AOE的度数为152°．【点评】本题主要考查了对顶角和邻补角的定义，利用对顶角相等的性质和互为邻补角的两个角的和等于180°求解是解答此题的关键．23．（7分）如图，已知点E在直线AB外，请用三角板与直尺画图，并回答第（3）题：（1）过E作直线CD，使CD∥AB；（2）过E作直线EF，使EF⊥AB，垂足为F；（3）请判断直线CD与EF的位置关系，并说明理由．【考点】N3：作图—复杂作图．【分析】（1）根据题意直接作出CD∥AB；（2）过点E利用三角尺作出EF⊥AB；（3）利用平行线的性质，进而得出直线CD与EF的位置关系．【解答】解：（1）、（2）如图所示：（3）CD⊥EF．理由：∵CD∥AB，∴∠CEF=∠EFB，∵EF⊥AB，∴∠EFB=90°，∴∠CEF=90°，∴CD⊥EF．【点评】此题主要考查了复杂作图以及平行线的性质等知识，根据题意作出正确图形是解题关键．24．（6分）如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE=∠E．求证：AD∥BC．【考点】J9：平行线的判定．【专题】14 ：证明题．【分析】首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件，内错角∠2和∠E相等，得出结论．【解答】证明：∵AE平分∠BAD，∴∠1=∠2，∵AB∥CD，∠CFE=∠E，∴∠1=∠CFE=∠E，∴∠2=∠E，∴AD∥BC．【点评】本题考查角平分线的性质以及平行线的判定定理．25．（8分）如图，△ABC中，A（﹣2，1）、B（﹣4，﹣2）、C（﹣1，﹣3），△A′B′C′是△ABC平移之后得到的图象，并且C的对应点C′的坐标为（4，1）（1）A′、B′两点的坐标分别为A′（3，5）、B′（1，2）；（2）作出△ABC平移之后的图形△A′B′C′；（3）求△A′B′C′的面积．【考点】Q4：作图﹣平移变换．【分析】（1）由点C（﹣1，﹣3）与点C′（4，1）是对应点，得出平移规律为：向右平移5个单位，向上平移4个单位，按平移规律即可写出所求的点的坐标；（2）按平移规律作出A、B的对应点A′，B′，顺次连接A′、B′、C′，即可得到△A′B′C′；（3）利用三角形所在的矩形的面积减去四周三个小直角三角形的面积即可求解．【解答】解：（1）∵△A′B′C′是△ABC平移之后得到的图象，并且C（﹣1，﹣3）的对应点C′的坐标为（4，1），∴平移前后对应点的横坐标加5，纵坐标加4，∴△ABC先向右平移5个单位，再向上平移4个单位得到△A′B′C′，∵A（﹣2，1），B（﹣4，﹣2），∴A′（3，5）、B′（1，2）；（2）△A′B′C′如图所示；（3）S=4×3﹣×3×1﹣×3×2﹣×1×4△A′B′C′=12﹣1.5﹣3﹣2=5.5．故答案为（3，5），（1，2）．【点评】本题考查了作图﹣平移变换，平移的规律，三角形的面积，准确找出对应点的位置是解题的关键，格点中的三角形的面积通常整理为长方形的面积与几个三角形的面积的差．青岛版数学七年级下册期中测试题（三）一、选择题（每小题3分，共42）1．在下列各数：3.1415926、、0.2、、、、中无理数的个数是（）A．2 B．3 C．4 D．5【考点】26：无理数．【分析】根据无理数的定义及常见的无理数的形式即可判定．【解答】解：在下列各数：3.1415926、、0.2、、、、中，根据无理数的定义可得，无理数有、两个．故选A．【点评】此题主要考查了无理数的定义，解题要注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．2．下列各式中，正确的是（）A．±=±B．±= C．±=±D．=±【考点】22：算术平方根．【分析】根据平方根的定义得到±=±，即可对各选项进行判断．【解答】解：因为±=±，所以A选项正确；B、C、D选项都错误．故选A．【点评】本题考查了算术平方根的定义：一个正数的正的平方根叫这个数的算术平方根；0的算术平方根为0．3．若|3﹣a|+=0，则a+b的值是（）A．2 B．1 C．0 D．﹣1【考点】23：非负数的性质：算术平方根；16：非负数的性质：绝对值．【分析】根据几个非负数的和为0时，这几个非负数都为0列出算式求出a、b 的值，计算即可．【解答】解：由题意得，3﹣a=0，2+b=0，解得，a=3，b=﹣2，a+b=1，故选：B．【点评】本题考查的是非负数的性质，掌握几个非负数的和为0时，这几个非负数都为0是解题的关键．4．估算﹣2的值（）A．在1到2之间B．在2到3之间C．在3到4之间D．在4到5之间【考点】2B：估算无理数的大小．【专题】11 ：计算题；511：实数．【分析】估算出的范围，即可确定出所求式子的范围．【解答】解：∵16＜21＜25，∴4＜＜5，即2＜﹣2＜3，则﹣2的值在2到3之间，故选B【点评】此题考查了估算无理数的大小，设实数为a，a的整数部分A为不大于a的最大整数，小数部分B为实数a减去其整数部分，即B=a﹣A；5．已知下列命题：①若a＞0，b＞0，则a+b＞0；②若a≠b，则a2≠b2；③两点之间，线段最短；④同位角相等，两直线平行．其中真命题的个数是（）A．1个B．2个C．3个D．4个【考点】O1：命题与定理．【专题】17 ：推理填空题．【分析】正确的命题叫真命题，错误的命题叫做假命题，据此逐项判断即可．【解答】解：∵若a＞0，b＞0，则a+b＞0，∴选项①符合题意；∵若a≠b，且|a|=|b|时，a2=b2，∴选项②不符合题意；∵两点之间，线段最短，∴选项③符合题意；∵同位角相等，两直线平行，∴选项④符合题意，∴真命题的个数是3个：①、③、④．故选：C．【点评】此题主要考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．6．同桌读了：“子非鱼焉知鱼之乐乎？”后，兴高采烈地利用电脑画出了几幅鱼的图案，请问：由图中所示的图案通过平移后得到的图案是（）A．B．C．D．【考点】Q1：生活中的平移现象．【分析】根据图形平移的性质对各选项进行逐一分析即可．【解答】解：A、由图中所示的图案通过旋转而成，故本选项错误；B、由图中所示的图案通过翻折而成，故本选项错误C、由图中所示的图案通过旋转而成，故本选项错误；D、由图中所示的图案通过平移而成，故本选项正确．故选D．【点评】本题考查的是生活中的平移现象，熟知图形平移变换的性质是解答此题的关键．7．如图，小明从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C处，此时需把方向调整到与出发时一致，则方向的调整应是（）A．右转80°B．左转80°C．右转100°D．左转100°【考点】IH：方向角．【专题】12 ：应用题．【分析】本题考查了方向角有关的知识，若需要和出发时的方向一致，在C点的方向应调整为向右80度．【解答】解：60°+20°=80°．由北偏西20°转向北偏东60°，需要向右转．故选：A．【点评】本题考查的是方向角，解答时要注意以北方为参照方向，进行角度调整．8．已知点P位于y轴右侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P坐标是（）A．（﹣3，4）B．（3，4）C．（﹣4，3）D．（4，3）【考点】D1：点的坐标．【分析】根据题意，P点应在第一象限，横、纵坐标为正，再根据P点到坐标轴的距离确定点的坐标．【解答】解：∵P点位于y轴右侧，x轴上方，∴P点在第一象限，又∵P点距y轴3个单位长度，距x轴4个单位长度，∴P点横坐标为3，纵坐标为4，即点P的坐标为（3，4）．故选B．【点评】本题考查了点的位置判断方法及点的坐标几何意义．9．在平面直角坐标系中，将点B（﹣3，2）向右平移5个单位长度，再向下平移3个单位长度后与点A（x，y）重合，则点A的坐标是（）A．（2，5）B．（﹣8，5）C．（﹣8，﹣1）D．（2，﹣1）【考点】Q3：坐标与图形变化﹣平移．【分析】让B的横坐标加5，纵坐标减3即可得到所求点A的坐标．【解答】解：∵将点B（﹣3，2）向右平移5个单位长度，再向下平移3个单位长度后与点A（x，y）重合，∴所求点A的横坐标为：﹣3+5=2，纵坐标为2﹣3=﹣1，∴所求点的坐标为（2，﹣1）．故选D．【点评】本题考查图形的平移变换，要牢记左右移动改变点的横坐标，左减，右加；上下移动改变点的纵坐标，下减，上加．10．如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（）A．（3，2）B．（﹣3，2）C．（3，﹣2）D．（﹣3，﹣2）【考点】D3：坐标确定位置．【专题】31 ：数形结合．【分析】先根据棋子“车”的坐标画出直角坐标系，然后写出棋子“炮”的坐标．【解答】解：如图，棋子“炮”的坐标为（3，﹣2）．故选C．【点评】本题考查了坐标确定位置：平面坐标系中的点与有序实数对一一对应；记住平面内特殊位置的点的坐标特征．11．已知点A（1，0），B（0，2），点P在x轴上，且△PAB的面积为5，则点P的坐标为（）A．（﹣4，0）B．（6，0）C．（﹣4，0）或（6，0）D．无法确定【考点】D5：坐标与图形性质；K3：三角形的面积．【分析】根据B点的坐标可知AP边上的高为2，而△PAB的面积为5，点P在x轴上，说明AP=5，已知点A的坐标，可求P点坐标．【解答】解：∵A（1，0），B（0，2），点P在x轴上，∴AP边上的高为2，又△PAB的面积为5，∴AP=5，而点P可能在点A（1，0）的左边或者右边，∴P（﹣4，0）或（6，0）．故选C．【点评】本题考查了直角坐标系中，利用三角形的底和高及面积，表示点的坐标．12．如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（）A．34°B．56° C．66° D．54°【考点】JA：平行线的性质．【分析】根据平行线的性质得到∠D=∠1=34°，由垂直的定义得到∠DEC=90°，根据三角形的内角和即可得到结论．【解答】解：∵AB∥CD，∴∠D=∠1=34°，∵DE⊥CE，∴∠DEC=90°，∴∠DCE=180°﹣90°﹣34°=56°．故选B．【点评】本题考查了平行线的性质，三角形的内角和，熟记平行线的性质定理是解题的关键．13．如图，直线AB∥CD，∠C=44°，∠E为直角，则∠1等于（）A．132°B．134°C．136°D．138°【考点】JA：平行线的性质．【分析】过E作EF∥AB，求出AB∥CD∥EF，根据平行线的性质得出∠C=∠FEC，∠BAE=∠FEA，求出∠BAE，即可求出答案．【解答】解：过E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠C=∠FEC，∠BAE=∠FEA，∵∠C=44°，∠AEC为直角，∴∠FEC=44°，∠BAE=∠AEF=90°﹣44°=46°，∴∠1=180°﹣∠BAE=180°﹣46°=134°，故选B．【点评】本题考查了平行线的性质的应用，能正确作出辅助线是解此题的关键．14．如图a是长方形纸带，∠DEF=20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（）A．110°B．120°C．140°D．150°【考点】PB：翻折变换（折叠问题）．【专题】16 ：压轴题．【分析】由题意知∠DEF=∠EFB=20°图b∠GFC=140°，图c中的∠CFE=∠GFC﹣∠EFG．【解答】解：∵AD∥BC，∴∠DEF=∠EFB=20°，在图b中∠GFC=180°﹣2∠EFG=140°，在图c中∠CFE=∠GFC﹣∠EFG=120°，故选B．【点评】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．二、填空题15．把命题“同角的余角相等”改写成“如果…那么…”的形式如果两个角是同一个角的余角，那么这两个角相等．【考点】O1：命题与定理．【分析】命题有题设和结论两部分组成，通常写成“如果…那么…”的形式．“如果”后面接题设，“那么”后面接结论．【解答】解：根据命题的特点，可以改写为：“如果两个角是同一个角的余角，那么这两个角相等”，故答案为：如果两个角是同一个角的余角，那么这两个角相等．【点评】本题考查命题的定义，根据命题的定义，命题有题设和结论两部分组成．。
青岛版七年级数学第二学期期中考试试题(含答案)
第二学期期中质量检测七年级数学试题（时间：120分钟 分数：120分）注意事项：1、本试卷分为第Ⅰ卷（选择题和填空题），第Ⅱ卷（解答题）两部分。
2、请考生将第Ⅰ卷的答案填写在第Ⅱ卷相应的横线上。
3、考试结束，只交第Ⅱ卷。
第I 卷一、选择题（本题共10小题，每小题3分，共30分）下面各题给出的四个选项中， 只有一项是正确的，请将正确选项的代号填写在第Ⅱ卷相应的横线上.1、下列四个图形中，能用∠1，∠AOB ，∠O 三种方法表示同一个角的（ ）A B C D2、在方程组⎩⎨⎧+==-1z 3y 1y x 2，⎩⎨⎧=-=1x y 32x ，⎩⎨⎧=-=+5y x 30y x ，⎩⎨⎧=+=3y 2x 1xy ，⎪⎩⎪⎨⎧=+=+1y x 1y 1x 1中，是二元一次方程组的有（）个。
A. 2B. 3C. 4D. 53、下列运算正确的是（）A. 623x 15x 5x 3=⋅B. ()32x y 8x y 2y 4-=-⋅B. ()532x 12x 4x 3-=⋅- D. ()()523a 54a 3a 2-=-⋅- 4、如图，∠1和∠2是内错角的是（ ）A B C D5、一个角的度数比它的余角的度数大20°，则这个角的度数为（ ）A. 20°B. 35°C. 45°D. 55°6、如图，∠AOB=120°，OC 是∠AOB 内部任意一条射线，OD 、OE 分别是∠AOC 、∠BOC 的角平分线，下列叙述正确的是（ ）A. ∠DOE 的度数不能确定B.∠AOD=21∠EOC C.∠AOD+∠BOE=60° D.∠BOE=2∠COD7、若将一副三角板按如图所示的方式放置，∠C 为45°角，∠D 为30°角，则下列结论不正确的是（）A. ∠1=∠3B. 如果∠2=30°，则有AC ∥DEC. 如果∠2=30°，则有BC ∥ADD. 如果∠2=30°，必有∠4=∠C8、计算()2019201852.0⨯-的结果是（）A. -1B. -5C. 1D.59、如图，已知直线a ∥b ，则∠1、∠2、∠3的关系是（ ）A. ∠1+∠2+∠3=360°B. ∠1+ ∠2-∠3=180°C.∠1-∠2+∠3=180°D. ∠1+ ∠2+∠3=180°7题图10、《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相等），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各重多少两？设每枚黄金重x 两，每枚白银重y 两，根据题意得（ ） A. ()()⎩⎨⎧=+-+=13y x 8x y 10y 9x 11 B. ⎩⎨⎧=++=+y 1113x 9y x 8x y 10 C. ()()⎩⎨⎧=+-+=13x y 10y x 8y 11x 9 D. ()()⎩⎨⎧=+-+=13y x 8x y 10y 11x 9 二、填空题（本题共8小题，每小题4分，共32分）请将答案填在第Ⅱ卷相应的横线上。
青岛版七年级下册数学期中考试题(附答案)
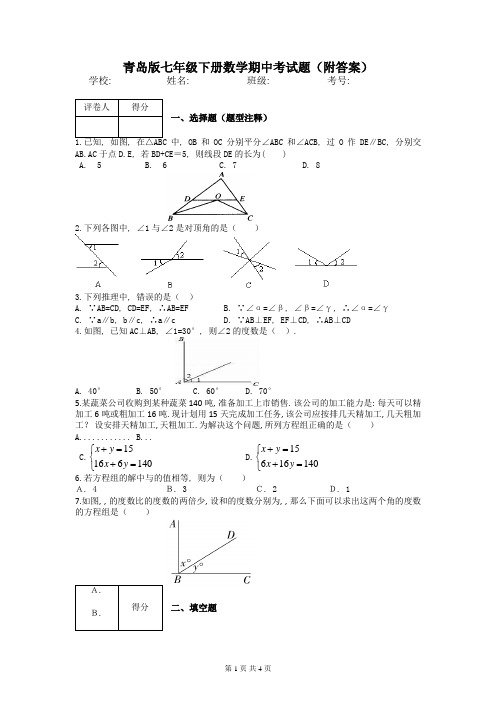
青岛版七年级下册数学期中考试题（附答案）学校:___________姓名: ___________班级: ___________考号: ___________评卷人得分一、选择题（题型注释）1.已知, 如图, 在△ABC中, OB和OC分别平分∠ABC和∠ACB, 过O作DE∥BC, 分别交AB.AC于点D.E, 若BD+CE＝5, 则线段DE的长为( )A. 5B. 6C. 7D. 82.下列各图中, ∠1与∠2是对顶角的是（）3.下列推理中, 错误的是（）A. ∵AB=CD, CD=EF, ∴AB=EFB. ∵∠α=∠β, ∠β=∠γ, ∴∠α=∠γC. ∵a∥b, b∥c, ∴a∥cD. ∵AB⊥EF, EF⊥CD, ∴AB⊥CD4.如图, 已知AC⊥AB, ∠1=30°, 则∠2的度数是（）.A. 40°B. 50°C. 60°D. 70°5.某蔬菜公司收购到某种蔬菜140吨, 准备加工上市销售. 该公司的加工能力是: 每天可以精加工6吨或粗加工16吨. 现计划用15天完成加工任务, 该公司应按排几天精加工, 几天粗加工？设安排天精加工, 天粗加工. 为解决这个问题, 所列方程组正确的是（）A............ B...C.15166140x yx y+=⎧⎨+=⎩D.15616140x yx y+=⎧⎨+=⎩6.若方程组的解中与的值相等, 则为（）Ａ. 4 Ｂ. 3 Ｃ. 2 Ｄ. 17.如图, , 的度数比的度数的两倍少, 设和的度数分别为, , 那么下面可以求出这两个角的度数的方程组是（）Ａ.Ｂ.得分二、填空题, 这个角等于______度.9.已知在△ABC 中, AC=3, BC=4, AB=5, 点P 是AB 上 （不与A.B 重合）, 过P 作PE ⊥AC, PF ⊥BC, 垂足分别是E 、F, 连结EF, M 为EF 的中点, 则CM 的最小值为 .10.已知是二元一次方程mx+y=3的解, 则m 的值是__.11.方程+=5是二元一次方程, 则m=____, n=_____.12.某铁路桥长1750m, 现有一列火车从桥上通过, 测得该火车从开始上桥到完全过桥共用了80s, 整列火车完全在桥上的时间共60s ；设火车的速度为xm/s, 火车的长度为ym, 根据题意三、解答题 15.如图, 已知AB ∥CD, BE 平分∠ABC, DE 平分∠ADC, ∠BAD ＝80°, 试求：（1）∠EDC 的度数；（2）若∠BCD ＝n °, 试求∠BED 的度数。
2022—2023学年山东省青岛市市南区七年级下学期期中数学试卷
2022—2023学年山东省青岛市市南区七年级下学期期中数学试卷一、单选题1. 下列运算正确的是（）A．B．C．D．2. 把用科学记数法表示为（）A．B．C．D．3. 下列说法正确的是（）A．相等的角是对顶角B．在同一平面内，平行于同一直线的两条直线互相平行C．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离D．两条直线被第三条直线所截，同位角相等4. 如图，在下列给出的条件中，不能判定AC∥DE的是（）A．∠1=∠A B．∠A=∠3C．∠3=∠4D．∠2+∠4=180° 5. 若一个三角形三个内角度数的比为，那么这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．等边三角形6. 若（﹣2 x+ a）（x﹣1）的结果中不含x的一次项，则a的值为（）A．1B．﹣1C．2D．﹣27. 从边长为的正方形内去掉-一个边长为b的小正方形(如图1)，然后将剩余部分剪拼成一个矩形（如图2），上述操作所能验证的等式是（）A．B．C．D．8. 星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼，她连续、匀速走了60min后回家，图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s （km）与行走时间t（min）之间的函数关系，则下列图形中可以大致描述蕊蕊妈妈行走的路线是（）A．B．C．D．二、填空题9. 已知，，那么的值是 _____ ．10. 若是一个完全平方式，则的值为 _______ ．11. 一个角的补角是它的余角的倍，则这个角余角的度数是 ________ ．12. 如图，是的中线，是边上的中点，连接，若的面积为，则的面积为 ______ ．13. 如图，直线，点分别在直线和直线上，点在两条平行线之间，和的角平分线交于点，已知，则的度数为 _________ ．14. 如图，某品牌自行车每节链条的长度为，交叉重叠部分的圆的直径为．（1）观察图形，填写如表；链条节数/…（节）链条长度/ ________ …（）（2）如果一辆自行车的链条（安装以后）共由节链条组成，那么链条的总长度是 __________ ．15. 如图，点是线段上的一点，以，为边向两边作正方形，设，两正方形的面积和，则图中阴影部分面积是 _______ ．16. A骑摩托车从甲地去乙地，开汽车从乙地去甲地，同时出发，匀速行驶，各自到达终点后停止，甲、乙两地间的距离为与甲行驶的时间为之间的关系如图所示．（1）甲、乙两地之间的路程为 ________ 千米；（2）甲出发 ____________________ 小时后甲、乙两地相距千米．三、解答题17. 作图题．用圆规，直尺作图，不写作法，但要保留作图痕迹．已知：点为线段外一点，求作直线，使．18. 计算：(1) ；(2) ；(3)用乘法公式计算：(4) ；(5) ；19. 先化简，再求值：，其中，．20. 已知：如图，△ABC中，AC⊥BC，若D、E在AB边上，点F在AC边上，DG⊥BC于点G，∠1＝∠2，求证：EF CD．将下列推理过程补充完整：证明：∵DG⊥BC，AC⊥BC，（已知）∴∠DGC＝∠ABC＝90°（）∴DG AC，（）∴∠2＝，（）∵∠1＝∠2∴∠1＝，（）∴EF CD（）21. 某经销商销售了一种水果，进价是元/千克，根据以往销售经验，每天的售价与销售量之间有如下关系：…价（元）每天销量（千克）……(1)从表格可以看出售价每下调元销售量就增加千克，每上涨元销售量就减少千克，直接写出每天销量（千克）与每千克售价（元）的函数关系式．(2)求出当售价从元/千克调整到元/千克时，求这一天的销售量是多少千克？利润多少元？22. 如图，已知．(1)问与平行吗？如果平行请说明理由．(2)若于E，平分，求的度数．23. 某数学兴趣小组在一组课题学习活动中以“钟表上时针与分针的重合时刻”为课题展开了研究．【问题提出】如图①是某钟表，图②是该钟表的简化平面示意图，设时针、分针所在直线在同一平面内，直线l表示钟表的数轴线．在～之间求时针与分针的重合时刻．【问题探究】设钟表中心为O，表示“12”的点为A，表示“1”的点为B，表示“3”的点为C，表示“6”的点为D，下面是小颖同学的研究过程：解题思路：建立函数关系的方法求解．(1)设自变量x和因变量y：设后再经过（），时针、分针分别与所成夹角度数为，，直接写出，关于x的关系式．(2)求解：【问题解决】请按照小颖的思路解答此问题；【问题拓展】求该钟表在1：15～1：30之间，时针与分针所在直线互相垂直的时刻．24. 已知直线，点A在直线MN上，点B、C为平面内两点，于点C．（1）如图1，当点B在直线MN上，点C在直线MN上方时，则和之间的数量关系是________；（2）如图2，当点C在直线MN上且在点A左侧，点B在直线MN与PQ之间时，过点B作交直线PQ于点D，为探究与的数量关系，小明过点B作，请根据他的思路，写出与的关系，并说明理由；（3）请从下面A，B两题中任选一题作答．A．如图3，在（2）的条件下，作∠ABD的平分线交直线MN于点E，当时直接写出的度数；B．如图4，当点C在直线MN上且在点A左侧，点B在直线PQ下方时，过点B作交直线PQ于点D，作∠ABD的平分线交直线MN于点E，当时，直接写出的度数．。
山东省青岛市2022-2023学年下学期期中数学学科素养七年级试题
2022—2023学年度第二学期期中学科素养测评七年级数学试题(考试时间:120分钟;满分:120分)说明：1.本试题分第Ⅰ卷和第Ⅱ卷两部分，共25题.第Ⅰ卷为选择题，共9小题，29分；第Ⅱ卷为填空题、作图题、解答题，共16小题，91分.2.所有题目均在答题卡上作答，在试题上作答无效.第Ⅰ卷(共29分)一、单项选择题（本题共7小题，每小题3分，共21分．在每个题给出的四个选项中，只有一项是符合题目要求的）1.下列运算正确的是（）A ．2⋅3=6B ．3−2=1C ．−223=−86D ．6÷2=32.科学家发现某种病毒近似于球体，它的半径约为0.00000000495米，用科学记数法表示为（）A ．4.95×10﹣9B ．0.495×10﹣8C ．4.95×10﹣8D ．495×10﹣93.如图，工人砌墙时，先在两个墙脚的位置分别插一根木桩，再拉一条直的参照线，就能使砌的砖在一条直线上．这样做应用的数学知识是（）A ．两点之间，线段最短B ．垂线段最短C ．两点确定一条直线D ．三角形两边之和大于第三边4.两个长方形的位置如图所示，若1124∠=︒，则∠2＝（）．A ．34°B ．56°C ．79°D ．146°5.如图所示，AD 、CE 、BF 是△ABC 的三条高，AB=5，BC=4，AD=3，则CE=A ．B ．3C ．4D ．56.如图，在△ABC 和△DEF 中，点A ，E ，B ，D 在同一直线上，AC ∥DF ，AC ＝DF ，只添加一个条件，能判定△ABC ≌△DEF 的是（）A ．BC ＝DEB ．∠ABC ＝∠DC ．∠A ＝∠DEFD ．AE ＝DB12第4题第6题第5题5127.如图，“漏壶”是一种古代计时器，在它内部盛一定量的水，不考虑水量变化对压力的影响，水从壶底小孔均匀漏出，壶内壁有刻度．人们根据壶中水面的位置计算时间，用t 表示漏水时间，h 表示壶底到水面的高度，下列图象适合表示h 与t 的对应关系的是（）A.B.C.D.二、多项选择题（本题共2小题，每小题4分，共8分．每小题的四个选项中，有多项符合题目要求，全部选对得4分，部分选对得2，有错选得0分）8.如图，在△ABC 中，BF ，CF 分别平分∠ABC 和∠ACB ，过点F 作DE//BC 交AB 于点D ，交AC 于点E ，下列结论正确的是( )A.∠DFB=∠DBFB.△EFC 为等腰三角形C.△ADE 的周长等于AB 与AC 的和D.∠BFC=90°+∠A 9.如图，AC=BC ，∠ACB=90°，AE 平分∠BAC ，BF ⊥AE ，交AC 的延长线于F ，且垂足为E.下列结论正确的是( )A.AD=BFB.BF=AFC.AC+CD=ABD.AD=2BE第Ⅱ卷（共91分）三、填空题（本大题共7小题，每小题3分，共21分）10.若4100=x，25100=y，则=-+12210y x 11.如果关于x 的多项式x 2−12x ＋m 是一个完全平方式，那么m ＝_______．12.如果一个三角形的两个内角α与β满足2α＋β＝90°，那么我们称这样的三角形为“准互余三角形”．若△ABC 是“准互余三角形”，∠C ＞90°，∠A ＝20°，则∠B ＝_______．13.如果(2m +n +3)(2m +n −3)＝40，则2m +n 的值为．14.如图，ABCD 为一长方形纸带，AB ∥CD ，将ABCD 沿EF 折叠，A ，D 两点分别与A ′，D ′对应，若∠CFE ＝2∠CFD ′，则∠AEF 的度数是2115.某超市进了一批草莓，出售时销售量x与销售总价y的关系如下表：销售量x（kg）12345…销售总价y（元）12＋0.524＋136＋1.548＋2.060＋2.5…请根据上表中的数据写出销售总价y（元）与销售量x（kg）之间的关系式：______________ 16.甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为s（单位：千米），甲行驶的时间为t（单位：小时），s与t 之间的关系如图所示，有下列结论：①出发1小时时，甲、乙在途中相遇；②出发1.5小时时，乙比甲多行驶了60千米；③出发3小时时，甲、乙同时到达终点；④甲的速度是乙速度的一半．其中，正确的有____________________（填序号）四、作图题（本题满分4分）用圆规、直尺作图，不写作法，但要保留作图痕迹．17.如图△ABC，请你利用尺规作出直线MN，使MN//AB，且MN经过点C．五、解答题（本大题共7个小题，共66分）18.计算（每小题4分，共16分）（1）−12+(2019−π)0−（−1）2019+（12）−2（2）(−22p2∙3xy÷(−62y)（3）20212−2019×2023（用乘法公式计算）（4）（2a−b）(a+2b)−(a+b)219.先化简，再求值（本题6分）(32y−xy2+12xy)÷(−12xy)其中3,2=-=y x20（本题4分）如图，EF//CD，∠1=∠2.求证：∠CGD+∠BCA=180°“五一黄金周”的某一天，小明全家上午8时自驾小汽车从家里出发，到距离180千米的某著名旅游景点游玩．该小汽车离家的距离s （千米）与时间t （时）的关系可以用图中的曲线表示．根据图象提供的有关信息，解答下列问题：（1）小明全家在旅游景点游玩了多少小时？（2）小明全家到家是什么时间？（3）若出发时汽车油箱中存油15升，汽车每行驶1千米耗油升．则需在几点前至少加一次油？加油总量至少为多少升？（加油所用时间忽略不计）22.（本题8分）如图，在△ABC 中，∠ACB ＝90°，AC ＝BC ，AD ⊥CD 于点D ，BE ⊥CD 于点E.（1）求证：△ACD ≌△CBE（2）若BE ＝6，DE ＝4，求△ACE的面积．91大泽山合作社向外地运送一批葡萄，由铁路运输每千克需运费6.0元；由公路运输，每千克需.0元，运完这批葡萄还需其他费用800元.运费25（1）该合作社运输的这批葡萄为xkg，选择铁路运输时，所需费用为1y元，选择公路运输时，所需费用为2y元.请分别写出1y，2y与x之间的关系式.（2）若合作社只支出运费1500元，则选用哪种运输方式运送更合算？24.（本题10分）已知AB ∥CD ，在AB ，CD 内有一条折线EPF ．（1）如图1，小明发现∠P=∠AEP+∠CFP ，他是这样思考的：过点P 作PQ //CD,...请你按照他的思路完成证明过程.（2）如图2，已知∠BEP 的平分线与∠DFP 的平分线相交于点Q ．①若∠P ＝60°，则∠Q=°②试探索∠P 与∠Q 之间的数量关系，并说理理由；（3）如图3，若∠BEQ ＝∠BEP ，∠DFQ ＝∠DFP ，请直接写出∠P 与∠Q 之间的数量关系：____________________A B CQ F EP A BCDFE图1图2QPDA BC DF E图3QP313125．（本题满分10分）如图，在长方形ABCD 中，AB=14厘米，BC=6厘米，动点P 从点A 开始以2厘米/秒速度沿AB 方向运动，向点B 运动；同时，点Q 从点C 以1厘米/秒速度沿CB 边向点B 运动；点Q 到达B 时，P ，Q 同时停止运动.设运动时间为t 秒(0<t<6)，解答下列问题：（1）当t 为何值时，BP=CQ?（2）连接BD ，当t 为何值时，△D BQ 的面积等于长方形ABCD 面积的?（3）设四边形DP QC 的面积为S cm 2，求S 与t之间的关系式；31。
青岛版七年级下册数学期中测试卷
期中测试卷一、选择题1.如图，已知AB∥CD∥EF，BC∥AD，AC平分∠BAD，那么图中与∠AGE相等的角有( )A.5个B.4个C.3个D.2个答案：A2.同一平面内的四条直线若满足a⊥b，b⊥c，c⊥d，则下列式子成立的是( )A.a∥dB.b⊥dC.a⊥dD.b∥c答案：C3.下列各式计算正确的是( )A.(a2)4=(a4)2B.2x3·5x2=10x6C.(-c)8÷(-c)6=-c2D.(ab3)2=ab6答案：A4.如图，已知AB∥CD，∠B=120°，∠D=150°，则∠P等于( )A.50°B.60°C.80°D.90°答案：D5.已知∠A=123°，则∠A的补角的余角为( )A.57°B.52°C.90°D.33°答案：D6.如图，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC 的度数分别为x，y，那么下面可以求出这两个角的度数的方程组是( )A.9015x yx yB.90215x yx yC.90152x yx yD.290215 xx y答案：B7.如图，∠DOB为直角，∠COA也是直角，则( )A.∠1=∠2B.∠3=12（∠1+∠2）C.∠1=∠3D.∠2=∠3答案：C8.已知x=2，y=1是方程kx-y=3的解，那么k的值为( )A.2B.-2C.1D.-1答案：A9.计算：(58)2 016×(-1.6) 2 017÷(-1) 2 015=( )A. 58B.-58C.85D.-85答案：C10.给出下列说法：①两条直线被第三条直线所截，同位角相等；②平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；③相等的两个角是对顶角；④从直线外一点到这条直线的垂线段，叫做这点到直线的距离.其中正确的有( )A.0个B.1个C.2个D.3个答案：B11.如图，若AB∥CD，CD∥EF，那么∠BCE=( )A.∠1+∠2B.∠2-∠1C.180°-∠1+∠2D.180°-∠2+∠1答案：D12.甲、乙两人按3∶2的比例投资开办了一家公司，约定除去各项支出外，所得利润按投资比例分成.若第一年甲分得的利润比乙分得的利润的2倍少3千元，求甲、乙二人各分得利润多少千元.若设甲分得x千元，乙分得y千元，由题意得( )A.2123x yy xB.2332x yx yC.2332x yy xD.23 23x yx y答案：C二、填空题13.计算：37°28′+44°49′= .答案：82°17′14.如图，AC⊥BC，AC=3，BC=4，AB=5，则点B到AC的距离为 .答案：415.如图，AB∥CD，直线EF分别交AB,CD于E,F，EG平分∠BEF，若∠1=72°，则∠2= .答案：54°16.方程2x n-3-y 3m+n-2+3=0是二元一次方程，则m= .答案：-1317.已知2,1x y是方程组31,5ax y x by的解，则a-b= .答案：-118.如图，△ABC 中，∠C=90°,∠BAD=13∠BAE ，∠ABD=13ABF ，则∠D= .答案：90°三、解答题19.解下列方程组. （1）3,3814;x yx y ①②（2）3416,5633.x y x y①②答案：解：（1）3?3814xyx y ，①，②由①得x=y+3，③把③代入②，得3(y+3)-8y=14，解得y=-1，把y=-1代入③，得x=2，所以21. xy，（2）3416 5633x yx y，①，②①×3，得9x+12y=48，③②×2，得10x-12y=66，④③+④，得19x=114，解得x=6，把x=6代入①，得y=-12，所以61.2 xy，20.若(x2+nx+3)(x2-3x+m)的展开式中不含x2和x3项，求m，n的值.答案：解：原式=x4-3x3+mx2+nx3-3nx2+mnx+3x2-9x+3m=x4+(n-3)x3+(m-3n+3)x2+(mn-9)x+3m.因为展开式中不含x2和x3项，所以n-3=0，m-3n+3=0，解得m=6，n=3.21.如图，根据下列条件，可以判定哪两条直线平行？并说明判定的根据是什么？①∠2=∠B；②∠1=∠D；③∠3+∠F=180°.答案：解：由①可判定AB∥DE，同位角相等，两直线平行.②可判定AC∥DF，内错角相等，两直线平行.③可判定AC∥DF，同旁内角互补，两直线平行.22.如图，△ABC中，AD⊥BC，AE平分∠BAC，∠B=40°，∠C=60°，求∠DAE的度数.答案：解：因为∠B=40°，∠C=60°，所以∠BAC=180°-∠B-∠C=180°-40°-60°=80°. 因为AE 平分∠BAC ，所以∠BAE=12∠BAC=12×80°=40°.因为AD ⊥BC ，所以∠BAD=90°-∠B=90°-40°=50°，所以∠DAE=∠BAD-∠BAE=50°-40°=10°. 23.已知方程组352,53x y m x ym 的解x,y 互为相反数，求m 的值.答案：解：由于方程组35253x y m x ym，的解x ，y 互为相反数，所以y=-x ，于是得到35253x x m x x m ，，整理得222x m xm ，，解得m=-1.24.某一天，蔬菜经营户老李用了145元从蔬菜批发市场批发一些黄瓜和茄子，到菜市场去卖，黄瓜和茄子当天的批发价与零售价如下表所示：品名黄瓜茄子批发价（元/kg ） 3 4 零售价（元/kg ）47当天他卖完这些黄瓜和茄子共赚了90元，这天他批发了黄瓜和茄子分别是多少千克？答案：解：设批发了黄瓜是x kg ，茄子是y kg ，由题意得34145437490 x yx y，，解得1525. xy，答：这天他批发了黄瓜15 kg，茄子25 kg.25.如图，已知直线a∥b，且c和a，b分别交于A，B两点，点P在AB上. （1）试找出∠1，∠2，∠3之间的关系并说明理由；（2）如果点P在A，B两点之间运动，问∠1,∠2，∠3之间的关系是否发生变化？（3）如果点P在A，B两点外侧运动时，试探究∠1，∠2，∠3之间的关系.（点P和点A，B不重合）答案：解：（1）∠3=∠1+∠2，理由如下：如图，过点P作d∥a，则∠4=∠1.因为a∥b，所以d∥b，所以∠5=∠2，所以∠3=∠4+∠5=∠1+∠2.（2）不发生变化.（3）当点P在线段AB的延长线上时，∠1=∠3+∠2;当点P在线段BA的延长线上时，∠２=∠３+∠１.。
青岛版七年级数学下册期中试卷
期中数学试卷一、选择题1．下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）A．B．C．D．2．已知，∠α与∠β互补，且∠α﹣∠β=30°，则∠α与∠β的大小关系依次为（）A．110°，70°B．105°，75°C．100°，70°D．110°，80°3．下列计算正确的是（）A．a2+a2=2a4B．（﹣a2b）3=﹣a6b3C．a2•a3=a6D．a8÷a2=a44．若A，B，C是直线l上的三点，P是直线l外一点，且PA=5cm，PB=4cm，PC=3cm，则点P到直线L的距离（）A．等于3cm B．大于3cm而小于4cmC．不大于3cm D．小于3cm5．要使（y2﹣ky+2y）（﹣y）的展开式中不含y2项，则k的值为（）A．﹣2B．0C．2D．36．如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=32°，则∠2的度数为（）A．25°B．28°C．30°D．32°7．用加减法解方程组时，要使方程中同一个未知数的系数相等或互为相反数，必须适当变形，以下四种变形正确的是（）（1）（2）（3）（4）A．（1）（2）B．（2）（3）C．（3）（4）D．（4）（1）8．如图，直线AB、CD交于点O，OT⊥AB于O，CE∥AB交CD于点C，若∠ECO=30°，则∠DOT等于（）A．30°B．45°C．60°D．120°9．古代有这样一个寓言故事：驴子和骡子一同走，它们驮着不同袋数的货物，每袋货物都是一样重的．驴子抱怨负担太重，骡子说：“你抱怨干吗如果你给我一袋，那我所负担的就是你的两倍；如果我给你一袋，我们才恰好驮的一样多！”那么驴子原来所托货物的袋数是（）A．5B．6C．7D．810．若a=240，b=332，c=424，则下列关系正确的是（）A．a＞b＞c B．b＞c＞a C．c＞a＞b D．c＞b＞a二、填空题11．若（m﹣3）x+2y|m﹣2|+8=0是关于x，y的二元一次方程，m=．12．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.000000076克，用科学记数法表示是克．13．若x n﹣1•x n+5=x10，则n﹣2=．14．如图，在三角形ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B=35°，∠C=65°，则∠EFD=．15．若实数m，m满足|m﹣2|+（n﹣2015）2=0，则m﹣1+n0=．16．已知关于x，y的二元一次方程组的解互为相反数，则k的值是．17．若（2x+5）（4x﹣10）=8x2+px+q，则p=，q=．18．五一前夕，某超市促销，由顾客抽奖决定折扣，某顾客购买甲乙两种商品，分别抽到七折（按售价70%）和九折销售，共付款386元，这两种商品原销售之和为500元，则甲乙两种商品原销售价分别为、．三、解答题19．化简求值：（1）a3•a3+（﹣2a3）2+（﹣a2）3，其中a=﹣1．（2）4x（x﹣1）﹣（2x+1）（2x﹣1），其中x=﹣5．20．解方程组（1）（2）．21．（1）一个角的余角与这个角的补角的和比平角的多1°，求这个角的度数．（2）已知5m=2，5n=3，求53m﹣2n．22．如图，直线EF，CD相交于点O，OA⊥OB，且OC平分∠AOF．（1）若∠AOE=40°，求∠BOD的度数；（2）若∠AOE=α，求∠BOD的度数．（用含α的代数式表示）23．某开发区去年出口创汇额为25亿美元，今年达到30.55亿美元，已知今年上半年出口创汇额比去年同期增长18%，下半年比去年同期增长25%，求去年上半年和下半年的出口创汇额各是多少亿美元？24．已知如图，在三角形ABC中，AC⊥AB，DG⊥BC，EF⊥AB，∠1=∠2，试判断CD与AB的位置关系？并说明理由．25．小亮在做“化简（2x+k）（3x+2）﹣6x（x+3）+5x+16并求x=2时的值”一题时，错将x=2看成x=﹣2，但结果却和正确答案一样，由此，你能推算出k值吗？26．如图，长青化工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨1 000元的原料运回工厂，制成每吨8 000元的产品运到B地．已知公路运价为1.5元/（t•km），铁路运价为1.2元/（t•km），且这两次运输共支出公路运输费15000元，铁路运输费97200元．求：（1）该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？（2）这批产品的销售款比原料费与运输费的和多多少元？参考答案一、选择题1．【解答】解：A、图中的∠AOB不能用∠O表示，故本选项错误；B、图中的∠1和∠AOB不是表示同一个角，故本选项错误；C、图中的∠1和∠AOB不是表示同一个角，故本选项错误；D、图中∠1、∠AOB、∠O表示同一个角，故本选项正确；故选：D．2．【解答】解：∵∠α与∠β互为补角，∴∠α+∠β=180°，又∵∠α﹣∠β=30°，∴，解得：，故选：B．3．【解答】解：A、a2+a2=2a2B，故A错误；B、（﹣a2b）3=﹣a6b3，故B正确；C、a2•a3=a5，故C错误；D、a8÷a2=a6，故D错误；故选：B．4．【解答】解：根据点到直线的距离的定义，点P到直线L的距离即为点P到直线L的垂线段的长度，垂线段的长度不能超过PC的长．故选C．5．【解答】解：∵（y2﹣ky+2y）（﹣y）的展开式中不含y2项，∴﹣y3+ky2﹣2y2中不含y2项，∴k﹣2=0，解得：k=2．故选：C．6．【解答】解：过A作AE∥NM，∵NM∥GH，∴AE∥GH，∴∠3=∠1=32°，∵∠BAC=60°，∴∠4=60°﹣32°=28°，∵NM∥AE，∴∠2=∠4=28°，故选：B．7．【解答】解：把y的系数变为相等时，①×3，②×2得，，把x的系数变为相等时，①×2，②×3得，．故选：C．8．【解答】解：∵CE∥AB，∴∠DOB=∠ECO=30°，∵OT⊥AB，∴∠BOT=90°，∴∠DOT=∠BOT﹣∠DOB=90°﹣30°=60°．故选：C．9．【解答】解：设驴子原来驮x袋，根据题意，得到方程：2（x﹣1）﹣1﹣1=x+1，解得：x=5，答：驴子原来所托货物的袋数是5．故选：A．10．【解答】解：∵a=240=328，b=332=818，c=424=648，∴b＞c＞a，故选：B．二、填空题11．【解答】解：根据题意，得|m﹣2|=1且m﹣3≠0，解得m=1．故答案为：1．12．【解答】解：0.000000076=7.6×10﹣8．故答案为：7.6×10﹣8．13．【解答】解：由x n﹣1•x n+5=x10，得x2n+4=x10，即2n+4=10，解得n=3．n﹣2=3﹣2=，故答案为：．14．【解答】解：∵EF∥AC，∴∠EFB=∠C=65°，∵DF∥AB，∴∠DFC=∠B=35°，∴∠EFD=180°﹣65°﹣35°=80°，故答案为：80°．15．【解答】解：由m，m满足|m﹣2|+（n﹣2015）2=0，得m﹣2=0，n﹣2015=0．解得m=2，n=2015．m﹣1+n0=+1=，故答案为：．16．【解答】解：解方程组得：，因为关于x，y的二元一次方程组的解互为相反数，可得：2k+3﹣2﹣k=0，解得：k=﹣1．故答案为：﹣1．17．【解答】解：已知等式整理得：8x2﹣50=8x2+px+q，则p=0，q=﹣50，故答案为：0，﹣5018．【解答】解：设甲、乙两商品的原价分别是x元，y元，则，解得．故答案为：320元；180元三、解答题19．【解答】解：（1）原式=a6+4a6﹣a6=4a6，当a=﹣1时，原式=4；（2）原式=4x2﹣4x﹣4x2+1=﹣4x+1，当x=﹣5时，原式=20+1=21．20．【解答】解：（1），①+②×4得：23x=23，即x=1，把x=1代入①得：y=2，则方程组的解为；（2），①×3+②得：14x=﹣14，即x=﹣1，把x=﹣1代入①得：y=3，则方程组的解为．21．【解答】解：（1）设这个角为x，根据题意得：90°﹣x+180°﹣x=180°×+1°，解得：x=67°，则这个角的度数为67°；（2）∵5m=2，5n=3，∴原式=（5m）3÷（5n）2=．22．【解答】解：（1）∵∠AOE+∠AOF=180°（互为补角），∠AOE=40°，∴∠AOF=140°；又∵OC平分∠AOF，∴∠FOC=∠AOF=70°，∴∠EOD=∠FOC=70°（对顶角相等）；∵∠BOE=∠AOB﹣∠AOE=50°，∴∠BOD=∠EOD﹣∠BOE=20°；（2）∵∠AOE+∠AOF=180°（互为补角），∠AOE=α，∴∠AOF=180°﹣α；又∵OC平分∠AOF，∴∠FOC=∠AOF=90°﹣α，∴∠EOD=∠FOC=90°﹣α（对顶角相等）；∵∠BOE=∠AOB﹣∠AOE=90°﹣α，∴∠BOD=∠EOD﹣∠BOE=α．23．【解答】解：设去年上半年出口创汇额为x亿美元，去年下半年的出口创汇额为y亿美元，则今年上半年出口创汇额为（1+18%）x=1.18x（亿美元），今年下半年的出口创汇额为（1+25%）y=1.25（亿美元），根据题意可列方程组，解得，答：去年上半年出口创汇额为10亿美元，去年下半年的出口创汇额为15亿美元．24．【解答】解：垂直．理由：∵AC⊥BC，DG⊥BC，∴AC∥DG，∴∠2=∠3，∵∠1=∠2，∴∠1=∠3，∴EF∥CD，∵EF⊥AB，∴CD⊥AB．25．【解答】解：原式=6x2+4x+3kx+2k﹣6x2﹣18x+5x+16=（3k﹣9）x+2k+16，由结果与x取值无关，得到3k﹣9=0，解得：k=3．26．【解答】解：（1）设工厂从A地购买了x吨原料，制成运往B地的产品y吨，根据题意得：，解得：．答：工厂从A地购买了400吨原料，制成运往B地的产品300吨．（2）300×8000﹣400×1000﹣15000﹣97200=1887800（元）．答：这批产品的销售款比原料费与运输费的和多1887800元．。
山东省青岛第三十九中学2022-2023学年七年级下学期数学期中试题(含部分答案)
2022-2023学年度第二学期期中质量检测七年级数学试题（满分：120分 时间：120分钟）说明：1.本试题分第Ⅰ卷和第Ⅱ卷两部分，共24题，第Ⅰ卷为选择题，共8小题，24.分；第Ⅱ卷为填空题、作图题、解答题，共16小题，96分.2.所有题目均在答题卡上作答，在试题上作答无效.第Ⅰ卷（共24分）一、选择题（本大题共8小题，每小题3分，共24分）1.计算所得结果是（ ）A. B.2023C.D.2.生物具有遗传多样性，遗传信息大多储存在DNA 分子上，一个DNA 分子直径约为0.0000002cm ，这个数量用科学记数法可表示为（ ）A. B. C. D.3.下表是研究弹簧长度与所挂物体质量关系的实验表格：所挂物体重量x （kg ）12345弹簧长度y （cm ）1012141618则弹簧不挂物体时的长度为（ ）.A.4cmB.6cmC.8cmD.10cm4.下列图形中，线段AD 的长表示点A 到直线BC 距离的是（）A. B.C. D.5.如图，为估计池塘岸边A 、B 两点的距离，小林在池塘的一侧选取一点O ，测得米，米，则A 、B 间的距离不可能是（）112023-⎛⎫ ⎪⎝⎭2023-12023-1202360.210cm-⨯6210cm-⨯70.210cm-⨯7210cm-⨯10OA =7OB =A.4米B.9米C.15米D.18米6.如图，点E 在.AD 延长线上，下列条件中不能判定的是（）A. B.C. D.7.如图，将一块含30°的三角板叠放在直尺上。
若，则（）A.45°B.50°C.60°D.70°8.如图1，正方形ABCD 的边BC 上有一定点E ，连接AE ，动点P 从正方形的顶点A 出发，沿A →D →C 以1cm/s 的速度匀速运动到终点C 图2是点P 运动时，的面积y （）随时间x （s ）变化的全过程图象，则EC 的长度为（）图1图2A.2cmB.2.5cmC.3cmD.3.5cm第Ⅱ卷（共96分）二、填空题（本大题共8小题，每小题3分，共24分）9.计算；______.10.若，，则______.//BC AD 12∠=∠C CDE ∠=∠34∠=∠180C ADC ∠+∠=︒140∠=︒2∠=APE △2cm 53a a ÷=2212x y -=6x y +=x y -=11.如图所示的网格由边长相同的小正方形组成，点A 、B 、C 、D 、E 、F 、G 在小正方形的顶点上，则的重心是点______.12.青岛与济南两地相距350千米，若汽车以平均80千米/小时的速度从青岛开往济南，则汽车距济南的路程y （千米）与行驶的时间x （小时）之间的关系式为______.13.已知，，则的值是______.14.如图，在中，AD 是角平分线，AE 是高，若，，则______.15.如图，，BF 平分，DF 平分，，那的度数为______°16.我们知道下面的结论：若（，且），则，利用这个结论解决下列问题：设，，.现给出m ，n ，p 三者之间的三个关系式：①，②；③.其中正确的是______.（填编号）三、作图题（本题满分4分）17.已知：如图，直线AB 和点P.ABC △210a b -=5ab =224a b +ABC △50B ∠=︒70C ∠=︒DAE ∠=//AB CD ABE ∠CDE ∠35BFD ∠=︒BED ∠m n a a =0a >1a ≠m n =23m =26n =212p =2m p n +=23m n p +=-²1n mp -=求作：直线CD ，使，且CD 经过点P .四、解答题（本题共7道小题，满分68分）18.计算（本题满分20分，每小题4分）（1）；（2）；（3）（用乘法公式）；（4）；（5）.19.（本小题满分6分）先化简，再求值：，其中，.20.（本小题满分6分）如图，直线AB 、BC 、AC 两两相交，交点分别为点A 、B 、C ，点D 在线段AB 上，过点D 作交AC 于点E ，过点E 作交BC 于点F .若，求的度数.请将下面的解答过程补充完整.解：①______（②_________________）∴③______（④_________________）（⑤_________________）⑥______°21.（本小题满分6分）小明家距离学校8千米，今天早晨，小明骑车上学途中，自行车出现故障，恰好路边有便民服务点，几分钟后车修好了，他增加速度骑车到校.我们根据小明的这段经历画了一幅图象（如图），该图描绘了小明行的路程s 与他所用的时间t 之间的关系.//CD AB ()()25344a a a-⋅+-3211322ab a b ab ab ⎛⎫⎛⎫ ⎪-+⎪ ⎝⎭⎝÷⎭-99.9100.1⨯()()()423241x x x x -+-+()()22a b c a b c +--+()()()2123222x y x y x y y ⎛⎫⎡⎤---+÷⎪⎣⎦⎝⎭2x =3y =//DE BC //EF AB 40ABC ∠=︒DEF ∠//DE BCDEF ∴∠=//EF ABABC =∠DEF ABC ∴∠=∠40ABC =︒DEF ∴∠=请根据图象，解答下列问题：（1）小明行了______千米时，自行车出现故障；小明共用了______分钟到学校.（2）小明修车用了多长时间？（3）如果自行车未出现故障，小明一直用修车前的速度行驶，那么他比实际情况早到或晚到多少分钟？22.（本小题满分8分）如图，已知，.（1）请你判断DA 与CE 的位置关系，并说明理由；（2）若DA 平分，于E ，，则______°.23.（本小题满分10分）【知识回顾】我们在学习代数式求值时，遇到这样一类题：代数式的值与x 的取值无关，求a 的值.通常的解题思路是：把x 、y 看作字母，a 看作系数，合并同类项。
青岛版七年级数学下册期中测试题(汇编)
BACDO5题图1AB FD C E2七年级数学期中试题一、选择题：（每题3分，）1、下列说法中正确的是（ ）Ａ、有且只有一条直线与已知直线垂直.Ｂ、从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离. Ｃ、互相垂直的两条线段一定相交. Ｄ、直线L 外一点A 与直线L 上各点连接而成的所有线段中最短的长是3厘米，则A 到L 的距离是3厘米。
2、下面四个图形中，∠1与∠2是对顶角的图形有（ ）A 、1个B 、2个C 、3个D 、4个3．判断两角相等，错误的是（ ）A 、对顶角相等B 、两条直线被第三条直线所截，内错角相等C 、两直线平行，同位角相等D 、∵∠1=∠2，∠2=∠3，∴∠1=∠34．下列说法中，正确的是 （ ） A 、有公共端点的两条射线组成的图形叫做角； B 、两条射线组成的图形叫做角； C 、两条线段组成的图形叫做角；D 、一条射线从一个位置移到另一个位置所形成的图形叫做角。
5、如图：已知AB ∥CD ，∠B=1200，∠D=1500，则∠O 等于（ ）. （A ）500 （B ）600 （C ）800 （D ）9006．如图，若AB ∥CD ，CD ∥EF ，那么∠BCE ＝（ ） A ．∠1＋∠2 B ．∠2－∠1 C ．180°－∠1＋∠2 D ．180°－∠2＋∠17. 下列四个图形中，能同时用∠1，∠ABC ，∠B 三种方法表示同一个角的图形是（ ）8、若∠1=5005' ∠2=50.50 则∠1与∠2的大小关系是（ ） A 、∠1=∠2 B 、∠1＞∠2 C 、∠1＜∠2 D 、无法确定9、下列说法正确的是（ ）A 、垂直于同一直线的两条直线互相垂直．B 、平行于同一条直线的两条直线互相平行．C 、平面内两个角相等，则他们的两边分别平行．D 、两条直线被第三条直线所截，那么有两对同位角相等．10、已知AB ∥CD ∥EF ，BC ∥AD ，AC 平分∠BAD ，那么图中与∠AGE 相等的角有( )（A ）5个． （B ）4个． （C ）3个． （D ）2个．11已知OC 是∠AOB 内部一条射线，下列所给条件中，不能判定OC 为∠AOB 的角平分线的是（ ）A 、∠AOC+∠BOC=∠AOB B 、∠AOC= ∠AOBC 、 ∠AOB =2∠AOCD 、 ∠AOC=∠BOC12、如图，AB ⊥BC ，∠ABD 的度数比∠DBC 的度数的两倍少15°，设∠ABD 和∠DBC 的度数分别为x 、y ，那么下面可以求出这两个角的度数的方程组是（ ）A 、9015x y x y +=⎧⎨=-⎩B 、90215x y x y +=⎧⎨=-⎩C 、90152x y x y +=⎧⎨=-⎩D 、290215x x y =⎧⎨=-⎩二：填空。
2022-2023学年山东省青岛重点中学七年级(下)期中数学试卷(含解析)
2022-2023学年山东省青岛重点中学七年级（下）期中数学试卷一、选择题（本大题共8小题，共24.0分。
在每小题列出的选项中，选出符合题目的一项）1. 下列运算正确的是( )A. a5+a5=a10B. (a3)3=a9C. (ab4)4=ab8D. a6÷a3=a22. 一个三角形的两边长分别为3和5，第三边长为偶数，则第三边长可能为( )A. 4或6B. 2或4C. 4D. 63. 若(x+a)(x−2)=x2+bx−2，则a+b的值为( )A. −2B. −1C. 0D. 24. 五一假期，小明去娱乐小镇游乐园游玩，坐上了他向往已久的摩天轮(如图所示).摩天轮上，小明离地面的高度ℎ(米)和他坐上摩天轮后旋转的时间t(分钟)之间的部分函数关系如图所示，则下列说法错误的是( )A. 摩天轮旋转一周需要6分钟B. 小明出发后的第3分钟和第9分钟，离地面的高度相同C. 小明离地面的最大高度为42米D. 小明出发后经过6分钟，离地面的高度为3米5.一副直角三角板按如图所示的位置摆放，点E在AB上，BC//EF，则∠1的度数是( )A. 60°B. 65°C. 70°D. 75°6. 小明有足够多的如图所示的正方形卡片A，B和长方形卡片C，如果他要拼一个长为(a+2b)，宽为(a+b)的大长方形，共需要C类卡片( )A. 3张B. 4张C. 5张D. 6张7. 如图，已知长方形纸片ABCD，点E，F在AD边上，点G，H在BC边上，分别沿EG，FH折叠，使点D和点A都落在点M处，若α+β=119°，则∠EMF的度数为( )A. 57°B. 58°C. 59°D. 60°8.如图，两个正方形的泳池，面积分别是S1和S2，两个泳池的面积之和S1+S2=16，点B是线段CG上一点，设CG=6，在阴影部分铺上防滑瓷砖，则所需防滑瓷砖的面积为( )A. 5B. 4C. 8D. 10二、填空题（本大题共8小题，共24.0分）9. 一个角的余角的2倍比这个角的补角少24°，那么这个角的度数是______．10. 2021年10月16日，我国神舟13号载人飞船与天和核心舱首次成功实现“径向对接”，对接过程的控制信息通过微波传递.微波理论上可以在0.000003秒内接收到相距约1km的信息.将数0.000003用科学记数法表示应为______ ．11. 若a5⋅(a y)4=a17，则y=______．12. 用“☆”定义一种新运算：对于任意有理数x和y，x☆y=a2x+ay+1(a为常数)，如：2☆3=a2⋅2+a⋅3+1=2a2+3a+1.若1☆2=3，则3☆6的值为______．13.如图，在△ABC中，点O是∠ABC和∠ACB的平分线的交点，点E，D分别是OB，OC延长线上的点，∠CBE和∠BCD的平分线交于则∠P的度数为.(用含α的代数式表示点P，∠A=α，)14. 平面镜在光学仪器中有广泛的应用.平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①，一束光线m射到平面镜a上，被a反射后的光线为n，则∠1=∠2.如图②，两平面镜OM，ON的夹角∠MON，若任何射到平面镜ON上的入射光线AB，经过平面镜ON，OM两次反射后，使得AB//CD，则∠MON=______°.15. 杨辉三角是中国古代数学的杰出研究成果之一.如图，在杨辉三角形中，斜线l的上方，从1开始箭头所示的数组成一个锯齿形数列：1，3，3，4，6，5，10，…，用a n表示这个数列的第n个数，则a99+a100=______ ．16. A，B两地相距640km，甲、乙两辆汽车从A地出发到B地，均匀速行驶，甲出发1小时后，乙出发沿同一路线行驶，设甲、乙两车相距s(km)，甲行驶的时间为t(ℎ)，s与t的关系如图所示，下列说法：①甲车行驶的速度是60km/ℎ，乙车行驶的速度是80km/ℎ；②甲出发4ℎ后被乙追上；ℎ；③甲比乙晚到53ℎ，甲，乙两车相距80km；④甲车行驶8ℎ或914其中正确的是______ ．三、解答题（本大题共8小题，共72.0分。
山东省青岛市2021-2022学年七年级下学期期中数学试题(含答案与解析)
【解析】
【分析】根据同底数幂的除法，合并同类项，同底数幂的乘法，幂的乘方与积的乘方对各选项进行判断即可；
【详解】解：选项A中，不是同同类项，不能相加，故选项A错误；
选项B中，x2x3=x5，同底数幂的乘法底数不变指数相加，故选项B错误；
选项C中，（﹣x3）2=x5，故选项C错误；
选项D中，x6÷x3=x3同底数幂的除法底数不变指数相减，故选项D正确；
A.a2﹣b2B.a2﹣2ab+b2C.a2+2ab﹣b2D.a2+2ab+b2
【4题答案】
【答案】B
【解析】
【分析】根据完全平方公式进行计算即可．
【详解】解：原式
故选B．
5.如果一个角的补角是150°，那么这个角的余角的度数是（ ）
A.30°B.60°C.90°D.120°
【5题答案】
【答案】B
【解析】
∠3=∠6（）
∴∠2+∠6=180°（）
∴a∥b（）
∴c∥b（）
20.已知 ， ，求下列式子的值：
（1） ；
（2）4ab．
21.如图，已知AD∥BE，∠A=∠E，求证：∠1=∠2．
22.小明在暑期社会实践活动中，以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售，在销售了40千克西瓜之后，余下的每千克降价0.4元，全部售完.销售金额与售出西瓜的千克数之间的关系如图所示；请你根据图象提供的信息完成以下问题：
∵AB∥CD，
∴∠EHD=180°−∠BGF=54°，
又∵HM平分∠EHD，
∴∠MHD= ∠EHD=27°.
故选D.
【点睛】本题主要考查了平行线的性质，掌握平行线的性质是解题的关键.
山东省青岛市胶州市、黄岛区、高新区、李沧区2022-2023学年七年级下学期期中数学试题
山东省青岛市胶州市、黄岛区、高新区、李沧区2022-2023学年七年级下学期期中数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题．．C ．D ．6．如图，从边长为(3cm )a +的正方形纸片中剪掉一个边长为(1)cm a +的正方形(0)a >，剩余部分沿虚线剪开，不重叠无缝隙地拼成一个长方形，则该长方形的面积为()A ．28cmB ．223(m )c a +C ．248(m )c a +D ．2(615)cm a +7．如图，下列各三角形中的三个数之间存在一定的规律，根据你发现的规律，确定最后一个三角形中y 与n 之间的关系式是（）A ．21y n =+B ．21n y n =+-C ．121n y n -=+-D ．2n y n=+8．如图，将两个边长为b 的小正方形放到边长为a 的大正方形内，若长方形ABCD 的面积为80，两个小正方形重叠的部分面积为48，则22a b +的值为（）A ．130B ．164C ．156D ．128二、多选题9．如图，给出的下列条件中能判断AB CD ∥的是（）A ．12∠=∠B ．3=4∠∠C ．5B ∠=∠D ．180B BCD ∠+∠=︒10．某校科技周期间，组织兴趣小组同学外出参观科技馆．他们先从学校匀速步行到科技馆，参观结束后，乘车原路匀速返回学校，兴趣小组的行驶路程s （米）与时间t （分）的图象如图，下列说法正确的是（）A ．兴趣小组的步行速度为80米/分B ．学校离科技馆1200米C ．乘车返回时速度是每分钟800米D ．兴趣小组在科技馆参观的时间是25分钟三、填空题16．已知()25164n =，则n =17．某路口红绿灯的平面示意图如图所示，已知BED ∠的度数是150︒，则∠18．观察2，12，27，…，发现这组数是按一定规律排列的．如果将第第2个数记为2a ，…，第n 个数记为为．四、解答题19．已知：四边形ABCD 20．计算(1)224212a b ab ⎛⎫+- ⎪⎝⎭；(2)()()()231x x x x +---；解：12，∠=∠∠=∠______)，AGB2((1)A、B两地相距___________(2)甲比乙早___________小时到达(3)求乙每小时行驶多少km？24．对于任意的有理数a和b，如果满足(1)BAC ∠与哪个角相等？为什么？(2)试判断AD 与FG 有怎样的位置关系，请说明理由．(3)若AD BC ⊥，30BFG ∠=︒，求26．如图，在四边形ABCD 中，点P 从点B 出发，沿BA 方向匀速运动，速度为同的速度沿CB 方向匀速运动，当点AC PC PQ ，，．设点P 的运动时间为(1)当t 为何值时，BP BQ =(2)设三角形APC 的面积为(2cm S (3)在运动过程中，是否存在某一时刻的值；若不存在，请说明理由．。
青岛版七年级数学下册期中检测卷(共4套)
期末测试一 一、选择题（每小题3分，共36分）1． 下列计算中，正确的是（ ）A.32x x x ÷=B.2m + 3n=5mnC.33x x x =⋅D.336x x x += 2、如图，三条直线相交于一点O ，其中，AB ⊥CO ，则∠1与∠2（ ）A ．互为补角B ．互为余角C ．相等D ．互为对顶角 3. 元一次方程组34,231x y x y +=⎧⎨-=-⎩的解是（ ）A ．11.x y =⎧⎨=⎩，B ．11.x y =-⎧⎨=-⎩，C ．22.x y =-⎧⎨=⎩，D ．21.x y =-⎧⎨=-⎩，4.一个多边形的内角和是外角和的2倍，则这个多边形的边数为（ ） A. 四 B. 六 C. 八 D.十5.下列计算不正确的是（ ） A. （21 x 3y ）2=41 x 6y 2 B. 2221)1(xx x x +=- C.22))((b a a b b a -=+- D. 2222)(y xy x y x ++=-- 6. 如图，已知∠AOC=∠BOD=90°，则图中相等的角共有（ ）A ．0对B ．1对C ．2对D ．3对第5题图第21题图7.下列分解因式正确的是（ ）A. 2a 2-3ab+a=a （2a-3b ） B.-x 2-2x=-x （x-2）C. 2πR-2πr=π（2R-2r ）D.5m 4+25m 2=5m 2（m 2+5） 8.已知10 x＝3，10 y＝4，则102x+3y=（ ）A. 574B.575C.576D.5779. 现有两根木棒，其长度分别为4cm 和9cm ，小明想要在墙壁上钉一个三角形木架，则可选用木棒的长度为（ ） A ．4cm B ．5cm C ．9cm D ．13cm10. 如图，在△ABC 中，∠A=α，∠ABC 的平分线与 ∠ACD 的平分线交于点A 1得∠A 1，∠A 1BC 的平分线与 ∠A 1CD 的平分线交于点A 2，得∠A 2，…，∠A 2008BC 的平分线与∠A 2008CD 的平分线交于点A 2009，得∠A 2009， 则∠A 2009=（ ） A.20082αB.20092αC.20102αD.20132α11、 已知：a+b=m ，ab=-4，化简（a-2）（b-2）的结果是（ ） A ．-2m B ．2m C ．2m-8 D ．612、 若点P （a ，a-2）在第四象限，则a 的取值不能是（ ） A ．1.1 B ．1.2 C ．1.8 D ．2 二、填空题（每小题4分，共20分） 13.生物具有遗传多样性，遗传信息大多储存在DNA 分子上．一个DNA 分子的直径约为0.0000002cm ．这个数量用科学记数法可表示为 _________cm ．14、如果226x x k ++恰好是一个整式的平方，那么常数K 的值为________.15.将一副直角三角板如图所示放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合，则∠1的度数为________. 16. 已知点P 在第四象限，它的横第15题图坐标与纵坐标的和为-3，则点P 的坐 标是____写出符合条件的一个点即可） 17.上海世博会期间，门票设个人票和 团队票两大类 ，个人普通票160元/张， 学生优惠票100元/张；成人团队票120 元/张，学生团队票50元/张.（1）如果2名老师、10名学生均购买个人票去参观世博会，一共要花 元钱购买门票；（2）如果某校共30名师生去参观世博会，并得知他们都是以团队形式购买门票，累计花去2200元.设该校本次分别有x 名老师、y 名学生参观世博会.根据题意可列出方程组 . 三、解答题18．（10分）分解因式：（1）x x -3 （2）9a 2(x-y)+4b 2(y-x)20．（12分）（1）计算(—3)0+(+0.2)2009×(+5)2010（2）化简求值：22()()()2a b a b a b a +-++-，其中133a b ==-，．21．（7分）解方程组：⎩⎨⎧=+-=300342150y x yx22.（8分）如图所示，AE∥BD，∠1=95°，∠2=28°，求∠C的度数。
青岛市七年级下学期数学期中考试试卷
青岛市七年级下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题（每小题3分，共30分） (共10题；共27分)1. （3分）下列方程组中，是二元一次方程组的是（）A .B .C .D .2. （3分）(2016·资阳) 下列运算正确的是（）A . x4+x2=x6B . x2•x3=x6C . （x2）3=x6D . x2﹣y2=（x﹣y）23. （3分） (2015八上·大石桥期末) 计算﹣12a6÷（3a2）的结果是（）A . ﹣4a3B . ﹣4a8C . ﹣4a4D . ﹣ a44. （2分）下列说法正确的是（）A . 同位角相等B . 在同一平面内，如果a⊥b，b⊥c，则a⊥cC . 相等的角是对顶角D . 在同一平面内，如果a∥b，b∥c，则a∥c5. （2分） (2018八上·长春月考) 计算(2+1)(22+1)(24+1)(28+1)+1的值是（）A . 1024B . 28+1C . 216+1D . 2166. （3分） (2017七下·平南期中) 关于x，y的二元一次方程组中，m与方程组的解中的x 或y相等，则m的值为（）A . 3或B . 2或﹣C . 3或D . 2或﹣7. （3分）如图，多边形的相邻两边互相垂直，则这个多边形的周长为（）．A . 21B . 26C . 37D . 428. （2分） (2020八上·天桥期末) 篮球比赛中，每场比赛都要分出胜负，每队胜1场得3分，负一场扣1分。
某队在8场比赛中得到12分，若设该该队胜的场数为x，负的场数为y，则可列方程组为（）A .B .C .D .9. （3分） (2018八上·江北期末) 下列各式分解因式正确的是（）A .B .C .D .10. （3分） (2019八下·乌拉特前旗开学考) 若(2a+3b)（）＝4a2﹣9b2 ，则括号内应填的代数式是（）A . ﹣2a﹣3bB . 2a+3bC . 2a﹣3bD . 3b﹣2a二、填空題（每小题2分，共12分） (共6题；共12分)11. （2分） (2017八下·安岳期中) =________；12. （2分） (2019七下·新密期中) ________.13. （2分）计算：（2a+b）（2a﹣b）﹣（a﹣b）2=________．14. （2分）当a=________时，方程组的解中，x与y的值互为相反数．15. （2分）(2018·苏州模拟) 在“三角尺拼角”实验中，小明同学把一副三角尺按如图所示的方式放置，则∠1=________°16. （2分） (2017八下·禅城期末) “a的3倍与12的差是一个非负数”用不等式表示为________．三、解答题（共58分） (共8题；共48分)17. （6分） (2016八上·海门期末) 解方程组：．18. （6分）992+2×99+1．19. （2分）如图，△ABC由△EDC绕C点旋转得到，B、C、E三点在同一条直线上，∠ACD=∠B，求证：△ABC 是等腰三角形.20. （6分）因式分解：（1）9－（2）＋2ab＋－421. （8分） (2016七下·谯城期末) 计算（1） |﹣1|﹣ +（π﹣3）0+2﹣2（2）（a+2b）（a﹣2b）（a2+4b2）22. （2分） (2018七上·澧县期中) 观察下列单项式：﹣x，3x2 ，﹣5x3 ， 7x4 ，…，﹣37x19 ， 39x20 ，…写出第 n 个单项式．为解决这个问题，特提供下面的解题思路：通过观察单项式的结构特征，分三步确定：先确定符号，再确定系数的绝对值，最后确定次数．（1）这组单项式系数的符号规律是________，系数的绝对值规律是________；（2）这组单项式的次数的规律是________；第六个单项式是________；（3）根据上面的归纳，可以猜想第 n 个单项式是________；（4）请你根据猜想，写出第 2018 个单项式是________．23. （8分）(2018·无锡模拟) 如图，C为∠AOB的边OA上一点，OC＝6，N为边OB上异于点O的一动点，P 是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．（1）若∠AOB＝60º，OM＝4，OQ＝1，求证：CN⊥OB．（2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．①问：的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．②设菱形OMPQ的面积为S1，△NOC的面积为S2，求的取值范围．24. （10.0分）某校规划在一块长AD为18m，宽AB为13m的长方形场地ABCD上，设计分别与AD，AB平行的横向通道和纵向通道（通道面积不超过总面积的），其余部分铺上草皮．（1）如图1，若设计两条通道，一条横向，一条纵向，4块草坪为全等的长方形，每块草坪的两边之比为3：4，并且纵向通道的宽度是横向通道宽度的2倍，问横向通道的宽是多少？（2）如图2，为设计得更美观，其中草坪①②③④为全等的正方形，草坪⑤⑥为全等的长方形（两边长BN：BM=2：3），通道宽度都相等，问：此时通道的宽度又是多少呢？参考答案一、选择题（每小题3分，共30分） (共10题；共27分) 1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空題（每小题2分，共12分） (共6题；共12分) 11-1、12-1、13-1、14-1、15-1、16-1、三、解答题（共58分） (共8题；共48分)17-1、18-1、19-1、20-1、21-1、21-2、22-1、22-2、22-3、22-4、23-1、23-2、24-1、24-2、。
初中数学练习题 2022-2023学年山东省青岛七年级(下)期中数学试卷
2022-2023学年山东省青岛五十九中七年级（下）期中数学试卷一、选择题（共10小题，每小题3分，满分30分）A ．-a <a <1B ．a <-a <1C ．1<-a <aD ．a <1<-a1．（3分）实数a在数轴上对应的点如图所示，则a ,-a ,1的大小关系正确的是（ ）A ．要了解一批节能灯的使用寿命，采用普查方式B ．调查你所在班级同学的身高，采用抽样调查方式C ．环保部门调查沱江某段水域的水质情况，采用抽样调查方式D ．调查全市中学生每天的就寝时间，采用普查方式2．（3分）下列调查方式中适合的是（ ）A ．3B ．4C ．5D ．63．（3分）已知a =5+2，b =5-2，则a 2+b 2+7的值为（ ）√√√A ．第一，二，三象限B ．第一，二，四象限C ．第二，三，四象限D ．第一，三，四象限4．（3分）已知一次函数y =kx -k ,若y 随x 的增大而减小，则该函数的图象经过（ ）A ．相交B ．外离C ．内含D ．外切5．（3分）两圆的圆心距为3，两圆的半径分别是方程x 2-4x +3=0的两个根，则两圆的位置关系是（ ）A ．247B ．73C ．724D ．136．（3分）直角三角形纸片的两直角边长分别为6，8，现将△ABC 如图那样折叠，使点A 与点B 重合，折痕为DE ，则tan ∠CBE 的值是（ ）√7．（3分）在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有（ ）二、填空题（共6小题，每小题5分，满分30分）A ．9箱B ．10箱C ．11箱D ．12箱A ．42cmB ．35cmC ．26cmD ．23cm8．（3分）如图，有一圆心角为120°，半径长为6cm 的扇形，若将OA 、OB 重合后围成一圆锥侧面，那么圆锥的高是（ ）√√√√A ．12B ．9C ．6D ．49．（3分）如图，已知双曲线y =k x（k <0）经过直角三角形OAB 斜边OA 的中点D ，且与直角边AB 相交于点C ．若点A 的坐标为（-6，4），则△AOC 的面积为（ ）A ．1B ．2C ．3D ．410．（3分）在一列数x 1，x 2，x 3，…中，已知x 1=1，且当k ≥2时，x k =x k −1+1−4([k −14]−[k −24])（取整符号[a ]表示不超过实数a 的最大整数），例如[2.6]=2，[0.2]=0，则x 2011等于（ ）11．（5分）由四舍五入法得到的近似数8.8×103，精确到 位，有 个有效数字．12．（5分）若分式x 2−x −2x 2+2x +1的值为0，则x 的值等于 ．13．（5分）不等式组V Y W Y X x −3(x −2)≥41+2x 3>x −1的解集是 ．14．（5分）“上升数”是一个数中右边数字比左边数字大的自然数（如：34，568，2469等）．任取一个两位数，是“上升数”的概率是 ．三、解答题（共8小题，满分60分）15．（5分）如图，在由24个边长都为1的小正三角形组成的正六边形网格中，以格点P 为直角顶点作格点直角三角形（即顶点均在格点上的三角形），请你写出所有可能的直角三角形斜边的长 ．16．（5分）如图，DB 为半圆的直径，A 为BD 延长线上一点，AC 切半圆于点E ，BC ⊥AC 于点C ，交半圆于点F ．已知BD =2，AD =1，则CF = ．17．（6分）先化简，再求值：（a 2−4a 2−4a +4-12−a ）÷2a 2−2a，其中a 是方程x 2+3x +1=0的根．18．已知关于x 的一元二次方程x 2+（2m -1）x +m 2=0有两个实数根x 1和x 2．（1）求实数m 的取值范围；（2）当（x 1+x 2）•（x 1-x 2）=0时，求m 的值．（友情提示：若x 1，x 2是一元二次方程ax 2+bx +c =0（a ≠0）的两根，则：x 1+x 2=−b a ，x 1．x 2=c a）19．（6分）一次函数y =kx +b 的图象与x 、y 轴分别交于点A （2，0），B （0，4）．（1）求该函数的解析式；（2）O 为坐标原点，设OA 、AB 的中点分别为C 、D ，P 为OB 上一动点，求PC +PD 的最小值，并求取得最小值时P 点的坐标．20．（8分）已知：角∠α，线段m .求作：等腰三角形△ABC ，使其顶角∠BAC =∠a ,∠BAC 平分线m .（尺规作图，保留作图痕迹，不写作法）21．（8分）为了解某品牌A ，B 两种型号冰箱的销售状况，王明对其专卖店开业以来连续七个月的销售情况进行了统计，并将得到的数据制成如下的统计表：月份一月二月三月四月五月六月七月A 型销售量（单位：台）10141716131414B 型销售量（单位：台）6101415161720（1）完成下表（结果精确到0.1）：平均数中位数方差A 型销售量14 4.3B 型销售量1418.6（2）请你根据七个月的销售情况在图中绘制成折线统计图，并依据折线图的变化趋势，对专卖店今后的进货情况提出建议（字数控制在20～50字）．22．（10分）如图，四边形ABCD 是菱形，点G 是BC 延长线上一点，连接AG ，分别交BD 、CD 于点E 、F，连接CE ．（1）求证：∠DAE =∠DCE ；（2）当AE =2EF 时，判断FG 与EF 有何等量关系？并证明你的结论．23．（10分）某镇道路改造工程，由甲、乙两工程队合作20天可完成．甲工程队单独施工比乙工程队单独施工多用30天完成此项工程．（1）求甲、乙两工程队单独完成此项工程各需要多少天？（2）若甲工程队独做a 天后，再由甲、乙两工程队合作 天（用含a 的代数式表示）可完成此项工程；（3）如果甲工程队施工每天需付施工费1万元，乙工程队施工每天需付施工费2.5万元，甲工程队至少要单独施工多少天后，再由甲、乙两工程队合作施工完成剩下的工程，才能使施工费不超过64万元？24．（12分）已知等腰梯形ABOC 在直角坐标系中如图所示，AB ∥OC ，OB =2，OA =23．（1）求点C 的坐标；（2）求经过点B ，O ，C 的抛物线解析式；（3）若点P 为（2）中所求抛物线上一动点，点Q 为y 轴上一动点，请探索是否存在点P 和点Q ，使得以B ，C ，P ，Q 为顶点的四边形是平行四边形？若存在，请求出所有对应的P ，Q 的坐标；若不存在，请说明理由．√。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B AC DO3题图七年级数学下册期中考试试题一、精心选一选，慧眼识金！（每题4分，共40分）1.三角形的一个外角小于与它相邻的内角,则这个三角形是( ) A.锐角三角形 B.钝角三角形; C.直角三角形 D.无法确定2、在平面直角坐标系中，线段A ′B ′是由线段AB 经过平移得到的，已知点A(－2，1)的对应点为A ′(3，1)，点B 的对应点为B ′(4，0)，则点B 的坐标为：（ ） A ．（9，0） B ．（－1，0） C ．（3，－1） D ．（－3，－1）3、如图：已知AB ∥CD ，∠B=1200，∠D=1500，则∠O 等于（ ）.（A ）500 （B ）600 （C ）800 （D ）9004.△ABC 中,∠A=13∠B=14∠C,则△ABC 是( )A.锐角三角形B.直角三角形;C.钝角三角形D.都有可能5、如图，AB ⊥BC ，∠ABD 的度数比∠DBC 的度数的两倍少15°，设∠ABD 和∠DBC 的度数分别为x 、y ，那么下面可以求出这两个角的度数的方程组是（ ）A 、9015x y x y +=⎧⎨=-⎩B 、90215x y x y +=⎧⎨=-⎩C 、90152x y x y +=⎧⎨=-⎩D 、290215x x y =⎧⎨=-⎩6.有两边相等的三角形的两边长为3cm,5cm,则它的周长为 ( )A.8cmB.11cmC.13cmD.11cm 或13cm7、一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数为： （ ） A ．7 B ．8 C ．9 D ．108、在下列点中，与点A （2-，4-）的连线平行于y 轴的是 （ ） A 、（2，4-） B 、（4，)2- C 、（-2，4） D 、（-4，2）9、甲、乙二人按3：2的比例投资开办了一家公司，约定除去各项支出外，所得利润按投资比例分成.若第一年甲分得的利润比乙分得的利润的2倍少3千元，求甲、乙二人各分得利润多少千元.若设甲分得x 千元，乙分得y 千元，由题意得（ ）A 、 x y y x 3212=-=B 、 y x y x 2332=+=C 、 x y y x 2332=-=D 、 yx y x 3232=+=10、给出下列说法：5题图ACB21FEDCBAGACBFDE1A B FD C E2（1） 两条直线被第三条直线所截，同位角相等；（2） 平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交； （3） 相等的两个角是对顶角；（4） 从直线外一点到这条直线的垂线段，叫做这点到直线的距离； 其中正确的有（ ）A 0个B 1个C 2个D 3个 11．如图，若AB ∥CD ，CD ∥EF ，那么∠BCE ＝（ ）A ．∠1＋∠2B ．∠2－∠1C ．180°－∠1＋∠2D ．180°－∠2＋∠112、a 、b 、c 为三角形的三边长，化简c b a c b a c b a c b a -+-+-----++，结果是 （ ）A 、0B 、c b a 222++C 、a 4D 、c b 22- 二、耐心填一填，你能行！（每题3分，共30分）13．在349x y +=中，如果2y = 6，那么x = 。
14、P （m-4，1-m ）在x 轴上，则m = 。
15、如图，AC ⊥BC ，AC=3，BC=4，AB=5，则点B 到AC 的距离为16.如图,AB ∥CD,直线EF 分别交AB 、CD 于E 、F,EG 平分∠BEF,若∠1=72°,•则∠2=________度.17、方程032233=+--+-n m n y x 是二元一次方程，则，m =n = ；21题图18、已知12==y x 是方程组 513=+=-by x y ax 的解，则b a -= ；19、如图,甲、乙两岸之间要架一座桥梁,从甲岸测得桥梁的走向是北偏东50•°,如果甲、乙两岸同时开工.要使桥梁准确连接,那么在乙岸施工时,应按β为_________度的方向动工。
20.有以下图形：①正三角形；②正方形；③正六边形；④正八边形。
现在要选其中的两种图形进行平面镶嵌，请你写出你所有的选择（填序号） 。
21、如图，△ABC 中，∠C=90°，∠BAD=31 ∠BAE ，∠ABD=31∠ABF ，则∠D 的大北βα北乙甲11题图15题图 16题图 19题图yx1234-1-2-3-4-4-3-2-104321小是 .22.一个多边形除了一个内角外,其余各内角之和为1680°,•那么这个多边形的边数为________.23、解下列方程组（每题5分，共10分）：（1） 14833=-=-y x y x （2） 33651643=-=+y x y x24.如图，根据下列条件，可以判定哪两条直线平行？并说明判定的根据是什么。
（6分） ①∠2=∠B ；②∠1=∠D ；③∠3+∠F=180°。
25.如图,△ABC 中,AD ⊥BC,AE 平分∠BAC,∠B=40°,∠C=60°,求∠DAE 的度数.（8分）26.在平面直角坐标系中,顺次连结A(-2,1),B(-2,-1),C(2,-2),D(2,3)各点,你会得到一个什么图形?试求出该图形的面积.（6分）27、已知方程组 my x m y x =++=+35253的解x 、y 互为相反数，求m 的值。
（8分）28、如图：直线DE 交△ABC 的边AB 、AC 于D 、E ，交BC 延长线于F ，若∠B ＝67°，∠ACB ＝74°，∠AED ＝48°，求∠BDF 的度数。
（8分）29、甲、乙两人共同解方程组⎩⎨⎧-=-=+ ②by x ①y ax 24155,由于甲看错了方程①中的a ,得到方程组的解为⎩⎨⎧-=-=13y x ；乙看错了方程②中的b ,得到方程组的解为⎩⎨⎧==45y x 。
试计算20072006101⎪⎭⎫⎝⎛-+b a 的值.（8分）30、一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车，已知过去两次租第一次 第二次 甲种货车辆数（单位：辆） 2 5 乙种货车辆数（单位：辆） 3 6 累计运货物吨数（单位：吨）15.535现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货，如果按每吨付运费30元计算，问货主应付运费多少元？（8分）31、（10分）如图，已知直线 1l ∥2l ，且3l 和1l 、2l 分别交于A 、B 两点，点P 在AB上。
（1）试找出∠1、∠2、∠3之间的关系并说出理由；(2)如果点P 在A 、B 两点之间运动时，问 ∠1、∠2、∠3 之间的关系是否发生变化？ (3)如果点P 在A 、B 两点外侧运动时，试探究 ∠1、∠2、∠3 之间的关系（点P 和A 、B 不重合）A PB 1l 2l 3l 1 23相信自己 一定会成功！初一数学参考答案及评分标准一、选择题（每题4分，共48分）1——5 BBDBB ； 6——10 DACCB ； 11、12 DA. 二、填空题；（每题3分，共30分）13、1-； 14、1； 15、4； 16、54； 17、31-，4； 18、1-； 19、130； 20、①②，①③，②④； 21、90°； 22、12. 三、解答题：（共72分）23、（1） 12-==y x （2） 216-==y x（每小题5分，每小题中前一个未知数对后一个未知数错得3分） 24、略（每小题2分，平行线1分，根据1分）25、略解：∠BAC=100° （3分） ∠BAE =40° （5分）∠BAD=50° （7分） ∠DAE=10° . （8分） 26、画图2分 梯形 3分 面积=14 6分27、略解：两式相加：2288+=+m y x （4分） 又0=+y x （5分） 022=+m （6分） 1-=m （8分）28、略解：∠A=39° （ 4分 ） 利用外角∠BDF=87° （8分）29、略解：10=b （3分） 1-=a （6分） 计算得：0 （8分）30、解；设甲种货车每辆一次运x 吨货物，设乙种货车每辆一次运y 吨货物。
由题意得：35655.1532=+=+y x y x （4分） 解得： 5.24==y x （6分）运费：)5.2534(30⨯+⨯⨯=735元 （8分）31、（1）∠3=∠1+∠2 （2分）证明：略 （5分）（2）不发生变化，仍然是 ∠3=∠1+∠2 （6分）（3）当点P 在线段AB 的延长线上时，∠1=∠2+∠3 （8分） 当点P 在线段BA 的延长线上时，∠2=∠1+∠3 （10分）。