ansys分布载荷作用下的悬臂梁应力计算
ANSYS悬臂梁等效应力分析教程

mikeliu65
工程软件教程系列
第 9 步,施加约束。
单击打开图示对话框。
- 11 -
mikeliu65
工程软件教程系列
在弹出的对话框内输入需要的面的编号或者选择对应的面。 按照下图路径打开编号显示目录。
在弹出的对话框内勾选 AREA number。单击 ok 退出。
- 12 -
mikeliu65
单击 line 下的 set,
。弹出 element size on picked line 对话框,
单击 pick all。在弹出的对话框里,设置线段网格大小。设置每一段网格长度为 0.05m。单击 ok,完成线段长度设置。
-9-
mikeliu65
工程软件教程系列
单击 mesh tool,弹出 mesh tool 对话框。选择 HEX 单击 mesh,开始划分网格。在弹出的 mesh volumes 对话框里单击 pick all。完成网格划分。
设置完成后如下图:
-6-
mikeliu65
工程软件教程系列
第 7 步,建立体悬臂梁三维实体。
点开下图所示的路径,在弹出的窗口里输入如下参数。
-7-
mikeliu65
工程软件教程系列
点击 ok,完成三维实体创建。
-8-
mikeliu65
工程软件教程系列
第 8 步,划分网格。
单击 mesh tool,弹出 mesh tool 对话框。
-1-
mikeliu65
工程软件教程系列
第 1 步打开软件,设置文件保存路径。
打开 ansys12.0
,设置文件保存路径,在 working 内输
入保存路径。例如我的保存路径设为 F:\mikeliu65\chapter-1
悬臂梁受均布载荷的应力和变形计算
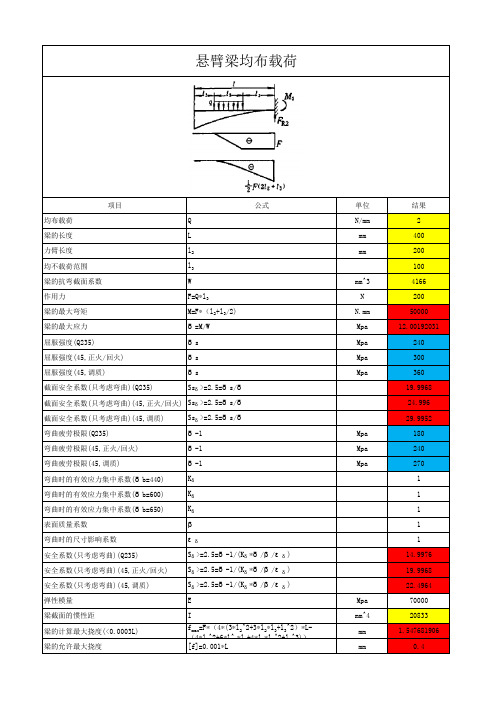
悬臂梁均布载荷项目公式单位结果均布载荷Q N/mm2梁的长度L mm400力臂长度l2mm200均不载荷范围l3100梁的抗弯截面系数W mm^34166作用力F=Q*l3N200梁的最大弯矩M=F*(l2+l3/2)N.mm50000梁的最大应力δ=M/W Mpa12.00192031屈服强度(Q235)δs Mpa240屈服强度(45,正火/回火)δs Mpa300屈服强度(45,调质)δs Mpa360截面安全系数(只考虑弯曲)(Q235)Ssδ>=2.5=δs/δ19.9968截面安全系数(只考虑弯曲)(45,正火/回火)Ssδ>=2.5=δs/δ24.996截面安全系数(只考虑弯曲)(45,调质)Ssδ>=2.5=δs/δ29.9952弯曲疲劳极限(Q235)δ-1Mpa180弯曲疲劳极限(45,正火/回火)δ-1Mpa240弯曲疲劳极限(45,调质)δ-1Mpa270弯曲时的有效应力集中系数(δb=440)Kδ1弯曲时的有效应力集中系数(δb=600)Kδ1弯曲时的有效应力集中系数(δb=650)Kδ1表面质量系数β1弯曲时的尺寸影响系数εδ1安全系数(只考虑弯曲)(Q235)Sδ>=2.5=δ-1/(Kδ*δ/β/εδ)14.9976安全系数(只考虑弯曲)(45,正火/回火)Sδ>=2.5=δ-1/(Kδ*δ/β/εδ)19.9968安全系数(只考虑弯曲)(45,调质)Sδ>=2.5=δ-1/(Kδ*δ/β/εδ)22.4964弹性模量E Mpa70000梁截面的惯性距I mm^420833mm 1.547681906梁的计算最大挠度(<0.0003L)f max=F*(4*(3*l2^2+3*l2*l3+l3^2)*L-(4*l2^2+6*l^2*l3+4*l2*l3^2+l3^3))梁的允许最大挠度[f]=0.001*L mm0.4。
ansys分布载荷作用下的悬臂梁应力计算

ansys 分布载荷作用下的悬臂梁应力计算分析模型如图1-1 所示, 梁的横截面为矩形 宽х高 = 1х 2 m 2. 受到分布载荷作用。
材料的弹性模量200GPa, 泊松比0.3。
习题文件名: Cantilever beam 。
注意:用实体单元离散,长度单位m, 力的单位 N ,对应应力单位 Pa ,按照平面应力处理。
1.1 进入ANSYS 程序 →ANSYSED 10.0 → input Initial jobname: Cantilever beam →OK1.2设置计算类型Main Menu: Preferences →select Structural → OK1.3选择单元类型Main Menu: Preprocessor →Element Type→Add/Edit/Delete →Add →select Solid Quad 4node 182 →OK (back to Element Types window) → Options →select K 1: Reduced integration → K3: Plane Stress →OK→Close (the Element Type window)1.4定义材料参数Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:200e9,PRXY:0.3→ OK1.5生成几何模型生成特征点Main Menu: Preprocessor →Modeling →Create →Key points →In Active CS →依次输入四个点的坐标(每次输入后按Apply,最后按OK):input:1(0,0,0), 2(10,0,0), 3(10,2,0), 4(0,2,0) →OK生成面Main Menu: Preprocessor → Modeling → Create→ Areas → Arbitrary → Through KPS →依次连接四个特征点,1 → 2 → 3 → 4 → OK注意:上面两步也可简化为:Main Menu: Preprocessor → Modeling → Create→Areas → Rectangle → By two corners → WPX, WP Y 均输入0, Width 输入10, Height 输入2 → OK1.6 网格划分=0Main Menu: Preprocessor →Meshing →Mesh Tool→(Size Controls) lines: Set →拾取长边: OK→input NDIV: 50→Apply→拾取短边: →input NDIV: 10 →OK →(back to the mesh tool window)Mesh: Areas, Shape: Quad, Mapped →Mesh →Pick All (in Picking Menu) → Close( the Mesh Tool window)1.7 模型施加约束给左边施加固定约束Main Menu: Solution →Define Loads →Apply →Structural→Displacement → On lines →选左边线→OK →select 第一行: ALL DOF →第四行 VALUE 选 0: → OK给梁的上边施加线性分布载荷ANSYS 命令菜单栏: Parameters →Functions →Define/Edit→1) 在下方的下拉列表框(第三行)内选择X作为设置的变量;2) 在Result窗口中出现{X},写入所施加的载荷函数(力的单位:N):10000-1000*{X};3) File → Save 输入my_q(文件扩展名:func) →返回:Parameters →Functions →Read from file:将需要的my_q.func文件打开,任给一个参数名qq, Local coordinatesystem id for (x,y,z) 栏选0→OKUtility menu → plotctrls → Symbols → Show pres andconvect as 表框内的Face outline下拉改为 arrowsMain Menu: Solution →Define Loads →Apply →Structural →Pressure →On Lines →拾取梁的上层线→OK →在下拉列表框中选择:Existing table →Apply →选择需要的载荷参数名qq→OKsolution→load step opts→write LSFile输入文件名(注意:显示的载荷箭头应当沿着长度有长短不同)1.8 分析计算Main Menu: Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK1.9 结果显示Main Menu: General Postproc →Plot Results →Deformed Shape… → select Def + Undeformed →OK (back to Plot Results window)→Contour Plot →Nodal Solu…→select: Stress → X Component of stress → OK1.10 退出系统ANSYS Utility Menu: File →Exit→ Save Everything→ OK。
悬臂梁变形及应力分析

基于ANSYS 10.0对悬臂梁的强度及变形分析姓名:***班级:机制0803班学号:************对悬臂梁的受力及变形分析摘要:本研究分析在ANSYS10.0平台上,采用有限元法对悬臂梁进行强度与变形分析、验证此悬臂梁设计的合理性。
一、问题描述长度L=254 mm的方形截面的铝合金锥形杆,上端固定,下端作用有均布拉力P=68.9 Mpa,上截面的尺寸50.8×50.8 mm,下截面尺寸25.4×25.4 mm(见右图),弹性模量E=7.071×104 Mpa,泊松比μ=0.3,试用确定下端最大轴向位移δ和最大轴向应力。
试将分析结果与理论解进行比较,说明有限元分析的误差。
(理论解:最大轴向位移δ=0.1238 mm)。
二、建立有限元模型:定义模型单元类型为:solid(实体)95号单元,材料常数为:弹性模量E=7.071×104 Mpa,泊松比μ=0.3。
三、有限元模型图:建立有限元模型时,观察模型的形状可知,我们可以先建立模型的上下底面,再根据有上下底面形成的八个关键点(keypoints)生成线,接着生成面,生成体。
最后生成该悬臂梁的模型图,示图如下:整个模型建立好之后即可对其划分网格,划分网格时,若选择自由划分则生成的网格比较混乱,不能比较准确的模拟该梁真实的受力变形情况。
故我们选择智能划分模式,并且分别对模型的各个棱边(lines)进行均匀分割,这样可以划分出比较理想的网格,更利于我们的研究和分析。
网格划分之后的模型图为:四、加载并求解:根据该悬臂梁的受力特点,我们在其下底面(比较大的底面)上进行六个自由度的位移约束,而在其上地面上施加大小为P=68.9 Mpa均布拉力,将载荷加载好之后便可进行运算求解,求解完成之后,我们得到其位移变形图如下:Z向位移云图为:Z向应力云图为:五、结果分析及结论:由以上两张云图和一张变形图中我们可以读出,悬臂梁的最大轴向(Z向)位移和轴向(Z向)最大应力分别为:最大轴向位移为:δ=0.123746 mm 最大轴向应力为:σ=68.224 Mpa 但是,我们知道,如果所划分的网格有差异时,计算结果将会产生一定的误差,由于设计要求的最大轴向位移不能超过0.1238mm,而我们的建模计算结果已经小于此设计要求值。
悬臂梁变形及应力分析

基于ANSYS 10.0对悬臂梁的强度及变形分析姓名:刘吉龙班级:机制0803班学号:200802070516对悬臂梁的受力及变形分析摘要:本研究分析在ANSYS10.0平台上,采用有限元法对悬臂梁进行强度与变形分析、验证此悬臂梁设计的合理性。
一、问题描述长度L=254 mm的方形截面的铝合金锥形杆,上端固定,下端作用有均布拉力P=68.9 Mpa,上截面的尺寸50.8×50.8 mm,下截面尺寸25.4×25.4 mm(见右图),弹性模量E=7.071×104 Mpa,泊松比μ=0.3,试用确定下端最大轴向位移δ和最大轴向应力。
试将分析结果与理论解进行比较,说明有限元分析的误差。
(理论解:最大轴向位移δ=0.1238 mm)。
二、建立有限元模型:定义模型单元类型为:solid(实体)95号单元,材料常数为:弹性模量E=7.071×104 Mpa,泊松比μ=0.3。
三、有限元模型图:建立有限元模型时,观察模型的形状可知,我们可以先建立模型的上下底面,再根据有上下底面形成的八个关键点(keypoints)生成线,接着生成面,生成体。
最后生成该悬臂梁的模型图,示图如下:整个模型建立好之后即可对其划分网格,划分网格时,若选择自由划分则生成的网格比较混乱,不能比较准确的模拟该梁真实的受力变形情况。
故我们选择智能划分模式,并且分别对模型的各个棱边(lines)进行均匀分割,这样可以划分出比较理想的网格,更利于我们的研究和分析。
网格划分之后的模型图为:四、加载并求解:根据该悬臂梁的受力特点,我们在其下底面(比较大的底面)上进行六个自由度的位移约束,而在其上地面上施加大小为P=68.9 Mpa均布拉力,将载荷加载好之后便可进行运算求解,求解完成之后,我们得到其位移变形图如下:Z向位移云图为:Z向应力云图为:五、结果分析及结论:由以上两张云图和一张变形图中我们可以读出,悬臂梁的最大轴向(Z向)位移和轴向(Z向)最大应力分别为:最大轴向位移为:δ=0.123746 mm 最大轴向应力为:σ=68.224 Mpa 但是,我们知道,如果所划分的网格有差异时,计算结果将会产生一定的误差,由于设计要求的最大轴向位移不能超过0.1238mm,而我们的建模计算结果已经小于此设计要求值。
有限元分析及应用报告-利用ANSYS软件分析带孔悬臂梁

有限元分析及应用报告题目:利用ANSY软件分析带孔悬臂梁姓名:xxx学号:xxx班级:机械xxx学院: 机械学院指导老师:xxx二零一五年一月问题概述图示为一隧道断面,其内受均布水压力q,外受土壤均布压力p;试采用不同单元计算断面内的位移及应力,并分别分析q=0或p=0时的位移和应力分布情况。
(材料为钢,隧道几何尺寸和压力大小自行确定)本例假定内圆半径为1m,外圆半径为2m,外受均布压力p=10000pa ,内受均布压力为q=20000pa 。
问题分析由题目可知,隧道的的长度尺寸远远大于截面尺寸,并且压力在长度方向上均匀分布,因此本问题可以看作为平面应变问题。
由于在一个截面内,压力沿截面四周均匀分布,且截面是对称的圆环,所以可以只取截面1/4进行有限元建模分析,这样不仅简化了建模分析过程,也能保证得到精确的结果。
由以上分析,可以选取单元类型plane42进行有限元分析,在option中选择K3 为plane strain。
三.有限元建模1.设置计算类型由问题分析可知本问题属于平面静应力问题,所以选择preferences 为structure 。
2.单元类型选定选取平面四节点常应变单元plane42,来计算分析隧道截面的位移和应力。
由于此问题为平面应变问题,在设置element type的K3时将其设置为plane strain。
3.材料参数隧道的材料为钢,则其材料参数:弹性模量E=2.1e11,泊松比(T =0.34.几何建模按照题目所给尺寸利用ansys的modeling依次建立keypoint :1(0,0),2(1,0),3(2,0),4(0,2),5(0,1) , create LINES 依次连接keypoint 2、3和4、5即可创建两条直线,使用create article 的By cent & radius 创建两条圆弧。
create AREAS依次选择四条线即建立了所需的1/4截面。
ansys workbench例题

Ansys Workbench是一款广泛应用于工程领域的有限元分析软件,可以用于解决各种结构力学、流体动力学、电磁场等问题。
本文将以Ansys Workbench为例,介绍一个结构力学的例题,并详细讲解解题过程。
1. 问题描述假设有一个悬臂梁,在梁的自由端施加一个集中力,要求计算梁的应力分布和挠度。
2. 建模打开Ansys Workbench软件,新建一个静力学分析项目。
在几何模型中,画出悬臂梁的截面,并确定梁的长度、宽度和厚度。
在材料属性中,选择梁的材料,并输入对应的弹性模量和泊松比。
在约束条件中,将梁的支座固定,模拟悬臂梁的真实工况。
在外部荷载中,施加一个与梁垂直的集中力,确定力的大小和作用位置。
3. 网格划分在建模结束后,需要对悬臂梁进行网格划分。
在Ansys Workbench 中,可以选择合适的网格划分方式和密度,以保证计算结果的准确性和计算效率。
通常情况下,悬臂梁的截面可以采用正交结构网格划分,梁的长度方向可以采用梁单元网格划分。
4. 设置分析类型在网格划分完成后,需要设置分析类型为结构静力学。
在分析类型中,可以选择加载和约束条件,在求解器中,可以选择计算所需的结果类型,如应力、应变、位移等。
5. 求解和结果分析完成以上步骤后,可以提交计算任务进行求解。
Ansys Workbench软件会自动进行计算,并在计算完成后给出计算结果。
在结果分析中,可以查看悬臂梁的应力分布图和挠度图,进一步分析梁的受力情况和变形情况。
6. 参数化分析除了单一工况下的分析,Ansys Workbench还可以进行参数化分析。
用户可以改变材料属性、外部加载、几何尺寸等参数,快速地进行批量计算和结果对比分析,以得到最优的设计方案。
7. 结论通过Ansys Workbench对悬臂梁的结构分析,可以得到悬臂梁在外部加载下的应力分布和挠度情况,为工程设计和优化提供重要参考。
Ansys Workbench还具有丰富的后处理功能,可以绘制出直观的分析结果图,帮助工程师和研究人员更好地理解和使用分析结果。
ANSYS悬臂梁的自由端受力的有限元计算[1]
![ANSYS悬臂梁的自由端受力的有限元计算[1]](https://img.taocdn.com/s3/m/6ed4c5c1da38376baf1faec4.png)
悬臂梁自由端受力的有限元计算一、计算目的1、掌握ANSYS软件的基本几何形体构造、网格划分、边界条件施加等方法。
2、熟悉有限元建模、求解及结果分析步骤和方法。
3、利用ANSYS软件对梁结构进行有限元计算。
4、梁的变形、挠曲线等情况的分析。
5、一维梁单元,二维壳单元,三维实体单元对计算结果的影响。
6、载荷施加在不同的节点上对结果的影响。
二、计算设备PC,ANSYS软件(版本为11.0)三、计算内容悬臂梁受力模型如上图所示,一段长100[mm]的梁,一端固定,另一段受到平行于梁截面的集中力F的作用,F=100[N]。
梁的截面为正方形,边长为10[mm]。
梁所用的材料:弹性模量E=2.0 105[MPa],泊松比0.3。
四、计算步骤(以梁单元为例)1、分析问题。
分析该物理模型可知,截面边长/梁长度=0.1是一个较小的值,我们可以用梁单元来分析这样的模型。
当然,建立合适的壳单元模型和实体单元模型也是可以的。
故拟采用这三种不同的方式建立模型。
以下主要阐述采用梁单元的模型的计算步骤。
2、建立有限元模型。
a)创建工作文件夹并添加标题;在个人的工作目录下创建一个文件夹,命名为beam,用于保存分析过程中生成的各种文件。
启动ANSYS后,使用菜单“File”——“Change Directory…”将工作目录指向beam 文件夹;使用/FILNAME,BEAM命令将文件名改为BEAM,这样分析过程中生成的文件均以BEAM为前缀。
偏好设定为结构分析,操作如下:GUI: Main Menu > Preferences > Structuralb)选择单元;进入单元类型库,操作如下:GUI: Main Menu > Preprocessor > Element Type > Add/Edit/Delete > Add…对话框左侧选择Beam选项,在右侧列表中选择2D elastic 3选项,然后单击OK按钮。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ansys 分布载荷作用下的悬臂梁应力计算
分析模型如图1-1 所示, 梁的横截面为矩形 宽х高 = 1х 2 m 2
. 受到分布载荷作用。
材料的弹性模量200GPa, 泊松比0.3。
习题文件名: Cantilever beam 。
注意:用实体单元离散,长度单位m, 力的单位 N ,对应应力单位 Pa ,按照平面应力处理。
1.1 进入ANSYS 程序 →ANSYSED 10.0 → input Initial jobname: Cantilever beam →OK
1.2设置计算类型
Main Menu: Preferences →select Structural → OK
1.3选择单元类型
Main Menu: Preprocessor →Element Type→Add/Edit/Delete →Add →select Solid Quad 4node 182 →OK (back to Element Types window) → Options →select K 1: Reduced integration → K3: Plane Stress →OK→Close (the Element Type window)
1.4定义材料参数
Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:200e9,PRXY:0.3→ OK
1.5生成几何模型
生成特征点
Main Menu: Preprocessor →Modeling →Create →Key points →In Active CS →依次输入四个点的坐标(每次输入后按Apply,最后按OK):input:1(0,0,0), 2(10,0,0), 3(10,2,0), 4(0,2,0) →OK
生成面
Main Menu: Preprocessor → Modeling → Create
→ Areas → Arbitrary → Through KPS →依次
连接四个特征点,1 → 2 → 3 → 4 → OK
注意:上面两步也可简化为:
Main Menu: Preprocessor → Modeling → Create
→Areas → Rectangle → By two corners → WP
X, WP Y 均输入0, Width 输入10, Height 输入
2 → OK
1.6 网格划分
=0
Main Menu: Preprocessor →Meshing →Mesh Tool→(Size Controls) lines: Set →拾取长边: OK→input NDIV: 50→Apply→拾取短边: →input NDIV: 10 →OK →(back to the mesh tool window)Mesh: Areas, Shape: Quad, Mapped →Mesh →Pick All (in Picking Menu) → Close( the Mesh Tool window)
1.7 模型施加约束
给左边施加固定约束
Main Menu: Solution →Define Loads →Apply →Structural
→Displacement → On lines →选左边线→OK →select 第
一行: ALL DOF →第四行 VALUE 选 0: → OK
给梁的上边施加线性分布载荷
ANSYS 命令菜单栏: Parameters →Functions →Define/Edit
→
1) 在下方的下拉列表框(第三行)内选择X作为设置的变量;
2) 在Result窗口中出现{X},写入所施加的载荷函数(力的单
位:N):10000-1000*{X};
3) File → Save 输入my_q(文件扩展名:func) →返回:
Parameters →Functions →Read from file:将需要的
my_q.func文件打开,任给一个参数名qq, Local coordinate
system id for (x,y,z) 栏选0→OK
Utility menu → plotctrls → Symbols → Show pres and
convect as 表框内的Face outline下拉改为 arrows
Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Lines →拾取梁的上层线→OK →在下拉列表框中选择:Existing table →Apply →选择需要的载荷参数名qq→OK
solution→load step opts→write LSFile输入文件名(注意:显示的载荷箭头应当沿着长度有长短不同)
1.8 分析计算
Main Menu: Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK
1.9 结果显示
Main Menu: General Postproc →Plot Results →Deformed Shape… → select Def + Undeformed →OK (back to Plot Results window)→Contour Plot →Nodal Solu…→select: Stress → X Component of stress → OK
1.10 退出系统
ANSYS Utility Menu: File →
Exit→ Save Everything→ OK。
