2019-2020年陕西省咸阳市实验中学高二(上)数学(理)第三次月考试题【含答案】
陕西省咸阳市实验中学2020-2021学年高二上学期第三次月考数学(理)试题
C．100D．99
8．若实数x、y满足 ，则 的取值范围是 ( )
A． B． C． D．
9． 满足约束条件 ，若目标函数 最大值为12，则 的最小值为（）
A．1B．2C．4D．
10．在R上定义运算：x*y＝x(1－y).若不等式(x－a)*(x＋a)＜1对任意实数x恒成立，则（）
（2）若 ，不等式 恒成立，求实数 的取值范围.
21．已知不等式 的解集为
（1）求实数 的值；
（2）若函数 在区间 上递增，求关于 的不等式 的解集．
22．某渔船在航行中不幸遇险，发出求救信号，我海军舰艇在A处获悉后，立即测出该渔船在方位角为45°、距离A为10海里的C处，并测得渔船正沿方位角105°的方向，以9海里/时的速度向某小岛B靠拢，我海军舰艇立即以21海里/时的速度前去营救，恰在小岛B处追上渔船.
A．6B．7C．8D．9
5．在△ABC中，a、b、c分别是角A、B、C的对边，如果2b=a+c，B=30°，△ABC的面积是 ，则b=（）
A．1+ B． C． D．2+
6．在 中，角 所对的边分 ．若 ，则 （）
A．- B． C．-1D．1
7．若数列{xn}满足lgxn＋1＝1＋lgxn(n∈N＋)，且x1＋x2＋x3＋…＋x100＝100，则lg(x101＋x102＋…＋x200)的值为( )
当直线 过点 时，在 轴上的截距最大，此时目标函数取得最大值，
又由 ，解得 ，
此时目标函数 取得最大值12，即 ，即 ，
则 ，
当且仅当 时，即 时等号成立，
所以 的最小值为4.
故选：C.
【点睛】
本题主要考查了线性规划问题和基本不等式求解函数的最值问题，其中解答中准确画出不等式组所表示的平面区域，求得 的关系式是解答的关键，着重考查数形结合思想，以及推理与运算能力.
陕西实验中学2019-2020年下学期高二理科数学第三次检测试题附答案
实验中学2019-2020年下学期第三次阶段检测试题高二数学（理科）试题命题人： 审阅人：注意事项：1．本试卷分为第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷为选择题，用2B 铅笔将答案涂在答题卡上。
第Ⅱ卷为非选择题，用0.5mm 黑色签字笔将答案答在答题纸上。
考试结束后，只收答题卡和答题纸。
2．答第Ⅰ、Ⅱ卷时，先将答题卡首和答题纸首有关项目填写清楚。
3．全卷满分150分，考试时间120分钟第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.复数7413iz i-=+在复平面内所对应的点位于（ ） A.第一象限B.第二象限C.第三象限D.第四象限2.设E （X ）=10，E （Y ）=3，则E （3X +5Y ）=（ ） A ．45B ．40C ．30D ．153.6本相同的数学书和3本相同的语文书分给9个人，每人1本，共有不同分法（ ）A ．CB ．AC ．AD ．AA4.由曲线y=，直线y=x ﹣2及y 轴所围成的图形的面积为（ ）A ．B ．4C ．D ．65.下面是利用数学归纳法证明不等式22(1)n n +-<（2n ≥，且*n ∈N ）的部分过程： “……假设当n k =（2k ≥）时，22(1)k k +-<，故当1n k =+时，有______，因为=<______，故2(1)(1)k k +-<+，……”则横线处应该填（ ）A.2(1)k +-2k <+21k +B.22(1)k k +-<+21k +C.2(1)k +-2k <+22k +D.22(1)k k +-<+22k +6.()()3411x x --的展开式2x的系数是（ ）A ．﹣6B ．﹣3C ．0D ．37.盒子里有25个外形相同的球，其中10个白的，5个黄的，10个黑的，从盒子中任意取出一球，已知它不是白球，则它是黑球的概率为（ ）A ．B ．C ．D ．8.函数x x y ln =过点()1,0-的切线为（ ）A.1--=x y B.1-=x yC.12-=x yD.不存在9.小红和小明利用体育课时间进行投篮游戏，规定双方各投两次，进球次数多者获胜.已知小红投篮命中的概率为35，小明投篮命中的概率为12，且两人投篮相互独立，则小明获胜的概率为（ ） A.1225 B.25 C.825 D.62510.某大学推荐7名男生和5名女生参加某企业的暑期兼职，该企业欲在这12人中随机挑选3人从事产品的销售工作，记抽到的男生人数为X ，则()E X =（ ） A.2B.74C.94D.3211.已知函数)(x f x y '=的图象如图所示（其中 )(x f '是函数)(x f 的导函数），下面四个图象中)(x f y =的图象大致是 ( )12定义在R 上的函数()f x 满足()()2e xf x f x '-<（e 为自然对数的底数），其中()f x '为()f x 的导函数，若2(2)4f e =，则()e 2x f x x >的解集为（ ） A.(,1)-∞B.(1,)+∞C.(,2)-∞D.(2,)+∞第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分.13.设z ∈C ，且（1﹣i ）z=2i （i 是虚数单位），则|z |= . 14.设当θ=x时，函数()x x x f cos 2sin -=取得最大值5，则=θcos ________.15.已知,0,0≥≥yx 且1=+y x ，则22yx +的取值范围 .16.甲罐中有5个红球，2个白球和3个黑球，乙罐中有4个红球，3个白球和3个黑球．先从甲罐中随机取出一球放入乙罐，分别以A 1，A 2和A 3表示由甲罐取出的球是红球，白球和黑球的事件；再从乙罐中随机取出一球，以B 表示由乙罐取出的球是红球的事件，则下列结论中正确的是 （写出所有正确结论的编号）．①；②；③事件B 与事件A 1相互独立； ④A 1，A 2，A 3是两两互斥的事件；⑤P （B ）的值不能确定，因为它与A 1，A 2，A 3中哪一个发生有关．三、解答题：（本大题共6小题，共70分. 解答应写出文字说明,证明过程或演算步骤）17. (本小题满分10分)已知a ，b 均为实数，求证：().2222b a b a +≥+18.(本小题满分12分)先阅读下列不等式的证法：已知12,a a ∈R ，121a a =＋，求证：221212a a +≥. 证明：构造函数222221212()()()22()f x x a x a x x a a =-+-=-++． 因为对一切x ∈R ，恒有()0f x ≥，所以2212Δ48()0a a =-+≤，从而得221212a a +≥. 再解决以下2题：(Ⅰ)若1212,,1n n a a a R a a a ∈+++=，，，请写出上述结论的推广式；(Ⅱ)参考上述解法，对你推广的结论加以证明．19.(本小题满分12分)数列{}n a 满足*153618,n n a a n n N ++=+∈，且14a =. （Ⅰ）写出{}n a 的前4项，并猜想其通项公式；（6分） （Ⅱ）用数学归纳法证明你的猜想.（6分）20.(本小题满分12分)某公司甲、乙、丙三位员工独立参加某项专业技能测试，根据平时经验，甲、乙、丙能达标的概率分别为，，；（Ⅰ）若甲、乙两位员工各自参加一次测试，各自测试达标与否互不影响，求甲、乙两位员工中恰好只有一人达标的概率；（6分）（Ⅱ）若三位员工各自参加一次测试，记达标的人数为X,求X 的分布列和数学期望.（6分）21.(本小题满分12分)设()42280128223x x a a x a x a x -+=+++⋅⋅⋅+.（Ⅰ）求0a 的值； （Ⅱ）求864aa a a +++的值.22.(本小题满分12分)已知函数()()0≠=a eaxx f x（e 为自然对数的底数）. （Ⅰ）讨论函数()f x 的单调性； （Ⅱ）若1=a 时，如果()t x f =有两个不等的实根21,xx ，求实数t的范围，并证明：.221>+x x高二数学（理）答案一．选择题：13.552-14. ⎥⎦⎤⎢⎣⎡1,2116. ②④ 三．解答题：17.略 18.略 19.（1）,22,16,10,44321====a a a a 猜想：16-=n a n（2）证明略 20.解： （1）125()60121=X E 21.（12分）解：（1）160=a ；（2）104984=+⋅⋅⋅++a a a 22.（12分） 解：(1),0>a ()x f 在()1,∞-上递增，在()+∞,1上递减； ,0<a ()x f 在()1,∞-上递减，在()+∞,1上递增（2）⎪⎭⎫ ⎝⎛∈e t 1,0 欲证122x x +>，即证212x x >-，因为1201x x <<<，故122,(1,)x x -∈+∞，又因为()f x 在(1,)+∞上单调递减，故只需证21()(2)f x f x <-，又因为12()()f x f x =，故也即证11()(2)f x f x <-，构造函数()()(2),(0,1)H x f x f x x =--∈，则等价于证明()0H x <对(0,1)x ∈恒成立.由221()()(2)(1)0x x xH x f x f x e e--'''=+-=->，则()H x 在(0,1)x ∈上单调递增，所以()(1)0H x H <=，即已证明()0H x <对(0,1)x ∈恒成立，故原不等式122x x +>亦成立.。
实验中学高二数学上学期第三次月考试题理含解析
所以 ,
所以 ,故选A．
8。若实数x、y满足 ，则 的取值范围是 （ ）
A。 B。 C. D。
【答案】A
【解析】
由 满足的约束条件画出可行域,如图:
目标函数 表示区域内的动点 与定点 连线的斜率
由图可知 是 最小值，故 的取值范围是
故答案选
点睛：线性规划转化为几何意义, 转化为可行域内的点到点 连线的斜率，先画出可行域，然后计算出斜率范围．
∴∠A＝60°.
在△ABC中,由正弦定理得sin B＝ ，
∵b2＝ac,∠A＝60°，
∴ ＝ ＝sin 60°＝ .
19。解关于x的不等式ax2－（a＋1)x＋1〈0。
【答案】见解析
【解析】
【分析】
将不等式化为(ax－1)（x－1）<0，再对 的取值范围讨论，分类解不等式.
【详解】原不等式可化为（ax－1）（x－1）<0
16。设 为正数， ，则 的最大值是___________
【答案】
【解析】
【分析】
根据柯西不等式直接求最值.
【详解】
当且仅当 时取等号
,即 的最大值是
故答案为：
【点睛】本题考查利用柯西不等式求最值，考查基本分析求解能力，属基础题.
三、解答题(本大题共6小题，共70分.)
17.已知等差数列{an｝中，a1=1，a3=﹣3．
(II）由（I）可知an=3﹣2n，
所以Sn= =2n﹣n2，
进而由Sk=﹣35，可得2k﹣k2=﹣35，
即k2﹣2k﹣35=0，解得k=7或k=﹣5，
又k∈N+,故k=7为所求．
点评：此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值，是一道基础题．
陕西省咸阳市实验中学2019-2020年高二上学期第三次月考英语试卷
英语试题第一部分听力(共两节, 满分30分)第一节(共5小题; 每小题1. 5分, 满分7. 5分)听下面5段对话。
每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。
听完每段对话后, 你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What can we know about the sports centre?A. It is under construction.B. It is very famous in the world.C. It is the most modern one in the country.2. Why does the woman want to get the blue coat?A. Because she prefers the color.B. Because the price is reasonable.C. Because it is on sale now.3. What musical instrument does the woman play the most?A. The violin.B. The flute.C. The guitar.4. What do we learn from the conversation?A. It rained heavily today.B. The man had a cold today.C. Many animals were on the street today.5. What was Sally doing?A. Lending money to a student.B. Asking for financial aid.C. Reading students’ applications.第二节(共15小题; 每小题1. 5分, 满分22. 5分)听下面5段对话。
陕西省咸阳市实验中学2019_2020学年高二数学上学期第三次月考试题理(含解析)
陕西省咸阳市实验中学2019-2020学年高二数学上学期第三次月考试题 理（含解析）一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中只有一项是符合题目要求的)1.在等差数列{}n a 中，若34567450a a a a a ++++=，则28a a +的值等于（ ） A. 45 B. 75C. 300D. 180【答案】D 【解析】试题分析：由已知得55285545090,2180a a a a a =∴=+==，故选D ． 考点：等差数列的性质．2.在ABC 中，若2sin b a B =，则角A 为（ ） A. 30°或60° B. 45°或60° C. 120°或60° D. 30°或150°【答案】D 【解析】 【分析】由正弦定理和题设条件，求得1sin 2A =，进而求得角A 的值，得到答案. 【详解】在ABC 中，因为2sin b a B =， 由正弦定理可得sin 2sin sin B A B =， 又由(0,)B π∈，则sin 0B >，所以1sin 2A =， 又因为(0,)A π∈，所以30A =或150A =. 故选：D.【点睛】本题主要考查了正弦定理的应用，以及特殊角的三角三角函数的应用，着重考查运算与求解能力.3.a∈R，且a 2＋a ＜0，那么－a ，－a 3，a 2的大小关系是( ) A a 2＞－a 3＞－a B. －a ＞a 2＞－a 3 C. －a 3＞a 2＞－aD. a 2＞－a ＞－a 3【答案】B 【解析】试题分析：由已知中a 2+a ＜0，解不等式可能求出参数a 的范围，进而根据实数的性质确定出a 3，a 2，-a ，-的大小关系．解：因为a 2+a ＜0，即a （a+1）＜0，所以-1＜a ＜0，根据不等式的性质可知－a ＞a 2＞－a 3，故选B. 考点：不等式比较大小点评：本题考查的知识点是不等式比较大小，其中解不等式求出参数a 的范围是解答的关键 4.设等差数列{a n }的前n 项和为S n ，若a 1＝－11，a 4＋a 6＝－6，则当S n 取最小值时，n 等于( ) A. 6 B. 7C. 8D. 9【答案】A 【解析】分析：条件已提供了首项，故用“a 1，d”法，再转化为关于n 的二次函数解得． 解答：解：设该数列的公差为d ，则a 4+a 6=2a 1+8d=2×（-11）+8d=-6，解得d=2， 所以S n =-11n+()n n 12-×2=n 2-12n=(n-6)2-36，所以当n=6时，S n 取最小值．故选A点评：本题考查等差数列的通项公式以及前n 项和公式的应用，考查二次函数最值的求法及计算能力．5.在ABC ∆中，,,a b c 分别为,,A B C 的对边，如果,,a b c 成等差数列，30B =︒，ABC ∆的面积为32，那么b =（ ）B. 1 D.2+【答案】B 【解析】试题分析：由余弦定理得22222cos ()22cos b a c c B a c ac ac B =+-=+--，又面积1sin 2ABC S ac B ∆=13642ac ac ==⇒=，因为a b c ，，成等差数列，所以2a c b +=，代入上式可得22412b b =--24b =+，解得1b =+B ．考点：余弦定理；三角形的面积公式．6.在ABC ∆中，角,,A B C 所对的边分,,a b c ．若cos sin a A b B =，则2sin cos cos A A B +=（ ）A. -12B.12C. -1D. 1【答案】D 【解析】试题分析：由cos sin a A b B =得2sin cos sin A A B =222sin cos cos sin cos 1A A B B B ∴+=+=考点：正弦定理及同角间的三角函数关系 点评：正弦定理sin sin sin a b cA B C==可实现三角形边与角的互相转化，同角间三角函数关系22sin cos 1B B +=7.若数列{x n }满足lg x n ＋1＝1＋lg x n (n ∈N ＋)，且x 1＋x 2＋x 3＋…＋x 100＝100，则lg(x 101＋x 102＋…＋x 200)的值为( ) A. 102 B. 101 C. 100 D. 99【答案】A 【解析】由1lg 1ln n n x x +=+，得110n nx x +=， 所以数列{}n x 是公比为10的等比数列，又10010010010111022200100,,,x x q x x q x x q =⋅=⋅=⋅，所以10010010210110220012100()1010010x x x q x x x +++=+++=⋅=，所以()101102200lg 102x x x +++=，故选A ．8.若实数x 、y 满足22000x y y x y --≥⎧⎪≥⎨⎪-≥⎩，则11y x-+的取值范围是 ( )A. 1[,1)2-B. 11[,]23-C. 1[,)2-+∞D. 1[1,]3-【答案】A 【解析】由,x y 满足的约束条件画出可行域，如图：目标函数11y x ω-=+表示区域内的动点(),x y 与定点()1,1P -连线的斜率 由图可知()011112PA k -==---是ω的最小值，故ω的取值范围是)112⎡-⎢⎣，故答案选A点睛：线性规划转化为几何意义，11y x -+转化为可行域内的点到点()1,1-连线的斜率，先画出可行域，然后计算出斜率范围．9.x y ，满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩，若目标函数(43)00z ax by a b =+>>，最大值为12，则11a b+的最小值为（ ） A. 1B. 2C. 4D.12【答案】C 【解析】 【分析】利用线性规划求得1a b +=，从而1111()()a b a b a b+=++，展开后利用基本不等式，即可求解.【详解】画出不等式组1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩所表示的平面区域，如图所示的阴影部分（包含边界），由直线43z ax by =+，可得433a z y x b b =-+，由0,0a b >>，可得403a b-<， 当直线433a zy x b b=+过点B 时，在y 轴上的截距最大，此时目标函数取得最大值， 又由122x y x y -=-⎧⎨-=⎩，解得(3,4)B ，此时目标函数43z ax by =+取得最大值12，即121212a b +=，即1a b +=，则1111()()2224b a b aa b a b a b a b a b+=++=++≥+⨯=， 当且仅当b aa b=时，即a b =时等号成立， 所以11a b+的最小值为4. 故选：C.【点睛】本题主要考查了线性规划问题和基本不等式求解函数的最值问题，其中解答中准确画出不等式组所表示的平面区域，求得,a b 的关系式是解答的关键，着重考查数形结合思想，以及推理与运算能力.10.定义在R 上的运算：()1x y x y *=-.若不等式()()1x a x a -*+<对任意实数x 都成立，则（ ） A. 3122a -<< B. 1322a -<< C. 11a -<< D. 02a <<【答案】B 【解析】 【分析】由题意得出2210x x a a -+-+>对任意实数x 都成立，由判别式小于0求解即可. 【详解】不等式()()1x a x a -*+<可化为()()11x a x a -⋅--<，即2210x x a a -+-+>对任意实数x 都成立，∴()21410a a ∆=-⨯-+<，解得1322a -<<.故选B. 【点睛】本题主要考查了一元二次不等式的恒成立问题，属于中档题.11.钝角三角形的三边为a ，1a +，2a +，其最大角不超过120︒，则a 的取值范围是（ ） A. 0<<3aB.332a ≤< C. 23a <≤D.512a ≤<【答案】B 【解析】钝角三角形的三边分别是a ，a+1，a+2，其最大内角不超过120°，∴()()()()222121210212a a a a a a a a ⎧+++⎪++-+⎨≥-⎪⋅+⎩＞＞，解得332a ≤＜，故选B ．点睛：在判断三角形的形状时，若三边长均含有参数，一定要考虑构成三角形的条件，即任意两边之和大于第三边，这也是本题的易错点. 12.已知函数221(),()()2x f x x g x m x =+=-，若任意的[]11,2x ∈，存在[]21,1x ∈-，使得()()12f x f x ≥，则实数m 的取值范围是（ ） A. )5,2⎡-+∞⎢⎣ B. [)1,-+∞ C. [)4,-+∞D.12⎡⎫-+∞⎪⎢⎣⎭【答案】A 【解析】 【分析】利用指数函数的的单调性求出()g x 是单调递减函数，利用导数判断()f x 为增函数，再根据题意()f x 的最小值大于等于()g x 的最小值即可求解.【详解】由于12x⎛⎫ ⎪⎝⎭是单调递减函数，故()g x 是单调递减函数，由于[]21,1x ∈-，故()g x 的最小值为()112g m =-， 对()f x 求导得()222f x x x '=-， 令()0f x '=，可得1x =，且1x >时，()f x 为增函数， 故()f x 的最小值为()1123f =+=，要使得()()12f x f x ≥，则有132m ≥-，解得52m ≥-. 故选：A【点睛】本题考查了指数函数的单调性、利用导数求函数的最值、含有一个量词的不等式恒成立问题，属于中档题.二、填空题(本大题共4小题，每小题5分，共20分.) 13.在△ABC 中，若a ＝cos C ＝13，S △ABC ＝b ＝________． 【答案】【解析】 由cosC=13， 得，所以S △ABC =12absinC=12×所以b=14.已知{a n }为等差数列，S n 为{a n }的前n 项和，n∈N *，若a 3=16，S 20=20，则S 10值为 ． 【答案】110 【解析】【详解】由题意a 3=16，故S 5=5×a 3=80，由数列的性质S 10﹣S 5=80+25d ，S 15﹣S 10=80+50d ，S 20﹣S 15=80+75d ， 故S 20=20=320+150d ，解之得d=﹣2 又S 10= =80+80+25d=160﹣50=110 故答案为110点评：本题考点是等差数列的性质，考查等差数列前n 项和的性质，以及数列的中项的运用，本题技巧性较强，属于等差数列的性质运用题，解答本题，要注意从题设条件中分析出应该用那个性质来进行转化．15.设点P(x ，y)在函数y ＝4－2x 的图象上运动，则9x＋3y的最小值为________． 【答案】18 【解析】试题分析：根据题意，由于点P(x ，y)在函数y ＝4－2x 的图象上运动，，则可知2x+y=4，由于9x＋3y18≥==，故可知当y=2,x=1时取得等号，故答案为18. 考点：均值不等式点评：主要是考查了不等式求解最值的运用，属于基础题．16.设,,a b c 为正数，241a b c ++=的最大值是___________【答案】2【解析】 【分析】根据柯西不等式直接求最值.【详解】22222225()(11((2)]22a b c +≤++++=当且仅当25,5a b c===时取等号1022a b c∴++≤，即2a b c++的最大值是10 2故答案为：10 2【点睛】本题考查利用柯西不等式求最值，考查基本分析求解能力，属基础题.三、解答题(本大题共6小题，共70分.)17.已知等差数列{a n}中，a1=1，a3=﹣3．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若数列{a n}的前k项和S k=﹣35，求k的值．【答案】（Ⅰ）a n=1+（n﹣1）×（﹣2）=3﹣2n（Ⅱ）k=7【解析】试题分析：（I）设出等差数列的公差为d，然后根据首项为1和第3项等于﹣3，利用等差数列的通项公式即可得到关于d的方程，求出方程的解即可得到公差d的值，根据首项和公差写出数列的通项公式即可；（II）根据等差数列的通项公式，由首项和公差表示出等差数列的前k项和的公式，当其等于﹣35得到关于k的方程，求出方程的解即可得到k的值，根据k为正整数得到满足题意的k的值．解：（I）设等差数列{a n}的公差为d，则a n=a1+（n﹣1）d由a1=1，a3=﹣3，可得1+2d=﹣3，解得d=﹣2，从而，a n=1+（n﹣1）×（﹣2）=3﹣2n；（II）由（I）可知a n=3﹣2n，所以S n==2n﹣n2，进而由S k=﹣35，可得2k﹣k2=﹣35，即k2﹣2k﹣35=0，解得k=7或k=﹣5，又k∈N+，故k=7为所求．点评：此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值，是一道基础题．18.在△ABC 中，a ，b ，c 分别是∠A 、∠B 、∠C 的对边长，已知a ，b ，c 成等比数列，且a 2－c 2＝ac －bc .求∠A 的大小及sin b Bc的值． 【答案】∠A ＝60°，sin 3b Bc =【解析】试题分析：由题意得2b ac =代入原式，求得222a b c bc =+-，进而根据余弦定理，求得cos A 的值，进而得到角A ，再把2b ac =和A 的值代入正弦定理，即可求解sin b Bc的值． 试题解析：∵a、b 、c 成等比数列，∴b 2＝ac. 又∵a 2－c 2＝ac －bc ， ∴b 2＋c 2－a 2＝bc.在△ABC 中，由余弦定理得cos A ＝＝＝，∴∠A＝60°.在△ABC 中，由正弦定理得sin B ＝，∵b 2＝ac ，∠A＝60°， ∴＝＝sin 60°＝.19.解关于x 的不等式ax 2－(a ＋1)x ＋1<0. 【答案】见解析 【解析】 【分析】将不等式化为(ax －1)(x －1)<0，再对a 的取值范围讨论，分类解不等式. 【详解】原不等式可化为(ax －1)(x －1)<0 当a ＝0时，原不等式解为x >1.当a <0时，不等式可化为1()(1)0x x a-->， ∵11a<，∴1x a <或x >1.当a >0时，原不等式可化为1()(1)0x x a--< 若11a <，即a >1，则11x a<<； 若11a=，即a ＝1，则x ∈∅； 若11a >，即0<a <1，则11x a <<. 综上所述，当a <0时，原不等式的解集为1{|x x a <或1}x >； 当a ＝0时，原不等式的解集为{x |x >1}；当0<a <1时，原不等式的解集为1{|1}x x a<<；当a ＝1时，原不等式的解集为∅；当a >1时，原不等式的解集为1{|1}x x a <<. 【点睛】本题考查一元二次不等式的解法，解题的关键是对参数的范围讨论，分类解不等式，属于中档题.20.设函数()|1||21|f x x x =-+-.（1）求不等式()2f x ≥的解集；（2）若x R ∀∈，不等式()||f x a x ≥恒成立，求实数a 的取值范围.【答案】（1）{|0x x ≤或4}3x ≥（2）1a ≤【解析】【分析】（1）根据绝对值定义将不等式转化为三个不等式组，求其并集得结果； （2）先讨论x 为零的情况，再对x 不为零的情况分离变量，利用绝对值三角不等式求最小值，解得结果.【详解】（1）1()21212x f x x x ≥⎧≥∴⎨-+-≥⎩ 或1121212x x x ⎧<<⎪⎨⎪-+-≥⎩或121122x x x ⎧≤⎪⎨⎪-+-≥⎩143x x ≥⎧⎪∴⎨≥⎪⎩或1122x x ⎧<<⎪⎨⎪≥⎩或120x x ⎧≤⎪⎨⎪≥⎩，43x ∴≥ 或x ∈∅或0x ≤， 即解集为{|0x x ≤或4}3x ≥（2）|1|(|2)||||1|f x a x a x x x -+≥-≥⇔当0x =时，20a R ≥∴∈当0x ≠时，||11|1||21||1||2|a x x x a x x ≥⇔---+-≥+ 因为1111|1||2||(1)(2)|1x x x x-+----=≥，所以1a ≤ 综上，1a ≤【点睛】本题考查分类讨论法解含绝对值不等式、利用绝对值三角不等式求最值，考查分类讨论思想方法以及综合分析求解能力，属中档题.21.已知不等式230x x t -+<的解集为{}1,x x m x R <<∈（1）求实数,t m 的值；（2）若函数()24f x x ax =-++在区间(],1-∞上递增，求关于x 的不等式()2log 320a mx x t -++-<的解集． 【答案】（1）22m t =⎧⎨=⎩；（2）130122x x x ⎧⎫<<<<⎨⎬⎩⎭或； 【解析】【分析】（1）根据不等式解集得对应方程230x x t -+=的根，根据韦达定理解得实数,t m 的值；（2）先根据二次函数单调性性质确定a 的范围，再根据对数函数单调性化简不等式，最后解一元二次不等式得结果.【详解】（1）由题意得1m ，为方程230x x t -+=的根，所以13212m m m t t +==⎧⎧∴⎨⎨⨯==⎩⎩， （2）因为函数()24f x x ax =-++在区间(],1-∞上递增，所以122a a ≥∴≥， 因此由()2log 320a mx x t -++-<得20321mx x t <-++-<,2 0231x x <-+<,301320112212x x x x x ⎧<<⎪⎪∴<<<<⎨⎪><⎪⎩或或,即130122x x x ⎧⎫<<<<⎨⎬⎩⎭或. 【点睛】本题考查一元二次不等式解集与一元二次方程根的关系、对数函数单调性以及解二次不等式，考查基本分析转化求解能力.22.某渔船在航行中不幸遇险，发出求救信号，我海军舰艇在A 处获悉后，立即测出该渔船在方位角为45°、距离A 为10海里的C 处，并测得渔船正沿方位角105°的方向，以9海里/时的速度向某小岛B 靠拢，我海军舰艇立即以21海里/时的速度前去营救，恰在小岛B 处追上渔船.（1）试问舰艇应按照怎样的航向前进？（2）求出舰艇靠近渔船所用的时间？(参考数据：133333cos 21.8,sin 21.8,tan 21.814==︒︒=︒) 【答案】（1）舰艇应按照北偏东66.8°的航向前进（2）舰艇靠近渔船所用的时间为23小时 【解析】【分析】 （1）设舰艇靠近渔船所用的时间为x 小时，则219AB x BC x ==，，根据渔船在方位角为45°，渔船正沿方位角105°的方向行驶，得到ACB ∠，利用正弦定理求得BAC ∠即可.（2）在ABC 中，结合（1）的结论，利用余弦定理求解即可.【详解】设舰艇靠近渔船所用的时间为x 小时，则219AB x BC x ==，，结合图形可知，275145∠=︒∠=︒，，则4575120ACB ∠=︒+︒=︒.（1）由正弦定理得，sin sin AB BC ACB BAC=∠∠，即219sin120sin x x BAC=︒∠，sin 14BAC ∴∠=， 218BAC ∴∠=︒．，21845668︒+︒=︒．．，∴舰艇应按照北偏东66.8°的航向前进.（2）在ABC 中，2222AB AC BC AC BC cos ACB =+-⋅⋅∠，即()()222211092109120x x x cos =+-⨯⨯⋅︒， 解得23x =或512x =-(不合题意，舍去)， ∴舰艇靠近渔船所用的时间为23小时. 【点睛】本题主要考查正弦定理、余弦定理在实际问题中的应用，还考查了运算求解的能力，属于中档题.。
咸阳市实验中学2019-2020学年高三上学期第三次月考试卷数学含答案
咸阳市实验中学2019-2020学年高三上学期第三次月考试卷数学含答案 班级__________ 座号_____ 姓名__________ 分数__________
一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）
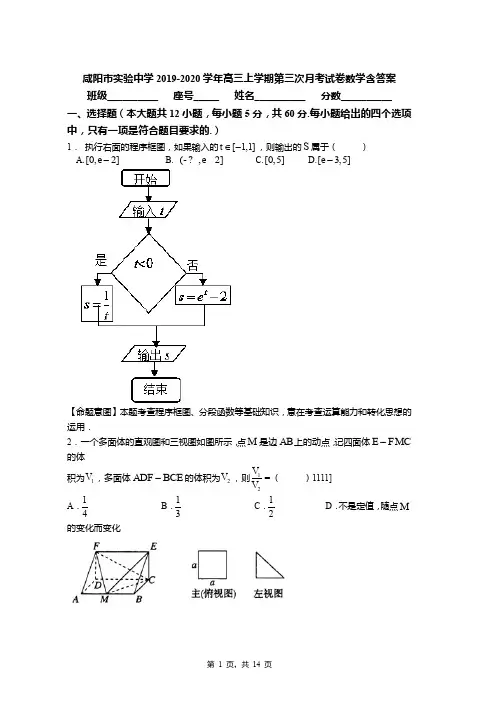
1． 执行右面的程序框图，如果输入的[1,1]t ∈-，则输出的S 属于（ ）
A.[0,2]e -
B. (,2]e -?
C.[0,5]
D.[3,5]e -
【命题意图】本题考查程序框图、分段函数等基础知识，意在考查运算能力和转化思想的
运用．
2． 一个多面体的直观图和三视图如图所示，点M 是边AB 上的动点，记四面体FMC E -的体
积为1V ，多面体BCE ADF -的体积为2V ，则
=2
1V V （ ）1111] A ．41 B ．31 C ．21 D ．不是定值，随点M 的变化而变化
3． 已知命题p ：∃x ∈R ，cosx ≥a ，下列a 的取值能使“￢p ”是真命题的是（ ） A ．﹣1 B ．0
C ．1
D ．2 4． 已知函数()f x 的定义域为[],a b ，函数()y f x =的图象如图甲所示，则函数(||)
f x 的图象是
图乙中的（ ）
5． 如图所示，已知四边形ABCD 的直观图是一个边长为的正方形，则原图形的周长为（ ）
A ．22
B ． C.
D ．42+2
6． 在极坐标系中，圆的圆心的极坐标系是( )。
A
B
C
D
7． 若集合A ＝{－1,1}，B ＝{0,2}，则集合{z|z ＝x ＋y ，x ∈A ，y ∈B}中的元素的个数为( )
A5
B4
C3。
陕西省咸阳市实验中学2019-2020学年高二上学期第三次月考数学(理科)试卷
数学试题(理)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中只有一项是符合题目要求的)1．在等差数列{a n}中，若a3＋a4＋a5＋a6＋a7＝450，则a2＋a8的值等于( ) A．45 B．75 C．180 D．3002．在△ABC中，若b＝2a sin B，则角A为( )A．30°或60° B．45°或60°C．120°或60° D．30°或150°3．a∈R，且a2＋a＜0，那么－a，－a3，a2的大小关系是( )A．a2＞－a3＞－a B．－a＞a2＞－a3C．－a3＞a2＞－a D．a2＞－a＞－a34．设等差数列{a n}的前n项和为S n.若a1＝－11，a4＋a6＝－6，则当S n取最小值时，n等于( )A．6 B．7 C．8 D．95．△ABC中，a、b、c分别为A、B、C的对边，如果a，b，c成等差数列，B＝30°，△ABC的面积为32，那么b＝( )A.1＋32B．1＋ 3 C.2＋32D．2＋ 36．在△ABC中，角A，B，C所对的边分别为a，b，c.若a cos A＝b sin B，则sin A cos A＋cos2B＝( )A．－12B.12C．－1 D．17．若数列{x n}满足lg x n＋1＝1＋lg x n(n∈N＋)，且x1＋x2＋x3＋…＋x100＝100，则lg(x101＋x102＋…＋x200)的值为( )A．102 B．101 C．100 D．998．实数x ，y 满足不等式组⎩⎨⎧y ≥0x －y ≥02x －y －2≥0，则ω＝y －1x ＋1的取值范围为( ) A ．[－1，13] B ．[－12，13] C ．[－12，＋∞) D．[－12，1)9．设x ，y 满足约束条件⎩⎨⎧x ＋y ≥1，x －y ≥－1，2x －y ≤2，若目标函数z ＝4ax ＋3by (a >0，b >0)最大值为12，则1a ＋1b的最小值为( )A ．1B ．2C ．4 D.1210．在R 上定义运算*：x *y ＝x (1－y )．若不等式(x －a )*(x ＋a )＜1对任意实数x 均成立，则( )A ．－1＜a ＜1B ．0＜a ＜2C ．－12＜a ＜32D ．－32＜a ＜1211．钝角三角形的三边为a ，a ＋1，a ＋2，其最大角不超过120°，则a 的取值范围是( )A ．0＜a ＜3 B.32≤a ＜3 C ．2＜a ≤3D ．1≤a ＜5212已知函数221(),()(),2x f x x g x m x=+=- 若[][]121,21,1∈∈-任意的x ，存在x 使得12x )()f f x ≥（，则实数m 的取值范围是( )A ．5,2⎡⎫-+∞⎪⎢⎣⎭B.[)1,-+∞C ． [)4,-+∞D ．12⎡⎫-+∞⎪⎢⎣⎭二、填空题(本大题共4小题，每小题5分，共20分．)13．在△ABC 中，已知a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________.14．已知{a n }是等差数列，S n 为其前n 项和，n ∈N *.若a 3＝16，S 20＝20，则S 10的值为________．15．设点P (x ，y )在函数y ＝4－2x 的图像上运动，则9x ＋3y 的最小值为________．16．设a,b,c 为正数，241a b c ++= 的最大值是 ___________ 三、解答题(本大题共6小题，共70分．)17．(本小题满分10分)已知等差数列{a n }中，a 1＝1，a 3＝－3.(1)求数列{a n }的通项公式；(2)若数列{a n }的前k 项和S k ＝－35，求k 的值．18．(本小题满分12分)在△ABC 中，a ，b ，c 分别是∠A 、∠B 、∠C 的对边长，已知a ，b ，c 成等比数列，且a 2－c 2＝ac －bc .求∠A 的大小及b sin Bc的值． 19．(本小题满分12分)解关于x 的不等式ax 2－(a ＋1)x ＋1＜0. 20．(本小题满分12分设函数()|1||21|f x x x =-+-(1)求不等式()2f x ≥ 的解集；(2)若x R ∀∈ ，不等式()||f x a x ≥ 恒成立，求实数a 的取值范围 21．(本小题满分12分)已知不等式x 2－3x ＋t ＜0的解集为{x |1＜x ＜m ，x ∈R }．(1)求t ，m 的值；(2)若函数f (x )＝－x 2＋ax ＋4在区间(－∞，1]上递增，求关于x 的不等式log a (－mx 2＋3x ＋2－t )＜0的解集．22．(本小题满分12分)某渔船在航行中不幸遇险，发出求救信号，我海军舰艇在A 处获悉后，立即测出该渔船在方位角为45°、距离A 为10海里的C 处，并测得渔船正沿方位角105°的方向，以9海里/时的速度向某小岛B 靠拢，我海军舰艇立即以21海里/时的速度前去营救，恰在小岛B 处追上渔船． (1)试问舰艇应按照怎样的航向前进？ (2)求出舰艇靠近渔船所用的时间？(参考数据：cos21.8°＝1314，sin21.8°＝3314，tan21.8°＝3313)数学（理）参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C DBABDADCCBA填空题13. 2 3 14. 110 15.18 16.10217. 解析： (1) a n ＝＝3－2n . (2)由(1)可知a n ＝3－2n ， 所以S n ＝n [1＋3－2n ]2＝2n －n 2.由S k ＝－35可得2k －k 2＝－35， 即k 2－2k －35＝0，解得k ＝7或k ＝－5. 又k ∈N *，故k ＝7.18. 解析： ∵a 、b 、c 成等比数列，∴b 2＝ac . 又∵a 2－c 2＝ac －bc ， ∴b 2＋c 2－a 2＝bc .在△ABC 中，由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝bc 2bc ＝12，∴∠A ＝60°.在△ABC 中，由正弦定理得sin B ＝b sin Aa， ∵b 2＝ac ，∠A ＝60°，∴b sin B c ＝b 2sin 60°ca ＝sin 60°＝32.19. 当a ＜0时，解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＜1a 或x ＞1；当a ＝0时，解集为{x |x ＞1}； 当0＜a ＜1时，解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1＜x ＜1a ；当a ＝1时，解集为∅； 当a ＞1时，解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1a ＜x ＜120.(1)4|0,3x x x ⎧⎫≤≥⎨⎬⎩⎭或 (2)1a ≤ 21.解析： (1)∵不等式x 2－3x ＋t ＜0的解集为{x |1＜x ＜m ，x ∈R }，∴⎩⎪⎨⎪⎧1＋m ＝3m ＝t 得⎩⎪⎨⎪⎧m ＝2t ＝2.(2)∵f (x )＝－⎝ ⎛⎭⎪⎫x －a 22＋4＋a 24在(－∞，1]上递增，∴a2≥1，a ≥2.又log a (－mx 2＋3x ＋2－t )＝log a (－2x 2＋3x )＜0， 由a ≥2，可知0＜－2x 2＋3x ＜1， 由2x 2－3x ＜0，得0＜x ＜32，由2x 2－3x ＋1＞0得x ＜12或x ＞1.所以原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪0＜x ＜12或1＜x ＜32.22. 解析：解：设舰艇靠近渔船所用的时间为x 小时，则AB ＝21x ，BC ＝9x ，结合图形可知，∠2＝75°，∠1＝45°，则∠ACB ＝45°＋75°＝120°.(1)由正弦定理得，AB sin ∠ACB ＝BCsin ∠BAC，即21x sin120°＝9x sin ∠BAC， ∴sin ∠BAC ＝3314，∴∠BAC ＝21.8°，21.8°＋45°＝66.8°， ∴舰艇应按照北偏东66.8°的航向前进． (2)在△ABC 中，AB 2＝AC 2＋BC 2－2AC ·BC ·cos∠ACB ，即(21x )2＝102＋(9x )2－2×10×9x ·cos120°，解得x ＝23或x ＝－512(不合题意，舍去)，∴舰艇靠近渔船所用的时间为23小时．。
陕西省咸阳市实验中学2019-2020学年高二上学期第三次月考物理试题(含答案)
物理试题一、单项选择题(共12小题，每小题4分，共48分。
)1．在图中，标有磁场B的方向，通电直导线中电流I的方向，以及通电直导线所受安培力F的方向，其中正确的是（）A. B. C. D.2．铅蓄电池的电动势为2V，这表示（）A. 铅蓄电池两极间的电压为2VB. 铅蓄电池能在1s内将2J的化学能转变成电能C. 电路中通过相同的电荷量时，铅蓄电池比1节干电池非静电力做的功多D. 铅蓄电池接入不同电路中，电动势会发生变化3．一直导线平行于通电螺线管的轴线放置在螺线管的上方，如图所示，如果直导线可以自由地运动且通以方向由a到b的电流，则导线ab受到安培力的作用后的运动情况为（）A．从上向下看顺时针转动并靠近螺线管B．从上向下看顺时针转动并远离螺线管C．从上向下看逆时针转动并远离螺线管D．从上向下看逆时针转动并靠近螺线管4．在描绘小灯泡的伏安特性曲线时，采用如图所示电路，实验中发现移动滑动变阻器的滑片时，电流表的示数变化而电压表的指针不动，下列原因可能的是（）A. 灯泡中灯丝已烧断B. 滑片接触不良C. 灯泡内部短路D. 滑动变阻器A端接触不良5．在法拉第时代，下列验证“由磁产生电”设想的实验中，能观察到感应电流的是（ ）A ．将绕在磁铁上的线圈与电流表组成一闭合回路，然后观察电流表的变化B ．在一通电线圈旁放置一连有电流表的闭合线圈，然后观察电流表的变化C ．将一房间内的线圈两端与相邻房间的电流表连接，往线圈中插入条形磁铁后，再到相邻房间去观察电流表的变化D ．绕在同一铁环上的两个线圈，分别接电源和电流表，在给线圈通电或断电的瞬间，观察电流表的变化6.如图所示，一根通电直导线垂直放在磁感应强度为1T 的匀强磁场中，以导线截面的中心为圆心，半径为r 的圆周上有a 、b 、c 、d 四个点，已知a 点的实际磁感应强度为0，则下列说法中正确的是（ ）A ．直导线中的电流方向垂直纸面向外B ．b 点的实际磁感应强度为T ，方向斜向右上方，与B的夹角为450C ．c 点的实际磁感应强度也为零D ．d 点的实际磁感应强度跟b 点的相同7.图甲所示，长直导线与闭合金属线框位于同一平面内，长直导线中的电流i 随时间t 的变化关系如图乙所示。
2019-2020学年陕西省咸阳市实验中学高二上学期第三次月考化学试题(解析版)
陕西省咸阳市实验中学2019-2020学年高二上学期第三次月考可能用到的相对原子质量：H-1 C-12 N-14 O-16 S-32 Cl-35.5一、选择题（本题包括16个小题，每小题3分，共48分）1.下列说法错误的是A. 反应产物的总焓与反应物的总焓之差，称为反应焓变B. 反应产物的总焓小于反应物的总焓，该反应为吸热反应C. 同一反应在不同温度下进行，其焓变是不同的D. 已知2NO2(g)=N2O4(g) △H1，N2O4(g)=2NO2(g) △H2，则△H1=－△H2『答案』B『解析』『详解』A．焓变=反应产物的总焓-反应物的总焓，故A正确；B．反应产物的总焓高于反应物的总焓，该反应为吸热反应，故B错误；C．物质本身具有的能量跟物质的状态有关，温度不同，物质的焓不同，则焓变不同，故C 正确；D．正反应是放热反应，其逆反应是吸热反应，反之也成立，故D正确；故选B。
2.用CH4催化还原NO x可以消除氮氧化合物的污染。
例如：①CH4（g）+4NO2（g）=4NO（g）+CO2（g）+2H2O（g）；△H=－574kJ/mol②CH4（g）+4NO（g）=2N2（g）+CO2（g）+2H2O（g）；△H=－1160kJ/mol下列说法中错误的是（）A. 等物质的量的CH4在反应①、②中转移电子数相同B. 由反应①可推知：CH4(g)+4NO2(g)=4NO(g)+CO2(g)+2H2O(l)；△H>－574kJ/molC. 4NO2（g）+2N2（g）=8NO（g）；△H=+586kJ/molD. 若用标准状况下4.48L CH4把NO2还原为N2，整个过程中转移的电子总数为1.6NA 『答案』B『解析』两个反应中甲烷都是转化为二氧化碳的，前后化合价变化相同，所以反应中等物质的量的甲烷的转移电子一定相同，选项A正确。
反应①中生成的为气态水，而气态水转化为液态水要对外放热，所以方程式变为CH4(g)+4NO2(g)=4NO(g)+CO2(g)+2H2O(l)时，反应对外放出的热量应该增加，所以△H＜－574kJ/mol，选项B错误。
陕西省咸阳市市实验中学2019-2020学年高二数学文月考试题含解析
陕西省咸阳市市实验中学2019-2020学年高二数学文月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。
在每小题给出的四个选项中，只有是一个符合题目要求的1. 某几何体的三视图如图，其正视图中的曲线部分为半个圆弧，则该几何体的表面积为（）A．16+6+4πB．16+6+3πC．10+6+4πD．10+6+3π参考答案：C【考点】由三视图求面积、体积．【分析】几何体为侧放的三棱柱与半圆柱的组合体，代入数据计算求出表面积．【解答】解：根据三视图可知，该几何体由两部分构成，底部为圆柱的一半，底面半径为1，高为3，上部为三棱柱，底面是直角边为2的等腰直角三角形，高为3，上部分几何体的表面积S上=+2×3+2×3=10+6，下部分几何体的表面积S下=π×12×2+×2π×1×3=4π，∴该几何体的表面积为S上+S下=10+6+4．故选：C．2. 给出下列四个命题：①有理数是实数；②有些平行四边形不是菱形；③∀x∈R，x2-2x>0；④∃x∈R，2x+1为奇数；以上命题的否定为真命题的序号依次是（）A．①④ B．①②④C．①②③④D．③参考答案：A略3. 到直线3x﹣4y﹣1=0的距离为2的直线方程是( )A．3x﹣4y﹣11=0 B．3x﹣4y﹣11=0或3x﹣4y+9=0C．3x﹣4y+9=0 D．3x﹣4y+11=0或3x﹣4y﹣9=0参考答案：B考点：直线的一般式方程；两条平行直线间的距离．专题：计算题；待定系数法．分析：设到直线3x﹣4y﹣1=0的距离为2的直线方程是 3x﹣4y+c=0，由两平行线间的距离公式得=2，解方程求出c值，即得所求的直线的方程．解答：解：设到直线3x﹣4y﹣1=0的距离为2的直线方程是 3x﹣4y+c=0，由两平行线间的距离公式得=2，c=﹣11，或 c=9．∴到直线3x﹣4y﹣1=0的距离为2的直线方程是 3x﹣4y﹣11=0，或 3x﹣4y+9=0，故选 B．点评：本题考查用待定系数法求平行直线方程的方法，以及两平行线间的距离公式的应用4. 设F1、F2是椭圆E：+=1（a＞b＞0）的左右焦点，P是直线x=a上一点，△F2PF1是底角为30°的等腰三角形，则椭圆E的离心率为( )A．B．C．D．参考答案：B【考点】椭圆的简单性质．【专题】计算题；圆锥曲线的定义、性质与方程．【分析】利用△F2PF1是底角为30°的等腰三角形，可得|PF2|=|F2F1|，根据P为直线x=a 上一点，可建立方程，由此可求椭圆的离心率．【解答】解：∵△F2PF1是底角为30°的等腰三角形，∴|PF2|=|F2F1|∵P为直线x=a上一点∴2（a﹣c）=2c∴e==故选：B．【点评】本题考查椭圆的几何性质，解题的关键是确定几何量之间的关系，属于基础题．5. 已知点M（a，b）在圆O：x2+y2=1外，则直线ax+by=1与圆O的位置关系是（▲）A．相切 B．相交 C．相离 D．不确定参考答案：B略6. 在下列命题中：①若、共线，则、所在的直线平行；②若、所在的直线是异面直线，则、一定不共面；③若、、三向量两两共面，则、、三向量一定也共面；④已知三向量、、，则空间任意一个向量总可以唯一表示为．其中正确命题的个数为（）A．3 B．2 C．1 D．0参考答案：D略7. 已知等比数列{a n}，满足a1+a2+a3+a4+a5=2，=，则a3=( ) A．﹣2 B．2 C．±2D．±4参考答案：C【考点】等比数列的通项公式．【专题】转化思想；整体思想；等差数列与等比数列．【分析】利用等比数列的性质可得：a1a5=a2a4=，分别通分即可得出．【解答】解：∵等比数列{a n}，满足a1+a2+a3+a4+a5=2，=，∴++=，∴++=，∴2=，解得a3=±2．故选：C．【点评】本题考查了等比数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题．8. 若函数内单调递增，则实数a的取值范围是（）A．B．C．D．（1，3]参考答案：B【考点】4N：对数函数的图象与性质；3G：复合函数的单调性．【分析】利用导函数讨论内层函数的单调性，根据复合函数的单调性判断即可得结论．【解答】解：由题意，函数内单调递增，∵y=x3﹣ax=x（x2﹣a），y＞0，a＞0，∴函数y的零点为0，，．则y′=3x2﹣a，令y′=0，可得，．∴函数y=x3﹣ax（y＞0）的单调增区间为[，]和[，+∞）．单调减区间为[，0]．当0＜a＜1时，（﹣，0）?[，0]．即：，可得：．∴实数a的取值范围是[，1）．故选B．【点评】本题考查了复合函数的单调性“同增异减”判断零点问题以及利用导函数讨论单调性．属于中档题．9. 若平面的法向量为，平面的法向量为，则平面与平面的夹角的余弦值为（）A． B． C．D．参考答案：A10. 函数f(x)=+(x-4)0的定义域为（）A． {x|x>2,x≠4} B.{x|x≥2,或x≠4} C. D.参考答案：C二、填空题:本大题共7小题,每小题4分,共28分11. 若双曲线C与双曲线－＝1有相同的渐近线，且过点A（3，），则双曲线C的方程为.参考答案：＝1略12. 在五个数字1，2，3，4，5中，若随机取出三个数字，则剩下两个数字至少有一个是偶数的概率为．（结果用数值表示）参考答案：0.7【考点】列举法计算基本事件数及事件发生的概率．【分析】基本事件总数为n==10，剩下两个数字至少有一个是偶数的对立事件是剩下两个数字都是奇数，由此利用对立事件概率计算公式能求出剩下两个数字至少有一个是偶数的概率．【解答】解：在五个数字1，2，3，4，5中，随机取出三个数字，基本事件总数为n==10，剩下两个数字至少有一个是偶数的对立事件是剩下两个数字都是奇数，∴剩下两个数字至少有一个是偶数的概率为：p=1﹣=0.7．故答案为：0.7．13. 底面边长为2m，高为1m的正三棱锥的全面积为m2．参考答案：【考点】棱柱、棱锥、棱台的侧面积和表面积．【分析】由已知中正三棱锥的底面边长为2m，高为1m，我们易出求棱锥的侧高，进而求出棱侧面积和底面面积即可求出棱锥的全面积．【解答】解：如图所示，正三棱锥S﹣ABC，O为顶点S在底面BCD内的射影，则O为正△ABC的垂心，过C作CH⊥AB于H，连接SH．则SO⊥HC，且，在Rt△SHO中，．于是，，．所以．故答案为14. 已知，且，则的最大值为参考答案：，略15. 正方体中，二面角的大小为__________．参考答案：略16. 与圆C：x2+y2﹣2x+4y=0外切于原点，且半径为2的圆的标准方程为．参考答案：（x+2）2+（y﹣4）2=20【考点】圆的标准方程．【专题】计算题；直线与圆．【分析】根据圆和圆的位置关系，求出圆心与半径，即可得到结论．【解答】解：圆C：x2+y2﹣2x+4y=0可化为圆C：（x﹣1）2+（y+2）2=5，设所求圆的圆心为C′（a，b），∵圆C′与圆C外切于原点，∴a＜0①，∵原点与两圆的圆心C′、C三点共线，∴=﹣2，则b=﹣2a②，由|C′C|=3，得=3③，联立①②③解得a=﹣2，则圆心为（﹣2，4），∴所求圆的方程为：（x+2）2+（y﹣4）2=20．故答案为：（x+2）2+（y﹣4）2=20．【点评】本题考查圆的方程，切点与两圆的圆心三点共线是关键，考查方程思想与运算能力，属于中档题．17. 已知，，且对任意都有：①②给出以下三个结论：（1）；（2）；（3）其中正确结论为参考答案：三、解答题：本大题共5小题，共72分。
实验中学高二数学上学期第三次月考试题理
陕西省咸阳市实验中学2020-2021学年高二数学上学期第三次月考试题 理一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1. 在下列命题中:①若空间向量a 、b 共线，则a 、b 所在的直线平行；②若空间向量a 、b 所在的直线是异面直线,则a 、b 一定不共面;③若空间向量a 、b 、c 两两共面,则a 、b 、c 三向量一定也共面；④已知空间三个向量a 、b 、c ，则空间任意一个向量p 总可以惟一表示为p ＝x a ＋y b ＋z c(x,y ，z 为实数)。
其中正确命题的个数为( ）A ．0B ．1C ．2D ．32．与椭圆9x 2＋4y 2＝36有相同焦点，且短轴长为4错误!的椭圆方程是( )A ．错误!＋错误!＝1B ．错误!＋错误!＝1C ．错误!＋错误!＝1D ．错误!＋错误!＝13。
已知椭圆错误!＋错误!＝1的左、右焦点分别为F 1、F 2,点P 在椭圆上．若12PF PF ,则点P 到x 轴的距离为（ ） A ．错误! B ．3 C ．错误!D．错误!4．已知向量a＝(2，4，5），b＝(3,x,y)分别是直线l1、l2的方向向量，若l1∥l2，则()A．x＝6，y＝15B．x＝3，y＝152C．x＝3，y＝15D．x＝6，y＝错误!5。
椭圆的一个焦点和短轴的两端点构成一个正三角形，则该椭圆的离心率为(）A。
错误! B. 错误! C.错误! D．不能确定6.点P是棱长为1的正方体ABCDA1B1C1D1内一点,且满足错误!＝错误!错误!＋错误!错误!＋错误!错误!,则点P到棱AB的距离为()A.错误!B.错误!C。
错误! D。
错误!7。
如图，正方体ABCD-A1B1C1D1的棱长为1，O是底面A1B1C1D1的中心，则O到平面ABC1D1的距离为（）A.错误!B。
错误!C。
错误! D。
错误!8．已知A(1,2，－1)关于平面xOy的对称点为B,而B关于x 轴的对称点为C，则错误!等于（）A ．（0，4，2）B ．(0,－4，－2)C ．(0，4，0）D ．（2，0，－2）9.已知正方体ABCD －A ′B ′C ′D ′ ，点E 是A ′C ′的中点,点F 是AE 的三等分点，且AF ＝错误!EF ，则错误!等于（ )A ．错误!＋错误!错误!＋错误!错误! B ．错误!错误!＋错误!错误!＋错误!错误!C ．错误!错误!＋错误!错误!＋错误!错误!D ．错误!错误!＋错误!错误!＋错误!错误!10。
2021-2022学年陕西省咸阳市实验中学高二年级上册学期第三次月考数学(理)试题【含答案】
2021-2022学年陕西省咸阳市实验中学高二上学期第三次月考数学（理）试题一、单选题1．不等式12x ->的解集为（ ） A ．()(),13,-∞-+∞ B ．()1,3- C ．()1,-+∞ D ．()3,+∞【答案】A【分析】由12x ->，可得12x ->或12x -<-，计算即可. 【详解】12x ->，∴12x ->或12x -<-， ∴3x >或1x <-，即解集为()(),13,-∞-+∞.故选：A2．下列结论中不正确的个数是（ ） ①命题“所有的四边形都是矩形”是特称命题； ②命题“R x ∀∈，210x ”是全称命题；③若命题p ：R x ∃∈，2210x x ++≤，则p ⌝：R x ∀∈，2210x x ++≤. A ．0 B ．1C ．2D ．3【答案】C【分析】根据全称命题以及特称命题的概念可判断①、②的正误；根据含有一个量词的命题的否定，可判断③的正误，可得答案.【详解】①命题“所有的四边形都是矩形”是全称命题，故①不正确； ②命题“R x ∀∈，210x ”是全称命题，正确；③若命题p ：R x ∃∈，2210x x ++≤，则p ⌝：R x ∀∈，2210x x ++>，故③不正确， 故选：C.3．若0a b <<，则下列不等式中成立的是（ ）A ．11a b -<-BC ．22a b >D ．11a b> 【答案】D【分析】根据不等式的性质可判断AB ，作差可判断CD.﹒【详解】对于A ，因为0a b <<，所以a b ->-，所以11a b ->-，故错误； 对于B ，因为0a b <<，所以0对于C ，因为0a b <<，所以0,0-<+>a b a b 所以()()220a b a b a b -=-+<，即22a b <，故错误；对于D ，因为0a b <<，所以0b a ->，所以110b a a b ab--=>，所以11a b >，故正确. 故选：D.4．若平面α与β的法向量分别是()2,4,3a =-，()1,2,2b =-，则平面α与β的位置关系是（ ） A ．平行 B ．垂直 C ．相交但不垂直 D ．无法确定【答案】B【分析】根据所给向量可知其数量积为零，故知两向量垂直.【详解】因为2,4,3)(1,2,2)0a b ⋅=-⋅-=（，所以a b ⊥，所以两平面垂直. 【点睛】本题主要考查了平面的法向量，向量的数量积，利用法向量判断平面的位置关系，属于中档题.5．若平面α的一个法向量为()1,2,2n →=，点()3,0,2A ，()5,1,3B ，A α，B α∈，A 到平面α的距离为（ ） A ．1 B ．2 C ．3 D ．4【答案】B【分析】求出AB →，点A 到平面α的距离：AB nnd →→→⋅=，由此能求出结果【详解】解：()3,0,2A ，()5,1,3B ，A α，B α∈，∴AB 为平面α的一条斜线，且(2,1,1)AB →=∴ 点A 到平面α的距离：236AB d nn→→→⋅==== 故选：B.6．如图，在三棱锥-P ABC 中，点N 为棱AP 的中点，点M 在棱BC 上，且满足2CM BM =，设PA a =，PB b =，PC c =，则MN =（ ）A ．121233a b c -+-B ．121233a b c +-C ．121233a b c --D ．121233a b c --+【答案】C【分析】利用空间向量基本定理可得答案.【详解】因为点N 为棱AP 的中点，2CM BM =，所以2132=++=-+MN MC CP PN BC PC PA 221121332332=--+=--+PC PB PC PA PC PB PA 121233=--a b c . 故选：C.7．设α、β是两个不同的平面，则αβ⊥的充要条件是（ ）. A ．平面α内任意一条直线与平面β垂直 B ．平面α、β都垂直于同一条直线 C ．平面α、β都垂直于同一平面 D ．平面α内存在一条直线与平面β垂直 【答案】D【解析】当两个平面垂直时，一个平面内的一条直线可以与另一个平面成任意角，可判断A 项不正确；垂直于同一条直线的两个平面互相平行，可判断B 项不正确；垂直于同一个平面的两个平面可以成任意角，可判断C 项错误；利用面面垂直的判定定理可以得到D 项正确；从而得到答案 【详解】若αβ⊥，则平面α内存在直线与平面β不垂直，选项A 不正确； 若平面α、β都垂直于同一条直线，则平面α与β平行，选项B 不正确；若平面α、β都垂直于同一平面，则平面α、β可以平行，也可以相交，选项C 不正确； 若平面α内存在一条直线与平面β垂直，则根据面面垂直的判定定理，可知αβ⊥， 若αβ⊥，则由面面垂直的性质定理知，平面α内垂直于平面β内的两条相交直线的直线一定垂直于平面β，故选项D 正确； 故选：D .【点睛】关键点点睛：该题考查的是有面面垂直的相关条件及结论，在做题的过程中，要注意： （1）要建立很强的空间立体感；（2）对空间关系对应的相关结论要非常熟悉； （3）可以随手制造模型.8．下列命题中正确的个数是（ ）．①若a 与b 共线，b 与c 共线，则a 与c 共线． ②向量a ，b ，c 共面，即它们所在的直线共面．③如果三个向量a ，b ，c 不共面，那么对于空间任意一个向量p ，存在有序实数组(),,x y z ，使得p xa yb zc =++．④若a ，b 是两个不共线的向量，而c a b λμ=+（,λμ∈R 且0λμ≠），则{},,a b c 是空间向量的一组基底． A ．0 B ．1 C ．2 D ．3【答案】B【分析】举例0b =，判断①，由向量共面的定义判断②，由空间向量基本定理判断③，由共面向量定理和空间向量基本定理判断④．【详解】①当0b =时，a 与c 不一定共线，故①错误；②当a ，b ，c 共面时，它们所在的直线平行于同一平面，或在同一平面内， 故②错误；由空间向量基本定理知③正确；④当a ，b 不共线且c a b λμ=+时，a ，b ，c 共面，故④错误． 故选：B ．9．李先生的私家车基本上每月需要去加油站加油两次，假定每月去加油时两次的油价略有差异.有以下两种加油方案：方案一：不考虑两次油价的升降，每次都加油200元； 方案二：不考虑两次油价的升降，每次都加油30升. 李先生下个月采用哪种方案比较经济划算?（ ） A ．方案一 B ．方案二 C ．一样划算 D ．不能确定【答案】A【分析】设第一次油价为a ，第二次油价为b ，计算两种方案的平均油价，作差比较得到答案. 【详解】设第一次油价为a ，第二次油价为b ，ab ，,0a b >，方案一的平均油价为：4002200200aba b a b=++；方案二的平均油价为：3030602a b a b++=. 则()()()()22420222ab a b a b ab a b a b a b a b -+--+-==<+++，故22ab a b a b +<+. 故选：A.10．已知命题p ：若//a b （0a ≠，0b ≠），则a a bb =，命题q ：函数2sin sin y x x =+，π,02x ⎡⎫∈-⎪⎢⎣⎭，最大值为3-，下列是真命题的为（ ） A ．()p q ⌝∧ B ．p q ∧ C ．()p q ∨⌝ D ．()()p q ⌝∧⌝【答案】A【分析】根据向量平行的性质判断p 的真假，由正弦函数及对勾函数的性质判断q 的真假，进而判断各选项中复合命题的真假即可. 【详解】当a 与b 方向相反时，a a bb =不成立，p 为假命题．令[)sin 1,0t x =∈-，则2y t t =+在[)1,0t ∈-上单调递减，max 3y ∴=-，q 为真命题．综上，()p q ⌝∧为真，p q ∧为假，()p q ∨⌝为假，()()p q ⌝∧⌝为假. 故选：A11．已知关于x 的不等式20ax bx c ++≥的解集为{3|x x ≤-或4}x ≥，则下列说法中正确的是（ ） A ．a<0B ．不等式0bx c +>的解集为{}4x x <-C ．不等式20cx bx a -+<的解集为{1|4x x <-或1}3x >D ．0a b c ++> 【答案】C【分析】根据关于x 的不等式20ax bx c ++≥的解集为{3|x x ≤-或4}x ≥可判断0a >，判断A;由此可得3,4-是20ax bx c ++=的两根，推得,12b a c a =-=-，即可求解0bx c +>以及20cx bx a -+<的解集，判断B,C ;结合题意将1x =代入2ax bx c ++，可退的结果为负，判断D. 【详解】由于关于x 的不等式20ax bx c ++≥的解集为{3|x x ≤-或4}x ≥， 故0a >，A 错误；由以上分析可知，3,4-是20ax bx c ++=的两根，则34,34b ca a -+=--⨯=，即,12b a c a =-=- ，故0bx c +>即120ax a -->，则12x <-，B 错误； 不等式20cx bx a -+<即22120,1210a ax x a x x -+<-∴->+，则14x <-或13x >，即不等式20cx bx a -+<的解集为{1|4x x <-或1}3x >，C 正确；由于关于x 的不等式20ax bx c ++≥的解集为{3|x x ≤-或4}x ≥，故20ax bx c ++<的解集为{|34}x x -<<，所以1x =时，2110a b c ⨯+⨯+<， 即0a b c ++<，故D 错误， 故选：C.12．已知四边形ABCD 为正方形GD ⊥平面ABCD ，四边形DGEA 与四边形DGFC 也都为正方形，连接EF ，FB ，BE ，H 为BF 的中点，有下述四个结论： ①DE ⊥BF ；②EF 与CH 所成角为3π；③EC ⊥平面DBF ；④BF 与平面ACFE 所成角为4π． 其中所有正确结论的编号是（ ） A ．①② B ．①②③ C ．①③④ D ．①②③④【答案】B【分析】根据题意，将几何体补形成一个正方体,进而建立空间直角坐标系，通过空间向量的坐标运算得到答案.【详解】由题意得，所得几何体可以补形成一个正方体，如图所示．以D 为坐标原点，DA ，DC ，DG 所在直线分别为x ，y ，z 轴，建立空间直角坐标系．设AD ＝DC ＝DG ＝2，则D (0，0，0)，C (0，2，0)，E (2，0，2)， F (0，2，2)，B (2，2，0)，H (1，2，1)．对①，()()2,0,2,2,0,2DE BF →→==-，所以()()2,0,22,0,24040DE BF →→⋅=⋅-=-++=， 则DE BF DE BF →→⊥⇒⊥，正确；对②，()()2,2,0,1,0,1BF CH →→=-=，设,CH BF 所成角为,(0,]2πθθ∈，所以1cos |cos ,|||23||||BF CH BF CH BF CH πθθ→→→→→→⋅=<>==⇒=，正确； 对③，()()()2,2,2,2,2,0,0,2,2EC DB DF →→→=--==，设(),,n x y z →=是平面DBF 的一个法向量，所以220220n DB x y n DF y z ⎧⋅=+=⎨⋅=+=⎩，令x =1，则()1,1,1n →=-，所以2//EC n EC n →→→→=-⇒，则EC ⊥平面DBF ，正确； 对④，由题意，EA ⊥平面ABCD ，则EA ⊥DB ，易得：DB ⊥AC ，EA 与AC 交于A ，则DB ⊥平面ACFE ，则()2,2,0DB →=是平面ACFE 的一个法向量，设BF 与平面ACFE 所成的角为,0,2παα⎡⎤∈⎢⎥⎣⎦，所以1sin |cos ,|||26||||DB BF DB BF DB BF παα→→→→→→⋅=<>==⇒=，错误. 故选：B.二、填空题 13．若1x >，则11x x +-的最小值为______． 【答案】3【分析】运用基本不等式即可. 【详解】因为11(1)121311x x x x +=-++≥+=--， 当且仅当111x x -=-时，即2x =，等号成立， 所以11x x +-的最小值为3. 即答案为:3.14．已知数列{}n a 满足①1N ,k k k a a ∀*+∈>，②1N ,2k k k a a ∀*+∈-≤，请写出一个满足条件的数列的通项公式________．（答案不唯一）【答案】()*n a n n N =∈【分析】判断数列的特征，从等差数列或等比数列入手考虑解答.【详解】*1k k k N a a +∀∈>，，说明数列是递增数列；由*12k k k N a a +∀∈-<，，不妨设该数列为等差数列， 则公差为1，首项为1， 所以n a n =.故答案为：()*n a n n N =∈15．若关于x 的不等式13x x m ++-<有实数解，则实数m 的取值范围为___________. 【答案】(4,2)-【分析】由绝对值的性质求得1x x m ++-的最小值后可得结论． 【详解】由绝对值三角不等式得11++-≥+x x m m ， 所以13m +<，解得42m -<<， 故答案为：(4,2)-．16．已知数列{}n a 满足22log 1n n a n +⎛⎫= ⎪+⎝⎭．给出定义：使数列{}n a 的前k 项和为正整数的k ()*k ∈N 叫做“好数”，则在[]1,2021内的所有“好数”的和为______． 【答案】2026【分析】先计算出数列{}n a 的前k 项和，然后找到使其为正整数的k ()*k ∈N ，相加即可得到答案．【详解】由题，22212222log log log 11211n n S n +++⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭222342log log log 231n n +⎛⎫=+++ ⎪+⎝⎭()()22222log log 2log 2log 212n n n +==+-=+-．所以，()2log 21k S k =+-．因为k S 为正整数，所以()2log 210k +->，即220k k +>⇒>． 令()2log 2m k =+，则22=-m k ．因为[]1,2021k ∈，所以[]23,2023m∈．因为2x y =为增函数，且12101122,24,,21024,22048====所以[]2,10m ∈．所以所有“好数”的和为210231022222222229202612-⨯-+-++-=-⨯=-．故答案为：2026．【点睛】本题考查了数列的新定义、对数运算法则，解题时应认真审题，找到规律，注意等比数列求前n 项和公式的灵活运用．三、解答题17．设函数()|23|||f x x x a =-+-. (1)若1a =-，解不等式()6f x ≥； (2)已知32a >，若3,2x a ⎡⎤∈⎢⎥⎣⎦时，()2f x ≤，求实数a 的取值范围. 【答案】(1)48(][,)33-∞-⋃+∞(2)3522a <≤【分析】（1）分类讨论x ，求绝对值不等式的解集即可.（2）由题设可得()3f x x a =+-，结合()2f x ≤在3,2x a ⎡⎤∈⎢⎥⎣⎦上恒成立，求a 的取值范围.【详解】（1）由题设，()|23||1|f x x x =-++， 当1x <-时，()32123f x x x x =---=-， 当312-≤<x 时，()3214f x x x x =-++=-， 当32x ≥时，()23132f x x x x =-++=-， ∴()6f x ≥，则1236x x <-⎧⎨-≥⎩得：43x ≤-；31246x x ⎧-≤<⎪⎨⎪-≥⎩，无解；32326x x ⎧≥⎪⎨⎪-≥⎩得：83x ≥；综上，()6f x ≥的解集为48(][,)33-∞-⋃+∞.（2）由题设，3,2x a ⎡⎤∈⎢⎥⎣⎦时()233f x x x a x a =--+=+-，由()2f x ≤，∴32x a +-≤，即5a x ≤-恒成立， ∴5a a ≤-，则52a ≤，故3522a <≤. 18．已知命题p ：实数x 满足2280x x --≤，命题q ：实数x 满足22m x m -≤≤+. (1)若p 是q 的充分不必要条件，求实数m 的取值范围；(2)若5m =，p q ∨为真命题，求实数x 的取值范围. 【答案】(1)[)4,+∞ (2)[]3,7-【分析】（1）通过解不等式化简命题p ，将p 是q 的充分不必要条件转化为[]2,4-是[]2,2m m -+的真子集，列出不等式组，求出m 的范围．（2）将复合命题的真假转化为构成其简单命题的真假，求出x 的范围即可. 【详解】（1）由2280x x --≤，得24x -≤≤， 若p 是q 的充分不必要条件，则[][]2,42,2m m --+，∴222422m m m m -≤-⎧⎪+≥⎨⎪-≤+⎩，解得4m ≥， ∴实数m 的取值范围是[)4,+∞；（2）当5m =时，命题q ：实数x 满足37x -≤≤， ∵p q ∨为真命题，∴24x -≤≤或37x -≤≤，即37x -≤≤， ∴实数x 的取值范围为[]3,7-.19．已知数列{}n a 满足132n n a a +=+，*n ∈N ，且11 a =. （1）求证数列{}1n a +是等比数列；（2）已知数列{}n b 的前n 项和为n S ，且312log 112n n a b +=-，求n S 的最小值. 【答案】（1）证明见解析（2）36-【解析】（1）根据等比数列定义,结合所给递推公式,证明111n n a a +++为常数即可.（2）由（1）可求得数列{}n a 的通项公式,代入表达式可得数列{}n b 的通项公式,结合通项公式即可判断n S 取得最小值时n 的值，进而求得结果. 【详解】（1）由11321311n n n n a a a a ++++==++,且112a += 则{}1n a +是以2为首项,3为公比的等比数列. （2）由（1）可知1123n n a -+=⨯.则1231n n a -=⨯-, 代入可得312log 112132n n a b n +=-=-, 由数列{}n b 的通项公式可知60b <,70b >,当n = 6时，n S 取得最小值，此时最小值为()1666=362b b S +=-. 20．在△ABC 中，设角A ，B ，C 的对边分别为a ，b ，c ，且a 2＋b 2＞c 2．现有以下四个条件： ①a ＝2，②b ＝3，③7cos 8A =，④11cos 16B =． (1)条件①、②成立的前提下，条件③和④能否同时成立?请说明理由；(2)请你从条件③和④中剔除一个，则同时满足余下三个条件的△ABC 是否存在?若存在，求c ；若不存在，说明理由．【答案】(1)③④不能同时成立(2)若剔除③，△ABC 不存在，若剔除④，ABC 是存在的，且54c =．【分析】（1）假设③④都成立，可得c 的值，但是不符合222a b c +>的条件；（2）分别讨论③④中有一个剔除的情况，然后对应求解即可．【详解】（1）③④不能同时成立，因为2a =，3b =，若③④成立，则在三角形中，可得sin A ==，sin B ==， 由正弦定理sin sin a b A B ===，此时117sin sin()sin cos cos sin 168C A B A B A B =+=+=+=， 由正弦定理sin sin a c A C == 解得4c =，22222231316a b c +=+=<=，所以③④不能同时成立；（2）若剔除③，由余弦定理可得2222cos b a c ac B =+-， 即211942216c c =+-⨯⨯，整理可得：2411200c c --=，解得4c =，2221316a b c +=<=，所以不符合222a b c +>．若剔除④，则余弦定理22223cos a b c c A =+-⨯⨯⨯， 即2749238c c =+-⨯⨯⨯， 整理可得：2421200c c --=，解得54c =或4c =， 再由222a b c +>可得54c =． 综上所述，剔除④满足余下三个条件的ABC ∆是存在的，且可得54c =． 21．已知直三棱柱111ABC A B C 中，ABC 为等腰直角三角形，90BAC ∠=︒，且1AB AA =，D ，E ，F 分别为11,,B A C C BC 的中点.(1)求证：直线//DE 平面ABC ；(2)求直线1AB 与平面AEF 所成角的大小.【答案】(1)见解析(2)3π【分析】根据图形，建立空间直角坐标系（1）求出平面ABC 的一个法向量m ，只需证明DE m ⊥，再结合DE ⊄平面ABC ，即可证明//DE 平面ABC ；（2）求出平面AEF 的一个法向量n ，设直线1AB 与平面AEF 所成角为([0,])2πθθ∈，则1sin cos ,AB n θ<=>，求出θ的值.【详解】（1）解：由直三棱柱，以及90BAC ∠=︒，可建立如图所示空间直角坐标系，因为ABC 为等腰直角三角形且1AB AA =，不妨设12AC AB AA ===，则(0,0,0),(2,0,0),(0,2,0),(1,0,1),(0,2,1)A B C D E(0,0,1)m =为平面ABC 的一个法向量，(1,2,0)DE =-，0m DE ∴⋅=，即m DE ⊥，又DE ⊄平面ABC ，//DE ∴平面ABC（2）()()12,0,2,1,1,0B F1(2,0,2)AB ∴=设(,,)n x y z =为平面AEF 的一个法向量，(0,2,1),(1,1,0)AE AF ==，200y z x y +=⎧∴⎨+=⎩，取(1,1,2)n =-， 设直线1AB 与平面AEF 所成角为([0,])2πθθ∈， 则12043sin cos ,226AB n θ++=<>==⨯ 又[0,]2πθ∈， 3πθ∴=.22．如图，在四棱锥M ABCD -中，底面ABCD 为直角梯形，//BC AD ，90ADC ∠=︒，MBC 与MCD △均为边长为2的等边三角形，12BC AD =.(1)求证：平面MBD ⊥平面ABCD ；(2)求二面角A MB C --的余弦值.【答案】(1)证明见解析 (2)6【分析】（1）取BD 的中点E ，连接ME 、CE ，证明出ME ⊥平面ABCD ，利用面面垂直的判定定理可证得结论成立；（2）由（1）以点E 为坐标原点，EC 、ED 、EM 所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法可求得二面角A MB C --的余弦值．【详解】（1）取BD 的中点E ，连接ME 、CE ，由MBC 与MCD △均为边长为2的等边三角形则2MB MC BC MD CD =====， E 为BD 的中点，则CE BD ⊥，同理可得ME BD ⊥，//AD BC ，90ADC ∠=，所以，90BCD ∠=，则22BD =，122CE BD ∴==222MB MD BD +=， 90BMD ∴∠=，则122ME BD == 所以，222CE ME MC +=，则CE ME ⊥，又ME BD ⊥CE BD E =，CE ⊂平面ABCD ，BD ⊂平面ABCD ，ME ⊄平面ABCD ， ME ∴⊥平面ABCD ，ME ⊂平面MBD ，所以，平面MBD ⊥平面ABCD ；（2）ME ⊥平面ABCD ，CE BD ⊥，以点E 为坐标原点，EC 、ED 、EM 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，由MBC 、MCD △的边长均为2，则(2M 、()0,2,0B 、()2,0,0C 、()22,2,0A -， 设平面ABM 的法向量为()111,,m x y z =，()22,0,0AB =，(2,2BM =，由00m AB m BM ⎧⋅=⎨⋅=⎩，可得11120220x z ⎧=⎪=，取11y =，可得()0,1,1m =-， 设平面BCM 的法向量为()222,,x n y z =，()2,2,0BC =， 由00n BC n BM ⎧⋅=⎨⋅=⎩，可得2222220220x z ==，取21y =-，可得()1,1,1n =-， 26cos ,23m nm n m n ⋅-<>===⨯⋅ 由图可知，二面角A MB C --为钝角，因此，二面角A MB C --的余弦值为6。
陕西省咸阳市实验中学2019-2020学年高二上学期检测数学(理)试卷
数学试卷 (理科)一.选择题（51050⨯=分）1.点P 是抛物线24y x =上一点，若点P 到焦点的距离为5，那么点P 的坐标是A.()4,4B.(或(3,-C. ()4,4-或 (4,4)--D.()4,4或(4,4)- 2. 已知椭圆2244x ky +=的一个焦点坐标是(0,1)，则实数k 的值是 A. 1 B. 2 C. 3 D. 4 3．在ABC ∆中, 若222sin sin sin A B C +<,则ABC ∆为A 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定 4．已知条件:0,p a <条件2:q a a >，则p ⌝是q ⌝的 A ．充分不必要条件B ．必要不充分条件C ． 充要条件D .既不充分也不必要条件 5. 已知{}n a 为等比数列，47562,8a a a a +==-，则110a a +=A ．7-B ．5C ．5-D . 76. 设,a b r r为向量，命题“若a b =-r r ，则a b =r r ”的否定是A ．若 a b ≠r r 则 a b ≠r rB ．若a b =-r r则 a b ≠r rC ．若 a b ≠r r ，则 a b ≠r rD . 若a b =r r ，则a b =-r r7. 设ln 2ln 3ln 5,,235a b c ===.则,,a b c 的大小关系为 A ．a b c >> B ．b c a >> C ．b a c >> D . c b a >>8.设P 为曲线C :223y x x =++上的点,且曲线在点P 处的切线的倾斜角的取值范围为0,4π⎡⎤⎢⎥⎣⎦,则点P 横坐标的取值范围为 A 11,2⎡⎤--⎢⎥⎣⎦B. []1,0-C. []0,1D. 1,12⎡⎤⎢⎥⎣⎦9. 双曲线22221(0,0)x y a b a b-=>>，过其右焦点且垂直于实轴的直线与双曲线交于M ，N两点，O 为坐标原点，若OM ON ⊥，则双曲线的离心率为A B C D10. 若正实数,x y 满足3x y xy ++=则A ．xy 的最小值是25B ．xy 的最大值是25C ． x y +的最小值是6D . x y +的最大值是6 二. 填空题（每题5分，共25分） 11.曲线21xy x =-在点(1,1)处的切线方程为 _____________. 12．设抛物线的顶点在原点,准线方程为2x =-,则抛物线方程为_____________.13.已知数列{}n a 的前n 项和2n S n =,求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T =____________.14.已知1423x y x y -<+<⎧⎨<-<⎩则23z x y =-的取值范围是(答案用区间表示)____________.15. 若对任意20,31xx a x x >≤++恒成立，则实数a 的取值范围是_____________. 三.解答题（共75分）16.（本小题满分12分）ABC ∆三个内角,,A B C 的对边分别为,,a b c .已知cos()cos 1,2A C B a c -+==求角C .17.（本小题满分12分）如图,从点1(0,0)P 做x 轴的垂线交曲线x y e =于点1(0,1)Q ,曲线在1Q 点处的切线与x 轴交于点2P ,再从2P 做x 轴的垂线交曲线于点2Q ,依次重复上述的过程得到一系列点: 1122,;,;,n n P Q P Q P Q L L 记k P 的坐标为(,0)(1,2,,,)k x k n =L L .(1).求1k x +与k x 的关系式;(1,2,,,)k n =L L (2)求1122n n PQ PQ PQ +++L .18.（本小题满分12分）某单位用2160万元购得一块空地,计划在该地上建造一栋至少10层,每层2000平方米的楼房,经测算,如果将楼房建为(10)x x ≥层,则每平方米的平均建筑费用为56048x +(单位:元),为了使楼房每平方米的平均综合费用最小,该楼房应建为多少层?(注:平均综合费用=平均建筑费+平均购地费用,平均购地费用=购地总费用÷建筑总面积，建筑总面积=单层的面积⨯层数)19.（本小题满分12分）如图,在长方体1111ABCD A B C D -中,11AA AD ==, E 为CD 的中点.(1) 求证: 11B E AD ⊥(2)在棱1AA 上是否存在点P ,使得DP P 平面1B AE ;(3)若二面角11A B E A --的大小为30o ，求AB 的长.20. （本小题满分13分）已知椭圆22221(0)x y a b a b+=>>,过点(,0),(0,)A a B b -的直线的倾斜角为6π,原点到该直线的距离为3.(1)求椭圆的方程;(2)是否存在实数k ,直线2y kx =+交椭圆于,P Q 两点,以PQ 为直径的圆过点(0,1)D ?若存在,求出k 值,若不存在,说明理由.21.（本小题满分14分） 已知函数1()ln(1)1xf x ax x-=+++,0x ≥.其中0a > （１） 若()f x 在1x =处取得极值,求a 值;, （２） 讨论()f x 的单调性;(2) 若()f x 的最小值为1,求a 的取值范围.数学参考答案(理科)一.选择题:(本大题共10小题,每小题5分,共50分) 1 2 3 4 5 6 7 8 9 10 DBCBABCADC二.填空题(本大题共5小题,每小题5分,共25分) 11 . 2y x =-+ 12. 28y x =-. 13.21nn + 14. 97z -≤≤15 . 1,5⎡⎤+∞⎢⎥⎣⎦三.解答题(本大题共6小题,共75分)16.(本小题满分12分)解： cos()cos 1cos()cos()1cos cos sin sin cos cos sin sin 2sin sin 1A CB AC A C A C A C A C A C A C -+=∴--+=+-+==Q又2112sin 2sin sin sin 42a c A C C C =⇒=⇒=⇒=，a c C >⇒Q 为锐角，6C π∴=17.(本小题满分12分)解: (1)因为xy e '=，所以曲线 xy e =在点(,)k xk x e 的切线方程为()k k x x k y e e x x -=-，令0y =得11k k x x +-=-(2) 121122nx x xn nPQ PQ PQ e e e +++=+++Q L L又111n n n nx x x x e e e e ++--==所以数列{}n x e 是首项为1，公比为1e -的等比数列，121112211()1nnx x x n n e PQ P Q P Q e e ee ---∴+++=+++=-L L18.解: (本小题满分12分)(1) 设每平方米的平均综合费用为 y 元，则1080056048(10)y x x x=++≥ 560248108002000≥+⨯= 当且仅当108004815x x x=⇒=时取等号. 19.(本小题满分12分)解:（1）建立空间直角坐标系如图所示设AB a =则11(0,0,0),(1,0,0),(1,,1),(0,0,1),(0,,0)2a D A B a D E1111(1,,1),(1,0,1)2110aB E AD B E AD =---=-∴⋅=-=u u u r u u u u r Q u u u r u u u u r∴11B E AD ⊥(2)假设在棱在棱1AA 上存在点P ,使得DP P 平面1B AE ，设(1,0,)P b设平面1B AE 的法向量为(,,)n x y z =r1(1,,1),(1,,0)22a aB E AE =---=-u u u r u u u r Q 又10022002a a x y z n B E x y a n AE z ay x y ⎧++=⎧⎧⎪⋅==⎪⎪⎪⇒⇒⎨⎨⎨⋅=⎪⎪⎪⎩=--+=⎩⎪⎩u u r u u u r uu r u u u r 取(,1,)2a n a =-r (1,0,)DP b =u u u r ，10022a n DP ab b ⋅=⇒-=⇒=u u r u u u r所以，存在点P 为1AA 的中点满足题设。
实验中学高二物理上学期第三次月考试题含解析
【点睛】本题考查电表改装原理的理解能力．当电流计的指针满偏时，电流表或电压表的指针满偏,所测量的电流或电压达到最大值．
A。 从上向下看顺时针转动并靠近螺线管
B。 从上向下看顺时针转动并远离螺线管
C。 从上向下看逆时针转动并远离螺线管
D。 从上向下看逆时针转动并靠近螺线管
【答案】D
【解析】
试题分析：通电导线因放在通电螺线管的磁场中故受到磁场力，因左右两侧磁场方向不同，故可以分左右两边分别分析研究,画出两侧的磁场方向，则由左手定则可判出磁场力的方向，根据受力情况可判出物体的转动情况．当导体转动后，我们可以认为电流向右偏内,受力也将发生变化，为了简便，我们可以判断导体转动到向里的位置判断导体的受力情况，再判出导体的运动情况．
5。在法拉第时代，下列验证“由磁产生电”设想 实验中，能观察到感应电流的是( ）
A。 将绕在磁铁上的线圈与电流表组合成一闭合回路,然后观察电流表的变化
B. 在一通电线圈旁放置一连有电流表的闭合线圈,然后观察电流表的变化
C。 将一房间内的线圈两端与相邻房间的电流表连接，往线圈中插入条形磁铁后,再到相邻房间去观察电流表的变化
6。如图所示,一根通电直导线垂直放在磁感应强度B＝1T的匀强磁场中，在以导线截面的中心为圆心、r为半径的圆周上有a、b、c、d四个点．已知a点的磁感应强度为0，则下列叙述正确的是( ）
A。 直导线中的电流方向垂直于纸面向外
B。b点的实际磁感应强度为 T,方向斜向右上方,与B的夹角为45°
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019-2020年陕西省咸阳市实验中学高二（上）数学（理）第三次月考试题一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中只有一项是符合题目要求的)1．在等差数列{a n}中，若a3＋a4＋a5＋a6＋a7＝450，则a2＋a8的值等于( ) A．45 B．75 C．180 D．3002．在△ABC中，若b＝2a sin B，则角A为( )A．30°或60° B．45°或60°C．120°或60° D．30°或150°3．a∈R，且a2＋a＜0，那么－a，－a3，a2的大小关系是( )A．a2＞－a3＞－a B．－a＞a2＞－a3C．－a3＞a2＞－a D．a2＞－a＞－a34．设等差数列{a n}的前n项和为S n.若a1＝－11，a4＋a6＝－6，则当S n取最小值时，n等于( )A．6 B．7 C．8 D．95．△ABC中，a、b、c分别为A、B、C的对边，如果a，b，c成等差数列，B＝30°，△ABC的面积为32，那么b＝( )A.1＋32B．1＋ 3 C.2＋32D．2＋ 36．在△ABC中，角A，B，C所对的边分别为a，b，c.若a cos A＝b sin B，则sin A cos A＋cos2B＝( )A．－12B.12C．－1 D．17．若数列{x n}满足lg x n＋1＝1＋lg x n(n∈N＋)，且x1＋x2＋x3＋…＋x100＝100，则lg(x101＋x102＋…＋x200)的值为( )A．102 B．101 C．100 D．998．实数x ，y 满足不等式组⎩⎨⎧y ≥0x －y ≥02x －y －2≥0，则ω＝y －1x ＋1的取值范围为( ) A ．[－1，13] B ．[－12，13] C ．[－12，＋∞) D．[－12，1)9．设x ，y 满足约束条件⎩⎨⎧x ＋y ≥1，x －y ≥－1，2x －y ≤2，若目标函数z ＝4ax ＋3by (a >0，b >0)最大值为12，则1a ＋1b的最小值为( )A ．1B ．2C ．4 D.1210．在R 上定义运算*：x *y ＝x (1－y )．若不等式(x －a )*(x ＋a )＜1对任意实数x 均成立，则( )A ．－1＜a ＜1B ．0＜a ＜2C ．－12＜a ＜32D ．－32＜a ＜1211．钝角三角形的三边为a ，a ＋1，a ＋2，其最大角不超过120°，则a 的取值范围是( )A ．0＜a ＜3 B.32≤a ＜3 C ．2＜a ≤3D ．1≤a ＜5212已知函数221(),()(),2x f x x g x m x=+=- 若[][]121,21,1∈∈-任意的x ，存在x 使得12x )()f f x ≥（，则实数m 的取值范围是( )A ．5,2⎡⎫-+∞⎪⎢⎣⎭B.[)1,-+∞C ． [)4,-+∞D ．12,2⎡⎫-+∞⎪⎢⎣⎭二、填空题(本大题共4小题，每小题5分，共20分．)13．在△ABC 中，已知a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________.14．已知{a n }是等差数列，S n 为其前n 项和，n ∈N *.若a 3＝16，S 20＝20，则S 10的值为________．15．设点P (x ，y )在函数y ＝4－2x 的图像上运动，则9x ＋3y 的最小值为________． 16．设a,b,c 为正数，241a b c ++= 2a b c 的最大值是 ___________ 三、解答题(本大题共6小题，共70分．)17．(本小题满分10分)已知等差数列{a n }中，a 1＝1，a 3＝－3.(1)求数列{a n }的通项公式；(2)若数列{a n }的前k 项和S k ＝－35，求k 的值．18．(本小题满分12分)在△ABC 中，a ，b ，c 分别是∠A 、∠B 、∠C 的对边长，已知a ，b ，c 成等比数列，且a 2－c 2＝ac －bc .求∠A 的大小及b sin Bc的值． 19．(本小题满分12分)解关于x 的不等式ax 2－(a ＋1)x ＋1＜0. 20．(本小题满分12分设函数()|1||21|f x x x =-+-(1)求不等式()2f x ≥ 的解集；(2)若x R ∀∈ ，不等式()||f x a x ≥ 恒成立，求实数a 的取值范围 21．(本小题满分12分)已知不等式x 2－3x ＋t ＜0的解集为{x |1＜x ＜m ，x ∈R }．(1)求t ，m 的值；(2)若函数f (x )＝－x 2＋ax ＋4在区间(－∞，1]上递增，求关于x 的不等式log a (－mx 2＋3x ＋2－t )＜0的解集．22．(本小题满分12分)某渔船在航行中不幸遇险，发出求救信号，我海军舰艇在A 处获悉后，立即测出该渔船在方位角为45°、距离A 为10海里的C 处，并测得渔船正沿方位角105°的方向，以9海里/时的速度向某小岛B 靠拢，我海军舰艇立即以21海里/时的速度前去营救，恰在小岛B 处追上渔船． (1)试问舰艇应按照怎样的航向前进？ (2)求出舰艇靠近渔船所用的时间？(参考数据：cos21.8°＝1314，sin21.8°＝3314，tan21.8°＝3313)数学（理）参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C DBABDADCCBA填空题13. 2 3 14. 110 15.18 16.10217. 解析： (1) a n ＝＝3－2n . (2)由(1)可知a n ＝3－2n ， 所以S n ＝n [1＋3－2n ]2＝2n －n 2.由S k ＝－35可得2k －k 2＝－35， 即k 2－2k －35＝0，解得k ＝7或k ＝－5. 又k ∈N *，故k ＝7.18. 解析： ∵a 、b 、c 成等比数列，∴b 2＝ac . 又∵a 2－c 2＝ac －bc ， ∴b 2＋c 2－a 2＝bc .在△ABC 中，由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝bc 2bc ＝12，∴∠A ＝60°.在△ABC 中，由正弦定理得sin B ＝b sin Aa， ∵b 2＝ac ，∠A ＝60°，∴b sin B c ＝b 2sin 60°ca ＝sin 60°＝32.19. 当a ＜0时，解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＜1a 或x ＞1；当a ＝0时，解集为{x |x ＞1}； 当0＜a ＜1时，解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1＜x ＜1a ；当a ＝1时，解集为∅； 当a ＞1时，解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1a ＜x ＜120.(1)4|0,3x x x ⎧⎫≤≥⎨⎬⎩⎭或 (2)1a ≤ 21.解析： (1)∵不等式x 2－3x ＋t ＜0的解集为{x |1＜x ＜m ，x ∈R }，∴⎩⎪⎨⎪⎧1＋m ＝3m ＝t 得⎩⎪⎨⎪⎧m ＝2t ＝2.(2)∵f (x )＝－⎝ ⎛⎭⎪⎫x －a 22＋4＋a 24在(－∞，1]上递增，∴a2≥1，a ≥2.又log a (－mx 2＋3x ＋2－t )＝log a (－2x 2＋3x )＜0， 由a ≥2，可知0＜－2x 2＋3x ＜1， 由2x 2－3x ＜0，得0＜x ＜32，由2x 2－3x ＋1＞0得x ＜12或x ＞1.所以原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪0＜x ＜12或1＜x ＜32.22. 解析：解：设舰艇靠近渔船所用的时间为x 小时，则AB ＝21x ，BC ＝9x ，结合图形可知，∠2＝75°，∠1＝45°，则∠ACB ＝45°＋75°＝120°.(1)由正弦定理得，AB sin ∠ACB ＝BCsin ∠BAC，即21x sin120°＝9x sin ∠BAC， ∴sin ∠BAC ＝3314，∴∠BAC ＝21.8°，21.8°＋45°＝66.8°， ∴舰艇应按照北偏东66.8°的航向前进． (2)在△ABC 中，AB 2＝AC 2＋BC 2－2AC ·BC ·cos∠ACB ，即(21x )2＝102＋(9x )2－2×10×9x ·cos120°，解得x ＝23或x ＝－512(不合题意，舍去)，∴舰艇靠近渔船所用的时间为23小时．。