考点14 圆周角(解析版)
2022年浙江各地数学中考真题(杭州温州金华嘉兴等)按知识点汇编专题14 圆(解析版)

专题14圆一、单选题1.(2022·宁波)已知圆锥的底面半径为4cm ,母线长为6cm ,则圆锥的侧面积为( )A .236πcmB .224πcmC .216πcmD .212πcm【答案】B【解析】4624S rl πππ==⋅⋅=侧2cm , 故选B .2.(2022·温州)如图,,AB AC 是O 的两条弦,⊥OD AB 于点D ,OE AC ⊥于点E ,连结OB ,OC .若130DOE ∠=︒,则BOC ∠的度数为( )A .95︒B .100︒C .105︒D .130︒【答案】B【解析】解:∵OD ⊥AB ,OE ⊥AC ,∴∠ADO =90°,∠AEO =90°,∵∠DOE =130°,∴∠BAC =360°-90°-90°-130°=50°,∴∠BOC =2∠BAC =100°,故选:B .3.(2022·丽水)某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m ,高为,则改建后门洞的圆弧长是( )A .5πm 3B .8πm 3C .10πm 3D .5π+2m 3⎛⎫ ⎪⎝⎭【答案】C 【解析】如图,连接AD ,BC ,交于O 点,∵90BDC ∠=︒ ,∴BC 是直径,∴4BC ===, ∵四边形ABDC 是矩形,∴122OC OD BC ===, ∵2CD =,∴OC OD CD ==,∴COD ∆是等边三角形,∴60COD ∠=︒,∴门洞的圆弧所对的圆心角为36060300︒-︒=︒ , ∴改建后门洞的圆弧长是11300300410221801803BC πππ︒⨯︒⨯⨯==︒︒(m), 故选:C4.(2022·杭州)如图,在平面直角坐标系中,已知点P (0,2),点A (4,2).以点P 为旋转中心,把点A 按逆时针方向旋转60°,得点B .在1M ⎛⎫ ⎪ ⎪⎝⎭,()21M -,()31,4M ,4112,2M ⎛⎫ ⎪⎝⎭四个点中,直线PB 经过的点是( ) A .1M B .2M C .3M D .4M【答案】B【解析】解:∵点A (4,2),点P (0,2),∴P A ⊥y 轴,P A =4,由旋转得:∠APB =60°,AP =PB =4,如图,过点B 作BC ⊥y 轴于C ,∴∠BPC =30°,∴BC =2,PC∴B (2,,设直线PB 的解析式为:y =kx +b ,则222k b b ⎧+=+⎪⎨=⎪⎩∴2k b ⎧=⎪⎨=⎪⎩∴直线PB 的解析式为:y +2,当y =0+2=0,x =∴点M 1(0)不在直线PB 上,当x =y =-3+2=1,∴M 2(-1)在直线PB 上,当x =1时,y ,∴M 3(1,4)不在直线PB 上,当x =2时,y ,∴M 4(2,112)不在直线PB 上. 故选:B .5.(2022·湖州)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD 中,M ,N 分别是AB ,BC 上的格点,BM =4,BN =2.若点P 是这个网格图形中的格点,连接PM ,PN ,则所有满足∠MPN =45°的△PMN 中,边PM 的长的最大值是( )A .B .6C .D .【答案】C【解析】 作线段MN 中点Q ,作MN 的垂直平分线OQ ,并使OQ =12MN ,以O 为圆心,OM 为半径作圆,如图,因为OQ 为MN 垂直平分线且OQ =12MN ,所以OQ =MQ =NQ ,∴∠OMQ =∠ONQ =45°,∴∠MON =90°,所以弦MN 所对的圆O 的圆周角为45°,所以点P 在圆O 上,PM 为圆O 的弦,通过图像可知,当点P 在P '位置时,恰好过格点且P M '经过圆心O ,所以此时P M '最大,等于圆O 的直径,∵BM =4,BN =2,∴MN ==∴MQ =OQ∴OM∴2P M OM '==故选 C .6.(2022·杭州)如图,已知△ABC 内接于半径为1的⊙O ,∠BAC =θ(θ是锐角),则△ABC 的面积的最大值为()A .()cos 1cos θθ+B .()cos 1sin θθ+C .()sin 1sin θθ+D .()sin 1cos θθ+【答案】D【解析】解:当△ABC 的高AD 经过圆的圆心时,此时△ABC 的面积最大,如图所示,∵AD ⊥BC ,∴BC =2BD ,∠BOD =∠BAC =θ,在Rt △BOD 中,sin θ= 1BD BD OB =,cos θ=1OD OD OB =, ∴BD =sin θ,OD =cos θ,∴BC =2BD =2sin θ,AD =AO +OD =1+cos θ,∴S △ABC =12AD •BC =12•2sin θ(1+cos θ)=sin θ(1+cos θ). 故选:D .二、填空题7.(2022·湖州)如图,已知AB 是⊙O 的弦,∠AOB =120°,OC ⊥AB ,垂足为C ,OC 的延长线交⊙O 于点D .若∠APD 是AD 所对的圆周角,则∠APD 的度数是______.【答案】30°##30度【解析】∵OC ⊥AB ,OD 为直径,∴BD AD =,∴∠AOB =∠BOD ,∵∠AOB =120°,∴∠AOD =60°,∴∠APD =12∠AOD =30°,故答案为:30°.8.(2022·宁波)如图,在△ABC 中,AC =2,BC =4,点O 在BC 上,以OB 为半径的圆与AC 相切于点A ,D 是BC 边上的动点,当△ACD 为直角三角形时,AD 的长为___________.【答案】32或65【解析】解:连接OA,①当D点与O点重合时,∠CAD为90°,设圆的半径=r,∴OA=r,OC=4-r,∵AC=4,在Rt△AOC中,根据勾股定理可得:r2+4=(4-r)2,解得:r=32,即AD=AO=32;②当∠ADC=90°时,过点A作AD⊥BC于点D,∵12AO•AC=12OC•AD,∴AD=AO AC OC⋅,∵AO=32,AC=2,OC=4-r=52,∴AD=65,综上所述,AD的长为32或65,故答案为:32或65.9.(2022·金华)如图,木工用角尺的短边紧靠⊙O于点A,长边与⊙O相切于点B,角尺的直角顶点为C,已知6cm,8cmAC CB==,则⊙O的半径为_____cm.【答案】253##183【解析】解:连接OB 、OA ,过点A 作AD ⊥OB ,垂足为D ,如图所示:∵CB 与O 相切于点B ,∴OB CB ⊥,∴90CBD BDA ACB ∠=∠=∠=︒,∴四边形ACBD 为矩形,∴8AD CB ==,6BD AC ==,设圆的半径为r cm ,在Rt △AOD 中,根据勾股定理可得:222OA OD AD =+,即r 2=(r −6)2+82,解得:253r =, 即O 的半径为253cm . 故答案为:253. 10.(2022·绍兴)如图,10AB =,点C 在射线BQ 上的动点,连接AC ,作CD AC ⊥,CD AC =,动点E 在AB 延长线上,tan 3QBE ∠=,连接CE ,DE ,当CE DE =,CE DE ⊥时,BE 的长是______.【答案】5或354【解析】解:如图,过点C 作CN ⊥BE 于N ,过点D 作DM ⊥CN 延长线于M ,连接EM ,设BN =x ,则CN =BN •tan ∠CBN =3x ,∵△CAD ,△ECD 都是等腰直角三角形,∴CA =CD ,EC =ED ,∠EDC =45°,∠CAN +∠ACN =90°,∠DCM +∠ACN =90°,则∠CAN =∠DCM ,在△ACN 和△CDM 中:∠CAN =∠DCM ,∠ANC =∠CMD =90°,AC =CD ,∴△ACN ≌△CDM (AAS ),∴AN =CM =10+x ,CN =DM =3x ,∵∠CMD =∠CED =90°,∴点C 、M 、D 、E 四点共圆,∴∠CME =∠CDE=45°,∵∠ENM =90°,∴△NME 是等腰直角三角形,∴NE =NM =CM -CN =10-2x ,Rt △ANC 中,AC =Rt △ECD 中,CD =AC ,CE 2CD , Rt △CNE 中,CE 2=CN 2+NE 2,∴()()()()2222110331022x x x x ⎡⎤++=+-⎣⎦, 2425250x x -+=,()()4550x x --=,x =5或x =54, ∵BE =BN +NE =x +10-2x =10-x ,∴BE =5或BE =354; 故答案为:5或354; 11.(2022·杭州)如图是以点O 为圆心,AB 为直径的圆形纸片,点C 在⊙O 上,将该圆形纸片沿直线CO 对折,点B 落在⊙O 上的点D 处(不与点A 重合),连接CB ,CD ,AD .设CD 与直径AB 交于点E .若AD =ED ,则∠B =_________度;BC AD的值等于_________.【答案】3635 2 +【解析】解:∵AD=DE,∴∠DAE=∠DEA,∵∠DEA=∠BEC,∠DAE=∠BCE,∴∠BEC=∠BCE,∵将该圆形纸片沿直线CO对折,∴∠ECO=∠BCO,又∵OB=OC,∴∠OCB=∠B,设∠ECO=∠OCB=∠B=x,∴∠BCE=∠ECO+∠BCO=2x,∴∠CEB=2x,∵∠BEC+∠BCE+∠B=180°,∴x+2x+2x=180°,∴x=36°,∴∠B=36°;∵∠ECO=∠B,∠CEO=∠CEB,∴△CEO∽△BEC,∴CE BE EO CE=,∴CE2=EO•BE,设EO=x,EC=OC=OB=a,∴a2=x(x+a),解得,x a(负值舍去),∴OE a,∴AE=OA-OE=a a,∵∠AED=∠BEC,∠DAE=∠BCE,∴△BCE∽△DAE,∴BC EC AD AE=,∴BC AD = 故答案为:36三、解答题12.(2022·绍兴)如图,半径为6的⊙O 与Rt △ABC 的边AB 相切于点A ,交边BC 于点C ,D ,∠B=90°,连接OD ,A D .(1)若∠ACB=20°,求AD 的长(结果保留π).(2)求证:AD 平分∠BDO .【答案】(1)43π;(2)见解析 【解析】(1)解:连接OA , ∵∠ACB =20°,∴∠AOD =40°, ∴180n r AD π=, 18040⨯π⨯6=43π=. (2)证明:OA OD =,OAD ODA ∠=∠∴, AB 切O 于点A ,OA AB ∴⊥,90B ∠=︒,//OA BC ∴,OAD ADB ∴∠=∠,ADB ODA ∴∠=∠,AD ∴平分BDO ∠.13.(2022·台州)如图,在ABC 中,AB AC =,以AB 为直径的⊙O 与BC 交于点D ,连接AD .(1)求证:BD CD =;(2)若⊙O 与AC 相切,求B 的度数;(3)用无刻度的直尺和圆规作出劣弧AD 的中点E .(不写作法,保留作图痕迹) 【答案】(1)证明见详解;(2)45B ∠=︒;(3)作图见详解【解析】 (1)证明:∵AB 是O 的直径, ∴90ADB ∠=︒, ∴AD BC ⊥, ∵AB AC =, ∴BD CD =. (2)∵O 与AC 相切, ∴90BAC ∠=︒, 又∵AB AC =, ∴45B ∠=︒.(3)如下图,点E 就是所要作的AD 的中点.14.(2022·湖州)如图,已知在Rt △ABC 中,90C ∠=︒,D 是AB 边上一点,以BD 为直径的半圆O 与边AC 相切,切点为E ,过点O 作OF BC ⊥,垂足为F .(1)求证:OF EC =;(2)若30A ∠=︒,2BD =,求AD 的长.【答案】(1)见解析;(2)1 【解析】(1)解:如图,连接OE ,∵AC 切半圆O 于点E ,∴OE ⊥A C ,∵OF ⊥BC ,90C ∠=︒, ∴∠OEC =∠OFC =∠C =90°. ∴四边形OFCE 是矩形, ∴OF =E C ; (2)∵2BD =, ∴112122OE BD ==⨯=, ∵30A ∠=︒,OE ⊥AC , ∴2212AO OE ==⨯=, ∴211AD AO DO =-=-=.15.(2022·嘉兴)如图,在廓形AOB 中,点C ,D 在AB 上,将CD 沿弦CD 折叠后恰好与OA ,OB 相切于点E ,F .已知120AOB ∠=︒,6OA =,则EF 的度数为_______;折痕CD 的长为_______.【答案】 60°##60度 46【解析】作O 关于CD 的对称点M ,则ON =MN 连接MD 、ME 、MF 、MO ,MO 交CD 于N∵将CD 沿弦CD 折叠∴点D 、E 、F 、B 都在以M 为圆心,半径为6的圆上∵将CD 沿弦CD 折叠后恰好与OA ,OB 相切于点E ,F . ∴ME ⊥OA ,MF ⊥OB ∴90MEO MFO ∠=∠=︒∵120AOB ∠=︒∴四边形MEOF 中36060EMF AOB MEO MFO ∠=︒-∠-∠-∠=︒ 即EF 的度数为60°;∵90MEO MFO ∠=∠=︒,ME MF = ∴MEO MFO ≅(HL )∴1302EMO FMO FME ∠=∠=∠=︒∴6cos cos30ME OM EMO ===∠︒∴MN =∵MO ⊥DC∴12DN CD ==∴CD =故答案为:60°;16.(2022·温州)如图1,AB 为半圆O 的直径,C 为BA 延长线上一点,CD 切半圆于点D ,BE CD ⊥,交CD 延长线于点E ,交半圆于点F ,已知5,3BC BE ==.点P ,Q 分别在线段AB BE ,上(不与端点重合),且满足54AP BQ =.设,BQ x CP y ==.(1)求半圆O 的半径.(2)求y 关于x 的函数表达式.(3)如图2,过点P 作PR CE ⊥于点R ,连结,PQ RQ . ①当PQR 为直角三角形时,求x 的值.②作点F 关于QR 的对称点F ',当点F '落在BC 上时,求CF BF ''的值. 【答案】(1)158;(2)5544y x =+;(3)①97或2111;②199 【解析】(1)解:如图1,连结OD .设半圆O 的半径为r .∵CD 切半圆O 于点D , ∴OD CD ⊥. ∵BE CD ⊥, ∴OD BE ∥,∴△∽△COD CBE , ∴OD CO BE CB=, 即535r r -=, ∴158r =,即半圆O 的半径是158.(2)由(1)得:1555284CA CB AB =-=-⨯=. ∵5,4AP BQ x BQ ==, ∴54AP x =. ∵CP AP AC =+, ∴5544y x =+. (3)①显然90PRQ ∠<︒,所以分两种情况. ⅰ)当90RPQ ∠=︒时,如图2.∵PR CE ⊥,∴90ERP ∠=︒. ∵90E ∠=︒,∴四边形RPQE 为矩形, ∴PR QE =.∵333sin 544PR PC C y x =⋅==+, ∴33344x x +=-,∴97x =.ⅰ)当90PQR ∠=︒时,过点P 作PH BE ⊥于点H ,如图3,则四边形PHER 是矩形,∴,PH RE EH PR ==. ∵5,3CB BE ==,∴4CE ==. ∵4cos 15CR CP C y x =⋅==+, ∴3PH RE x EQ ==-=, ∴45EQR ERQ ∠=∠=︒, ∴45PQH QPH ∠=︒=∠, ∴3HQ HP x ==-,由EH PR =得:33(3)(3)44x x x -+-=+, ∴2111x =. 综上所述,x 的值是97或2111.②如图4,连结,AF QF ',由对称可知QF QF =',F QR EQR ∠=∠'∵BE ⊥CE ,PR ⊥CE , ∴PR ∥BE ,∴∠EQR =∠PRQ ,∵BQ x =,5544CP x =+, ∴EQ =3-x , ∵PR ∥BE , ∴CPR CBE △∽△,∴CP CBCR CE=, 即:x CR +=555444,解得:CR =x +1, ∴ER =EC -CR =3-x , 即:EQ = ER∴∠EQR =∠ERQ =45°, ∴45F QR EQR ∠=∠='︒ ∴90BQF ∠='︒, ∴4tan 3QF QF BQ B x ==⋅='. ∵AB 是半圆O 的直径, ∴90AFB ∠=︒, ∴9cos 4BF AB B =⋅=, ∴4934x x +=, ∴2728x =, ∴319119CF BC BF BC BF BF BF x -==''''=-='-. 17.(2022·宁波)如图1,O 为锐角三角形ABC 的外接圆,点D 在BC 上,AD 交BC 于点E ,点F 在AE 上,满足,∠-∠=∠∥AFB BFD ACB FG AC 交BC 于点G ,BE FG =,连结BD ,DG .设ACB α∠=.(1)用含α的代数式表示BFD ∠.(2)求证:△≌△BDE FDG .(3)如图2,AD 为O 的直径. ①当AB 的长为2时,求AC 的长. ②当:4:11=OF OE 时,求cos α的值. 【答案】(1)902︒∠=-BFD α;(2)见解析;(3)①3;②5cos 8α=【解析】(1)∵∠-∠=∠=AFB BFD ACB α,①又∵180∠+∠=︒AFB BFD ,② ②-①,得2180∠=︒-BFD α, ∴902︒∠=-BFD α.(2)由(1)得902︒∠=-BFD α,∵∠=∠=ADB ACB α,∴180902∠=︒-∠-︒-∠=FBD ADB BFD α,∴DB DF =. ∵FGAC ,∴∠=∠CAD DFG . ∵CAD DBE ∠=∠, ∴∠=∠DFG DBE . ∵BE FG =,∴()BDE FDG SAS △≌△. (3)①∵△≌△BDE FDG , ∴∠=∠=FDG BDE α,∴2∠=∠+∠=BDG BDF EDG α. ∵DE DG =, ∴()11809022∠=︒-∠=︒-DGE FDG α, ∴在BDG 中,3180902∠=︒-∠-∠=︒-DBG BDG DGE α, ∵AD 为O 的直径, ∴90ABD ∠=︒.∴32∠=∠-∠=ABC ABD DBG α. ∴AC 与AB 的度数之比为3∶2.∴AC 与AB 的的长度之比为3∶2, ∵2AB =, ∴3=AC . ②如图,连结BO .∵OB OD =,∴∠=∠=OBD ODB α,∴2∠=∠+∠=BOF OBD ODB α. ∵2∠=BDG α, ∴∠=∠BOF BDG . ∵902∠=∠=︒-BGD BFO α,∴△∽△BDG BOF ,设BDG 与BOF 的相似比为k , ∴==DG BDk OF BO. ∵411=OF OE , ∴设4OF x =,则114OE x DE DG kx ===,, ∴114==+=+OB OD OE DE x kx , 154==+BD DF x kx ,∴154154114114++==++BD x kx kBO x kx k, 由154114+=+kk k,得247150+-=k k ,解得154k =,23k =-(舍), ∴11416=+=OD x kx x ,15420=+=BD x kx x , ∴232==AD OD x , 在Rt ABD △中,205cos 328∠===BD x ADB AD x , ∴5cos 8α=.18.(2022·金华)如图1,正五边形ABCDE 内接于⊙O ,阅读以下作图过程,并回答下列问题,作法:如图2,①作直径AF ;②以F 为圆心,FO 为半径作圆弧,与⊙O 交于点M ,N ;③连接,,AM MN NA .(1)求ABC ∠的度数.(2)AMN 是正三角形吗?请说明理由.(3)从点A 开始,以DN 长为半径,在⊙O 上依次截取点,再依次连接这些分点,得到正n 边形,求n 的值. 【答案】(1)108︒;(2)是正三角形,理由见解析;(3)15n = 【解析】(1)解:∵正五边形ABCDE . ∴BC CD DE AE AB ====,∴360725AOB BOC COD DOE EOA ︒∠=∠=∠=∠=∠==︒, ∵3AEC AE =,∴AOC ∠(优弧所对圆心角)372216︒︒=⨯=, ∴1121610822AOC ABC ∠=⨯︒=∠=︒;(2)解:AMN 是正三角形,理由如下: 连接,ON FN ,由作图知:FN FO =,∵ON OF =, ∴ON OF FN ==, ∴OFN △是正三角形,∴60OFN ∠=︒,∴60AMN OFN ∠=∠=︒, 同理60ANM ∠=︒,∴60MAN ∠=︒,即AMN ANM MAN ∠=∠=∠, ∴AMN 是正三角形; (3)∵AMN 是正三角形,∴2120A N A N M O =∠=︒∠. ∵2AD AE =,∴272144AOD ∠=⨯︒=︒, ∵DN AD AN =-,∴14412024NOD ∠=︒-︒=︒, ∴3601524n ==. 19.(2022·丽水)如图,以AB 为直径的O 与AH 相切于点A ,点C 在AB 左侧圆弧上,弦CD AB ⊥交O 于点D ,连接,AC AD .点A 关于CD 的对称点为E ,直线CE 交O 于点F ,交AH 于点G .(1)求证:CAG AGC ∠=∠;(2)当点E 在AB 上,连接AF 交CD 于点P ,若25EF CE =,求DP CP的值; (3)当点E 在射线AB 上,2AB =,以点A ,C ,O ,F 为顶点的四边形中有一组对边平行时,求AE 的长. 【答案】(1)证明过程见解析 (2)57352或22【解析】 【分析】(1)设CD 与AB 相交于点M ,由O 与AH 相切于点A ,得到90BAG ,由CD AB ⊥,得到90AMC ∠=,进而得到AG CD ∥,由平行线的性质推导得,CAG ACD ,AGC FCD ,最后由点A 关于CD 的对称点为E 得到FCD ACD ∠=∠即可证明.(2)过F 点作FK AB ⊥于点K ,设AB 与CD 交于点N ,连接DF ,证明FAD ADC ∠=∠得到DP AP =,再证明CPA FPD △≌△得到PF PC =;最后根据KEF NEC △∽△及APN AFK △∽△得到25KE EF EN CE 和512PA ANAF AK ,最后根据平行线分线段成比例求解.(3)分四种情形:如图1中,当∥OC AF 时,如图2中,当∥OC AF 时,如图3中,当AC OF ∥时,如图4中,当AC OF ∥时,分别求解即可.. (1)证明:如图,设CD 与AB 相交于点M ,∵O 与AH 相切于点A ,∴90BAG ,∵CD AB ⊥,∴90AMC ∠=,∴AG CD ∥,∴CAG ACD ,AGC FCD ,∵点A 关于CD 的对称点为E ,∴FCD ACD ∠=∠,∴CAG AGC ∠=∠.(2)解:过F 点作FK AB ⊥于点K ,设AB 与CD 交于点N ,连接DF ,如下图所示:由同弧所对的圆周角相等可知:FCD FAD ,∵AB 为O 的直径,且CD AB ⊥,由垂径定理可知:AC AD =, ∴ACD ADC ∠=∠,∵点A 关于CD 的对称点为E ,∴FCD ACD ∠=∠,∴FAD FCD ACD ADC ∠=∠=∠=∠,即FAD ADC ∠=∠, ∴DP AP =,由同弧所对的圆周角相等可知:ACP DFP ,且CPA FPD ,∴CPA FPD △≌△, ∴PC PF =,∵FK AB ⊥,AB 与CD 交于点N ,∴90FKE CNE . ∵KEF NEC ,90FKE CNE , ∴KEF NEC △∽△, ∴25KEEF EN CE ,设KE =2x ,EN =5x ,∵点A 关于CD 的对称点为E ,5AN EN x ∴==,10AE AN NE x =+=,12AK AE KE x =+=, 又FK PN ∥,∴APN AFK , ∴551212PA ANx AF AK x . ∵FCD CDA ,∴CF AD ∥, ∴57DPAP AP CP PF AF AP ; (3)解:分类讨论如下:解:如图1中,当∥OC AF 时,连接OC ,OF ,设AGF α∠=,则CAG ACD DCF AFG α∠=∠=∠=∠=,∵∥OC AF ,OCF AFC α∴∠=∠=,OC OA =,3OCA OAC α∴∠=∠=,45OAG ∠=︒,490α∴=︒,22.5α∴=︒,OC OF =,OA OF =,22.5OFC OCF AFC ∴∠=∠-∠=︒,45OFA OAF ∴∠=∠=︒,AF ∴==,∵∥OC AF ,AE AF OE OC∴=∴, 1OA =,2AE ∴=如图2中,当∥OC AF 时,连接OC ,设CD 交AE 点M .设OAC α∠=,∵∥OC AF ,FAC OCA α∴∠=∠=,2COE FAE α∴∠=∠=,AFD D ∠=∠,AGF D ∠=∠,3AGC AFG AEC FAE α∴∠=∠=∠+∠=, 90AGC AEC ∠+∠=︒,490α∴=︒,22.5α∴=︒,245α=︒,COM ∴∆是等腰直角三角形,OC ∴,OM ∴=1AM =,22AE AM ∴==如图3中,当AC OF ∥时,连接OC ,OF ,设AGF α∠=,2ACF ACD DCF α∠=∠+∠=, ∵AC OF ∥,2CFO ACF α∴∠=∠=,4CAO ACO α∴∠=∠=,180AOC OAC ACO ∠+∠+∠=︒, 10180α∴=︒,18α∴=︒,36COE ECO CFO ∴∠=∠-∠=︒, OCE FCO ∴∆∆ 、,2OC CE CF ∴=⋅ 、, ()11CE CE ∴=+ 、,CE AC OE ∴===AE OA OE ∴=-; 如图4中,当AC OF ∥时,连接OC ,OF ,BF .设FAO α∠=,∵AC OF ∥,CAF OFA α∴∠=∠=,2COF BOF α∴∠=∠=,AC AE =,AEC CAE EFB ∴∠=∠=∠, BF BE ∴=,由OCF OBF ∆≅∆,CF BF BE ∴==,E COF ∠=∠,COF CEO ∴∆∆,2OC CE CF ∴=⋅,BE CF ∴==AE AB BE ∴=+=.综上所述,满足条件的AE 的长为22352或。
圆心角与圆周角(4种题型)-2023年新九年级数学核心知识点与常见题型(浙教版)(解析版)

圆心角与圆周角(4种题型)【知识梳理】一.圆心角、弧、弦的关系(1)定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.(2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.(3)正确理解和使用圆心角、弧、弦三者的关系三者关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合.(4)在具体应用上述定理解决问题时,可根据需要,选择其有关部分.二.圆周角定理(1)圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.①顶点在圆上.②角的两条边都与圆相交,二者缺一不可.(2)圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.(3)在解圆的有关问题时,常常需要添加辅助线,构成直径所对的圆周角,这种基本技能技巧一定要掌握.(4)注意:①圆周角和圆心角的转化可通过作圆的半径构造等腰三角形.利用等腰三角形的顶点和底角的关系进行转化.②圆周角和圆周角的转化可利用其“桥梁”﹣﹣﹣圆心角转化.③定理成立的条件是“同一条弧所对的”两种角,在运用定理时不要忽略了这个条件,把不同弧所对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角.三.圆内接四边形的性质(1)圆内接四边形的性质:①圆内接四边形的对角互补.②圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).(2)圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来.在应用时要注意是对角,而不是邻角互补.四.相交弦定理(1)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.(经过圆内一点引两条线,各弦被这点所分成的两段的积相等).几何语言:若弦AB、CD交于点P,则P A•PB=PC•PD(相交弦定理)(2)推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项.几何语言:若AB是直径,CD垂直AB于点P,则PC2=P A•PB(相交弦定理推论).【考点剖析】一.圆心角、弧、弦的关系(共9小题)1.(2023•杭州二模)如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是()A.∠OBA=∠OCA B.四边形OABC内接于⊙OC.AB=2BC D.∠OBA+∠BOC=90°【分析】过O作OD⊥AB于D交⊙O于E,由垂径定理得到=,于是得到==,推出AE=BE =BC,根据三角形的三边关系得到2BC>AB,故C错误;根据三角形内角和得到∠OBA=(180°﹣∠AOB)=90°﹣∠BOC,∠OCA=(180°﹣∠AOC)=90°﹣∠BOC,推出∠OBA≠∠OCA,故A错误;由点A,B,C在⊙O上,而点O在圆心,得到四边形OABC不内接于⊙O,故B错误;根据余角的性质得到∠OBA+∠BOC=90°,故D正确;【解答】解:过O作OD⊥AB于D交⊙O于E,则=,∴AE=BE,∠AOE=∠BOE=AOB,∵∠AOB=2∠BOC,∴∠AOE=∠BOE=∠BOC,∴==,∴AE=BE=BC,∴2BC>AB,故C错误;∵OA=OB=OC,∴∠OBA=(180°﹣∠AOB)=90°﹣∠BOC,∠OCA=(180°﹣∠AOC)=90°﹣∠BOC,∴∠OBA≠∠OCA,故A错误;∵点A,B,C在⊙O上,而点O在圆心,∴四边形OABC不内接于⊙O,故B错误;∵∠BOE=∠BOC=AOB,∵∠BOE+∠OBA=90°,∴∠OBA+∠BOC=90°,故D正确;故选:D.【点评】本题考查了圆心角,弧,弦的关系,垂径定理,三角形的三边关系,正确的作出辅助线是解题的关键.2.(2022秋•鄞州区校级期末)如图,AB,CD是⊙O的直径,,若∠AOE=32°,则∠COE的度数是.【分析】根据在同圆中,等弧所对的圆心角相等,可推出∠BOD=∠AOE=32°,再根据对顶角相等,可推出∠AOC=∠BOD=32°,最后用∠COE=∠COA+∠AOE即可求解.【解答】解:∵,∠AOE=32°,∴∠BOD=∠AOE=32°,∵∠AOC=∠BOD=32°,∴∠COE=∠COA+∠AOE=32°+32°=64°.故答案为:64°.【点评】本题主要考查等弧和圆心角的关系,熟知在同圆中,等弧所对的圆心角相等,和对顶角相等是解题的关键.3.(2022秋•越城区期末)如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4,则⊙O 的周长为()A.4πB.6πC.8πD.9π【分析】如图,连接OD、OC.根据圆心角、弧、弦的关系证得△AOD是等边三角形,则⊙O的半径长为BC =4cm;然后由圆的周长公式进行计算.【解答】解:如图,连接OC、OD∵AB是⊙O的直径,四边形ABCD内接于⊙O,BC=CD=DA=4,∴==,∴∠AOD=∠DOC=∠BOC=60°.又OA=OD,∴△AOD是等边三角形,∴OA=AD=4,∴⊙O的周长=2×4π=8π.故选:C.【点评】本题考查了圆心角、弧、弦的关系,等边三角形的判定与性质.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距也相等,即四者有一个相等,则其它三个都相等.4.(2023•越城区模拟)如图,AB,AC是⊙O的两条弦,OD⊥AB于点D,OE⊥AC于点E,连结OB,OC.若∠DOE=140°,则∠BOC的度数为()A.70°B.80°C.90°D.100°【分析】根据四边形的内角和等于360°计算可得∠BAC=50°,再根据圆周角定理得到∠BOC=2∠BAC,进而可以得到答案.【解答】解:∵OD⊥AB,OE⊥AC,∴∠ADO=90°,∠AEO=90°,∵∠DOE=140°,∴∠BAC=360°﹣90°﹣90°﹣140°=40°,∴∠BOC=2∠BAC=80°,故选:B.【点评】本题考查的是圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.5.(2023•路桥区校级二模)如图,弧AB所对圆心角∠AOB=90°,半径为8,点C是OB中点,点D弧AB上一点,CD绕点C逆时针旋转90°得到CE,则AE的最小值是.【分析】如图,连接OD,以OC为边向下作正方形OCTH,连接AT,ET.利用勾股定理求出AT,再证明△OCD≌△TCE(SAS),推出ET=OD=8,由AE≥AT﹣ET=4﹣8,可得结论.【解答】解:如图,连OD,以OC为边向下作正方形OCTH,连AT,ET.∵OA=OB=8,OC=CB=CT=OH=HT=4,∴AH=AO+OH=12,∴AT===4,∴∠OCT=∠ECD=90°,∴∠OCD=∠RCE,在△OCD和△TCE中,,∴△OCD≌△TCE(SAS),∴ET=OD=8,∴AE≥AE﹣ET=4﹣8,∴AE的最小值为4﹣8.故答案为:4﹣8.【点评】本题考查全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.6.(2023•宁波模拟)传统服饰日益受到关注,如图1为明清时期女子主要裙式之一的马面裙,如图2马面裙可以近似地看作扇环,其中AD长度为米,BC长度为米,圆心角∠AOD=60°,则裙长AB 为.【分析】由题意知,==,==计算求解OA ,OB 的值,然后根据AB =OB ﹣OA 计算求解即可.【解答】解:由题意知,==,==,解得OA =1,,∴=0.8(米), 故答案为:0.8米.【点评】本题考查了扇形的弧长公式.解题的关键在于正确的计算.7.(2023•萧山区校级模拟)如图,BD 是⊙O 的直径,点A ,C 在⊙O 上,AB =AD ,AC 交BD 于点E ,已知∠COD =135°.(1)求∠AEB 的度数,(2)若CO =1,求OE 的长.【分析】(1)根据圆周角定理以及等腰直角三角形的性质可求出答案;(2)由相似三角形的判定和性质得出=,进而得到=,而OE+BE =OB =1,代入求解即可.【解答】解:(1)∵BD 是⊙O 的直径,点A 在⊙O 上,∴∠BAD =90°,∵AB =AD ,∴∠ABD =∠ADB =45°,∵∠COD =135°,∴∠BOC =180°﹣135°=45°,∴∠BAC=∠BOC=22.5°,∴∠AEB=180°﹣45°﹣22.5°=112.5°;(2)在Rt△ABD中,AB=AD,BD=2OC=2,∴AB=×BD=,∵∠ABC=∠BOC=45°,∴AB∥OC,∴△COE∽△ABE,∴=,即=,而OE+BE=OB=1,∴OE=﹣1.【点评】本题考查圆心角、弦、弧之间的关系,圆周角定理,相似三角形的判定和性质,掌握圆心角、弦、弧之间的关系,圆周角定理是正确解答的前提.8.(2023•玉环市二模)如图,点A、B、C、D是⊙O上的点,AD为直径,AB∥OC.(1)求证:点C平分弧BD.(2)利用无刻度的直尺和圆规作出AB的中点P(保留作图痕迹).【分析】(1)连接OB,由平行线的性质,等腰三角形的性质,得到∠DOC=∠COB,由此点C平分.(2)分别以A、B为圆心,大于AB的长为半径画弧,得到两弧的交点,从而得到点P.【解答】(1)证明:连接OB,∵OC∥AB,∴∠DOC=∠OAB,∠COB=∠OBA.∵OA=OB,∴∠DOC=∠COB,∴点C平分.(2)作法:①分别以A、B为圆心,大于AB的长为半径画弧,两弧交于M,②连接OM交AB于P,∴点P即为所求作的点.【点评】本题考查平行线的性质,圆心角、弧、弦的关系,尺规作图,关键是掌握圆心角、弧、弦的关系,用尺规作线段垂直平分线的方法.9.(2023•婺城区模拟)如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.(1)求证:CF=BF;(2)若CD=6,AC=8,求⊙O的半径及CE的长.【分析】(1)要证明CF=BF,可以证明∠ECB=∠DBC;AB是⊙O的直径,则∠ACB=90°,又知CE⊥AB,则∠CEB=90°,则∠DBC=90°﹣∠ACE=∠A,∠ECB=∠A,则∠ECB=∠DBC;(2)在直角三角形ACB中,AB2=AC2+BC2,又知,BC=CD,所以可以求得AB的长,即可求得圆的半径;再利用面积法求得CE的长.【解答】(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠A=90°﹣∠ABC.∵CE⊥AB,∴∠ECB=90°﹣∠ABC,∴∠ECB=∠A.又∵C是的中点,∴=,∴∠DBC=∠A,∴∠ECB=∠DBC,∴CF=BF;(2)解:∵=,∴BC=CD=6,∵∠ACB=90°,∴AB===10,∴⊙O的半径为5,∵S△ABC=AB•CE=BC•AC,∴CE===.【点评】此题考查了相似三角形的判定与性质、全等三角形的判定与性质、圆周角定理、等腰三角形的性质以及角平分线的性质等知识.此题综合性很强,难度适中,注意数形结合思想与方程思想的应用.二.圆周角定理(共11小题)10.(2023•鹿城区一模)如图,AC是⊙O的直径,B,D是⊙O上的两点,连结AB,BC,CD,BD,若∠A+∠D=80°,则∠ACB的度数为()A.40°B.50°C.60°D.80°【分析】根据圆周角定理得出∠ABC=90°,∠A=∠D=40°,根据直角三角形的性质求解即可.【解答】解:∵AC是⊙O的直径,∴∠ABC=90°,∴∠A+∠ACB=90°,∵∠A+∠D=80°,∠A=∠D,∴∠A=40°,∴∠ACB=50°,故选:B.【点评】此题考查了圆周角定理,熟记圆周角定理是解题的关键.11.(2023•西湖区校级三模)如图,点A、B、C在圆O上,若∠A=50°,则∠OBC的度数为()A.40°B.45°C.50°D.55°【分析】根据圆周角定理求得∠BOC的度数,然后利用三角形内角和定理及等边对等角即可求得答案.【解答】解:∵∠A=50°,∴∠BOC=2∠A=100°,∵OB=OC,∴∠OBC=∠OCB=(180°﹣100°)÷2=40°,故选:A.【点评】本题主要考查圆周角定理及等腰三角形性质,它们均为几何中重要知识点,必须熟练掌握.12.(2023•宁波模拟)如图,AB是⊙O的直径,C,D两点在圆上,连接AD,CD,且=,∠CAB=25°,P为上一动点,在运动过程中,DP与AC相交于点M,当△CDM为等腰三角形时,∠PDC的度数为.【分析】根据=,∠CAB=25°,得∠CAD=∠CAB=25°,由AB是⊙O的直径,得∠C=40°,然后分三种情况讨论即可求出答案.【解答】解:∵=,∠CAB=25°,∴∠CAD=∠CAB=25°,∵AB是⊙O的直径,∴∠C=40°,当△CDM为等腰三角形时,①当MD=MC时,∠PDC=∠C=40°,②当CD=CM时,∠PDC==70°,③当DM=DC时,∠PDC=180°﹣2×40°=100°,故答案为:40°或70°或100°.【点评】本题主要考查了圆周角定理,关键是求出∠C的度数和分三种情况讨论求角.13.(2023AB是⊙O的直径,弦CD与AB交于点E,若∠ABD=60°,∠AED=100°,则∠ABC=.【分析】连接AC,根据圆周角定理及三角形外角性质求解即可.【解答】解:连接AC,∵AB是⊙O的直径,∴∠ACB=∠BCD+∠ACD=90°,∵∠ACD=∠ABD=60°,∴∠BCD=90°﹣60°=30°,∵∠AED=100°,∴∠BED=∠BCD+∠ABC=80°,∴∠ABC=∠BED﹣∠BCD=80°﹣30°=50°,故答案为:50°.【点评】此题考查了圆周角定理,熟记“直径所对的圆周角等于90°”是解题的关键.14.(2023•杭州)如图,在⊙O中,半径OA,OB互相垂直,点C在劣弧AB上.若∠ABC=19°,则∠BAC=()A.23°B.24°C.25°D.26°【分析】连接OC,根据圆周角定理可求解∠AOC的度数,结合垂直的定义可求解∠BOC 的度数,再利用圆周角定理可求解.【解答】解:连接OC,∵∠ABC=19°,∴∠AOC=2∠ABC=38°,∵半径OA,OB互相垂直,∴∠AOB=90°,∴∠BOC=90°﹣38°=52°,∴∠BAC=∠BOC=26°,故选:D.【点评】本题主要考查圆周角定理,掌握圆周角定理是解题的关键.15.(2023•余杭区模拟)如图,AB是半圆O的直径,点D是弧AC的中点,若∠DAC=25°.则∠BAC等于()A.40°B.42°C.44°D.46°【分析】利用圆周角定理和弧与圆心角的关系求解即可.【解答】解:连接OC,OD,∵点D是弧AC的中点,∴弧AD=弧CD,又∠DAC=25°,∴∠AOD=∠COD=2∠DAC=50°,∴∠BOC=180°﹣∠AOD﹣∠COD=80°,∴,故选:A.【点评】本题考查圆周角定理、弧与圆心角的关系,熟练掌握圆周角定理是解答的关键.16.(2023•杭州模拟)如图是以点O为圆心,AB为直径的圆形纸片,点C在⊙O上,将该圆形纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E.若AD=ED,则∠B=度;的值等于.【分析】由等腰三角形的性质得出∠DAE=∠DEA,证出∠BEC=∠BCE,由折叠的性质得出∠ECO=∠BCO,设∠ECO=∠OCB=∠B=x,证出∠BCE=∠ECO+∠BCO=2x,∠CEB=2x,由三角形内角和定理可得出答案;证明△CEO∽△BEC,由相似三角形的性质得出,设EO=x,EC=OC=OB=a,得出a2=x(x+a),求出OE=a,进而可得出答案.【解答】解:∵AD=DE,∴∠DAE=∠DEA,∵∠DEA=∠BEC,∠DAE=∠BCE,∴∠BEC=∠BCE,∵将该圆形纸片沿直线CO对折,∴∠ECO=∠BCO,又∵OB=OC,∴∠OCB=∠B,设∠ECO=∠OCB=∠B=x,∴∠BCE=∠ECO+∠BCO=2x,∴∠CEB=2x,∵∠BEC+∠BCE+∠B=180°,∴x+2x+2x=180°,∴x=36°,∴∠B=36°;∵∠ECO=∠B,∠CEO=∠CEB,∴△CEO∽△BEC,∴,∴CE2=EO•BE,设EO=x,EC=OC=OB=a,∴a2=x(x+a),解得,x=a(负值舍去),∴OE=a,∴AE=OA﹣OE=a﹣a=a,∴==.故答案为:36,.理,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.17.(2023•钱塘区三模)如图,AB是⊙O的直径,半径OD⊥AB,点E在OB上,连接DE并延长交⊙O于点C,连接BC.(1)求∠B﹣∠D的值.(2)当∠B=75°时,求的值.(3)若BC=CE,△DOE与△CBE的面积分别记为S1,S2,求的值.【分析】(1)由圆周角定理求出∠BCD=∠BOD=45°,由等腰三角形的性质推出∠OBC﹣∠ODC=∠OCB ﹣∠OCD=∠DCB=45°;(2)由直角三角形的性质得到=,由等腰三角形的性质得到CD=OD,即可求出的值;(3)由OC∥BD,得到△CBD的面积=△ODB的面积,因此△CBE的面积=△OED的面积,即可解决问题.【解答】解:(1)连接OC,∵半径OD⊥AB,∴∠BOD=90°,∴∠BCD=∠BOD=45°,∵OC=OD,∴∠OCD=∠ODC,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC﹣∠ODC=∠OCB﹣∠OCD=∠DCB=45°;(2)∵∠B=75°,∠DCB=45°,∴∠CEB=60°,∴∠OED=60°,∴=,∵OB=OC,∴∠OCB=∠OBC=75°,∴∠BOC=30°,∴∠COD=∠BOD+∠BOC=120°,∴CD=OD,∴==.(3)连接BD,∵BC=CE,∴∠CBE=∠CEB,∵∠BCE=45°,∴∠CBE=67.5°,∵OC=OB,∴∠OCB=∠CBE=67.5°,∴∠OCE=∠OCB﹣∠BCD=22.5°,∵∠BOC=180°﹣∠OCB﹣∠OBC=45°,∴∠BDC=∠BOC=22.5°,∴∠OCE=∠BDC,∴OC∥BD,∴△CBD的面积=△ODB的面积,∴△CBE的面积=△OED的面积,∴=1.【点评】本题考查圆周角定理,直角三角形的性质,等腰三角形的性质,平行线的判定,三角形的面积,关键是由圆周角定理∠BCD=45°,由等腰三角形的性质即可求出∠OBC﹣∠ODC=45°;由直角三角形的性质,等腰三角形的性质求出OE、CD与OD的数量关系,即可求出的值;由OC∥BD,即可得到△CBE的面积=△OED的面积.18.(2023•衢州二模)如图,在⊙O中,OA,OB是直径,C是劣弧上的一点.且∠AOB=120°.(1)求∠ACB的度数;(2)若AC=BC.求证:四边形ACBO是菱形.【分析】(1)由题意可得劣弧=120°,从而可得优弧=240°,再由圆周角定理即可求∠ACB的度数;(2)连接OC,利用SSS可证得△AOC≌△BOC,则有∠AOC=∠BOC,可求得∠AOC=∠BOC=60°,可得△AOC是等边三角形,则有AO=AC=OC,同理得BO=BC=OC,故AO=AC=BC=BO,即可判定四边形ACBO 是菱形.【解答】(1)解:∵C是劣弧上的一点,且∠AOB=120°,∴劣弧的度数为:120°,∴优弧的度数为:240°,∴∠ACB=×240°=120°;(2)证明:连接OC,如图,∵OA,OB是半径,点C在⊙O上,∴OA=OB=OC,在△AOC与△BOC中,,∴△AOC≌△BOC(SSS),∴∠AOC=∠BOC,∵∠AOB=120°,∴∠AOC=∠BOC=60°,∴△AOC是等边三角形,∴AO=AC=OC,同理得:BO=BC=OC,∴AO=AC=BC=BO,∴四边形ACBO是菱形.【点评】本题主要考查圆周角定理,菱形的判定,圆心角,弦,弧的关系,解答的关键是熟记相应的知识并灵活运用.19.(2023•金东区二模)如图,已知AB,CD是⊙O的直径,点E是CA延长线的一点,射线ED交⊙O点于F,连结AD,CF,∠CDA=∠EDA,∠CAB=30°,AB=8.(1)求证:AB∥FE.(2)求∠FCA的度数.(3)求CE的长.【分析】(1)由OA=OD,得到∠ODA=∠OAD,而∠CDA=∠EDA,因此∠OAD=∠EDA,即可证明AB∥FE;(2)由AB∥FE,得到∠E=∠CAB=30°,由圆周角定理得到∠EFC=90°,由直角三角形的性质,即可得到∠FCA的度数;(3)可以证明DC=DE,由圆周角定理得到AD⊥CE,因此CE=2CA,由cos∠DCA==,CD=AB=8,求出AC的长,即可得到CE的长.【解答】(1)证明:∵OA=OD,∴∠ODA=∠OAD,∵∠CDA=∠EDA,∴∠OAD=∠EDA,∴AB∥FE;(2)解:∵AB∥FE,∴∠E=∠CAB=30°,∵CD是圆的直径,∴∠EFC=90°,∴∠FCA=90°﹣∠E=60°;(3)解:∵OC=OA,∴∠OCA=∠OAC=30°,∵∠E=30°,∴∠OCA=∠E=30°,∴DC=DE,∵DC是圆的直径,∴AD⊥CE,∴CA=EA,∴CE=2CA,∵cos∠DCA==,CD=AB=8,∴AC=4,∴CE=2×4=8.【点评】本题考查圆周角定理,解直角三角形,等腰三角形的判定和性质,平行线的判定,掌握以上知识点是解题的关键.20.(2023•滨江区一模)如图1,AB为⊙O的直径,CD⊥AB于点E,,BF与CD交于点G.(1)求证:CD=BF.(2)若BE=1,BF=4,求GE的长.(3)连结GO,OF,如图2,求证:.【分析】(1)由AB为⊙O的直径,CD⊥AB于点E得,又由,得到,从而得到,即,即可得证;(2)连接BC,由(1)得:,CD=BF=4,从而得到∠FBC=∠BCD,则BG=CG,设EG=x,则BG =CG=2﹣x,在△BEG中,EG2+BE2=BG2,即x2+12=(2﹣x)2,即可得到答案;(3)连接OC交BF于I,则OC⊥BF,通过证明△OCG≌△OBG(SSS),得到∠IOB=2∠EOG,再由等腰三角【解答】(1)证明:∵AB为⊙O的直径,CD⊥AB于点E,∴,∵,∴,∴,即,∴BF=CD;(2)解:如图所示:连接BC,由(1)得:,CD=BF=4,∴∠FBC=∠BCD,∴BG=CG,∵AB为⊙O的直径,CD⊥AB于点E,∴,设EG=x,则BG=CG=2﹣x,在△BEG中,EG2+BE2=BG2,即x2+12=(2﹣x)2,解得:,∴GE的长为;(3)解:如图所示:连接OC交BF于I,∴,在△OCG和△OBG中,,∴△OCG≌△OBG(SSS),∴∠COG=∠BOG,∴∠IOB=2∠EOG,∵OF=OB,OC为半径,∴OC⊥BF,∴∠OIB=90°,∵∠IOB+∠IBO=90°,∴.【点评】本题主要考查了圆周角定理,全等三角形的判定与性质,三角形外角的性质,勾股定理,熟练掌握圆周角定理,全等三角形的判定与性质,三角形外角的性质,添加恰当的辅助线是解题的关键.三.圆内接四边形的性质(共11小题)21.(2022秋•嘉兴期末)已知,在圆内接四边形ABCD中,∠A:∠B:∠C=1:2:5,则∠D的度数为()A.30°B.60°C.120°D.150°【分析】先根据在圆内接四边形ABCD中∠A:∠B:∠C=1:2:5,设∠A=x,则∠B=2x,∠C=5x,再根据圆内接四边形的对角互补求出x的值,进而可得出结论.【解答】解:∵圆内接四边形ABCD中∠A:∠B:∠C=1:2:5,设∠A=x,则∠B=2x,∠C=5x,∵∠A+∠C=180°,即x+5x=180°,解得x=30°,∴2x=60°.即∠B=60°,∵∠B+∠D=180°,∴D=120°.故选:C.22.(2023•宁波模拟)圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A=°.【分析】根据圆内接四边形的性质得到∠BCD=180°﹣∠A,根据三角形的外角的性质计算即可.【解答】解:∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣∠A,∵∠CBF=∠A+∠E,∠DCB=∠CBF+∠F,∴180°﹣∠A=∠A+∠E+∠F,即180°﹣∠A=∠A+40°+60°,解得∠A=40°.故答案为:40.【点评】本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补、圆内接四边形的任意一个外角等于它的内对角是解题的关键.23.(2023•龙港市一模)如图,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连结CE,若∠BAD =110°,则∠DCE=度.【分析】由∠DAB+∠DCB=180°,再结合圆周角定理,即可计算∠DCE的大小.【解答】解:∵四边形ABCD是⊙O的内接四边形,∠BAD=110°,∴∠DAB+∠DCB=180°,∴∠DCB=180°﹣110°=70°,∵BE是⊙O的直径,∴∠DCE+∠DCB=90°,【点评】本题考查了圆内接四边形的性质、圆周角定理,熟练掌握圆内接四边形的性质是解题的关键.24.(2022秋•仙居县期末)如图,四边形ABCD是⊙O的内接四边形,点C是弧BD的中点,连接BD,若∠CBD=35°,求∠A的度数.【分析】根据圆的性质及等腰三角形的性质得出∠CBD=∠CDB=35°,根据三角形内角和推出∠C=110°,再根据圆内接四边形的性质即可求解.【解答】解:∵点C是弧BD的中点,∴=,∴BC=CD,∴∠CBD=∠CDB=35°,∴∠C=180°﹣35°﹣35°=110°,∵四边形ABCD是⊙O的内接四边形,∴∠A+∠C=180°,∴∠A=70°.【点评】此题考查了圆内接四边形的性质,熟记“圆内接四边形的对角互补”是解题的关键.25.(2023•绍兴)如图,四边形ABCD内接于圆O,若∠D=100°,则∠B的度数是.【分析】由圆内接四边形的性质:圆内接四边形的对角互补,即可得到答案.【解答】解:∵四边形ABCD内接于圆O,∴∠B+∠D=180°,∵∠D=100°,【点评】本题考查圆内接四边形的性质,关键是掌握圆内接四边形的性质.26.(2023•萧山区二模)如图,四边形ABCD内接于⊙O,点C是弧BD的中点,延长AB到点E,使得BE =AD,连结AC,CE.(1)求证:AC=CE.(2)若,,∠BCD=120°,求BC的长.【分析】(1)根据圆内接四边形性质易得∠D=∠CBE,再根据圆心角、弧、弦的关系可得CD=CB,再结合已知条件证得△ACD≌△ECB,从而证得结论;(2)作CM⊥AB交AB于点M,结合(1)中所求易得AE的长度,再根据圆内接四边形性质及圆心角、弧、弦的关系可得∠CBM=30°,利用三线合一及三角函数可求得CM,BM的长度,最后利用勾股定理即可求得答案.【解答】解:(1)∵四边形ABCD为⊙O的内接四边形,∴∠D+∠ABC=180°,∵∠ABC+∠CBE=180°,∴∠D=∠CBE,∵点C时的中点,∴CD=CB,在△ACD与△ECB中,,∴△ACD≌△ECB(SAS),∴AC=CE;(2)如图,作CM⊥AB交AB于点M,∵AD=4,BE=AD,∴BE=4,∵AB=6,∴AE=AB+BE=6+4=10,∵AC=CE,CM⊥AB,∴AM=AE=5,∴BM=AB﹣AM=6﹣5=,∵四边形ABCD为⊙O的内接四边形,∴∠BCD+∠BAD=180°,∵∠BCD=120°,∴∠BAD=60°,∵CD=CB,∴∠CAM=∠BAD=30°,∵∠AMC=90°,∴tan∠CAM=tan30°==,∴CM=5×=5,∴BC====2.【点评】本题主要考查圆的相关性质及全等三角形的判定及性质,(2)中作CM⊥AB交AB于点M,构造直角三角形及利用三线合一求得线段长度是解题的关键.27.(2023•金华三模)在⊙O中,点A,B,C,D都在圆周上,OB∥DC,OD∥BC,则∠A的度数为()A.45°B.50°C.55°D.60°【分析】根据圆内接四边形的性质得出∠C+∠A=180°,根据平行线的性质得出∠C+∠OBC=180°,∠BOD+∠OBC=180°,求出∠C=∠BOD,根据圆周角定理得出∠BOD=2∠A,求出∠C=2∠A,再求出∠A即可.【解答】解:∵点A,B,C,D都在圆周上,∴∠C+∠A=180°,∵OB∥DC,OD∥BC,∴∠C+∠OBC=180°,∠BOD+∠OBC=180°,∴∠C=∠BOD,∵∠BOD=2∠A,∴∠C=2∠A,即3∠A=180°,∴∠A=60°,故选:D.【点评】本题考查了圆周角定理,圆内接四边形的性质,平行线的性质等知识点,能求出∠C+∠A=180°和∠BOD=2∠A是解此题的关键.28.(2023•萧山区校级模拟)如图,A、B、C、D四个点均在⊙O上,∠AOD=α,AO∥DC,∠B=β,则α,β满足关系为()A.2α﹣β=90°B.α+β=90°C.2β+α=180°D.α+9β=540°【分析】先根据平行线的性质得出∠ODC=∠AOD=α,再由等腰三角形的性质与三角形内角和定理求得∠即可.【解答】解:连接OC,∵AO∥DC,∴∠ODC=∠AOD=α,∵OD=OC,∴∠ODC=∠OCD=α,∴∠DOC=180°﹣2α,∴∠AOC=∠AOD+∠DOC=180°﹣α,∴∠ABC=∠AOC=90°﹣α,即β=90°﹣α,∴2β+α=180°.故选:C.【点评】本题考查等腰三角形的性质,平行线的性质,三角形内角和定理,圆周角定理,熟练掌握圆周角定理是解题的关键.29.(2022秋•上城区期末)如图,四边形ABCD是半圆O的内接四边形,AB是直径,CD=BC.若∠DCB =100°,则∠ADC的度数为()A.100°B.110°C.120°D.130°【分析】连接BD,分别求出∠ADB,∠CDB,可得结论.【解答】解:连接BD.∵AB是直径,∵CD=CB,∠C=100°,∴∠CDB=∠CBDD=40°,∴∠ADC=∠ADB+∠CDB=90°+40°=130°.故选:D.【点评】本题考查圆内接四边形的性质,圆周角定理,等腰三角形的性质等知识,解题关键是灵活运用所学知识解决问题,属于中考常考题型.30.(2022秋•嵊州市期末)如图,四边形ABCD内接于⊙O,分别延长BC,AD,使它们相交于点E,AB=8,且DC=DE.(1)求证:∠A=∠AEB.(2)若∠EDC=90°,点C为BE的中点,求⊙O的半径.【分析】(1)根据圆内接四边形的对角互补可得∠A+∠BCD=180°,再由邻补角互补可得∠BCD+∠DCE=180°,根据同角的补角相等可得∠A=∠DCE,再根据等边对等角可得∠E=∠DCE,再根据等量代换可得∠A=∠AEB.(2)连接AC,根据直角所对的弦是直径得出AC为⊙O的直径,根据勾股定理求出AC,即可求解.【解答】(1)证明:∵四边形ABCD内接于⊙O,∴∠A+∠BCD=180°,∵∠BCD+∠DCE=180°,∴∠A=∠DCE,∵DC=DE∴∠E=∠DCE,(2)解:如图,连接AC,∵∠EDC=90°,∴AC是⊙O的直径,∴∠ABC=90°,∵∠A=∠AEB∴AB=BE∵AB=8,∴BE=8,∵点C为BE的中点,∴,在Rt△ABC中,,∴⊙O的半径为.31.(2023•杭州二模)如图,四边形ABCD是⊙O的内接四边形,点F是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.(1)求证:AB=AC.(2)若BD=11,DE=2,求CD的长.【分析】(1)根据角平分线的定义、圆内接四边形的性质解答;(2)过点A作AG⊥BD,分别证明Rt△AED≌Rt△AGD和Rt△AEC≌Rt△AGB,根据全等三角形的性质计算.【解答】(1)证明:∵AD平分∠BDF,∴∠ADF=∠ADB,∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,∴∠ADF=∠ABC,∵∠ACB=∠ADB,∴∠ABC=∠ACB,∴AB=AC;(2)解:过点A作AG⊥BD,垂足为点G.∵AD平分∠BDF,AE⊥CF,AG⊥BD,∴AG=AE,∠AGB=∠AEC=90°,在Rt△AED和Rt△AGD中,,∴Rt△AED≌Rt△AGD,∴GD=ED=2,在Rt△AEC和Rt△AGB中,,∴Rt△AEC≌Rt△AGB(HL),∴BG=CE,∵BD=11,∴BG=BD﹣GD=11﹣2=9,∴CE=BG=9,∴CD=CE﹣DE=9﹣2=7.【点评】本题考查的是圆内接四边形的性质、全等三角形的判定和性质,掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键.四.相交弦定理(共4小题)32.(2021秋•东阳市月考)已知四边形ABCD两条对角线相交于点E,AB=AC=AD,AE=3,EC=1,则BE•DE的值为()A.6B.7C.12D.16【分析】由题意可知AB=AC=AD,点D、C、B在以点A为圆心的圆周上运动,由相交弦定理可得,BE•DE =CE•EF即可求出答案.【解答】解:∵AB=AC=AD,∴点D、C、B在以点A为圆心的圆周上运动,AE=3,EC=1,∴AC=AF=AE+CE=3+1=4,EF=AE+AF=3+4=7,由相交弦定理可得,BE•DE=CE•EF=1×7=7,故选:B.【点评】本题考查了相交弦定理,根据圆心和半径构建圆是解题的关键.33.(2021秋•余姚市期中)如图,⊙O的弦AB、CD相交于点P,若AP=6,BP=8,CP=4,则CD长为()A.16B.24C.12D.不能确定【分析】由相交线定理可得出AP•BP=CP•DP,再根据AP=6,BP=8,CP=4,可得出PD的长,从而得出CD即可.【解答】解:∵AP•BP=CP•DP,∴PD=,∵AP=6,BP=8,CP=4,∴PD=12,∴CD=PC+PD=12+4=16.故选:A.【点评】本题考查了相交线定理,圆内两条弦相交,被交点分成的两条线段的积相等.34.(2022秋•温州期末)已知四边形ABCD两条对角线相交于点E,AB=AC=AD,AE=3,EC=1,则BE •DE的值为()A.6B.7C.12D.16.【分析】由题意可知AB=AC=AD,点D、C、B在以点A为圆心的圆周上运动,由相交弦定理可得,BE•DE =CE•EF即可求出答案.【解答】解:∵AB=AC=AD,∴点D、C、B在以点A为圆心的圆周上运动,AE=3,EC=1,∴AC=AF=AE+CE=3+1=4,EF=AE+AF=3+4=7,由相交弦定理可得,BE•DE=CE•EF=1×7=7,故选:B.【点评】本题考查了相交弦定理,根据圆心和半径构建圆是解题的关键.35.(2022秋•嵊州市期末)如图,AB是⊙O的直径,弦CD与AB相交于点E,若AE=2,BE=8,CE=2DE,则O到CD的距离为.【分析】连接AD、BC、OC,过O作OH⊥CD交CD于H,先根据圆周角定理和相似三角形的判定证明△ADE∽△CBE,再利用相似三角形的性质求得进而求得,进而求得,然后利用垂径定理和勾股定理求得OH即可求解.【解答】解:如图,连接AD、BC,则∠ADE=∠CBE,∠DAE=∠BCE,∴△ADE∽△CBE,∴,∵AE=2,BE=8,CE=2DE,∴2DE2=AE•BE=2×8=16,AB=10,∴,,∴, 过O 作OH ⊥CD 交CD 于H ,连接OC ,则, 在Rt △OHC 中,, ∴,即O 到CD 的距离为, 故答案为:.【点评】本题考查圆周角定理、垂径定理、相似三角形的判定与性质、勾股定理,熟练掌握圆周角定理和垂径定理,会利用相似三角形的判定与性质求线段长是解题的关键.【过关检测】一、单选题 1.(2022秋·浙江·九年级专题练习)如图,在O 中,45CD A AB OB =∠=︒,则COD ∠=( )A .60︒B .45︒C .30︒D .40︒【答案】B 【分析】根据同圆中等弧所对的圆心角相等,即可求解.【详解】解:∵,45CD A AB OB =∠=︒,∴COD ∠=45︒,故选:B .【点睛】本题考查了同圆或等圆中,等弧所对的圆心角相等,掌握同圆或等圆中,等弧所对的圆心角相等是解题的关键. 2.(2023·浙江·九年级假期作业)如图,点A ,B ,C ,D 在O 上,则图中一定与ABC ∠相等的角是( )A .BAD ∠B .ACD ∠C .BCD ∠ D .ADC ∠【答案】D 【分析】根据同弧所对等圆周角相等求解即可.【详解】∵ABC ∠所对应的弧为AC ,∴ADC ABC ∠=∠,故选:D .【点睛】本题考查了圆周角定理,熟练掌握圆周角定理是解题的关键.3.(2023·浙江·九年级假期作业)如图,四边形ABCD 内接于⊙O ,AB 为直径,BC CD =,连接AC .若40DAB ∠=︒,则B ∠的度数为( )A .70°B .60°C .50°D .40°【答案】A 【分析】连接AC ,根据等弧所对的圆周角相等可得1202DAC BAC DAB ∠=∠=∠=︒,再根据直径所对的圆周角为直角可得90ACB ∠=︒,最后根据三角形的内角和即可求解.【详解】解:连接AC ,∵点C 为BD 的中点 ∴1202DAC BAC DAB ∠=∠=∠=︒∵AB 为O 的直径∴90ACB ∠=︒∴180902070ABC ∠=︒−︒−︒=︒故选:A .【点睛】本题主要考查了在同圆或等圆中,同弧或等弧所对的圆周角相等,直径所对的圆周角为直角,三角形的内角和,解题的关键是熟练掌握相关知识并灵活运用.4.(2023·浙江·模拟预测)已知弦AB 把圆周分成1:3两部分,则弦AB 所对圆心角的度数为( )【分析】分优弧,劣弧两种情况,求解即可.【详解】解:∵弦AB 把圆周分成1:3两部分,∴劣弧AB 的度数为:1360904°´=°,即:劣弧所对的圆心角的度数为90︒, 优弧AB 的度数为:33602704︒⨯=︒,即:优弧所对的圆心角的度数为270︒,∴弦AB 所对圆心角的度数为90︒或270︒;故选C .【点睛】本题考查弦,弧,角之间的关系.注意弦分弧为优弧和劣弧两种情况. 5.(2023秋·浙江台州·九年级统考期末)如图,CD 是O 的直径,弦AB 垂直CD 于点E ,连接AC ,BC ,AD ,BD ,则下列结论不一定...成立的是( )。
九年级圆周角知识点

九年级圆周角知识点圆周角是指以圆心为顶点,两边分别为弧所对应的角。
在九年级数学学习中,圆周角是一个重要的概念,掌握圆周角的知识对于理解和解决相关问题至关重要。
本文将详细介绍九年级圆周角的相关知识点,帮助同学们更好地理解和应用。
1. 圆周角的定义圆周角是指以圆心为顶点,两边分别为弧所对应的角。
圆周角的度数等于所对应的弧度数,并且圆周角满足角度的加法定理,即两个相邻的圆周角的度数之和等于360度(或2π弧度)。
2. 圆周角的性质- 如果两个角的顶点在同一个圆上,并且两个角的两边分别与同一个弧相交,则这两个角互为圆周角,它们的度数相等。
- 如果两个角的顶点在同一个圆上,并且两个角的一边分别与同一个弦相交,则这两个角互为补角,它们的度数之和等于180度。
- 如果两个角的顶点在同一个圆上,并且两个角的一个角是直角,则另一个角也是直角。
3. 判断圆周角的大小对于给定的圆周角,可以通过以下方法来判断它的大小:- 将角的度数与360度(或2π弧度)进行比较,如果小于360度(或2π弧度),则圆周角是锐角;如果等于360度(或2π弧度),则圆周角是整圆角;如果大于360度(或2π弧度),则圆周角是钝角。
4. 圆周角的应用圆周角的概念在解决与圆相关的问题中发挥着重要作用,例如:- 弧长与角度之间的关系:圆周角的度数与所对应的弧长之间存在着等量关系,即弧长等于圆周角的弧度数乘以半径长度;- 扇形面积的计算:扇形是由圆心、两个半径所组成的图形,扇形的面积等于所对应的圆周角所占据的圆的面积的比例乘以整个圆的面积;- 弧度制的应用:弧度制是一种角度度量单位,它与度数之间存在着特定的换算关系,在解决复杂问题时非常有用。
总结:九年级的圆周角知识点对于数学学习至关重要,通过理解圆周角的定义、性质和判断方法,我们可以更好地解决与圆相关的问题,并灵活运用到实际生活中。
在学习过程中,我们还要注意弧长和扇形面积的计算,以及掌握弧度制的应用。
人教版九年级数学上章节知识点深度解析 圆周角 第1课时 圆周角定理及推论

证明:由圆周角定理推出∠ A =∠ C ,∠ D =∠B ,
在△ ADM 和△ CBM 中,
∠=∠,
ቐ=,
∠=∠,
∴△ ADM ≌△ CBM (ASA).∴ AM = CM .
1
2
3
4
5
谢谢观看
Thank you for watching!
.
定理的 2.半圆(或直径)所对的圆周角是 直角
推论 90°的圆周角所对的弦是 直径 .
,
图例
90°直径ຫໍສະໝຸດ 圆周角内容图例
①在圆中,利用“直径所对的圆周角是直
解题
角”构造直角三角形解题.
策略
②一条弦所对的圆周角有两种情况:相等
或互补.
当堂检测
1. 如图,已知圆心角∠ BOC =78°,则圆周角∠ BAC
的度数是( C
)
A. 156°
B. 78°
C. 39°
D. 12°
第1题图
1
2
3
4
5
2. 如图, AB 是圆 O 的直径,点 C 在圆 O 上,若∠ A =
30°,则∠ B 的度数为( B
A. 75°
B. 60°
C. 45°
D. 15°
)
第2题图
1
2
3
4
5
3. 如图, AB , BC 是☉ O 的弦, AB =3,∠ ACB =
30°,则☉ O 的半径等于(
A. 1.5
B. 3
C. 4.5
D. 6
)
B
第3题图
1
2
3
圆周角—知识讲解(基础)
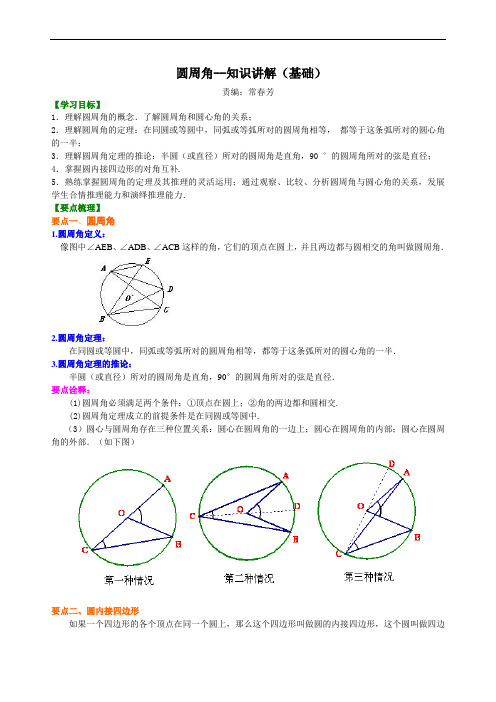
圆周角--知识讲解(基础)责编:常春芳【学习目标】1.理解圆周角的概念.了解圆周角和圆心角的关系;2.理解圆周角的定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,•都等于这条弧所对的圆心角的一半;3.理解圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90•°的圆周角所对的弦是直径;4.掌握圆内接四边形的对角互补.5.熟练掌握圆周角的定理及其推理的灵活运用;通过观察、比较、分析圆周角与圆心角的关系,发展学生合情推理能力和演绎推理能力.【要点梳理】要点一、圆周角1.圆周角定义:像图中∠AEB、∠ADB、∠ACB这样的角,它们的顶点在圆上,并且两边都与圆相交的角叫做圆周角.2.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.3.圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.要点诠释:(1)圆周角必须满足两个条件:①顶点在圆上;②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.(3)圆心与圆周角存在三种位置关系:圆心在圆周角的一边上;圆心在圆周角的内部;圆心在圆周角的外部.(如下图)要点二、圆内接四边形如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.圆内接四边形的对角互补.圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).要点诠释:圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来.在应用时要注意是对角,而不是邻角互补.【典型例题】类型一、圆周角、圆心角、弧、弦之间的关系及应用1.如图,在⊙O中,,求∠A的度数.【答案与解析】.【总结升华】在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的圆周角相等,所对的弦也相等.举一反三:【变式】如图所示,正方形ABCD内接于⊙O,点E在劣弧AD上,则∠BEC等于( )A.45° B.60° C.30° D.55°【答案】A.∵ AB=BC=CD=DA,∴»»»»90 AB BC CD DA====°,∴∠BEC=45°.类型二、圆周角定理及应用2.观察下图中角的顶点与两边有何特征? 指出哪些角是圆周角?【思路点拨】根据圆周角的定义去判断,顶点在圆上,并且两边都和圆相交的角叫做圆周角.【答案与解析】(a)∠1顶点在⊙O内,两边与圆相交,所以∠1不是圆周角;(b)∠2顶点在圆外,两边与圆相交,所以∠2不是圆周角;(c)图中∠3、∠4、∠BAD的顶点在圆周上,两边均与圆相交,所以∠3、∠4、∠BAD是圆周角.(d)∠5顶点在圆上,一边与圆相交,另一边与圆不相交,所以∠5不是圆周角;(e)∠6顶点在圆上,两边与圆均不相交,由圆周角的定义知∠6不是圆周角.【总结升华】紧扣定义,抓住二要素,正确识别圆周角.3.(2015•台州)如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;(2)求证:∠1=∠2.【答案与解析】(1)解:∵BC=DC,∴∠CBD=∠CDB=39°,∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,∴∠BAD=∠BAC+∠CAD=39°+39°=78°;(2)证明:∵EC=BC,∴∠CEB=∠CBE,而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,∴∠2+∠BAE=∠1+∠CBD,∵∠BAE=∠CBD,∴∠1=∠2.【总结升华】本题主要考查了圆周角定理和等腰三角形的性质,熟悉圆的有关性质是解决问题的关键.举一反三:【变式】(2015•安顺)如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为()A.2B.4C.4D.8【答案】C.提示:∵∠A=22.5°,∴∠BOC=2∠A=45°,∵⊙O的直径AB垂直于弦CD,∴CE=DE,△OCE为等腰直角三角形,∴CE=OC=2,∴CD=2CE=4.故选:C.类型三、圆内接四边形4.如图,在圆的内接四边形ABCD中,∠ABC=120°,则四边形ABCD的外角∠ADE的度数是()A.130° B.120° C.110° D.100°【思路点拨】先根据圆内接四边形的对角互补及邻补角互补得出∠ADC+∠B=180°,∠ADC+∠ADE=180°,然后根据同角的补角相等得出∠ADE=∠B=120°.【答案】B;【解析】解:∵四边形ABCD是圆内接四边形,∴∠ADC+∠B=180°,∵∠ADC+∠ADE=180°,∴∠ADE=∠B.∵∠B=120°,∴∠ADE=120°.【总结升华】本题考查的是圆内接四边形的性质,熟知圆内接四边形对角互补的性质是解答此题的关键.举一反三:【变式】如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若CF平分∠DCE,则∠DCF的大小是()A.52°B.54°C.56°D.60°【答案】B.解:∵四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,∴∠DCE=∠BAD=108°.∵CF平分∠DCE,∴∠DCF=∠DCE=54°.5.如图,四边形ABCD内接于圆O,若∠BOD=130°,则∠DCE=°.【思路点拨】由圆周角定理,可求得∠A的度数,又由圆的内接四边形的性质,可得∠DCE=∠A.【答案】65;解:∵∠BOD=130°,∴∠A=∠BOD=65°,∵∠A+∠BCD=180°,∠DCE+∠BCD=180°,∴∠DCE=∠A=65°.【总结升华】此题考查了圆的内接四边形的性质以及圆周角定理.此题难度不大,注意掌握数形结合思想的应用.举一反三:【变式】如图,点C是AB上一点,O是圆心,且∠AOB=120°,则∠ACB=度.【答案】120;解:设点E是优弧AB上的一点,∵∠AOB=120°,∴∠AEB=60°,∴∠ACB=180°﹣∠AEB=120°.。
2022年中考数学真题-专题14 圆与正多边形(1)(全国通用解析版)

专题14 圆与正多边形一.选择题1. 如图,在⊙O 中,∠BOC =130°,点A 在BAC 上,则∠BAC 的度数为( )A. 55°B. 65°C. 75°D. 130°【答案】B【解析】【分析】利用圆周角直接可得答案. 【详解】解: ∠BOC =130°,点A 在BAC 上, 165,2BACBOC故选B 【点睛】本题考查的是圆周角定理的应用,掌握“同圆或等圆中,同弧所对的圆周角是它所对的圆心角的一半”是解本题的关键.2. 如图,在O 中,弦,AB CD 相交于点P ,若48,80A APD ∠=︒∠=︒,则B 的大小为( )A. 32︒B. 42︒C. 52︒D. 62︒ 【答案】A【解析】【分析】根据三角形的外角的性质可得C A APD ∠+∠=∠,求得32C ∠=︒,再根据同弧所对的圆周角相等,即可得到答案.【详解】C A APD ∠+∠=∠,48,80A APD ∠=︒∠=︒,32C ∴∠=︒32B C ∴∠=∠=︒故选:A .【点睛】本题考查了圆周角定理及三角形的外角的性质,熟练掌握知识点是解题的关键.3. 如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )A. 23πB. 23π-C. 43π-D. 43π【答案】B【解析】 【分析】阴影部分的面积等于扇形面积减去三角形面积,分别求出扇形面积和等边三角形的面积即可.【详解】解:如图,过点OC 作OD ⊥AB 于点D ,∵∠AOB =2×36012︒=60°, ∴△OAB 是等边三角形, ∴∠AOD =∠BOD =30°,OA =OB =AB =2,AD =BD =12AB =1,∴OD =∴阴影部分的面积为260212236023ππ⋅⨯-⨯=- 故选:B .【点睛】本题考查了扇形面积、等边三角形的面积计算方法,掌握扇形面积、等边三角形的面积的计算方法是正确解答的关键.4. 如图,在四边形材料ABCD 中,AD BC ∥,90A ∠=︒,9cm AD =,20cm AB =,24cm BC =.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )A. 110cm 13B. 8cmC.D. 10cm【答案】B【解析】【分析】如图所示,延长BA 交CD 延长线于E ,当这个圆为△BCE 的内切圆时,此圆的面积最大,据此求解即可.【详解】解:如图所示,延长BA 交CD 延长线于E ,当这个圆为△BCE 的内切圆时,此圆的面积最大,∵AD BC ∥,∠BAD =90°,∴△EAD △△EBC ,∠B =90°, △EA AD EB BC=,即92024EA EA =+, ∴12cm EA =,∴EB =32cm ,∴40cm EC ==,设这个圆的圆心为O ,与EB ,BC ,EC 分别相切于F ,G ,H ,∴OF =OG =OH ,∵=EBC EOB COB EOC S S S S ++△△△△, ∴11112222EB BC EB OF BC OG EC OH ⋅=⋅+⋅+⋅, ∴()2432=243240OF ⨯++⋅,∴8cm OF =,∴此圆的半径为8cm ,故选B .【点睛】本题主要考查了三角形内切圆半径与三角形三边的关系,勾股定理,正确作出辅助线是解题的关键.5. 如图,四边形ABCD 内接于O ,连接OB ,OD ,BD ,若110C ∠=︒,则OBD ∠=( )A. 15︒B. 20︒C. 25︒D. 30【答案】B【解析】 【分析】根据圆内接四边形的性质求出A ∠,根据圆周角定理可得BOD ∠,再根据OB OD =计算即可.【详解】∵四边形ABCD 内接于O ,∴18070A BCD ∠︒-∠︒== ,由圆周角定理得,2140BOD A ∠=∠=︒ ,∵OB OD = ∴180202BOD OBD ODB ︒-∠∠=∠==︒ 故选:B .【点睛】此题考查圆周角定理和圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.6. 如图,点E 是ABC 的内心,AE 的延长线和ABC 的外接圆相交于点D ,与BC 相交于点G ,则下列结论:△BAD CAD ∠=∠;△若60BAC ∠=︒,则120∠=︒BEC ;△若点G 为BC 的中点,则90BGD ∠=︒;△BD DE =.其中一定正确的个数是( )A. 1B. 2C. 3D. 4 【答案】D【解析】【分析】根据点E 是ABC 的内心,可得BAD CAD ∠=∠,故①正确;连接BE ,CE ,可得∠ABC +∠ACB =2(∠CBE +∠BCE ),从而得到∠CBE +∠BCE =60°,进而得到∠BEC =120°,故②正确; BAD CAD ∠=∠,得出BD CD =,再由点G 为BC 的中点,则90BGD ∠=︒成立,故③正确;根据点E 是ABC 的内心和三角形的外角的性质,可得()12BED BAC ABC ∠=∠+∠,再由圆周角定理可得()12DBE BAC ABC ∠=∠+∠,从而得到∠DBE =∠BED ,故④正确;即可求解. 【详解】解:∵点E 是ABC 的内心,∴BAD CAD ∠=∠,故①正确;如图,连接BE ,CE ,∵点E 是ABC 的内心,∴∠ABC =2∠CBE ,∠ACB =2∠BCE ,∴∠ABC +∠ACB =2(∠CBE +∠BCE ),∵∠BAC =60°,∴∠ABC +∠ACB =120°,∴∠CBE +∠BCE =60°,∴∠BEC =120°,故②正确;∵点E 是ABC 的内心,∴BAD CAD ∠=∠,∴BD CD =,∵点G 为BC 的中点,∴线段AD 经过圆心O ,∴90BGD ∠=︒成立,故③正确;∵点E 是ABC 的内心, ∴11,22BAD CAD BAC ABE CBE ABC ∠=∠=∠∠=∠=∠, ∵∠BED =∠BAD +∠ABE , ∴()12BED BAC ABC ∠=∠+∠, ∵∠CBD =∠CAD ,∴∠DBE =∠CBE +∠CBD =∠CBE +∠CAD , ∴()12DBE BAC ABC ∠=∠+∠, ∴∠DBE =∠BED ,∴BD DE =,故④正确;∴正确的有4个.故选:D【点睛】本题主要考查了三角形的内心问题,圆周角定理,三角形的内角和等知识,熟练掌握三角形的内心问题,圆周角定理,三角形的内角和等知识是解题的关键.7. 如图所示,等边ABC 的顶点A 在△O 上,边AB 、AC 与△O 分别交于点D 、E ,点F 是劣弧DE 上一点,且与D 、E 不重合,连接DF 、EF ,则DFE ∠的度数为( )A. 115︒B. 118︒C. 120︒D. 125︒【答案】C【解析】【分析】根据等边三角形的性质可得60A ∠=︒,再根据圆内接四边形的对角互补即可求得答案. 【详解】解:ABC 是等边三角形,60A ∴∠=︒,180120DFE A ∴∠=︒-∠=︒,故选C .【点睛】本题考查了等边三角形的性质及圆内接四边形的性质,熟练掌握圆内接四边形的对角互补是解题的关键.8. 大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF ,若对角线AD 的长约为8mm ,则正六边形ABCDEF 的边长为( )A. 2mmB.C.D. 4mm 【答案】D【解析】【分析】如图,连接CF 与AD 交于点O ,易证△COD 为等边三角形,从而CD =OC =OD =12AD ,即可得到答案.【详解】连接CF 与AD 交于点O ,∵ABCDEF 为正六边形,∴∠COD = 3606︒=60°,CO =DO ,AO =DO =12AD =4mm ,∴△COD 为等边三角形,∴CD =CO =DO =4mm ,即正六边形ABCDEF 的边长为4mm ,故选:D .【点睛】本题考查了正多边形与圆的性质,正确把握正六边形的中心角、半径与边长的关系是解题的关键.9. 如图,⊙O 是等边△ABC 的外接圆,若AB =3,则⊙O 的半径是( )A. 32 B. 2 D. 52【答案】C【解析】【分析】作直径AD ,连接CD ,如图,利用等边三角形的性质得到∠B =60°,关键圆周角定理得到∠ACD =90°,∠D =∠B =60°,然后利用含30度的直角三角形三边的关系求解.【详解】解:作直径AD ,连接CD ,如图,∵△ABC 为等边三角形,∴∠B =60°,∵AD 为直径,∴∠ACD =90°,∵∠D =∠B =60°,则∠DAC =30°,∴CD =12AD , ∵AD 2=CD 2+AC 2,即AD 2=(12AD )2+32,∴AD∴OA =OB =12AD 故选:C .【点睛】本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了等边三角形的性质、圆周角定理和含30度的直角三角形三边的关系.10. 如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA ,PB 分别相切于点A ,B ,不倒翁的鼻尖正好是圆心O ,若28OAB ∠=°,则APB ∠的度数为( )A. 28︒B. 50︒C. 56︒D. 62︒【答案】C【解析】【分析】连OB,由AO=OB得,∠OAB=∠OBA=28°,∠AOB=180°-2∠OAB=124°;因为P A、PB分别相切于点A、B,则∠OAP=∠OBP=90°,利用四边形内角和即可求出∠APB.【详解】连接OB,∵OA=OB,∴∠OAB=∠OBA=28°,∴∠AOB=124°,∵P A、PB切⊙O于A、B,∴OA⊥P A,OP⊥AB,∴∠OAP+∠OBP=180°,∴∠APB+∠AOB=180°;∴∠APB=56°.故选:C【点睛】本题考查切线的性质,三角形和四边形的内角和定理,切线长定理,等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,构造等腰三角形解决问题.11. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连接PM,PN,则所有满足∠MPN =45°的△PMN中,边PM的长的最大值是()A. B. 6 C. D.【答案】C【解析】【分析】根据同弧所对的圆周角等于所对圆心角的一半,过点M、N作以点O为圆心,∠MON=90°的圆,则点P在所作的圆上,观察圆O所经过的格点,找出到点M距离最大的点即可求出.MN,以O为【详解】作线段MN中点Q,作MN的垂直平分线OQ,并使OQ=12圆心,OM为半径作圆,如图,MN,所以OQ=MQ=NQ,因为OQ为MN垂直平分线且OQ=12∴∠OMQ=∠ONQ=45°,∴∠MON=90°,所以弦MN所对的圆O的圆周角为45°,所以点P在圆O上,PM为圆O的弦,通过图像可知,当点P在P'位置时,恰好过格点且P M'经过圆心O,所以此时P M'最大,等于圆O的直径,∵BM=4,BN=2,∴MN=△MQ=OQ△OM==△2P M OM'==故选C.【点睛】此题考查了圆的相关知识,熟练掌握同弧所对的圆周角相等、直径是圆上最大的弦,会灵活用已知圆心角和弦作圆是解题的关键.12. 如图,圆锥底面圆半径为7cm,高为24cm,则它侧面展开图的面积是()A. 175π3cm2 B.175π2cm2 C. 175πcm2 D. 350πcm2【答案】C【解析】【分析】先利用勾股定理计算出AC=25cm,由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,则可根据扇形的面积公式计算出圆锥的侧面积.【详解】解:在Rt AOC△中,25AC =cm , ∴它侧面展开图的面积是127251752ππ⨯⨯⨯=cm 2. 故选:C【点睛】本题考查了圆锥的计算,理解圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长是解题的关键. 13. 如图,ABC 内接于⊙,46O C ∠=︒,连接OA ,则OAB ∠=( )A. 44︒B. 45︒C. 54︒D. 67︒【答案】A【解析】 【分析】连接OB ,由2∠C =△AOB ,求出△AOB ,再根据OA =OB 即可求出△OAB .【详解】连接OB ,如图,△△C =46°,△△AOB =2△C =92°,△△OAB +△OBA =180°-92°=88°,△OA =OB ,△△OAB =△OBA ,△△OAB =△OBA =12×88°=44°,故选:A .【点睛】本题主要考查了圆周角定理,根据圆周角定理的出△AOB =2△C =92°是解答本题的关键.14. 已知圆锥的底面半径为4cm ,母线长为6cm ,则圆锥的侧面积为( )A. 236πcmB. 224πcmC. 216πcmD. 212πcm【答案】B【解析】【分析】利用圆锥侧面积计算公式计算即可:S rl π=侧;【详解】4624S rl πππ==⋅⋅=侧2cm ,故选B .【点睛】本题考查了圆锥侧面积的计算公式,比较简单,直接代入公式计算即可. 15. 如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧(AB ),点O 是这段弧所在圆的圆心,半径90m OA =,圆心角80AOB ∠=︒,则这段弯路(AB )的长度为( )A. 20m πB. 30m πC. 40m πD. 50m π【答案】C【解析】 【分析】根据题目中的数据和弧长公式,可以计算出这段弯路(AB )的长度.【详解】解:∵半径OA =90m ,圆心角∠AOB =80°,∴这段弯路(AB )的长度为:809040(m)180ππ⨯=, 故选C 【点睛】本题考查了弧长的计算,解答本题的关键是明确弧长计算公式.180n r l π=16. 如图,,AB AC 是O 的两条弦,⊥OD AB 于点D ,OE AC ⊥于点E ,连结OB ,OC .若130DOE ∠=︒,则BOC ∠的度数为( )A. 95︒B. 100︒C. 105︒D. 130︒【答案】B【解析】 【分析】根据四边形的内角和等于360°计算可得∠BAC =50°,再根据圆周角定理得到∠BOC =2∠BAC ,进而可以得到答案.【详解】解:∵OD ⊥AB ,OE ⊥AC ,∴∠ADO =90°,∠AEO =90°,∵∠DOE =130°,∴∠BAC =360°-90°-90°-130°=50°,∴∠BOC =2∠BAC =100°,故选:B .【点睛】本题考查的是圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.17. 如图,点I 为的ABC 内心,连接AI 并延长交ABC 的外接圆于点D ,点E 为弦AC 的中点,连接CD ,EI ,IC ,当2AI CD =,6IC =,5ID =时,IE 的长为( )A. 5B. 4.5C. 4D. 3.5【答案】C【解析】【分析】延长ID到M,使DM=ID,连接CM.想办法求出CM,证明IE是△ACM 的中位线即可解决问题.【详解】解:延长ID到M,使DM=ID,连接CM.∵I是△ABC的内心,∴∠IAC=∠IAB,∠ICA=∠ICB,∵∠DIC=∠IAC+∠ICA,∠DCI=∠BCD+∠ICB,∴∠DIC=∠DCI,∴DI=DC=DM,∴∠ICM=90°,∴CM=,∵AI=2CD=10,∴AI=IM,∵AE=EC,∴IE是△ACM的中位线,CM=4,∴IE=12故选:C.【点睛】本题考查三角形的内心、三角形的外接圆、三角形的中位线定理、直角三角形的判定、勾股定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题.18. 某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m ,高为,则改建后门洞的圆弧长是( )A. 5πm 3B. 8πm 3C. 10πm 3D. 5π+2m 3⎛⎫ ⎪⎝⎭【答案】C【解析】【分析】利用勾股定理先求得圆弧形的门洞的直径BC ,再利用矩形的性质证得COD ∆是等边三角形,得到60COD ∠=︒,进而求得门洞的圆弧所对的圆心角为36060300︒-︒=︒,利用弧长公式即可求解.【详解】如图,连接AD ,BC ,交于O 点,∵90BDC ∠=︒ ,∴BC 是直径,∴4BC ===,∵四边形ABDC 是矩形,∴122OC OD BC ===, ∵2CD =,∴OC OD CD ==,∴COD ∆是等边三角形,∴60COD ∠=︒,∴门洞的圆弧所对的圆心角为36060300︒-︒=︒ , ∴改建后门洞的圆弧长是11300300410221801803BC πππ︒⨯︒⨯⨯==︒︒(m), 故选:C【点睛】本题考查了弧长公式,矩形的性质以及勾股定理的应用,从实际问题转化为数学模型是解题的关键.19. 如图,正六边形ABCDEF 内接于△O ,若△O 的周长等于6π,则正六边形的边长为( )C. 3D. 【答案】C【解析】 【分析】连接OB ,OC ,由△O 的周长等于6π,可得△O 的半径,又由圆的内接多边形的性质,即可求得答案.【详解】解:连接OB ,OC ,∵△O 的周长等于6π,∴△O 的半径为:3,∵∠BOC 61=⨯360°=60°, ∵OB =OC ,∴△OBC 是等边三角形,∴BC =OB =3,∴它的内接正六边形ABCDEF 的边长为3,故选:C .【点睛】此题考查了正多边形与圆的性质.此题难度适中,注意掌握数形结合思想的应用.20. 家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件,已知扇形的圆心角∠BAC =90°,则扇形部件的面积为( )A. 12π米2 B. 14π米2 C. 18π米2 D. 116π米2 【答案】C【解析】 【分析】连接BC ,先根据圆周角定理可得BC 是O 的直径,从而可得1BC =米,再解直角三角形可得AB AC = 【详解】解:如图,连接BC ,90BAC ∠=︒,BC ∴是O 的直径,1BC ∴=米,又AB AC =,45ABC ACB ∴∠=∠=︒,sin AB AC BC ABC ∴==⋅∠=(米),则扇形部件的面积为290123608ππ⨯=(米2), 故选:C .【点睛】本题考查了圆周角定理、解直角三角形、扇形的面积公式等知识点,熟练掌握圆周角定理和扇形的面积公式是解题关键.二.填空题21. 如图,在正六边形ABCDEF 中,AB =6,点M 在边AF 上,且AM =2.若经过点M 的直线l 将正六边形面积平分,则直线l 被正六边形所截的线段长是_____.【答案】 【解析】【分析】如图,连接AD ,CF ,交于点O ,作直线MO 交CD 于H ,过O 作OP ⊥AF 于P ,由正六边形是轴对称图形可得:,ABCO DEFO S S 四边形四边形 由正六边形是中心对称图形可得:,,AOMDOHMOFCHOSSSS,OM OH = 可得直线MH 平分正六边形的面积,O 为正六边形的中心,再利用直角三角形的性质可得答案. 【详解】解:如图,连接AD ,CF ,交于点O ,作直线MO 交CD 于H ,过O 作OP ⊥AF 于P ,由正六边形是轴对称图形可得:,ABCODEFO S S 四边形四边形由正六边形是中心对称图形可得:,,AOMDOHMOFCHOSSSS,OM OH =∴直线MH 平分正六边形的面积,O 为正六边形的中心, 由正六边形的性质可得:AOF 为等边三角形,60,AFO而6,AB =6,3,AB AF OF OA AP FP226333,OP2,AM 则1,MP 2213327,OM247.MHOM故答案为:【点睛】本题考查的是正多边形与圆的知识,掌握“正六边形既是轴对称图形也是中心对称图形”是解本题的关键.22. 如图,用一个半径为6 cm 的定滑轮拉动重物上升,滑轮旋转了120︒,假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了_________cm .(结果保留π)【答案】4π 【解析】【分析】利用题意得到重物上升的高度为定滑轮中120°所对应的弧长,然后根据弧长公式计算即可.【详解】解:根据题意,重物的高度为12064180ππ⨯⨯=(cm ).故答案为:4π.【点睛】本题考查了弧长公式:180n Rl π⋅⋅=(弧长为l ,圆心角度数为n ,圆的半径为R ).23. 如图是以点O 为圆心,AB 为直径的圆形纸片,点C 在⊙O 上,将该圆形纸片沿直线CO 对折,点B 落在⊙O 上的点D 处(不与点A 重合),连接CB ,CD ,AD .设CD 与直径AB 交于点E .若AD =ED ,则∠B =_________度;BCAD的值等于_________.【答案】 △. 36 △. 32+ 【解析】【分析】由等腰三角形的性质得出∠DAE =∠DEA ,证出∠BEC =∠BCE ,由折叠的性质得出∠ECO =∠BCO ,设∠ECO =∠OCB =∠B =x ,证出∠BCE =∠ECO +∠BCO =2x ,∠CEB =2x ,由三角形内角和定理可得出答案;证明△CEO ∽△BEC ,由相似三角形的性质得出CE BEEO CE=,设EO =x ,EC =OC =OB =a ,得出a 2=x (x +a ),求出OE a ,证明△BCE ∽△DAE ,由相似三角形的性质得出BC ECAD AE=,则可得出答案.【详解】解:∵AD =DE , ∴∠DAE =∠DEA ,∵∠DEA =∠BEC ,∠DAE =∠BCE , ∴∠BEC =∠BCE ,∵将该圆形纸片沿直线CO 对折, ∴∠ECO =∠BCO , 又∵OB =OC , ∴∠OCB =∠B ,设∠ECO =∠OCB =∠B =x , ∴∠BCE =∠ECO +∠BCO =2x , ∴∠CEB =2x ,∵∠BEC +∠BCE +∠B =180°, ∴x +2x +2x =180°, ∴x =36°, ∴∠B =36°;∵∠ECO =∠B ,∠CEO =∠CEB , ∴△CEO ∽△BEC , ∴CE BEEO CE=, ∴CE 2=EO •BE ,设EO =x ,EC =OC =OB =a , ∴a 2=x (x +a ),解得,x a (负值舍去),∴OE a ,∴AE =OA -OE =a -12a =32-a ,∵∠AED =∠BEC ,∠DAE =∠BCE , ∴△BCE ∽△DAE ,∴BC EC AD AE=,∴32BCAD==.故答案为:36,32+.【点睛】本题是圆的综合题,考查了圆周角定理,折叠的性质,等腰三角形的判定与性质,三角形内角和定理,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.24. 如图,已知AB是⊙O的弦,∠AOB=120°,OC⊥AB,垂足为C,OC的延长线交⊙O于点D.若∠APD是AD所对的圆周角,则∠APD的度数是______.【答案】30°##30△【解析】【分析】根据垂径定理得出△AOB=△BOD,进而求出△AOD=60°,再根据圆周角定理可得△APD=12△AOD=30°.【详解】△OC⊥AB,OD为直径,△BD AD=,△△AOB=△BOD,△△AOB=120°,△△AOD=60°,△△APD=12△AOD=30°,故答案为:30°.【点睛】本题考查了圆周角定理、垂径定理等知识,掌握垂径定理是解答本题的关键.25. 某中学开展劳动实习,学生到教具加工厂制作圆锥,他们制作的圆锥,母线长为30cm ,底面圆的半径为10 cm ,这种圆锥的侧面展开图的圆心角度数是_____. 【答案】120︒ 【解析】【分析】设这种圆锥的侧面展开图的圆心角度数为n ,30210180n =⨯⨯ππ,进行解答即可得.【详解】解: 设这种圆锥的侧面展开图的圆心角度数为n°,30210180n =⨯⨯ππ 120n =︒故答案为:120︒.【点睛】本题考查了圆锥侧面展开图的圆心角,解题的关键是掌握扇形的弧长公式.26. 如图,在△ABC 中,AC =2,BC =4,点O 在BC 上,以OB 为半径的圆与AC 相切于点A ,D 是BC 边上的动点,当△ACD 为直角三角形时,AD 的长为___________.【答案】32或65【解析】【分析】根据切线的性质定理,勾股定理,直角三角形的等面积法解答即可. 【详解】解:连接OA ,①当D点与O点重合时,∠CAD为90°,设圆的半径=r,∴OA=r,OC=4-r,∵AC=4,在Rt△AOC中,根据勾股定理可得:r2+4=(4-r)2,解得:r=32,即AD=AO=32;②当∠ADC=90°时,过点A作AD⊥BC于点D,∵12AO•AC=12OC•AD,∴AD=AO AC OC,∵AO=32,AC=2,OC=4-r=52,∴AD=65,综上所述,AD的长为32或65,故答案为:32或65.【点睛】本题主要考查了切线的性质和勾股定理,熟练掌握这些性质定理是解决本题的关键.27. 一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦AB长20厘米,弓形高CD为2厘米,则镜面半径为____________厘米.【答案】26【解析】【分析】令圆O的半径为OB=r,则OC=r-2,根据勾股定理求出OC2+BC2=OB2,进而求出半径.【详解】解:如图,由题意,得OD垂直平分AB,∴BC=10厘米,令圆O的半径为OB=r,则OC=r-2,在Rt△BOC中OC2+BC2=OB2,∴(r-2)2+102=r2,解得r=26.故答案为:26.【点睛】本题考查垂径定理和勾股定理求线段长,熟练地掌握圆的基本性质是解决问题的关键.28. 若扇形的圆心角为120 ,半径为32,则它的弧长为___________.【答案】π【解析】【分析】根据题目中的数据和弧长公式,可以计算出该扇形的弧长.【详解】解:∵扇形的圆心角为120°,半径为32, ∴它的弧长为:31202,180ππ⨯=故答案为:π【点睛】本题考查弧长的计算,解答本题的关键是明确弧长的计算公式.180n rl π=29. 如图,⊙O 的半径为2,点A ,B ,C 都在⊙O 上,若30B ∠=︒.则AC 的长为_____(结果用含有π的式子表示)【答案】23π 【解析】【分析】利用同弧所对的圆心角是圆周角的2倍得到60AOC ∠=︒,再利用弧长公式求解即可.【详解】2AOC B ∠=∠,30B ∠=︒,60AOC ∴∠=︒,⊙O 的半径为2,60221803AC ππ⨯∴==, 故答案为:23π.【点睛】本题考查了圆周角定理和弧长公式,即180n rl π=,熟练掌握知识点是解题的关键.30. 如图,在Rt ABC △中,90C ∠=︒,6AC =,BC =1的O在Rt ABC △内平移(O 可以与该三角形的边相切),则点A 到O 上的点的距离的最大值为________.【答案】1 【解析】【分析】设直线AO 交O 于M 点(M 在O 点右边),当O 与AB 、BC 相切时,AM 即为点A 到O 上的点的最大距离.【详解】设直线AO 交O 于M 点(M 在O 点右边),则点A 到O 上的点的距离的最大值为AM 的长度当O 与AB 、BC 相切时,AM 最长 设切点分别为D 、F ,连接OB ,如图∵90C ∠=︒,6AC =,BC =∴tan ACB BC==AB = ∴60B ∠=︒∵O 与AB 、BC 相切 △1302OBD B ∠=∠=︒ △O 的半径为1 ∴1OD OM ==∴BD ==∴AD AB DB =-=∴OA===∴1=+=AM OA OM∴点A到O上的点的距离的最大值为1.【点睛】本题考查切线的性质、特殊角度三角函数值、勾股定理,解题的关键是确定点A到O上的点的最大距离的图形.31. 如图,在扇形AOB中,点C,D在AB上,将CD沿弦CD折叠后恰好与OA,OA=,则EF的度数为_______;折痕OB相切于点E,F.已知120AOB∠=︒,6CD的长为_______.【答案】△. 60°##60△ △.【解析】【分析】根据对称性作O关于CD的对称点M,则点D、E、F、B都在以M为圆心,半径为6的圆上,再结合切线的性质和垂径定理求解即可.【详解】作O关于CD的对称点M,则ON=MN连接MD、ME、MF、MO,MO交CD于N△将CD沿弦CD折叠∴点D 、E 、F 、B 都在以M 为圆心,半径为6的圆上△将CD 沿弦CD 折叠后恰好与OA ,OB 相切于点E ,F .∴ME ⊥OA ,MF ⊥OB∴90MEO MFO ∠=∠=︒∵120AOB ∠=︒∴四边形MEOF 中36060EMF AOB MEO MFO ∠=︒-∠-∠-∠=︒即EF 的度数为60°;∵90MEO MFO ∠=∠=︒,ME MF =∴MEO MFO ≅(HL ) ∴1302EMO FMO FME ∠=∠=∠=︒∴6cos cos30ME OM EMO ===∠︒∴MN =∵MO ⊥DC∴12DN CD ====∴CD =故答案为:60°;【点睛】本题考查了折叠的性质、切线的性质、垂径定理、勾股定理;熟练掌握折叠的性质作出辅助线是解题的关键.三.解答题32. 如图,在Rt ABC △中,90ACB ∠=︒,以BC 为直径作⊙O ,交AB 边于点D ,在CD 上取一点E ,使BE CD =,连接DE ,作射线CE 交AB 边于点F .(1)求证:A ACF ∠=∠;(2)若8AC =,4cos 5ACF ∠=,求BF 及DE 的长. 【答案】(1)见解析 (2)BF =5,4225DE = 【解析】【分析】(1)根据Rt ABC △中,90ACB ∠=︒,得到∠A +∠B =∠ACF +∠BCF =90°,根据BE CD =,得到∠B =∠BCF ,推出∠A =∠ACF ;(2)根据∠B =∠BCF ,∠A =∠ACF ,得到AF =CF ,BF =CF ,推出AF =BF =12 AB ,根据4cos cos 5AC ACF A AB ∠===,AC =8,得到AB =10,得到BF =5,根据6BC ==,得到3sin 5BC A AB ==,连接CD ,根据BC 是⊙O 的直径,得到∠BDC =90°,推出∠B +∠BCD =90°,推出∠A =∠BCD ,得到3sin 5BD BCD BC ∠==,推出185BD =,得到75DF BF BD =-=,根据∠FDE =∠BCE ,∠B =∠BCE ,得到∠FDE =∠B ,推出DE ∥BC ,得到△FDE ∽△FBC ,推出DE DF BC BF =,得到4225DE =. 【小问1详解】解:∵Rt ABC △中,90ACB ∠=︒,∴∠A +∠B =∠ACF +∠BCF =90°,∵BE CD =,∴∠B =∠BCF ,∴∠A =∠ACF ;【小问2详解】∵∠B =∠BCF ,∠A =∠ACF∴AF =CF ,BF =CF ,∴AF =BF =12 AB , ∵4cos cos 5AC ACF A AB ∠===,AC =8,∴AB=10,∴BF=5,∵6 BC==,∴3 sin5BCAAB==,连接CD,∵BC是⊙O的直径,∴∠BDC=90°,∴∠B+∠BCD=90°,∴∠A=∠BCD,∴3 sin5BDBCDBC∠==,∴185 BD=,∴75 DF BF BD=-=,∵∠FDE=∠BCE,∠B=∠BCE,∴∠FDE=∠B,∴DE∥BC,∴△FDE∽△FBC,∴DE DF BC BF=,∴4225 DE=.【点睛】本题主要考查了圆周角,解直角三角形,勾股定理,相似三角形,解决问题的关键是熟练掌握圆周角定理及推论,运用勾股定理和正弦余弦解直角三角形,相似三角形的判定和性质.33. 如图,已知AC为O的直径,直线P A与O相切于点A,直线PD经过O 上的点B且CBD CAB∠=∠,连接OP交AB于点M.求证:(1)PD 是O 的切线;(2)2AM OM PM =⋅【答案】(1)见解析 (2)见解析【解析】【分析】(1)连接OB ,由等边对等角及直径所对的圆周角等于90°即可证明; (2)根据直线P A 与O 相切于点A ,得到90OAP ∠=︒,根据余角的性质得到OAM APM ∠=∠,继而证明OAM APM ,根据相似三角形的性质即可得到结论.【小问1详解】连接OB ,OA OB OC ==,,OAB OBA OBC OCB ∴∠=∠∠=∠,AC 为O 的直径,ABC OBA OBC ∴∠=∠+∠,CBD CAB∠=∠,OBA CBD∴∠=∠,90CBD OBC OBD∴∠+∠=︒=∠,∴PD是O的切线;【小问2详解】直线P A与O相切于点A,90OAP∴∠=︒,∵PD是O的切线,90AMO AMP OAP∴∠=∠=∠=︒,90OAM PAM PAM APM∴∠+∠=∠+∠=︒,OAM APM∴∠=∠,OAM APM∴,AM OMPM AM∴=,∴2AM OM PM=⋅.【点睛】本题考查了切线的判定和性质,相似三角形的判定和性质,圆周角定理,等腰三角形的性质,熟练掌握知识点是解题的关键.34. 如图,点C在以AB为直径的O上,CD平分ACB∠交O于点D,交AB于点E,过点D作O的切线交CO的延长线于点F.(1)求证:FD AB∥;(2)若AC=BC=,求FD的长.【答案】(1)见解析(2)15 8【解析】【分析】(1)连接OD,由CD平分△ACB,可知AD BD=,得△AOD=△BOD=90°,由DF是切线可知△ODF=90°=△AOD,可证结论;(2)过C作CM⊥AB于M,已求出CM、BM、OM的值,再证明△DOF∽△MCO,得CM OMOD FD,代入可求.【小问1详解】证明:连接OD,如图,△CD平分△ACB,△AD BD=,△△AOD=△BOD=90°,△DF是△O的切线,△△ODF=90°△△ODF=△BOD,△DF∥AB.【小问2详解】解:过C作CM⊥AB于M,如图,∵AB是直径,∴∠ACB=90°,∴AB2222(25)(5)5BC.∴1122AB CM AC BC=,即115255 22CM,∴CM=2,∴2222(5)21BM BC CM,∴OM=OB -BM=135122,∵DF∥AB,∴∠OFD=∠COM,又∵∠ODF=∠CMO=90°,∴△DOF ∽△MCO,∴CM OM OD FD,即32252FD,∴FD=158.【点睛】本题考查了圆的圆心角、弦、弧关系定理、圆周角定理,切线的性质,相似三角形的判定与性质,勾股定理,解题的关键是熟练掌握这些定理,灵活运用相似三角形的性质求解.35. 如图,AB 为O的直径,点C是O上一点,点D是O外一点,BCD BAC∠=∠,连接OD交BC于点E.(1)求证:CD是O的切线.(2)若4,sin5CE OA BAC=∠=,求tan CEO∠的值.【答案】(1)见解析;(2)3【解析】【分析】(1)连接OC ,根据圆周角定理得到∠ACB =90°,根据OA =OC 推出∠BCD =∠ACO ,即可得到∠BCD +∠OCB =90°,由此得到结论;(2)过点O 作OF ⊥BC 于F ,设BC =4x ,则AB =5x ,OA =CE =2.5x ,BE =1.5x ,勾股定理求出AC ,根据OF ∥AC ,得到1BF OB CF OA==,证得OF 为△ABC 的中位线,求出OF 及EF ,即可求出tan CEO ∠的值.【小问1详解】证明:连接OC ,∵AB 为O 的直径,∴∠ACB =90°,∴∠ACO +∠OCB =90°,∵OA =OC ,△∠A =∠ACO ,∵BCD BAC ∠=∠,∴∠BCD =∠ACO ,∴∠BCD +∠OCB =90°,∴OC ⊥CD ,∴CD 是O 的切线.【小问2详解】解:过点O 作OF ⊥BC 于F , ∵4,sin 5CE OA BAC =∠=, ∴设BC =4x ,则AB =5x ,OA =CE =2.5x ,∴BE =BC -CE =1.5x ,∵∠C =90°,∴AC 3x =,∵OA =OB ,OF ∥AC , ∴1BF OB CF OA==, ∴CF =BF =2x ,EF =CE -CF =0.5x ,∴OF 为△ABC 的中位线,∴OF =1 1.52AC x =, ∴tan CEO ∠= 1.530.5OF x EF x ==.【点睛】此题考查了圆周角定理,证明直线是圆的切线,锐角三角函数,三角形中位线的判定与性质,平行线分线段成比例,正确引出辅助线是解题的关键. 36. 如图,AB 为O 的弦,OC OA ⊥交AB 于点P ,交过点B 的直线于点C ,且CB CP =.(1)试判断直线BC 与O 的位置关系,并说明理由;(2)若sin 85A OA ==,求CB 的长. 【答案】(1)相切,证明见详解(2)6【解析】【分析】(1)连接OB ,根据等腰三角形的性质得出A OBA ∠=∠,CPB CBP ∠=∠,从而求出90AOC OBC ∠=∠=︒,再根据切线的判定得出结论; (2)分别作OM AB ⊥交AB 于点M ,CN AB ⊥交AB 于N ,根据sin 8A OA ==求出OP ,AP 的长,利用垂径定理求出AB 的长,进而求出BP 的长,然后在等腰三角形CPB 中求解CB 即可.【小问1详解】证明:连接OB ,如图所示:CP CB OA OB ==,,∴A OBA ∠=∠,CPB CBP ∠=∠,APO CPB ∠=∠,APO CBP ∴∠=∠,OC OA ⊥,即90AOP ︒=∠,90A APO OBA CBP OBC ∴∠+∠=︒=∠+∠=∠,OB BC ∴⊥, OB 为半径,经过点O ,∴直线BC 与O 的位置关系是相切.【小问2详解】分别作OM AB ⊥交AB 于点M ,CN AB ⊥交AB 于N ,如图所示:AM BM ∴=,CP CB AO CO =⊥,,A APO PCN CPN ∴∠+∠=∠+∠,PN BN =,PCN BCN ∠=∠A PCN BCN ∴∠=∠=∠sin A =,8OA =,sin OM OP A OA AP ∴===4OM AM OP AP ∴====,25AB AM ∴==,111()(22255PN BN PB AB AP ∴===-=⨯-=sin sin BN A BCN CB ∴=∠==,6CB ∴===. 【点睛】本题考查了切线的证明,垂径定理的性质,等腰三角形,勾股定理,三角函数等知识点,熟练掌握相关知识并灵活应用是解决此题的关键,抓住直角三角形边的关系求解线段长度是解题的主线思路.37. 如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A 、B 、C 、D 、M 均为格点.【操作探究】在数学活动课上,佳佳同学在如图①的网格中,用无刻度的直尺画了两条互相垂直的线段AB 、CD ,相交于点P 并给出部分说理过程,请你补充完整:解:在网格中取格点E ,构建两个直角三角形,分别是△ABC 和△CDE . 在Rt △ABC 中,1tan 2BAC ∠=在Rt △CDE 中, ,所以tan tan BAC DCE ∠∠=.所以∠BAC =∠DCE .因为∠ACP + ∠DCE =∠ACB =90°,所以∠ACP+∠BAC=90°,所以∠APC=90°,即AB⊥CD.(1)【拓展应用】如图②是以格点O为圆心,AB为直径的圆,请你只用无刻度的直尺,在BM上找出一点P,使PM=AM,写出作法,并给出证明:(2)【拓展应用】如图③是以格点O为圆心的圆,请你只用无刻度的直尺,在弦AB上找出一点P.使2AM=AP·AB,写出作法,不用证明.【答案】(1)1tan2DCE∠=;见解析(2)见解析【解析】【分析】(1)取格点N,作射线AN交BM于点P,则AN MO⊥根据垂径定理可知,点P即为所求作;(2)取格点I,连接MI交AB于点P,点P即为所求作.利用正切函数证得∠FMI=∠MNA,利用圆周角定理证得∠B=∠MNA,再推出△P AM∽△MAB,即可证明结论.【小问1详解】解:【操作探究】在网格中取格点E,构建两个直角三角形,分别是△ABC和△CDE.在Rt△ABC中,1 tan2BAC∠=在Rt△CDE中,1 tan2DCE∠=,所以tan tan BAC DCE ∠∠=.所以∠BAC =∠DCE .因为∠ACP + ∠DCE =∠ACB =90°,所以∠ACP +∠BAC =90°,所以∠APC =90°,即AB ⊥CD . 故答案为:1tan 2DCE ∠=; 取格点N ,作射线AN 交BM 于点P ,点P 即为所求作;11tan ,tan 33MOD NAC ∠=∠= MOD NAC ∴∠=∠90NAC ANC ∠+∠=︒90ANC DOM ∴∠+∠=︒∴AN OM ⊥AM PM ∴=【小问2详解】解:取格点I ,连接MI 交AB 于点P ,点P 即为所求作;证明:作直径AN ,连接BM 、MN ,在Rt △FMI 中,1an 3t FMI ∠=, 在Rt △MNA 中,1an 3t MNA ∠=, 所以tan tan FMI MNA ∠∠=.。
《圆周角》知识全解

圆周角概念定理推论满足两个条件计算与证明计算与证明《圆周角》知识全解课标要求1.理解圆周角的概念,让学生探索和掌握圆周角定理,并能灵活地应用圆周角定理解决圆的有关说理和计算问题;2.让学生在探究过程中体会“由特殊到一般”、“分类”、“化归”等数学思想;3.培养学生观察、比较、分析、推理及小组合作交流的能力和创新能力,通过解决问题增强自信心,激发学习数学的兴趣.知识结构内容解析一、圆心角、圆周角的定义及其度量1.圆心角:顶点在圆心的角叫做圆心角;圆心角的度数等于它所对的弧的度数.2.圆周角:顶点在圆上,且两边都与圆相交的角叫做圆周角;圆周角的度数等于它所对的弧的度数的一半.3.区别:(1)顶点的位置不同:圆心角的顶点在圆心,而圆周角的顶点在圆周上.(2)与所对弧的关系不同:圆心角的度数与它所对弧的度数相等,圆周角的度数是它所对弧度数的一半.联系:同弧所对的圆周角是圆心角的一半.二、圆周角与圆心角的关系1.同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;它包含两层含义:(1)圆周角与圆周角的关系:同弧或等弧所对的圆周角相等.这是圆中论证角相等非常重要的依据.(2)圆周角与圆心角的关系:一条弧所对的圆周角等于它所对的圆心角的一半.圆周角和圆心角关系的纽带是“弧”,该“弧”确定了圆周角和圆心角的位置关系.2.半圆(或直径)所对的圆周角都相等,都等于90°(直角);90°(直角)的圆周角所对的弦是直径.它包含两层含义:(1)这时圆中最特殊的弦(直径)产生了最特殊的角(直角),体现了特殊的位置确定特殊的结果;(2)这个结论为在圆中确立直角,构造垂直关系创造了条件.在圆中见直径应联想到直角,圆周角是直角联想到直径,简记为:直径对直角,直角对直径.重点难点本节的重点是:经历探索“圆周角与圆心角的关系”的过程;教学重点的解决方法:为了突出重点,我设计了一系列的探究活动由浅入深,循序渐进.①一条弧对的圆心角有几个,圆周角有几个?②圆心与圆周角有几种位置关系? 当学生摆出三种位置关系时,教师提问是否还存在其他的位置关系,是否有遗漏?当确定只有这三种位置时,作出三个图中的圆心角,③同一条弧所对的圆周角∠BAC与圆心角∠BOC 的度数,你有什么发现等等.本节的难点是:了解圆周角的分类,用化归思想合情推理验证“圆周角与圆心角的关系”.教学难点的解决方法:为突破难点,在学生验证猜想时,教师要给学生充分探索的时间和空间,因为难点处是学生互相学习互相交流思维的最佳时机,相信学生的思维闪光点也正是在学生互相讨论中挖掘出来的.若学生一时难以找到证明的途径,教师提示可把第二类圆内部的图形想象成一面三角旗、则第一类、第三类分别想象成两面三角旗合并、两面三角旗叠成,化抽象为具体、化一般为特殊.向学生有机渗透“由特殊到一般”、“分类”、“化归”等数学思想.教法导引根据教材本身探究性较强的特点,我以“探究式教学法”为主,讲授法、发现法、分组交流合作法、启发式教学法等多种方法相结合的教学模式实施教学,由浅入深,鼓励学生采用观察分析、自主探索、合作交流的学习方式,让学生经历数学知识的形成与应用过程.俗话说:“听不如看,看不如做”.在新课教学时,借助教具学具的演示,使学生非常直观地掌握圆周角的特征,并且为学生如何使用学具完成一系列的探究活动做了很好的示范.为了简便快捷地充分利用好学具,我将学具中的塑料棒改为皮筋.学具的使用不仅激发了学生兴趣,充分调动了学生的学习积极性,使学生乐于探索,还体现了自主、探索、合作与实践的学习方式,让学生成为了学习的主人,让学生的主体意识、能动性得到了发展.学法建议探究式学习和有意义接受式学习都是学生的重要学习方式,本课尝试做两者相结合的学习方式的指导.力图转变学生以往只是认真听讲、单纯记忆、练习巩固的被动学习方式.引导学生在动手实践、自主探索、合作交流活动中发现新知和发展能力,与此同时教师通过适时的精讲、点拨使观察、实验、猜想、验证、归纳、推理贯穿整个学习过程.。
专题14 圆中的两解及多解问题分类讨论思想)归类集训-2023年中考数学二轮复习核心考点拓展训练

专题14 圆中的两解及多解问题(分类讨论思想)归类集训(解析版)类型一讨论弦上某点或端点的位置1.在半径为10的⊙O中,弦AB的长为16,点P在弦AB上,且OP的长为8,AP长为 .思路引领:作OC⊥AB于点C,根据垂径定理求出OC的长,根据勾股定理求出PC的长,分当点P在线段AC上和当点P在线段BC上两种情况计算即可.解:作OC⊥AB于点C,∴AC=12AB=8,由勾股定理得,OC=OA2―AC2=6,∴PC=OP2―OC2=27,当点P在线段AC上时,AP=AC﹣PC=8﹣27,当点P在线段BC上时,AP=8+27,故答案为:8﹣27或8+27.总结提升:本题考查的是垂径定理的应用和勾股定理的应用,正确作出辅助线构造直角三角形、运用分情况讨论思想是解题的关键.2.(2021•无棣县模拟)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )A.25cm B.43cm C.25cm或45cm D.23cm或43cm思路引领:分两种情况,根据题意画出图形,先根据垂径定理求出AM的长,连接OA,由勾股定理求出OM的长,进而可得出结论.解:连接AC,AO,∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,∴AM=12AB=12×8=4(cm),OD=OC=5(cm),当C点位置如图1所示时,∵OA=5cm,AM=4cm,CD⊥AB,∴OM=OA2―AM2=52―42=3(cm),∴CM=OC+OM=5+3=8(cm),∴AC=AM2+CM2=42+82=45(cm);当C点位置如图2所示时,同理可得:OM=3cm,∵OC=5cm,∴MC=5﹣3=2(cm),在Rt△AMC中,AC=AM2+CM2=42+22=25(cm);综上所述,AC的长为45cm或25cm,故选:C.总结提升:本题考查的是垂径定理和勾股定理等知识,根据题意画出图形,利用垂径定理和勾股定理求解是解答此题的关键.3.(2020•黑龙江)在半径为5的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP = .思路引领:如图1,作OE⊥AB于E,OF⊥CD于F,连接OD、OB,如图,根据垂径定理得到AE=BE=12AB=2,DF=CF=12CD=2,根据勾股定理在Rt△OBE中计算出OE=1,同理可得OF=1,接着证明四边形OEPF为正方形,于是得到PA=PC=1,根据三角形面积公式求得即可.解:作OE⊥AB于E,OF⊥CD于F,连接OD、OB,则AE=BE=12AB=2,DF=CF=12CD=2,如图1,在Rt△OBE中,∵OB=5,BE=2,∴OE=OB2―BE2=1,同理可得OF=1,∵AB⊥CD,∴四边形OEPF为矩形,∴PE=PF=1,∴PA=PC=1,∴S△APC=12×1×1=12;如图2,同理:S△APC=12×3×3=92;如图3,同理:S△APC=12×1×3=32;故答案为:12或32或92.总结提升:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.类型二圆心在两弦之间或者两弦之外4.(2021•商河县校级模拟)一下水管道的截面如图所示.已知排水管的直径为100cm,下雨前水面宽为60cm.一场大雨过后,水面宽为80cm,求水面上升多少?思路引领:分两种情形分别求解即可解决问题.解:作半径OD⊥AB交AB于C,连接OB,如图所示,由垂径定理得:BC=12AB=30cm,在Rt△OBC中,OC=502―302=40cm,当水位上升到圆心以下,水面宽80cm时,则OC′=502―402=30cm,水面上升的高度为:40﹣30=10cm;当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,综上可得,水面上升的高度为10cm或70cm.总结提升:本题考查的是垂径定理的应用,掌握垂径定理、灵活运用分情况讨论思想是解题的关键.5.(1)半径为1的圆中有一条弦,如果它的长为3,那么这条弦所对的圆周角的度数等于 ;(2)在半径为1的⊙O中,弦AB,AC的长分别为3和2,则∠BAC的度数是 ;(3)已知圆内接△ABC中.AB=AC,圆心O到BC的距离为3cm,圆的半径为7cm,求腰长AB.思路引领:(1)根据垂径定理求得AD的长,再根据三角形函数可得到∠AOD的度数,再根据圆周角定理得到∠ACB的度数,根据圆内接四边形的对角互补即可求得∠AEB的度数;(2)连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据垂径定理求出AE、FA值,根据解直角三角形的知识求出∠OAB和∠OAC,然后分两种情况求出∠BAC即可;(3)可根据勾股定理先求得BD的值,再根据勾股定理可求得AB的值.注意:圆心在内接三角形内时,AD=10cm;圆心在内接三角形外时,AD=4cm.解:(1)如图1,过O作OD⊥AB,则AD=12AB=12×3=32.∵OA=1,∴sin∠AOD=ADOA=32,∠AOD=60°.∵∠AOD=12∠AOB=60°,∠ACB=12∠AOB,∴∠ACB=∠AOD=60°.又∵四边形AEBC是圆内接四边形,∴∠AEB=180°﹣∠ACB=180°﹣60°=120°.故这条弦所对的圆周角的度数等于60°或120度.故答案为:60°或120度.(2)解:有两种情况:①如图2所示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,∴∠OEA=∠OFA=90°,由垂径定理得:AE=BE=32,AF=CF=32,cos∠OAE=AEOA=32,cos∠OAF=AFOA=22,∴∠OAE=30°,∠OAF=45°,∴∠BAC=30°+45°=75°;②如图3所示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,∴∠OEA=∠OFA=90°,由垂径定理得:AE=BE=32,AF=CF=22,cos∠OAE=AEOA=32,cos∠OAF=AFOA=22,∴∠OAE=30°,∠OAF=45°,∴∠BAC=45°﹣30°=15°,故答案为:75°或15°;(3)分圆心在内接三角形内和在内接三角形外两种情况讨论,如图4,假若∠A是锐角,△ABC是锐角三角形,连接OB,作AD⊥BC于D,连接OD,∵AB=AC,∴AD是BC的中垂线,∴OD也是BC的中垂线,∴A、O、D三点共线,∵OD=3cm,OB=7cm,∴AD=10cm,∴BD=OB2―OD2=210cm,∵OD⊥BC,∴BD=CD,∵AB=AC,∴AD⊥BC,∴AB=AD2+BD2=235cm;如图5,若∠A是钝角,则△ABC是钝角三角形,和图4解法一样,只是AD=7﹣3=4cm,∴AB=AD2+BD2=214cm,综上可得腰长AB=235cm或214cm.总结提升:本题主要考查了垂径定理和勾股定理,注意分圆心在内接三角形内和在内接三角形外两种情况讨论,解题的关键是根据题意作出图形,求出符合条件的所有情况.类型三讨论点在优弧上或劣弧上6.(2022秋•双城区期末)已知⊙O的半径为2,弦AB的长为23,则弦AB的中点到这条弦所对的弧的中点的距离为 .思路引领:由垂径定理得出AC,再由勾股定理得出OC,从而得出CD和CE的长.解:如图,∵C是弦AB的中点,AB=23,∴OC⊥AB,AC=12AB=3,∴AD=BD,AE=BE,在Rt△AOC中,OC=22―(3)2=1,∴CD=2﹣1=1cm,CE=2+1=3.故答案为:1或3.总结提升:本题考查了垂径定理和勾股定理,熟练掌握垂径定理和勾股定理是解题的关键.8.(2021秋•凉州区校级期末)如图,AB、AC分别与⊙O相切于点B、C,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是 .思路引领:此题分为两种情况,如图p点的位置有两个,所以∠BPC可能是锐角,也有可能是钝角,分别连接O、C;O、B;B、P1;B、P2;C、P1;C、P2各点.(1)当∠BPC为锐角,也就是∠BP1C时,根据AB,AC与⊙O相切,结合已知条件,在△ABC中,即可得出圆心角∠COB的度数,根据同弧所对的圆周角为圆心角的一半,即可得出∠BP1C的度数;(2)如果当∠BPC为钝角,也就是∠BP2C时,根据⊙O的内接四边形的性质,即可得出∠BP2C的度数.解:分别连接O、C;O、B;B、P1;B、P2;C、P1;C、P2各点,(1)当∠BPC为锐角,也就是∠BP1C时:∵AB,AC与⊙O相切于点B,C两点∴OC⊥AC,OB⊥AB,∵∠A=50°,∴在△ABC中,∠COB=130°,∵在⊙O中,∠BP1C为圆周角,∴∠BP1C=65°,(2)如果当∠BPC为钝角,也就是∠BP2C时∵四边形BP1CP2为⊙O的内接四边形,∵∠BP1C=65°,∴∠BP2C=115°故答案为:65°或115°.总结提升:本题考查圆的切线性质,在解题过程中还要注意对圆的内接四边形、圆周角、圆心角的有关性质的综合应用.类型四弦所对的圆周角7.(2018秋•泗阳县期中)若圆的一条弦把圆分成度数的比为1:3的两条弧,则该弦所对的圆周角等于 .思路引领:圆的一条弦把圆分成度数之比为1:3的两条弧,则所分的劣弧的度数是90°,当圆周角的顶点在优弧上时,这条弦所对的圆周角等于45°,当这条弦所对的圆周角的顶点在劣弧上时,这条弦所对的圆周角等于135°.解:如图,弦AB将⊙O分成了度数比为1:3两条弧.连接OA、OB;则∠AOB=90°;①当所求的圆周角顶点位于D点时,这条弦所对的圆周角∠ADB=12∠AOB=45°;②当所求的圆周角顶点位于C点时,这条弦所对的圆周角∠ACB=180°﹣∠ADB=135°.故答案为:45°,135°.总结提升:本题考查的是圆心角、弧、弦的关系及圆周角定理,在解答此类问题时要注意是在“同圆或等圆中”才适用,这是此类问题的易错点.9.(2020秋•溧阳市期末)已知△ABC是半径为2的圆内接三角形,若BC=23,则∠A的度数为( )A.30°B.60°C.120°D.60°或120°思路引领:首先根据题意画出图形,然后由圆周角定理与含30°角的直角三角形的性质,求得答案.解:如图,作直径BD,连接CD,则∠BCD=90°,∵△ABC是半径为2的圆内接三角形,BC=23,∴BD=4,∴CD=BD2―BC2=2,∴CD=12 BD,∴∠CBD=30°,∴∠A=∠D=60°,∴∠A′=180°﹣∠A=120°,∴∠A的度数为:60°或120°.故选:D.总结提升:此题考查了圆周角定理与含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.类型五讨论圆内接三角形的形状10.(2019•绥化)半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连接OB、OC,延长CO交弦AB 于点D.若△OBD是直角三角形,则弦BC的长为 .思路引领:如图1,当∠ODB=90°时,推出△ABC是等边三角形,解直角三角形得到BC=AB=53,如图2,当∠DOB=90°,推出△BOC是等腰直角三角形,于是得到BC=2OB=52.解:如图1,当∠ODB=90°时,即CD⊥AB,∴AD=BD,∴AC=BC,∵AB=AC,∴△ABC是等边三角形,∴∠DBO=30°,∵OB=5,∴BD =32OB =532,∴BC =AB =53,如图2,当∠DOB =90°,∴∠BOC =90°,∴△BOC 是等腰直角三角形,∴BC =2OB =52,综上所述:若△OBD 是直角三角形,则弦BC 的长为53或52,故答案为:53或52.点睛:本题考查了三角形的外接圆与外心,等边三角形的判定和性质,等腰直角三角形的性质,正确的作出图形是解题的关键.101.已知等腰△ABC 的三个顶点都在半径为5的⊙O 上,如果底边BC 的长为8,求BC 边上的高.思路引领:从圆心向BC 引垂线,交点为D ,则根据垂径定理和勾股定理可求出,OD 的长,再根据圆心在三角形内部和外部两种情况讨论.解:连接AO 并延长交BC 于D 点,∵AB =AC ,∴AB =AC ,根据垂径定理得AD ⊥BC ,则BD =4,根据勾股定理得OD =3①圆心在三角形内部时,三角形底边BC 上的高=5+3=8;②圆心在三角形外部时,三角形底边BC 上的高=5﹣3=2.所以BC 边上的高是8或2.总结提升:本题综合考查了垂径定理和勾股定理在圆中的应用,因三角形与圆心的位置不明确,注意分情况讨论.类型六讨论点与圆的位置关系12.(2020•南通模拟)若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为 .思路引领:点P可能在圆内,也可能在圆外;当点P在圆内时,直径为最大距离与最小距离的和;当点P在圆外时,直径为最大距离与最小距离的差;再分别计算半径.解:若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b,若这个点在圆的内部或在圆上时,圆的直径为a+b,因而半径为a+b 2;当此点在圆外时,圆的直径是a﹣b,因而半径是a―b 2;故答案为:a+b2或a―b2.总结提升:本题考查了点与圆的位置关系,培养学生分类的思想及对点P到圆上最大距离、最小距离的认识.13.已知点P到⊙O的最长距离为6cm,最短距离为2cm.试求⊙O的半径长.思路引领:分两种情况进行讨论:①点P在圆内;②点P在圆外,进行计算即可解:①当P在⊙O外时,如图,∵P当⊙O的最长距离是为6cm,最短距离为2cm,∴PB=6cm,PA=2cm,∴AB=4cm,∴⊙O的半径为2cm';当P在⊙O内时,,此时AB=8cm,⊙O的半径为4cm.即⊙O的半径长为2cm或4cm.解题秘籍:本题考查了点和圆的位置关系,分类讨论是解此题的关键.类型七讨论直线与圆的位置关系14.(2021•崇明区二模)已知同一平面内有⊙O和点A与点B,如果⊙O的半径为3cm,线段OA=5cm,线段OB=3cm,那么直线AB与⊙O的位置关系为( )A.相离B.相交C.相切D.相交或相切思路引领:根据点与圆的位置关系的判定方法进行判断.解:∵⊙O的半径为3cm,线段OA=5cm,线段OB=3cm,即点A到圆心O的距离大于圆的半径,点B到圆心O的距离等于圆的半径,∴点A在⊙O外.点B在⊙O上,∴直线AB与⊙O的位置关系为相交或相切,故选:D.总结提升:本题考查了直线与圆的位置关系,正确的理解题意是解题的关键.15.(2021秋•信都区校级月考)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,若以点C为圆心,r为半径的圆与边AB所在直线相离,则r的取值范围为 ;若⊙C与AB边只有一个公共点,则r的取值范围为 .思路引领:如图,作CH⊥AB于H.利用勾股定理求出AB,再利用面积法求出CH即可判断.解:如图,作CH⊥AB于H.在Rt△ABC中,∵∠ACB=90°,BC=8,AC=6,∴AB=AC2+BC2=62+82=10,∵S△ABC=12•AC•BC=12•AB•CH,∴CH=24 5,∵以点C为圆心,r为半径的圆与边AB所在直线相离,∴r的取值范围为r<24 5,∵⊙C与AB边只有一个公共点,∴r的取值范围为6<r≤8或r=24 5,故答案为:r<245,6<r≤8或r=245.总结提升:本题考查直线与圆的位置关系,解直角三角形等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.16.(衢州中考)如图,已知直线l的解析式是y=43x﹣4,并且与x轴、y轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l 相切时,则该圆运动的时间为( )A.3秒或6秒B.6秒C.3秒D.6秒或16秒思路引领:由y=43x﹣4可以求出与x轴、y轴的交点A(3,0)、B(0,﹣4)坐标,再根据勾股定理可得AB=5,当C在B上方,根据直线与圆相切时知道C到AB的距离等于1.5,然后利用三角函数可得到CB,最后即可得到C运动的距离和运动的时间;同理当C在B下方,利用题意的方法也可以求出C 运动的距离和运动的时间.解:如图,∵x=0时,y=﹣4,y=0时,x=3,∴A(3,0)、B(0,﹣4),∴AB=5,当C在B上方,直线与圆相切时,连接CD,则C到AB的距离等于1.5,∴CB=1.5÷sin∠ABC=1.5×53=2.5;∴C运动的距离为:1.5+(4﹣2.5)=3,运动的时间为:3÷0.5=6;同理当C在B下方,直线与圆相切时,连接CD,则C运动的距离为:1.5+(4+2.5)=8,运动的时间为:8÷0.5=16.故选:D.总结提升:此题首先注意分类讨论,利用了切线的性质和三角函数等知识解决问题.17.(2018•浦东新区二模)已知l1∥l2,l1、l2之间的距离是3cm,圆心O到直线l1的距离是1cm,如果圆O 与直线l1、l2有三个公共点,那么圆O的半径为 cm.思路引领:根据题意可以画出相应的图形,从而可以解答本题.解:如下图所示,设圆的半径为r如图一所示,r﹣1=3,得r=4,如图二所示,r+1=3,得r=2,故答案为:2或4.总结提升:本题考查直线和圆的位置关系,解答本题的关键是明确题意,画出相应的图形,利用数形结合的思想解答.18.(2021秋•新荣区月考)综合与实践问题情境:数学活动课上,老师出示了一个直角三角板和量角器,把量角器的中心O 点放置在AC 的中点上,DE 与直角边AC 重合,如图1所示,∠C =90°,BC =6,AC =8,OD =3,量角器交AB 于点G ,F ,现将量角器DE 绕点C 旋转,如图2所示.(1)点C 到边AB 的距离为 245 .(2)在旋转过程中,求点O 到AB 距离的最小值.(3)若半圆O 与Rt △ABC 的直角边相切,设切点为K ,求BK 的长.思路引领:(1)如图1,过点C 作CH ⊥AB 于点H ,利用勾股定理求得AB ,再利用AB •CH =AC •BC ,即可求得答案.(2)当CD ⊥AB 时,点O 到AB 的距离最小,再由OH =CH ﹣OC ,即可求得答案.(3)分两种情况:①当半圆O 与BC 相切时,如图2,设切点为K ,连接OK ,运用勾股定理即可求得答案;②当半圆O 与AC 相切时,如图3,设切点为K ,连接OK ,运用勾股定理求得CK ,再利用勾股定理即可求得BK .解:(1)如图1,过点C 作CH ⊥AB 于点H ,∵∠ACB =90°,BC =6,AC =8,∴AB =AC 2+BC 2=62+82=10,∵CH ⊥AB ,∴AB •CH =AC •BC ,∴CH =AC ⋅BC AB=6×810=245,即点C 到边AB 的距离为245,故答案为:245.(2)∵O 为AC 的中点,∴OC =12AC =12×8=4,当CD ⊥AB 时,点O 到AB 的距离最小,∴OH =CH ﹣OC =245―4=45,∴点O 到AB 距离的最小值为45.(3)①当半圆O 与BC 相切时,如图2,设切点为K ,连接OK ,∴∠OKC =90°,在Rt △OCK 中,OK =3,OC =4,∴CK =OC 2―OK 2=42―32=7,∴BK =BC ﹣CK =6―7;②当半圆O 与AC 相切时,如图3,设切点为K ,连接OK ,∴∠OKC =90°,在Rt △OCK 中,OK =3,OC =4,∴CK =OC 2―OK 2=42―32=7,在Rt △BCK 中,BK =BC 2+CK 2=62+(7)2=43;综上所述,BK 的长为7或43.解题秘籍:本题是几何综合题,考查了圆的性质,切线的性质,旋转变换的性质,勾股定理,三角形面积,解题关键是熟练掌握旋转变换的性质等相关知识,运用分类讨论思想解决问题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年八年级数学《暑假作业�新课程无忧衔接》(苏科版)考点14圆周角【知识点梳理】圆周角的定义:顶点在圆上,并且两边都和圆相交的角叫做圆周角圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
圆内接四边形:如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.圆内接四边形的对角互补.圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).【新课程预习练·无忧衔接】一、单选题1.如图,AB是⊙O的直径,点C在⊙O上,连接OC,AC,若26OCA∠=︒,则BOC∠=()A.60°B.56°C.52°D.48°【答案】C【分析】先说明OA=OC,进而得到⊙BAC=⊙OCA=26°,然后再根据圆周角定理解答即可.【详解】解:⊙AB 是⊙O 的直径,点C 在⊙O 上⊙OC =OA⊙⊙BAC =⊙OCA =26°⊙BOC ∠=2⊙BAC =52°.故选C .【点睛】考查了圆周角定理、等腰三角形的判定与性质等知识点,掌握圆周角定理成为解答本题的关键. 2.如图,在Rt ⊙ACB 中,⊙ACB =90︒,AC =6,BC =8,若以AC 为直径的⊙O 交AB 于点D ,则CD 的长为( )A .125B .135C .245D .5【答案】C【分析】根据勾股定理求得AB 的长,然后根据直径所对圆周角为90︒得到90ADC ∠=︒,然后根据三角形面积即可求解.【详解】在Rt ⊙ACB 中,22226810ABAC BC , ⊙AC 为O 的直径,⊙90ADC ∠=︒,⊙1122ABC S AC BC AB CD ==, ⊙6824105AC BC CD AB ⨯===, 故选C . 【点睛】考查了圆周角定理,勾股定理,关键是判断90ADC ∠=︒.3.如图,AB 为O 的直径,AC 为O 的弦,D 是弧BC 的中点,E 是AC 的中点.若CD =6AC =,则DE =( )AB .5CD .【答案】A 【分析】连接OC 、BC 、OE 、BD ,OE 交O 于F ,OD 交BC 于G ,连接OE 并延长交AC 于点F ,如图,先根据垂径定理得到OD BC ,OE AC ⊥,再计算出90DOF ∠=︒,设O 的半径为r ,则3DG r =-,利用勾股定理得到=5r ,然后利用勾股定理计算DE 的长.【详解】解:连接OC 、BC 、BD ,OD 交BC 于G ,连接OE 并延长交AC 于点F ,⊙D 是弧BC 的中点,⊙OD BC ,BD CD ==BOD COD ∠=∠,⊙E 是AC 的中点,⊙OE AC ⊥,AF CF =,⊙AOF COF ∠=∠, ⊙1180902DOF ∠=⨯︒=︒, ⊙OA OB =,BG CG =,⊙//OG AC ,132==OG AC , 设O 的半径为r ,则3DG r =-,在Rt OBG 中,2223BG r =-,在Rt DBG △中,(()2223BG r =--,⊙(()22293r r -=--, 解得:12r =-(舍去),35r =,⊙5OD =,⊙4BG =,易得四边形OGCE 为矩形,⊙4OE CG BG ===,在Rt DOE 中,DE =故选:A .【点睛】考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.4.如图,四边形ABCD 内接于O ,:2:1,2ABC ADC AB ∠∠== ,点C 为BD 的中点,延长AB 、DC 交于点E ,且60E ∠=,则O 的面积是( )A .πB .2πC .3πD .4π【答案】D 【分析】连接BD ,根据圆内接四边形的外角等于其内对角可得⊙D =⊙CBE =60°,根据等边对等角以及三角形内角和定理求出⊙BCE =60°,可得⊙A =60°,点C 为BD 的中点,可得出⊙BDC =⊙CBD =30°,进而得出⊙ABD =90°,AD 为直径,可得出AD =2AB =4,再根据面积公式计算得出结论;【详解】解:连接BD ,⊙ABCD 是⊙O 的内接四边形,⊙⊙CBE =⊙ADC ,⊙BCE =⊙A⊙:2:1ABC ADC ∠∠=⊙:2:1ABC CBE ∠∠=⊙⊙CBE =⊙ADC=60°,⊙CBA =120°⊙60E ∠=⊙⊙CBE 为等边三角形⊙⊙BCE =⊙A=60°,⊙点C 为BD 的中点,⊙⊙CDB =⊙DBC=30°⊙⊙ABD =90°,⊙ADB =30°⊙AD 为直径⊙AB =2⊙AD =2AB =4⊙O 的面积是=224ππ⨯=故答案选:D【点睛】考查了圆内接四边形的性质,圆周角定理,等边三角形的判定与性质,三角形内角和定理,掌握相关性质及公式是解题的关键.5.如图,AB 为圆O 的直径,且AB =8,C 为圆上任意一点,连接AC 、BC ,以AC 为边作等边三角形ACD ,以BC 为边作正方形BCEF ,连接DE .若AC 为a ,BC 为b ,DE 为c ,则下列关系式成立的是( )A .260ab c +=B .2222a b c +=C .2223a c b +=D .264ab c +=【答案】D 【分析】延长DC ,过E 作DC 延长线的垂线,垂足为M ,在⊙E CM 中,分别表示出EM 和CM ,得到DM ,在⊙DEM 中,利用勾股定理得到222a b ab c ++=,结合直径AB =8即可得到结果.【详解】解:延长DC ,过E 作DC 延长线的垂线,垂足为M ,⊙AB 为圆O 的直径,⊙⊙ACB =90°,⊙四边形BCEF 为正方形,⊙⊙BCE =90°,即A ,C ,E 三点共线,⊙⊙ACD 为正三角形,⊙⊙ACD =60°,⊙⊙E CM=60°,在⊙E CM 中,EM =EC ·sin60°=2b , CM=EC ·sin30°=12b , ⊙DM =DC +CM=a +12b , 在⊙DEM 中,222DM EM DE +=,⊙22212a b c ⎫⎛⎫++=⎪ ⎪⎪⎝⎭⎝⎭, 整理可得:222a b ab c ++=,⊙AB =8,⊙222264AC BC a b +=+=,⊙264ab c +=,故选D .【点睛】考查了等边三角形的性质,正方形的性质,三角函数的定义,勾股定理,圆周角定理,解题的关键是作出辅助线,得到a ,b ,c 的关系式222a b ab c ++=.6.如图,AB 与CD 是O 的两条互相垂直的弦,交点为点P ,70ABC ∠=︒,点E 在圆上,则BED ∠的度数为( )A .10︒B .20︒C .30D .40︒【答案】B 【分析】利用垂直的定义和圆周角定理解答即可.【详解】解:⊙AB CD ⊥,⊙90BPC ∠=︒,⊙70ABC ∠=︒,⊙180180709020BED BCP ABC BPC ∠=∠=︒-∠-∠=︒-︒-︒=︒ ,故选:B .【点睛】考查了圆周角定理,解答此题的关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.7.如图,点A ,D ,B ,C 是圆O 上的四个点,连接AB ,CD 相交于点E ,若38BOD ∠=︒,132AOC ∠=︒,则AEC ∠的度数为( )A .95°B .90°C .85°D .80°【答案】C【分析】首先连接BC ,根据⊙BOD 和⊙BCD 是同弧所对的圆心角和圆周角,得出⊙BCD 的度数,再根据⊙AOC 和⊙ABC 是同弧所对的圆心角和圆周角,得出⊙ABC 的度数,再根据三角形的外角,得出⊙AEC =⊙EBC +⊙ECB ,即可求出⊙AEC 的度数.【详解】连接BC ,⊙BOD ∠ 和BCD ∠ 是BD 所对的圆心角和圆周角, 11381922BCD BOD ,又AOC ∠ 和ABC ∠ 是AC 所对的圆心角和圆周角, 111326622ABC AOC ,又⊙⊙AEC 是⊙BEC 的外角,⊙196685AECEBC ECB , 故选:C .【点睛】考查了同弧所对的圆周角是圆心角的一半,三角形的外角,解题关键是连接辅助线,构造同弧所对的圆周角和圆心角.8.如图,O 中所对的圆周67ACB ∠=︒,点P 在劣弧AB 上,42AOP ∠=︒,则BOP ∠的度数为( )A .25︒B .90︒C .92︒D .109︒【答案】C【分析】根据圆周角定理可得2134AOB ACB ∠=∠=︒,再根据角的和差即可得出答案. 【详解】 解:O 中所对的圆周67ACB ∠=︒,2134AOB ACB ∴∠=∠=︒点P 在劣弧AB 上,42AOP ∠=︒,1344292BOP AOB AOP ∴∠=∠-∠=︒-︒=︒故选C .【点睛】考查了圆周角定理,熟练掌握定理是解题的关键.9.如图,ABC 内接于O ,CD 是O 的直径,20ABC ∠=︒,则ACD ∠的度数是( )A .40︒B .50︒C .60︒D .70︒【答案】D 【分析】由CD 是⊙O 的直径,根据直径所对的圆周角是直角,得出⊙CAD =90°,根据直角三角形两锐角互余得到⊙ACD 与⊙D 互余,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得⊙D 的度数,继而求得⊙ACD 的度数. 【详解】解:⊙CD 是⊙O 的直径, ⊙⊙CAD =90°, ⊙⊙ACD +⊙D =90°. ⊙⊙ADC =⊙ABC =20°, ⊙⊙ACD =90°-⊙ADC =70°. 故选:D .【点睛】考查了三角形的外接圆与外角,圆周角定理,直角三角形的性质,难度不大,注意掌握数形结合思想的应用.10.如图,ABC 内接于O ,其外角BAE ∠的平分线交O 于点D ,点A 为弧CD 的中点.若28ABC ∠=︒,则ACB ∠的大小为( )A .84°B .85°C .86°D .88°【答案】A连接AO 并延长与O 交于点F ,连接FC ,FD ,根据圆周角定理得出28AFC DFA ∠=∠=︒,根据直角三角形两锐角互余与外角平分线得出BAF ∠度数,进一步计算可得ACB ∠的度数. 【详解】解:连接AO 并延长与O 交于点F ,连接FC ,FD ,⊙AF 是直径,⊙90ACF ADF ∠=∠=︒,⊙点A 为弧CD 的中点,28ABC ∠=︒, ⊙=28DFA AFC ∠=∠︒, ⊙62FAD FAC ∠=∠=︒,⊙180626256DAE ∠=︒-︒-︒=︒, ⊙AD 平分BAE ∠, ⊙56DAB DAE ∠=∠=︒,⊙62566BAF FAD DAB ∠=∠-∠=︒-︒=︒, ⊙6BCF ∠=︒,⊙90684ACB ∠=︒-︒=︒,【点睛】考查圆周角定律,三角形内角和,作出合理辅助线是解题关键.11.如图,C ,D 是O 上直径AB 两侧的两点.设25ABC ∠=︒,则BDC ∠=( )A .85︒B .75︒C .70︒D .65︒【答案】D 【分析】先利用直径所对的圆周角是直角得到⊙ACB =90°,从而求出⊙BAC ,再利用同弧所对的圆周角相等即可求出⊙BDC . 【详解】解:⊙C ,D 是⊙O 上直径AB 两侧的两点, ⊙⊙ACB =90°, ⊙⊙ABC =25°, ⊙⊙BAC =90°-25°=65°, ⊙⊙BDC =⊙BAC =65°, 故选:D .【点睛】考查了圆周角定理的推论,即直径所对的圆周角是90°和同弧或等弧所对的圆周角相等,解决本题的关键是牢记相关概念与推论,本题蕴含了属性结合的思想方法. 12.如图,AB 是O 的直径,点C 在O 上.40OCA ∠=︒.则BOC ∠的度数为( )A .80︒B .90︒C .100︒D .50︒【答案】A【分析】先利用等腰三角形的性质得到⊙A =⊙OCA =40°,然后根据圆周角定理得到⊙BOC 的度数. 【详解】 解:⊙OC =OA , ⊙⊙A =⊙OCA =40°, ⊙⊙BOC =2⊙A =80°. 故选:A .【点睛】考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半. 二、填空题13.如图,已知正方形ABCD 的边长为6,点F 是正方形内一点,连接,CF DF ,且ADF =DCF ∠∠,点E 是AD 边上一动点,连接,EB EF ,则EB EF +长度的最小值为___________.【答案】3【分析】根据正方形的性质得到⊙ADC=90°,推出⊙DFC=90°,点F在以DC为直径的半圆上移动,,如图,设CD 的中点为O,作正方形ABCD关于直线AD对称的正方形APGD,则点B的对应点是P,连接PO交AD于E,交半圆O于F,则线段FP的长即为BE+FE的长度最小值,根据勾股定理即可得到结论.【详解】解:⊙四边形ABCD是正方形,⊙⊙ADC=90°,⊙⊙ADF+⊙CDF=90°,∠∠,⊙ADF=DCF⊙⊙DCF+⊙CDF=90°,⊙⊙DFC=90°,⊙点F在以DC为直径的半圆上移动,如图,设CD的中点为O,作正方形ABCD关于直线AD对称的正方形APGD,则点B的对应点是P,连接PO交AD于E,交半圆O于F,则线段FP的长即为BE+FE的长度最小值,OF=3,⊙⊙G=90°,PG=DG=AB=6,⊙OG=9,⊙OP=,⊙FP=3,⊙BE+FE的长度最小值为3,故答案为:3.【点睛】考查了轴对称−最短路线问题,正方形的性质,勾股定理以及圆的基本性质.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.14.如图,劣弧BC与AD的度数之差为20°,弦AB与CD交于点E,⊙CEB=60°,求⊙CAB的度数________.【答案】35°【分析】根据圆周角定理,可得:⊙A-⊙C=10°;根据三角形外角的性质,可得⊙CEB=⊙A+⊙C=60°;联立两式可求得⊙A的度数.【详解】解:由题意,弧BC与弧AD的度数之差为20°,⊙两弧所对圆心角相差20°,⊙2⊙A-2⊙C=20°,⊙⊙A-⊙C=10°…⊙;⊙⊙CEB是⊙AEC的外角,⊙⊙A +⊙C =⊙CEB =60°…⊙; ⊙+⊙,得:2⊙A =70°,即⊙A =35°. 故答案为:35°.【点睛】考查圆周角定理,三角形外角的性质等知识,解题的关键是熟练掌握圆周角定理,属于中考常考题型.15.如图,点A ,B ,C 在O 上,50B C ∠+∠=︒,则BOC ∠的度数为______.【答案】100︒【分析】根据点A 、B 、C 在圆上,利用等腰三角形性质,可得⊙OAB =⊙B ,⊙OAC =⊙C ,根据同圆中同弧所对的圆周角等于圆心角的一半解答即可. 【详解】 解:连结OA ,点、、A B C 在O 上, ⊙OA =OB =OC ,⊙⊙OAB =⊙B ,⊙OAC =⊙C , ⊙50B C ∠+∠=︒,⊙50BAC OAB OAC B C ∠=∠+∠=∠+∠=︒,2100BOC BAC ∴∠∠︒==.故答案为:100︒.【点睛】考查的圆的半径相等,等腰三角形性质,圆周角定理,熟记定理内容是解题的关键. 16.如图,在O 中,55,15CBO CAO ∠=︒∠=︒,则AOB ∠的度数是______°.【答案】80【分析】首先连接OC ,由OA =OC =OB ,可得⊙ACO =⊙CAO =15°,⊙BCO =⊙CBO =55°,继而求得⊙ACB 的度数,然后由圆周角定理,求得⊙AOB 的度数. 【详解】 解:连接OC , ⊙OA =OC =OB ,⊙⊙ACO =⊙CAO =15°,⊙BCO =⊙CBO =55°, ⊙⊙ACB =⊙BCO −⊙ACO =40°, ⊙⊙AOB =2⊙ACB =80°. 故答案是:80.【点睛】考查了圆周角定理以及等腰三角形的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用. 三、解答题17.请阅读下列材料,并完成相应的任务.克罗狄斯·托勒密(约90年-168年),古希腊天文学家、地理学家和光学家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理,托勒密定理的内容如下:圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.即:如图1,若四边形ABCD 内接于O ,则有______.任务:(1)材料中划横线部分应填写的内容为_______.(2)已知,如图2,四边形ABCD 内接于O ,BD 平分ABC ∠,120COD ∠=︒,求证:BD AB BC =+.【答案】(1)AC BD AB CD BC AD ⋅=⋅+⋅;(2)见解析 【分析】(1)由托勒密定理可直接求解;(2)连接AC ,通过证明⊙ACD 是等边三角形,可得AC =AD =CD ,由AC•BD=AB•CD+BC•AD ,可求解.【详解】解:(1)由托勒密定理可得:AC BD AB CD BC AD ⋅=⋅+⋅故答案为:AC BD AB CD BC AD ⋅=⋅+⋅(2)如图,连接AC⊙120COD ∠=︒,⊙60CBD CAD ∠=∠=︒⊙BD 平分ABC ∠⊙60ABD CBD ∠=∠=︒⊙60ACD ∠=︒⊙ACD △是等边三角形⊙AC AD CD ==,⊙四边形ABCD 是圆内接四边形⊙AC BD AB CD BC AD ⋅=⋅+⋅⊙BD AB BC =+.【点睛】考查了圆的内接四边形的性质,圆的有关知识,阅读理解题意是本题的关键.18.如图,等边三角形ABC 内接于O ,D 是BC 上一动点,连接AD ,BD ,CD ,延长DC 到点E ,使CE BD =,连接AE .(1)求证:ADE 是等边三角形;(2)填空:⊙若1BD =,2CD =,则AD 的长为____________;⊙当BAD ∠的度数为_________时,四边形OBDC 为菱形.【答案】(1)证明见解析;(2)⊙3;⊙30°.【分析】(1)根据等边三角形的性质可得AB =AC =BC ,⊙AB C=⊙ACB =⊙BAC =60°,根据圆周角定理可得⊙CBD =⊙CAD ,⊙ABC =⊙ADC ,根据角的和差关系及外角性质可得⊙ABD =⊙ACE ,利用SAS 可证明⊙ABD ⊙⊙ACE ,可得AD =AE ,即可得⊙ADE 是等边三角形;(2)⊙根据线段的和差关系可得DE 的长,由(1)可知⊙ADE 是等边三角形,可得AD =DE ,即可得答案;⊙如图,连接OB 、OC ,根据圆周角定理可知⊙BOC =2⊙BAC =120°,根据等腰三角形的性质可得⊙OCB =30°,根据菱形的性质可得⊙BCD =30°,根据圆周角定理可得⊙BAD =⊙BCD =30°,可得答案.【详解】(1)⊙⊙ABC 是等边三角形,⊙AB =AC =BC ,⊙AB C=⊙ACB =⊙BAC =60°,⊙⊙CBD 与⊙CAD 是CD 所对的圆周角,⊙⊙CBD =⊙CAD ,同理可得:⊙ABC =⊙ADC =60°,⊙⊙ACE=⊙ABC+⊙CBD=⊙ABD,在⊙ABD和⊙ACE中,AB ACABD ACE BD CE=⎧⎪∠=∠⎨⎪=⎩,⊙⊙ABD⊙⊙ACE,⊙AD=AE,⊙⊙ADE是等边三角形.(2)⊙⊙BD=CE=1,DE=CD+CE,CD=2,⊙DE=3,⊙⊙ADE是等边三角形,⊙AD=DE=3.故答案为:3⊙如图,连接OB、OC,⊙⊙BAC和⊙BOC分别是BC所对的圆周角和圆心角,⊙⊙BOC=2⊙BAC=120°,⊙OB=OC,⊙⊙OCB=30°,⊙四边形OBDC为菱形,⊙⊙BCD=⊙OCB=30°,⊙⊙BAD和⊙BCD都是BD所对的圆周角,⊙当BAD ∠的度数为30°时,四边形OBDC 为菱形.故答案为:30°【点睛】考查全等三角形的判定与性质、圆周角定理、等边三角形的判定与性质及菱形的性质,熟练掌握相关性质及判定定理是解题关键.19.小亮在学习中遇到如下一个问题:如图1,点C 是半圆AmB 上一动点,线段AB =6,CD 平分ACB ∠,过点A 作//AD BC 交CD 于点D ,连接BD .当BCD △为等腰三角形时,求线段AC 的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是他尝试结合学习函数的经验研究此问题.将线段AC 的长度作为自变量x ,BC ,BD 和CD 的长度都是x 的函数,分别记为BC y ,BD y 和CD y .请将下面的探究过程补充完整:(1)根据点C 在半圆AmB 上的不同位置,画出相应的图形,测量线段AC ,BC ,BD 的长度,得到下表的几组对应值:⊙上表中a 的值是______⊙操作中发现,“无需测量线段CD 的长度即可得到CD y 关于x 的函数解析式”.请直接写出CD y 关于x 的函数解析式.(2)小亮已在平面直角坐标系xOy 中画出了函数BD y 的图象,如图2所示.⊙请在同一个坐标系中画出函数BC y 和CD y 的图象;⊙结合图象直接写出当BCD △为等腰三角形时,线段AC 长度的近似值(结果保留一位小数).【答案】(1)⊙4.0;⊙CD y;(2)⊙见解析;⊙2.7或4.2 【分析】(1)⊙根据直径所对的圆周角是直角,得到⊙ACB 是直角三角形,用勾股定理求出边长即可;⊙根据等腰直角三角形三角形的性质,再根据勾股定理求出即可;(2)⊙根据条件画出图形即可;⊙根据等腰直角三角形的性质,分类讨论,利用勾股定理求出边长即可.【详解】解:(1)⊙⊙AB是圆的直径,⊙⊙ACB=90°,在Rt⊙ACB中,⊙ACB=90°,由勾股定理得:BC=当AC=4.5时, 3.96BC=,⊙a≈4.0;⊙⊙AB是圆的直径,⊙⊙ACB=90°,⊙CD平分ACB∠,⊙⊙ACD=⊙BCD=45°,AD BC,⊙//⊙⊙ADC=⊙BCD=45°,⊙AC=AD,⊙⊙CAD=180°-⊙ADC-⊙BCD=90°,⊙⊙ACD是等腰直角三角形,⊙CD,y=⊙CD(2)⊙如图所示.⊙当BC=BD时,BC与BD即为交点,AD BC,⊙⊙ACB=90°,//⊙⊙CAD=90°,⊙⊙ADC=⊙BCD,⊙CD平分ACB,⊙⊙ACD=⊙BCD,⊙⊙ACD=⊙ADC=45°,⊙AC=AD,⊙BC=CD,⊙BDC=⊙BCD=45°,⊙⊙ADB=90°,⊙四边形ABDC为矩形,⊙AC=AD,⊙AC=BC,⊙AB=6,⊙AC = 4.22AB =≈, 当BC=CD 时,图象无交点,则BC ≠CD ,当BD =CD 时,⊙BDC =⊙BCD =45°,⊙⊙BDC =90°,则在等腰直角⊙ACD 中,CD ==,在等腰直角⊙BCD 中,2BC x ==,在Rt ⊙ABC 中,222AB AC BC =+,⊙x =⊙ 2.75AC =≈, 故AC 的长为:2.7或4.2.【点睛】考查了圆的性质、等腰直角三角形的性质与勾股定理,关键在于运用分类讨论的思想. 20.如图,在Rt ABC 中,90ACB ∠=︒.点D 为边AC 上一点,DE AB ⊥于点E ,点G 为BD 上一点.连结CG 并延长与AB 相交于点F ,连结EG .已知12∠=∠.(1)若BD 平分ABC ∠,求证:DBC △⊙DBE .(2)若4BD =,求CG 的长.(3)若80EGF ∠=︒,求A ∠的读数.【答案】(1)见解析;(2)2;(3)40°【分析】(1)利用角平分线的定义及AAS 定理证明三角形全等;(2)根据等腰三角形的判定和性质求解;(3)解法一:结合等边对等角,角平分线的定义及三角形内角和定理计算求解;解法二:利用圆周角定理求解.【详解】解:(1)证明:⊙DE AB ⊥,⊙90DEB ∠=︒,⊙90ACB ∠=︒,⊙DEB ACB ∠=∠.⊙BD 平分ABC ∠,⊙ABD CBD ∠=∠.又⊙BD BD =,⊙DBC △⊙DBE (AAS ).(2)⊙在BDE 中,90DEB ∠=︒,⊙190DBE ∠+∠=°,290BEG ∠+∠=°.⊙12∠=∠,⊙DBE BEG ∠=∠,⊙DG EG BG ==.⊙在Rt DBC 中,122CG BD ==. (3)解法一:⊙80EGF ∠=︒,⊙180100EGC EGF ∠=-∠=°°.⊙DG EG CG ==, ⊙()()11118018022CDE CDG DGE DGC ∠=∠+∠=-∠+-∠°° ()11802DGC DGE =-∠+∠° 11801302EGC =-∠=°°. ⊙9040A CDE ∠=∠-=°°.解法二:⊙DG EG BG CG ===,⊙点C ,D ,E ,B 在以点G 为圆心的圆上, ⊙()111805022ABC EGC EGF ∠=∠=-∠=°°, ⊙9040A ABC ∠=-∠=°°.【点睛】考查全等三角形的判定和性质,等腰三角形的判定和性质,也考查圆周角定理,掌握相关性质定理正确推理计算是解题关键.。
