第二十二章 二次函数 复习小结
第二十二章 二次函数单元小结与复习
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
★考点一 ★考点二 ★考点三 ★考点四 ★考点五 ★考点六 ★考点七
(人教版新课标)九年级数学第22章《二次函数》知识小结
函数是初中数学知识的主线，而二次函数是这条主线上的高潮.我们通过探索二次函数与方程的关系，让我们领悟到事物之间相互联系的辨证关系.我们能够利用二次函数解决实际问题，培养数学建模的能力. 【知识结构】【知识梳理】1、定义：形如 c bx ax y ++=2（a 、b 、c 是常数，a≠0）的函数叫做x 的二次函数. 二次函数的一般形式是c bx ax y ++=2（a≠0），还可以用配方法化为k h x a y +-=2)(的形式，它可直接看出其顶点坐标为（k h ,），故把k h x a y +-=2)(叫做二次函数的顶点式.2、图象：二次函数的图象是抛物线，它是轴对称图形，其对称轴平行于y 轴. 注意：二次函数c bx ax y ++=2的图象的形状、大小、开口方向只与a 有关，所以，c bx ax y ++=2的图象可通过2ax y =的 图象平移得到．平移可按照如下口诀进行：上加下减，左加右减，即向上或向左用加，向下或向右用减.例如，将22x y =向左平移1个单位为()212+=x y ，再向下平移3个单位为()3122-+=x y ．3、性质注意：二次函数的性质要结合图象，认真理解，灵活应用，不要死记硬背． 4、二次函数与一元二次方程的关系对于二次函数c bx ax y ++=2（a≠0），当y =0时，就变成了一元二次方程02=++c bx ax ．二次函数c bx ax y ++=2（a≠0）的图象与x 轴的交点有三种情况： 当ac b 42-﹥0时，有两个交点； 当ac b 42-=0时，有一个交点； 当ac b 42-﹤0时，无交点.当二次函数c bx ax y ++=2（a≠0）的图象与x 轴的有交点时，其交点横坐标就是方程02=++c bx ax 的根． 【易错点剖析】一、忽略二次项系数不等于0例1已知二次函数263y kx x =-+的图象与x 轴有交点，则k 的取值范围 是（ ）（A ）k ＜3 (B) k ＜3 且k ≠0 (C) k ≤3 (D) k ≤3 且k ≠0 错解:选C.由题意,得△=()26-－4 k ×3≥0,解得k ≤3,故选C.错解分析:当k =0时,二次项系数为0,此时原函数不是二次函数.欲求k 的取值范围,须同时满足:①函数是二次函数;②图象与x 轴有交点,上面的解法只注重了△≥0而忽略了二次项系数不等于0的条件.正解: 选D.由题意,得△=()26-－4 k ×3≥0且k ≠0,即k ≤3 且k ≠0,故应选D. 二、忽略隐含条件例2如图,已知二次函数2y x bx c =++的图象与y 轴交于点A, 与x 轴正半轴交于B,C 两点,且BC ＝2,ABC S ∆ ＝3,则b 的值为( )（A ）-5 (B)4或-4 (C) 4 (D)-4错解: 选 B.依题意BC ＝2,ABC S ∆ ＝3,得点A(0,3),即c ＝3.又BC ＝2,得方程20x bx c ++=的两根之差为2,2-=,解得b =±4.故选B.错解分析:上面的解法忽略了“抛物线的对称轴x ＝-2b在y 轴的右侧”这一隐含条件,正确的解法应是同时考虑-2b＞0,得b ＜0,∴b =4应舍去,故应选D. 正解: 选D.例3 若y 关于x 的函数y =(a -2)x 2-(2a -1)x +a 的图象与坐标轴有两个交点，则a 可取的值是多少？错解：因为函数y =(a -2)x 2-(2a -1)x +a 的图象与坐标轴有两个交点，而其中与y 轴有一个交点(0,a )，则与x 轴就只有一个交点，所以关于x 的一元二次方程y =(a -2)x 2-(2a -1)x +a有两个相等的实数根，所以判别式[-(2a-1)]2-4×(a-2)a=0，解得a=-14.错解分析：本题关于函数的描述是“y关于x的函数”，并没有指明是二次函数，所以需要分“y关于x的一次函数”和“y关于x的二次函数”两种情况进行讨论.当函数y是关于x的二次函数时，函数y=(a-2)x2-(2a-1)x+a的图象与y轴有一个交点(0,a)，与坐标轴三、忽略数形结合思想方法的应用例4 求二次函数y=2x+4x+5(-3≤x≤0)的最大值和最小值.错解:当x=-3时,y=2; 当x=0时,y=5;所以，-3≤x≤0时,y最小=2,y最大=5.错解分析:上面的解法错在忽略了数形结合思想方法的应用,误以为端点的值就是这段函数的最值.解决此类问题,画出函数图象,借助图象的直观性求解即可.四、求顶点坐标时混淆符号例5 求二次函数y =-x 2+2x -2的顶点坐标. 错解1 用配方法y =-x 2+2x -2=-(x 2-2x )-2=-(x 2-2x +1-1)-2=-(x 2-2x +1) -1=-(x -1) 2-1所以二次函数y =-x 2+2x -2的顶点坐标为(-1,-1).错解2 用公式法 在二次函数y =-x 2+2x -2中，a =-1，b =2，c =-2，则2122(1)b a ==-⨯-，22424(1)(2)142(1)b ac a --⨯-⨯-==⨯- 所以二次函数y =-x 2+2x -2的顶点坐标为(-1,1).错解分析：二次函数y =a (x -h )2+k 的顶点坐标为(h ,k ),即横坐标与配方后完全平方式中的常数项互为相反数，而非相等，也就是说不是(-h ,k ).二次函数y =ax 2+bx +c (a ≠0)的顶点坐标为(-2b a ,244b ac a-)，横坐标前面带“-”，纵坐标的分子为4ac -b 2,不要与一元二次方程根的判别式b 2-4ac 混淆.另外，把一般式转化为顶点式，常用配方法，如果二次项系数是1，则常数项为一次项系数一半的平方；如果二次项系数不是1，则先提出二次项系数（注意：不能像解方程一样把二次项系数消去），使括号中的二次项系数变为1，再对括号中进行配方.五、忽视根的判别式的作用例6 已知抛物线y=-12x2)x+m-3与x轴有两个交点A，B，且A，B关于y轴对称，求此抛物线解析式.错解：因为A与B关于y轴对称，所以抛物线对称轴为y轴，即直线x=-02ba==.解得m=6或m=-6.当m=6时，方程抛物线解析式为y=-12x2+3.错解分析：抛物线与x轴有两个交点为A，B，等价于：相应的一元二次方程有两个不相等的实数根，所以b2-4ac>0.如果忽视根的判别式在解题中的作用，就不能排除不符合题意的解，扩大了解的范围，导致错误.。
22章二次函数小结与复习导学案
第22章二次函数复习考点一：二次函数的定义：1. 下列函数中，哪些函数是y 关于x 的二次函数？(1) 32283y x x =-+ (2) 21x y -= (3) 21y mx x =-- （4）(1)y x x =- （5）2x y = 2、当=m _____时，函数()222-+=m x m y 为二次函数．2、抛物线2x y -=不具有的性质是( )．A 、开口向下B 、对称轴是y 轴C 、与y 轴不相交D 、最高点是原点 3、二次函数222+-=x x y 有( )． A 、最小值1 B 、最小值2 C 、最大值1D 、最大值24、已知点A ()1,1y 、B ()2,2y -、C ()3,2y -在函数()21122-+=x y 上，则1y 、2y 、3y 的大小关系是( )． A 、321y y y >>B 、131y y y >>C 、213y y y >>D 、312y y y >>5、已知抛物线c bx ax y ++=2的开口向下,顶点坐标为（2，－3） ,那么该抛物线有最 值 。
6、若点A ()m ,2在函数12-=x y 上，则A 点的坐标为_______．7、二次函数()223+-=x y 的对称轴是__________．8、函数()132+--=x y 中，当x _____时，y 随x 的增大而减小．9、将322+-=x x y 化为()k h x a y +-=2的形式，则=y _____________． 考点三：二次函数平移问题：y O平移法则：遵循“左加右减，上加下减”原则，左右针对x ，上下针对y 。
1、抛物线2x y =向左平移4个单位，再向上平移3个单位可以得到抛物线__________________的图像． 2、已知k h x a y +-=2)(是由抛物线221x y -=向上平移2个单位，再向右平移1个单位得到的抛物线，求出k 、、h a 的值。
人教版数学九年级上册 第二十二章《二次函数》章节知识点归纳复习总结
人教版数学九年级上学期《二次函数》章节知识点归纳总结一、二次函数概念：1．二次函数的概念：（1）一般地，形如2y ax bx c =++（a b c ，，是常数，a ≠0）的函数，叫做二次函数。
（2）这里需要强调：和一元二次方程类似，二次项系数a ≠0，而b c ，可以为零．二次函数的定义域(x)是全体实数．2. 二次函数 2y ax bx c =++ 的结构特征：（1）等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． （2）a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．3. 二次函数解析式的几种形式（1）一般式：y=ax 2+bx+c （a ，b ，c 为常数，a ≠0） （2）顶点式：y=a(x-h)2+k [抛物线的顶点P （ h ，k ）]（3）交点式：y=a(x-x 1)(x-x 2)[仅限于与x 轴有交点A （x 1，0）和 B （x 2，0）的抛物线]其中x 1,x 2是抛物线与x 轴的交点的横坐标，即一元二次方程ax 2+bx+c ＝0的两个根，a ≠0. x 1,x 2 = (-b ±ac 4b 2-)/2a在三种形式的互相转化中，有如下关系:h= -b / 2a ； k=(4ac-b 2) / 4a ； x 1,x 2 = (-b ±ac 4b 2-) / 2a说明：(1)任何一个二次函数通过配方都可以化为顶点式y＝a(x-h)2+k，抛物线的顶点坐标是(h,k)；(2) 当h＝0时，抛物线y＝ax2+k的顶点在y轴上；当k＝0时，抛物线a(x-h)2的顶点在x轴上；当h＝0且k＝0时，抛物线y＝ax2的顶点在原点；(3) 如果图像经过原点，并且对称轴是y轴，则设y=ax2；如果对称轴是y轴，但不过原点，则设y=ax2+k4.抛物线的性质（1）.抛物线是轴对称图形。
对称轴为直线 x = -b/2a。
对称轴与抛物线唯一的交点为抛物线的顶点P。
新人教版初中数学第二十二章二次函数知识点总结附例题
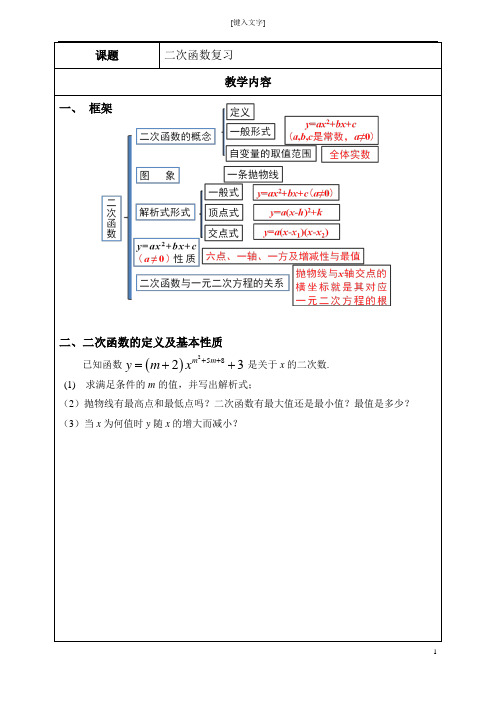
课题 二次函数复习教学内容一、 框架二、二次函数的定义及基本性质已知函数 是关于x 的二次数.(1) 求满足条件的m 的值，并写出解析式；（2）抛物线有最高点和最低点吗？二次函数有最大值还是最小值？最值是多少？ （3）当x 为何值时y 随x 的增大而减小？()25823m m y m x ++=++三、二次函数图象的对称性x2+bx+c的部分图象如图所示，则当y>0时，x的取值范围是.四、二次函数图象的变换抛物线y=a(x-h)2+k的平移规律：左右平移，括号内左加右减；上下平移，括号外上加下减.要得到抛物线y=2(x-4)2-1,可以将抛物线y=2x2 ( )A.向左平移4个单位长度，再向上平移1个单位长度B.向左平移4个单位长度，再向下平移1个单位长度C.向右平移4个单位长度，再向上平移1个单位长度D.向右平移4个单位长度，再向下平移1个单位长度五、二次函数图象与系数的关系抛物线y=ax2+bx+c中的符号问题:①a的符号决定开口方向；②a、b的符号共同决定对称轴的位置，“左同右异”；③c的符号决定抛物线与y轴的交点位置.如图，二次函数y＝ax2＋bx＋c（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，且对称轴为直线x＝1，点B坐标为（-1，0）．则下面的四个结论：①2a＋b＝0；②4a－2b＋c>0；③abc＞0；④当y ＜0时，x＜-1或x＞3．其中正确的是（）A.①②B. ①③C.①④D. ②③如图，函数y=ax2-2x+1和y=ax+a（a是常数，且a≠0)在同一平面直角坐标系的图象可能是（）六、二次函数与一元二次方程的关系已知抛物线y=ax2+bx+c的图象如图所示，则关于x的方程ax2+bx+c-8=0的根的情况是（）A.有两个不相等的正实数根B.有两个异号实数根C.有两个相等的实数根D.没有实数根七、待定系数法求二次函数的解析式你能求出图中抛物线的解析式吗？课堂总结。
第22章《二次函数》全章小结pp
2．练习，巩固所学二次函数内容
问题2 用配方法求出函数 y = -2x 2 - 4x + 6 的图象的对称 轴、顶点坐标，画出函数图象，并说明图象是由抛物线 y = -2x 2 经过怎样的平移得到的．
2 （x + 1） +8 y = -2
（ -1 ， 8）
2．练习，巩固所学二次函数内容
y 8
6
4
S = x（6 - x）= - x 2 + 6x（0＜x＜6）． （2）请你设计一个方案，使获得的设计费最多， 并求出这个设计费用．
当 x = 3 时，设计费最多，为 9 000 元．
2．练习，巩固所学二次函数内容
问题5 某商场销售一批名牌衬衫，平均每天可售出 20 件， 进价是每件 80 元，售价是每件 120 元，为了扩大销售， 增加盈利， 减少库存， 商场决定采取适当的降价措施， 经调查发现，如果每件衬衫降低 1 元， 商场平均每天可 多售出 2 件，但每件最低价不得低于 108 元． （1）若每件衬衫降低 x 元（x 取整数），商场平均 每天盈利 y 元， 试写出 y 与 x 之间的函数关系式，并写 出自变量 x 的取值范围．
1．复习知识，回顾方法
问题1 （1）二次函数的定义：_____________； （2）二次函数的图象： ① 开口方向、对称轴、顶点坐标 名称 表达式 开口方向 对称轴 顶点坐标 一般式
顶点式 ② 与坐标轴的交点： 与 x 轴的公共点坐标__________，与 y 轴的公共点 坐标_______________．
结论:①ab<0;②b2>4a;③0<a+b+c<2;④0<b<1;⑤当x&g A.5个 C.3个 B.4个 D.2个 )
2024九年级数学上册“第二十二章 二次函数”必背知识点
2024九年级数学上册“第二十二章二次函数”必背知识点一、二次函数的定义与表达式定义：一般地，自变量x和因变量y之间存在如下关系：y = ax² + bx + c（a, b, c为常数，a ≠ 0）。
这样的函数称为二次函数，其中a决定函数的开口方向，b和a共同决定对称轴的位置，c决定抛物线与y轴的交点。
三种表达式：1. 一般式：y = ax² + bx + c （a, b, c为常数，a ≠ 0）。
2. 顶点式：y = a(x - h)² + k，其中(h, k)为抛物线的顶点坐标。
3. 交点式：y = a(x - x₁)(x - x₂)，仅限于与x轴有交点A(x₁, 0)和B(x₂, 0)的抛物线。
二、二次函数的图像与性质图像：二次函数的图像是一条抛物线。
开口方向与大小：由二次项系数a决定。
当a > 0时，开口向上；当a < 0时，开口向下。
|a|越大，开口越小；|a|越小，开口越大。
对称轴：1. 一般式：对称轴为直线x = -b/2a。
2. 顶点式：对称轴为直线x = h。
3. 交点式：对称轴为直线x = (x₁ + x₂)/2。
顶点坐标：1. 顶点式直接给出为(h, k)。
2. 一般式可通过公式计算得到(-b/2a, (4ac - b²)/4a)。
最值：1. 当a > 0时，函数有最小值，最小值为(4ac - b²)/4a，此时x = -b/2a。
2. 当a < 0时，函数有最大值，最大值为(4ac - b²)/4a，此时x = -b/2a。
三、二次函数与一元二次方程当二次函数y = ax² + bx + c中y = 0时，即转化为一元二次方程ax² + bx + c = 0。
函数图像与x轴的交点即为该方程的根。
根据判别式Δ = b² - 4ac的值，可以判断抛物线与x轴的交点个数：1. Δ > 0时，抛物线与x轴有两个交点。
初中数学第二十二单元 二次函数知识点总结
- 1 -第二十二单元 二次函数一、二次函数概念：1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。
这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． 2. 二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2．⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项． 二、二次函数的基本形式二次函数的基本形式()2y a x h k =-+的性质： a 的绝对值越大，抛物线的开口越小。
三、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：向右(h >0)【或左(h <0)】平移 |k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向右(h >0)【或左(h <0)】平移|k|个单位向右(h >0)【或左(h <0)】平移|k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向上(k >0)【或向下(k <0)】平移|k |个单位y=a (x-h )2+ky=a (x-h )2y=ax 2+ky=ax 22. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”． 概括成八个字“左加右减，上加下减”． 方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中a 的符号开口方向 顶点坐标 对称轴 性质0a > 向上()h k ， X=hx h >时，y 随x 的增大而增大；x h <时，y随x 的增大而减小；x h =时，y 有最小值k ．0a <向下 ()h k ，X=hx h >时，y 随x 的增大而减小；x h <时，y随x 的增大而增大；x h =时，y 有最大值k ．- 2 -2424b ac b h k a a-=-=，． 五、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y a x b x c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a=-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，． 当2b x a <-时，y 随x 的增大而减小；当2bx a>-时，y 随x 的增大而增大；当2b x a =-时，y 有最小值244ac ba-． 2. 当0a <时，抛物线开口向下，对称轴为2bx a=-，顶点坐标为2424b ac b aa ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而增大；当2bx a >-时，y 随x 的增大而减小；当2b x a =-时，y 有最大值244ac ba-．七、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴．ab 的符号的判定：对称轴abx 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异”)04(2422≥--±-=ac b aac b b x二次函数解析式的确定：一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．九、一元二次方程根与系数的关系如果方程)0(02≠=++a c bx ax 的两个实数根是21x x ，，那么a b x x -=+21，acx x =21。
第22章 二次函数小结第1课时 知识结构与要点-九年级数学上册课件(人教版)
解：∵ 当 x = −2 或 4 时，y = −16，且函数的最大值为 2.
∴ 对称轴为直线
.
∴ 顶点为 (1，2).
设二次函数解析式为 y = a(x − 1)2 + 2，
把 (−2，−16) 代入得 −16 = 9a + 2，解得 a = −2.
∴ y = −2(x − 1)2 + 2.
∴ 二次函数解析式为 y = −2x2 + 4x.
6 已知二次函数 y = x2 − 2mx + m2 − 1( m 为常数).
求证：不论 m 为何值，该函数的图象与 x 轴总有两个公共点.
证明：(−2m)2 − 4(m2 − 1) = 4＞0，
故不论 m 为何值，该函数的图象与 x 轴总有两个公共点.
时，y 随 x 的增大而增大；
2
x＞−
时，y 随 x 的增大而减小.
2
当 x＜函数与一元二次方程的关系
抛物线与 x 轴的交点
数形结合
2 + bx + c
y
=
ax
y
y >0
y >0
x1 O
一元二次方程 ax2 + bx + c = 0 的根
y <0
x2
x
二次函数 y = ax2
)
2
4
对称轴：x=2
3.一般式 y = ax²+ bx + c (a≠0) 的图和性质
a> 0
a< 0
y
O
当
x=−
2
y
x
时，y最小值 =
第二十二章《二次函数》知识点总结人教版数学九年级上册
《二次函数》知识点总结【知识点1 二次函数的表达式】1. 一般式： . 顶点坐标： . 对称轴： .2. 顶点式： .顶点坐标： . 对称轴： . 【知识点2 二次函数的图象与性质】 1. 二次项系数a 决定抛物线的 开口方向 ；①当0>a 时，抛物线的 ； ②当0<a 时，抛物线的 ； ③ ||a 越大，抛物线的开口 .3.常数项c 决定抛物线 与y 轴 交点的位置 . ①当0=c ，抛物线与y 轴交于 ； ②当0>c ，抛物线与y 轴交于 ； ③当0<c ，抛物线与y 轴交于 .5.根据a 、b 、c 的符号，画出二次函数的草图:①已知 a <0、b <0、c <0 ②已知 a>0、b <0、c >0 6.描述下面二次函数c bx ax y ++=2的增减性： 【知识点3 抛物线与坐标轴的交点】 1. 抛物线c bx ax y ++=2与x 轴的交点个数，即02=++c bx ax . ①当 ，抛物线与x 轴有两个交点； ②当 ，抛物线与x 轴有1个交点； ③当 ，抛物线与x 轴有没有交点；2.求抛物线c bx ax y ++=2与x 轴的交点的过程： 3.求抛物线c bx ax y ++=2与y 轴的交点的过程：4.函数 y = ax 2 + bx + c 的图象如图，那么 ①方程 ax 2 + bx + c =2 的根是 ______________;2.系数a 和b 共同决定抛物线 对称轴的位置 . ①a 和b 同号，对称轴在原点的 ； ②a 和b 异号， .4.根据图象判断出a 、b 、c 的符号：方法总结：第一步：求出对称轴；第二步：用箭头在对称轴两侧标出上升和下降；第三步：描述增减性.①当 时，随的增大而减小； ②当 时， 随的增大而增大；∵轴上的点， 为零，∴ . ∵轴上的点， 为零，∴ .②不等式 ax 2 + bx + c >0 的解集是 ___________; ③不等式 ax 2 + bx + c <2 的解集是 _________.④ a + b + c 0 ，4a 2 b + c 0 ， 9a +3 b + c 0 .【知识点4 抛物线的平移】二次函数 y = ax 2 + bx + c 的平移口诀：“上下平移， ；左右平移， .” 【 * *知识点5 抛物线的对称 ** 】抛物线c bx ax y ++=2关于x 轴对称的解析式为 . 抛物线c bx ax y ++=2关于y 轴对称的解析式为 . 【 * *知识点6 二次函数图象的画法 ** 】 画出二次函数3-2-2x x y =的的图象.【典型例题 】1.m2+1+2x −是二次函数，则m 的值为( )C. −1D. 1或−12.【求顶点坐标 】抛物线y =2(x −3)4的顶点坐标是( ) A. (3,4)B. (−3,4)C. (3,−4)D. (2,4)3.【与坐标轴的交点 】抛物线y =−x 2+4x −4与坐标轴的交点个数为( ) A. 0B. 1C. 2D. 34.【平移】将函数y =x 2的图象用下列方法平移后，所得的图象不经过点A(1,4)的方法是( ) A. 向左平移1个单位 B. 向右平移3个单位C. 向上平移3个单位D. 向下平移1个单位5.【平移】抛物线y =x 2+6x +7可由抛物线y =x 2如何平移得到的( )A. 先向左平移3个单位，再向下平移2个单位B. 先向左平移6个单位，再向上平移7个单位C. 先向上平移2个单位，再向左平移3个单位D. 先向右平移3个单位，再向上平移2个单位 6.【图象与性质】对于抛物线y =−3(x +1)2−2，下列说法正确的是( ) A. 抛物线开口向上 B. 当x >−1时，y 随x 的增大而减小 C. 函数最小值为−2D. 顶点坐标为(1,−2)7.【增减性】已知(−3,y 1)，(−1,y 2)，(2,y 3)是抛物线y =−3x 2+6x +m 上的三个点.则( ) A. y 1<y 3<y 2B. y 3<y 2<y 1C. y 1<y 2<y 3D. y 2<y 1<y 38.【最值】已知二次函数y=x2−4x+2，关于该函数在−1≤x≤3的取值范围内，下列说法正确的是( )A. 有最大值−1，有最小值−2B. 有最大值0，有最小值−1C. 有最大值7，有最小值−1D. 有最大值7，有最小值−29.【系数与图象】二次函数y=ax2+bx+c(a≠0)与一次函数y=ax+c在同一坐标系中的图象大致为( )A. B. C. D.10.【求解析式】如图所示，已知二次函数y=ax2+bx+c的图象，求二次函数的解析式．11.如图，已知二次函数y=ax2−4x+c的图象经过点A(−1,−1)和点B(3,−9)．(1)求该二次函数的解析式、对称轴及顶点坐标；(2)点C是抛物线与x轴的一个交点，点D是抛物线与y轴的交点，求三角形ACD 的面积；(3)已知点M（x1，y1）和N（1+x1，y2）在抛物线对称轴的右侧，判段y1和y2的大小.12.在运动会比赛时，九年级的一名男同学推铅球，已知铅球经过的路线是某二次函数图象的一部分(如图所示)，如果这名男同学的出手处A点的坐标为(0,2)，铅球路线的最高处B点的坐标为(6,5)．(1)求出这个二次函数的解析式；(2)请求出这名男同学比赛时的成绩？13.如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m．(1)建立平面直角坐标系，求抛物线的解析式；(2)如果水面下降1m，则水面宽度是多少米？14.某商场一种商品的进价为每件30元，售价为每件50元．每天可以销售48件，为尽快减少库存，商场决定降价促销．(1)若该商品连续两次下调相同的百分率后售价降至每件40.5元，求两次下降的百分率；(2)经调查，若该商品每降价2元，每天可多销售16件，那么每天要想获得最大利润，每件售价应多少元？最大利润是多少？。
人教版九年级数学上册第二十二章二次函数章末小结课件
b
如果a＞0，当 x＜ 时，y随x的增大而减小，当 x＞ 时，y随x的增大而
2a
2a
增大；
b
b
x
＜
x
＞
如果a＜0，当
时，y随x的增大而增大，当
时，y随x的增大而
2a
2a
减小.
8.二次函数y=ax2+bx+c的图象与a、b、c的关系：
向上
向下
y
左
右
正
负
9.二次函数解析式的类型及适用情况：
2
(h＞0、k＞0)
y a x h
向
上
或
下
)
)
平
移
k
个
单
位
向左(或右)
平移h个单位
(
(
向
上
或
下
2
向左(或右)
平移h个单位
平
移
k
个
单
位
2
y a x h k
2
7.二次函数y=ax2+bx+c的性质：
y ax 2 bx c
配 方
b 4ac b 2
y a x
2a
4a
2
b 4ac b 2
b
对称轴是直线 x ，顶点是 ，
.
2a
4a
2a
2
b
4ac
b
如果a＞0时，那么当 x 时，y最小值=
；
2a
4a
b
4ac b 2
如果a＜0时，那么当 x 时，y最大值=
第22章《二次函数》小结与复习课件
(2)∵∠F =∠A = 45°，∠CBF =∠ABC = 90°，
∴∠BGF =∠F = 45°，1BG = BF1 = 2x -130. 1
所= 以 32Sx△2D+EF60-xS-△4G5BF0.= 2DE2 - 2BF2 = 2 x2 - 2 (2x - 30)2
若点 A(x1，y1)，B(x2，y2)在此函数图象上，且
x1＜x2＜1，则 y1 与 y2 的大小关系是 ( B )
A．y1≤y2 B．y1＜y2 C．y1≤y2 D．y1＞y2
x
【解析】由图象看出，抛物线开口向下，对称轴是 x＝1， 当 x＜1时，y 随 x 的增大而增大．∵x1＜x2＜1，∴ y1＜y2.
解：W = (x-60)•(-x+120) = -x2+180x-7200 = -(x-90)2 +900，
∵抛物线的开口向下， ∴当 x＜90 时，W 随 x 的增大而增大. 而 60≤x≤60×(1 + 45%)，即 60≤x≤87. ∴当 x = 87 时，W 有最大值，
此时 W = -(87- 90)2 + 900 = 891.
售量 y (件)与销售单价 x (元)符合一次函数 y＝kx＋b，且 x＝65
时，y＝55；x＝75 时，y＝45.
(1) 求一次函数的解析式；
解：根据题意，得
65k 75k
b b
55，解得
45.
k
=
-1，b
=
120.
故所求一次函数的解析式为 y = -x + 120.
第二十二章 二次函数小结与复习
C．y1≥y2
D．y1>y2
【解析】由图像看出，抛物线开口向下，对称轴是x
＝1，当x＜1时，y随x的增大而增大．
∵x1<x2<1，∴y1<y2 . 故选B.
针对训练 针对训 练 2.下列函数中，当x＞0时，y值随x值增大而减小的是 （ D） A. y= x
2
B.y=x-1
3 C. y x 4
D.y=-3x2
第二十二章 二次函数
小结与复习
要点梳理 考点讲练 课堂小结 课后作业
要点梳理
1.二次函数的概念
一般地，形如 y＝ax2＋bx＋c
数，
(a，b，c是常
__)的函数，叫做二次函数． a ≠０
[注意 ] (1)等号右边必须是整式； (2)自变量的 最高次数是2；(3)当b＝0，c＝0时，y＝ax2是特殊 的二次函数．
针对训练 3.已知二次函数y=－x2＋2bx＋c，当x＞1时，y的值随
x值的增大而减小，则实数b的取值范围是（
A．b≥－1 B．b≤－1
）
C．b≥1
D．b≤1
解析：∵二次项系数为－1＜0，∴抛物线开口向下，
在对称轴右侧，y的值随x值的增大而减小，由题设可知，
当x＞1时，y的值随x值的增大而减小，∴抛物线y=－x2
情况:有两个交点,有两个重合的交点,没有交点.当二
次函数y＝ax2＋bx＋c的图象和x轴有交点时,交点的
横坐标就是当y=0时自变量x的值,即一元二次方程
ax2＋bx＋c=0的根.
二次函数y＝ax2 一元二次方程 一元二次方程 ＋bx＋c的图像和 ax2＋bx＋c=0的 ax2＋bx＋c=0根的 x轴交点 根 判别式（b2-4ac） 有两个交点 有两个重合 的交点 没有交点 有两个相异的 实数根 有两个相等的 实数根 b2-4ac > 0 b2-4ac = 0
第22章二次函数全章知识点归纳总结人教版九年级数学上册
初三上学期二次函数全章知识点归纳总结【例1】下列函数是二次函数的有（）①y＝（x+1）2﹣x2；②y＝﹣3x2+5；③y＝x3﹣2x；④y＝x2−1x+3．A．1个B．2个C．3个D．4个【变式11】下列函数中，是二次函数的有（）①y=√x2+2；②y＝﹣x2﹣3x；③y＝x（x2+x+1）；④y=11+x2；⑤y＝﹣x+x2．A．1个B．2个C．3个D．4个【例2】若y＝（a+1）x|a+3|﹣x+3是关于x的二次函数，则a的值是（）A．1B．﹣5C．﹣1D．﹣5或﹣1【变式21】函数y＝（a﹣5）x a2+4a+5+2x﹣1，当a＝时，它是一次函数；当a＝时，它是二次函数．【例3】关于函数y＝（500﹣10x）（40+x），下列说法不正确的是（）A．y是x的二次函数B．二次项系数是﹣10C．一次项是100D．常数项是20000【例4】下列具有二次函数关系的是（）A．正方形的周长y与边长x B．速度一定时，路程s与时间tC．正方形的面积y与边长x D．三角形的高一定时，面积y与底边长x【例5】某种商品的价格是2元，准备进行两次降价．如果每次降价的百分率都是x，经过两次降价后的价格y（单位：元）随每次降价的百分率x的变化而变化，则y关于x的函数解析式是（）A．y＝2（x+1）2B．y＝2（1﹣x）2C．y＝（x+1）2D．y＝（x﹣1）2【变式51】据省统计局公布的数据，合肥市2021年第一季度GDP总值约为2.4千亿元人民币，若我市第三季度GDP总值为y千亿元人民币，平均每个季度GDP增长的百分率为x，则y关于x的函数表达式是（）A．y＝2.4（1+2x）B．y＝2.4（1﹣x）2C．y＝2.4（1+x）2D．y＝2.4+2.4（1+x）+2.4（1+x）【例1】用配方法将下列函数化成y＝a（x+h）2+k的形式，并指出抛物线的开口方向，对称轴和顶点坐标．（1）y=12x2﹣2x+3；（2）y＝（1﹣x）（1+2x）．【变式11】把下列二次函数化成顶点式，即y＝a（x+m）2+k的形式，并写出他们顶点坐标及最大值或最小值．（1）y＝﹣2x﹣3+12x2（2）y＝﹣2x2﹣5x+7【变式12】用配方法可以解一元二次方程，还可以用它来解决很多问题例如：因为5a2≥0，所以5a2+1≥1，即：当a＝0时，5a2+1有最小值1．同样，因为﹣5（a2+1）≤0，所以﹣5（a2+1）+6≤6有最大值1，即当a＝1时，﹣5（a2+1）+6有最大值6．（1）当x＝时，代数式﹣3（x﹣2）2+4有最（填写大或小）值为．（2）当x＝时，代数式﹣x2+4x+4有最（填写大或小）值为．（3）矩形花园的一面靠墙，另外三面的栅栏所围成的总长度是14m，当花园与墙相邻的边长为多少时，花园的面积最大？最大面积是多少？利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点. 【例2】已知二次函数y ＝ax 2+bx +c 中，函数y 与自变量x 的部分对应值如下表：x … 0 1 2 3 4 … y…52125…（1）求该二次函数的表达式； （2）当x ＝6时，求y 的值；（3）在所给坐标系中画出该二次函数的图象．【变式21】如图，已知二次函数y =−12x 2+bx +c 的图象经过A （2，0）、B （0，﹣6）两点． （1）求这个二次函数的解析式；（2）求该二次函数图象的顶点坐标、对称轴以及二次函数图象与x 轴的另一个交点； （3）在右图的直角坐标系内描点画出该二次函数的图象及对称轴． 【知识点3 二次函数的图象与各系数之间的关系】在y 轴的右侧则0<ab ，概括的说就是“左同右异” ③常数项c ：总结起来，c 决定了抛物线与y 轴交点的位置． 【知识点4 二次函数图象的平移变换】 （1）平移步骤：变式21例2①将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ①保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【例4】把抛物线y ＝ax 2+bx +c 的图象先向右平移2个单位，再向上平移2个单位，所得的图象的解析式是y ＝（x ﹣3）2+5，则a +b +c ＝ ．【变式41】要得到函数y ＝﹣（x ﹣2）2+3的图象，可以将函数y ＝﹣（x ﹣3）2的图象（ ） A ．向右平移1个单位，再向上平移3个单位 B ．向右平移1个单位，再向下平移3个单位 C ．向左平移1个单位，再向上平移3个单位 D ．向左平移1个单位，再向下平移3个单位 【知识点5 二次函数图象的对称变换】 （1）关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；（2）关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；（3）关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； （4）关于顶点对称（即：抛物线绕顶点旋转180°）()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．向上 向下【例1】已知二次函数y ＝x 2﹣2x ﹣3的自变量x 1，x 2，x 3对应的函数值分别为y 1，y 2，y 3．当﹣1＜x 1＜0，1＜x 2＜2，x 3＞3时，y 1，y 2，y 3三者之间的大小关系是（ ） A ．y 1＜y 2＜y 3B ．y 2＜y 3＜y 1C ．y 3＜y 1＜y 2D ．y 2＜y 1＜y 3【例2】在二次函数y ＝﹣x 2+bx +c 中，函数y 与自变量x 的部分对应值如下表：则m 、n 的大小关系为x … ﹣1 1 3 4 … y … ﹣6m n﹣6…A ．m ＜nB ．m ＞nC ．m ＝nD ．无法确定0a >0a <【变式21】二次函数y＝ax2+bx+c（a≠0）中x，y的部分对应值如下表：x…﹣2﹣1012…y…0﹣4﹣6﹣6﹣4…则该二次函数图象的对称轴为（）A．y轴B．直线x=12C．直线x＝1D．直线x=32【知识点1 二次函数图象与x轴的交点情况决定一元二次方程根的情况】二次函数的图象【例1】抛物线y＝（x﹣x1）（x﹣x2）+mx+n与x轴只有一个交点（x1，0）．下列式子中正确的是（）A．x1﹣x2＝m B．x2﹣x1＝m C．m（x1﹣x2）＝n D．m（x1+x2）＝n【变式11】抛物线y＝x2+2x﹣3与坐标轴的交点个数有（）A．0个B．1个C．2个D．3个【例2】二次函数与一元二次方程有着紧密的联系，一元二次方程问题有时可以转化为二次函数问题．请你根据这句话所提供的思想方法解决如下问题：若s，t（s＜t）是关于x的方程1+（x﹣m）（x﹣n）＝0的两根，且m＜n，则m，n，s，t的大小关系是（）A．s＜m＜n＜t B．m＜s＜n＜t C．m＜s＜t＜n D．s＜m＜t＜n【知识点1 解二次函数的实际应用问题的一般步骤】审：审清题意，弄清题中涉及哪些量，已知量有几个，已知量与变量之间的基本关系是什么，找出等量关系（即函数关系）；设：设出两个变量，注意分清自变量和因变量，同时还要注意所设变量的单位要准确；列：列函数解析式，抓住题中含有等量关系的语句，将此语句抽象为含变量的等式，这就是二次函数；解：按题目要求结合二次函数的性质解答相应的问题；检：检验所得的解，是否符合实际，即是否为所提问题的答案；答：写出答案.【例1】为优化迪荡湖公园的灯光布局，需要在一处岸堤（岸堤足够长）为一边，用总长为80m的灯带在湖中围成了如图所示的①②③三块灯光喷泉的矩形区域，且要求这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．（1）求y与x之间的函数关系式，并注明自变量x的取值范围；（2）x为何值时，y有最大值？最大值是多少？【变式11】爱动脑筋的小明在学过用配方法解一元二次方程后，他发现二次三项式也可以配方，从而解决一些问题．例如：x2﹣6x+10＝（x2﹣6x+9﹣9）+10＝（x﹣3）2﹣9+10＝（x﹣3）2+1≥1；因此x2﹣6x+10有最小值是1，只有当x＝3时，才能得到这个式子的最小值1．同样﹣3x2﹣6x+5＝﹣3（x2+2x+1﹣1）+5＝﹣3（x+1）2+8，因此﹣3x2﹣6x+5有最大值是8，只有当x＝﹣1时，才能得到这个式子的最小值8．（1）当x＝时，代数式﹣2（x﹣3）2+5有最大值为．（2）当x＝时，代数式2x2+4x+3有最小值为．（3）矩形自行车场地ABCD一边靠墙（墙长10m），在AB和BC边各开一个1米宽的小门（不用木板），现有能围成14m长的木板，当AD长为多少时，自行车场地的面积最大？最大面积是多少？【例2】如图，在矩形ABCD中，AB＝12cm，BC＝9cm．P、Q两点同时从点B、D出发，分别沿BA、DA 方向匀速运动（当P运动到A时，P、Q同时停止运动），已知P点的速度比Q点大1cm/s，设P点的运动时间为x秒，△P AQ的面积为ycm2，（1）经过3秒△P AQ的面积是矩形ABCD面积的1时，求P、Q两点的运动速度分别是多少？3（2）以（1）中求出的结论为条件，写出y与x的函数关系式，并求出自变量x的取值范围．【变式31】廊桥是我国古老的文化遗产，如图，是某座抛物线型的廊桥示意图．已知水面AB宽40米，抛物线最高点C到水面AB的距离为10米，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，求这两盏灯的水平距离EF．（结果保留根号）。
九年级数学上册第二十二章二次函数知识点总结归纳(带答案)
九年级数学上册第二十二章二次函数知识点总结归纳单选题1、定义：我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”．如图，在正方形OABC 中，点A (0,2)，点C (2,0)，则互异二次函数y =(x −m )2−m 与正方形OABC 有交点时m 的最大值和最小值分别是（ ）A ．4，-1B ．5−√172，-1C ．4，0D ．5+√172，-1 答案：D分析：分别讨论当对称轴位于y 轴左侧、位于y 轴与正方形对称轴x =1之间、位于直线x =1和x =2之间、位于直线x =2右侧共四种情况，列出它们有交点时满足的条件，得到关于m 的不等式组，求解即可． 解：由正方形的性质可知：B （2,2）；若二次函数y =(x −m )2−m 与正方形OABC 有交点,则共有以下四种情况:当m ≤0时，则当A 点在抛物线上或上方时，它们有交点，此时有{m ≤0m 2−m ≤2， 解得：−1≤m <0；当0<m ≤1时，则当C 点在抛物线上或下方时，它们有交点，此时有{0<m ≤1(2−m )2−m ≥0， 解得：0<m ≤1；当1<m ≤2时，则当O 点位于抛物线上或下方时，它们有交点，此时有{1<m ≤2m 2−m >0， 解得：1<m ≤2；当m >2时，则当O 点在抛物线上或下方且B 点在抛物线上或上方时，它们才有交点，此时有{m >2m 2−m ≥0(2−m )2−m ≤2 ，解得：2<m≤5+√17；2，−1．综上可得：m的最大值和最小值分别是5+√172故选：D．小提示：本题考查了抛物线与正方形的交点问题，涉及到列一元一次不等式组等内容，解决本题的关键是能根据图像分析交点情况，并进行分类讨论，本题综合性较强，需要一定的分析能力与图形感知力，因此对学生的思维要求较高，本题蕴含了分类讨论和数形结合的思想方法等．2、如图，二次函数y=ax2+bx+c的图象关于直线x=1对称，与x轴交于A(x1,0)，B(x2,0)两点，若−2< x1<−1，则下列四个结论：①3<x2<4，②3a+2b>0，③b2>a+c+4ac，④a>c>b．正确结论的个数为（）A．1个B．2个C．3个D．4个答案：B分析：根据二次函数的对称性，即可判断①；由开口方向和对称轴即可判断②；根据抛物线与x轴的交点已经x=-1时的函数的取值，即可判断③；根据抛物线的开口方向、对称轴，与y轴的交点以及a－b＋c＜0，即可判断④．∵对称轴为直线x=1，-2<x1<-1，∴3＜x2＜4，①正确，∵−b= 1，2a∴b=- 2а，∴3a＋2b= 3a-4a= -a，∵a＞0，∴3a+2b<0，②错误；∵抛物线与x轴有两个交点，∴b2 - 4ac > 0，根据题意可知x=-1时，y<0，∴a－b＋c<0，∴a＋c<b，∵a＞0，∴b=-2a<0，∴a＋c<0，∴b2 -4ac > a+ c，∴b2＞a＋c＋4ac，③正确；∵抛物线开口向上，与y轴的交点在x轴下方，∴a＞0，c<0，∴a>c，∵a-b＋c<0，b=-2a，∴3a+c<0，∴c<-3a，∴b=–2a，∴b＞c，以④错误；故选B小提示：本题主要考查图象与二次函数系数之间的关系，解题的关键是掌握数形结合思想的应用，注意掌握二次函数图象与系数的关系，掌握二次函数的对称性．3、抛物线y＝x2+3上有两点A（x1，y1），B（x2，y2），若y1＜y2，则下列结论正确的是( )A．0≤x1＜x2B．x2＜x1≤0C．x2＜x1≤0或0≤x1＜x2D．以上都不对答案：D分析：根据二次函数图象及性质，即可判定．∵抛物线y＝x2+3开口向上，在其图象上有两点A（x1，y1），B（x2，y2），且y1＜y2，∴|x1|＜|x2|，∴0≤x1＜x2，或x2＜x1≤0，或x2＞0，x1≤0且x2+x1＞0，或x2＜0，x1＞0且x2+x1＜0，故选：D．小提示：本题考查了二次函数的图象及性质，熟练掌握和运用二次函数的图象及性质是解决本题的关键．4、如图，某公司准备在一个等腰直角三角形ABC的绿地上建造一个矩形的休闲书吧PMBN，其中点P在AC上，点NM分别在BC，AB上，记PM=x，PN=y，图中阴影部分的面积为S，若NP在一定范围内变化，则y与x，S与x满足的函数关系分别是（）A．反比例函数关系，一次函数关系B．二次函数关系，一次函数关系C．一次函数关系，反比例函数关系D．一次函数关系，二次函数关系答案：D分析：先求出AM=PM，利用矩形的性质得出y=﹣x+m，最后利用S=S△ABC－S矩形PMBN得出结论．设AB=m（m为常数）．在△AMP中，∠A=45°，AM⊥PM，∴△AMP为等腰直角三角形，∴AM=PM，又∵在矩形PMBN中，PN=BM，∴x+y=PM+PN=AM+BM=AB=m，即y=﹣x+m，∴y与x成一次函数关系，∴S =S △ABC －S 矩形PMBN =12m 2-xy =12m 2-x （﹣x +m ）=x 2-mx +12m 2， ∴S 与x 成二次函数关系．故选D ．小提示：本题考查了一次函数的实际应用及二次函数的实际应用，解题的关键是掌握根据题意求出y 与x 之间的函数关系式．5、二次函数y =x 的图象经过的象限是（ ）A ．第一、二象限B ．第一、三象限C ．第二、四象限D ．第三、四象限答案：A分析：由抛物线解析式可得抛物线开口方向及顶点坐标，进而求解．∵y =x 2， ∴抛物线开口向上，顶点坐标为（0，0），∴抛物线经过第一，二象限．故选：A ．小提示：本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系．6、关于x 的方程ax 2+bx +c =0有两个不相等的实根x 1、x 2，若x 2=2x 1，则4b −9ac 的最大值是（ ）A ．1B ．√2C ．√3D ．2答案：D分析：根据一元二次方程根与系数的关系，求得两根之和和两根之积，再根据两根关系，求得系数的关系，代入代数式，配方法化简求值即可．解：由方程ax 2+bx +c =0有两个不相等的实根x 1、x 2可得，a ≠0，x 1+x 2=−b a ，x 1x 2=c a ∵x 2=2x 1，可得3x 1=−b a ，2x 12=c a ，即2(−b 3a )2=c a 化简得9ac =2b 2 则4b −9ac =−2b 2+4b =−2(b 2−2b)=−2(b −1)2+2故4b −9ac 最大值为2故选D小提示：此题考查了一元二次方程根与系数的关系，涉及了配方法求解代数式的最大值，根据一元二次方程根与系数的关系得到系数的关系是解题的关键．7、已知抛物线y=x2+kx−k2的对称轴在y轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则k的值是（）A．−5或2B．−5C．2D．−2答案：B分析：根据二次函数图象左加右减，上加下减的平移规律进行解答即可．解：函数y=x2+kx−k2向右平移3个单位，得：y=(x−3)2+k(x−3)−k2；再向上平移1个单位，得：y=(x−3)2+k(x−3)−k2+1，∵得到的抛物线正好经过坐标原点∴0=(0−3)2+k(0−3)−k2+1即k2+3k−10=0解得：k=−5或k=2∵抛物线y=x2+kx−k2的对称轴在y轴右侧∴x=−k＞02∴k＜0∴k=−5故选：B．小提示：此题主要考查了函数图象的平移，要求熟练掌握平移的规律：左加右减，上加下减．8、在同一平面直角坐标系中，函数y=ax2+bx与y＝ax＋b的图象不可能是( )A．B．C．D．答案：D分析：根据二次函数与一次函数的图象与性质进行判断即可．解：当a>0，b>0时，y=ax2+bx的开口上，与x轴的一个交点在x轴的负半轴，y=ax+b经过第一、二、三象限，且两函数图象交于x的负半轴，无选项符合；当a>0，b<0时，y=ax2+bx的开口向上，与x轴的一个交点在x轴的正半轴，y=ax+b经过第一、三、四象限，且两函数图象交于x的正半轴，故选项A正确，不符合题意题意；当a<0，b>0时，y=ax2+bx的开口向下，与x轴的一个交点在x轴的正半轴，y=ax+b经过第一、二、四象限，且两函数图象交于x的正半轴，C选项正确，不符合题意；当a<0，b<0时，y=ax2+bx的开口向下，与x轴的一个交点在x轴的负半轴，y=ax+b经过第二、三、四象限，B选项正确，不符合题意；只有选项D的两图象的交点不经过x轴，故选D.小提示：本题考查二次函数与一次函数图象的性质，解题的关键是根据a、b与0的大小关系进行分类讨论．9、已知二次函数y=mx2−4m2x−3（m为常数，m≠0），点P(x p,y p)是该函数图象上一点，当0≤x p≤4时，y p≤−3，则m的取值范围是（）A．m≥1或m<0B．m≥1C．m≤−1或m>0D．m≤−1答案：A分析：先求出抛物线的对称轴及抛物线与y轴的交点坐标，再分两种情况：m>0或m<0，根据二次函数的性质求得m的不同取值范围便可．解：∵二次函数y=mx2−4m2x−3，∴对称轴为x=2m，抛物线与y轴的交点为(0,−3)，∵点P(x p,y p)是该函数图象上一点，当0≤x p≤4时，y p≤−3，∴①当m>0时，对称轴x=2m>0，此时，当x=4时，y≤−3，即m⋅42−4m2⋅4−3≤−3，解得m≥1；②当m<0时，对称轴x=2m<0，当0≤x≤4时，y随x增大而减小，则当0≤x p≤4时，y p≤−3恒成立；综上，m的取值范围是：m≥1或m<0．故选：A．小提示：本题考查了二次函数的性质，关键是分情况讨论．10、如图，某涵洞的截面是抛物线形，现测得水面宽AB＝1.6m，涵洞顶点O与水面的距离CO是2m，则当水位上升1.5m时，水面的宽度为（）A．0.4mB．0.6mC．0.8mD．1m答案：C分析：根据题意可建立平面直角坐标系，然后设函数关系式为y=ax2，由题意可知A(−0.8,−2)，代入求解函数解析式，进而问题可求解．解：建立如图所示的坐标系：设函数关系式为y=ax2，由题意得：A(−0.8,−2)，∴−2=0.8×0.8×a，，解得：a=−258∴y=−25x2，8x2，当y=-0.5时，则有−0.5=−258解得：x=±0.4，∴水面的宽度为0.8m；故选C．小提示：本题主要考查二次函数的应用，熟练掌握二次函数的应用是解题的关键．填空题11、已知抛物线y=x2−x−1与x轴的一个交点为(m,0)，则代数式−3m2+3m+2022的值为______．答案：2019分析：先将点（m，0）代入函数解析式，然后求代数式的值即可得出结果．解：将（m，0）代入函数解析式得，m2-m-1=0，∴m2-m=1，∴-3m2+3m+2022=-3（m2-m）+2022=-3+2022=2019．所以答案是：2019．小提示：本题考查了二次函数图象上点的坐标特征及求代数式的值，解题的关键是将点（m，0）代入函数解析式得到有关m的代数式的值．12、如图，在平面直角坐标系中，抛物线y=−x2+2mx+m−2（m为常数，且m>0）与直线y＝2交于A、B两点．若AB＝2，则m的值为______．答案：√21−12分析：设A（x1，2），B（x2，2），抛物线y=−x2+2mx+m−2中，令y=2，得x2−2mx−m+4=0，利用根与系数关系求得AB，可建立关于m的方程并解出即可．解：设A（x1，2），B（x2，2），抛物线y=−x2+2mx+m−2中，令y=2，得：−x2+2mx+m−2=2，即：x2−2mx−m+4=0∴x1+x2=2m,x1x2=−m+4，∴AB=|x2−x1|=√(x2+x1)2−4x1x2=√(2m)2−4(−m+4)=2，∴m2+m−5=0，解得：m1=√21−12,m2=−√21−12(舍去)，所以答案是：√21−12．小提示：本题考查了抛物线与x轴的交点、二次函数与一元二次方程的关系、二次函数图象上点的坐标特征，熟练掌握这三个知识点的综合应用是解题关键．13、平移二次函数的图象，如果有一个点既在平移前的函数图象上，又在平移后的函数图象上，我们把这个点叫做“关联点”．现将二次函数y=x2+2x+c（c为常数）的图象向右平移得到新的抛物线，若“关联点”为(1,2)，则新抛物线的函数表达式为_______．答案：y=(x−3)2−2分析：将（1，2）代入y=x2+2x+c，解得c=-1，设将抛物线y=x2+2x-1=（x+1）2-2，向右平移m个单位，则平移后的抛物线解析式是y=（x+1-m）2-2，然后将（1，2）代入得到关于m的方程，通过解方程求得m的值即可．解：将（1，2）代入y=x2+2x+c，得12+2×1+c=2，解得c=-1．设将抛物线y=x2+2x-1=（x+1）2-2，向右平移m个单位，则平移后的抛物线解析式是y=（x+1-m）2-2，将（1，2）代入，得（1+1-m）2-2=2．整理，得2-m=±2．解得m1=0（舍去），m2=4．故新抛物线的表达式为y=（x-3）2-2．故答案是：y=(x−3)2−2．小提示：本题主要考查了二次函数图象与几何变换，二次函数图象上点的坐标特征以及待定系数法确定函数关系式，解题的关键是理解“关联点”的含义．14、如图是一个横断面为抛物线形状的拱桥，当水面在正常水位的情况下，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．则当水位下降m=________时，水面宽为5m？答案：1.125分析：以抛物线的顶点为原点建立坐标系，则可以设函数的解析式是y=ax2，然后求得水面与抛物线的交点坐标，利用待定系数法求解抛物线的解析式，再利用点的坐标特点即可求解．解：如图，建立如下的坐标系：水面与抛物线的交点坐标是（-2，-2），(2,−2)，设函数的解析式是y=ax2，则4a=-2，解得a=−12，则函数的解析式是y=−12x2．当水面宽为5米时，把x=52代入抛物线的解析式可得：y=12×(52)2=258=3.125,∴3.125−2=1.125（米），所以答案是：1.125．小提示：本题考查了待定系数法求二次函数的解析式，二次函数的性质，建立合适的平面直角坐标系，求得水面与抛物线的交点是解题的关键．15、根据物理学规律，如果不考虑空气阻力，以40m/s的速度将小球沿与地面成30°角的方向击出，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间的函数关系是ℎ=−5t2+20t，当飞行时间t为___________s时，小球达到最高点．答案：2分析：将函数关系式转化为顶点式即可求解．根据题意，有ℎ=−5t2+20t=−5(t−2)2+20，当t=2时，ℎ有最大值．所以答案是：2．小提示：本题考查二次函数解析式的相互转化及应用，解决本题的关键是熟练二次函数解析式的特点及应用．解答题16、某公司电商平台，在2021年五一长假期间，举行了商品打折促销活动，经市场调查发现，某种商品的周销售量y（件）是关于售价x（元/件）的一次函数，下表仅列出了该商品的售价x，周销售量y，周销售利润W（元）的三组对应值数据．（2）若该商品进价a（元/件），售价x为多少时，周销售利润W最大？并求出此时的最大利润；（3）因疫情期间，该商品进价提高了m（元/件）（m>0），公司为回馈消费者，规定该商品售价x不得超过55（元/件），且该商品在今后的销售中，周销售量与售价仍满足（1）中的函数关系，若周销售最大利润是4050元，求m的值．答案：（1）y=−3x+300；（2）售价60元时，周销售利润最大为4800元；（3）m=5分析：（1）①依题意设y=kx+b，解方程组即可得到结论；（2）根据题意得W=(−3x+300)(x−a)，再由表格数据求出a=20，得到W=(−3x+300)(x−20)=−3(x−60)2+4800，根据二次函数的顶点式，求出最值即可；（3）根据题意得W=−3(x−100)(x−20−m)(x⩽55)，由于对称轴是直线x=60+m2>60，根据二次函数的性质即可得到结论．解：（1）设y=kx+b，由题意有{40k+b=180 70k+b=90，解得{k=−3b=300，所以y关于x的函数解析式为y=−3x+300；（2）由（1）W=(−3x+300)(x−a)，又由表可得：3600=(−3×40+300)(40−a)，∴a=20，∴W=(−3x+300)(x−20)=−3x2+360x−6000=−3(x−60)2+4800．所以售价x=60时，周销售利润W最大，最大利润为4800；（3）由题意W=−3(x−100)(x−20−m)(x⩽55)，其对称轴x=60+m2>60，∴0<x⩽55时上述函数单调递增，所以只有x=55时周销售利润最大，∴4050=−3(55−100)(55−20−m)．∴m=5．小提示：本题考查了二次函数在实际生活中的应用，重点是掌握求最值的问题．注意：数学应用题来源于实践，用于实践，在当今社会市场经济的环境下，应掌握一些有关商品价格和利润的知识，总利润等于总收入减去总成本，然后再利用二次函数求最值．17、“八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：①统计售价与需求量的数据，通过描点（图1），发现该蔬菜需求量y1（吨）关于售价x（元/千克）的函数图象可以看成抛物线，其表达式为y1=ax2+ c，部分对应值如表：221．③1~7月份该蔬菜售价x1（元/千克），成本x2（元/千克）关于月份t的函数表达式分别为x1=12t+2，x2=1 4t2−32t+3，函数图象见图2．请解答下列问题：(1)求a，c的值．(2)根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由．(3)求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．答案：(1)a=−15,c=9(2)在4月份出售这种蔬菜每千克获利最大，见解析(3)该蔬菜供给量与需求量相等时的售价为5元/千克，按此价格出售获得的总利润为8000元分析：（1）运用待定系数法求解即可；（2）设这种蔬菜每千克获利w元，根据w=x售价−x成本列出函数关系式，由二次函数的性质可得结论；（3）根据题意列出方程，求出x的值，再求出总利润即可．（1）把{x=3,y=7.2，{x=4,y=5.8代入y需求=ax2+c可得{9a+c=7.2,①16a+c=5.8.②②-①，得7a=−1.4，解得a=−15，把a=−15代入①，得c=9，∴a=−15,c=9．（2）设这种蔬菜每千克获利w元，根据题意，有w=x售价−x成本=12t+2−(14t2−32t+3)，化简，得w=−14t2+2t−1=−14(t−4)2+3，∵−14<0,t=4在1≤t≤7的范围内，∴当t=4时，w有最大值．答：在4月份出售这种蔬菜每千克获利最大．（3）由y供给=y需求，得x−1=−15x2+9，化简，得x2+5x−50=0，解得x1=5,x2=−10（舍去），∴售价为5元/千克．此时，y供给=y需求=x−1=4（吨）=4000（千克），把x=5代入x售价=12t+2，得t=6，把t=6代入w=−14t2+2t−1，得w=−14×36+2×6−1=2，∴总利润=w⋅y=2×4000=8000（元）．答：该蔬菜供给量与需求量相等时的售价为5元/千克，按此价格出售获得的总利润为8000元．小提示：此题主要考查了函数的综合应用，结合函数图象得出各点的坐标，再利用待定系数法求出函数解析式是解题的关键．18、一隧道内设双行公路，隧道的高MN为6米．下图是隧道的截面示意图，并建立如图所示的直角坐标系，它是由一段抛物线和一个矩形CDEF的三条边围成的，矩形的长DE是8米，宽CD是2米．（1）求该抛物线的解析式；（2）为了保证安全，要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离．若行车道总宽度PQ （居中，两边为人行道）为6米，一辆高3.2米的货运卡车（设为长方形）靠近最右边行驶能否安全？请写出判断过程；（3）施工队计划在隧道门口搭建一个矩形“脚手架”ABHG ，使H 、G 两点在抛物线上，A 、B 两点在地面DE 上，设GH 长为n 米，“脚手架”三根木杆AG 、GH 、HB 的长度之和为L ，当n 为何值时L 最大，最大值为多少？ 答案：（1）y=-14x 2+4；（2）能安全通过，见解析；（3）n=4时，L 有最大值，最大值为14分析：（1）根据题意和函数图象，可以设出抛物线的解析式，然后根据抛物线过点F 和点M 即可求得该抛物线的解析式；（2）先求出抛物线的解析式，再根据题意判断该隧道能通过的车辆的最高高度，便可判断该车辆能安全通过．（3）射出H 的坐标，用n 表示出L ，利用二次函数的性质求解即可．解：（1）由题意得M （0，4），F （4，0）可设抛物线的解析式为y=ax 2+4，将F （4，0）代入y=ax 2+4中，得a=-14， ∴抛物线的解析式为y=-14x 2+4； （2）当x=3，y=74， 74+2-12=3.25>3.2，∴能安全通过； （3）由GH=n ，可设H （n 2，−n 216+4），∴GH+GA+BH=n+（−n 216+4）×2+2×2=−18n 2+n +12，∴L=−18n 2+n +12，∵a ＜0，抛物线开口向下，∴当n=-b=4时，L有最大值，最大值为14．2a小提示：本题考查了二次函数的实际应用，解题的关键是要注意自变量的取值范围必须使实际问题有意义．。
人教版九年级数学上册第22章《二次函数》知识小结与复习
解:(1)∵抛物线过点(3,8)，(-1,0)，(0,5)，
8 则 0
9a 3b c， a b c，
解得
a b
1， 4，
5 c.
c 5.
∴该二次函数关系式为y=-x2+4x+5
(2)顶点M的坐标为(2，9)， 对称轴为直线x=2,则B点坐标为(5，0)， 过M作MN⊥AB于N，则
S四边形ABMD =S△AOD+S梯形DONM +S△MNB
教学反思
本课时是对本章知识点的全面总结，教学 时，教师注重引导学生回忆知识点并构建知识 结构框图，同时辅以典型例题，复习和巩固所 学知识点，最后教师详细讲解解题思路和分析 过程.
4.已知抛物线y
1 2
x
2
3
x
5 2
.
(1)求抛物线的开口方向、对称轴及顶点坐标；
(2)求抛物线与x轴、y轴的交点坐标；
解:(1)
y
1 2
x
2
3
x
5 2
.
1 2
(
x
3)2
7.
开口:向上，
对称轴:x=3,
顶点坐标:(3，-7).
(2)
0
1 2
(x轴的交点：
(3 14，0)，(3 14，0).
ab<0；②b2-4ac>0；③9a-3b+c<0；④b-4a=0；
⑤方程ax2+bx=0的两个根为x1=0, x2=-4. y 其中正确的结论有（ B ）
A.①③④ B.②④⑤
-4 -2 O
x
C.①②⑤ D.②③⑤
专题训练四 二次函数与一元二次方程的关系
（黑龙江牡丹江中考）已知二次函数y=kx2+(2k-1)x-1与x轴
人教版数学九年级上册第二十二章二次函数小结第1课时课件
第1课时
初中数学 九年级上册 RJ
知识梳理
二次函数的概念
一般地，形如y＝ax2＋bx＋c(a ≠0，a，b，c是常数)的
函数，叫做二次函数． 注意：
(1)等号两边都是整式；
(2)自变量的最高次数是2；
(3)只含有一个未知数.
知识梳理 二次函数的解析式 一般式：y＝ax2＋bx＋c(a ≠0，a，b，c是常数)，已知
图象上三点的坐标，通常设一般式. 顶点式：y=a(x-h)2+k (a ≠0，h，k是常数)，顶点坐标(h,k)，
已知图象的顶点坐标或对称轴，通常设顶点式. 交点式：y=a(x-x1)(x-x2)(a ≠0,（x1,0 ）,（x2,0）为抛 物线与x轴的交点)．已知图象与x轴的交点坐标，
通常设交点式.
抛物线y=-x2+6x+1可以看成抛物线y=-x2向上平移10个
单位长度后，再向右平移3个单位长度得到的．
2.二次函数 y＝－x2＋bx＋c的图象如图所示，若点A(x1， y1)，B(x2，y2)在此函数图象上，且x1<x2<1，则y1与y2
的大小关系是( B )
A. y1≤y2
B. y1<y2
C. y1≥y2
配方得
1 已知抛物线y=-x2+6x+1，
(2) 求出抛物线与坐标轴的公共点；
分析： 坐标轴
解：当 x = 0 时,y=0+0+1=1． ∴抛物线与 y 轴的公共点是(0，1)．
y轴
x 轴 当 y=0 时，-x2+6x+1=0.
( x = 0 ) ( y = 0 ) 解得x1 3 10 ，x2 3 10 ．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
b 2a
的位置:
ab>0 ab=0 ab<0
(4)Δ确定抛物线与x轴的交点个数：
Δ>0
Δ=0 Δ<0
典型例题 知识点1：二次函数的图象和性质 【例1】 抛物线y=-5（x+2）2-6的对称轴和顶点分别是（ C ） A. x=2和（2，-6） B. x=2和（-2，-6） C. x=-2和（-2，-6） D. x=-2和（2，-6）
典型例题 知识点3：二次函数的实际应用及综合问题 【例3】 某商店经销一种双肩包，已知这种双肩包的成 本价为每个30元. 市场调查发现，这种双肩包每天的销 售量y（单位：个）与销售单价x（单位：元）有如下关 系：y=-x+60（30≤x≤60）. 设这种双肩包每天的销售 利润为W元.
（1）求W与x之间的函数解析式；
（2）存在.当AB为平行四边形的边长时，如答图22-
28-2，答图22-28-3，M1，M2为所求点. ①∵四边形ANM1B为平行四边形， ∴△ANH≌△BM1G. 则M1的横坐标为-2，代入二次函数表达式， 解得M1坐标为（-2，5）；
②∵四边形AM2NB为平行四边形， ∴△ABG≌△M2NH. 则M2的横坐标为4，代入二次函数表达式， 解得M2的坐标为（4，5）； ③当AB为平行四边形的对角线时，如答图22-28-4
，M3与点C重合，故M3（0，-3）. 故点M的坐标为（0，-3），（4，5），（-2，5）.
a<0时，对称轴左侧(x<- 2a )， 函数值y随x的增大而增大 ；对称轴
右侧(x>减小 。
2a
)，函数值y随x的增大而
（2） a>0时，y最小=
4ac-b2 4a
a<0时，y最大=
4ac-b2 4a
一、定义
使用
二、图象的特点 和性质
一般式
解析式
范围
y=ax2+bx+c
三个点的 坐标
三、解析式的求法
解：（1）W=（x-30）·y =（x-30）（-x+60）=-x2+30x+60x-1 800 =-x2+90x-1 800，
即W与x之间的函数解析式为W=-x2+90x-1 800.
（2）这种双肩包销售单价定为多少元时，每天的销售 利润最大？最大利润是多少元？
（2）由（1）得 W=-x2+90x-1 800 =-（x-45）2+225.
C组 5.如图，抛物线y=ax2+bx+c经过点A（2，-3），且与x 轴的交点坐标为（-1，0）和（3，0）. （1）求抛物线的解析式；
解：（1）y=x2-2x-3. （2）若点M在抛物线上，点N 在抛物线的对称轴上，是否存 在以点A，B，M，N为顶点的四 边形是平行四边形？若存在，直接写出所有符合条件的 点M的坐标；若不存在，请说明理由.
解：设矩形的面积为S，一边长为a，则
S=
.
∴当a=15时，S取得最大值，此时S=225.
答：这个矩形的面积与其一边长的关系式是S=-
a2+30a，当矩形面积取得最大值时，长和宽都是15.
4.如图，抛物线y=x2-2x+k与x轴交于A,B两点，与y轴交 于点C（0，-3）.
（1）k=_____-_3____，点A的坐标为_（__-_1_，__0_）__，点B的 坐标为__（__3_，_0_）___；
一、定义
二、图象特点和性质
三、解析式的求法
四、图象位置与a、 b、c、 的正负关 系
一般地，形如 y=ax2+bx+c(a，b，c
是常数，a≠0)的函数， 叫做二次函数.
1.二次函数 y=ax2 (a≠0)的图象和性质 (一) 图象:
图 26.2.1
(1)是一条抛物线； (2)对称轴是y轴； (3)顶点在原点； (4)开口方向: a>0时,开口向上； a<0时,开口向下.
∵a=-1＜0， ∴当x=45时，W有最大值，最大值是225，即当 销售单价定为45元时，每天的销售利润最大，最 大利润为225元.
变式训练 1.如图，抛物线y=ax2+2x+c经过点A（0，3），B（-1，0）. （1）求抛物线的解析式； （2）点F在抛物线的对称轴上运动，是否存在点F，使 △BFC的面积为4，如果存在，求出点F的坐标；如果不存在 请说明理由.
（2）设抛物线的顶点为M，求四边形ABMC的面积. 解： （2）如图，连接OM. 由（1）知，A（-1，0），B （3，0），则OA=1，OB=3. ∵抛物线y=x2-2x+3的顶点为M， ∴M（1，-4）. ∴S四边形ABMC=S△AOC+S△OMC+S△BOM = OA·OC+ OC·Mx+ OB·My = ×1×3+ ×3×1+ ×3×4=9. 即四边形ABMC的面积是9.
(一) 图象:
(1)是一条抛物线；
(2)对称轴是:x=- 2a
(3)顶点坐标是:(- ,2a
)4ac-b2 4a
(4)开口方向:
a>0时,开口向上；
a<0时,开口向下.
图 26.2.4
图 26.2.4
(二) 性质：
（函1数）值ay>随0时x的，增对大称而轴减左小侧；( x对< 称-2a轴)， 右侧(x>- )，函数值y随x的增大而 增大 。 2a
图 26.2.1
(二) 性质：
（1） a>0时，y轴左侧，函数 值y随x的增大而减小 ； y轴右 侧，函数值y随x的增大而增大 。
a<0时， y轴左侧，函数值 y随x的增大而增大 ； y轴右侧， 函数值y随x的增大而减小 。
（2） a>0时，y最小=0
a<0时，y最大=0
2.二次函数 y=ax2+bx+c(a≠0)的图象和性质
顶点（h,k)
四、图象位置与a、顶点式 b、c、 的正负 关系
y=a(x-h)2+k
及另一个 点坐标
与x轴的
交点式
y=a(x-x1)(x-x2)
两个交点 及另一个
点坐标
(1)a确定抛物线的开口方向：
a>0
a<0
y
(2)c确定抛物线与y轴的交点位置:
c>0
c=0 c<0
0
x
(3)a、b确定对称轴
x=-
解：（1）y=-2（x-2）2+4. （2）与y轴的交点为（0,-4），与x轴的 交点为（2+ ，0）和（2- ，0）.
变式训练 1.二次函数y=x2+bx+c的图象经过点（4，3）和点（3， 0）. （1）求二次函数的解析式； （2）该函数的图象可以由y=x2的图象经过怎样的平移 得到？
解：（1）y=x2-4x+3. （2）y=x2-4x+3=（x-2）2-1,可以由y=x2的图象向右 平移2个单位长度，再向下平移1个单位长度得到.
解：（1）抛物线的解 析式为y=-x2+2x+3.
（2）点F在抛物线的对称轴上运动，是否存在点F，使
△BFC的面积为4，如果存在，求出点F的坐标；如果不
存在，请称轴为x=1，且
B（-1，0），∴C（3，0）.
设F（1，m），
∵△BFC的面积为4，∴
.
∴ =2.解得m=2或m=-2.
∴点F的坐标为（1，2）或（1，-2）.
分层训练
A组
1.抛物线y=2（x-3）2+4的顶点坐标是
（ A）
A. （3，4）
B. （-3，4）
C. （3，-4）
D. （2，4）
2.抛物线y=x2-2x-3与y轴的交点的纵坐标为 （ A ）
A. -3 B. -1 C. 1 D. 3
B组 3.已知矩形的周长为60，请表示出这个矩形的面积与其 一边长的关系，并求出当矩形面积取得最大值时，矩形 的边长.
变式训练 1.下列关于抛物线y=-x2+2的说法正确的是 （ D ） A. 抛物线开口向上 B. 顶点坐标为（-1，2） C. 在对称轴的右侧，y随x的增大而增大 D. 抛物线与x轴有两个交点
典型例题 知识点2：用待定系数法求抛物线的解析式 【例2】 已知抛物线的顶点为（2，4），并过点（1，2）. （1）求抛物线的解析式； （2）求抛物线与x轴，y轴的交点坐标.