自适应阵列信号处理
自适应阵最优化处理稳态性能极限与维纳解

3.4 复信号的相关矩阵:
对复矢量:
{ } R xx = E X * X T { } R xy = E X *Y T
另一种定义:
{ } R xx = E XX H { } R xy = E XY H
(3.4.1)
(3.4.2)
(3.4.3) (3.4.4)
表示共轭,T表示转置,H表示共轭转置(Hermite Conjugate Transpose)。后者正好是前者矩阵的复 共轭,只要前后采用同一个定义,所得结果(所得
|| X ||= X T X || X ||= X H X
(实) (3.5.1) (复)(3.5.2)
2. 梯度和梯度算子
梯 度:从数学上说是沿某一方向的导数。
梯度算子:作用于矢量 y 的标量值函数 f ( y ) 以得到 沿 y 的各个方向的偏导数。
实变量场合,梯度算子是矢量算子。
y =[
,L, y1
性能量度)是一样的。
由定义可得
RxHx = Rxx
RxHy = Ryx
(3.4.5)
Rxx , Ryx 也叫Hermite阵(矩阵等于它的共轭转置)。
3.5 矢量或复矢量的有关运算:
最优化问题就是对不同性能量度求其最符合要求的复加权 矢量。其中要使用复矢量的模,梯度和协方差距阵或相关矩 阵等。
1、希尔伯特空间的模:||x||代表矢量长度
3.1 复信号:
采用复信号的好处:实信号的频谱是共轭对称的,从信息 的角度来看,其负谱部分是冗余的,复信号的频谱不存在共 轭对称性,信号占有的频带减小了一半,有利于无线通信。
1、解析信号:
表达复信号 Z(t)的最简单的方法是用所 给定的实信
号S(t) = a(t)cos[ (t )]作其实部,并另外构造 一“虚拟信
阵列信号处理
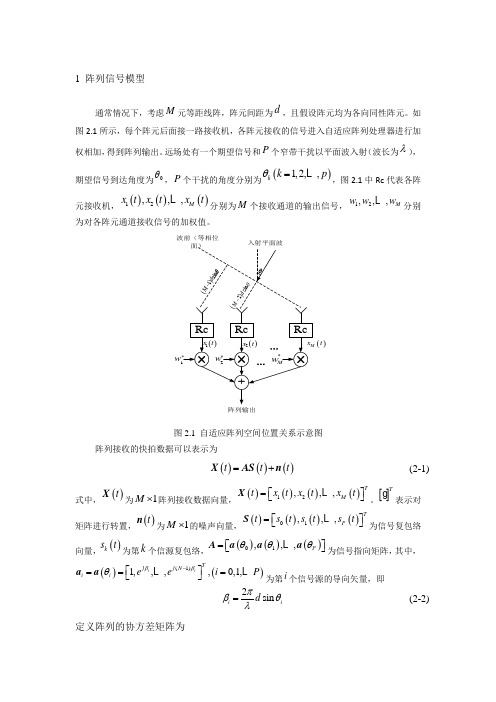
1 阵列信号模型通常情况下,考虑M 元等距线阵,阵元间距为d ,且假设阵元均为各向同性阵元。
如图2.1所示,每个阵元后面接一路接收机,各阵元接收的信号进入自适应阵列处理器进行加权相加,得到阵列输出。
远场处有一个期望信号和P 个窄带干扰以平面波入射(波长为λ),期望信号到达角度为0θ,P 个干扰的角度分别为()1,2,,k k p θ= ,图2.1中Rc 代表各阵元接收机,()()()12,,,M x t x t x t 分别为M 个接收通道的输出信号,12,,,M w w w 分别为对各阵元通道接收信号的加权值。
()t w 阵列输出波前(等相位图2.1 自适应阵列空间位置关系示意图阵列接收的快拍数据可以表示为()()()t t t =+X AS n(2-1)式中,()t X 为1M ⨯阵列接收数据向量,()()()()12,,,TM t x t x t x t =⎡⎤⎣⎦X 。
[]T表示对矩阵进行转置,()t n 为1M ⨯的噪声向量,()()()()01,,,TP t s t s t s t =⎡⎤⎣⎦S 为信号复包络向量,()k s t 为第k 个信源复包络,()()()01,,,P θθθ=⎡⎤⎣⎦A a a a 为信号指向矩阵,其中,()()(1)1,,,,0,1,i iTj j N i i e e i P ββθ-⎡⎤===⎣⎦a a 为第i 个信号源的导向矢量,即2sin i i d πβθλ=(2-2)定义阵列的协方差矩阵为()()2H H x s n E t t σ⎡⎤==+⎣⎦R X X AR A I (2-3)式中,()()H s E t t ⎡⎤=⎣⎦R S S 为信号的协方差矩阵,I 为M 维单位矩阵,2n σ为阵元的噪声功率,本文中约定,[]T表示转置,[]*表示共轭,[]H表示共轭转置。
式(2-3)常由接收数据采样协方差矩阵ˆx R 代替,即()()11ˆNH xiii t t N==∑R x x(2-4)如图2.1所示的自适应阵列模型,阵列的M 个通道接收信号经加权处理后,最后的输出信号为()()()1MH i i i y t w x t t *===∑w x(2-5)阵列的方向图()p θ定义为()()H p θθ=w a(2-6)调整自适应阵列的权矢量w ,可以改变阵列的方向图,即改变各个方向上入射信号增益。
阵列信号处理

B
B
1 有 zB t 2
B
2
z e jt d z B t
因此
s r , t z B t e j0t e j0 s 0, t e j0
2
小结: 信号带宽足够小使得波到达 r 处时的复包络基本 不变。 T r 表示了波传播的空间信息(方向、位置), 它仅含于载波项中,而与信号复包络无关。
s exp[ j t r ]d
T
这里函数 s 是任意的,只要其Fourier变换存在即 可。该式表达了沿同一方向 传播的任意波形(信 号),其频率分量任意。
B. 波动方程球坐标系中的解
球坐标系 r , , ,但是,当波动方程的解具有球形 对称时,函数s r , , , t 并不依赖于 和 ,使解简化, 这时波动方程可简化为:
T
波动方程的任意解可以分解为无穷多个“单频” 解的迭加(传播方向和频率分量均任意)。
波动方程的单频解可以写成单变量的函数:
s r , t A exp[ j (t k r ) A exp[ j t r ]
T T
k ,其大小等于传播速度的倒数,其方向与 式中
时间频率 空间频率
b) 任意解:由四维Fourier变换表示: j t k r 1 s r, t s u , e d kd 4 2 j t k r s k , s t , r e d rdt 其中
T
a t 带宽越宽,信号起伏越快。窄带条件即要求a t cos 变化比 0t t 变化慢。
阵列信号处理技术

动通信的用户很多,一方面通过空间不同位置进行区分,另 一方面通过不同的编码等方法实现多用户和大容量。 现代超分辨技术,使系统能够分辨空间和时间上都很靠 近的信号。
概括起来说:
波束的控制和管理
时间和空间信号的高分辨 五、主要研究内容 1、阵列构形研究 均匀直线阵、平面阵、元阵、随机阵、共形阵。 2、波束形成和超分辨新方法的研究(不是热点)
军用雷达:
火炮雷动:炮位侦校雷达、炮瞄雷达
战场侦察雷达:(坦克、直升机等目标的检测与识别)
步兵侦察雷达:
空中警戒雷达:(对空监视雷达) 机载雷达气象雷达: 天气预报、人工降雨)
探地雷达: (探测地下管道,检查高速公路施工质量,
接收信号
X T = [ x1 , x 2 , L , x N ]
(2.1.1)
方向图形成网络: W = [ w1 , w 2 , L , w N ]
(2.1.2)
(形成最优权 和系统输出)
y(t ) = W T X = X T W
(2.1.3)
自适应处理器: ( 例如MVDR:Minimum Variance Distortionless Response) 求解约束性问题:
0 ≤ t ≤ T
(2.2.5)
所需信号和噪声的矢量可以表达为:
s1 (t ) S (t ) = 2 M s N (t )
n1 (t ) n (t ) = 2 M n N (t )
0 ≤ t ≤ T
所需信号分量可精确已知,粗略近视已知,或仅在统计意 义上已知。
3、理想的传播模型
3、应用性研究(热点)
在一个具体的领域或工程项目上,如何应用这些理论和
方法,实际系统的误差很大,比如阵列通道之间的性能差异, 频率特性,阵列传感器的位置误差等情况下的一些理论算法 和性能。
阵列信号处理技术

旁 瓣零 陷 。之后 , 又 提 出 了 自适 应 阵列 求 最 优 他 权 的最 大信 干噪 比 (I ) SNR 准则 。16 9 7年 Wirw do
提 出 了最小均 方 ( MS 自适应 算法 。1 6 L ) 9 9年 C . a
研制的集成 自 适应阵列信号处理技术的多功能数 字阵列 雷达 。英 国 防御 评估 研 究 局 、 门子普 莱 西
赛 防务系 统公 司 以及 罗克 马诺 尔研究 有 限公 司合 作 开 发 的 多 功 能 电 子 扫 描 自 适 应 雷 达
( SR等。 ME A )
pn提 出了最 小方 差无 失 真 响 应 ( D ) o MV R 波束 形 成器 , 通过求 解约 束最 优化 问题来 求权 。F ot rs将 单 一 的无失 真 响应 约 束 推广 为 多 个 线性 约 束 , 提 出 了线 性 约束 最 小 方 差 波束 形 成 器 ( C L MV)线 , 性 约束 由最 初 的方 向约束 推广到 导数 约束 和特征 向量 约 束 。V n en总 结 分 析 了 L MV 波 束 形 aV e C
自上世 纪 4 0年 代 起 , S A P已经 有 近 7 0年 的
向发展。这些问题 的解决也必将使 阵列处理技术 的发 展迈 向新 的 台阶 。
值 得一提 的是 , 由于外界 环境 复杂 多变 , 自 盲 适应 波束 成形 最 近 受 到许 多 学 者 的 广泛 关 注 , 并
发展历 史 , 根据 典型技 术 的提 出 ,S A P大致 可分 为
摘 要 : 阵列信 号处理 (S ) A P 由于其 广泛应 用于雷达 、 信 、 通 声学 、 生物 信 息处理 等诸 多领域 而受
到 了长期 的关注 , 至今 还是一 个研 究热 点。现 回顾 了( S ) A P 的发展 与研 究现状 , 介绍 了阵列信 号
自适应信号处理

自适应信号处理-唐正必马长芳科学出版社赵春晖哈尔滨工程大学出版社本书全面系统地阐述了自适应信号处理的理论及其应用,包括确定性信号与随机过程(平稳与非平稳信号)滤波检测理论,不用训练序列的本身自适应的盲信号处理理论,从一维到多维、线性到非线性、经典自适应到神经智能自适应等近代信号处理。
它将信息论、时间序列分析、系统辨识、谱估计理论、高阶谱理论、优化理论、进化计算,以及神经网络理论等学科知识综合而成一体。
本书共十章,内容有自适应滤波基本原理、自适应LMS滤波器、自适应RLS滤波器、自适应格型滤波器、自适应递归滤波器、自适应谱线增强与谱估计、自适应噪声干扰抵消器、自适应均衡器、自适应阵列处理与波束形成,以及自适应神经信息处理。
对于盲信号处理的理论与方法,将分散在最后三章中论述。
本书取材新颖,内容丰富;叙述深入浅出,系统性强,概念清楚。
它总结了自适应信号处理的最新成果,其中包括作者在该领域内所取得的科研成果,是一部理论联系实际的专业理论专著。
可作为信息与通信、雷达、声纳、自动控制、生物医学工程等专业的研究生的教材或主要参考书,也可供广大科研人员阅读。
第1章绪论1.1 自适应滤波的基本概念1.2 自适应信号处理的发展过程1.3 自适应信号处理的应用第2章维纳滤波2.1 问题的提出2.2 离散形式维纳滤波器的解2.3 离散形式维纳滤波器的性质2.4 横向滤波器的维纳解第3章最小均方自适应算法3.1 最陡下降法3.2 牛顿法3.3 LMS算法3.4 LMS牛顿算法第4章改进型最小均方自适应算法4.1 归一化LMS算法4.2 块LMS算法4.3 快速块LMS算法第5章最小均方误差线性预测及自适应格型算法5.1 最小均方误差线性预测5.2 Lev ins on-Durbi n算法5.3 格型滤波器5.4 最小均方误差自适应格型算法第6章线性最小二乘滤波6.1 问题的提出6.2 线性最小二乘滤波的正则方程6.3 线性最小二乘滤波的性能6.4 线性最小二乘滤波的向量空间法分析第7章最小二乘横向滤波自适应算法7.1 递归最小二乘算法7.2 R LS算法的收敛性7.3 R LS算法与LMS算法的比较7.4 最小二乘快速横向滤波算法第8章最小二乘格型自适应算法8.1 最小二乘格型滤波器8.2 LSL自适应算法第9章非线性滤波及其自适应算法9.1 非线性滤波概述9.2 Volterra级数滤波器9.3 LMS Volterra级数滤波器9.4 R LS Volterra级数滤波器9.5 形态滤波器结构元优化设计的自适应算法9.6 自适应加权组合广义开态滤波器9.7 层叠滤波器的自适应优化算法第10章自适应信号处理的应用10.1 自适应模拟与系统辨识10.2 自适应逆模拟10.3 自适应干扰对消10.4 自适应预测计算机实验实验1 LMS算法的收敛性实验2 LMS自适应线性预测实验3 LMS自适应模型识别实验4 LMS自适应均衡实验5 RLS自适应线性预测实验6 RLS自适应模型识别实验7 RLS自适应均衡实验8 自适应格型块处理迭代算法仿真附录A 矩阵和向量A.1 矩阵A.2 向量A.3 二次型……附录B 相关矩阵附录C 时间平均相关矩阵参考文献《自适应信号处理》课程教学大纲课程编号:S0105603C课程名称:自适应信号处理开课院系:电子与信息技术研究院任课教师:邹斌(副教授)胡航(副教授)先修课程:数字信号处理适用学科范围:信息与通信工程学时:36 学分:2.0开课学期:春季学期开课形式:课堂讲授课程目的和基本要求:本课程是一门理论性较强、并在实际中获得广泛应用的课程。
毕业设计(论文)-lms及rls自适应干扰抵消算法的比较[管理资料]
![毕业设计(论文)-lms及rls自适应干扰抵消算法的比较[管理资料]](https://img.taocdn.com/s3/m/e45ae55891c69ec3d5bbfd0a79563c1ec4dad715.png)
前言自适应信号处理的理论和技术经过40 多年的发展和完善,已逐渐成为人们常用的语音去噪技术。
我们知道, 在目前的移动通信领域中, 克服多径干扰, 提高通信质量是一个非常重要的问题, 特别是当信道特性不固定时, 这个问题就尤为突出, 而自适应滤波器的出现, 则完美的解决了这个问题。
另外语音识别技术很难从实验室走向真正应用很大程度上受制于应用环境下的噪声。
自适应滤波的原理就是利用前一时刻己获得的滤波参数等结果, 自动地调节现时刻的滤波参数, 从而达到最优化滤波。
自适应滤波具有很强的自学习、自跟踪能力, 适用于平稳和非平稳随机信号的检测和估计。
自适应滤波一般包括3个模块:滤波结构、性能判据和自适应算法。
其中, 自适应滤波算法一直是人们的研究热点, 包括线性自适应算法和非线性自适应算法, 非线性自适应算法具有更强的信号处理能力, 但计算比较复杂, 实际应用最多的仍然是线性自适应滤波算法。
线性自适应滤波算法的种类很多, 有RLS自适应滤波算法、LMS自适应滤波算法、变换域自适应滤波算法、仿射投影算法、共扼梯度算法等[1]。
其中最小均方(Least Mean Square,LMS)算法和递归最小二乘(Recursive Least Square,RLS)算法就是两种典型的自适应滤波算法, 它们都具有很高的工程应有价值。
本文正是想通过这一与我们生活相关的问题, 对简单的噪声进行消除, 更加深刻地了解这两种算法。
我们主要分析了下LMS算法和RLS算法的基本原理, 以及用程序实现了用两种算法自适应消除信号中的噪声。
通过对这两种典型自适应滤波算法的性能特点进行分析及仿真实现, 给出了这两种算法性能的综合评价。
1 绪论自适应噪声抵消( Adaptive Noise Cancelling, ANC) 技术是自适应信号处理的一个应用分支, 年提出, 经过三十多年的丰富和扩充, 现在已经应用到了很多领域, 比如车载免提通话设备, 房间或无线通讯中的回声抵消( AdaptiveEcho Cancelling, AEC) , 在母体上检测胎儿心音, 机载电子干扰机收发隔离等, 都是用自适应干扰抵消的办法消除混入接收信号中的其他声音信号。
多通道信号处理中的自适应阵列处理技术

多通道信号处理中的自适应阵列处理技术自适应阵列处理技术在多通道信号处理中扮演着重要的角色。
它是一种利用多个传感器接收并处理信号的方法,通过选择性地增强所需信号、抑制干扰信号,提高通信质量和可靠性。
本文将通过介绍自适应阵列处理技术的原理和应用领域,探讨其在多通道信号处理中的重要性和优势。
一、自适应阵列处理技术原理自适应阵列处理技术基于波束形成和空间滤波的原理,通过计算传感器阵列中各个传感器之间的差异信息,调整传感器的增益和相位,实现对指定方向信号的增强以及对干扰信号的抑制。
1. 波束形成波束形成是指通过合理选择传感器的权值,使得波束指向指定的方向,从而增强来自该方向的信号。
传感器阵列接收的信号中,如果目标信号来自于阵列的指定方向,那么经过相位和幅度的调整后,信号在阵列中各个传感器上的相位将趋于一致,从而在合成波束上形成最大增益。
2. 空间滤波空间滤波是指对传感器阵列接收到的信号进行加权叠加,通过调整权值达到抑制干扰信号的目的。
通过传感器阵列之间的相位差异来调整权值,可以选择性地滤除不需要的信号,提高接收信号的质量。
二、自适应阵列处理技术的应用领域自适应阵列处理技术具有广泛的应用领域,包括无线通信、雷达与声纳、医学图像处理等。
1. 无线通信在无线通信系统中,自适应阵列处理技术可以用于空中接口中的信号增强和干扰抑制。
通过自适应阵列处理技术,可以提高无线信号的接收灵敏度和抗干扰能力,增强通信质量和可靠性。
2. 雷达与声纳自适应阵列处理技术在雷达与声纳系统中有着重要的应用。
通过波束形成和空间滤波,可以实现对目标信号的精确定位和抑制来自其他方向的杂乱信号,提高雷达与声纳系统的探测性能。
3. 医学图像处理在医学领域,自适应阵列处理技术可用于医学图像处理中的噪声抑制和信号增强。
通过选择性地增强医学图像中的有用信息,可以提高图像的清晰度和准确性,辅助医生进行诊断和治疗。
三、自适应阵列处理技术的优势自适应阵列处理技术在多通道信号处理中具有许多优势,以下是其中几个主要的优势:1. 强抗干扰能力通过自适应阵列处理技术,可以实现对干扰信号的抑制,提高信号的纯净度和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
缺少期望信号的先验知识 不能确定参考信号
解决方案
对权值进行线性约束
LCMV
波束形成要求
期望信号的波达方向(DOA)(缺点)
ASPASP 小组报告@航大
2014-5-25
11
基于LCMV准则波束形成
MVDR最小方差无失真响应
当 w H a(0 ) 1时, 使 J (w) w H Rw 最小化
w (n) 2 x(t )e* (t )
LMS算法优点:实现简单 严重缺陷:收敛速率太慢
ASPASP 小组报告@航大
2014-5-25
15
ASPASP 小组报告@航大
2014-5-25
8
自适应阵列概述
自适应阵列处理目的:提取所需信号源和信号属性等 信息 自适应阵列处理内容
经典波束形成技术 波束形成技术 盲波束形成技术 阵列输出经过加权求和,调整到 阵列接收的方向增益聚集在一个 方向,相当于形成一个波束。
波束形成 物理意义
ASPASP 小组报告@航大
def
S(k)和 n(k)统计 独立
R AE s(k )s H (k ) A H E n(k )n H (k ) APA H 2I
ASPASP 小组报告@航大
2014-5-25
4
阵列信号处理概述(续)
式中
P E s(k )s H (k )
def
各阵元的噪 声不相关, 且强度相等
5
阵列信号处理的主要内容
自适应波束形成技术 • 目的:增强有用(所需)信号,抑制干扰和噪声 信号 • 应用:雷达、通信、声纳等领域 超分辨空间谱估计技术 • 目的:估计空间信号的到达方向 • 应用:雷达、声纳、地震勘探以及射电天文等领 域
6
ASPASP 小组报告@航大
2014-5-25
自适应波束形成
2014-5-25
9
自适应阵列概述
最小均方误差(MMSE)准则
最优化准则
最大信噪比(Max SNR)准则
线性约束最小方差(LCMV)准则
ASPASP 小组报告@航大
2014-5-25
10
自适应波束形成 ——经典的方法 (续)
线性约束最小方差(LCMV)
问题引出
期望信号幅度未知
最大SNR失效 SLC和MMSE失效
E n(k )n H ( k ) 2I
R UU iuiuiH
H M
H H us sus u n nun i ui uiH 2 i 1
i 1
P
i P 1
H u u i i
M
信号子 空间
ASPASP 小组报告@航大
噪声子 空间
2014-5-25
约束条件 wH a(0 ) g
H 输出功率最小化 min w Rw w
R 1a(0 ) Lagrange法求得 w g H a (0 )R 1a(0 )
ASPASP 小组报告@航大
2014-5-25
13
最小均方(LMS)算法
MSE准则:wo R1p 波束形成:y(t ) w H x(t ) 期望输出:d (t ) 误差:e(t ) y(t ) d (t )
自适应阵列信号处理
阵列信号处理概述
阵列信号处理的引入
延伸推广
一维信号
多维信号
传感器阵列
时域
天线阵列
空域
阵列信号处理
ASPASP 小组报告@航大
2014-5-25
2
阵列信号处理概述
阵列信号模型
阵列所 处环境 传 感 器 阵 列
目标参数 估计输出 处理器
目标
… …
先验知识
ASPASP 小组报告@航大
实现:通过增加期望信号的贡献,抑制掉干扰源来实现。
ASPASP 小组报告@航大
2014-5-25
7
自适应波束形成技术
普通波束形成的优缺点: 优点:是一个匹配滤波器,在主瓣方向信号相干积累,实 现简单,在白噪声背景下它是最优的,在色噪声背景下, 维纳滤波是最优的。 缺点: 波束宽度限制了方向角的分辨。 存在旁瓣,强干扰信号可以从旁瓣进入。 加窗处理可以降低旁瓣,但同时也会展宽主瓣。 总之,普通波束形成依赖于阵列几何结构和波达方 向角,而与信号环境无关,且固定不变,抑制干扰能力 差。
J (w ) 2p 2Rw w
ASPASP 小组报告@航大
2014-5-25
14
最小均方(LMS)算法
LMS思想(widrow提出):用瞬态值代替稳态值.
J (w) 2x(t )e* (t )
迭代算法: w (n 1) w (n) J (w )
2014-5-25
3
阵列信号处理概述(续)
统计模型:Βιβλιοθήκη 在第m个阵元上第k次快拍的采样值为
xm (k ) si (k )e
i 1
P
j
2
( m 1) d sin i
nm (k )
将各阵元上第k次快拍的采样写成向量形式
x( k ) As(k ) n(k )
R E x(k )x H (k )
定义:要求自适应阵形成个很窄的主波束,自动对准所要的 观测的目标;在干扰方向上自动形成零陷,使干扰信号得到 最大限度的抑制。 目的:波束形成就是通过传感器阵列重构源信号。 阵列采用自适应处理的动因:
在阵列天线上容易进行自适应阵列波束形成 提高系统的可靠性 实现机扫到相扫的转变 有利于多目标远距离的监测和跟踪
* 2 H H H J ( w ) E e ( t ) e ( t ) w p p w w Rw 代价函数: d
J ( w )
H * 2 E x ( t ) x ( t ) w E x ( t ) d (t ) * * 2E x ( t ) y ( t ) d ( t ) * 2E x ( t ) e (t )
R 1a(0 ) 解得 w H a (0 )R 1a(0 )
与Max SNR准则所 得 W 具有相同信噪比
优点:具有最佳信噪比增益 缺点:低的信噪比条件限制了其高分辨性能
ASPASP 小组报告@航大
2014-5-25
12
基于LCMV准则波束形成
LCMV
基本思想:使感兴趣的波达方向信号以特定增益与相位 通过,而输出信号能量或方差最小化 代价函数 J (w) w H Rw
