间接效用函数
第二讲 间接效用函数与支出函数
• 假设消费者的偏好是良好性状的。
• A点为最初的选择，B点为征从量税的最优选 择，C点为征所得税的最优选择。可见，在政 府向消费者征收相同数量的税收条件下，消费 者在政府课征所得税时的境况要好些。
X2
征从量税的预算线
初始预算线
X2*
B• •C •A
征所得税的预算线
O
X1*
X1
思考：
➢ 在政府征收从量税和等额所得税的情况下，消费 者的境况有没有可能一样好？如果有，是在什么 情况下？ 有，折拗性偏好，例如：完全互补
y p1
p2
请求消费者的马歇尔需求函数。
求解
v(p1,p2,y ) p1
y(p1
p
2
)
2
,
v(
p1,p p 2
2
,y
)
y(p1
p 2 )2
v(p1,p2,y ) y
(p1
p 2 )1
利用罗尔恒等式
v(p ,y )
pi v(p ,y )
xi*
xi(p ,y )
y 0
v(p1,p2,y )
我们有x1(p1,p2,y )
p1 v(p1,p2,y )
y(p1 p 2 )2 (p1 p 2 )1
y
y(p1 p 2 )1
v(p1,p2,y )
x 2(p1,p2,y )
p 2 v(p1,p2,y )
y(p1 p 2 )2 (p1 p 2 )1
y
y(p1 p 2 )1
（三）间接效用函数的应用
• 可以分析价格和收入变动对消费者福利的影 响。
p ， *
u(x* )
i xi
0(偏好满足单调性），pi
8效用函数、间接效用函数和支出函数
j 1,
,n
证明： ①先求分子
v( p, m) u( x( p, m))
v u xi p j i 1 xi p j
n
u 又 pi xi
(i 1,
, n)
（最大化一阶条件）
n xi v pi p j p j i 1
同时 即
px m
max u x max u x tp x tm t 0 px m
（二） p ' p时 , v p ', m v p, m 证：记 B x px m B x px m
显然 B B
v x j p j (1)
v m
(2)
包络定理
• 考察参数变化对值函数的影响 • 假设f(x,a)是x和a的函数，a为决定于所研究 问题之外的一个参数，x为所研究的变量。 假定选择x来最大化这一函数，对于每一个 a，存在一个不同的x的最优选择。 • 定义值函数M(a)=f(x(a),a) • 现在我们想知道a的变动如何影响M(a)的变 动，即dM(a)/da
故 v( p1 , p2 , m) x x
* * 1 2 2
m 4 p1 p2
p1 0.25, p2 1, m 2
2 * x1 2 0.25 4 2 * x2 1 2 1
时
v( p1 , p2 , m) v(0.5,1, 2) 4
maxu ( x )满足x属于B B， B B B k，因为v(p, m) k和v(p, m) k
（五）罗伊（Roy identity）等式：
v p, m 0 如果 m
第二讲间接效用函数与支出函数D
* 故 v( p1 , p2 , m) = x1* x2
m = 4 p1 p2
2
p1 =0.25, p2 =1, m= 2
2 * x1 = 2 × 0.25 = 4 2 * x2 = =1 2 ×1
时
v( p1 , p2 , m) = v(0.5,1, 2) = 4
现在假设政府对商品1按0.25元/ 单位征收消费税，即
两边同时对pj偏微分
∂xi x j + ∑ pi =0 ∂p j i =1
n
∂ v = λ ∂ p j
∑
n
p
i=1
i
∂ x ∂ p
i j
故
∂v = −λ x j ∂p j
（1）
②再求分母
Q v( p, m) = u ( x( p, m))
对m求偏微分
∂v = ∂m
∑
n
i =1 n
∂u ( x ) ∂xi ∂xi ∂m ∂ xi pi ∂m
∂e( p, u ) ⋅ ∂pi
(1)
由谢泼特引理知
∂e = hi ( p , u ) ∂pi
且
hi ( p , u ) = x i ( p , e ( p , u )) = xi ( p , m )
即
∂e = xi ( p, m) ∂p i
代入(1)式变形即可得
∂x j ∂pi = ∂h j ( p, v( p, m)) ∂pi − xi ∂x j ( p, m) ∂m
第二讲间接效用函数与支出函数
•
Outline of Today’s Class
• • • • • 1.间接效用函数 2.罗伊（Roy identity）等式 3.支出最小化问题 支出最小化问题 4.支出函数 5.希克斯（补偿）需求函数
间接效用函数求马歇尔需求函数
间接效用函数求马歇尔需求函数马歇尔需求函数是经济学中用于描述消费者的需求行为的一个工具。
它表示了消费者的需求与价格、收入等因素之间的关系，从而帮助我们理解消费者对商品的需求程度。
在求解马歇尔需求函数之前，我们首先要了解一下间接效用函数和马歇尔需求函数的定义及特点。
间接效用函数是消费者效用函数的一种表达形式。
效用函数用来表示消费者对商品的偏好程度，而间接效用函数则是通过价格和收入等因素，将消费者偏好程度转化为需求数量的函数。
间接效用函数的变量包括商品的价格、消费者的收入以及其他可能影响消费者对商品需求的因素，如替代品和补品的价格。
马歇尔需求函数是在给定价格和消费者收入的条件下，描述消费者对其中一种商品需求数量和价格之间关系的函数。
马歇尔需求函数由间接效用函数推导得到，它以价格和收入为变量，表示消费者在价格和收入的限制下对其中一种商品的需求数量。
下面我们来以一种具体的商品为例，推导马歇尔需求函数。
假设一些消费者的效用函数为U(X,Y)，其中X表示商品X的数量，Y 表示其他商品的数量。
消费者的收入为M，商品X的价格为PX，商品Y的价格为PY。
根据微观经济学的理论，消费者会在给定收入的情况下，选择使得效用最大化的消费组合。
这个选择取决于消费者对商品的边际效用以及商品的价格。
边际效用表示消费者对商品的额外满足程度，即消费者对商品的需求强度。
消费者的效用最大化问题可以表达为以下数学方程：Max U(X,Y) = X^a * Y^bSubject to: PX*X + PY*Y ≤ M其中，a和b是效用函数中的参数，代表消费者对商品X和Y的偏好程度。
假设a和b都是正数。
为了求解上述问题，我们需要使用拉格朗日乘数法，根据约束条件构建拉格朗日函数：L(X,Y,λ)=U(X,Y)-λ(PX*X+PY*Y-M)其中，λ是拉格朗日乘数。
然后我们对L(X,Y,λ)分别对X、Y和λ求偏导，并置导数等于零，解得：dL/dX=a*X^(a-1)*Y^b-λ*PX=0①dL/dY=b*X^a*Y^(b-1)-λ*PY=0②PX*X+PY*Y-M=0③根据上面的三个方程，我们可以解出X和Y的函数关系：根据①式，可以解出λ为：λ=(a*X^(a-1)*Y^b)/PX④根据②式，可以解出λ为：λ=(b*X^a*Y^(b-1))/PY⑤将④式代入③式，可以得到一个只包含X和Y的方程：PX*X+PY*Y-M=0带入式⑤，并整理可得：a*X^a*Y^b*PX/PY-M=0化简后，可得：X^a*Y^b=M*(PY/PX)⑥根据式⑥，我们可以得到马歇尔需求函数：X=(M*(PY/PX))^(1/a)*Y^(b/a)⑦通过马歇尔需求函数，我们可以推导出马歇尔需求曲线，即在给定价格和收入的条件下，消费者对其中一种商品的需求数量与价格之间的关系。
间接效用函数-详解
间接效用函数-名词详解间接效用函数(Indirect Utility Function)目录• 1 什么是间接效用函数• 2 间接效用函数的内容• 3 间接效用函数的性质• 4 相关条目什么是间接效用函数间接效用函数是指消费者在进行消费活动时，当自变量商品价格向量C和消费者的消费预算S．T．发生冲突时，即C．Z＞S．T．时，在满足C．Z≤S．T．情况下，让效用函数u(z)取得最大值。
间接效用函数的内容在实际中，消费者在购买一种商品时会面临许多选择，例如同种商品有许多不同的品牌，或者是消费者要购买的这种商品可以被其他相类似的商品而替代。
因此，消费者在购买商品时做出的决定其实是一个决策问题效用实际上是消费者在进行消费的过程中，从销售商提供的商品或者服务中是否能得到满足感。
我们给效用附加上一个效用值，通过比较不同商品或者服务的效用值来做出购买的决定。
间接效用函数表示收入和价格两个变量下消费者的最优消费时的效用。
间接效用函数的存在对于说明政府水平的福利影响有比较便利的条件成立。
间接效用函数的性质间接效用函数 v(p, m) 是价格和收入的函数，消费者的最大化效用，是消费束x的函数。
可以由预算约束（收入m）和外在的相对价格（p）关系间接地表达。
具有如下性质：1.关于p和m是零次齐次的，即对于所有t>0，是零次齐次的，都有v(p,m)=v(t p,t m)。
2.对于p是非递增的和拟凸的，即是非递增的和拟凸的，v(p,m)≤0。
3.对于m是严格递增的，即是严格递增的，v(p,m)>0。
4.对于所有的p>0和m>0是连续的，即如果u(x)连续，则是连续的，连续其最大化的一阶导数值也是连续的。
其最大化的一阶导数值也是连续的。
5.满足罗伊恒等式(Roy’sidentity)。
相关条目•需求函数•效用函数-全文完-。
第二讲间接效用函数与支出函数 第一节间接效用函数 间接效用函数的定义
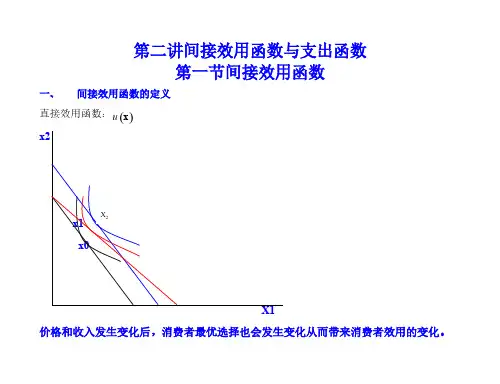
x1*
y 2p1
2 2*0.5
2
税收总量=2*0.25=0.5。与所得税相同。
v (.) y y
22 =1.41
2p1 2p2 2 * 0.5 2 *1
商品税带来的效用损失大于所得税。
为什么？
第二节支出函数 一、 支出函数的定义
y
y
0
0
4.间接效用函数v p, y关于价格 p 递减
设 x*i 0, 用与（3）同样的方法可证：
v(p, pi
y)
L(x*, *)
pi
* x *i
〈0
5、间接效用函数v p, y在p, y上拟凸
定义 A1.27：一个函数 f : D ? 是拟凸函数，当且仅当对于所
有 X1, X2 D ，有： f (Xt ) max[ f (X1), f (X2 )] 。即凸组合的函
x
px,
x
x
x
?
n
,u
x
u,u
?
两元空间支出最小化：
ep,u p1x1h p1, p2,u p2x2h p1, p2,u
min x1, x2
p1x1
p1,
p2 , u
p2
x2
p1,
p2 , u
,
s.t., u x1, x2 u
x2
p0 p0 p1
X0
X1
p1
希克斯需求函数（补偿需求函数，或实际收入不变的需求函数）
第二讲间接效用函数与支出函数 第一节间接效用函数
一、 间接效用函数的定义
直接效用函数：u x
x2
X2
间接效用函数与消费中的对偶性
间接效用函数与消费中的对偶性（一）间接效用函数1、直接效用函数：效用是消费量的函数，)(x u u =。
2、间接效用函数：令),(w p x x **=为效用最大化问题的解，)],([),(w p x u w p v *=为间接效用函数。
w 为收入。
3、直接效用函数描述的偏好独立于市场，间接效用函数反映最优化程度和市场价格。
4、推导罗伊恒等式ww p v p w p v w p x j j ∂∂∂∂-=),(),(),(，n j ,,2,1 = 推导：由于)(max ),(x u w p v =，所以，),(w p v 关于w p ,得偏导数，按包络定理等于求)(max x u 关于w p ,的导数，求导如下：)()(),(x p w x u x L ⋅-+=λλ),(),(),(w p x x w x L w m p v =***=∂∂=∂∂λλx px L p m p v ⋅-=∂∂=∂∂***λλ),(),( x wm p v p m p v =∂∂∂∂-),(),( 罗伊恒等式的含义：如果间接效用函数已知，且连续可导，那么，就可以求出马歇尔需求函数。
（二）对偶性定理1、对偶性问题：是指一些成对的问题和概念，它们阐述的行为原则是一致的，只是（目标函数和约束条件的）表达正好相反。
（见肖红叶著《高级微观经济学》35页。
）2、用对偶性定理描述直接效用函数与间接效用函数的关系，或直接效用函数与间接效用函数间存在对偶关系。
显示偏好理论（46页）（参阅厉以宁《西方经济学》67-71页、肖红叶著《高级微观经济学》18页、黄亚钧、姜纬《微观经济学》第一版63-67页）1、前面是从偏好（或效用函数）到最优选择，显示偏好理论则是从主体的选择行为观察主体的偏好。
2、假定（见肖红叶著《高级微观经济学》18页。
）（一）显示偏好弱公理1、在0p 价格下，消费者既可以购买0q （这是一个商品组合！），也可以购买1q （这是一个商品组合！），但他购买了0q ，这一行为显示消费者相对于1q 更偏好0q 。
经济学第二讲笔记
意义：控制消费者的消费行为实质上可以通过 p《价 格政策，价格改革》及 y《收入政策》 二、间接效用函数的性质 如果 u(x)在Rn + 是连续且严格递增的，则 v(p,y)= max u(x) x∈ Rn + st: px≤y 有
n 1、在Rn ++ × R + 是连续的
2、关于（p,y）是零次齐次的 3、对于 y 严格递增 4、对于 p 严格递减 5、满足罗尔恒等式 即 v(p,y)在点（p0 ,y 0 ）可等且
= =
1
x 2 1
1
−1 2
x2 - p1 λ = 0
−1
1 2
⋯⋯① ⋯⋯②
1 2 2 x x 2 1 2
- p2 λ = 0
= y − p1 x1 − p2 x2 = 0 ⋯ ⋯ ③
x2 x1
由①②有 即
= p1
2
p
x 2 = p 1 x1
2
p
代入③有
∗ x1 = 2p ∗ x2 = 2p y
y
ρ
+ 1]
有
p 1 ρ −1 p2
ρ ρ −1 ρ
= u[
+ 1]
−1 ρ 1 ρ −1
=u[p1
+ p2 ] . p2
γ −1 p2 )γ .
1
ρ −1 ρ −1 ρ
γ =u(p1
+
p2
γ−1
⋯⑥
代⑥给④有
h x1 =up1
1 ρ −1
. p2
−1 ρ −1
γ (p1
+
γ −1 p2 )γ .
1
p2
3、总效应<TE> SE + IE= TE 讨论题： 住房由福利分房改为货币分房，分析其效应 配合上图
第2章 间接效用函数与支出函数
运用包络定理，可得到：
e( p, u ) L( x* , * ) h xi xi ( p, u ) * pi pi
例：
min( p1 x1 p2 x2 )
x1 , x2
1
由u( x1 , x2 ) ( x1 x2 ) , 0 1),求支出函数.
p
r 1 1
up2 ( p p )
r 1
1 1 r r 2
p
r 1 2
u( p p )
r 1
1 r r 2
求上式对于p1的偏导，可直接验证谢泼特引理。
四、预算份额
如果收入为y，消费的商品数量和价格分别为： ( x1, x2 , , xn )和( p1, p2 , pn )
pi xi 则称： Si 为购买xi的收入（预算）份额。 y 如果i=1,2，则 p1 x1 S1 S2 1 S1 y
因此， * 0
v( p, y ) 0 y
（4）满足罗尔恒等式。
v ( p , y ) ( p , y ) 如果间接效用函数 在点上 是可导的，
v ( p, y ) 0 且 y
v( p, y) x j ( p, y) p j
v( p, y) , j 1, 2, y
两式相除，就可以得到罗尔恒等式。
3.间接效用函数的应用:政府税收对效用的影响 设效用函数为: u( x1 , x2 ) x1 x2 最大化问题为: max x1 x2
s.t. p1x1 p2 x2 y
L x1 x2 ( y p1 x1 p2 x2 )
L 0 x1 L 0 x2
,n
max u f ( p, y ) s.t px y 写出Lagrange方程 L(x, )=u(x)+(y-px) v ( p, y ) L ( x , ) |x x ( p , y ) y y v ( p, y ) L ( x , ) |x x ( p , y ) x p p
间接效用函数
数学附录
• ４ 内点和界点：欧氏空间中一个子集X的点x叫做一个 内点，如果它的某一个邻域B(x,)整个被包含在X内； 称x为X的一个界点，如果x的每一个邻域既包含X的点 也包含余集Xc的点。X的全体内点之集记为Int(X)，X 的全体界点之集记为Bdy(X)。 • 一个开集G的每个点都是内点，一个闭集F包含它所有 界点。 • ５ 紧致性：欧氏空间中一个子集X叫做紧致的（序列 紧），如果X中每一个序列都有子序列收敛于X本身某 个点。可以证明，欧氏空间中的每个有界闭集都是紧 致集，反之亦然。
偏好和效用
• 消费集：考虑一个有M种商品的经济。一个各分 量非负的M-维向量x=(x1,...,xM)就称为一个商品向 量，这个向量的第m个分量xm表示第m种商品的量。 一个消费者i意欲消费的商品向量的全体Xi构成他 的消费集。在一般情况下，我们认为Xi=RM+。 • 容许消费集：对消费者i来说，一个商品向量称为 容许的，如果他的收入足够支付购买这个商品向 量所需的花费。对于给定的价格向量p和给定的收 入I, 消费者i的所有容许商品向量构成他的容许消 费集，记为Bi(p,I)。
数学附录
• 9 凹函数： Assume that a real-valued function f is defined on a convex set Xn. f is said to be concave if for any x’ and x” in X, and any real number (0, 1), it holds that
数学附录 • ７ 凸集：A set Xn is said to be a convex set if for any two points x’ and x” in X and any real number [0, 1], the point x=(1-)x’+x” is contained in X. The intersection of any number of convex set is also convex. • ８. For any m points x1,…,xm in n, and any 1,…,m in [0, 1] such that ii=1, x=iixi is said to be a convex combination of x1,…,xm.
间接效用函数
间接效用函数
1 什么是间接效用函数
间接效用函数是指一种实现某个社会理想状态（如极大消费者满
意度和卓越企业家利润）所必需的行动，通常用来表示消费者和企业
家的兴趣间的效用交换。
它通过向消费者提供不同的好处来获取更大
的收益，而企业家也会得到更大的收益，从而达到实现一定的社会理
想状态的目的。
2 间接效用函数的作用
间接效用函数通常用来衡量一个经济体如何服务于它的消费者，
它可以用来判断消费者和企业家之间的激励关系。
它推动了经济状况
的发展，有助于实现可持续发展的战略目标。
同时它也有助于企业领
导者制定合理的经营战略，有利于企业长期可持续经营及实现企业家
利润最大化目标。
3 间接效用函数的形成方式
间接效用函数形成的主要因素有技术发展、政府政策和市场变化
三个方面。
技术的发展是形成间接效用函数的关键动力，它改善了消
费者的购买力，增强了企业家的实力。
政府政策则是对市场行为把关，它可以建立健全监管制度，减少市场操纵，改善企业家利润和消费者
收益之间的不平衡状态。
市场变化是根据客观定律而发生的，它影响
着间接效用函数的形成。
4 结论
间接效用函数是实现极大消费者满意和卓越企业家利润的重要指标，它的形成主要受到技术发展、政府政策和市场变化的影响，它不仅有助于实现可持续发展的战略目标，更有助于领导者制定合理的经营战略。
第三讲 间接效用函数与支出函数
x( p1 , w1 )
x R : u ( x) v
2
5、罗伊恒等关系
• 如果间接效用函数 v( p, w) 在点上 ( p , w ) 是可导的且 v( p, w) 0 ， w • 一定存在
v( p, w) x j ( p, w) p j
性质5证明
由 max u f ( p, y ) s.t px y 得，L(x, )= u(x)+ (y- px) v ( p, y ) L( x , ) |x x ( p , y ) y y v ( p, y ) L( x , ) |x x ( p , y ) x p p
p
y
• 现在应用效用最大化理论来分析两个实际问题：所得税与 销售税的比较，价格补贴发放办法比较。 • 问题1：所得税与销售税哪一种对消费者更为有利？ • 国家向居民征税有两种办法，一种是征收所得税，另一种 是征收销售税。假定不论采取哪种办法，居民缴纳的税额 是一样的。那么，哪一种征税办法对居民更为有利些? • 问题2：涨价补贴对消费者是否有利？ • 商品涨价，国家要发放价格补贴。一种办法是控制价格， 不许涨价，把价格补贴发给生产者。另一种办法是允许涨 价，把价格补贴发给消费者。那么，哪一种补贴办法对消 费者更为有利？ • 为了分析这两个问题，设当前的市场价格体系为 p，消费 者收入为 r，消费者的选择为 xD( p, r)。
1 1 2
1
1 1
1 1 p2 p1
1 1 2
x2
yp p1
1
p2
1 1 1
1
间接效用函数与支出函数
(2)
∂ψ ∂x j
= α j Ax1α1 LL xαj j −1L xnα n
− λp j1 = 0
(3)
∂ψ ∂x1
=
αn
Ax1α1
xα 2 2
LLL
xnα
n
−1
−
λpn
=0
(4)
∑ ∂ψ
∂λ
n
=m−
i =1
pi xi
=0
(5)
由 (2) 得: (3)
xi
=
αi pjxj α j pi
;
把上两式分别代入（5）式得:
1
1
1
( ) e( p,u) =
p1⎜⎜⎝⎛
2up2 p1
⎟⎟⎠⎞3
+
p2 ⎜⎜⎝⎛
up12 4 p22
⎟⎟⎠⎞ 3
=
2up12 p2
1 3
+
⎜⎜⎝⎛
up12 p2 4
⎟⎟⎠⎞
3
1
e(
p,u)
=
3⎜⎜⎝⎛
up12 p2 4
⎟⎟⎠⎞ 3
也可根据间接效用函数与支出函数互为倒函数的关系直接得出：
1
v( p, m)
=
αim
n
pi α j
j =1
；因为
n
αj
j =1
=
1 ；所以
xi
(
p,
m)
=
αim pi
；
我们还可以通过对其效用函数进行单调变化，进而可方便的得出其马歇尔需求函数；
n
∑ ln u(x) = ln A + αi ⋅ ln xi i =1
（2）把上所得的马歇尔需求函数代入目标函数得间接效用函数：
间接效用函数
在财富上是严格递增的，而在价格上则是严格递减的。
• 代入支出px得最小支出称为支出函数： 它对于价格和财富是零次齐次的，即价格和财富的同比例变化并不影响效用水平。
（2）间接效用函数的性质
记为e(p,y) 在财富上是严格递增的，而在价格上则是严格递减的。
即最优的消费束都在预算线的上界。
（1）基本概念：即是在满足消费预算约束的条件下，消费者获得的最大的效用水平时的解。
• （1）基本概念
• 若 v(p,y)ux成(p 立,y，)则
就v为( p间, 接y ) 效用函数。
• 间接效用函数表示收入和价格两个变量下消费者
的最优消费时的效用。
• 间接效用函数的存在对于说明政府水平的福利影 响有比较便利的条件
一、间接效用函数
• （2）间接效用函数的性质
• A.它对于价格和财富是零次齐次的，即价格和财 富的同比例变化并不影响效用水平。
它对于价格和财富是零次齐次的，即价格和财富的同比例变化并不影响效用水平。
（2）马歇尔需求函数的推导
如果间接效用函数 在点上 是可导的且
，
在价格和财富上是连续的。
二、支出函数
二、支出函数
• 2.希克斯需求函数 • 希克斯的需求函一般记为：h ( p , u ) • 前者是为达到既定的效用水平u，选择的最小支
•建立L函数
L ( x 1 ,x 2 , ) ( x 1 x 2 ) 1 ( w p 1 x 1 p 2 x 2 )
•得到的一阶条件为
L x1
1
( x1
x
2
)
1
1
x11
p1 0
L x2
1
( x1
x
2
)
效用最大化问题中的三个函数——需求函数、间接效用函数、支出函数
效⽤最⼤化问题中的三个函数——需求函数、间接效⽤函数、⽀出函数需求函数：性质：关于所有价格和收⼊零次齐次性（所有商品价格与收⼊乘以t倍），最优化需求数量保持不变。
1. CES需求函数CES需求函数的函数形式为：构造朗格朗⽇表达式：求偏导数得到⼀阶条件：根据上式求得需求函数：从上式看出我们确实可以得到⼀个对于任意的CES函数的需求函数。
但是个⼈建议，由于CES函数有不同的“形式”（⽐如说也是⼀种CES函数，所以在实际做题求解CES函数的需求函数的过程中，建议重复上述证明步骤，⽤构造拉格朗⽇表达式，利⽤⼀阶条件来求解需求函数）当的时候，此时为完全互补效⽤函数，利⽤消费者为了效⽤最⼤化只会选择L型⽆差异曲线顶点消费的特征来直接求解，就不⽤构造朗格朗⽇表达式了。
除此之外，联系弹性和之前讲过的（点击链接回顾）的概念，我们不难发现，，即替代弹性等于1为分界线。
举例说明：当的时候，此时商品x花费的收⼊份额为不是常数，越⾼，x的相对价格越⾼，它所花费的收⼊份额就越⼩。
换⾔之，x的需求对其价格的反应就⾮常敏感，价格的上升减少了x的总花费。
不过收⼊的变化并不影响消费份额。
U (x ,y )=+δx δδy δf =+δx δ+δy δλ(I −p x −x p y )y ⎩⎨⎧=x −λp =0∂x ∂f δ−1x =x −λp =0∂x∂f δ−1x =I −p x −p y =0∂λ∂f x y ⎩⎨⎧x =p (1+())x p y p x 1−δδy =p (1+())y p x p y 1−δδI δU =(αx +11ραx )22ρρ1δ→∞δ=0σ=1−δ1δ=0.5x =p (1+())x p y p x I p x /I =x 1/[1+(p /p )]x y p x2. 柯布道格拉斯需求函数柯布-道格拉斯效⽤函数的表达式为：同样可以利⽤朗格朗⽇法来算出需求函数，由于过程重复，在此不做赘述，得到如下的结果：由此我们得到⼀个重要的结论，在柯布道格拉斯效⽤函数情形下，消费者会花费⽐例的收⼊去购买商品x，⽤的⽐例去购买y。
斯勒斯基方程(补充1)
Chapter Seven: 斯勒斯基方程这一章主要用数学方法对收入效应和替代效应进行讨论。
由于在经济学中对替代效应有两种描述方法，因此我们也将对有关的概念作简要的介绍。
一、直接效用函数、间接效用函数和支出函数（一）直接效用函数就是由商品的消费量所决定的效用函数。
其一般描述为：)(x u u =，其中x 是向量。
在序数效用论中，直接效用函数本身没有经济意义，但是在一定效用值下的消费束x *是有意义的。
因此，我们只关心直接效用函数值达到最大时的需求。
（二）间接效用函数根据约束条件下的极值问题，求出最优选择之后，可以将x *带回间接效用函数中去，从而得到一个新的效用函数，这个效用函数是价格和收入的函数，我们将这个效用函数称作间接效用函数。
一般描述为：),,(21m p p v 。
间接效用函数是通过求解下述效用最大化问题得到的，即mx p x p t s x x u u =+=221121..),(max由此：（1）求出马歇尔需求函数：),,(21m p p x i ，所有变量都可度量。
（2）将其带回目标函数，可以求出间接效用函数 ),,(21m p p v（三）支出函数消费者均衡一般是指在一定的预算约束条件下可以给消费者带来最大效用的商品消费数量。
实际上，问题也可以反过来提出，即在一定的效用水平上的最小货币支出数量是多少。
支出函数衡量的是与一定的效用水平相对应的在消费者均衡条件下的最小货币支出数量。
它是与马歇尔需求函数相对应的最小支出函数，是通过求解下述支出最小化问题得到的，即),(..min 212211x x u u t s x p x p =+由此：（1）求出希克斯需求函数：),,(21u p p x i ，其中包含不可度量因素。
（2）将其带回目标函数，可以求出支出函数 ))(,,(21x u p p e二、用货币度量的直接和间接效用函数（一）用货币侧度的直接效用函数假定在价格向量q 条件下与消费束向量x 相对应存在一个效用水平)(x u u =。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二、支出函数
p1 p2
1
1
一、间接效用函数
令
r 1
x1 x2
yp1r 1 p1r p2r
yp2r 1 p1r p2r
一、间接效用函数
• （3）马歇尔需求函数的性质 • A.在价格和收入上，需求函数是零次齐次的。
即对于任意给定的p、y，都有a>0，使得 成立。 x(ap, ay) x( p, y) • B.瓦尔拉斯定理。即最优的消费束都在预算线 的上界。 x R, px y
• A.它对于价格和财富是零次齐次的，即价格和财 富的同比例变化并不影响效用水平。
• B.在财富上是严格递增的，而在价格上则是严格 递减的。
• C.拟凸的。 • D.在价格和财富上是连续的。
一、间接效用函数
• (3) 罗伊恒等式
• 如果间接效用函数 v( p在, y)点上 ( p是, 可y)导的
且 ， v( p, w) 0 w
• 一定存在 x j
(
p,
y)
v( p, p j
y)
v( p, y) , j 1, 2, y
,n
由 max u f ( p, w)
s.t px w
得，L(x, )= u(x)+ (w - px)
v( p, w) w
L( x , )
w
|x x( p,w)
v( p, w) p
L( x , )
第二章 间接效用函数与支出函数
内蒙古财经大学 张建斌
一、间接效用函数
• 1.马歇尔需求函数 （1）基本概念：即是在满足消费预算约束的条
件下，消费者获得的最大的效用水平时的解。 • 记为：x* x( p, y) • 这时消费者的所有的支出将与其收入达到一致。
满足：px=y
一、间接效用函数
• （2）马歇尔需求函数的推导
一、间接效用函数
• 2.间接效用函数
• （1）基本概念
• 若 v( p, y) u x成( p立, y，) 则
就v为( p间, 接y)效用函数。
• 间接效用函数表示收入和价格两个变量下消费者
的最优消费时的效用。
• 间接效用函数的存在对于说明政府水平的福利影 响有比较便利的条件
一、间接效用函数
• （2）间接效用函数的性质
p
| x x ( p ,w)
x
二、支出函数
• 1.支出函数： • 这是个支出最小化问题，选择合适的x使得满足
约束条件
min
px
s.t
u( x) u
L=p x- u( x) - u
L xi
pi
u ( x ) xi
0
L
u ( x ) - u 0
pi pj
u ( x ) u ( x )
1
u( x1, x2 ) ( x1 x2 ) , 0 1, 求xi xi ( p1, p2 , y), i 1, 2
•建立L函数
1
L ( x1, x2 , ) ( x1 x2 ) (w p1x1 p2 x2 )
•得到的一阶条件为
L x1
1
( x1
x2
)
1
1
x11
p1
0
L x2
1
( x1
x2
)
1
1
x12
p2
0
L
w p1 x1 p2 x2 0
一、间接效用函数
1
x1 x2
p1 p2
,x1 x2 Biblioteka y p1 x1 p2 x2
y
x2
1
p1 1
p2 1
p2 1
x2
1
yp2 1
p1 1 p2 1
x1
1
yp1 1
p1 1 p2 1
xi x j
二、支出函数
• 求出的最小解称为 • 希克斯需求函数： • 记为：xi xih ( p, u), i 1, 2,...n • 代入支出px得最小支出称为支出函数：
记为e(p,y)
二、支出函数
二、支出函数
• 2.希克斯需求函数 • 希克斯的需求函一般记为：h( p, u) • 前者是为达到既定的效用水平u，选择的最小支