人教版初三数学导学案锐角三角函数
濠知教育初三数学锐角三角函数导学案
学 生教 师 吴老师 日 期 2013/12/22 年 级 初三学 科数学时 段10:10-11:40学 情 分 析 锐角三角函数在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题,题型常以填空、选择、简答或综合出现,分值一般在20%左右,有时也单独成题,形成创新与探索型试题;有利于培养学生的综合素质。
课 题 锐角三角函数学习目标与 考点分析 本节知识的考查一般以填空题和选择题的形式出现,主要考查锐角三角函数的意义,即运用sin a 、cos a 、tan a 、cot a 准确表示出直角三角形中两边的比(a 为锐角),考查锐角三角函数的增减性,特殊角的三角函数值以及互为余角、同角三角函数间的关系。
学习重点 难 点让学生熟练掌握解题的方法,会运用知识灵活计算,并能正确地进行相关题目的运算教学方法 讲练结合、互动启发教学过程【例1】在Rt △ABC 中,∠C =900,AC =12,BC =15。
(1)求AB 的长;(2)求sinA 、cosA 的值; (3)求A A 22cos sin +的值; (4)比较sinA 、cosB 的大小。
变式:(1)在Rt △ABC 中,∠C =900,5=a ,2=b ,则sinA = 。
(2)在Rt △ABC 中,∠A =900,如果BC =10,sinB =0.6,那么AC = 。
濠知教育学科导学案【例2】计算:020045sin 30cot 60sin +⋅【例3】已知,在Rt △ABC 中,∠C =900,25tan =B ,那么cosA ( ) A 、25 B 、35C 、552 D 、32变式:已知α为锐角,且54cos =α,则ααcot sin += 。
【例4】已知3cot tan =+αα,α为锐角,则αα22cot tan += 。
评注:由锐角三角函数定义不难推出1cos sin 22=+A A ,1cot tan =⋅αα,它们是中考中常用的“等式”。
锐角三角函数(1)

雨母山中学 九年级数学导学案 主备人 .周扬清
锐角三角函数(1)
课型 :预+展 班级 小组 小主人姓名 编号sx 09031
【抽测】
【目标要求】
1 认识锐角三角函数及它们的值的取值范围。
(重点)
2 在利用相似三角形知识测量、计算物体高度的过程中,联想函数概念,观察、发现、建立锐角三角函数概念。
(难点)
3
在运用知识解决问题的过程中,观察、联想、分析、推断可以获得数学发现,体验数学活动充满探索性和创造性。
【自主探究】
知识点一:锐角三角形函数的概念
在△ABC 中,∠C=900,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,且满足a:b =3:4,求∠B 的四个三角函数。
知识点二:同角三角函数关系及互余角的三角函数的关系
如图,在△ABC 中,∠C=900,AC,BC 均为直角边,AB 为斜边,求2
2
sin cos A A +与
sin tan cos A A A
-
的值。
【小试牛刀】。
1 在△ABC 中,∠C=900,AC=9,BC=12,则sin A +sin B = 。
2 在△ABC 中,∠C=900,AB=2,AC=1,则tan B = 。
3 在△ABC 中,∠C=900,BC=4,sin A =23,求AC 边的长。
【整理评价】
1 整理今天所学内容,展示 次,质疑 次,参与 次。
2 反思我这节课的表现,学习状态( )
A 很认真,值得表扬
B 还可以,继续努力
C 还得加油
【课后作业】
课本P80 复习题 第2、3、7题 P81 第10题.。
(初三数学教案)人教版初中九年级数学下册第28章锐角三角函数28.2.2 应用举例第3课时教学设计

28.2 解直角三角形及其应用28.2.2 应用举例(第3课时)一、教学目标【知识与技能】1.正确理解方向角、坡度、坡角的概念;2.能运用解直角三角形知识解决方向角、坡度的问题;3.能够解决与解直角三角形有关的实际问题,如航海航空、建桥修路、测量技术、图案设计等.【过程与方法】通过实际问题的求解,总结出用解直角三角形的知识解决问题的一般过程,增强分析问题和解决问题的能力。
【情感态度与价值观】渗透数形结合的思想方法,增强学生的数学应用意识和能力.二、课型新授课三、课时第3课时共3课时四、教学重难点【教学重点】用三角函数有关知识解决方位角问题.【教学难点】学会准确分析问题并将实际问题转化成数学模型.五、课前准备教师:课件、直尺、三角板等.学生:直尺、三角板.六、教学过程(一)导入新课(出示课件2)宜宾是国家级历史文化名城,大观楼是其标志性建筑之一(如图①).喜爱数学的小伟决定用所学的知识测量大观楼的高度,如图②所示,他站在点B处利用测角仪测得大观楼最高点P的仰角为45°,又前进了12 m到达点A处,测得点P的仰角为60°.请你帮助小伟算一算大观楼的高度(测角仪的高度忽略不计,结果保留整数).(二)探索新知知识点1 方向角的有关问题(出示课件4)方向角的定义:指北或指南方向线与目标方向线所成的小于90°的角.教师强调:(出示课件5)(1)因为方向角是指北或指南方向线与目标方向线所成的角,所以方向角通常都写成“北偏……”,“南偏……”,的形式.(2)解决实际问题时,可利用正南、正北、正西、正东方向线构造直角三角形来求解.(3)观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的,通常借助于此性质进行角度转换.考点1 有关方向角的实际问题——距离.(出示课件6)例如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?学生独立思考后师生共同解决:(出示课件7)解:如图,在Rt△APC中,PC=PA·cos(90°-65°)=80×cos25°≈80×0.91=72.505.在Rt△BPC中,∠B=34°,sinPCBPB=,()72.505130n mile.sin sin34PCPBB∴==≈因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130n mile.教师强调:利用解直角三角形的知识解决实际问题的一般过程是:(出示课件8)(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;(3)得到数学问题的答案;(4)得到实际问题的答案.出示课件9,学生独立解决,一生板演,教师订正.考点2 有关方向角的实际问题——预测路线.(出示课件10)例海中有一个小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?学生独立思考后,师生共同解决:(出示课件13~14)解:过A 作AF ⊥BC 于点F ,则AF 的长是A 到BC 的最短距离.∵BD ∥CE ∥AF ,∴∠DBA=∠BAF=60°,∠ACE=∠CAF=30°,∴∠BAC=∠BAF -∠CAF=60°-30°=30°.又∵∠ABC=∠DBF -∠DBA=90°-60°=30°=∠BAC ,∴BC=AC=12海里,∴cos 30?AF AC ==海里),,故渔船继续向正东方向行驶,没有触礁的危险.出示课件13~14,学生独立解决,一生板演,教师订正. 知识点2 坡度、坡角有关的问题解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝或山的高度h时,8392.1036>≈我们无法直接测量,我们又该如何呢?(出示课件15)教师问:如图,从山脚到山顶有两条路AB 与BC ,问哪条路比较陡?如何用数量来刻画哪条路陡呢?(出示课件16)学生思考后,师生共同总结:(出示课件17)坡角:坡面与水平面的夹角叫做坡角,用字母α表示.坡度(坡比):坡面的铅直高度h 和水平距离l 的比叫做坡度,用字母i 表示,如图,坡度通常写成tan h i lα==的形式.教师强调:坡度越大,坡角越大,坡面越陡.出示课件18,学生独立解决并口答,教师订正.考点1 利用坡度、坡角解答大坝问题例 如图,防洪大堤的横截面是梯形 ABCD ,其中AD ∥BC ,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20m ,求改造后的坡长AE .(结果保留根号)(出示课件19)学生独立思考后,师生共同解答:(出示课件20)解:过点A 作AF ⊥BC 于点F ,在Rt △ABF 中,∠ABF=∠α=60°,则AF=AB ·sin60°=,在Rt △AEF 中,∠E=∠β=45°,则sin 45AF AE ==故改造后的坡长AE 为m.出示课件21~22,学生独立解决,一生板演,教师订正. 考点2 利用坡度、坡角解答山坡问题例 如图,一山坡的坡度为i=1:2.小刚从山脚A 出发,沿山坡向上走了240m 到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m )?(出示课件23)学生独立思考后,师生共同解答:(出示课件24) 解:用α表示坡角的大小,由题意可得1tan 0.52α==,因此α≈26.57°.在Rt △ABC 中,∠B=90°,∠A=26.57°,AC=240m , 因此sin 240BC BC AC α==, 从而BC=240×sin26.57°≈107.3(m ).答:这座山坡的坡角约为26.57°,小刚上升了约107.3m . 出示课件25,学生独立解决,教师订正.(三)课堂练习(出示课件26-36)练习课件26-36页题目,巩固所学知识点,约用时20分钟。
锐角三角函数的定义 导学案
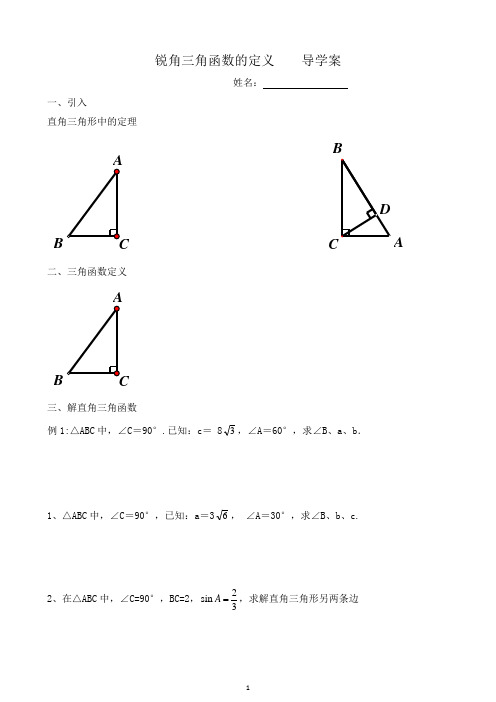
锐角三角函数的定义导学案姓名:一、引入直角三角形中的定理BD CBA二、三角函数定义B三、解直角三角函数例1:△ABC中,∠C=90°.已知:c= 83,∠A=60°,求∠B、a、b.1、△ABC中,∠C=90°,已知:a=36,∠A=30°,求∠B、b、c.2、在△ABC中,∠C=90°,BC=2,2sin3A ,求解直角三角形另两条边3、在△ABC 中,∠ACB =90°,cosA=33,AB =8cm ,则△ABC 的面积为4、由下列条件解直角三角形:在Rt △ABC 中,∠C=90°:(1)已知a=4,c=24, (2)已知b=10,∠B=60°.例2:在Rt △ABC 中,∠C =90°,a =2,b =3,则cosA = ,sinB = ,tanB = 。
1、直角三角形ABC 的面积为24cm 2,直角边AB 为6cm ,∠A 是锐角,则sinA = 。
2、如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =2,AC =3,则sinB 的值是( )3、在△ABC 中,∠C=90°,AB=5,AC=4,则cosB = ,sinA = ,tanA = 。
cosA = ,sinB = ,tanB = 。
4、如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB ,tan ∠BCD=,AC=12,则BC= .5、在Rt△ABC 中,∠C=90°,AB=3,BC=1,则sinA="______," tanA=" _______," cosA=_______ SinB="______," tanB=" _______," cosB=_______6、如图,在菱形ABCD 中,DE ⊥AB , 垂足为E , DE =8cm , , 则菱形ABCD 的面积是__________.7、如图,正方形网格中,每一个小正方形的边长都是 , 四边形的四个顶点都在格点上,为边的中点,若把四边形绕着点顺时针旋转.【小题1】画出四边形旋转后的图形;【小题2】设点旋转后的对应点为 , 则;【小题3】求点在旋转过程中所经过的路径长.例3:已知tan α=125,α是锐角,则sin α= 。
精品!九年级数学锐角三角函数整章导学案教案含答案解析

知识点:锐角三角函数的概念问题情境1:求一个锐角的正弦问题模型:已知锐角*,求它的正弦.求解模型:(1)找出(或构造)锐角★所在的直角三角形(2)确定锐角★的对边和斜边的长(3)求出★的正弦值例题:如图,在Rt^ABC中,/ C=90° ,求sinA和sinB的值.分析:要求sinA和sinB的值,只需求出/ A、/ B的对边以及斜边的长解:⑴在Rt^ABC中,AC=4,BC=3贝U AB=;AC2+ BC2 =5BC 3 故sinA=——=一AB 5 sinB= AC 4 AB 5(2)在RtzXABC中,AB=13,BC=5RJ ACK,AB2— BC2 =12士A* ,八BC 5故sinA=——=—,sinB=AB 13 AC 12 AB 13练习:1.如图,已知直线11 // I2 // I3 // I4 ,相邻两条平行直线间的距离都是的四个顶点分别在四条直线上,则sina=.5【答案】—51 ,如果正方形ABCDAB =4, AC =2,则 sin B 的值是( )5 7A. ----- 14 3.在 Rt△ ABC 中,/ C=90 sinA= 1 ,则 BC : AC : AB 等于( 2 A.1 : 2 : 5B.1 : <3<5 C.1 : V 3 : 2 D.1 : 2 : J 3 【答案】C 4.把RtAABC 的三边都扩大十倍,关于锐角 A 的正弦值:甲同学说扩大十倍;乙同学说不 变;丙同学说缩小十倍.那么你认为正确的说法应是( C.丙 D.都不正确AC=12 ,求 sinA 、sinB 的值。
A.甲B.乙 【答案】B 1 _【答案】:如图,过点 B 作BDL BC 于D,过点 A 作A 已BC 于E,贝U BD=- AC=6), 在 Rt^ABC 中, BD sin / BAC= ---AB•.S A ABC= 1 AC- 248 AE=—5AB=10, AD=6 故 BD=8,_ _8 _ 4一 10 一 51八BD- BC- AE2AE• • sin Z ABE= ---------- AB48 51024 25问题情境2:求一个锐角的余弦 问题模型:已知锐角支,求它的余弦. 求解模型:2.在^ ABC 中,/ A = 120°,找出(或构造)锐角★所在的直角三角形(1)找出(或构造)锐角★所在的直角三角形(2)确定锐角★的邻边和斜边的长(3)求出★的余弦值例题:如图,直径为10的。
人教版初三数学下册锐角三角函数——余弦、正切 教案

∠A的邻边b∠A的对边a斜边cC
B
A
(1)34C
B
A
长沙市中(小)学教师统一备课用纸 科目 数学 年级 九年级 班级 时间 年 月 日 课题 锐角三角函数——余弦、正切 教学目标
1、感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实。
2、培养学生观察、比较、分析、概括的思维能力。熟练运用锐角三角函数的概念进行有关计算。
教材分析 重点:余弦、正切的概念; 难点:锐角三角函数的运用。
实 施 教 学 过 程 设 计
【课前热身】 如图1,在直角△ABC中,∠C=90o,若AB=5,AC=4,则sinA=______,sinB=______.
【合作探究】 •在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比是 ,
则:∠A的邻边与斜边的比呢? ∠A的对边与邻边的比呢?
【知识归纳】 1、余弦、正切定义:如图,在Rt△ABC中,∠C=90°,
把∠A的邻边与斜边的比叫做∠A的____,记作cosA,即cosA=A的邻边斜边=ac;
把∠A的对边与邻边的比叫做∠A的____,记作tanA,即tanA=AA的对边的邻边=ab. 2、锐角A的正弦、余弦、正切统称为∠A的 . 【合作探究】 知识点一 已知直角三角形的边长,求锐角的三角函数 例1: 求出下列直角三角形中两个锐角的正弦值、余弦值、正切值,发现什么规律?
sin A= sin B= cos A= cos B= tan A= tan B=
6C
B
A
知识点二 已知直角三角形中一个锐角的三角函数值,求其他三角函数值 例2:如图,在Rt△ABC中,∠C=90°,BC=•6,sinA=35,求cosA、tanB的值.
变式1:如图,在Rt△ABC中,∠C=90°,sinA=135,求cosA、tanB的值. 【针对训练】 1. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
则sinA=CD==
九年级数学下册锐角三角函数(3)《特殊角三角函数值》导学案

28.1 锐角三角函数(3)——特殊角三角函数值【学习目标】⑴: 能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
⑵: 能熟练计算含有30°、45°、60°角的三角函数的运算式【学习重点】熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式【学习难点】根据函数值说出对应的锐角度数 【学法指导】小组合作 教师点拨学习过程:一、新课引入1、在Rt △ACB 中, ∠C=90°,∠A=30 °若BC=1,则AB=____,AC= ____,∠B=_____2、在Rt △ACB 中,若∠A =45°,BC=1,则AB=____,AC= ____,∠B=_____。
3、让学生回忆 正弦、余弦、正切的定义 sinA=斜边的对边A ∠,cosA=斜边的邻边A ∠,tanA=的邻边的对边A A ∠∠ 二、自学指导一:阅读课本P65中的探究,并完成下面问题1、一副三角板中有几个不同的锐角?2、如何求出这几个锐角的正弦值、余弦值、正切值。
请写出推导过程。
提示:设每块三角尺较短的边长均为1,利用勾股定理和锐角三角函数的定义可以求出这些锐角三角函数值.1、特殊角的三角函数值表:请用五分钟熟记这些三角函数值,再跟同学分享你牢记的方法。
自学检测一:1.请快速回答出下列三角函数值sin45°= sin60°= sin30°=cos45°= cos60°= cos30°=tan45°= tan60°= tan30°=2.根据函数值说出对应的锐角度数Sin___°= sin___°= sin___°= Cos___°=cos___°= cos____°= tan___°= tan___°= tan____°=3.同桌之间互相出题,一人出题,两人回答,看谁回答得又快又对.三、自学指导二:P66例31.cos 260°表示什么意思? 锐角θ 三角函数 30° 45° 60° sin θ cos θ tan θ C B A B A2.如何计算含有30°、45°、60°角的三角函数的运算式自学检测二:1、计算:(1)2sin30°(2)cos245°(3)2sin30°-cos45°(4)sin60°·cos60°(5)cos230°+sin230°.(6)co s45sin45︒︒(7)co s45sin45︒︒-tan45°2.P67 1四、阅读课本66页例41.如何求出直角三角形中锐角的度数?同桌之间互相讨论得出解题方法。
锐角三角函数3——特殊角的三角函数值

3、思考 P83 第 9、10 题
忻州市十二中学
九年级 (数学)导学案 (教师版)
主备人:王小平 审核人:刘文华
授课人: 学生姓名:
授课时间: 小组: 课时
班级: 得分: 备注 (教师复备栏及学 生笔记)
课题 :28.1 锐角三角函数(3) 【学习目标】
1、 能推导并熟记 30°、45°、60°角的三角函数值,并能根据这 些值说出对应锐角度数。 2、 能熟练计算含有 30°、45°、60°角的三角函数的运算式。 【重点】熟记 30°、45°、60°角的三角函数值,能熟练计算含有 30°、45°、60°角的三角函数的运算式 【难点】30°、45°、60°角的三角函数值的推导过程。 【自学指导】仔细看:课本 P79—P80 例 4 结束。 想一想:1、30°、45°、60°角的三角函数值的推导过程。测】 课本 P80 练习 1、2。
【合作探究】
忻州市十二中学
九年级 (数学)导学案 (教师版)
【总结反思】
【当堂训练】 1、课本 P82 第 3 题
2、若( 3 tanA-3)2+│2cosB- 3 │=0,则△ABC( ) . A.是直角三角形 B.是等边三角形 C. 是含有 60°的任意三角形 D. 是顶角为钝角的等腰三角形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
濠知教育-----您值得信赖的中小学辅导专家
1
学 生 教 师 吴老师 日 期
2015/12/05
年 级 初三 学 科 数学 时 段
学 情
分 析
针对初三下册所学的知识点进行简要系统的复习与预习。
课 题 锐角三角函数
学习目标与
考点分析
1、使学生了解方位角的命名特点,能准确把握所指的方位角是指哪一个角
2、逐步培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.
3、巩固用三角函数有关知识解决问题,学会解决方位角问题.
学习重点
难 点
重点:用三角函数有关知识解决方位角问题
难点:学会准确分析问题并将实际问题转化成数学模型
教学方法 讲练结合、互动启发
【知识回顾】
例1热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋离楼底部的俯角为60°,热
气球与高楼的水平距离为120 m.这栋高楼有多高(结果精确到0.1m)?
分析:在中,,.所以可以利用解直角三角形的知识求出BD;类似地可以求
出CD,进而求出BC.
濠知教育学科导学案
濠知教育-----您值得信赖的中小学辅导专家
2
(三)巩固再现
1、为测量松树AB的高度,一个人站在距松树15米的E处,测得仰角∠ACD=52°,已知人的高度
是1.72米,求树高(精确到0.01米).(tan52=1.28)
2、在宽为30米的街道东西两旁各有一楼房,从东楼底望西楼顶仰角为45°,从西楼顶望东楼顶,俯角为
10°,求西楼高(精确到0.1米).
3、上午10时,我军驻某海岛上的观察所A发现海上有一艘敌军舰艇正从C
处向海岛驶来,当时的
俯角,经过5分钟后,舰艇到达D处,测得俯角。已知观察所A距水面高度为
80
米,我军武器射程为100米,现在必须迅速计算出舰艇何时驶入我军火力射程之内,以便及时还击。
(1/tan5.71=10, 1/tan7.59=7.5 )
濠知教育-----您值得信赖的中小学辅导专家
3
(二)教学互动
1、上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,正以每小时10海里的速
度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
3、如图6-32,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,
在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛
A位于北偏东30°,如果鱼船不改变航向继续向东航行.有没有触礁的危险?
1. 坡度与坡角
坡面的铅直高度h和水平宽度l的比叫做坡度(或叫做坡比),一般用i表示。即i=,常写成i=1:
m的形式如i=1:2.5 把坡面与水平面的夹角α叫做坡角.
i=hl=tan 这一关系在实际问题中经常用到.
濠知教育-----您值得信赖的中小学辅导专家
4
练习(1)一段坡面的坡角为60°,则坡度i=______; ______,坡角______度.
坡面铅直高度一定,其坡角、坡度和坡面水平宽度有什么关系?
坡面水平宽度一定,铅直高度与坡度有何关系
如图,铅直高度AB一定,水平宽度BC增加,α将变小, 坡度减小,因为 tan=ABBC,AB不变,tan
随BC增大而减小(2)与(1)相反,水平宽度BC不变,α将随铅直高度增大而增大,tanα 也随之增大,
因为tan=BCAB不变时,tan随AB的增大而增大
例:
利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图6-35阴影部分是挖去部分),已知渠道内
坡度为1∶1.5,渠道底面宽BC为0.5米,求:
①横断面(等腰梯形)ABCD的面积;
②修一条长为100米的渠道要挖去的土方数.
