《控制系统CAD》实验指导书
控制系统CAD与仿真实验指导书
实验一MATLAB的实验环境及基本命令一实验目的：1．学习了解MA TLAB的实验环境2．在MA TLAB系统命令窗口练习有关MA TLAB命令的使用。
二实验步骤1．学习了解MA TLAB的实验环境：在Windows桌面上，用mouse双击MA TLAB图标，即可进入MA TLAB系统命令窗口：图1-1 MA TLAB系统命令窗口①在命令提示符”>>”位置键入命令:help此时显示MA T ALAB 的功能目录， 其中有“Matlab\general ”，“toolbox\control ”等；阅读目录的内容；② 键入命令：intro此时显示MA TLAB 语言的基本介绍，如矩阵输入、数值计算、曲线绘图等。
要求阅读命令平台上的注释内容，以尽快了解MA TLAB 语言的应用。
③ 键入命令：help help显示联机帮助查阅的功能，要求仔细阅读。
④ 键入命令：into显示工具箱中各种工具箱组件和开发商的联络信息。
⑤ 键入命令：demo显示MA TLAB 的各种功能演示。
2． 练习MA TLAB 系统命令的使用。
① 表达式MA TLAB 的表达式由变量、数值、函数及操作符构成。
实验前应掌握有关变量、数值、函数及操作符的有关内容及使用方法。
练习1-1: 计算下列表达式:要求计算完毕后，键入相应的变量名，查看并记录变量的值。
②．向量运算： )6sin(/250π=d 2/)101(+=a )sin(3.2-=e c i b 53+=n 维向量是由n 个成员组成的行或列数组。
在MA TLAB 中，由分号分隔的方括号中的元素产生一个列向量；由逗号或空号分隔的方括号中的元素产生一个列向量；同维的向量可进行加减运算，乘法须遵守特殊的原则。
练习1-2已知：X=[2 ；-4；8]求 ：Y=R ＇；P=5*R ；E=X .*Y ；S=X ＇* Y练习1-3⑴产生每个元素为1的4维的行向量；⑵产生每个元素为0的4维的列向量；⑶产生一个从1到8的整数行向量，默认步长为1；⑷产生一个从π到0，间隔为π/3的行向量；③矩阵基本运算操作。
控制系统计算机辅助设计CAD实验
控制系统计算机辅助设计实验一、实验教学目标与基本要求上机实验是本课程重要的实践教学环节。
实验的目的不仅仅是验证理论知识，更重要的是通过上机加强学生的实验手段与实践技能，掌握应用MATLAB/Simulink 求解控制问题的方法，培养学生分析问题、解决问题、应用知识的能力和创新精神，全面提高学生的综合素质。
通过对MATLAB/Simulink进行求解，基本掌握常见控制问题的求解方法与命令调用，更深入地认识和了解MATLAB语言的强大的计算功能与其在控制领域的应用优势。
二、题目及解答第一部分：MATLAB 必备基础知识、控制系统模型与转换、线性控制系统的计算机辅助分析：编写文件：function dx=rossler(t,x)dx=[-x(2)-x(3);x(1)+*x(2);+(x(1)*x(3)];主函数：>> x0=[0;0;0];[t,y]=ode45('rossler',[0,100],x0);plot3(y(:,1),y(:,2),y(:,3)),grid>> plot3(y(:,1),y(:,2),y(:,3)),grid>> plot(y(:,1),y(:,2)),grid所的图像：三维相轨迹（下图）xoy平面投影2.编写文件：function y=c2exmobj(x)y=x(1)^2-2*x(1)+x(2);编写文件：function [c,ce]=c2exmcon(x)ce=[];c=[4*x(1)^2+x(2)^2-4];主函数为：A=[];B=[];Aeq=[];Beq=[];xm=[0;0];xM=[];x0=[0;0];ff=optimset;=1e-10;=1e-20;x=fmincon('c2exmobj',x0,A,B,Aeq,Beq,xm,xM,'c2exmcon',ff)运行结果：Warning: Trust-region-reflective method does not currently solve this type of problem,using active-set (line search) instead.> In fmincon at 422Optimization terminated: first-order optimality measure less thanand maximum constraint violation is less than .Active inequalities (to within = 1e-006):lower upper ineqlin ineqnonlin2 1x =3.(a).程序代码为：>> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5))运行结果为：Transfer function:s^3 + 4 s + 2------------------------------------------------------ s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3 (b). 程序代码为：>> z=tf('z',;H=(z^2+/((z-1)*(z^*z+)运行结果为：Transfer function:z^2 +-----------------------------z^3 - z^2 + z -Sampling time:4.将方程两边进行拉式变换后可得传递函数，代码如下：>> tf('s');G=2/(s^3+13*s^2+4*s+5)Transfer function:2----------------------s^3 + 13 s^2 + 4 s + 5转换为状态空间方程为：>> G1=ss(G)a =x1 x2 x3x1 -13 -1x2 4 0 0x3 0 1 0b =u1x1x2 0x3 0c =x1 x2 x3y1 0 0 1d =u1y1 0Continuous-time model.转换为零极点模型为：>> G2=zpk(G)Zero/pole/gain:2----------------------------------(s+ (s^2 + +5.如题可设采样时间为，代码如下：>> z=tf('z',;H=(z+2)/(z^2+z+运行结果为：Transfer function:z + 2--------------z^2 + z +Sampling time:6.编写函数：function H=feedback(G1,G2,key)if nargin==2; key=-1; end, H=G1/(sym(1)-key*G1*G2); H=simple(H); 代码如下：syms J Kp Ki s;G=(s+1)/(J*s^2+2*s+5);Gc=(Kp*s+Ki)/s;GG=feedback(G*Gc,1);G1=collect(GG,s)运行结果为：G1 =(s+1)*(Kp*s+Ki)/(J*s^3+(Kp+2)*s^2+(Ki+Kp+5)*s+Ki)7.(a):代码如下：>> s=tf('s');G=*s+/(s+20)/(s+/(s+;Gc=*s+400)/s/(s+4);H=1/*s+1);GG=feedback(G*Gc,H)运行结果为：Transfer function:s^3 + s^2 + s + 127056----------------------------------------------------------------------------------s^6 + s^5 + s^4 + 2444 s^3 + s^2 + s + 127056状态方程如下：>> ss(GG)a =x1 x2 x3 x4 x5 x6x1x2 128 0 0 0 0 0x3 0 64 0 0 0 0x4 0 0 32 0 0 0x5 0 0 0 8 0 0x6 0 0 0 0 2 0b =u1x1 4x2 0x3 0x4 0x5 0x6 0c =x1 x2 x3 x4 x5 x6y1 0 0d =u1y1 0Continuous-time model.零极点模型转换如下：>> zpk(GG)Zero/pole/gain:(s+100) (s+ (s+-----------------------------------------------------------------------(s^2 + + (s^2 + + (s^2 + +(b).程序代码如下：可先设系统采样周期为>> z=tf('z',;G=*z^2+108444*z^3)/(4*z+1)/(20*z+1)/(1+*z);Gc=z/(1-z);H=z/;GG=feedback(G*Gc,H)运行结果为：Transfer function:-108444 z^5 + z^4 + z^3--------------------------------------------------------------------- z^5 + z^4 + z^3 + z^2 + z +Sampling time:状态方程转换如下：>> ss(GG)a =x1 x2 x3 x4 x5x1x2 0 0 0 0x3 0 0 0 0x4 0 0 0 0x5 0 0 0 0b =u1x1 1x2 0x3 0x4 0x5 0c =x1 x2 x3 x4 x5y1d =u1y1Sampling time:Discrete-time model.零极点模型转化如下：>> zpk(GG)Zero/pole/gain:z^3 (z+----------------------------------------------------------(z+ (z+ (z+ (z^2 - +Sampling time:8.程序代码如下：s=tf('s');c1=feedback(1/(s+1)*s/(s^2+2),(4*s+2)/(s+1)^2);c2=feedback(1/s^2,5 0);c3=feedback(c1*c2,(s^2+2)/(s^3+14));G=3*c3;G运行结果为：Transfer function:3 s^6 + 6 s^5 + 3 s^4 + 42 s^3 + 84 s^2 + 42 s-----------------------------------------------------------------------------------------------------s^10 + 3 s^9 + 55 s^8 + 175 s^7 + 300 s^6 + 1323 s^5 + 2656 s^4 + 3715 s^3 + 7732 s^2 + 5602 s + 14009.程序代码如下：>> s=tf('s');G=(s+1)^2*(s^2+2*s+400)/(s+5)^2/(s^2+3*s+100)/(s^2+3*s+2500);G1=c2d(G,,G2=c2d(G,,G3=c2d(G,1)运行结果如下：Transfer function:z^5 - z^4 + z^3 + z^2 - z +------------------------------------------------------------------------------------------z^6 - z^5 + z^4 - z^3 + z^2 - z +Sampling time:Transfer function:z^5 - z^4 - z^3 + z^2 - z +-------------------------------------------------------------------------------------z^6 - z^5 + z^4 - z^3 + z^2 - z +Sampling time:Transfer function:z^5 - z^4 + z^3 + z^2 - z +--------------------------------------------------------------------------------------------z^6 - z^5 - z^4 - z^3 + z^2 - z +Sampling time: 1绘制曲线如下：>> subplot(221),step(G)subplot(222),step(G1)subplot(223),step(G2)subplot(224),step(G3)图像为：10.(a)程序代码如下：>> s=tf('s');G=1/(s^3+2*s^2+s+2);eig(G)运行结果如下：ans =+-可得系统为临界稳定(b)程序代码如下：>> num=1;den=[6 3 2 1 1];G=tf(num,den);eig(G)运行结果为：ans =+-+-可得有一对共轭复根在右半平面，所以系统不稳定。
控制系统CAD实验报告
控制系统CAD实验报告一、实验目的1. 掌握如何使用Matlab进行系统的根轨迹分析。
2. 掌握如何使用Matlab进行系统的稳定性分析。
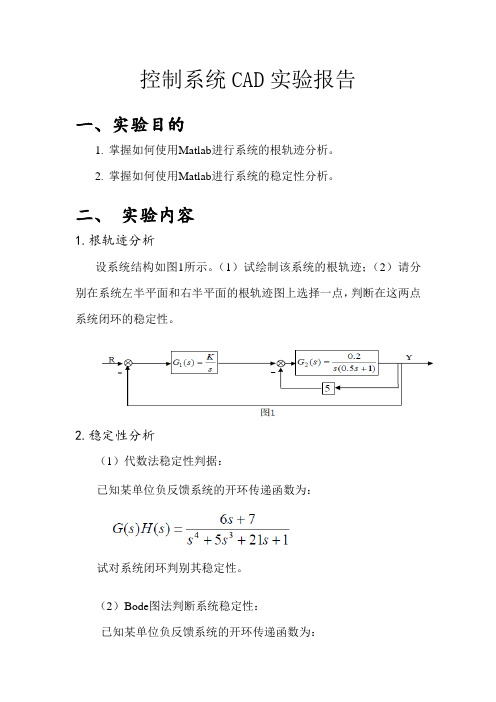
二、实验内容1.根轨迹分析设系统结构如图1所示。
（1）试绘制该系统的根轨迹；（2）请分别在系统左半平面和右半平面的根轨迹图上选择一点，判断在这两点系统闭环的稳定性。
2.稳定性分析（1）代数法稳定性判据：已知某单位负反馈系统的开环传递函数为：试对系统闭环判别其稳定性。
（2）Bode图法判断系统稳定性：已知某单位负反馈系统的开环传递函数为：试绘制系统的Bode图和Nyquist曲线，分别用两种方法判断闭环系统的稳定性，并求出系统的频域性能指标w，γ与时域性能指标σ%、s t。
c三、预习报告1.根轨迹分析g1=tf(1,[1 0])g2=tf(0.2,[0.5 1 0])sys=g1*g2+5*g2rlocus(sys)Gridnyquist(G)2.稳定性分析(1)G=tf([6 7],[1 5 0 27 8]) %闭环环传递函数den=[1 5 0 27 8]p=roots(den)i=find(real(p)>=0)n=length(i)if(n>0) disp('系统不稳定，不稳定根个数为：')nelse disp('系统稳定')end四、上机实验结果1.根轨迹分析2.稳定性分析（1）代数法稳定性判据：Transfer function:6 s + 7----------------------s^4 + 5 s^3 + 27 s + 8den =1 5 0 27 8p =-5.76950.5307 + 2.1137i0.5307 - 2.1137i-0.2920i =23n = 2系统不稳定，不稳定根个数为：n =2（2）Transfer function:0.3 s + 1------------------s^3 + 12 s^2 + 5 s Gm = Inf Pm = 69.1650 Wcg =InfWcp =0.1842五、实验总结对知识的掌握不足，对知识点理解错误。
控制系统CAD及数字仿真实验指导书
控制系统CAD及数字仿真实验指导书自动化系目录第一章前言............... (2)第二章控制系统CAD及数字仿真实验1．控制系统稳定性的MATLAB辅助分析 (3)2．数据处理方法的MATLAB实现 (4)3．控制系统数字仿真的实现． (5)4．基于双闭环PID控制的一阶倒立摆控制系统仿真实验 (6)5．双闭环直流调速系统设计仿真实验．........... .... .... .... .7 6．水箱液位控制仿真实验．.......................... .. .... . .8第一章前言本实验课程是与学科基础选修课程《控制系统CAD及数字仿真》相配合的实践课程。
作为联系自动控制理论、自动控制系统设计、课程设计、毕业设计等教学环节的仿真技术类课程，其不仅可以使学生加强课程的学习效果，而且还可为学生在毕业设计中提供一个强有力的工具，有效加强教学中的实践性教学环节，提高学生的独立工作能力和创造性思维能力。
开设本课程的目的，主要是培养学生运用MATLAB语言进行编程和仿真的能力，为今后从事科研工作和与专业有关的工程技术工作打好基础。
一、上机实验要求1、要求学生熟悉MATLAB中的控制系统工具箱与SIMULINK软件包。
2、能根据有关控制算法，编写有关的MATLAB程序。
3、能对实验结果进行分析和讨论，得到相关的实验结论。
二、上机实验的基本程序：1、明确实验任务。
2、提出实验方案。
3、编制有关的MATLAB程序或利用SIMULINK工具建立系统的仿真模型。
4、进行实验操作，作好观测和记录，保存有关的实验数据。
5、整理实验数据，得出结论，撰写实验报告。
在进行上机实验时，上述程序应让学生独立完成，教师给予必要的指导，以培养学生的动手能力。
要做好各个上机实验，就应做到：实验前做准备，实验中有条理，实验后勤分析。
实验一控制系统稳定性的MATLAB辅助分析一、实验目的学会在MATLAB环境下对线性控制系统进行稳定性分析。
“控制系统数字仿真与CAD”实验指导书.
写，均要求用标准Ａ４纸进行撰写，单栏排版，单面打印，并左侧装订，以便于报告最终的批阅与存档，（对于存在“逻辑混乱” 、“文字不清” 、“作图潦草” 、“排版混乱”等问题的报告，将予以退回重新撰写）。
封页：（参考最后一页的“封页”格式）正文：（小四字体）仿真实验题目 1、 2、 3、 4、 5、五、思考题 1．在系统启动过程的第 2 阶段中，理想的电流特性为：实际值小于给定/设定值，试说明为何？引言原理/建模设计/分析/论述仿真实验/结果分析结论（思考题解答） 2．动态性能中，电流/转速特性的“超调量”与理论值是否有偏差？；如有偏差，试给出分析/解释。
3．在“双闭环直流电动机调速系统”中，电流调节器与速度调节器的输出都要设置“限幅” ，试说明：你是如何选取限幅值的？ 4．假设系统中的励磁电压减小/增加，试说明：系统转速将可能怎样变化？参考文献： [1] 张晓华主编《控制系统数字仿真与 CAD》第 3 版机械工业出版社 2009 [2] 张晓华主编《系统建模与仿真》清华大学出版社 2006 [3] 陈伯时主编《电力拖动自动控制系统》第 3 版机械工业出版社 2008 25
“控制系统数字仿真与CAD” 仿真实验报告姓班学名：级：号：联系电话： Email: 提交日期： 26。
AutoCAD实验指导书(范例)
AutoCAD实验指导书(范例)目录一、实验目的与要求二、方法与步骤三、实验过程及内容正文一、实验目的与要求二、方法与步骤三、实验过程及内容四、实验报告填写要求学生需要及时填写实验报告，填写内容为各实验项目最后一项综合练题的解题步骤，并注明各步骤的命令参数。
由于实验时间有限，学生对课程的掌握不同，除安排上机实验之外应另外自行安排时间研究、解决相关知识及问题。
本实验旨在对学生进行AutoCAD的综合考核。
在考核中，学生将需要绘制一份符合要求的二维或三维图形，并添加文字、表格、尺寸标注等信息。
通过本考核，学生将展示他们在AutoCAD中所学的知识和技能，检验他们的实际操作能力。
以“单元平面图zoom练”文件为练对象。
1）使用“选择”命令，选择“主卧”区域内的所有图形对象。
2）使用“选择”命令，选择“主卧”区域内的某一个图形对象。
3）使用“选择”命令，选择“主卧”区域外的所有图形对象。
4）使用“选择”命令，选择“主卧”区域外的某一个图形对象。
4．捕捉快捷菜单的调用1）在“单元平面图zoom练”文件中，选择一个图形对象，右键单击鼠标，调出捕捉快捷菜单。
2）在捕捉快捷菜单中，选择“中心点”，观察图形对象中心点的位置。
1. 按照教材第39页的案例，我们可以使用两种方法来绘制一个200长，100高的矩形。
第一种是参数法，我们可以指定第一点后，使用参数D，然后按照提示，分别输入200和100。
第二种是相对坐标法，我们可以指定第一点后，输入相对坐标“@200,100”。
3. 按照教材第41页的案例，我们可以使用正多边形命令来绘制一个正六边形。
5. 按照教材2.4节的内容，我们可以练图案填充命令，如图2-6所示。
1. 实验目的：学会AutoCAD的基本修改命令，能够根据绘图要求采用适当绘图命令与修改进行图形绘制。
- 复制命令：打开随书光盘“案例文件\第3章\3.1.1复制copy例图”文件，执行复制命令，将例图中的矩形随意复制。
《控制系统仿真与CAD》课程设计指导书
《控制系统仿真与CAD》课程设计指导书一、目的和任务配合《控制系统仿真与CAD》课程的理论教学，通过课程设计教学环节，使学生掌握当前流行的演算式MATLAB语言的基本知识，学会运用MATLAB语言进行控制系统仿真和辅助设计的基本技能，有效地提高学生实验动手能力。
基本要求：1、利用MATLAB提供的基本工具，灵活地编制和开发程序，开创新的应用。
2、熟练地掌握各种模型之间的转换，系统的时域、频域分析及根轨迹绘制。
3、熟练运用SIMULINK对系统进行仿真。
4、掌握PID控制器参数的设计。
二、设计要求1、编制相应的程序，并绘制相应的曲线。
2、对设计结果进行分析。
3、撰写和打印设计报告（包括程序、结果分析、仿真结构框图、结果曲线）。
三、设计内容1、本次设计有八个可以选择的题目，至少选择两个题目进行设计。
2、“设计报告”要按规定的格式撰写（对于存在“逻辑混乱”、“文字不清”、“作图潦草”等问题的报告，将予以退回重新撰写）。
3、无论计算机录入/打印还是手工书写，均要求用标准A4纸进行撰写，以便于报告最终的批阅与存档。
四、时间安排1、课程设计时间为一周。
2、第1天布置设计题目，讲授设计的要求。
3、第2～4天学生进行设计。
4、第5天教师验收，然后学生撰写和打印设计报告。
选题一：二阶弹簧—阻尼系统的PID 控制器设计及参数整定考虑弹簧－阻尼系统如图1所示，其被控对象为二阶环节，传递函数()G s 如下，参数为M=1kg ，b=2N.s/m ，k=25N/m ，()1F s =。
设计要求：（1）控制器为P 控制器时，改变比例系数大小，分析其对系统性能的影响并绘制相应曲线。
（2）控制器为PI 控制器时，改变积分系数大小，分析其对系统性能的影响并绘制相应曲线。
(例如当Kp=50时，改变积分系数大小)（3）设计PID 控制器，选定合适的控制器参数，使闭环系统阶跃响应曲线的超调量σ%<20%，过渡过程时间Ts<2s, 并绘制相应曲线。
控制系统CAD实验指导书2011
《控制系统CAD 》上机实验指导书一、课程实验目的通过运用MATLAB 软件进行控制系统的分析和设计，对控制类课程进行理论验证实验和设计实验，使学生能够进一步熟悉控制系统的原理和设计方法，更直观的了解自动控制系统的运动过程，从而提高学生对控制系统的分析和设计能力。
二、上机实验要求（1） 在MATLAB 环境下独立完成实验内容。
（2） 根据实验结果写出分析报告，报告中附上实验中所编写的程序，同时要提交该程序的电子版。
另外，实验报告中，对每一个实验除了说明实验过程及实验结果以外，要对实验中出现的问题进行分析，并进行小结。
封面要注明姓名、学号、专业等信息。
提交程序电子版时，请以学号建立一个文件夹，将实验中的程序放入该文件夹里，并建立一个readme.txt 文件，用以说明程序和实验的对应关系，以及姓名等个人信息。
三、上机实验内容（8学时）实验一（1学时）：（1）熟悉MATLAB 环境；（2）控制系统模型及其转换。
实验二（3学时）：二阶控制系统在时域和频域内的分析。
实验三（3学时）：编制程序，实现串联校正（超前、滞后、超前--滞后校正），要得到校正装置的元件数值的大小，并标称化。
① 设一单位负反馈控制系统，如果控制对象的传递函数为：)80)(4()(++=s s s K s G p 试设计一个串联超前校正装置。
要求：相角裕度≥45。
；当系统的输入信号是单位斜坡信号时，稳态误差e ss ≤0.04；取C=1μF 时，确定该串联超前校正装置的元件数据；绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。
(提示：稳态误差e ss ≤0.04 —> 取kv=1/e ss =25，k0=8000 )② 设一单位负反馈控制系统，其控制对象的传递函数为：)80)(4()(++=s s s K s G p 试设计一个串联滞后校正装置。
要求：相角裕度≥45。
；当系统的输入信号是单位斜坡信号时，稳态误差e ss ≤0.04；取C=100μF 时，确定该串联滞后校正装置的元件数据；绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。
《控制系统CAD》实验指导书
《控制系统CAD及仿真》实验指导书自动化学院自动化系实验一SIMULINK 基础与应用一、实验目的1、熟悉并掌握Simulink 系统的界面、菜单、工具栏按钮的操作方法；2、掌握查找Simulink 系统功能模块的分类及其用途，熟悉Simulink 系统功能模块的操作方法；3、掌握Simulink 常用模块的内部参数设置与修改的操作方法；4、掌握建立子系统和封装子系统的方法。
二、实验内容：1. 单位负反馈系统的开环传递函数为：1000()(0.11)(0.0011)G s s s s =++应用Simulink 仿真系统的阶跃响应曲线。
2．PID 控制器在工程应用中的数学模型为：1()(1)()d p i d T s U s K E s T s T s N=++ 其中采用了一阶环节来近似纯微分动作，为保证有良好的微分近似效果，一般选10N ≥。
试建立PID 控制器的Simulink 模型并建立子系统。
三、预习要求：利用所学知识，编写实验程序，并写在预习报告上。
实验二 控制系统分析一、 实验目的1、掌握如何使用Matlab 进行系统的时域分析2、掌握如何使用Matlab 进行系统的频域分析3、掌握如何使用Matlab 进行系统的根轨迹分析4、掌握如何使用Matlab 进行系统的稳定性分析5、掌握如何使用Matlab 进行系统的能观测性、能控性分析 二、 实验内容： 1、时域分析（1）根据下面传递函数模型：绘制其单位阶跃响应曲线并在图上读标注出峰值，求出系统的性能指标。
8106)65(5)(232+++++=s s s s s s G （2）已知两个线性定常连续系统的传递函数分别为1G (s)和2G (s)，绘制它们的单位脉冲响应曲线。
451042)(2321+++++=s s s s s s G ， 27223)(22+++=s s s s G （3）已知线性定常系统的状态空间模型和初始条件，绘制其零输入响应曲线。
控制系统CAD上机实验
《控制系统CAD》实验指导书编者：刘辉姓名：专业班级：测控学号：*****指导老师：实验一 Matlab 使用方法和程序设计一、实验目的1. 掌握Matlab 软件使用的基本方法；2. 熟悉Matlab 的基本运算和程序控制语句；3. 熟悉Matlab 程序设计的基本方法。
二、实验内容1.求多项式的根4532)(234++++=x x x x x P程序：>> p=[1 2 3 5 4]; >> x=roots(p)结果截图：结果： x =0.2166 + 1.5199i 0.2166 - 1.5199i -1.2166 + 0.4657i -1.2166 - 0.4657i2已知)()()(224224224b a c a c b c b a f -+-+-=,试使用符号运算的方法对其因式分解。
程序：>> syms a b c;>> f=a^4*(b^2-c^2)+b^4*(c^2-a^2)+c^4*(a^2-b^2); >> r=factor(f)结果截图：结果： r =(c-a)*(c+a)*(b-a)*(b+a)*(b-c)*(b+c)3.编写一个函数，完成求和s=1+2+3+...+i+...+n 。
程序：求1000个数相加的和 >> sum=0;>> for i=1:1000 sum=sum+i; end结果截图：4.已知一传递函数452)(2+++=s s s s F ，试将其分解为部分分式。
程序：>> num=[1 2]; >> den=[1 5 4];>> [res,poles,k]=residue(num,den)结果截图：结果：F （S ）=0.6667/(S+4)+0.3333/(S+1)实验二一、 实验目的1. 掌握如何使用Matlab 进行系统的时域分析。
《控制系统仿真与CAD》实验指导书
《控制系统仿真与CAD》实验指导书适用自动化、测控、电气、电控荷专业电气自动化系自动化教研室2011年2月实验1：M函数的编写1. 实验目的掌握在Matlab环境下编写并运行M函数的操作方法。
2. 实验内容对给定的二阶欠阻尼传递函数，编制一个函数程序，计算阶跃响应的特征参数：超调量б% 、峰值时间Tp、上升时间Tr、过渡过程时间Ts（2%）。
b=7500; a=[1, 34.5, 7500];3. 实验步骤(1) 开机后在Windows状态下，启动Matlab7.1环境；(2) MATLAB的Editor/Debugger窗口来编辑程序；(3) 输入下列源程序：% mp：超调量，Tp：峰值时间，Tr：上升时间，T s：调节时间function [mp,Tp,Tr,Ts]=exp1(num,den)t=0:0.005:1;y=step(num,den,t);plot(t,y);%求mp与TpN=length(t);yss=y(N); %yss:稳态值[ymax,i]=max(y);mp=(ymax-yss)*100/yss;Tp=t(i);%求Tryr1=0.1*yss;yr2=0.9*yss;i=1;while y(i)<yr1i=i+1;endt1=t(i);while y(i)<yr2i=i+1;endt2=t(i);Tr=t2-t1;%求Ts：调节时间symbol=0; %symbol：超标标志for i=1:1:Nfor j=1:1:N-iif(abs(y(i+j)-yss)/yss>0.02)symbol=1;endendif symbol==1symbol=0;elsebreak;endendTs=t(i);i=N;while abs(y(i)-yss)/yss<=0.02i=i-1;endTs=t(i);(4) 把源程序以文件形式保存到MATLAB的Work子目录下；(5) 调用编写的函数程序，运行源程序；(6) 打印源程序清单，并将二阶欠阻尼系统性能指标的结果保存。
控制系统CAD及计算机仿真实验指导书
2
求矩阵A的特征多项式；求特征多项式中未知数为20时的值。 A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4] poly(A) polyval(ans,20) 4、基本绘图命令 （1）绘制余弦曲线y=cos(t)，t∈[0，2π]。 t=0:pi/100:2*pi; plot(t,cos(t)) （2）在同一坐标系中绘制余弦曲线y=cos(t-0.25)和正弦曲线y=sin(t-0.5)，t∈[0， 2π]。 t=0:pi/100:2*pi; y1=plot(t,cos(t-0.25)); hold on y2=plot(t,sin(t-0.5)); 5、基本绘图控制 绘制[0，4π]区间上的y=10sint曲线，并要求： （1）线形为点划线、颜色为红色、数据点标记为加号； （2）坐标轴控制：显示范围、刻度线、比例、网络线； （3）标注控制：坐标轴名称、标题、相应文本。 t=0:0.1:4*pi; y=10*sin(t); plot(t,y,'r-.+') grid on; title('y=10*sin(t)'); xlabel('t') ylabel('y') 6、基本程序设计 （1）编写命令文件：计算1+2+⋯ +n<2000时的最大n值； s=0; for i=1:1:100; s=s+i; if s>=2000; %满足条件（1）
4
实验二 SIMULINK 仿真
一、实验目的 学习使用SIMULINK进行系统仿真的方法。 二、实验内容 1、Simulink的基本操作： （1）运行 Simulink； （2）常用的标准模块； （3）模块的操作； （4）参数设置。 2、系统仿真及参数设置： （1）算法设置（Solver） ； （2）工作空间设置（Workspace I/O） 。 3、已知系统结构图如下
控制系统CAD实验
实验内容1 系统的传递函数为：22251()23s s G s s s ++=++ 绘制出系统的根轨迹、Bode 图和Nyquist 图。
2 系统的开环传递函数为：1）27(5)()(10)(1)s G s s s s +=++ 2） 21000(2)()(32)(5)(1)s G s s s s s +=++++ 绘制系统的Bode 图和Nyquist 图，并讨论其稳定性以及计算系统的幅值裕度和相角裕度。
3 系统的闭环传递函数为22(0.5)()(0.1)1s G s s +=++ 利用Routh 判据、Hurwitz 判据判断系统的稳定性。
4 系统的特征方程为6543228122016160s s s s s s ++++++=试利用Routh 判据和Hurwitz 判据判断系统的稳定性。
sys=tf([2,5,1],[1,2,3])Transfer function:2 s^2 + 5 s + 1---------------s^2 + 2 s + 3>> rlocus(sys)>> [x,y]=ginput(2);p=x+i*yp =-2.8169 + 1.6351i-0.2222 - 0.0140i>> sys=tf([2,5,1],[1,2,3])Transfer function:2 s^2 + 5 s + 1---------------s^2 + 2 s + 3>> rlocus(sys)>> num=[2,5,1];den=[1,2,3];bode(num,den)>> num=[2,5,1];den=[1,2,3];nyquist(num;den)??? nyquist(num;den)|Error: Expression or statement is incorrect--possibly unbalanced (, {, or [.>> G=tf([2,5,1],[1,2,3]);nyquist(G)>> G=tf([1000,2000],[1,11,10,0]);>> nyquist(G)>> bode(G)>> axis('square')>> G_close=feedback(G,1);>> roots(G_close,den{1})??? Cell contents reference from a non-cell array object.>>>> G=tf([1000,2000],[1,11,10,0]);>> nyquist(G)??? Invalid parameter/value pair arguments.??? Error using ==> axesError while evaluating line ButtonDownFcn.??? Invalid parameter/value pair arguments.??? Error using ==> axesError while evaluating line ButtonDownFcn.??? Invalid handle object.??? Error while evaluating line ButtonDownFcn.>> bode(G)>> G=tf([1000,2000],[1,11,10,0]);>> roots(G.den{1})ans =-10-1>> G=tf([1000,2000],[1,11,10,0]);>> G_close=feedback(G,1);>> [Gm,Pm,Wcg,Wcp]=margin(G)Gm =InfPm =16.1004Wcg =InfWcp =30.8643>> den=[1,0.2,1.01];function H=hurwitz(den)n=length(den)-1;for i=1:n, i1=floor(i/2);if i==i1*2, hsub1=den(1:2:n+1); i1=i1-1;else, hsub1=den(2:2:n+1); endl1=length(hsub1);H(i,:)=[zeros(1,i1),hsub1,zeros(1,n-i1-l1)];end[key,sdet]=posdef(H)??? function H=hurwitz(den)|Error: Function definitions are not permitted at the prompt or in scripts.>> den=[1,0.2,1.01];function H=hurwitz(den)n=length(den)-1;for i=1:n, i1=floor(i/2);if i==i1*2, hsub1=den(1:2:n+1); i1=i1-1;else, hsub1=den(2:2:n+1); endl1=length(hsub1);H(i,:)=[zeros(1,i1),hsub1,zeros(1,n-i1-l1)];endH=hurwitz(den)[key,sdet]=posdef(H)??? function H=hurwitz(den)|Error: Function definitions are not permitted at the prompt or in scripts.>> den=[1,0.2,1.01];>> H=hurwitz(den)H =0.2000 01.0000 1.0100>> [key,sdet]=posdef(H)key =1sdet =0.2000 0.2020>> den=1,0.2,1.01];??? den=1,0.2,1.01];|Error: Unbalanced or misused parentheses or brackets.>> den=[1,0.2,1.01];>> [rtab,msg]=roth(den)??? Undefined command/function 'roth'.>> den=[1,0.2,1.01];>> [rtab,msg]=routh(den)rtab =1.0000 1.01000.2000 01.0100 0msg =[]>> den=[1,2,8,12,20,16,16];>> H=hurwitz(den)H =2 12 16 0 0 01 8 20 16 0 00 2 12 16 0 00 1 8 20 16 00 0 2 12 16 00 0 1 8 20 16>> [key,sdet]=posdef(H)key =sdet =2 4 0 0 0 0>> [rtab,msg]=routh(den)rtab =1.0000 8.0000 20.0000 16.00002.0000 12.0000 16.0000 02.0000 12.0000 16.0000 04.0000 12.0000 0 06.0000 16.0000 0 01.3333 0 0 016.0000 0 0 0 msg =All elements in row 4 are zeros;>>。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《控制系统CAD及仿真》实验指导书
自动化学院
自动化系
实验一SIMULINK 基础与应用
一、
实验目的
1、熟悉并掌握Simulink 系统的界面、菜单、工具栏按钮的操作方法；
2、掌握查找Simulink 系统功能模块的分类及其用途，熟悉Simulink 系统功能模块的操作方法；
3、掌握Simulink 常用模块的内部参数设置与修改的操作方法；
4、掌握建立子系统和封装子系统的方法。
二、
实验内容：
1. 单位负反馈系统的开环传递函数为：
1000
()(0.11)(0.0011)
G s s s s =
++
应用Simulink 仿真系统的阶跃响应曲线。
2．PID 控制器在工程应用中的数学模型为：
1
()(1)()d p i d T s U s K E s T s T s N
=+
+ 其中采用了一阶环节来近似纯微分动作，为保证有良好的微分近似效果，一般选10N ≥。
试建立PID 控制器的Simulink 模型并建立子系统。
三、
预习要求：
利用所学知识，编写实验程序，并写在预习报告上。
实验二 控制系统分析
一、 实验目的
1、掌握如何使用Matlab 进行系统的时域分析
2、掌握如何使用Matlab 进行系统的频域分析
3、掌握如何使用Matlab 进行系统的根轨迹分析
4、掌握如何使用Matlab 进行系统的稳定性分析
5、掌握如何使用Matlab 进行系统的能观测性、能控性分析 二、 实验内容： 1、时域分析
（1）根据下面传递函数模型：绘制其单位阶跃响应曲线并在图上读标注出峰值，求出系统
的性能指标。
8
106)
65(5)(2
32+++++=s s s s s s G （2）已知两个线性定常连续系统的传递函数分别为1G (s)和2G (s)，绘制它们的单位脉冲响
应曲线。
4
5104
2)(2
321+++++=s s s s s s G ， 27223)(22+++=s s s s G （3）已知线性定常系统的状态空间模型和初始条件，绘制其零输入响应曲线。
⎥⎦
⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤
⎢⎢⎢⎣
⎡∙∙212107814.07814.05572.0x x x x []⎥⎦
⎤⎢⎣⎡=214493
.69691.1x x y ⎥⎦⎤
⎢⎣⎡=01)0(x 2、频域分析 设线性定常连续系统的传递函数分别为1G (s)、2G (s)和3G (s)，将它们的Bode
图绘制在一张图中。
151)(1+=
s s G ，4
53.0)(22++=s s s G ，16.0)(3
+=s s G 3、根轨迹分析 根据下面负反馈系统的开环传递函数，绘制系统根轨迹，并分析系统稳定
的K 值范围。
)
2)(1()()(++=
s s s K
s H s G
4、系统稳定性分析
（1）代数法稳定性判据：（用求分母多项式的根和routh 函数两种方法）
已知系统的开环传递函数为：(2)
()100(1)(20)
s G s s s s +=++试对系统闭环判别其稳定性
（2）根轨迹法判断系统稳定性：
已知一个单位负反馈系统开环传递函数为：2
(3)
()(5)(6)(22)
s G s k
s s s s s +=++++ 试在系统的闭环根轨迹图上选择一点，求出该点的增益及其系统的闭环极点位置， 并判断在该点系统闭环的稳定性。
（3）Bode 图法判断系统稳定性：
已知两个单位负反馈系统的开环传递函数分别为：
123232
2.7 2.7
();()5454G s G s s s s s s s
=
=+++- 用Bode 图法判断系统闭环的稳定性。
5、系统能控性、能观性分析
已知连续系统的传递函数模型，
32
()102718
s G s s s s α
+=
+++ 当α分别取－1，0，＋1时，判别系统的能控性与能观性 三、预习要求：
利用所学知识，编写实验程序，并写在预习报告上。
实验三 基于BODE 图法的控制系统设计
一、
实验目的
1、BODE 图法串联超前校正器设计 ；
2、BODE 图法串联滞后校正器设计 ；
3、BODE 图法反馈校正器设计 ； 二、
实验内容：
1、已知单位负反馈控制系统的开环传递函数为：
0100
()(0.11)(0.011)
=
++G s s s s
设计超前校正装置，使校正后系统满足：
1v K 100s -= ，1c 50s -ω=，%30%σ≤
2、已知单位负反馈控制系统的开环传递函数为：
0100
()(0.11)(0.011)
=
++G s s s s
设计超前校正装置，使校正后系统满足：
1v K 100s -= ，1c 5s -ω≥，%40%σ≤
3、已知控制系统方框图如图3-1所示。
图中：
11G (s)K 200== ，210
()(0.11)(0.011)
=
++G s s s ，30.1()=G s s
若要求校正后系统在单位斜坡输入作用下的稳态误差ss 1
e 200
= ，相角裕度c ()45γω≥o ，试确定反馈校正装置c G (s) 的形式与参数。
图3-1
三、预习要求：利用所学知识，编写实验程序，并写在预习报告上。
实验四 控制系统的
PID 设计和工程整定方法
一、实验目的
1、使用MATLAB 分析比例、微分、积分环节对控制系统性能的影响；
2、掌握MATLAB 实现工程整定的方法； 二、实验内容
1、系统的结构图如图4-1所示。
图中
()(1)=++i c p d K G s K K s s ，1()--=Ts
h e G s s
当系统对象取p15G (s)(0.5s 1)(0.1s 1)=++，或p21G (s)s(0.1s 1)
=+时，分别时间相应的PID 控
制器。
图4-1
2、已知被控系统对象的传递函数为10
()(1)(2)(3)(4)
=
++++G s s s s s ，试设计P 控制器、
PI 控制器、PID 控制器。
（使用齐格勒——尼柯尔斯整定法） 三、预习要求
利用所学知识，编写实验程序，并写在预习报告上。
实验五 现代控制系统设计
一、实验目的
1、掌握用状态反馈配置极点的方法；
2、掌握状态观测器设计方法； 二、实验内容
系统传递函数为： 2100
() 3.928103.57
=
++G s s s ，用状态反馈将系统极点配置在
17.35j7.5λ=-+ ，17.35j7.5λ=--，并用状态观察器实现状态反馈，观测器极点为：s 0.1j0=-± 。
【注】 函数place()用来配置系统（A ，B ，C ，D ）的闭环极点，其调用格式为：
K=place(A ，B ，P)
其中，参数P 为系统要配置的闭环极点向量；返回变量K 为状态反馈向量。
三、预习要求
利用所学知识，编写实验程序，并写在预习报告上。
实验六 基于SIMULINK 的控制系统综合仿真
一、实验目的
1、了解MATLAB 系统仿真的研究方法和实现手段；
2、掌握基本的系统仿真实现的技巧和能力。
二、实验内容
1、系统结构图如图6-1所示。
输入为信号电平1~6，非线性环节的上、下限为1± ，取步长h 0.1= ，仿真时间为10s ，试绘制系统的响应曲线。
图6-1
2、已知钢铁厂车间加热炉传递函数与温度传感器及其变送器的传递函数模型分别为：
80s 019.9G e 120s 1-=
+ ，020.107
G 10s 1
=
+ 设定控制所用的PID 调节器传递函数为
2c 29286s 240s 1.5G 521s 145s
++=+
试对系统的PID 控制进行分析、设计与仿真。
三、预习要求
利用所学知识，编写实验程序，并写在预习报告上。
2c 29286s 240s 1.5
G 521s 145s
++=
+。