乘法公式(提高)巩固练习
乘法公式练习题

乘法公式练习题乘法公式练习题乘法是数学中最基础、最常用的运算之一。
在我们日常生活中,乘法无处不在。
从计算购物账单到解决实际问题,乘法都扮演着重要的角色。
为了提高我们的乘法运算能力,下面将提供一些乘法公式练习题,帮助我们巩固和提高技能。
1. 两位数乘一位数首先,我们从最简单的乘法开始,即两位数乘一位数。
例如,计算78乘以6。
我们可以按照下面的步骤进行计算:78x 6------468首先,我们将6乘以8,得到48。
然后,我们将6乘以7,得到42。
最后,将两个结果相加,得到468。
这就是78乘以6的结果。
2. 两位数乘两位数接下来,我们来看一下两位数乘以两位数的乘法。
例如,计算34乘以56。
我们可以按照下面的步骤进行计算:34x 56--------204 (34乘以6)+ 170 (30乘以6,再乘以10)1904 (34乘以50,再加上前面两个结果)首先,我们将34乘以6,得到204。
然后,我们将30乘以6,再乘以10,得到170。
最后,将这两个结果相加,并将34乘以50的结果加上去,得到1904。
这就是34乘以56的结果。
3. 三位数乘以两位数现在,我们来看一下三位数乘以两位数的乘法。
例如,计算123乘以45。
我们可以按照下面的步骤进行计算:123x 45--------615 (123乘以5)+ 4920 (120乘以5,再乘以10)--------5535 (123乘以40,再加上前面两个结果)首先,我们将123乘以5,得到615。
然后,我们将120乘以5,再乘以10,得到4920。
最后,将这两个结果相加,并将123乘以40的结果加上去,得到5535。
这就是123乘以45的结果。
4. 两位数乘以三位数最后,我们来看一下两位数乘以三位数的乘法。
例如,计算67乘以321。
我们可以按照下面的步骤进行计算:67--------201 (67乘以1)+ 4020 (60乘以1,再乘以10)+ 2010 (7乘以300,再乘以10)--------21507 (67乘以300,再加上前面三个结果)首先,我们将67乘以1,得到201。
提高小学生乘法技巧的练习题

提高小学生乘法技巧的练习题一、基础乘法运算1. 8 × 6 = ________2. 4 × 9 = ________3. 5 × 3 = ________4. 7 × 2 = ________5. 2 × 10 = ________二、扩展乘法运算1. 35 × 2 = ________2. 12 × 5 = ________3. 6 × 8 = ________4. 21 × 4 = ________5. 17 × 3 = ________三、乘法口诀表填入适当的数字:× 1 2 3 4 5 6 7 8 9 10----------------------------------------------1 | 123456789 102 | 2 4 6 8 10 12 14 16 18 203 | 3 6 9 12 15 18 21 24 27 304 | 4 8 12 16 20 24 28 32 36 405 | 5 10 15 20 25 30 35 40 45 506 | 6 12 18 24 30 36 42 48 54 607 | 7 14 21 28 35 42 49 56 63 708 | 8 16 24 32 40 48 56 64 72 809 | 9 18 27 36 45 54 63 72 81 9010| 10 20 30 40 50 60 70 80 90 100四、填空练习1. 12 × ________ = 962. ________ × 7 = 493. 9 × ________ = 814. ________ × 4 = 245. 15 × ________ = 75五、解决问题1. 小明每天早上骑自行车上学,一共耗时10分钟。
乘法公式(提高)巩固练习

【巩固练习】1.下列各多项式相乘,可以用平方差公式的有( ).①()()2552ab x x ab -++ ②()()ax y ax y ---③()()ab c ab c --- ④()()m n m n +--A.4个B.3个C.2个D.1个2. (2016•濮阳校级自主招生)若x 2+mx +k 是一个完全平方式,则k 等于( )A .m 2B .m 2C .m 2D .m 23.下面计算()()77a b a b -++---正确的是( ).A.原式=(-7+a +b )[-7-(a +b )]=-27-()2a b +B.原式=(-7+a +b )[-7-(a +b )]=27+()2a b +C.原式=[-(7-a -b )][-(7+a +b )]=27-()2a b +D.原式=[-(7+a )+b ][-(7+a )-b ]=()227a b +-4.(a +3)(2a +9)(a -3)的计算结果是( ).A.4a +81B.-4a -81C. 4a -81D.81-4a 5.下列式子不能成立的有( )个.①()()22x y y x -=- ②()22224a b a b -=- ③()()()32a b b a a b -=--④()()()()x y x y x y x y +-=---+ ⑤()22112x x x -+=-- A.1 B.2 C.3 D.46.(2015春•开江县期末)计算20152﹣2014×2016的结果是( )A .﹣2B .﹣1C .0D .1二.填空题7.(2016•湘潭)多项式x 2+1添加一个单项式后可变为完全平方式,则添加的单项式可以 是 (任写一个符合条件的即可).8. 已知15a a +=,则221a a+的结果是_______. 9. 若把代数式223x x --化为()2x m k -+的形式,其中m ,k 为常数,则m +k =_______.10.(2015春•深圳期末)若A=(2+1)(22+1)(24+1)(28+1)+1,则A 的末位数字是 .11.对于任意的正整数n ,能整除代数式()()()()313133n n n n +---+的最小正整数是_______.12. 如果()()221221a b a b +++-=63,那么a +b 的值为_______.三.解答题13.计算下列各值.22(1)10199+ ()()()2222(2)224m m m +-+(3)()()a b c a b c +--+ 2(4)(321)x y -+14.(2015春•成华区月考)如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”,如:4=22﹣02,12=42﹣22,20=62﹣42,因此4、12、20都是这种“神秘数”.(1)28和2012这两个数是“神秘数”吗?试说明理由;(2)试说明神秘数能被4整除;(3)两个连续奇数的平方差是神秘数吗?试说明理由.15. 已知:()26,90,a b ab c a -=+-+=求a b c ++的值.。
乘法公式练习题

乘法公式练习题乘法公式是数学运算中非常重要的工具,熟练掌握并运用乘法公式可以大大提高计算的效率和准确性。
下面我们就通过一些练习题来巩固和加深对乘法公式的理解。
一、平方差公式平方差公式:(a + b)(a b) = a² b²练习题 1:计算(5 + 3)(5 3)解析:直接运用平方差公式,a = 5,b = 3,可得:(5 + 3)(5 3) = 5² 3²= 25 9 = 16练习题 2:化简(x + 2y)(x 2y)解析:同样使用平方差公式,a = x,b = 2y,得到:(x + 2y)(x 2y) = x²(2y)²= x² 4y²练习题 3:计算 98×102解析:将 98 看成 100 2,102 看成 100 + 2,那么:98×102 =(100 2)(100 + 2) = 100² 2²= 10000 4 = 9996二、完全平方公式完全平方公式:(a + b)²= a²+ 2ab + b²,(a b)²= a² 2ab +b²练习题 1:计算(3 + 4)²解析:运用完全平方公式,a = 3,b = 4,可得:(3 + 4)²= 3²+ 2×3×4 + 4²= 9 + 24 + 16 = 49练习题 2:化简(2x 3)²解析:a = 2x,b = 3,所以:(2x 3)²=(2x)² 2×2x×3 + 3²= 4x² 12x + 9练习题 3:已知(a + 1)²= 9,求 a 的值。
解析:因为(a + 1)²= 9所以 a²+ 2a + 1 = 9a²+ 2a 8 = 0(a + 4)(a 2) = 0则 a + 4 = 0 或 a 2 = 0解得 a =-4 或 a = 2三、乘法公式的综合运用练习题 1:计算(2x + 3y)²(2x 3y)²解析:先分别运用完全平方公式展开:(2x + 3y)²= 4x²+ 12xy + 9y²(2x 3y)²= 4x² 12xy + 9y²然后相减:(4x²+ 12xy + 9y²) (4x² 12xy + 9y²) = 4x²+ 12xy + 9y² 4x²+ 12xy 9y²= 24xy练习题 2:化简(x + 2)²(x 1)(x + 1)解析:先展开(x + 2)²得到 x²+ 4x + 4,再用平方差公式计算(x 1)(x + 1) 得到 x² 1,然后相减:(x²+ 4x + 4) (x² 1) = x²+ 4x + 4 x²+ 1 = 4x + 5练习题 3:已知 a + b = 5,ab = 3,求 a²+ b²的值。
初二上册数学乘法公式练习题

初二上册数学乘法公式练习题在初二上册的数学学习中,乘法公式是一个重要的内容。
乘法公式是指将两个或多个数相乘时使用的特定公式。
通过掌握乘法公式,我们能够更快、更准确地进行乘法计算。
本文将为大家提供一些乘法公式的练习题,帮助大家巩固乘法公式的运用。
练习题一:单项乘法公式运算1. 52 * 7 = ____。
答案:364。
2. 63 * 9 = ____。
答案:567。
3. 85 * 6 = ____。
答案:510。
4. 97 * 4 = ____。
答案:388。
5. 34 * 12 = ____。
答案:408。
练习题二:多项乘法公式运算1. (6 + 9) * 4 = ____。
答案:60。
2. (5 - 3) * (8 + 2) = ____。
答案:20。
3. (7 + 2) * (6 - 3) = ____。
答案:27。
4. (8 - 4) * (10 + 2) = ____。
答案:48。
5. (9 + 3) * (7 - 2) = ____。
答案:60。
练习题三:应用乘法公式解决实际问题1. 某书店每天卖出50本书,如果连续卖出7天,共卖出多少本书?答案:350本。
2. 某超市原价为每袋4.5元的大米进行促销,打8折后售价为多少?答案:3.6元。
3. 一包纸巾共有8包,每包纸巾有36张,共有多少张纸巾?答案:288张。
4. 一直线上有10个点,每两个点之间都有一段直线连接,共有多少段直线?答案:45段。
5. 小明在一周内每天早上跑步,每天跑5公里,共跑了多少公里?答案:35公里。
通过以上练习题,我们可以巩固数学乘法公式的运用。
通过反复练习,大家可以更加熟练地应用乘法公式解决实际问题。
希望大家能善于运用乘法公式,提高数学计算的准确性和效率。
2020年秋人教版八年级数学乘法公式能力提升练习
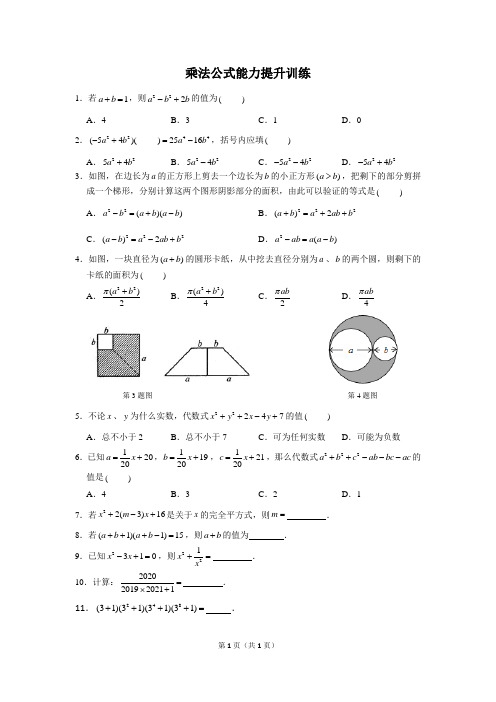
乘法公式能力提升训练1.若1a b +=,则222a b b -+的值为( )A .4B .3C .1D .02.22(54)(a b -+ 44)2516a b =-,括号内应填( )A .2254a b +B .2254a b -C .2254a b --D .2254a b -+3.如图,在边长为a 的正方形上剪去一个边长为b 的小正方形()a b >,把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )A .22()()a b a b a b -=+-B .222()2a b a ab b +=++C .222()2a b a ab b -=-+D .2()a ab a a b -=- 4.如图,一块直径为()a b +的圆形卡纸,从中挖去直径分别为a 、b 的两个圆,则剩下的卡纸的面积为( )A .22()2a b π+ B .22()4a b π+ C .2ab π D .4ab π第3题图 第4题图5.不论x 、y 为什么实数,代数式22247x y x y ++-+的值( )A .总不小于2B .总不小于7C .可为任何实数D .可能为负数 6.已知12020a x =+,11920b x =+,12120c x =+,那么代数式222a b c ab bc ac ++---的值是( )A .4B .3C .2D .17.若22(3)16x m x +-+是关于x 的完全平方式,则m = .8.若(1)(1)15a b a b +++-=,则a b +的值为 .9.已知2310x x -+=,则221x x += . 10.计算:2020201920211=⨯+ . 11.248(31)(31)(31)(31)++++= .12.已知35a b b c -=-=,2221a b c ++=,则ab bc ca ++的值等于 . 13.记248(12)(12)(12)(12)(12)n x =++++⋯+,且12812x +=,则n = .14.先阅读下面的内容,再解决问题例题:若2222690m mn n n ++-+=,求m 和n 的值解:2222690m mn n n ++-+=2222690m mn n n n ∴+++-+=22()(3)0m n n ∴++-=0m n ∴+=,30n -=3m ∴=-,3n =问题:(1)若2222440x y xy y +-++=,求2y 的值;(2)试探究关于x 、y 的代数式22591262028x y xy x +--+是否有最小值,若存在,求出最小值及此时x 、y 的值;若不存在,说明理由15.从边长为a 的正方形中剪掉一个边长为b 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)探究:上述操作能验证的等式是: (请选择正确的一个). A .22()()a b a b a b -=+- B .2()a ab a a b +=+ C .2222()a ab b a b -+=-(2)应用:利用你从(1)选出的等式,完成下列各题:①已知224924x y -=,238x y +=,求23x y -的值;②计算:2222211111(1)(1)(1)(1)(1)23452020-⨯-⨯-⨯-⨯⋯⨯-.。
整式的乘法公式练习题

整式的乘法公式练习题在代数学中,整式的乘法是一项基本的运算,它在解决各种代数问题中起着重要的作用。
本文将为大家提供一些整式的乘法公式练习题,通过练习巩固并加深对整式乘法的理解。
练习题一:将下列整式相乘,并将结果化简。
1. (2x + 3)(x + 4)解析:首先使用分配律,将前一项的每个项与后一项的每个项相乘:= 2x * (x + 4) + 3 * (x + 4)接下来使用分配律将每个相乘得到的结果进行合并并化简:= 2x^2 + 8x + 3x + 12最终结果为:2x^2 + 11x + 122. (3x - 5)(2x + 7)解析:同样地,使用分配律将每个项相乘:= 3x * (2x + 7) - 5 * (2x + 7)然后合并并化简结果:= 6x^2 + 21x - 10x - 35最终结果为:6x^2 + 11x - 35练习题二:将下列整式相乘,并将结果化简。
1. (a + 5)(a - 2)解析:使用分配律将每一项相乘:= a * (a - 2) + 5 * (a - 2)合并并化简结果:= a^2 - 2a + 5a - 10最终结果为:a^2 + 3a - 102. (2x + 3)(2x - 3)解析:应用分配律进行乘法运算:= 2x * (2x - 3) + 3 * (2x - 3)合并并化简结果:= 4x^2 - 6x + 6x - 9最终结果为:4x^2 - 9练习题三:将下列整式相乘,并将结果化简。
1. (3a - 2b)(4a + 5b)解析:通过使用分配律进行乘法运算:= 3a * (4a + 5b) - 2b * (4a + 5b)合并并化简结果:= 12a^2 + 15ab - 8ab - 10b^2最终结果为:12a^2 + 7ab - 10b^2 2. (2x - 3y)(x + 4y)解析:使用分配律将每一项相乘:= 2x * (x + 4y) - 3y * (x + 4y)合并并化简结果:= 2x^2 + 8xy - 3xy - 12y^2最终结果为:2x^2 + 5xy - 12y^2通过以上的练习题,我们可以对整式乘法公式进行更好的掌握。
乘法公式专项练习题

乘法公式专项练习题乘法是数学中非常重要的运算之一,掌握乘法公式对于解决各种数学问题至关重要。
在这份文档中,我们将提供一系列乘法公式的专项练习题,帮助您巩固和加深对乘法公式的理解和应用。
练习题1:计算下列乘积:1) (2x)(-3x)2) (4a)(-5b)3) (-6)(2x^2)练习题2:简化下列乘积表达式:1) 3x^2 * 5x^32) -4a^2 * 2a^43) -6x^3 * -2x^2练习题3:计算下列表达式的值:1) (4 + 2)(6 - 3)2) (5 - 3)^23) (2x + 3)(4x - 5)练习题4:计算下列表达式的值:1) (2 + 3) + (4 - 1)2) (5 - 2) * 33) (2x + 5) - (3x - 4)练习题5:利用分配律计算下列表达式的值:1) 2(3x + 4)2) -5(2a - 3)3) -x(2x^2 - 3x + 1)练习题6:计算下列乘积并简化结果:1) (3a + 2b)(3a - 2b)2) (-4x - 5y)(4x + 5y)3) (2x^2 + 3xy - 5y^2)(2x^2 - 3xy + 5y^2)练习题7:计算下列表达式的值:1) (-2)^32) 3^2 * 2^43) (-5)^2 * (-3)^3练习题8:计算下列乘积:1) -2 * (-3)2) 0 * 53) 7 * (-4)练习题9:计算下列乘积并用科学计数法表示结果:1) 2.5 * 10^4 * 1.2 * 10^32) 6.8 * 10^5 * 3.2 * 10^23) 5.2 * 10^7 * 7.6 * 10^1练习题10:计算下列乘积并用适当的单位表示结果:1) 5 km * 2 h2) 3 m * 4 s3) 10 g * 5 cm^3以上是乘法公式的专项练习题,通过解答这些题目,您将更加熟悉和掌握乘法公式的运用。
如果您遇到了困难或有任何疑问,建议您向老师寻求帮助,他们将为您提供更详细的解答和指导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
④(x + y X x -y ) = (-x -y X-x + y )⑤ 1-(1 + x ) =-x2-2x
A.1
B.2
C.3
D.4
(2015春?开江县期末)计算 20152- 2014 >2016的结果是(
)
A . - 2
B .- 1
C . 0
D . 1
二.填空题
6. 7. 多项式X 2 -8x +k 是一个完全平方式,则 k =
8.
1 2 1
已知a+-=5,贝U a +飞的结果是
a a
9. 0 2 若把代数式 X 2
—2x —3化为(X — m ) +k 的形式,其中 m , k 为常数,则 m + k =
10. (2015春?深圳期末)若A= (2+1 ) (22
+1) (24
+1) ( 28
+1) +1,则A 的末位数字是 11.对于任意的正整数 n ,能整除代数式(3n +U 3n-1)-(3-n X 3+ n )的最小正整数是
【巩固练习】 一.选择题
1•下列各多项式相乘,可以用平方差公式的有 ()
①(-2ab +5x \5x +2ab )②(ax — y X -ax- y )
③(—ab-c Xab-c )
④(m + n X -m-n ) A.4个
B.3个
C.2个
D.1个
2.若X 2
+kx + -是完全平方式,则 k 值是(
4
A. ±2
B. ±1
C. ±4
D. 1
3.下面计算(—7+a +b X -7 —a —b )正确的是(
A.原式=(—7 + a + b )[ — 7— ( a + b )] =— 72
,2
—
(a + b )
4. B.原式=(—7 + a + b )[ — 7—( a + b )] = 7? + C.原式=[—(7 — a — b )][ — (7 + a + b )] = 7
2
(a +b )
.2
—(a +
2 2
D.原式=[—(7 + a ) + b ][ — (7 + a ) — b ] = (7 + a ) -b (a + 3)( a 2 + 9)( a — 3)的计算结果是
.
4
A. a + 81 4
B. — a —
4
C. a — 81 4
D.81 — a
5. 下列式子不能成立的有()个.
2 2 2
①(x -y ) =(y -x ) ②(a -2b ) 2
- 2
=a -4b ③(a -b ) =(b -a )(a -b )
2 ..2
12.如果(2a +2b +1 x 2a +2b _1 尸 63,那么 a + b 的值为 三.解答题 13.计算下列各值.
2 2 2 2
(2) (m + 2 ) (m -2) (m 2
+4 )
14. (2015春?成华区月考)如果一个正整数能表示为两个连续偶数的平方差,那么称这个
正整数为 神秘数”女口: 4=22 - 02, 12=42- 22, 20=62- 42
,因此4、12、20都是这种
神
秘数”
(1) (2) (3)
2
15.已知:a-b=6, ab +(c -a )+9 = 0,求 a +b + c 的值.
【答案与解析】 -.选择题
1. 【答
案】 B ;
【解析】 ①,②,③可用平方差公式
.
2. 【答
案】
B ;
【解析】
X 2±2X
〔1
]X
+〔
1
]
=x2±kx+1
所以k = ± 1.
3. 【答案】 C;
4. 【答案】 C ;
【解析】
(a + 3)( a 2 + 9)( a — 3) = (a 2-9)(a 2 + 9) =a 4 -81
5. 【答案】 B ;
【解析】②,③不成立.
6. 【答
案】
D ;
【解析】
解:原式=20152
- (2015 - 1) X (2015+1 )=20152
— (20152
- 1)=20152
—
20152
+1=1, 故选D.
X 2-8x +k = X 2-2^ 4x 中42
,二 k = 16.
二.填空题
7. 【答
案】
16;
(1) 1012 +992
(3) (a + b-c)(a-b +c)
(4) (3x-2y +1)2
28和2012这两个数是 神秘数”吗?试说明理由; 试说
明神秘数能被 4整除;
两个连续奇数的平方差是神秘数吗?试说明理由. 【解析】
8 . 【答案】【解析】
9 . 【答
案】
23;
甘1)2=25,a2 +2 + 2=25,a2+厶=23. a a a
—3
;
【解析】X 2-2X -3=X
2
-2x+1-1-3=(x-1) —4, m = 1, k =-4.
2
10. 【答案】6; 2 4 8 【解析】解:(
2+1) (2 +1) (2 +1) (2 +1) +1 2 4 8
=(2 - 1) (2+1) (2 +1) (2 +1) (2 +1) +1,
2 2 4
=(2 - 1) (2 +1) (2 +1) 4 八"4 8
=(2 - 1) (2 +1) (2 +1)
8 八 "8
=(2 - 1) (2 +1) +1 , =(216 - 1) (216+1) +1, =2 32
- 1+1 , 因为232
的末位数字是6,所以原式末位数字是 6 • 故答案
为:6 • 11. 【答案】10;
8 (2+1) +1 , + 1 ,
【解析】利用平方差公式化简得 10( n 2
-1),故能被10整除. 12.【答案】± 4; 2
【解析】(2a +2b+ 1X2a +2b-1) = (2a+2b ) -1=63, 2a + 2b = ±8, a + b = ±4. 三.解答题 13.【解析】
原式= 2 2 (100 + 1)+(100-1 ) =10000+200+1+10000-200 + 1=20002
原式= 2 2 2
(m 2 -4) (m 2 +4) =(m 4 -16) =m 8-32m 4 +256
原式= a 2 -(b-C 2 =&2 -b 2 -c 2
+2bc 原式=
2 2 2
(3x-2y+1) =(3x ) +(2y ) +1-2x3xx2y + 2畑-2個
= 9x 2
+4y 2 -12xy + 6x -4y +1 14.【解析】 解: 15.
(1 )是,理由如下:
2 2 2 2 •/ 28=8 - 6 , 2012=504 - 502 , • 28是“神秘数” ;2012是“神秘数”; (2) “神秘数”是4的倍数.理由如下: 2 2 (2k+2) -( 2k ) = (2k+2+2k ) (2k+2 - 2k ) =2 (4k+2) =4 (2k+1), ••• “神秘数”是4的倍数;
(3)
设两个连续的奇数为: 2k+1 , 2k - 1,贝U
(2k+1 ) 2
-( 2k - 1) 2
=8k ,
而由(2)知“神秘数”是 4的倍数,但不是8的倍数, 所以两个连续的奇数的平方差不是神秘数.
【解析】
解: •/ a -b =6, ••• a =b
+6
2
•: ab +(c-a) +9 = 0,
2
•(b +6 p +(c-a ) +9=0,
2 2
•(b+3) +(c-a ) =0, /. b = —3, c = a
a =( —3 )+6=3, c = 3 ••• a+b+c = 3 + (£)+3 = 3.。
