四年级奥数图形面积

合集下载

四年级奥数题及答案-求格点图案面积

四年级奥数题及答案-求格点图案面积
【题目】以下这张图里的三个格点图案面积分别是多少?
【解析】
这三个图形都适合用格点面积公式计算面积：
格点多边形面积 = 内格点个数 + 边格点数÷ 2 - 1
这个公式是皮克(Pick)在1899年给出的，被称为“皮克定理”，这是一个实用而有趣的定理。

我们先来看喇叭图案：
这个图案周界上有8个格点，图内却没有格点，那么利用格点面积公式我们可以求得这个喇叭形状的面积为：0+8÷2-1=3;
接下来这只小猫的图案：
小猫图案的周界上有20个格点，而图内有2个格点，面积为：2+20÷2-1=11;
小狗图案同理：
我们可以看到小狗图案是由两个格点多边形组成，那我们可以将两个图案分开求解，先求出每个格点多边形的面积，再求出总面积。

躯干面积：0+12÷2-1=5;
尾巴面积：0+4÷2-1=1;
总面积：5+1=6。

我们在计算像小狗图案这样的有两个或以上的独立格点多边形组成的图案时，可以先求每个独立的格点多边形的面积，再进行求和计算总面积，这样可以避免数漏多个独立图形公共格点而导致计算错误。

四年级奥数详解答案第6讲面积的计算

四年级奥数详解答案第6讲第六讲面积的计算一、知识概要1. 面积：面积是围成的平面图形的大小。

2. 各种图形的计算公式1. 三角形面积=底×高÷2 用字母表示为：S=ah ÷2(注：高，就是从三角形的顶点向它的对边所做的那条垂线段)}是特殊的平行四边形为：用字母表示边长边长面积正方形为：用字母表示宽长面积长方形2a S . 3.ab S .2=⨯==⨯= 4. 平行四边形面积=底×高用字母表示为：S=ah5. 梯形面积=(上底+下底)×高÷2 用字母表示为：S=2h b)a ⨯+（ {注：解梯形应用题常用到梯形的中位线。

中位线就两腰的中立的连线。

中位线等于两底边之和的一半，即，中位线=(a+b)÷2}}二、典型题目精讲1. 用同样大小的长方形纸片摆成下图，已知每张小纸片的宽是4厘米，阴影部分的面积是多少平方厘米？分析：(如图)5个长方形的长等于3个长十3个宽即5a=3a+3b,则2a=3b,a=3×4÷2=6(cm) 图中阴影部分是三个相等的小正方形，其一个正方形的边长为长-宽，即6-4=2(cm),这样，全部阴影部分面积就是(2×2×3)cm 2了。

解：①3×4÷2=6(cm)②6-4=2(cm)③2×2×3=12(cm 2)答：阴影部分的面积是12 cm 2。

2. 下图是一个边长为20厘米的正方形和一个长方形的组合图形，求阴影部分的面积。

分析：作二条辅助线，交于正点使EF=20cm ，EG=10 cm(如图)则阴影面积=上、下两个长方形面积之和-∆ABC 的面积-∆ADE 的面积解：①S ∆ABC=(20+10+4)×14÷2=238(cm 2) ②S ∆ADE=(20+10)×(20+14)÷2=510(cm 2) ③34×14+30×20=1076(cm 2) ④1076-(238+510)=328(cm 2)答：阴影部分的面积等于328cm2。

四年级奥数巧算面积

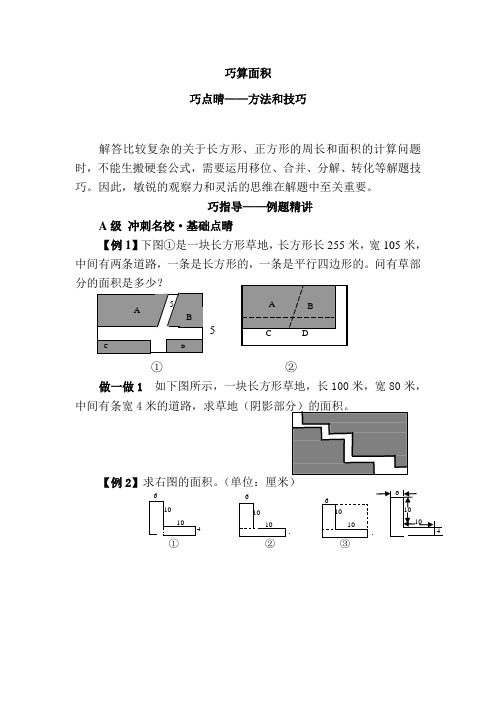
巧算面积巧点晴——方法和技巧解答比较复杂的关于长方形、正方形的周长和面积的计算问题时，不能生搬硬套公式，需要运用移位、合并、分解、转化等解题技巧。

因此，敏锐的观察力和灵活的思维在解题中至关重要。

巧指导——例题精讲A级冲刺名校·基础点晴【例1】下图①是一块长方形草地，长方形长255米，宽105米，中间有两条道路，一条是长方形的，一条是平行四边形的。

问有草部分的面积是多少？5①②做一做1如下图所示，一块长方形草地，长100米，宽80米，中间有条宽4【例2】做一做2 计算下列图形的面积。

（单位：厘米）【例3】如右图，一块菜地长18米，宽10米，菜地中间留了宽2米的路，把菜地平均分成四小块，每一小块的面积是多少？分析与解1 已知这块菜地的长和宽，能求出这块菜地的总面积（大长方形），再减去道路的面积，就得到四小块菜地面积之和；也可直接求出每小块菜地的长和宽，从而求出小块菜地的面积。

每一小块菜地宽为：（10－2）÷2=4（米）每一小块菜地长为：（18－2）÷2=8（米）每一小块菜地的面积为：4×8=32（平方米）分析与解2 如右图，注意横道和竖道面积有一个重合部分，即虚线围成的小正方形，计算面积时，避免计算两次。

2×10＋2×18－2×2=52（平方米）或（10－2）×2＋18×2=52（平方米）（18×10－52）÷4=32（平方米）分析与解3 我们还可以运用平移的办法（面积不变）将道路平衡到菜地的边沿，如右图，先直接求一个小长方形的面积。

（18－2）×（10－2）=128（平方米） 128÷4=32（平方米）答：每一小块的面积是32平方米。

小结敏锐的观察力和灵活的思维在解本题时至关重要。

做一做3 如下图，一条白底的正方形手帕，它的边长是18厘米，手帕上横竖各有两道红条（图中的阴影部分），红条的宽都是2厘米。

奥数四年级—长方形和正方形面积

7
2021/8/14
分段
例4、如图，正方形中套一长方形，正方形的边长是 15，长方形的四个顶点恰好分别把正方形的四条边都分成两段，其中长的一段都是短的2倍。这个长方形的面积是多少？ (单位:厘米) 15÷3=5
5×2=10。
三角形面积： 5×5÷2=12.5 10×10÷2=50
12.5×2=25 50×2=100
15
2021/8/14
练 5、如图，是由9个小长方形组成的，按图中习编号，第1，2，3，4，5号的面积分别是1平
方米，2平方米，3平方米，4平方米，5平方米，那么，第6号长方形和面积是多少呢？
1×1=1
16
2021/8/14
3×2.5=7.5
练 6、如图，一个正方形中套着一个长方形，
习已知正方形的边长是20分米，长方形的四个
例1、有一块长方形的土地，长是宽的2倍，中间有一座雕塑，雕塑的底面是一个正方形，周围是草坪，草坪的面积是多少平方米？(单位：米)
20÷2=10 米
20×10=200 平方米
1×1=1 平方米
2
200-1=199 平方米 2021/8/14
拆分
例2、如图，是由6个相同的等腰三角形拼成的图形，求这个图形的面积是多少？
最多能裁出12张长4宽1厘米的纸条
10
2021/8/14
练 1.用48厘米长的一根铁丝围成一个正方形，习它的面积是多少？用这根铁丝围成一个长15
厘米的长方形，它的面积是多少？
48÷4=12 12×12=144
15×2=30
48-30=18 18÷2=9
15×9=135
11
2021/8/14
练 2、有一个长方形的市民广场，长100米，宽习 80米。广场中间留了宽4米的人行道，把广

四年级奥数面积求解

四年级奥数面积求解1.四边形面积：下图中AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE的面积是___平方厘米四边形AFDC的面积=三角形AFD+三角形ADC=（1/2×FD×AF）+（1/2×AC×CD）=1/2（FE+ED）×AF+1/2（AB+BC）×CD= （1/2×FE×AF+1/2×ED×AF）+（1/2×AB×CD+1/2×BC×CD）。

所以阴影面积=四边形AFDC-三角形AFE-三角形BCD=（1/2×FE×AF+1/2×ED×AF）+（1/2×AB×CD+1/2×BC×CD）-1/2×FE×AF-1/2×BC×CD=1/2×ED×AF+1/2×AB×CD=1/2×8×7+1/2×3×12=28+18=46。

2.如图所示，四边形ABCD与AEGF都是平行四边形，请你说明它们的面积相等。

连接 BE，根据前面介绍的模型，的面积既是平行四边形 ABCD面积的一半，又是平面积的两倍，因此相行四边形AEGF 面积的一半，所以这两个平行四边形的面积均为等。

3.三角形面积：如图，四边形ABCD和四边形DEFG都是正方形，已知三角形AFH的面积为6平方厘米，求三角形CDH的面积．通常求三角形的面积，都是先求它的底和高．题目中没有一条线段的长度是已知的，所以我们只能通过创造等积的方法来求．直接找三角形HDC 与三角形AFH 的关系还很难，而且也没有利用\四边形ABCD和四边形DEFG 是正方形\这一条件．我们不妨将它们都补上梯形DEFH 这一块．寻找新得到大三角形CEF 和大直角梯形DEFA 之间的关系．经过验算，可以知道它们的面积是相等的．从而得到三角形 HDC与三角形AFH面积相等，也是6平方厘米．4. 如下图，有21个点，每相邻三个点成\1的等边三角形.计算三角形ABC的面积.如图（2）所示，在△ABC内连接相邻的三个点成△DEF，再连接DC、EA、FB后是△ABC可看成是由△DEF分别延长FD、DE、EF边一倍、一倍、二倍而成的，不难得到S△ACD=2，S△AEB=3，S△FBC=4，所以S△=1+2+3+4=10（面积单位）.5.如图，平行四边形ABCD的面积是40平方厘米，图中阴影部分的面积是多少？解答：连接BD,由三角形等积变形，ΔBOD的面积等于阴影部分的面积，又ΔADB的面积等于ΔBCD的面积，都是平行四边形ABCD的一半，所以阴影部分的面积是平行四边形ABCD的1/4，面积为10平方厘米。

小学四年级奥数第15讲图形问题(含答案分析)

第15讲图形问题一、知识要点解答有关“图形面积”问题时，应注意以下几点：1.细心观察，把握图形特点，合理地进行切拼，从而使问题得以顺利地解决；2.从整体上观察图形特征，掌握图形本质，结合必要的分析推理和计算，使隐蔽的数量关系明朗化。

二、精讲精练【例题1】人民路小学操场长90米，宽45米。

改造后，长增加10米，宽增加5米。

现在操场面积比原来增加了多少平方米？练习11、有一块长方形的木板，长22分米，宽8分米。

如果长和宽分别减少10分米、3分米，面积比原来减少多少平方分米？2、一块长方形铁板，长18分米，宽13分米。

如果长和宽各减少2分米，面积比原来减少多少平方分米？【例题2】一个长方形，如果宽不变，长增加6米，那么它的面积增加54平方米；如果长不变，宽减少3米，那么它的面积减少36平方米。

这个长方形原来的面积是多少平方米？练习21、一个长方形，如果宽不变，长减少3米，那么它的面积减少24平方米；如果长不变，宽增加4米，那么它的面积增加60平方米。

这个长方形原来的面积是多少平方米？2、一个长方形，如果宽不变，长增加5米，那么它的面积增加30平方米；如果长不变，宽增加3米，那么它的面积增加48平方米。

这个长方形原来的面积是多少平方米？【例题3】下图是一个养禽专业户用一段16米的篱笆围成的一个长方形养鸡场，求它的占地面积。

练习31、下图是某个养禽专业户用一段长13米的篱笆围成的一个长方形养鸡场，求养鸡场的占地面积。

2、用56米长的木栏围成长或宽是20米的长方形，其中一边利用围墙，怎样才能使围成的面积最大？【例题4】街心花园中一个正方形的花坛四周有1米宽的水泥路，如果水泥路的总面积是12平方米，中间花坛的面积是多少平方米？练习41、有一个正方形的水池，如下图的阴影部分，在它的周围修一个宽8米的花池，花池的面积是480平方米，求水池的边长。

2、已知大正方形比小正方形的边长多4厘米，大正方形的面积比小正方形面积大96平方厘米（如下图）。

四年级奥数第12讲-图形面积(教)

学科教师辅导讲义学员编号：年级：四年级课时数：3学员姓名：辅导科目：奥数学科教师：授课主题第12讲-图形面积授课类型 T 同步课堂 P 实战演练 S 归纳总结教学目标① 熟悉掌握基本图形面积的求法。

② 熟悉运用分解、平移、合并等技巧成基本图形，利用长方形、正方形面积计算公式求解。

③ 能够分析图形的特点，提高几何图形的观察能力和思维转换能力。

授课日期及时段T （Textbook-Based ）——同步课堂解答有关“图形面积”问题时，应注意以下几点：1.细心观察，把握图形特点，合理地进行切拼，从而使问题得以顺利地解决；2.从整体上观察图形特征，掌握图形本质，结合必要的分析推理和计算，使隐蔽的数量关系明朗化。

例1、人民路小学操场长90米，宽45米。

改造后，长增加10米，宽增加5米。

现在操场面积比原来增加了多少平方米？【解析】用操场现在的面积减去操场原来的面积，就得到增加的面积。

操场现在的面积是（90+10）×（45+5）=5000平方米，操场原来的面积是90×45=4050平方米。

所以，现在的面积比原来增加5000－4050=950平方米。

例2、一个长方形，如果宽不变，长增加6米，那么它的面积增加54平方米；如果长不变，宽减少3米，那么它的面积减少36平方米。

这个长方形原来的面积是多少平方米？【解析】由“宽不变，长增加6米，面积增加54平方米”可知，它的宽为54÷6=9米；由“长不变，宽减少3米，面积减少36平方米”可知，它的长为36÷3=12米。

知识梳理典例分析所以，这个长方形原来的面积是12×9=108平方米。

例3、下图是一个养禽专业户用一段16米的篱笆围成的一个长方形养鸡场，求它的占地面积。

【解析】根据题意，因为一面利用着墙，所以两条长加一条宽等于16米。

而宽是4米，那么长是（16－4）÷2=6米，占地面积是6×4=24平方米。

小学四年级奥数思维问题之图形面积

图形面积问题教学目标：①知识与技能目标:借助所学知识计算组合图形的面积②过程与方法目标:通过对数量关系地分析，让学生在解决问题过程中掌握一些解决问题的基本策略③情感态度与价值观目标:感受所学知识与现实生活的紧密联系教学重点：图形面积公式的运用教学难点：组合图形的面积计算[知识引领与方法]1.细心观察，把握图形特点，合理的进行切拼，从而使问题得以顺利解答2.从整体上观察图形的特征，掌握图形本质，结合必要的分析，推理和计算，使隐蔽的数量关系明朗化[例题精选及训练]【例1】一块长方形铁板，长18分米，宽15分米。

若长和宽分别减少3分米，面积比原来的减少多少平方分米？练习：1.人民路小学操场长90米,宽45米，改造后,长和宽分别增加10米。

现在操场面积比原来增加了多少平方米?2.有一块长方形的木板，长22分米,宽8分米。

如果长和宽分别减少10分米和3分米，木板的面积比原来减少多少平方分米?3.一块长方形地，长是80米，宽是45米，如果把宽增加5米，要使面积不变，长应减少多少米?【例2】一个长方形，如果宽不变，长增加5米，那么它的面积增加30平方米；如果长不变，宽增加3米，那么它的面积增加48平方米。

问这个长方形原来的面积是多少平方米？练习：1.一个长方形，如果宽不变,长减少3米，那么它的面积减少24平方米;如果长不变，宽增加4米，那么它的面积增加60平方米。

这个长方形原来的面积是多少平方米?2.一个长方形,如果宽不变，长增加6米,那么它的面积增加54平方米;如果长不变，宽减少3米，那么它的面积减少36平方米。

问这个长方形原来的面积是多少平方米?3.一个长方形花圃，如果它的长减少5米，或它的宽减少6米,那么它的面积都减少60平方米。

求这个长方形花圃原来的面积。

【例3】下图是一个养鸡专业户用一段长17米的篱笆围成的一个长方形养鸡场，那么这个养鸡场的占地面积是多少平方米？练习：1.右图是某个养鸡专业户用一段长13米的篱笆围成一个长形的养鸡场，则养鸡场的占地面积有多大?2.用56米长的木栏围成长或宽是20米的长方形,其中一边利用围墙，怎样才能使围成的面积最大?【例4】街心花园中一个正方形的花坛四周有一条1米宽的水泥路，如果水泥路的总面积是12平方米，那么中间花坛的面积是多少平方米？练习：1.有一个正方形的水池，如右图阴影部分所示，在它的周围修了一个宽8米的花池,花池的面积是480平方米,求水池的边长。

四年级奥数试题与解析：面积问题【三篇】

四年级奥数试题与解析：面积问题【三篇】芬芳袭人花枝俏，喜气盈门捷报到。

心花怒放看通知，梦想实现今日事，喜笑颜开忆往昔，勤学苦读最美丽。

在学习中学会复习，在运用中培养能力，在总结中不断提高。

以下是小编为大家整理的《四年级奥数试题与解析：面积问题【三篇】》供您查阅。

【第一篇】如图，已知大正方形的边长为4，小正方形的边长为3，那么阴影部分的面积为（）。

分析：由图意可知：阴影部分是一个三角形，且其底和高都等于小正方形的边长，于是利用三角形的面积S=（1/2）ah，代入数据即可求解．解答：解：(1/2)_3_3=4.5；答：阴影部分的面积是4.5．故答案为：4.5．点评：解答此题的关键是明白：阴影部分是一个三角形，且其底和高都等于小正方形的边长，从而利用三角形的面积公式即可求解．【第二篇】1．用60米长的篱笆围成一个长方形养鸡场，其中一面利用墙，如图．求这个养鸡场的面积是（）米。

考点：长方形、正方形的面积．分析：设养鸡场宽为_米，则长为（60-2_）米，再通过枚举法由长方形的面积公式S=ab，即可求出面积．解答：解：设养鸡场宽为_米，则长为（60-2_）米，根据题意宽为1米时，长是58米，面积是58_1=58（平方米），宽是2米时，长是56米，面积是56_2=_2（平方米），宽是3米时，长是54米，面积是54_3=_2（平方米），宽是4米时，长是52米，面积是52_4=2_（平方米），宽是5米时，长是50米，面积是50_5=250（平方米），宽是6米时，长是48米，面积是48_6=288（平方米），宽是7米时，长是46米，面积是46_7=3_（平方米），宽是8米时，长是44米，面积是44_8=352（平方米），宽是9米时，长是42米，面积是42_9=378（平方米），宽是_米时，长是40米，面积是40__=4_（平方米），宽是_米时，长是38米，面积是38__=4_（平方米），宽是_米时，长是36米，面积是36__=432（平方米），宽是_米时，长是34米，面积是34__=442（平方米），宽是_米时，长是32米，面积是32__=448（平方米），宽是_米时，长是30米，面积是30__=450（平方米），宽是_米时，长是28米，面积是28__=448（平方米），由此看出当宽是_米时，长是30米，面积，为30__=450（平方米），答：这个养鸡场的面积是450平方米．故答案为：450平方米．点评：根据长方形的面积公式，利用枚举法，得出如何围才能够使面积．【第三篇】‘四年级奥数试题与解析：面积问题【三篇】.到电脑，方便收藏和打印：。

四年级奥数第三讲：图形面积问题

第三讲：图形面积问题
姓名：
例1、一块长方形铁板，长18分米，宽15分米。

若长和宽分别减少3分米，面积比原来减少多少平方分米？
练习1、人民路小学操场长90米，宽45米，改造后，场合宽分别增加10米。

现在操场面积比原来增加了多少平方米？
练习2、一块长方形地，长80米，宽45米，如果把宽增加5米，要使面积不变，长应该减少多少米？
例2、一个长方形，如果宽不变，长增加5米，那么它的面积增加30平方米；如果长不变，宽增加3米，那么它的面积增加48平方米。

问这个长方形原来的面积时多少平方米？
练习1、一个长方形花圃，如果它的长减少5米，或它的宽减少6米，那么它的面积都减少60平方米。

求这个长方形花圃原来的面积时多少平方米？
例3、右图是一个养鸡专业户用一段长17米的篱笆围成的一个长方形养鸡场，那么这个养鸡场的占地面积是多少平方米？
练习1、用56米长的木栏围成长或宽是20米的长方形，其中一边利用围墙，怎样才能使围成的面积最大？
例4、街心花园中一个正方形的花坛四周有一条1米宽的水泥路，如果水泥路的总面积是12平方米，那么中间花坛的面积是多少平方米？
练习1、有一个正方形的水池，如右图阴影部分所示，在它的周围修了一个宽8米的花池，花池的面积是480平方米，求水池的边长是多少米？
例5、一块正方形的钢板，先截去宽5分米的长方形，又截去宽8分米的长方形（如下图所示），这样面积就比原来的正方形减少了181平方分米。

原来正方形的边长是多少分米？
练习1、一个正方形一条边减少6分米，另一条边减少10分米后变成一个长方形，这个长方形的面积比正方形的面积少260平方分米，求原来正方形的边长是多少分米？。

奥数四年级第15讲图形面积一

第15讲图形面积（一）解题策略：用好割补法。

【金牌例题1】暨阳小学操场长90m ，宽45m 。

改造后，长增加10m ，宽增加5m 。

现在操场面积比原来增加了多少m 2？【葛老师指路】现在面积－原来面积=增加的面积。

现在面积：(90+10)×(45+5)=5000m 2原来面积：90×45=4050m 2增加面积：5000-4050=950m 2方法二：画出右图，阴影部分就是增加的面积。

10×45+90×5+5×10=950 m 2金牌练习1 1.一块长方形木板，长22dm ，宽8dm 。

若长、宽分别减少10、3dm ，面积比原来减少几？22×8=176dm 2；12×5=60dm 2；176-60=116dm 2 2.一块长方形铁板，长18dm ，宽13dm 。

若长和宽各减少2dm ，面积比原来减少几？18×13=234dm 2；16×11=176dm 2；234-176=58dm 2。

3.一块长方形地，长80m ，宽45m 。

若把宽增加5m ，要使面积不变，长应减少几m ？80×45=3600m 2；3600÷（45+5）=72m ；80-72=8m ……减少8m【金牌例题2】一个长方形，若宽不变，长增加6m ，则它的面积增加54m 2；若长不变，宽减少3m ，则它的面积减少36m 2。

这个长方形原来的面积是多少？【葛老师指路】(长加)6m ×宽=54m 2，宽= 。

54÷6=9m ……宽；36÷3=12m ……长；12×9=108m 2……长方形面积金牌练习21.一个长方形，若宽不变，长减少3m ，则它的面积减少24m 2；若长不变，宽增加4m ，则它的面积增加60m 2。

长方形原来的面积是多少？24÷3=8m ……宽；60÷4=15m ……长；8×15=120m 2。

小学四年级奥数第十四讲求面积(四年级)

第十四讲求面积一、例题精讲姓名：例1、从长100厘米，宽60厘米的长方形纸上剪下一个最大的正方形，这张正方形的面积是多少？还剩下多大面积的纸？例2、有一个正方形水池，在它的周围修一个宽8米的花园，花园面积为480平方米，求水池的面积？（如图）例3、用篱芭围成一个长方形的养鸡场地，一边利用20米长的墙壁，篱笆共长40米，求养鸡场的面积？例4、有一个长方形，如果它的宽减少2米或它的长减少3米，那么它的面积就减少24 平方米，求原来这个长方形的面积？二、巩固练习成绩：1、求下面图形的面积？（单位：厘米）2、把一张长为4米，宽3米的长方形木板，剪成一个面积最大的正方形，这个正方形木板的面积是多少平方米？3、学校里有一个正方形花坛，四周种了一圈绿篱，绿篱总长20米，求花坛面积是多少平方米？4、一个长方形如果宽不变，长增加8米面积就增加72平方米，如果长不变，宽减少4米，面积就减少48平方米，这个长方形的面积是多少平方米？10335三、拓展提高姓名：1、有两个相同的长方形，长是8厘米，宽是3厘米，如果安下图叠放，这个图形的面积是多少？2、求下面图形的面积？（单位厘米）14233、有大小两个正方形部分重合，两块没有重合的阴影部分面积相差多少平方厘米？（单位：厘米）1064、如图，四个一样大的长方形和一个小正方形拼成一个大正方形，大正方形的面积是64平方厘米，小正方形的面积是4平方厘米，问长方形的宽（短边）是多少厘米？4422445324四、趣味作业1、求下面图形的面积？（单位：厘米）2、一个长方形若长增加2厘米，面积就增加10平方厘米，若宽减少3厘米，面积就减少18平方厘米，求原来长方形的面积？3、一块长方形铁皮，长12分米，宽9分米，把它剪成一个面积最大的正方形，剪成的正方形的面积是多少平方米？4、两张边长4厘米的正方形纸，二部分叠在一起放在桌上（如图），问桌与被盖住的面积是多少？家长意见:家长签字:。

苏教版四年级奥数第15周图形面积问题

第15周图形面积问题专题简析：解答有关图形面积问题时，应注意以下几点：1、细心观察，把握图形特点，合理地进行切拼，从而使问题得以顺利解答。

2、从整体上来观察图形特征，掌握图形本质，结合必要的分析、推理和计算，使隐蔽的数量关系明朗化。

例1:一块长方形铁板，长18分米，宽15分米。

若长和宽分别减少3分米，面积比原来的减少多少平方分米？练习一：1、人民小学操场长90米，宽45米，改造后，长和宽分别增加10米。

现在操场面积比原来增加了多少平方米？2、有一块长方形的木板，长22分米，宽8分米。

如果长和宽分别减少10分米和3分米，木板的面积比原来减少多少平方分米？3、一块长方形地，长是80米，宽是45米，如果把宽增加5米，要使面积不变，长应减少多少米？例2:一个长方形，如果宽不变，长增加5米，那么它的面积增加30平方米；如果长不变，宽增加3米，那么它的面积增加48平方米。

问这个长方形原来的面积是多少平方米？练习二：1、一个长方形，如果宽不变，长减少3米，那么它的面积减少24平方米；如果长不变，宽增加4米，那么它的面积增加60平方米。

这个长方形原来的面积是多少平方米？2、一个长方形，如果宽不变，长增加6米，那么它的面积增加54平方米；如果长不变，宽减少3米，那么它的面积减少36平方米。

问这个长方形原来的面积是多少平方米？3、一个长方形，如果它的长减少3米，或它的宽减少2米，那么它的面积都减少36平方米。

求这个长方形原来的面积？例3:右图是一个养鸡专业户用一段长17米的篱笆围成的一个长方形养鸡场，那么这个养鸡场的占地面积是多少平方米？练习三：1、右图是某个养鸡专业户用一段长13米的篱笆围成一个长方形的养鸡场，则养鸡场的占地面积有多大？2、用56米长的木栏围成长或宽是20米的长方形，其中一边利用围墙，怎样才能使围成的面积最大？3、用15米长的栅栏沿着围墙围一个种植花草的长方形苗圃，其中一面利用围墙。

如果每边的长度都是整数，怎样才能使围成的面积最大？例4:街心花园中一个正方形的花坛四周有一条1米宽的水泥路，如果水泥路的总面积是12平方米，那么中间花坛的面积是多少平方米？练习四：1、有一个正方形的水池，如右图阴影部分所示，在它的周围修了一个宽8米的花池，花池的面积是480平方米，求水池的边长。

四年级奥数：面积问题

四年级奥数：面积问题
面积是数学中的一个重要概念，它用来描述平面上的形状或图形所占据的空间大小。

四年级的奥数也涉及到了面积问题，下面我们来介绍一些常见的面积问题及解决方法。

正方形的面积
正方形是一个四边都相等且角均为90度的特殊矩形。

要计算正方形的面积，只需要将正方形的边长乘以它自己即可。

例如，一个边长为5厘米的正方形的面积是25平方厘米。

长方形的面积
长方形是另一种常见的图形，它有两对相等的边和四个角均为90度。

计算长方形的面积需要知道它的长和宽，然后将长乘以宽即可得到面积。

例如，一个长为7厘米，宽为4厘米的长方形的面积是28平方厘米。

三角形的面积
三角形是一个具有三条边和三个角的多边形。

计算三角形的面积需要知道底边的长度和高的长度。

将底边乘以高的一半即可得到三角形的面积。

例如，一个底边长度为6厘米，高为3厘米的三角形的面积是9平方厘米。

平行四边形的面积
平行四边形是一个具有两对平行边和四个角的四边形。

计算平行四边形的面积需要知道底边的长度和高的长度。

将底边乘以高即可得到平行四边形的面积。

例如，一个底边长度为8厘米，高为5厘米的平行四边形的面积是40平方厘米。

总结
面积是描述平面图形所占据空间大小的概念。

在四年级的奥数中，我们经常会遇到正方形、长方形、三角形和平行四边形的面积问题。

要计算这些图形的面积，只需要记住相应的公式，并将已知的值代入求解即可。

通过练习这些面积问题，我们能够更好地理解图形的特点和面积的计算方法，提高自己的数学水平。

四年级巧求面积奥数题

四年级巧求面积奥数题一、例题1. 题目一个长方形，如果宽不变，长增加6米，那么它的面积增加54平方米；如果长不变，宽减少3米，那么它的面积减少36平方米。

这个长方形原来的面积是多少平方米？2. 解析（1）根据“宽不变，长增加6米，面积增加54平方米”，由长方形面积公式S = 长×宽，可得宽为54÷6 = 9米。

（2）再根据“长不变，宽减少3米，面积减少36平方米”，可得长为36÷3 = 12米。

（3）所以原来长方形的面积为12×9 = 108平方米。

3. 题目如图，大正方形比小正方形的边长多4厘米，大正方形的面积比小正方形面积大96平方厘米。

小正方形的面积是多少？（这里假设小正方形边长为a厘米，大正方形边长为a + 4厘米）4. 解析（1）大正方形面积为(a + 4)^2平方厘米，小正方形面积为a^2平方厘米。

（2）已知大正方形面积比小正方形面积大96平方厘米，则可列出等式(a + 4)^2-a^2=96。

（3）展开式子得到a^2+8a + 16 a^2=96，化简后为8a+16 = 96。

（4）先计算8a=96 16 = 80，解得a = 10。

（5）所以小正方形面积为a^2=10^2=100平方厘米。

5. 题目有一个长方形菜园，如果把宽改成50米，长不变，那么它的面积减少680平方米；如果使宽为60米，长不变，那么它的面积比原来增加2720平方米。

原来的长和宽各是多少米？6. 解析（1）由“宽改成50米，长不变，面积减少680平方米”，可得长为680÷(原来的宽 50)。

（2）由“宽为60米，长不变，面积比原来增加2720平方米”，可得长为2720÷(60 原来的宽)。

（3）因为长不变，所以680÷(原来的宽 50)=2720÷(60 原来的宽)。

（4）设原来的宽为x米，则(680)/(x 50)=(2720)/(60 x)。

面积

四年级奥数之图形的面积知识点：一、基本图形的面积公式：1、平行四边形的面积=底×高2、三角形的面积=底×高÷23、梯形面积=（上底+下底）×高÷2二、常用方法：1.分割2.拼接3.旋转4.平移例题解析：例1：下图大小两个正方形有一部分重合，两块没有重合的阴影部分面积相差是多少?(单位：厘米)例2：如图，一张长方形纸片，长7厘米，宽5厘米．把它的右上角往下折叠，再把左下角往上折叠，未盖住的阴影部分的面积是多少平方厘米？巩固练习：1．一个长方形，如果长减少5厘米，宽减少2厘米，那么面积就减少66平方厘米，这时剩下部分刚好成为一个正方形。

求原来长方形的面积。

2．图11中“风车”（阴影部分）的面积等于多少平方厘米？3.图是两个正方形，边长分别是8厘米和4厘米，那么阴影部分的面积是多少？4.下图是一个方格网，计算阴影部分的面积．5、求下图的面积（单位：厘米）6、一个边长为10米的正方形花坛，依次连接四边中点得到一个小正方形的喷泉，求小正方形喷泉的面积。

7、如图，大小两个正方形对应边的距离均为2厘米，如果两个正方形之间部分的面积是40平方厘米，那么小正方形的面积是多少平方厘米？8、一个长方形，如果宽增加2厘米，或长增加3厘米，他们的面积都增加120平方厘米，原来长方形的面积是多少？（2400平方厘米）9、右图是由5个相同的小长方形拼成的一个大长方形，大长方形的周长是44厘米，求大长方形的面积。

10.如图，四边形ABCD和四边形DEFG都是正方形，已知三角形AFH的面积为6平方厘米，求三角形CDH的面积.11.一个边长是7厘米的正方形纸片，最多能裁出多少个长是4厘米，宽是1厘米的长方形纸条？12. 巧求面积:7个完全相同的长方形拼成了图中阴影部分，图中空白部分的面积是多少平方厘米？13.如右图，正方形ABCD的边长是6厘米，过正方形内的任意两点画直线，可把正方形分成9个小长方形。