组合数学第2章
顺序结构的优缺点
优点： 优点： 算法简单，容易实现，随机存取。 算法简单，容易实现，随机存取。 缺点： 缺点： 插入和删除操作复杂，移动大量的数据元素， 插入和删除操作复杂，移动大量的数据元素， 在插入操作时， 在插入操作时，还要涉及到重新分配大块空 间问题. 间问题. 使用情况： 使用情况： 建立结构后只做大量的查询而很少做插入、 建立结构后只做大量的查询而很少做插入、 删除的场合。 删除的场合。
线性表(Linear List)定义
n个具有相同特性的数据元素组成的有限序列 个具有相同特性的数据元素组成的有限序列 个具有相同特性的数据元素组成的
(a1,…,ai-1,ai,ai+1,…,an)
ai
前驱： 前驱： ai-1 n: 线性表的长度， 线性表的长度 长度， n=0时 ：空表 时
位序： 位序： i 后继： 后继：ai+1
可以随机 存取
0 1 i-1 i n-1 MAXSIZE-1
… a1
a2
…
ai-1
ai
ai+1
…
an
…
线性表的起始地址 称作线性表的基地址
顺序表用元素的物理关系 存储位置） （存储位置）表达了数据 元素的逻辑关系
线性表的顺序表Biblioteka 和实现0 1 i-1 i n-1 MAXSIZE-1
a1
a2
…
ai-1
设在第i个 位置删除的概率为pi；
n
1 n n −1 Ein = ∑ pi (n − i ) = ∑ (n − i ) = i =1 n i =1 2
时间复杂度为O（ ） 时间复杂度为 （n）
顺序表上基本运算的实现(4)
按值查找 :
该算法的时间复杂度为 O(ListLength(L))
int SeqListLocate(SeqList L, ElemType x) { //在顺序表 中查找第一个与x值相等的元素。若查找成功， 在顺序表L中查找第一个与 值相等的元素。若查找成功， 在顺序表 中查找第一个与 值相等的元素 则返回它在顺序表中的位置 否则，返回0 位置； 则返回它在顺序表中的位置；否则，返回0。 i=1; while(i<=L.length && L.data[i-1]!=x) //第i个元素的下标为 [i-1] 个元素的下 第 个元素的 i++; if (i<=L.length) return i; //返回数据元素的位置 返回数据元素的位置 else return 0; //查找失败 查找失败 }
插入算法的时间复杂度分析
基本操作：移动数据 在第i个位置插入x：an到ai都要向后移动一个位置，共移 动 n-i+1个元素； +1 i的取值范围为： 1 ≤ i ≤ n ，即有n＋1个位置插入； ＋ 1 pi = 设在第i个 位置插入的概率为pi； ( n + 1) 平均移动数据元素的次数（期望值）为： Ein = n+1 pi (n − i + 1) ∑ i =1 设 pi = 1
线性结构 • 线性结构是 一个数据元素的有序集。 一个数据元素的有序集。
线性结构
• 在数据元素的非空的有限集合中： 在数据元素的非空的有限集合中：
– 存在唯一的一个“第一个”的数据元素 存在唯一的一个“第一个” – 存在唯一的一个“最后一个”的数据元素 存在唯一的一个“最后一个” – 除第一个元素外，每个元素都有且仅有一个（直 除第一个元素外，每个元素都有且仅有一个（ 接）前驱 – 除最后一个元素外，每个元素都有且仅有一个 除最后一个元素外， （直接）后继 直接）
第二章 线性表
问题
• • • • •
什么是数据结构？ 什么是抽象数据类型？ 什么是渐进时间复杂度？ 有几种类型逻辑结构？ 物理结构指的是什么？
Objective
1. 2. 3. 4. 5.
学习用抽象数据类型定义线性表 学会利用基本操作编写关于线性表的操作 学会线性表的顺序表示和实现 学会线性表的链式表示和实现 学会其他链表
顺序表上基本运算的实现(2)
插入运算: 个位置，插入元素e 插入运算:在第 i 个位置，插入元素 思想：把第i个位置开始的元素 个位置开始的元素， 思想：把第 个位置开始的元素，依次后移 步骤： 步骤：
1.当前表是否已经满？ 当前表是否已经满？ 当前表是否已经满 2.输入是否有效？ 输入是否有效？ 输入是否有效 3.插入元素 插入元素 4. 长度+1 长度
顺序表上基本运算的实现(2)
插入元素 : void SeqListInsert(SeqList L,int i,ElemType x) { //在顺序表中的第 i 个位置插入元素 x //在顺序表中的第 if (L.length==MAXSIZE) {printf(＂表满＂); exit(0); } //表满， 表满， ＂表满＂ 表满 退出 if(i<1 || i>L.length+1) {printf(“位置错 位置错”); exit(0); } 位置错 开始， L.data[i-1]； //插入位置错。下标 从0开始，第i个是 L.data[i-1]； 插入位置错。 插入位置错 for(j=L.length-1;j>=i-1;j--) L.data[j+1]=L.data[j]; //第i个后的元素逐一后移 第 个后的元素逐一后移 L.data[i-1]=x; //新元素插入到第 个位置 新元素插入到第i个位置 新元素插入到第 L.length++; //顺序表长度加 顺序表长度加1 顺序表长度加 }
ai
ai+1
…
an
…
顺序存储结构定义 typedef struct {ElemType data[MAXSIZE]; int length; }SeqList;
用数组表 示顺序表
//数组 //数组
// 顺序表的长度
顺序表上基本运算的实现(1)
顺序表的初始化 : SeqList SeqListInit( ) {//构造一个空的线性表L //构造一个空的线性表 //构造一个空的线性表 SeqList L; L.length=0; return L; } //定义 为顺序表 //定义L为顺序表 定义 //顺序表的长度为0 //顺序表的长度为0 顺序表的长度为
算法的时间复杂度显然为： 算法的时间复杂度显然为： O(ListLength(La)+ ListLength(Lb))
线性表的顺序表示和实现
线性表的顺序表示 :
在内存中用地址连续的一块存储空间顺序存放线性表的各 在内存中用地址连续的一块存储空间顺序存放线性表的各 地址连续 元素，用这种存储形式存储的线性表称为顺序表 顺序表。 元素，用这种存储形式存储的线性表称为顺序表。 的存储地址为Loc(a 设 a１的存储地址为Loc(a１)，每个数据元素占 L 个存 储单元，则第i个数据元素的地址为： 储单元，则第i个数据元素的地址为： )+(i1≤ Loc(ai)=Loc(a1)+(i-1)*L 1≤i≤n
线性表举例2 续（合并线性表L） 合并线性表L 合并线性表
while(i<=La_len) {// 已空，将La表的剩余部分复制到新表 //Lb已空 // 已空， 表的剩余部分复制到新表 ai=ListGet(La,i++); ListInsert(Lc,++k,ai); } while(j<=Lb_len) {// 已空，将Lb表的剩余部分复制到新表 //La已空 // 已空， 表的剩余部分复制到新表 bj=ListGet (Lb,j++); ListInsert(Lc,++k,bj); } return(Lc); }// //ListMerge //
删除算法的时间复杂度分析
n-(i+1)+1=n-i 基本操作：移动数据； 删除第i个元素：从ai＋1 到an都要向前移动一个位置，共需移动 n-i 个元素； i的取值范围为： 1 ≤ i ≤ n n 平均移动数据元素的次数（期望值）为： Ede = ∑ pi (n − i )
1 pi = n
i= i =1
例子：遍历线性表L 遍历线性表L
ListTraverse(List L，visit()) ， {//遍历线性表 //遍历线性表 // if(ListEmpty(L)) printf(“空表”); 空表” 空表 else for(i=1;i<=ListLength(L);i++) visit(ListGet(L,i))； ； }
例子：合并线性表L 合并线性表L
List ListMerge(List La,List Lb) {//La和Lb 是两个非递减有序的线性表 ， 将线性表 La 和Lb 合并成一个 //La和 是两个非递减有序的线性表， La和 //La Lb是两个非递减有序的线性表 将线性表La Lb合并成一个 新的线性表Lc Lc也非递减 Lc， 也非递减。 新的线性表Lc，Lc也非递减。 ListInit(Lc); i=j=1;k=0; La_len=ListLength(La);Lb_len=ListLength(Lb); while((i<=La_len)&&(j<=Lb_len)) {// 和Lb均非空 //La和 均非空 // ai=ListGet(La,i); bj=ListGet(Lb,j); if(ai<=bj) {ListInsert(Lc,++k,ai);++i;} else {ListInsert(Lc,++k,bj);++j;} }
1.要检查删除位置的有效性。 要检查删除位置的有效性。 要检查删除位置的有效性 2.依次移动元素 依次移动元素 3.长度减 长度减1 长度减
组合数学第二章
课堂中的“空白”艺术所谓“空白”，就是指空着，没有被填满或没有被利用的部分。
在绘画艺术中就有一种美叫做空白美。
那么以此为鉴，在课堂教学中也有一种方法称之为——“空白”艺术。
现代教育理论认为，数学教学要提供给学生充分体验与交流的机会，使他们真正理解和掌握数学思想和方法。
走进新课标，教学的最高宗旨和核心理念是“一切为了每一个学生的发展”。
而“发展”是一个生成性的动态过程，作为教师要不断地为学生创设一种“可持续发展”的时间与空间。
特别是伴随着新一轮基础教育课程改革的实施和推进，教师的教学行为和学生的学习方式都发生了巨大的改变。
在课堂上，教育者要善于适时、适度地巧设“空白”，秉承“学生只有通过自己的真切体验，才能真正对所学内容有所感悟，进而内化为己有，在学习活动实践中逐步学会学习”的课改理念，让学生自主、合作、探究地学习，使他们充分发挥自己的创造性，尽情展示、描绘出属于他们的精彩。
教学内容：北京市21世纪教材九年义务教育教材数学实验本第1册第十一单元《统计初步知识》。
[片段一]课堂练习1：猜丁克游戏（石头、剪子、布）。
师：大家玩过这个游戏吗？（学生辨认游戏中的手势。
）下面请同座位的两个人为一组玩这个游戏，要求统计出你们各自赢的次数填入表格中。
学生一边玩一边用自己喜欢的方式记录如下：第一种用符号表示：……第二种用画图表示：……第三种用实物表示：小棒、学具卡片……第四种用数字表示：1、2、3、……第五种用“正”字表示。
学生游戏后，在实物投影上展示自己的记录方式并汇报统计结果。
[评析：这里老师只是提出了学习任务，即“统计出你们各自赢的次数填入表格中”，但对于学习方式即怎样统计、如何记录并没有作出任何要求。
因此为学生创设了创新实践的空间，这样的“留白”使学生能够得以彰显其鲜明的个性，并满足其渴望同辈群体认可的价值需求。
][片段二]课堂练习3：数一数屋里一共有多少个小朋友？学生提出质疑：屋外的这些鞋摆放得太乱了！不好数，能不能摆整齐再数呀？师：题目要求是数人，你们为什么想到要数鞋呢？生：因为有一双鞋就等于有一个人。
组合数学第2章答案
组合数学第2章答案2.1 求序列{0，1，8，27，…3n …}的母函数。
解：()()++++++=++++++=nn n x n x x x x G x a x a x a x a a x G 3323322102780()46414321313=+-+--==-----n n n n n n n a a a a a n a n a左右同乘再连加：464:0464:0464:0464:4321543211123455012344=+-+-=+-+-=+-+-=+-+-----------n n n n n n n n n n n n a a a a a x a a a a a x a a a a a x a a a a a x母函数：()()42162036-+-=x x x x G2.2 已知序列()()3433{,,……()33,,n +……}，求母函数。
解：1(1)nx -的第k 项为：11()k n n +-- ，对于本题，n=4， ∴母函数为：41(1)x -2.3 已知母函数G （X ）=25431783x x x--+,求序列{ n a }解：G （X ）=)61)(91(783x x x +-+=)61()91(x Bx A ++-从而有： ⎩⎨⎧-==⇒⎩⎨⎧=-=+4778963B A B A B A G （X ）=)61(4)91(7x x +-+-G （X ）=7)999x (13322 ++++x x -4))6((-6)(-6)x (13322 +-+++x xn a =7*n )6(*49n -- 2.4．已知母函数239156xx x ---，求对应的序列{}n a 。
解：母函数为239()156x G x x x -=--39(17)(18)xx x -=+- A BG(x)17x 18xA(18x)B(17x)39x=++--++=-令 A B 38A +7B =9+=⎧⎨--⎩解得：A=2 B=1所以 ii i 0i 021G(x)2*(7x)(8x)17x 18x ∞∞===+=-++-∑∑n n n a 2*(7)8=-+2.5 设n n F G 2=，其中F n 是第n 个Fibonacci 数。
组合数学第二章二章六节
应用举例：斐波那契数列求解
• 斐波那契数列定义：$F_0 = 0, F_1 = 1, Fn = F{n-1} + F_{n-2} (n \geq 2)$
应用举例：斐波那契数列求解
生成函数求解
设斐波那契数列的生成函数为$F(x) = sum_{n=0}^{infty} F_n x^n$
根据递推关系和初始条件，得到$F(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + cdots$
05
生成函数与递推关系
生成函数定义及性质
乘积性质
两个生成函数的乘积对应于序列 的卷积。
线性性质
生成函数的线性组合对应于序列 的线性组合。
微分性质
生成函数的微分对应于序列的差 分。
定义
生成函数是一种将离散数学中的 序列通过幂级数形式表示出来的 函数，常用于组合数学中的计数
问题。
积分性质
生成函数的积分对应于序列的部 分和。
04
容斥原理与错排问题
容斥原理表述与证明
容斥原理的表述
对于两个集合A和B，它们的并集元素个数等于各自元素个数之和减去它们的交 集元素个数，即∣A∪B∣=∣A∣+∣B∣−∣A∩B∣。
容斥原理的证明
通过分类讨论和数学归纳法可以证明容斥原理的正确性。
应用举例：错排问题求解
错排问题的定义
在n个元素的全排列中，不是其自然排列（即每个元 素都不在其原来的位置上）的排列称为错排。
递推关系建立与求解方法
02
01
03
建立递推关系 通过组合问题的具体背景，分析问题的递推结构。 利用已知的初始条件和边界条件，建 Nhomakorabea递推关系式。
组合数学第二章课后习题答案
2.1题（陈兴）求序列{ 0，1，8，27，3n }的母函数。
解：由序列可得到32333()23n G x x x x n x =+++++因为23111n x x x x x =++++++- 2311()'12341n x x x nx x-=++++++-设 2311()()'23(1)1n np x x x x x n x nx x-==++++-+-2222221[()]'123(1)n n p x x x x n x n x --=+++++-+设 2223212()[()]'23(1)n nq x x p x x x x n x n x -==++++-+3323231[()]'123(1)n n q x x x n x n x --=++++-+ 3233313[()]'23(1)n n x q x x x x n x n x -=+++-+ 由以上推理可知[()]'x q x =,[7*94*(6)],n n +-所以可通过求得[()]'x q x 得到序列的母函数：32()4G x x x x =++2321()()[34(3)]6n H x F x dx x x n x +==++++⎰2.2题（陈兴）已知序列343,,,,333n ⎧+⎛⎫⎛⎫⎛⎫⎫⎨⎬ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎭⎩，求母函数 解： 3*2*14*3*2(3)*(2)*(1)()3*2*13*2*13*2*1nn n n G x x +++=+++=1[3.2.1 4.3.2(3)(2)(1)]6n x n n n x ++++++211()()[3.2 4.3(3)(2)]6n F x G x dx x x n n x +==+++++⎰ 2321()()[34(3)]6n H x F x dx x x n x +==++++⎰3431()()[]6n I x H x dx x X x ++==++⎰因为23111n x x x x+=+++++-所以211()(1)61I x x x x=----所以31()[]'''61x G x x=-就是所求序列的母函数。
组合数学 第2章 母函数
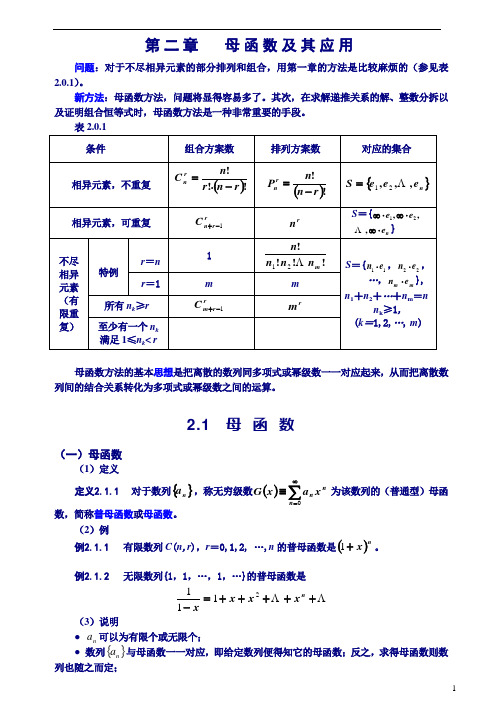
第二章 母函数及其应用问题：对于不尽相异元素的部分排列和组合，用第一章的方法是比较麻烦的（参见表2.0.1）。
新方法：母函数方法，问题将显得容易多了。
其次，在求解递推关系的解、整数分拆以及证明组合恒等式时，母函数方法是一种非常重要的手段。
母函数方法的基本思想是把离散的数列同多项式或幂级数一一对应起来，从而把离散数列间的结合关系转化为多项式或幂级数之间的运算。
2.1 母 函 数（一）母函数（1）定义定义2.1.1 对于数列{}n a ，称无穷级数()∑∞=≡0n nnxax G 为该数列的（普通型）母函数，简称普母函数或母函数。
（2）例例2.1.1 有限数列C (n ,r )，r ＝0,1,2, …,n 的普母函数是()nx +1。
例2.1.2 无限数列{1，1，…，1，…}的普母函数是+++++=-nxx x x2111（3）说明● n a 可以为有限个或无限个； ● 数列{}n a 与母函数一一对应，即给定数列便得知它的母函数；反之，求得母函数则数列也随之而定；例如，无限数列{0，1，1，…，1，…}的普母函数是 +++++n x x x 20＝xx -1● 这里将母函数只看作一个形式函数，目的是利用其有关运算性质完成计数问题，故不考虑“收敛问题”，而且始终认为它是可“逐项微分”和“逐项积分”的。
（4）常用母函数（二）组合问题（1）组合的母函数定理2.1.1 组合的母函数：设{}m m e n e n e n S ⋅⋅⋅=,,,2211 ,且n 1＋ n 2＋…＋ n m ＝n ，则S 的r 可重组合的母函数为()x G ＝∏∑==⎪⎪⎭⎫ ⎝⎛mi n j ji x 10＝∑=n r r r x a 0 (2.1.1) 其中，r 可重组合数为rx 之系数r a ，r ＝0,1,2, …,n .定理2.1.1的最大优点在于：● 将无重组合与重复组合统一起来处理；● 使处理可重组合的枚举问题变得非常简单。
卢开澄《组合数学》习题答案第二章
2.1 求序列{0，1，8，27，…3n …}的母函数。
解：()()++++++=++++++=nn n x n x x x x G x a x a x a x a a x G 3323322102780()046414321313=+-+--==-----n n n n n n n a a a a a n a n a左右同乘再连加：464:0464:0464:0464:4321543211123455012344=+-+-=+-+-=+-+-=+-+-----------n n n n n n n n n n n n a a a a a x a a a a a x a a a a a x a a a a a x母函数：()()42162036-+-=x x x x G2.2 已知序列()()3433{,,……()33,,n +……}，求母函数。
解：1(1)nx -的第k 项为：11()k n n +-- ，对于本题，n=4， ∴母函数为：41(1)x - 2.3 已知母函数G （X ）= 25431783x x x--+,求序列{ n a }解：G （X ）=)61)(91(783x x x +-+=)61()91(x Bx A ++-从而有： ⎩⎨⎧-==⇒⎩⎨⎧=-=+4778963B A B A B AG （X ）=)61(4)91(7x x +-+-G （X ）=7)999x (13322 ++++x x -4))6((-6)(-6)x (13322 +-+++x xn a =7*n )6(*49n -- 2.4．已知母函数239156xx x---，求对应的序列{}n a 。
解：母函数为239()156x G x x x -=--39(17)(18)xx x -=+- A BG(x)17x 18xA(18x)B(17x)39x=++--++=-令 A B 38A +7B =9+=⎧⎨--⎩解得：A=2 B=1所以 ii i 0i 021G(x)2*(7x)(8x)17x 18x ∞∞===+=-++-∑∑n n n a 2*(7)8=-+2.5 设n n F G 2=，其中F n 是第n 个Fibonacci 数。
组合数学_第2章
xi
1i n
ln xi e exp( ln xi ) 1i n
第二章 基本计数原理 即积式可转化为和式来处理。条件xi＞0并无实质性的限制，因 若 某 个 xi=0 ， 则 整 个 积 式 为 0 ， 又 恰 有 k 项 取 负 时 ， 可 先 对 （2.1.8）式两边乘(-1)k，以确保xi＞0， 最后再将其恢复过来。
第二章 基本计数原理 2.2.2 乘法原理(Multiplication Principle) 设 A， B为二不同类事件，若事件A有m种产生方式，事件B 有n种产生方式，则“事件A与事件B”有mn种产生方式 用集合论的术语，乘法原理也可描述如下： 设S，T为二集，若S为m元集，T为n元集，则S与T的叉积之 集合S×T为mn元集。 推广的乘法原理是：如果Ti为ni元集(i=1, 2, …, r)，则
0i k
a a
2i j 0
k
2j
第二章 基本计数原理 3. 双下标
( a11 a12 a1n ) ( a21 a22 a2 n ) ( am1 am 2 amn )
1 j n
a
1j
a2 j
iN n
a
i
第二章 基本计数原理 命题 1 用和号∑表示的和式中，通项下标的改变不影响和 式。 例如
0i n
a , a 及 a
i 0 j n j 0 k n
k
都表示同一和式。 当通项下标不取连续整数时，也希望能寻找一些规律，以 便于用和式写出简单的表示式，下面给出一些特殊和式的例子。
第二章 基本计数原理 · 对（2.1.9）式的算法 №1 输入N №2 M 1；（累乘器M置1） №3 对k=2, N, 做
组合数学第二篇习题解答
2.11 an (n 1)2,G anxn 1 4x ... (n 1)2 xn ... n0
证明（1-3x+3x2-x3)G是一个多项式，并求母函数G
G [x 2x2 ... (n 1)xn1 ...]'
2.34 求解：an=an-1+C(n+2,3),a0=0
an an1 C(n 2,3) a1 C(3,3) a2 C(3,3) C(4,3) a3 C(3,3) C(4,3) C(5,3) ............................................... an C(3,3) C(4,3) C(5,3) ... C(n 2,3) C(3,0) C(4,1) C(5,2) C(6,3) C(7,4)... C(n 2, n 1) C(3,0) C(4,1) C(5,2) C(6,3) C(7,4)... C(3 (n 1), n 1)) C(n 3, n 1)
G(x)
b0 (b1 b0)x 1 x x2
4 3x 1 x x2
2.26 逐项展开，两边合并。
2.27 求下列递推关系的一般解
(a)an-4an-1=5n
an 4an 1 5an1 20an2 0 an 9an 1 20an2 0 特征方程的解为4和5 一般解为 : r1 4n r2 5n
[
(1
x x)
2
]'
(1 x)2 2x(1 x) (1 x)4
1 x2 (1 x)4
1 x (1 x)3
《组合数学》教案 2章(母函数)及课后习题讲解
第二章母函数及其应用问题：对于不尽相异元素的部分排列和组合，用第一章的方法新方法：母函数方法。
基本思想：把离散的数列同多项式或幂级数一一对应起来，算。
2.1 母函数（一）母函数（1）定义【定义2.1.1】对于数列{}n a ，称无穷级数()∑∞=≡0n n n x a x G 为该数列的（普通型）母函数，简称普母函数或母函数。
（2）例【例2.1.1】有限数列rn C （r ＝0, 1, 2, …, n ）的普母函数：()x G ＝nn n n n nx C x C x C C ++++ 2210＝()nx +1【例2.1.2】无限数列{1, 1. …, 1, …}的普母函数：()x G ＝ +++++nx x x 21＝x-11（3）说明● n a 可以为有限个或无限个。
● 数列{}n a 与母函数一一对应。
{0, 1, 1, …, 1, …}↔ +++++n x x x 20＝xx -1 ● 将母函数视为形式函数，目的是利用其有关运算性质完成计数问题，故不考虑“收敛问题”。
（4）常用母函数（二） 组合问题 （1）组合的母函数【定理2.1.1】组合的母函数：设{}m m e n e n e n S ⋅⋅⋅=,,,2211 ,且n 1＋n 2＋…＋n m ＝n ，则S 的r 可重组合的母函数为()x G ＝∏∑==⎪⎪⎭⎫ ⎝⎛mi n j j i x 10＝∑=n r r r x a 0其中，r 可重组合数为rx 之系数r a ，r ＝0, 1, 2, …, n 。
理论依据：多项式的任何一项与组合结果一一对应。
【例2.1.3】设有6个红球，7个黑球，8个白球，问 （1） 共有多少种不同的选取方法，试加以枚举？ （2） 若每次从中任取3个，有多少种不同的取法？ （解）（1）元素符号化（x ，y ，z ↔红、黑、白球），元素的个数以符号的指数区分。
母函数G (x , y , z ) ＝(1＋x ＋x 2) (1＋y ) (1＋z )＝1＋(x ＋y ＋z )＋(x 2＋xy ＋xz ＋yz )＋(x 2x ＋x 2x ＋xxx )＋( x 2yz )5种情况：① 数字1表示一个球也不取的情况，共有1种方案； ② 取1个球的方案有3种，即红、黑、白三种球只取1个； ③ 取2个球的方案有4种，即2红、1红1黑、1红1白、1黑1白； ④ 取3个球的方案有3种，即2红1黑、2红1白、三色球各一； ⑤ 取4个球的方案有1种，即全取。
组合数学—第二章鸽巢原理和Ramsey定理(2)
定理推广（2） 将T 划分成E1, E2, … , Ek
设r,k≥1, qi≥r, i=1, 2, … , k, 是给定正整数，则存 在一个最小的正整数R(q1, q2, … , qk; r)，使得当 n≥R(q1,q2,…,qk;r) 时, 当n元集S 的所有r 元子集 划分成k 个子集族T1, T2, … , Tk，那么存在S 的q1 元子集A1, 其所有的r元子集属于T1, 或者存在S 的 q2元子集A2，A2的所有r 元子集属于T2, … ,或者 存在S 的qk 元子集Ak, 其所有的r元子集属于Tk .
2013年7月9日 第二章 鸽巢原理和Ramsey定理
推论2.2.1 若 n(r－1) + 1个物品放入n个盒 子。则至少有一个盒子里含有r个或者更多 的物品。 推论2.2.2 若设有n个正整数m1 , m2 , … , mn 满足下面的不等式 (m1 + … +mn)/n > r－1, 则 m1,…, mn中至少有一个数≥ r 推论2.2.3 设m和n都是正整数且m>n，若将 m个物体放入n个盒子中，则至少有一个盒 m 子中有大于等于 n 个物体
8 28 56 84 101 216 127 495 216 1031 282 1870
9 36 69 115 121 316 169 780 232 1713 317 3583 565 6588
10 40 43 92 149 141 442 178 1171 2826
6090
580 12677 798 23556
2013年7月9日
第二章 鸽巢原理和Ramsey定理
推论2.2.3 设m和n都是正整数且m>n，若将 m个物体放入n个盒子中，则至少有一个盒 m 子中有大于等于 n 个物体