经济数学2014 年上半年第二次作业

合集下载

(完整word版)经济学基础第二次形考作业

江苏开放大学形成性考核作业学号___________________________ 姓名___________________________ 所在教学点______________________________ 课程代码110139 _______ 课程名称经济学基础评阅教师________________________________ 第二次任务共四次任务【第二次形成性考核】（理论教学）第一部分习题3.短期总成本曲线一条从原点出以，向右上方倾斜的曲线。

4 ?短期边际成本曲线与短期平均成本曲线相交于短期平均成本曲线的占八、、6 ?在停止营业点上，价格只能弥补可变成本7.在经济分析中，利润最大化的原则是&在完全竞争市场上，对整个行业来说，需求曲线是一条线是一向右下方倾斜的曲线：对个别企业来说需求曲条水平线。

9 .在完全竞争市场上，企业短期均衡的条件是 MR=MC 且MR > AVC ，长期均衡的条件是P=MR=SMC=LMC=SAC=LAC=AR10 .垄断市场上短期均衡的条件是 SMC=MR ，长期均衡的条件是 LMC=SMC=MR 。

11.在垄断竞争市场上，短期均衡的条件是 SMC=MR ，长期均衡的条件是LMR=LMC 和P= LAR =LAC 。

12 ?边际替代率递减决定了等产量曲线凸向原点。

13 .在长期内，一切生产要素都是可以调整的，没有固定成本。

14 .在完全竞争市场中，需求曲线、平均收益曲线、边际收益曲线和 __________________ 曲线都从合在一起，且平行于用于表示需求量的横轴。

15 .在价格不变条件下 MR = MC,在价格递减条件下 MR V MG二、选择题（15*2=30分）1.一个企业使用 50单位的劳动，可以生产出1800单位的产量；使用60单位的劳动，可以生产出 2100单位的产量。

生产额外一单位劳动的边际产量是（B ）A. 3B. 30C. 300D. 36边际产量曲线与平均产量曲线相交时（B. 边际产量达到最大C .边际产量为0D.平均产量最低一、填空题（15*2=30分）1.平均产量；在相交后，边际产量产量；在相交时，平均产量达到最大。

(2021年整理)东北三省三校2014年高三第二次联合模拟考试数学(理)试卷及答案

整)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（东北三省三校2014年高三第二次联合模拟考试数学(理)试卷及答案(推荐完整)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为东北三省三校2014年高三第二次联合模拟考试数学(理)试卷及答案(推荐完整)的全部内容。

(推荐完整)编辑整理:张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方，但是我们任然希望东北三省三校2014年高三第二次联合模拟考试数学（理）试卷及答案（推荐完整）这篇文档能够给您的工作和学习带来便利。

同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力.本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为 <东北三省三校2014年高三第二次联合模拟考试数学（理)试卷及答案（推荐完整)> 这篇文档的全部内容。

东北三省三校2014年高三第二次联合模拟考试（哈师大附中、东北师大附中、辽宁实验中学)数学理试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题)两部分,共150分,考试时间120分钟。

第Ⅰ卷（选择题共60分)一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中,只有一项是符合题目要求的。

）1。

若}7,6,5{}3,2,1{}8,7,6,5,4,3,2,1{===B A U ，，，则()()U U C A C B = A 。

｛4,8} B. {2，4,，6，8｝ C. {1,3，5，7｝ D. {1，2，3,5,6，7}2。

经济数学基础12》形考作业2参考答案

经济数学基础12》形考作业2参考答案1.注意网上题目是随机的，不同学生的题目可能是不同的，同一人第二次做与第一次做也会不一样。

2.删除明显有问题的段落。

3.改写每段话。

参考答案：单项选择题（每题5分，共100分）1.下列函数中，cosx是sin(x^2)/x的一个原函数。

答案：B2.下列函数中，2sin(x)/x^2是cos(x)的一个原函数。

答案：C3.下列函数中，-cos(x)/2是xsin(x)的一个原函数。

答案：D4.若∫f(x)dx=sin(x)+5ln|x-1|+c，则f(x)=cos(x)-5/(x-1)。

答案：C5.若∫(1/x)f(x)dx=xln(x^2)+c，则f(x)=1-1/(2x^2)。

答案：C6.若∫f(x)dx=2x+2ln|x+1|+c，则f(x)=2+2/(x+1)。

答案：B7.∫(tanx)'dx=tan(x)+c。

答案：A8.d/dx ∫cos(x)dx=cos(x)。

答案：A9.∫(sinx)'dx=-cos(x)+c。

答案：C10.∫(x^2-2x-3)/(x-3)dx=x^2+x+2ln|x-3|+c。

答案：C11.∫(x^2-25)/(x-5)dx=2xln|x-5|+x^2+c。

答案：D12.下列等式成立的是13x<14x。

答案：错误。

1d(cosx)B．sinxxdxcosxd(lnx)C．sinxxdxcosxd(ln(cosx))D．sinxxdxcosxd(tanx)答案：B1.将文章格式错误删除，小幅度改写每段话：1.题目中的积分公式应该为 $\int \sin x dx$，然后可以将其化简为 $\int \sin x \frac{1}{x^2} x^2 dx$，再利用分部积分法得到 $\int \frac{\cos x}{x} dx$。

2.常用分部积分法计算的是 $\int \ln x dx$。

3.常用分部积分法计算的是 $\int x \sin 2x dx$。

新疆乌鲁木齐地区2014年高三年级第二次诊断性测验理科数学试卷及答案

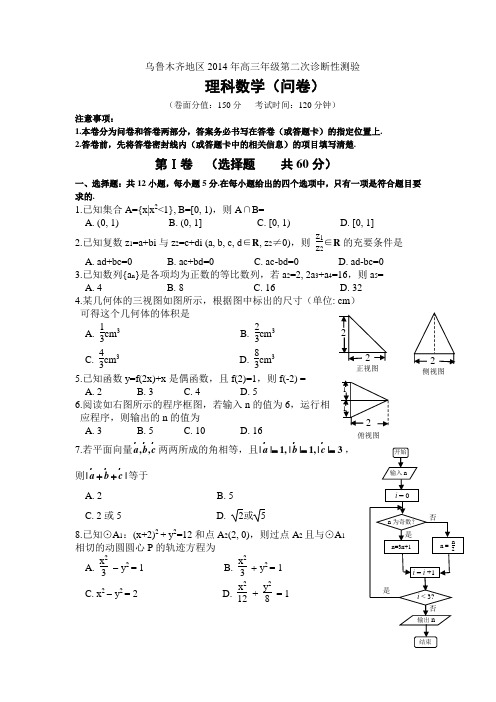
乌鲁木齐地区2014年高三年级第二次诊断性测验理科数学（问卷）（卷面分值：150分考试时间：120分钟）注意事项：1.本卷分为问卷和答卷两部分，答案务必书写在答卷（或答题卡）的指定位置上.2.答卷前，先将答卷密封线内（或答题卡中的相关信息）的项目填写清楚.第Ⅰ卷（选择题共60分）一、选择题：共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合A={x|x2<1}, B=[0, 1)，则A∩B=A. (0, 1)B. (0, 1]C. [0, 1)D. [0, 1]2.已知复数z1=a+bi与z2=c+di (a, b, c, d∈R, z2≠0)，则z1z2∈R的充要条件是A. ad+bc=0B. ac+bd=0C. ac-bd=0D. ad-bc=03.已知数列{a n}是各项均为正数的等比数列，若a2=2, 2a3+a4=16，则a5=A. 4B. 8C. 16D. 324.某几何体的三视图如图所示，根据图中标出的尺寸（单位: cm）可得这个几何体的体积是A. 13cm3 B. 23cm3C. 43cm3 D. 83cm35.已知函数y=f(2x)+x是偶函数，且f(2)=1，则f(-2) =A. 2B. 3C. 4D. 56.阅读如右图所示的程序框图，若输入n的值为6，运行相应程序，则输出的n的值为A. 3B. 5C. 10D. 167.若平面向量,,a b c两两所成的角相等，且||1,||1,||3a b c===，则||a b c++等于A. 2B. 5C. 2或5D. 2或 58.已知⊙A1：(x+2)2 + y2=12和点A2(2, 0)，则过点A2且与⊙A1 相切的动圆圆心P的轨迹方程为A. x23- y2 = 1 B. x23+ y2 = 1C. x2 - y2 = 2D. x212+y28= 1正视图侧视图俯视图9.将函数f(x)=sin(2x+θ) (-π2 < θ < π2 )的图象向右平移φ（φ > 0）个单位长度后得到函数g(x)的图象，若f(x), g(x)的图象都经过点P(0, 32)，则φ的值可以是A. 5π3B. 5π6C. π2D. π6 10.设a = log 0.10.2，b = log 0.20.4，c = log 0.30.6，则A. a > b> cB. a > c > bC. b > c > aD. c > b > a 11.从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数，这个数能被3整除的概率为A. 827B. 1927C. 1954D. 3554 12.若直线ax + by + c = 0与抛物线y 2=2x 交于P ，Q 两点，F 为抛物线的焦点，直线PF ，QF 分别交抛物线于点M ，N ，则直线MN 的方程为A. 4cx -2by + a=0B. ax -2by + 4c=0C. 4cx + 2by + a=0 C.ax + 2by + 4c=0 第Ⅱ卷（非选择题共90分）本卷包括必考题和选考题两部分.第13题 ~ 第21题为必考题，每个试题考生都必须作答.第22题 ~ 第24题为选考题，考生根据要求作答. 二、填空题：本大题共4小题，每小题5分13.设等差数列{a n }的前n 项和为S n ，若S 9=11，S 11=9，则S 20= ； 14.如图，矩形OABC 内的阴影部分由曲线f(x)=sinx 及直线x=a(a ∈(0,2π) )与x 轴围成.向矩形OABC 内随机掷一点，该点落在阴影部分的概率为12，则a= ；15.直三棱柱ABC -A 1B 1C 1的各个顶点都在同一个球面上. 若AB=AC=AA 1=2，∠BAC=120°，则此球的表面积等于 . 16.已知直线x+y+1=0与曲线C ：y = x 3-3px 2相交于点A ，B ，且曲线C 在A ，B 处的切线平行，则实数p 的值为 .三、解答题第17~21题每题12分，解答应在答卷的相应各题中写出文字说明，证明过程或演算步骤.17.（本小题满分12分）如图，已知OPQ 是半径为3，圆心角为π3的扇形，C 是扇形弧上的动点，ABCD 是扇形的内接矩形，记∠COP 为x ，矩形ABCD 的面积为f(x)。

湖北省2014届高三八校二次联考数学试题及答案

鄂南高中华师一附中黄冈中学黄石二中荆州中学孝感高中襄阳五中襄阳四中2014届高三第二次联考数学（理工类）命题学校：孝感高中命题人：彭西骏韩松桥审题人：徐新斌黄鹏考试时间：2014年3月20日下午15：00—17：00本试卷共4页，共22题，其中第15、16题为选考题。

满分150分。

考试用时120分钟。

★ 祝考试顺利 ★注意事项：1．答题前，考生务必将自己的姓名、班级、准考证号填写在答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B 铅笔将答题卡上试卷类型A 方框涂黑。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

答在试题卷、草稿纸上无效。

3．填空题和解答题的作答：用黑色墨水签字笔将答案直接答在答题卡上对应的答题区域内。

答在试题卷、草稿纸上无效。

4．选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。

考生应根据自己选做的题目准确填涂题号，不得多选。

答题答在答题卡上对应的答题区域内，答在试题卷、草稿纸上无效。

5．考生必须保持答题卡的整洁。

考试结束后，请将答题卡上交。

一、选择题：本大题共10小题，每小题5分，共50分．在每个小题给出的四个选项中，只有一项是符合题目要求的． 1．若复数z 满足i z i 21)1(+=+(其中i 是虚数单位)，则z 对应的点位于复平面的 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．设集合2{(3)30}A x x a x a =-++=，2{540}B x x x =-+=，集合A B 中所有元素之和为8，则实数a 的取值集合为A ．{0}B ．{03}，C ．{13,4}，D ．{013,4}，， 3．下列说法正确的是A ．“a b >”是“22a b >”的必要条件B ．自然数的平方大于0C ．“若a b ，都是偶数，则+a b 是偶数”的否命题为真D ．存在一个钝角三角形，它的三边长均为整数4．已知某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是A ．48cm 3B ．98cm 3C ．88cm 3D ．78cm 3 5．把函数()sin y x x R =∈的图象上所有的点向左平移6π个单位长度，再把所得图象上所有点的横坐标变为原来的2倍（纵坐标不变），得到图象的函数表达式为A ．sin 2,3y x x R π⎛⎫=-∈ ⎪⎝⎭B ．sin 2,3y x x R π⎛⎫=+∈ ⎪⎝⎭ C ．1sin ,26y x x R π⎛⎫=+∈ ⎪⎝⎭D ．1sin ,26y x x R π⎛⎫=-∈ ⎪⎝⎭6．已知双曲线)0( 14222>=-a y a x 的一条渐近线与圆8)322=+-y x （相交于N M ,两点，且4=MN ，则此双曲线的离心率为A ．5B ．355C ．533D ．57．把一个带+q 电量的点电荷放在r 轴上原点处，形成一个电场，距离原点为r 处的单位电荷受到的电场力由公式2F=k qr（其中k 为常数）确定，在该电场中，一个单位正电荷在电场力的作用下，沿着r 轴的方向从a r =处移动到a r 2=处，与从a r 2=处移动到a r 3=处，电场力对它所做的功之比为 A ．23 B ．13 C ．32D ．38．如图，在半径为R 的圆C 中，已知弦AB 的长为5，则AB AC =A ．52B ．252C ．52R D ．252R 9．将一颗骰子连续抛掷三次, 已知它落地时向上的点数恰好依次成等差数列, 那么这三次抛掷向上的点数之和为12的概率为 A ．185 B ． 91 C ．183D ．72110．函数223,0()2ln ,0x x x f x x x ⎧--+≤⎪=⎨->⎪⎩，直线y m =与函数()f x 的图像相交于四个不同的点，从小到大，交点横坐标依次记为,,,a b c d ，下列说法错误的是A ．[)3,4m ∈B ．)40,abcd e ⎡∈⎣C ．562112,2a b c d e e e e ⎡⎫+++∈+-+-⎪⎢⎣⎭D ．若关于x 的方程()=f x x m +恰有三个不同实根，则m 取值唯一二、填空题：本大题共6个小题，考生共需作答5小题，每小题5分，共25分．请将答案填在答题卡．．．对应题号．．．．的位置上．答错位置，书写不清，模棱两可均不得分．（一）必考题（11—14题）11．记集合{}22(,)|4A x y x y =+≤和集合{}(,)|20,0,0B x y x y x y =+-≤≥≥表示的平面区域分别为1Ω和2Ω，若在区域1Ω内任取一点(,)M x y ，则点M 落在区域2Ω的概率为 .湖北省八校BAC第8题图第4题图第15题图第21题图第19题图12．已知正数x, y, z 满足x+2y+3z=1, 则xz z y y x +++++3932421的最小值为．13．定义某种运算⊗，b a S ⊗=的运算原理如右图所示．设)3()0()(x x x x f ⊗-⊗=.则=)3(f ______；()f x 在区间[]3,3-上的最小值为______．14．数学与文学之间存在着许多奇妙的联系.诗中有回文诗，如：“云边月影沙边雁，水外天光山外树”，倒过来读，便是“树外山光天外水，雁边沙影月边云”，其意境和韵味读来是一种享受！数学中也有回文数，如：88，454，7337，43534等都是回文数，无论从左往右读，还是从右往左读，都是同一个数，称这样的数为“回文数”，读起来还真有趣！二位的回文数有11，22，33，44，55，66，77，88，99，共9个；三位的回文数有101，111，121，131，…，969，979，989，999，共90个；四位的回文数有1001，1111，1221，…，9669，9779，9889，9999，共90个；由此推测：11位的回文数总共有个．(二) 选考题（请考生在第15、16两题中任选一题做答，请先在答题卡指定位置将你所选的题目序号所在方框用2B 铅笔涂黑．如果全选，则按第15题作答结果计分．） 15．（选修4-1：几何证明选讲）如图，△ABC 为圆的内接三角形，BD 为圆的弦，且BD//AC ．过点A 作圆的切线与DB 的延长线交于点E ， AD 与BC 交于点F ．若AB = AC ，AE = 35， BD = 4，则线段CF 的长为______．16．（选修4-4：坐标系与参数方程）在直角坐标系中，以原点为极点，x 轴的正半轴为极轴建立极坐标系，两种坐标系取相同的单位长度．已知曲线 54532:1⎪⎪⎩⎪⎪⎨⎧=+=t y t x C （t 为参数）和曲线θθρcos 2sin :22=C 相交于A B 、两点，设线段AB 的中点为M ，则点M 的直角坐标为．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知向量22cos ,3m x =（），1,sin 2n x =（），函数()f x m n =⋅ ．（Ⅰ）求函数()f x 的最小正周期；（Ⅱ）在∆ABC 中，c b a ,,分别是角,,A B C 的对边，且()3,1f C c ==，32=ab ，且b a >，求b a ,的值．18．（本小题满分12分）已知数列{}n a 的前n 项和是n S ，且113n n S a +=)(*∈N n ．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设41log (1)n n b S +=-)(*∈N n ，12231111n n n T bb b b b b +=+++ ，求使10072016n T ≥成立的最小的正整数n 的值．19．（本小题满分12分）如图，在三棱锥C P A B -中，,,AB BC PB BC ⊥⊥5,PA PB ==64,AB BC ==，点M 是PC 的中点，点N 在线段AB 上,且MN AB ⊥．（Ⅰ）求AN 的长；（Ⅱ）求二面角M NC A --的余弦值．20．（本小题满分12分）甲乙两个地区高三年级分别有33000人，30000人，为了了解两个地区全体高三年级学生在该地区二模考试的数学成绩情况，采用分层抽样方法从两个地区一共抽取了105名学生的数学成绩，并作出了如下的频数分布统计表，规定考试成绩在[120，150]内为优秀．甲地区：乙地区：（Ⅰ）计算x ，y 的值；（Ⅱ）根据抽样结果分别估计甲地区和乙地区的优秀率；若将此优秀率作为概率，现从乙地区所有学生中随机抽取3人，求抽取出的优秀学生人数的数学期望；（Ⅲ）根据抽样结果，从样本中优秀的学生中随机抽取3人，求抽取出的甲地区学生人数η的分布列及数学期望．21．（本小题满分13分）如图所示，已知椭圆C 1和抛物线C 2有公共焦点)0,1(F ,C 1的中心和C 2的顶点都在坐标原点，过点M （4,0）的直线l 与抛物线C 2分别相交于A 、B 两点. （Ⅰ）写出抛物线C 2的标准方程；（Ⅱ）求证：以AB 为直径的圆过原点；（Ⅲ）若坐标原点O 关于直线l 的对称点P 在抛物线C 2上，直线l 与椭圆C 1有公共点，求椭圆C 1的长轴长的最小值．22．（本小题满分14分）已知函数)1,0(,2)1ln()(2≠≥+-+=k k x k x x x f 且．（Ⅰ）当2=k 时，求曲线)(x f y =在点))1(,1(f 处的切线方程；（Ⅱ）求)(x f 的单调减区间；（Ⅲ）当0=k 时，设)(x f 在区间)](,0[*N n n ∈上的最小值为n b ，令n n b n a -+=)1ln(，求证：)(,112*2421231423121N n a a a a a a a a a a a a a n nn ∈-+<⋅⋅⋅⋅⋅⋅+⋅⋅⋅++-．？？湖北八校2014届高三第二次联考参考答案数学（理工类）一、选择题A D DBC BD B A D二、填空题：11,π21; 12, 18 ; 13, 3- 12- ; 14, 900000 ； 15, 553 ; 16, ），（431641 . 三、解答题：17.（1）22()(2cos ,3)(1,sin 2)2cos 3sin 2f x m n x x x x =⋅=⋅=+cos 213sin 22sin(2)16x x x π=++=++. (3)分故最小正周期22T ππ== (5)分(2）31)62sin(2)(=++=πC C f ，1)62sin(=+∴πC ，C 是三角形内角，∴262ππ=+C 即：.6π=C (7)分232cos 222=-+=∴ab c a b C 即：722=+b a ． ……………………9分将32=ab 代入可得：71222=+aa ，解之得：32=a 或4,23或=∴a ，32或=∴b (11)分3,2,==∴>b a b a (12)分18.（1）当1n =时，11a s =，由11113134S a a +=⇒=， ……………………1分当2n ≥时，11111113()01313n n n n n n n n S a S S a a S a ----⎧+=⎪⎪⇒-+-=⎨⎪+=⎪⎩114nn a a -⇒= ∴{}n a 是以34为首项，14为公比的等比数列． ……………………4分故1311()3()444n n n a -== )(*∈N n …………………6分（2）由（1）知111111()34n n n S a +++-==，14141log (1)log ()(1)4n n n b S n ++=-==-+ ………………8分11111(1)(2)12n n b b n n n n +==-++++ nT =1223111111111111()()()23341222n n b b b b b b n n n +++⋅⋅⋅+=-+-+⋅⋅⋅+-=-+++1110072014222016n n -≥⇒≥+，故使10072016n T ≥成立的最小的正整数n 的值2014n =. ………………12分19.解：（1）方法一、如图，分别取AB 、AC 的中点O 、Q,连接OP 、OQ ，设AN a =以O 为坐标原点，OP 为x 轴，OA 为y 轴，OQ 为z 轴建立空间直角坐标系，则3(400),(0,34),(2,2),(0)2P C M N a -，，，，-，3-,0设0(00)N x ，，，则9(00),(),2A B M N a == ，-6，-2，-，-2 由MN A B ⊥得()990,6200=22AB MN a a a ⎛⎫=+--⨯⇒ ⎪⎝⎭即-2- 所以29=AN …………………6分方法二：如图，取AB 的中点为O ，PB 的中点为Q ，连接MQ 、NQ ， M 、Q 分别为PB 、PC 的中点∴MQ BC 又 AB BC ⊥ ∴AB MQ ⊥ 又 MN AB ⊥∴AB MNQ ⊥平面 AB NQ ⊥，又 PA PB =且O 为AB 的中点 ∴OP AB ⊥ ∴NQ OP又 Q 为AB 中点 ∴N 为OB 中点∴113242BN OB AB ===∴92AN =………………6分（2） 3(2),(0.),2MN NC =-=- ，0，-2，4设平面MNC 的一个法向量为()1000,,n x y z = ，则0000220034002x z m MN y z m NC --=⎧⎧∙=⎪⎪⇒⎨⎨-+=∙=⎪⎪⎩⎩试卷类型：A 试卷类型：A令03z =，则003,y 8x =-=，即()13,8,3n =-………………9 分平面ANC 的一个法向量为()20,0,1n =，则121212382cos ,82n n n n n n ∙<>==故二面角M NC A--的余弦值为38282. ………………12分 20.解 (I )6,7x y == ………………4分 (II) 甲地区优秀率为2,11乙地区优秀率为22,0,1,2,3,(3,)55B ξξ= ，ξ的数学期望为26()3.55E ξ=⨯= ………………6分(III)()320330570203C P C η===，()121020330951203C C P C η=== ()211020330452203C C P C η===，()31033063203C P C η=== η的分布列为 η 0 1 2 3P57203 95203 45203 6203 ………………10分 η的数学期望为5795456()0+1+2+3=1.203203203203E η=⨯⨯⨯⨯ ………………12分 21.解： (1) 设抛物线的标准方程为),0(22>=p px y由)0,1(F 得2=p , x y C 4:22=∴; …………………3分 (2) 可设ny x AB +=4:,联立x y 42= 得 01642=--ny y , 设1616,16),,(),,(222121212211==-=yy x x y y y x B y x A 则 12120O A O B x x y y ∴⋅=+=,即以AB 为直径的圆过原点; ………………8分(3)设)4,4(2t t P ,则，l t t OP 上在直线的中点)2,2(2⎪⎩⎪⎨⎧-=+=∴n tt ntt 2244242得1±=n 0<t4,1+==∴y x l n ：直线 ………………10分设椭圆:1C 112222=-+a y a x ，与直线4:+=y x l 联立可得： ()()22242218117160a y a y a a -+--+-=3402a ∆≥≥，∴长轴长最小值为34 ………………13分 22.(1)当2=k 时，2)1ln()(x x x x f +-+= x xx f 2111)(+-+=' 2ln )1(,23)1(=='∴f f ………………2分∴曲线)(x f y =在点))1(,1(f 处的切线方程为：)1(232ln -=-x y 即 032ln 223=-+-y x ………………3分（2）),1(,1)1()(+∞-∈+-+='x x k kx x x f ①当0=k 时，00)(,1)(><'+-='x x f x xx f 则令），的单调减区间为：（∞+∴0)(x f ②当1001<<>-k k k 即时，k k x x f -<<<'100)(则令），的单调减区间为：（k k x f -∴10)( ③当101><-k k k 即时，010)(<<-<'x kk x f 则令）的单调减区间为：（0,1)(k kx f -∴ (7)分（3）当0=k 时，],0[)(n x f 在上单调递减 n n n f b n -+==∴)1l n ()()(,)1l n (*N n n b n a n n ∈=-+=∴ ………………9分1212121221222121121)2()12)(12(6754532312642)12(5312222264212531--+=-++<+=+<+⨯+-⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯=⨯⋅⋅⋅⨯⨯⨯-⨯⋅⋅⋅⨯⨯⨯=⋅⋅⋅⋅⋅⋅∴-n n n n n n n n n n nn a a a a a a a a nn………………12分)(,112112)1212()35()13(*2421231423121N n a n n n a a a a a a a a aa a a n nn ∈-+=-+=--++⋅⋅⋅+-+-<⋅⋅⋅⋅⋅⋅+⋅⋅⋅++∴-试卷类型：A 试卷类型：A。

经济数学考试题及答案

经济数学考试题及答案1.从标志与统计指标的对应关系来看，标志通常与( )相同。

2.某连续变量数列，其首组为开口组，上限为80，又知其邻组的组中值为95，则首组的组中值为( )。

3.国民收入中消费额和累积额的比例为1：0.4，这就是( )相对指标。

4.在+A的公式中，A称为( )。

5.峰度就是指次数原产曲线项峰的( )，就是次数原产的一个关键特征。

6.用水平法求平均发展速度本质上是求( )平均数。

7.按习惯作法，使用平均值调和平均值形式基本建设的物量指标指数，其计算公式实际上就是( )综合指数公式的变形。

8.对一个确定的总体，抽选的样本可能个数与( )和( )有关。

9.用以充分反映重回直线代表性大小和因变量估计值精确程度的指标表示( )。

二、是非题(每小题1分，共10分)1.统计数据史上，将国势学派和图表学派泛称为社会经济统计数据学派。

2.统计总体与总体单位在任何条件下都存在变换关系统计学原理试题及答案统计学原理试题及答案。

3.学生按体重分组，适合使用等距分组。

4.根据组距数列计算求得的算术平均数是一个近似值。

5.基尼系数的基本公式可以转变为2(S1+S2+S3)。

6.对连续时点数列求序时平均数，应采用加权算术平均方法。

7.分段平均法的数学依据就是Σ(Y-YC)2=最小值。

8.平均数、指数都有静态与动态之分。

9.在不能重复样本下，从总体N中提取容量为n的样本，则所有可能将的样本个数为Nn个10.根据每对x和y的等级计算结果ΣD2=0，说明x与y之间存在完全正相关。

三、单项选择题(每小题2分后，共10分后)1.在综合统计指标分析的基础上，对社会总体的数量特征作出归纳、推断和预测的方法是A.大量观察法B.统计数据分组法C.综合指标法D.模型推测法2.对同一总体选择两个或两个以上的标志分别进行简单分组，形成A.无机分组B.层叠分组C.平行分组体系D.无机分组体系3.交替标志方差的最大值为A.1B.0.5C.0.25D.04.如果采用三项移动平均修匀时间数列，那么所得修匀数列比原数列首尾各少A.一项数值B.二项数值C.三项数值D.四项数值5.可变权数是指在一个指数数列中，各个指数的A.同度量因素就是变动的B.基期就是变动的C.指数化因数是变动的D.时期是变动的.四、多项选择题(每小题2分后，共10分后)1.反映以经济指标为中心的三位一体的指标总体系包括A.社会统计数据指标体系B.专题统计数据指标体系C.基层统计指标体系D.经济统计指标体系E.科技统计数据指标体系2.典型调查A.就是一次性调查B.就是专门非政府的调查C.是一种深入细致的调查D.调查单位是有意识地选取的E.需用专访法获得资料3.下列指标中属于总量指标的有A.月末商品库存额B.劳动生产率C.历年产值增加额D.年末固定资金额E.某市人口天量增加数4.重复抽样的特点是A.各次抽取互不影响B.各次抽取相互影响C.每次抽选时，总体单位数逐渐减少D.每次抽取时，总体单位数始终不变E.各单位被抽中的机会在各次抽选中相等5.以下关系中，相关系数大于0的现象存有A.产品产量与耗电量的关系B.单位成本与产品产量的关系C.商品价格与销售量的关系D.纳税额与总收入的关系E.商品流通费用率与商品销售额的关系五、计算题(每小题10分后，共60分后)要求：(1)写下必要的计算公式和排序过程，否则，酌情处罚。

《经济数学基础12》形考作业2参考答案

经济数学基础形考作业2参考答案特别说明：供同学们参考，请同学们一定注意网上题目是随机的，不同学生的题目可能是不同的，同一人第二次做与第一次做也会不一样，务必看清楚再选择，不能照搬照抄。

单项选择题（每题5分，共100分）1、1．下列函数中，（）是21sinx x 的一个原函数．A ．1sinxB ．1cos xC ．1sin x -D ．1cos x -答案：B1、2．下列函数中，（AB．CD．答案：B1、3．下列函数中，（）是2sin x x 的一个原函数．A ．21cos 2x B ．22cos x C ．22cos x - D ．21cos 2x - 答案：D 2、1．若()d sin 5x f x x x c -=++⎰，则()f x =（）.A ．cos 5ln5x x -+B ．cos 5ln5xx --+C ．cos 5ln5x x --D ．cos 5ln5xx ---答案：C 2、2．若1()d f x x x c x=++⎰，则()f x =（）．A ．2ln 2x x +B ．2ln 2x x + C ．211x -D ．211x+ 答案：C 2、3．若c x x x f x++=⎰22d )(，则()f x =（）.A ．22x +B ．2ln22x +C ．22ln 2x +D ．22ln 2x x cx ++ 答案：B3、1．(tan )d x x '=⎰（）．A ．tan x c +B ．cot x c +C ．21sin c x -+ D ．21cos c x+答案：A3、2．dcos d d x x x=⎰（）. A ． cos x B ． cos x c + C ． sin x - D ． sin x c -+ 答案：A3、3．⎰='x x d )sin (（）.A ．sin xB ．cos xC ．sin x c +D ．cos x c -+ 答案：C4、1．223d 3x x x x --=-⎰（）．A ．2x x c ++ B ．212x x c -+ C ．212x x c ++ D ．2x x c -+ 答案：C4、2．225d 5x x x -=-⎰（）．A ．25x x c ++B ．25x x c -+C ．252x x c ++ D ．252x x c -+ 答案：C4、3．24d 2x x x -=+⎰（）． A ．2122x x c -+ B ．2122x x c ++ C ．22x x c -+ D ．22x x c ++答案：A5、1．下列等式成立的是（）．A ．21d d(tan )sin x x x= B ．3d d(3)ln 3x xx =C ．211d d()x x x -= D x = 答案：D5、2．下列等式成立的是（）．A ．32d d()3x x x =B ．1d d(ln )x x x= C ．e d d(e )xxx --= D ．cos d d(sin )x x x -= 答案：B5、3．下列等式成立的是（）．A ．)d(cos d sin x x x =B ．)d(22ln 1d 2x xx =C ．)1d(d ln xx x = D ．x x xd d 1=答案：B6、1．若c x F x x f +=⎰)(d )(，则(3ln )d f x x x+=⎰（）.A ．(ln )F x c +B ．(ln )F x c x+ C ．()3ln F x c x ++ D ．()3ln F x c ++答案：D 6、2．若()d ()f x x F x c =+⎰，则(e )e d x x f x --=⎰（）．A ．(e )x F c -+B ．(e )x F c --+C ．(e )e x x F c ---+D ．(e )e x x F c --+ 答案：B 6、3．若c x F x x f +=⎰)(d )(，则(32)d f x x -=⎰（）.A ．3()2F x -B ．()32F x c -+C ．()332F x c -+D ．()1323F x c -+ 答案：D7、1．用第一换元法求不定积分21cosd x x x ⎰，则下列步骤中正确的是（）．A ．221cos11d d(sin )x x x x x=⎰⎰ B ．221cos11d d(sin )x x x x x=-⎰⎰ C ．21cos11d cos d()x x x x x =⎰⎰D ．21cos11d cos d()x x x x x =-⎰⎰答案：D7、2．用第一换元法求不定积分sin d cos xx x ⎰，则下列步骤中正确的是（）． A ．sin 1d d(cos )cos cos x x x x x =⎰⎰B ．sin 1d d(cos )cos cos x x x x x =-⎰⎰C ．sin d sin d(sin )cos xx x x x =⎰⎰ D ．sin 1d sin d()cos sin x x x x x=⎰⎰ 答案：B7、3．用第一换元法求不定积分⎰x xx d sin ，则下列步骤中正确的是（）．A ．x=-B ．x =⎰C ．2x=⎰D ．12x =⎰答案：C8、1．下列不定积分中，常用分部积分法计算的是（）．A ．ln d xx x⎰ B ．22d 1x x x +⎰ C ．2cos d x x x ⎰ D ．ln d x x ⎰ 答案：D8、2．下列不定积分中，常用分部积分法计算的是（）．A ．x ⎰B ．2e d x x x ⎰C ．23sin d x x x ⎰D ．1d (1ln )x x x +⎰答案：B8、3．下列不定积分中，常用分部积分法计算的是（）．A ．cos(21)d x x +⎰B ．⎰-x x x d 12C ．⎰x x x d 2sin D ．⎰+x x xd 12答案：C9、1．用分部积分法求不定积分⎰+x x 1)d ln(，则下列步骤中正确的是（）．A ．ln d ln ln d x x x x x x x =-⎰⎰B ．ln d ln d(ln )x x x x x x x =-⎰⎰C ．221ln d ln d(ln )22x x x x x x x =-⎰⎰ D ．221ln d ln ln d()22x x x x x x x =-⎰⎰ 答案：C9、2．用分部积分法求不定积分2ln d xx x ⎰，则下列步骤中正确的是（）． A ．2ln ln 1d d(ln )x x x x x x x=-⎰⎰ B ．2ln ln 1d d(ln )x x x x x x x =--⎰⎰ C ．2ln ln 1d d(ln )x x x x x x x =-+⎰⎰ D ．2ln ln 1d d(ln )x x x x x x x=+⎰⎰ 答案：C9、3．用分部积分法求不定积分⎰+x x 1)d ln(，则下列步骤中正确的是（）．A ．ln(1)d ln(1)d(ln(1))x x x x x x +=+-+⎰⎰B ．ln(1)d ln(1)d(ln(1))x x x x x +=+-+⎰⎰C ．ln(1)d ln(1)d(ln(1))x x x x x +=+-+⎰⎰D ．ln(1)d ln(1)d(ln(1))x x x x +=+-+⎰⎰答案：A10、1．π22d sin(1)d d x x x +=⎰（）. A ．2sin(1)x + B ．22cos(1)x x + C ．0 D ．2π3答案：D10、2．π2d sin d d x x x =⎰（）．A ．0B ．1C ．sin xD ．sin x c + 答案：A10、3．e1d ln d d x x x =⎰（）. A ．ln x B ．1xC ．1D ．0 答案：D 11、1．设02()ln(1)d xP x t t =+⎰，则()P x '=（）．A ．0B ．2ln(1)x + C ．2ln(1)x -+ D ．221xx + 答案：C 11、2．设2e ()d 2txP x t -=⎰，则()P x '=（）. A ．22exx - B ．2exx - C ．2e2x - D ．2ex x --答案：C 11、3．设0()xP x t =⎰，则()P x '=（）.A ．BCD ．0答案：A12、1．下列定积分计算正确的是（）． A ．11d 0x -=⎰B ．10e d e xx =⎰ C ．π2π2cos d 0x x -=⎰ D ．123d 2x x -=-⎰答案：D12、2．下列定积分计算正确的是（）． A ．ππcos d 0x x -=⎰B ．32d 1x -=⎰C ．22d 0x x -=⎰D ．21d 1x x -=⎰答案：A12、3．下列定积分计算正确的是（）． A ．102d 2x x =⎰B ．15d 161=⎰-xC ．1e d e x x =⎰D ．πsin d 2x x =⎰答案：D13、1．下列定积分计算正确的是（）．A ．11(1)d 0x x -+=⎰B ．11sin d 0x x x -=⎰C ．11cos d 0x x x -=⎰D ．11(2+2)d 0x x x --=⎰答案：C13、2．下列定积分计算正确的是（）．A ．121(1)d 0x x -+=⎰B ．121sin d 0x x x -=⎰C ．121cos d 0x x x -=⎰D ．11(1)d 0x x -+=⎰答案：B13、3．下列定积分计算正确的是（）．A ．1231()d 0x x x -+=⎰ B ．11e e d 02x xx --+=⎰ C ．11sin d 0x x x -=⎰ D ．11e e d 02x xx ---=⎰ 答案：D 14、1．212d x x --=⎰（）． A ．32 B ．52 C ．72 D ．92答案：D 14、2．121d x x -+=⎰（）．A．1B．12C．32D．52答案：D14、3．计算定积分211dx x--⎰，则下列步骤中正确的是（）．A．22111d(1)dx x x x ---=-⎰⎰B．2121111d(1)d(1)d x x x x x x ---=-+-⎰⎰⎰C．2121111d(1)d(1)d x x x x x x ---=-+-⎰⎰⎰D．22111d(1)dx x x x ---=-⎰⎰答案：C15、1．用第一换元法求定积分1dlnxx x⎰，则下列步骤中正确的是（）．A．111d d()lnxx x x x=⎰⎰B．2111d d()ln lnxx x x x=-⎰⎰C．11d d(ln)ln lnx xx x x=⎰⎰D．11d d(ln)lnx xx x x=⎰⎰答案：C15、2．用第一换元法求定积分12d1xxx+⎰，则下列步骤中正确的是（）．A．11222001d d() 11xx xx x=++⎰⎰B．112200d d(ln(1+)) 1xx x xx=+⎰⎰C．112220011d d() 121xx xx x=++⎰⎰D．11222001d2d() 11xx xx x=++⎰⎰答案：C15、3．用第一换元法求定积分3e1x⎰，则下列步骤中正确的是（）．A．33e e11)x x=⎰⎰B ．33e e111d(1ln )x x x =+⎰⎰C ．33e e11x =⎰⎰D ．33e e1112d x x =⎰⎰答案：A16、1．用分部积分法求定积分π2cos d x x x ⎰，则下列步骤正确的是（）．A ．1110e d e de x x x x x x x =-⎰⎰B ．111000e d e e d x x x x x x x =-⎰⎰C ．111000e d e e d x x x x x x x =+⎰⎰D ．1110e d e de x x x x x x x =+⎰⎰答案：B16、2．用分部积分法求定积分π2sin d x x x ⎰，则下列步骤正确的是（）．A ．πππ22200sin d cos cos d x x x x x x x =-⎰⎰B ．πππ22200sin d cos cos d x x x x x x x =--⎰⎰C ．πππ22200sin d cos cos d x x x x x x x =+⎰⎰D ．πππ22200sin d cos cos d x x x x x x x =-+⎰⎰答案：D16、3．用分部积分法求定积分π2cos d x x x ⎰，则下列步骤正确的是（）．A ．πππ22200cos d cos cos d x x x x x x x =-⎰⎰B ．πππ22200cos d cos sin d x x x x x x x =-⎰⎰C ．πππ22200cos d sin sin d x x x x x x x =-⎰⎰D ．πππ22200cos d sin cos d x x x x x x x =-⎰⎰答案：C17、1．下列无穷积分中收敛的是（）．A．1x +∞⎰B ．11d x x +∞⎰ C．1x +∞⎰ D ．1cos d x x +∞⎰ 答案：C17、2．下列无穷积分中收敛的是（）．A．1x +∞⎰B ．1ln d x x +∞⎰C ．311d x x +∞⎰D ．⎰∞+1d 1x x 答案：C17、3．下列无穷积分中收敛的是（）．A ．⎰∞+1d 1x x B ．⎰∞+12d 1x x C ．⎰∞+0de x x D ．⎰∞+1d sin x x答案：B18、1．求解可分离变量的微分方程()()y f x g y '=，则下列步骤正确的是（）．A ．()()1d ()d ()y f x g y y f x x g y '== B ．()()()d ()d y f x g y g y y f x x'=-=C ．()()()d ()d y f x g y g y y f x x'== D ．()()1d ()d ()y f x g y y f x x g y '==- 答案：A18、2．求解可分离变量的微分方程y x xy '=+，则下列步骤正确的是（）．A ．d d 1y x xyyx xy'=+=+ B ．d d y x xyyx xy'=+=C ．d d y x xy y y x x'=+= D ．(1)d d y x xy y y x x'=++=答案：A18、3．求解可分离变量的微分方程ex yy +'=，分离变量后可得（）．A ．e d e d yxy x = B ．d e d eyx xy =C ．d de e y x y x = D ．d e d ex y y x = 答案：D19、1．根据一阶线性微分方程的通解公式求解1y xy x'-=，则下列选项正确的是（）．A ．1(),()P x Q x x x == B ．1(),()P x x Q x x== C ．1(),()P x x Q x x =-= D ．1(),()P x Q x x x==- 答案：C19、2．根据一阶线性微分方程的通解公式求解22(1)x y xy x '++=，则下列选项正确的是（）．A ．2(),()P x x Q x x == B ．2(),()P x x Q x x ==C ．222(),()11xy x P x Q x x x ==++D ．222(),()11x x P x Q x x x ==++ 答案：D19、3．根据一阶线性微分方程的通解公式求解32x y xy =-'，则下列选项正确的是（）．A ．32(),()P x Q x x x ==B ．32(),()P x Q x x x =-= C ．32(),()P x Q x x x ==- D ．32(),()P x Q x x x=-=- 答案：B20、1．微分方程2e x yy +'=满足0)0(=y 的特解为（）．A ．2e 2e 3yx -=+ B ．2e 2e 3yx -=-+ C ．2e2e 3y x -=- D ．2e2e 3yx -=--答案：B20、2．微分方程1y x '=+满足0)0(=y 的特解为（）．A ．212x y x =++B ．22x y x =+ C ．2y x x =+ D ．22y x x =+ 答案：B20、3．微分方程yx y -='2e满足0)0(=y 的特解为（）．A ．21e e 2yx c =+ B ．21e e 2y x =C ．211e e 22yx =+ D ．2e e y x = 答案：C。

湖北省孝感市2014届高三第二次统一考试数学理试题含答案

孝感市２０１３—２０１４学年度高中三年级第二次统一考试数学（理科）(含答案)本试卷满分１５０分，考试时间１２０分钟．注意事项：１２照题号顺序在各题的答题区域内作答，超出答题区域书写的答案无效．３一、选择题：本大题共１０小题，每小题５分，共５０分．在每小题给出的四个选项中，只有一项是符合题目要求的．１的共轭复数是Ａ.Ｂ.Ｃ.Ｄ.２，，，则｜ａ＋ｂ＋ｃ｜＝Ａ.０Ｂ.３Ｃ.Ｄ.３集数据如下：经检验，这组样本数据具有线性相关关系，那么对于加工零件的个数ｘ与加工时间ｙ这两个变量，下列判断正确的是ＡＢ０，７６）ＣＤ４ξ服从正态分布，若，则Ｐ（ξ＜０）＝Ａ５，则输入的ｘ可能为Ａ.－１Ｂ.０Ｃ.１Ｄ.５６的最大值是Ａ.２Ｂ.Ｃ.７的最大值是Ａ.２Ｂ.１Ｃ.Ｄ.３８与ｘ轴交于Ａｎ、Ｂｎ两点，以ＡｎＢｎ表示这两点间的距离，则Ａ１Ｂ１＋Ａ２Ｂ２＋…＋Ａ２０１４Ｂ２０１４的值是Ａ. Ｂ. Ｃ.Ｄ.９{１，２，３}，Ｎ＝{１，２，３，４}．定义映射ｆ：Ｍ→Ｎ，则从中任取一个映射满足由点Ａ（１，ｆ（１）），Ｂ（２，ｆ（２）），Ｃ（３，ｆ（３））构成△ＡＢＣ且ＡＢ＝ＢＣ的概率为Ａ. Ｂ. Ｃ. Ｄ.１０(ａ＞０，ｂ＞０)的右焦点为Ｆ，过点Ｆ作与ｘ轴垂直的直线ｌ交两渐近线于Ａ、Ｂ两点，且与双曲线在第一象限的交点为Ｐ，设Ｏ为坐标原点，若(λ，μ∈Ｒ)，λμ＝，则该双曲线的离心率为Ａ. Ｂ. Ｃ. Ｄ二、填空题：本大题共６小题，考生共需作答５小题，每小题５分，共２５分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分．（一）必考题（１１－１４题）１１簧伸长的长度成正比．如果２０Ｎ的力能使弹簧伸长３ｃｍ，则把弹簧从平衡位置拉长６ｃｍ（在弹性限度内）时所做的功为．（单位：焦耳）１２．若目标函数ｚ＝ａｂｘ＋ｙ（ａ＞０，ｂ＞０）的最大值为８，则ａ＋ｂ的最小值为．１３．１４续偶数２、４；第三次取３个连续奇数５、７、９；第四次取４个连续偶数１０、１２、１４、１６；第五次取５个连续奇数１７、１９、２１、２３、２５．按此规则一直取下去，得到一个子数列１，２，４，５，７，９，１０，１２，１４，１６，１７，…．则在这个子数列中，由１开始的第２９个数是，第２０１４个数是．（二）选考题（请考生在第１５、１６两题中任选一题作答，如果全选，则按第１５题作答结果计分）１５△ＡＢＣ的面积，则∠ＢＡＣ＝．１６取相同的长度单位．已知直线ｌ的极坐标方程为，圆Ｃ的参数方程为（θ为参数），则直线ｌ被圆Ｃ截得的弦长为．三、解答题：本大题共６小题，满分７５分，解答应写出文字说明，证明过程或演算步骤．１７．（本小题满分１２分）已知函数，ｘ∈Ｒ．（１）求函数ｆ（ｘ）的最小正周期及单调增区间；（２）在△ＡＢＣ中，角Ａ、Ｂ、Ｃ所对的边分别是ａ、ｂ、ｃ，又，ｂ＝２，△ＡＢＣ的面积等于３，求边长ａ的值．１８题满分１２分）已知{ａｎ}为等差数列，Ｓｎ为其前ｎ项和，且．（１）求ａｎ，Ｓｎ；（２）若ａｋ，ａ２ｋ－２，ａ２ｋ＋１（ｋ∈Ｎ{ｂｎ}的前三项，设Ｔｎ＝ａ１ｂ１＋ａ２ｂ２＋ａ３ｂ３＋…＋ａｎｂｎ，求Ｔｎ．１９交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念性指数值，交通指数取值范围为０～１０，分为五个级别，０～２畅通；２～４基本畅通；４～６轻度拥堵；６～８中度拥堵；８～１０严重拥堵．早高峰时段，从某市交通指挥中心随机选取了四环以内的５０个交通路段，依据其交通指数数据绘制的直方图如右图．（１）这５０个路段为中度拥堵的有多少个？（２）据此估计，早高峰四环以内的三个路段至少有一个是严重拥堵的概率是多少？（３）某人上班路上所用时间若畅通时为２０分钟，基本畅通为３０分钟，轻度拥堵为３６分钟，中度拥堵为４２分钟，严重拥堵为６０分钟，求此人所用时间的数学期望．２０如图①，在平面内，ＡＢＣＤ是∠ＢＡＤ＝６０°且ＡＢ＝ａ的菱形，ＡＤＭＡ１和ＣＤＮＣ１都是正方形．将两个正方形分别沿ＡＤ，ＣＤ折起，使Ｍ与Ｎ重合于点Ｄ１．设直线ｌ过点Ｂ且垂直于菱形ＡＢＣＤ所在的平面，点Ｅ是直线ｌ上的一个动点，且与点Ｄ１位于平面ＡＢＣＤ同侧（图②）．（１）求证：不管点Ｅ如何运动都有ＣＥ∥面ＡＤＤ１；（２）当线段ＢＥ＝时，求二面角Ｅ—ＡＣ—Ｄ１的大小．２１已知曲线Ｃ１：和曲线Ｃ２：（０＜λ＜１）．曲线Ｃ２的左顶点恰为曲线Ｃ１的左焦点．（１）求λ的值；（２）设Ｐ（ｘ０，ｙ０）为曲线Ｃ２上一点，过点Ｐ作直线交曲线Ｃ１于Ａ，Ｃ两点，直线ＯＰ交曲线Ｃ１于Ｂ，Ｄ两点，若Ｐ为ＡＣ中点．①求证：直线ＡＣ的方程为ｘ０ｘ＋２ｙ０ｙ＝２；②四边形ＡＢＣＤ的面积是否为定值？若是，请求出该定值；若不是，请说明理由．２２已知函数ｆ（ｘ）＝ａｌｎｘ－ａｘ－３（ａ∈Ｒ）．（１）讨论函数ｆ（ｘ）的单调性；（２）若函数ｙ＝ｆ（ｘ）的图象在点（２，ｆ（２））处的切线的倾斜角为４５°，对于任意的ｔ∈［１，２］，函数在区间（ｔ，３）上总不是单调函数，求实数ｍ的取值范围；（３）求证：。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

经济数学2014 年上半年第二次作业
一、单项选择题（每小题3分，共30分）
1.函数f(x)在区间 [a,b] 上连续，则以下结论正确的是 ( B )
(A)f (x)可能存在，也可能不存在，x ∈[a ，b]。

(B)f (x)在 [a ，b] 上必有最大值。

(C)f (x)在 [a ，b] 上必有最小值，但没有最大值。

(D)f (x)在 (a,b) 上必有最小值。

2.设函数x x y sin =，则该函数是（ A ）．
A ．奇函数
B ．偶函数
C ．非奇非偶函数
D ．既奇又偶函数
3.当k =（A ）时，函数⎩⎨⎧=≠+=00,,1)(2x k
x x x f ，在0=x 处连续. A ．1 B ．2 C ．1- D ．0
4.满足方程0)(='x f 的点一定是函数)(x f 的（ A ）。

A ．极值点
B ．最值点
C ．驻点
D ．间断点
5.设)(x f 是连续的奇函数，则定积分
=⎰a a x x f -d )(（ D ） A ．⎰0-d )(2a x x f B ．⎰0
-d )(a x x f C ．⎰a
x x f 0d )( D ． 0 6.微分方程1+='y y 的通解是（B ）
A. 1e
-=Cx y ； B. 1e -=x C y ； C. C x y +=； D. C x y +=221 7. 若c x x f x x +-=⎰1
1
e d e )(，则
f (x ) =（ C ）．
A ．
x 1 B ．-x 1 C ．21x D ．-21x
8.当+∞→x 时，下列变量为无穷小量的是（ B ）．
A ．x x sin
B ． 12+x x
C ．21
e x - D ．)1ln(x + 9. ⎰=π
0|cos |dx x ( A )
（Ａ）2 （Ｂ）1 （Ｃ）
21 （Ｄ）41
10．下列积分值为0的是（ A ）．
A ．⎰ππ-d sin x x x
B ．⎰-+1
1-d 2e e x x
x C ．⎰--1
1-d 2e e x x
x D ．⎰-+ππx x x d )(cos
二、填空题（每小题3分，共15分） ⒈函数241
)(x x f -=的定义域是．
⒉若24sin lim 0=→kx
x x ，则=k 2 ． ⒊已知x x f ln )(=，则)(x f ''= ．
⒋若⎰
=x x s d in ．
⒌微分方程y x e x y y x +='+'''sin )(4的阶数是．
三、微积分计算题（每小题10分，共40分） ⒈计算极限4
23lim 222-+-→x x x x ．
⒉设x x y 3cos 5sin +=，求y '
.
⒊计算不定积分
x x x d )1(2⎰+
⒋计算定积分
⎰π0d sin 2
x x x
五、应用题（本题15分）
已知某产品的销售价格p（单位：元／件）是销量q（单位：件）的函数p
q
=-
400
2
，而
总成本为C q q
()=+
1001500（单位：元），假设生产的产品全部售出，求产量为多少时，利润最大？最大利润是多少？？。