第五节曲线的凹凸性拐点与渐近线培训资料
合集下载
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线、函数作图

定义
设有曲线段 y = f ( x ) , x ∈ ( a , b ) ,
若函数 f 在 (a , b) 上为凸函数(凹函数) 即对于其上任 上为凸函数(凹函数) ,即 , 上方(或 何两点 A, B , 弦 AB 总位于所夹曲线弧 AB 的 上方 或 向下凸(或向上凸)。 下方 ),则称曲线段 y = f ( x ) 在 (a , b) 内向下凸 或向上凸 。 ,
y
y = f ( x)
A
o a x1
D B
C
x
x2 b x
y
A
D y = f ( x) B
C
x2 b x
5
向下凸
o a x1 x 向上凸
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图 函数的凹凸与曲线的凸向、
定理 6
内可导, 设函数 f 在区间 I 内可导,且导函数 f ′( x )
的拐点, (3)若 ( x0 , f ( x0 )) 是曲线 y = f ( x ) 的拐点, 且 f ′′( x ) 连续, 反之未必。 在 点 x0 连续,则 f ′′( x0 ) = 0 ,反之未必。
例如: 例如: f ( x ) = x 4 , f ′′( x ) = 12 x 2 ,有 f ′′(0) = 0 ,但 (0,0)不是拐点。 不是拐点。
14
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图 函数的凹凸与曲线的凸向、
3、斜渐近线 、
f ( x) lim 若 = a, x→∞ x ( 或 x → +∞ )
( 或 x → −∞ )
x→∞ ( 或 x → +∞ ) ( 或 x → −∞ )
lim [ f ( x ) − ax ] = b ,
曲线的渐近线

2若在a, b内,f x 0,则f x在a, b上的图形是凸的。
证明 对于(1),设 x1, x2 a, b, 且 x1 x2 ,
记 x0
x1 x2 , 2
并记
x2 x0 x0 x1 h,
则 x2 x0 h, x1 x0 h,
lim
x x0
x3
x2
x1
x
3 0
x
2 0
x0
1
所以该曲线既无水平渐近线,
也无铅直渐近线。
5 f 1 32 , f 1 16 ,
3 27 3 27 f (1) 0 得到函数图形上三个点:
1 , 32 3 27
x
x
x
则y C是 函 数y f ( x)的 一 条 水 平 渐 近 线
(2)、垂直渐近线
若 lim f ( x) (或 lim f ( x) ;lim f ( x) )
xx0 0
x x0
xx0 0
则x x0是函数y f ( x)的一条铅直渐近线。
第五节 曲线的凹凸和函数作图
C
B
D A
a
b
弧ACB与弧ADB的凹向不同。
1
1.凹凸性的定义
f x1 f x2
2
f x1
f
x1
2
x2
f
x2
f
x1
2
x2
f x1 f x2
f x1 2 f x2
例1. 画出y x 3 x 2 x 1的图形.
曲线的凹凸性与拐点及图象

注意:若 f ( x0 ) 不存在,点 ( x0 , f ( x0 )) 也可能
是连续曲线 y f ( x)的拐点.
练习:讨论曲线 y (x 1)3 x5 的凹凸性与拐点.
解 函数的定义域为 (,) .
由于
y
x
8 3
5
x3
,
y
8 3
5
x3
5 3
2
x3
,
y
40 9
x
2 3
10 9
1
x3
10 9
4x
3
练习: 作函数 (x)
1
x2
e2
的图形.
2
解 D : (,), W : 0 ( x) 1 0.4.
2
偶函数,图形关于y轴对称.
( x)
x
x2
e 2,
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
2
令 ( x) 0, 得驻点 x 0,
令 ( x) 0, 得特殊点 x 1, x 1.
例3 作函数 f ( x) x3 x2 x 1 的图形.
解 D : (,), 无奇偶性及周期性.
f ( x) (3x 1)( x 1), f ( x) 2(3x 1). 令 f ( x) 0, 得驻点 x 1 , x 1.
3 令 f ( x) 0, 得特殊点 x 1 .
x (,3) 3 (3,2) 2 (2,0) 0 (0,)
f ( x)
0 不存在
f (x)
0
f (x)
拐点
(3, 26) 9
极值点
3
间 断 点
补充点 : (1 3,0), (1 3,0);
是连续曲线 y f ( x)的拐点.
练习:讨论曲线 y (x 1)3 x5 的凹凸性与拐点.
解 函数的定义域为 (,) .
由于
y
x
8 3
5
x3
,
y
8 3
5
x3
5 3
2
x3
,
y
40 9
x
2 3
10 9
1
x3
10 9
4x
3
练习: 作函数 (x)
1
x2
e2
的图形.
2
解 D : (,), W : 0 ( x) 1 0.4.
2
偶函数,图形关于y轴对称.
( x)
x
x2
e 2,
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
2
令 ( x) 0, 得驻点 x 0,
令 ( x) 0, 得特殊点 x 1, x 1.
例3 作函数 f ( x) x3 x2 x 1 的图形.
解 D : (,), 无奇偶性及周期性.
f ( x) (3x 1)( x 1), f ( x) 2(3x 1). 令 f ( x) 0, 得驻点 x 1 , x 1.
3 令 f ( x) 0, 得特殊点 x 1 .
x (,3) 3 (3,2) 2 (2,0) 0 (0,)
f ( x)
0 不存在
f (x)
0
f (x)
拐点
(3, 26) 9
极值点
3
间 断 点
补充点 : (1 3,0), (1 3,0);
高等数学--45曲线凸性、拐点与渐近线-精品文档
)存在且连续 , 证: f (x) 二阶可导 , f(x
则 f ( x ) [ f ( x ) ] 在 x 两边变 , 0
f ( x ) 在 x 取得极值 , 由可导函数取极值的条件. 0
又 ( x ,f ( x ) ) 是拐点 , 0 0
(x f . 0) 0
在 ( 0 , ) 内 , y 0 ,曲线在 [ 0 , ) 上是凸的 .
3 点 ( 0 , 0 ) 是曲线 y x 的拐点 .
9
信息学院
考研题欣赏 (2019年3,4)设
罗捍东
f( x )xx ( 1 ) ,则
(A)x=0是f(x)的极值点,但(0,0)不是曲线y=f(x)的拐点。 (B)x=0不是f(x)的极值点,但(0,0)是曲线y=f(x)的拐点。 (C)x=0是f(x)的极值点,且(0,0)是曲线y=f(x)的拐点。
3
信息学院
2 3 y x , y 6 x , 解:
罗捍东
3 例1:判断曲线 yx 的凹凸性 .
当 x0 时,y 0 ,
曲线 在 ( , 0 ] 为凸的;
0 y , 当 x0 时, 曲线 在 [ 0 , ) 为凹的;
(0,0)是曲线由凸变凹的分界 点 . 注意到, 点
信息学院
4.5.1 曲线凸性与拐点
罗捍东
C
B
A
o
x
yf( x )
第五节 曲线凸性、拐点与渐近线 y
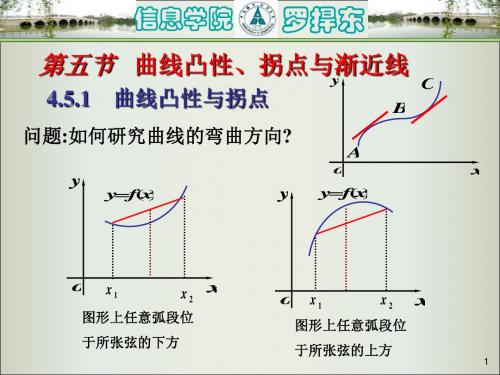
问题:如何研究曲线的弯曲方向?
y
yf( x )
y
o
x1
x2 x
图形上任意弧段位 于所张弦的下方
o x1
x2
x
3-5 凹凸性 拐点.渐近线

0
0
f ( x ) 递增
y 0
f ( x ) 递减
y 0
机动
目录
上页
下页
返回
结束
例1. 判断曲线
解: 函数的定义域为
的凹凸性.
1 y , x 1 y 2 x
所以在函数的定义域 由定理1知 曲线
1 内,y 2 0 x
是凸的.
机动
目录
上页
下页
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2 x 3
y x 2 为曲线的斜渐近线 . 无水平渐近线 .
机动 目录 上页 下页 返回 结束
y 0是曲线的水平渐近线
1 x lim +ln(1+e ) = x 0 x
x 0是曲线的垂直渐近线
机动
目录
上页
下页
返回
结束
1 例3 求曲线y=f(x)= +ln(1+e x )的渐近线 x f ( x) 1 ln(1+e x ) lim 2 + 考虑斜渐近线. lim x x x x x
第五节
第三章
曲线的凹凸性,拐点与渐近线
一、曲线的凹凸性 二、曲线的拐点 三、渐近线
机动
目录
上页
下页
返回
结束
1、曲线凹凸性的概念
定义 . 设函数 在区间 I 上连续 ,
(1) 若恒有
图形是凹的; (2) 若恒有
B
则称
则称
A 图形是凸的 .
yy
oo
x1 x x1 x x1x1 2 2x2x2 x x 2 2
§4.5 曲线的凹向、拐点与渐近线

15/25
2.1、 2.1、渐近线的定义 若曲线y=f(x)上的动点 沿曲线无限远离坐标原 上的动点P沿曲线无限远离坐标原 若曲线 上的动点 点时,该点P与某条定直线 的距离趋于零, 与某条定直线L的距离趋于零 点时,该点 与某条定直线 的距离趋于零,则称该 定直线L为曲线 为曲线y=f(x)的一条渐近线. 的一条渐近线. 定直线 为曲线 的一条渐近线 2.2、 2.2、分类 ⑴水平渐近线 (平 于 轴 渐 线 行 x 的 近 ) 如 果 lim f (x) = b或lim f (x) = b (b为 数 常 )
x = 0是不可导点, y′, y′′均不存在 .
但在( −∞ ,0)内, y′′ > 0, 曲线在 ( −∞ ,0 ]上是凹的 ;
y
y =3 x
在(0,+∞ )内, y′′ < 0,
曲线在[0,+∞ )上是凸的.
o
x
∴ 点(0,0)是曲线 y = 3 x的拐点.
微积分四 微积分四⑤
10/25
xe 的凹向区间及拐点. 例5.求曲线 y = 的凹向区间及拐点.
y
y = f (x)
y
C
B
A
x
y = f (x)
o
y
o
x1
x2 x
o
x1
x2
x
曲线向上弯曲的弧段 位于其上任一点处切 上凹. 线的上方, 称为上凹 线的上方 称为上凹
微积分四 微积分四⑤
曲线向下弯曲的弧段 位于其上任一点处切 线的下方,称为下凹. 称为下凹 线的下方 称为下凹
4/25
1.2、 1.2、曲线凹向的定义 定义4.3 若在某个区间内 曲线弧位于其上任一 若在某个区间内, ⑴定义 点的切线上方, 则称曲线在该区间内是上 点的切线上方 则称曲线在该区间内是上凹的; 若 曲线弧位于其上任一点的切线下方, 曲线弧位于其上任一点的切线下方 则称曲线在该 区间内是下 区间内是下凹的. 简称凹 也称下凸 下凸; 简称凸 也称上凸 上凸. 注: 上凹简称凹, 也称下凸 下凹简称凸, 也称上凸 y = f (x) ⑵图形分析 B y y y= f (x) B =
凹凸性、渐近线、作图资料
[解] 定义域:(,), 是偶函数.
因 为 lim e x2 0, 所 以 直 线y 0 x
是 水 平 渐 近 线.
y 2xex2
y 2ex2 (2x2 1)
令 y 0 驻点:x 0
令 y 0 x 1
10/15/2019
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x
(,
1 )
5
y '' -
y凸
1
5
0
8 25
拐点
(1 , ) 5
+
凹
在 x 1 两侧 y ''符号发生改变,则(1 , 8 )是拐点.
5
5 25
1
例3.求曲线 y x3 的拐点.
1
解:函数 y x3 的定义域为 (, )
函数的凹凸性、渐近线 与作图
一、函数的凹凸性 二、曲线的渐近线 三、函数作图
10/15/2019
1
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
f (x2 )
则称f (x)在该区间上的图形是凸的.
10/15/2019
4
凹曲线的一阶导数变化规律:
若 f (x)是凹函数,则 f (x)单调增加;
10/15/2019
5
凸曲线的一阶导数变化规律:
若 f (x)是凸函数,则 f (x)单调减少.
10/15/2019
6
因 为 lim e x2 0, 所 以 直 线y 0 x
是 水 平 渐 近 线.
y 2xex2
y 2ex2 (2x2 1)
令 y 0 驻点:x 0
令 y 0 x 1
10/15/2019
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x
(,
1 )
5
y '' -
y凸
1
5
0
8 25
拐点
(1 , ) 5
+
凹
在 x 1 两侧 y ''符号发生改变,则(1 , 8 )是拐点.
5
5 25
1
例3.求曲线 y x3 的拐点.
1
解:函数 y x3 的定义域为 (, )
函数的凹凸性、渐近线 与作图
一、函数的凹凸性 二、曲线的渐近线 三、函数作图
10/15/2019
1
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
f (x2 )
则称f (x)在该区间上的图形是凸的.
10/15/2019
4
凹曲线的一阶导数变化规律:
若 f (x)是凹函数,则 f (x)单调增加;
10/15/2019
5
凸曲线的一阶导数变化规律:
若 f (x)是凸函数,则 f (x)单调减少.
10/15/2019
6
高等数学-曲线的凹凸性及拐点
曲线的凹凸性和拐点的判别
例3 求曲线 =
解
3
的凹凸区间和拐点.
定义域为(−∞, +∞).
′
=
1
3
3 2
,
″
=−
2
39Leabharlann 2. = 0时, ′ ,′′都不存在.
+
凹
0
凸
由表可知,曲线的凹区间为(−∞, 0) ,凸区间为(0, + ∞),
曲线的拐点为 (0,0).
9
″ () = 12 2 − 30 + 12 = 6(2 − 1)( − 2),
令 ″ ()
= 0,得1 =
+
凹
1
,2
2
0
= 2.
凸
0
+
凹
1
由表可知,曲线的凹区间为(−∞, )和(2, +∞),凸区间为
2
1
1 7
( , 2),曲线的拐点为( , )和(2, −5).
2
2 16
8
02
微分中值定理及导数的应用
第6讲
曲线的凹凸性及拐点
本节内容
01 曲线的凹凸性和拐点的定义
02 曲线的凹凸性和拐点的判别
2
01 曲线的凹凸性和拐点的定义
定义3.2
设函数 = ()在开区间(, )内可导,在该
区间内如果曲线位于其任何一点切线的上方,
那么称此曲线在区间(, )内是凹的,区间
区间(, )内具有二阶导数.
(1)在(, )内,若 ″ () > 0,那么曲线 = ()在
[, ]上是凹的.
(2)在(, )内,若 ″ () < 0,那么曲线 = ()在
曲线的凹凸性和拐点、函数图像的描绘
高等数学
曲线的凹凸性和拐点、函数图 像的描绘
一、曲线的凹凸性与拐点 1.曲线凹凸性的定义及其判定
首先观察图3-9所示的两条曲线。
图3-9
如图3-9所示,有一类曲线向上弯曲,它在任何点处的切 线总位于曲线的下方;另一类曲线向下弯曲,它在任何点处的 切线总位于曲线的上方,由此我们给出关于曲线凹凸的定义:
x x0
则称直线 x x0 为曲线 y f (x)的垂直渐近线。
其一般步骤如下:
2.函数图像的描绘
(1)确定函数 y f (x) 的定义域、间断点及函数所具有的某些特 性(如奇偶性、周期性等); (2)求出函数的一阶导数 f (x) 和二阶导数 f (x),解方程
f (x)=0,f (x) 0 在定义域内的全部实根及 f (x) 和 f (x)不存在的 点,应用这些根和点,将函数的定义域划分为若干个子区间; (3)列表讨论 f (x)和 f (x) 在(2)中所得各子区间内的符号,由 此确定函数的单调性、极值、曲线的凹凸性和拐点; (4)如有渐近线,求出渐近线,并确定其他变化趋势; (5)求辅助点,如曲线与坐标轴的交点等; (6)在直角坐标系中,根据上面讨论,描点作图。
例2 求曲线 y x4 2x3 1 的凹凸点区间和拐点。 解 函数 y x4 2x3 1 的定义域为( , )
y 4x3 6x2 y 12x2 12x 12x(x 1) , 令 y 0,得 x 0 和 x 1。 列表讨论如下:
x y
曲线
( ,0) +
0 0 拐点 (0,1)
如果将定理中的区间改为其他区间,结论仍然成立。
例1 判定曲线 y x3 的凹凸性。 解 函数的定义域为 ( , ) ,y 3x2,y 6x
(当 x 0 时,y 0 ,故曲线在 ( ,0] 内是凸的;当 x 0 时,y 0,股曲线在 [0 , ) 内是凹的;当x 0时,y 0。 点(0,0)是曲线 y x3由凸变凹的分界点(图3-11)
曲线的凹凸性和拐点、函数图 像的描绘
一、曲线的凹凸性与拐点 1.曲线凹凸性的定义及其判定
首先观察图3-9所示的两条曲线。
图3-9
如图3-9所示,有一类曲线向上弯曲,它在任何点处的切 线总位于曲线的下方;另一类曲线向下弯曲,它在任何点处的 切线总位于曲线的上方,由此我们给出关于曲线凹凸的定义:
x x0
则称直线 x x0 为曲线 y f (x)的垂直渐近线。
其一般步骤如下:
2.函数图像的描绘
(1)确定函数 y f (x) 的定义域、间断点及函数所具有的某些特 性(如奇偶性、周期性等); (2)求出函数的一阶导数 f (x) 和二阶导数 f (x),解方程
f (x)=0,f (x) 0 在定义域内的全部实根及 f (x) 和 f (x)不存在的 点,应用这些根和点,将函数的定义域划分为若干个子区间; (3)列表讨论 f (x)和 f (x) 在(2)中所得各子区间内的符号,由 此确定函数的单调性、极值、曲线的凹凸性和拐点; (4)如有渐近线,求出渐近线,并确定其他变化趋势; (5)求辅助点,如曲线与坐标轴的交点等; (6)在直角坐标系中,根据上面讨论,描点作图。
例2 求曲线 y x4 2x3 1 的凹凸点区间和拐点。 解 函数 y x4 2x3 1 的定义域为( , )
y 4x3 6x2 y 12x2 12x 12x(x 1) , 令 y 0,得 x 0 和 x 1。 列表讨论如下:
x y
曲线
( ,0) +
0 0 拐点 (0,1)
如果将定理中的区间改为其他区间,结论仍然成立。
例1 判定曲线 y x3 的凹凸性。 解 函数的定义域为 ( , ) ,y 3x2,y 6x
(当 x 0 时,y 0 ,故曲线在 ( ,0] 内是凸的;当 x 0 时,y 0,股曲线在 [0 , ) 内是凹的;当x 0时,y 0。 点(0,0)是曲线 y x3由凸变凹的分界点(图3-11)
曲线的凹凸性、拐点与渐近线
x1 x2 f ( x 1 ) f ( x2 ) f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凸的(凸弧)。 x x y y f( )
如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在; x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在, x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1:设 f ( x )在区间 I 上连续,如果对于 I 上任意两点 x1 , x2, x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧);
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断,且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在; x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在, x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1:设 f ( x )在区间 I 上连续,如果对于 I 上任意两点 x1 , x2, x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧);
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断,且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)式与(2)式相加得
[f( x 2 ) f( x 1 )x ] 2 ( x 1 ) 0
故 f(x2)f(x1) 从而 f (x) 单调增加.
定理4.11 设函数 f ( x)在区间(a,b)内有 二阶导数, 那么 ①如果x(a,b)时, 恒有 f(x)0,
则曲线 f ( x) 在区间(a,b) 内是凹曲线; ②如果x(a,b)时, 恒有 f(x)0,
例2
试证明
0x时,有
sin
x 2
x
.
(99年考题)
证明 f(x)sinx x 2
又 f(0)0 f()0
f(x)12cos2x1
f(x)1sinx 0 42
所以曲线是凸的
故 0x 时
f(x)sinx x 0
2 即 sin x x .
2
二.曲线的拐点 定义 曲线凹与凸的分界点称为曲线的拐点. 拐点定理 如果P(x0, f(x0))为曲线 f ( x) 的拐点,
设函数 y y(x) 由方程 ylnyxy0确定,
试判断曲线 y y(x) 在点 ( 1 , 1 ) 附近的凹凸性.
解 ylny2y10 y 1
ln y 2
1 y
y
(ln
y y 2)2
1 y(ln y 2)3
0
y y(x) 在点 ( 1 , 1 ) 附近是凸的.
利用凹凸性证明不等式
y f(x)
c是 f ( x)的间断点
P
xc是铅垂渐近线
第五节 曲线的凹凸性、拐点与渐近线
y
oa
b
x
一.曲线的凹凸性 定义1 直观定义.
注 (1)凹 凸
(2)凹也称上凹、下凸 凸也称上凸、下凹.
y
y
oa
bx o a
bx
定义2 如果在某个区间内, 曲线位于其上 任一点切线的上方, 则称该曲线在 这个区间内是凹曲线; 如果在某个区间内, 曲线位于其上 任一点切线的下方, 则称该曲线在 这个区间内是凸曲线;
则必有 f(x0)0或 f (x0) 不存在.
f(x)0 f (x)不存在
注 (1)一般来说圈中的点为 有限多个.
(2)拐点是曲线上的点,表 示拐点要用两个坐标.
例3 讨论曲线 f(x)x42x31拐点.
解 f ( x)的定义域为(,)
f(x)4x36x2
f(x)1x 2 (x1 )
令 f(x)0得 x0,x1
定义3 如果对某区间内任意两点x1, x2 有
f(x1x2)f(x1)f(x2),
2
2
则称曲线为凹曲线;
如果对某区间内任意两点x1, x2 有
f(x1x2)f(x1)f(x2),
2
2
则称曲线为凸曲线.
定理4.10 如果函数 f ( x)在区间 (a,b)内可导,
则曲线 f ( x)在区间(a,b) 内凹(凸)
则曲线 f ( x) 在区间(a,b) 内是凸曲线.
例1 讨论曲线 f(x)x42x31的凹凸性.
解 f ( x)的定义域为(,)
f(x)4x36x2
f(x)1x 2 (x1 )
令 f(x)0得 x0,x1
x
f (x) f (x)
( ,0)
(0,1)
(1, )
补充:07年考研真题10分
x
f (x) f)
(0,1) 1 0
(1, )
拐点(1,0)
例4 讨论曲线 f(x)(x1)3 x5 的凹凸性与拐点 解 f ( x)的定义域为(,)
f(x)8x53 5x32 33
令 f(x)0得 x
1 4
f(x) 10 4x1 9 3x
另 f (0)不存在
x ( ,0) 0
1 (0, )
4
1 4
( 1 , ) 4
f(x) 不存在
0
13
f (x)
(0,0)
( ,
)
4 163 16
三.曲线的渐近线 定义 如果曲线上的动点 P沿着曲线无限
地远离原点时,点 P与某一固定直线 的距离趋于零,则称该直线为曲线的 渐近线.
1.水平渐近线
渐近线 2.垂直渐近线或铅垂渐近线 3.斜渐近线
1.水平渐近线
y b是水平渐近线
y y f(x)
lim [f(x)b]0 x
P
b
或 lim [f(x)b]0 x
limf(x)b x
o xx
或 limf(x)b
x
例5
求曲线 y
1 x
的水平渐近线.
解 因 lim 1 0 水平渐近线为 y 0.
x x
2.垂直渐近线或铅垂渐近线
y
f ( x 1 ) f ( x 2 ) f ( x 2 )x 1 ( x 2 )
从而
f ( x 2 ) f ( x 1 ) f ( x 1 ) x 2 ( x 1 ) ( 1 )
f ( x 1 ) f ( x 2 ) f ( x 2 ) x 1 ( x 2 ) ( 2 )
[f() f(x 0 )x ] ( x 0 ) 0
• ••
a x0
•x
• b
所以 f(x ) f(x 0 ) f(x 0 )x ( x 0 )
故曲线为凹曲线.
(条件:曲线 f ( x), 结论: f (x) )
设 x1 x2是 (a,b) 内任意两点 曲线上过x1 处的切线: y f(x 1 ) f(x 1 )x ( x 1 )
只需证 f(x ) f(x 0 ) f(x 0 )x ( x 0 )(x x0)
设 f (x) 单调增加, 对 x(a,b)
f(x ) [f(x 0 ) f(x 0 )x ( x 0 )]
[ f ( x ) f ( x 0 ) ] f ( x 0 )x (x 0 )
f()x (x 0 ) f( x 0 )x (x 0 )
曲线上过x 2 处的切线: y f(x 2 ) f(x 2 )x ( x 2 )
因曲线
f
(
x
)
,
故
f( x ) f( x 1 ) f( x 1 )x (x 1 )
f( x ) f( x 2 ) f( x 2 )x (x 2 )
从而
f ( x 2 ) f ( x 1 ) f ( x 1 )x 2 ( x 1 )
导函数 f (x) 在区间 (a,b) 内单调增加(减少).
证 (条件: f (x) ,结论:曲线 f ( x) )
曲线: y f(x) 曲线上任一点 x 0 处的切线: y f(x 0 ) f(x 0 )x ( x 0 )即 y f(x 0 ) f(x 0 )x ( x 0 ) 只需证 f(x ) f(x 0 ) f(x 0 )x ( x 0 )(x x0)
