三角函数的化简求值
三角函数的化简求值(含答案)

三角函数的化简求值一、单选题(共10道,每道10分)1.化简的结果是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简2.化简的结果是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简3.下列选项中,不是化简的结果的是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简4.化简的结果的是( )A.,其中B.,其中C.,其中D.,其中答案:B解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简5.函数()的值域为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简6.函数()的值域为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简7.已知函数,若为偶函数,则的一个值为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简8.函数()的值域为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简9.函数()的值域为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简10.函数()的值域是( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:形如asinx+bcosx的化简。
三角函数式的化简求值训练

)=cos_αcos_β+sin_αsin_β; (2)C (α+β):cos(α+β)=cos_αcos_β-sin_αsin_β; (3)S (α+β):sin(α+β)=sin_αcos_β+cos_αsin_β; (4)S (α-β):sin(α-β)=sin_αcos_β-cos_αsin_β;(5)T (α+β):tan(α+β)=tan α+tan β1-tan αtan β;(6)T (α-β):tan(α-β)=tan α-tan β1+tan αtan β. 2.二倍角的正弦、余弦、正切公式.二倍角的正弦、余弦、正切公式 (1)S 2α:sin 2α=2sin_αcos_α;(2)C 2α:cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α;(3)T 2α:tan 2α=2tan α1-tan 2α. 3.有关公式的逆用、变形等.有关公式的逆用、变形等(1)tan α±tan β=tan(α±β)(1∓tan_αtan_β);(2)cos 2α=1+cos 2α2,sin 2α=1-cos 2α2;(3)1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2,sin α±cos α=2sin èæøöα±π4. =α+β2-α-β2;α-β2=èæøöα+β2-èæøöα2+β.原则: 用已知表示待求用已知表示待求 (2) 化简技巧:切化弦、“1”的代换等.的代换等. 6 三个变化三个变化(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”. (2)变名:变名:通过变换函数名称达到减少函数种类的目的,通过变换函数名称达到减少函数种类的目的,通过变换函数名称达到减少函数种类的目的,其手法通常有其手法通常有“切化弦”、“升幂与降幂”等.等.(3)等.等.二 典型题目1 三角函数式的化简【例1】►化简2cos 4x -2cos 2x +122tan èæøöπ4-x sin 2èæøöπ4+x. 【训练1】 化简 (sin cos 1)(sin cos 1)sin 2a a a a a+--+:. 1三角三角函数式函数式的化简求值训练 一.重要公式与方法技巧:1 两角和与差的两角和与差的正弦正弦、余弦、正切公式、余弦、正切公式(1)C (α-β):cos(α-β4.函数f (α)=a cos α+b sin α(a ,b 为常数),可以化为f (α)=a 2+b 2sin(α+φ)或f (α)=a 2+b 2c os(α-φ),其中φ可由a ,b 的值唯一确定.的值唯一确定. 5两个技巧两个技巧(1)拆角、拼角技巧:2α=(α+β)+(α-β);α=(α+β)-β;β变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”、“逆用变用公式”、“通分约分”、“分解与分解与组合组合”、“配方与配方与平方平方”<π2<α<π,且cos èæøöα-β2=-19,sin èæøöα2-β=23,求cos(α+β)的值.的值.【训练2】 已知α,β∈èæøö0,π2,sin α=45,tan(α-β)=-13,求cos β的值.的值.三 三角函数的求角问题三角函数的求角问题【例3】►已知cos α=17,cos(α-β)=1314,且0<β<α<π2,求β. 【训练3】 已知α,β∈èæøö-π2+33x +4=0的两个根,求α+β的值.的值.四 三角函数的综合应用三角函数的综合应用【例4】►已知函数f (x )=2cos 2x +sin 2x .(1)求f èæø-π62二 三角三角函数式函数式的求值的求值【例2】►已知0<β,π2,且tan α,tan β是方程x 2öπ3的值;(2)求f (x )的最大值和最小值.和最小值.【训练4】 已知函数f (x )=2sin(π-x )cos x . (1)求f (x )的最小正周期;的最小正周期;(2)求f (x )在区间ëéûù,π2上的最大值和最小值.上的最大值和最小值.一、给值求值一、给值求值一般是给出某些角的三角函数式的值,求另外一些角的求另外一些角的三角函数值三角函数值,解题的关键在于“变角”,如α=(α+β)-β,2α=(α+β)+(α-β)等,把所求角用含已知角的式把所求角用含已知角的式子表示子表示,求解时要注意角的范围的讨论.角的范围的讨论.3【示例】►已知tan èæøöx +π4=2,则tan =12,tan β,π2. (1)求sin θ和cos θ的值;的值;(2)若5cos(θ-φ)=35cos φ,0<φ<π2,求cos φ的值.的值.【课后巩固】1.81cos sin =×a a ,且4p <a <2p,则a a sin cos -的值为:的值为:A 、23B 、23-C 、43D 、43-2.已知a a aa a cos 3sin 2cos sin ,2tan +--=则的值是的值是A 、-1 B 、1 C 、-3 D 、3 3.已知=-=+-=-)sin(,21sin cos ,43cos sin a b b a b a 则A 、3219B 、3219-C 、0 D 、1916-4.已知 5.已知3sin(),45x p -=则sin 2x 的值为的值为 ( )A.1925 B.1625 C.1425 D.7256.已知1sin cos 5q q -=,则sin 2q 的值是的值是A 、45B 、45-C 、2425D 、-24257.已知54)cos(-=-b a 54)cos(=+b a ),2(p p b a Î-)2,23(p p b a Î+则cos2a =( ) xtan 2x 的值为________.二、给值求角二、给值求角“给值求角”:实质上也转化为“给值求值”,关键也是变角,把所求角用含已知角的式把所求角用含已知角的式子表示子表示,由所得的函数值结合该函数的单调由所得的函数值结合该函数的单调区间区间求得角.求得角.【示例】►已知tan(α-β)=-17,且α,β∈(0,π),求2α-β的值.的值. ▲三角恒等变换与▲三角恒等变换与向量向量的综合问题的综合问题 两角和与差的两角和与差的正弦正弦、余弦、正切公式作为解题工具,是每年余弦、正切公式作为解题工具,是每年高考高考的必考内容,常在选择题中以条件求值的形式考查.近几年该部分内容与向量的综合问题常出现在解答题中,并且成为高考的一个新考查方向.高考的一个新考查方向.【示例】► 已知向量a =(sin θ,-2)与b =(1,cos θ)互相互相垂直垂直,其中θ∈èæøö0q tam 和)4(q p-tam 是方程02=++q px x 的两根,则p 、q 间的关系是:间的关系是: A 、01=+-q p B 、01=++q p C 、01=-+q p D 、01=--q p4A 、257-B 、257C 、1-D 、1 8.22cos 75cos 15cos75cos15++ 的值等于(的值等于( ) A 、62 B 、32 C 、54D 、1+349.已知tan(α+β)=52,tan(β-4p )=41,那么tan(α+4p )的值是的值是A .1813 B .223 C .2213 D .18310.若,(0,)2pa b Î,3cos()22ba -=,1sin()22a b -=-,则cos()a b +的值等于 (A )32-(B )12- (C )12(D )32 11、已知tan 2a =,求2212sin cos cos sin a a a a +-12.求tan200+tan400+3tan200tan400的值. 13.已知3110,tan 4tan 3pa p a a<<+=-(Ⅰ)求tan a的值;(Ⅱ)求225sin 8sin cos 11cos 822222sin 2a a a a p a ++-æö-ç÷èø 14.已知40,sin 25pa a <<=(Ⅰ)求22sin sin 2cos cos 2a a a a++的值;(Ⅱ)求5tan()4pa -的值。
高中数学专题:三角函数的化简与求值

2+3,
则常数 a=________.
解析
1+2cos2x-1 f(x)= 2cos x +sin
x+a2sinx+π4
=cos x+sin x+a2sinx+π4
= 2sinx+4π+a2sinx+π4 =( 2+a2)sinx+4π. 依题意有 2+a2= 2+3, ∴a=± 3.
答案 ± 3
α
=2
2sin
α=-2
5
5 .
答案 A
高考题型精练 1 2 3 4 5 6 7 8 9 10 11 12
4.已知f(x)=sin2
x+4π,若a=f(lg
5),b=f(lg
1 5
),则(
)
A.a+b=0
B.a-b=0
C.a+b=1
D.a-b=1
解析 a=f(lg 5)=sin2(lg 5+4π)
1-cos2lg
2 .
又∵cosπ4-β2= 33,-2π<β<0, ∴sinπ4-β2= 36,
高考题型精练 1 2 3 4 5 6 7 8 9 10 11 12
∴cosα+2β=cosπ4+α-π4-β2 =cosπ4+αcosπ4-β2+sinπ4+αsinπ4-β2 =13× 33+232× 36=593. 答案 C
=-41+34+1=23.
点评 熟练运用诱导公式和基本关系式,并确定相应三角 函数值的符号是解题的关键.另外,切化弦是常用的规律 技巧.
变式训练2 (1)(四川)已知sin α+2cos α=0, 则2sin αcos α-cos2α的值是________. 解析 ∵sin α+2cos α=0, ∴sin α=-2cos α, ∴tan α=-2, 又∵2sin αcos α-cos2α=2sinsiαn2cαo+s αc-osc2αos2α
(完整版)三角函数化简求值证明技巧
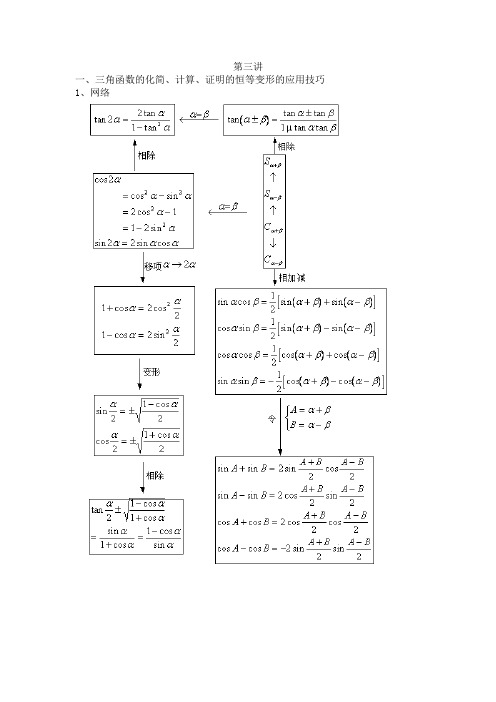
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
高考题集三角函数,化简求值通用步骤.doc

高考题集三角函数,化简求值通用步骤求解三角函数的性质通常情况下需利用三角函恒等变换公式将函数的解析式转化为y=Asin(wx+φ)+B的形式,然后根据基本三角函数y=sinx的性质结合整体代换的思想求解,这点大家还是很熟悉了,下面一起来看下
解三角函数化简步骤:诱导公式(π,2π,,,)→和差角公式(π/6,π/4,π/6)→正弦二倍角逆用公式(sinxcosx,)→降幂公式(sin²x,cos²x)→辅助角公式(asinx+bcosx)→y=Asin(wx+φ)+B
在化简过程中这个步骤非常好用,括号里的就是题目条件中会给到的常见的数学公式符号特征,只要按照相应公式展开即可,快速又简便
题中sin(x-π/6),就是特征,按正弦差角公式展开,由于π/6的正余弦值知晓,所以就化简一层了,接着乘法张开,就发现降幂公式使用以后,就化成同角正余弦了,最后直接用辅助角公式即可化成y=Asin(wx+φ)+B,然后根据基本三角函数y=sinx的性质结合整体代换的思想求解。
方法还是非常独特的思路,利用和差角公式,凑出y+z,y-z,再加减消元,y即求出,只是这个方法考试的时候还是需要慎用,因为一不小心算不出来,找不到关系,就意味着要重新计算,耽误时间,心里压力又加大,老生常谈的话就是用你最拿手的办法,解你自己的题,不管别人如何解,走
自己的路让别人说去吧。
方法3就是凑角,恒等变换求结果
三角函数这部分的知识,化简恒等变换就是重点,是求性质的前提,所以把化简步骤记忆掌握就尤其重要了,解题往往是在前往通法的道路上,找到适合此题的又独特解法,方法是死的,人是活的,脑子是活的,你想怎么用,想先用哪个都随你心,加油哦。
考点15 三角函数式的化简与求值(答案)

,故选 B.
3.【2017
届广西玉林市、贵港市高中毕业班质量检测】若
cos
−
3sin
=
0
,则
tan
−
4
=
(
)
−1
1
A. 2
B.-2
C. 2
D.2
【答案】A
【解析】由 cos
− 3sin
=
0
tan
,知
=
1 3
,则
tan
− 4
=
tan −1 1+ tan
=
−
1 2
,故选 A
.
4.【山西省孝义市 2017 届高三下学期高考考前质量检测三(5 月)】已有角 的顶点与坐标原点重合,
+ cos2
sin ”;(3)化正弦、余弦为正切,即 cos
=
tan
;
tan = sin
(4)化正切为正弦、余弦,即
cos ;( 5 ) 正 弦 、 余 弦 和 ( 差 ) 与 积 的 互 化 , 即
(sin cos )2 =1 2sin cos .
tan = 3
1− sin 2 =
【变式 1】【例题中的条件不改变,所求三角函数式改变】若
【解析】
16 8 ,选 D.
【方法技巧归纳】二倍角公式的正用、逆用、变形用是公式的种主要应用手段,特别是二倍角的余弦 公式,其变形公式在求值与化简中有广泛的应用,在综合使用两角和与差、二倍角公式化简求值时,要注 意以下几点:(1)熟练掌握公式的正用、逆用和变形使用;(2)擅于拆角、配角;(3)注意二倍角的相对性; (4)注意角的范围;(5)熟悉常用的方法和技巧,如切化弦、异名化同名、异角化同角等.
三角函数化简求值的技巧

三角函数化简求值的技巧
一、三角函数的重要性质:
1、正弦函数sin x、余弦函数cos x、正切函数tanx和其逆函数的
关系:
sin x=1/cos x,cos x=1/sin x,tan x=1/cot x,cot x=1/tan x,cos x=1/csc x,csc x=1/cos x。
2、三角函数的基本性质:
sin2x+cos2x=1,sin2x=2sin(x/2)cos(x/2),cos2x=cos2(x/2)
-sin2(x/2),2sin xcos x=sin2x+cos2x=2sin2(x/2)=2cos2(x/2)。
3、三角函数的对称性:
sin(-x)=-sin x,cos(-x)=cos x,tan(-x)=-tan x,cot(-x)=-cot x,csc(-x)=-csc x。
二、用三角函数化简求值的常用方法:
1、用公式和定义:
用三角函数的基本公式来把表达式中的各个项拆分开明确每个项的意义,然后把各个项的值累加求值。
2、用对称性:
对变量进行绝对值化,然后利用三角函数的对称性变换变量或表达式,从而达到化简的目的。
3、用反函数求值:
把表达式中的三角函数换成其对应的反函数,然后利用反函数的性质进行化简,获得原函数的表达式。
四、利用三角函数化简求值的实例:
例1:求Sin(60°)
解:
1、用公式求值:
可以用公式sin 2x=2sin xcos x来求值。
三角函数化简求值典型例题

三角函数化简求值典型例题三角函数,哎呀,这可真是个既神秘又有趣的世界!我们在生活中,常常能看到三角函数的身影,像是在建筑、导航,甚至是音乐中,都有它的身影。
你有没有想过,三角函数其实就像一个调皮的小孩,时不时就会给你带来一些意想不到的挑战。
今天,我们就来聊聊这些三角函数的化简与求值,带你一起深挖这个“秘密花园”。
咱们得了解一下三角函数的基本概念。
最常见的,可能就是正弦、余弦和正切了。
别看它们名字听起来复杂,其实它们就是个“角”的游戏。
就像在游乐园里,正弦和余弦这对好朋友总是一起玩耍。
你想象一下,正弦就像是一个在过山车上尖叫的小孩,余弦则是那个在旁边冷静地观察的朋友。
他们的关系其实很微妙,正弦的最高点和余弦的最低点,总是能碰到一起,真是有趣得很!我们来说说这些三角函数的化简。
化简就像是把一个复杂的拼图变得简单明了。
比如说,咱们有一个表达式,像是sin²(x) + cos²(x),这看起来是不是有点复杂?但它有个神秘的特性,就是总能化简成1。
这就好比你在忙碌的一天中,突然发现原来生活中的小确幸其实一直都在。
每次看到这个化简,我都忍不住想笑,真是简单又快乐!再看看这个正切函数,tanj = sinj/cosj。
这个家伙有点特别,常常让人捉摸不透。
有时候它显得那么高深莫测,但只要你理解了正弦和余弦的关系,正切就乖乖听话了。
比如说,当你求一个角的正切值时,记得去找它的对边和邻边,这样你就能轻松地求出结果。
这种感觉,就像是揭开了一个谜底,瞬间明亮了许多。
不过,三角函数不仅仅是计算,它背后有个更深层次的故事。
比如,当我们在计算某个角的值时,其实是在寻找这个角在生活中的意义。
它就像一个指引,让我们能在复杂的世界中找到方向。
记得有一次,我在爬山的时候,忽然想到三角函数,心里有种说不出的亲切感。
仿佛每一步的攀登,都与这些函数息息相关。
山的高度、斜率,甚至每一个呼吸,都与三角函数有着千丝万缕的联系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【知识要点】
利用同角三角函数的基本关系式——平方关系、商数关系、倒数关系和两角和差倍半角公式来化简求值. 和差化积、积化和差公式:
sin sin 2sin cos 22αβ
αβαβ+-+= sin sin 2sin cos 22
αβαβαβ-+-=
cos cos 2cos cos 22αβαβαβ+-+= cos cos 2sin sin 22
αβαβαβ+--= 1sin cos [sin()sin()]2αβαβαβ=++- 1cos sin [sin()sin()]2
αβαβαβ=+-- 1cos cos [cos()cos()]2αβαβαβ=++- 1sin sin [cos()cos()]2αβαβαβ=+--
【典型例题】
例1求234cos cos cos cos 9999
π
πππ的值.
例2化简下列各式:
(1)2sin10cos 20sin 20︒-︒︒
(2)22sin sin cos sin cos tan 1x x x x x x +---(3)66441sin cos 1sin cos θθθθ----
例3已知tan 2α=,求:(1)
4sin 2cos 5sin 3cos αααα
-+;(2)223sin 3sin cos 2cos αααα+-.
例4已知sin()410πα-
=,7cos 225α=,求sin α及tan()3πα+的值.
例5已知α为第二象限内的角,3sin 5α=
,β为第一象限内的角,5cos 13
β=,求tan (2α-β)的值.
【课堂练习】
1.若sin cos 2sin cos x x x x
+=-,则sin cos x x =( ).
A . 34
B . 310±
C . 310 D. 310
-
2.若sin cos cos θθ=,则θ所在象限是( ).
A .第一象限
B .第二象限
C .第三象限 D.第四象限
3.已知tan α与cot α是方程2
220x x m -+=的两根,则sin α的值为( ).
A B . ±C -4.化简:22sin 2cos 1cos 2cos 2αααα
⋅=+( ). A . tan α B . tan 2α C . 1 D.
12 5. sin 7cos15sin8cos7sin15sin8︒+︒︒=︒-︒︒
( ).
A . 2+
B
C . 26.在ABC ∆中,若cos()tan sin sin()
C B B A C B -=+-,则这个三角形的形状是( ). A .锐角三角形 B .直角三角形
C .钝角三角形 D.等腰三角形或直角三角形
7.cos43cos77sin 43cos167︒︒+︒︒的值为 .
8.已知αβ、均为锐角,且cos()sin()αβαβ+=-,则tan α= .
9.设sin cos θθ、是方程221)0x x m -++=的两根.
(1)求m 与22sin cos sin cos cos sin θθθθθθ
+--的值;(2)求sin cos θθ、及此时θ的值.
10.已知α为锐角,且1tan 2α=,求sin 2cos sin sin 2cos 2ααααα
-的值.
11.化简:
(1
α是第三象限角)(2
(3)222222sin sin sin sin cos cos αβαβαβ+-+
12.已知α是第三象限角,且)
sin()cot()23tan()2cos()sin()(αππαπααπαπα----+
---=f 。
(1)化简)(αf ; (2)若51)23cos(=-πα,求)(αf 的值;(3)若 1860-=α,求)(αf 的值。
【课后作业】
1.若cos 2xcos 3x =sin 2xsin 3x ,则x 的一个值是( )
° ° ° °
2.若ABC ∆的内角A 满足2sin 23
A =,则sin cos A A += ( )
A B .C .53
D .53- °tan 20°+3 (tan 10°+tan 20°)等于( )
A . 23 C . 3 D. 6
4.若02πβα<<<且45513
cos(),sin()αβαβ+=
-=,那么2cos α的值是( ) A .6365 B .6365- C .3365 D .5665或1365- 5.︒
︒-︒+︒+︒︒-︒-︒-8tan 7tan 8tan 7tan 18tan 7tan 8tan 7tan 1= . 6.设tan α=31,tan (β-α)=-2,则tan β= . 7.若tan (α+β)=m ,tan (α-β)=n ,且mn ≠-1,则tan 2β= .
8. °°+°°的值等于 .
9.若A =22°,B =23°则(1+tanA )(1+tanB )的值是 . °+tan 40°+3tan 20°tan 40°= .
11.求值:
︒︒+20sin 220cos 1-sin 10°(cot 5°-tan 5°)
12.已知:sin α+sin β=
21,cos α+cos β=31,求cos (α-β)的值.
13.已知cos (α-
2β)=-91,sin (2α-β)= 32,2π<α<π,0<β<2
π,求cos (α+β)之值.
14.求值:︒︒+20sin 220cos 1-sin 10°(cot 5°-tan 5°)
15. 化简︒-︒+︒+︒+40cos 40sin 140cos 40sin 1。
