材料科学基础作业
材料科学基础习题

查看文本习题一、名词解释金属键; 结构起伏; 固溶体; 枝晶偏析; 奥氏体; 加工硬化; 离异共晶; 成分过冷; 热加工; 反应扩散二、画图1在简单立方晶胞中绘出()、(210)晶面及[、[210]晶向。
2结合Fe-Fe3C相图,分别画出纯铁经930℃和800℃渗碳后,试棒的成分-距离曲线示意图。
3如下图所示,将一锲形铜片置于间距恒定的两轧辊间轧制。
试画出轧制后铜片经再结晶后晶粒大小沿片长方向变化的示意图。
4画出简单立方晶体中(100)面上柏氏矢量为[010]的刃型位错与(001)面上柏氏矢量为[010]的刃型位错交割前后的示意图。
5画图说明成分过冷的形成。
三、Fe-Fe3C相图分析1用组织组成物填写相图。
2指出在ECF和PSK水平线上发生何种反应并写出反应式。
3计算相图中二次渗碳体和三次渗碳体可能的最大含量。
四、简答题1已知某铁碳合金,其组成相为铁素体和渗碳体,铁素体占82%,试求该合金的含碳量和组织组成物的相对量。
2什么是单滑移、多滑移、交滑移?三者的滑移线各有什么特征,如何解释?。
3设原子为刚球,在原子直径不变的情况下,试计算g-Fe转变为a-Fe时的体积膨胀率;如果测得910℃时g-Fe和a-Fe的点阵常数分别为0.3633nm和0.2892nm,试计算g-Fe转变为a-Fe的真实膨胀率。
4间隙固溶体与间隙化合物有何异同?5可否说扩散定律实际上只有一个?为什么?五、论述题τC结合右图所示的τC(晶体强度)—ρ位错密度关系曲线,分析强化金属材料的方法及其机制。
晶须冷塑变六、拓展题1 画出一个刃型位错环及其与柏士矢量的关系。
2用金相方法如何鉴别滑移和孪生变形?3 固态相变为何易于在晶体缺陷处形核?4 画出面心立方晶体中(225)晶面上的原子排列图。
综合题一:材料的结构1 谈谈你对材料学科和材料科学的认识。
2 金属键与其它结合键有何不同,如何解释金属的某些特性?3 说明空间点阵、晶体结构、晶胞三者之间的关系。
《材料科学基础》作业

《材料科学基础》作业(七)
1.铜和镍固态完全互溶,它们的熔点分别是TCu=1083℃,TNi=1452℃,问:
Ni-10%Cu及Ni-50%Cu两种合金在浇铸和凝固条件相同的条件下,哪种合金形成
柱狀晶的倾向大?哪种合金的枝晶偏析严重?为什么?
2.画图并说明共晶成分的AL-Si合金在快冷条件下得到亚共晶组织 +( +Si)的
5)上坡扩散是指_______________。下坡扩散是指______________________________。
反应扩散是____________________________原子扩散是_____________________________
6)扩散通量为____________________________________
4.fcc结构晶体的滑移面(密排晶面)是—————,滑移方向(密排晶向)是—————;bcc
结构晶体的滑移面是——————,滑移方向为——————;hcp结构的滑移面是——————,
滑移方向为————————。
5.某晶体的致密度为74%,该晶体的晶体结构为————————————————————。
三.问答题
③若此单位位错是纯螺型位错在(11 )晶面上运动受阻后将交滑移到哪一个晶面上?
④若此单位位错在(11 )晶面内可以分解为扩展位错,写出位错分解的反应式并判断能否进行。
⑤若扩展位错在(11 )晶面内滑移受阻还能否运动?如何运动?
6.在面心立方结构的(11 )晶面上有b= [ 01]的单位位错以及b= [12 ]的肖克莱部分位错,两
第三章晶体结构习题课习题(二)
1.判断下列位错是否能够进行:
(1)a [100]+a [010]→ [111] + [11 ](2)a [100]→ [111] + [1 ]
材料科学基础习题

第1章固体结构1.何谓晶体?晶体与非晶体有何区别?2.已知MgO晶体中Mg2+和O2-在三维空间有规律地相间排列,其晶体结构相当于两套面心立方点阵互相套叠在一起,晶胞常数a=b=c=4.20 ,α=β=γ=90℃,请回答:①画出MgO晶体二维和三维空间的晶体结构图.②从①的图形中抽象出MgO晶体的空间点阵图形.③从②中划分出单位空间格子,计算其结点数.④画出晶胞结构图,指出晶胞中的分子数.3.何谓元素电负性,有何意义?在元素周期表中分布规律如何?4.何谓晶格能,用途?试计算MgO晶格能。
已知:MgO属NaCl型结构,立方面心点阵N0=6.023×1023,e=4.8×10-10静电单位,r =1.32 , r =0.78 ,A=1.74765.画出MgO晶体(立方面心点阵)在(1 0 0)、(1 1 0)、(1 1 1)晶面上的结点和离子排布图.6.立方晶系中①画出下列晶面:(0 0 1)、(1 0)、(1 1 1)②在①所画晶面上分别标出下列晶向:[2 1 0]、[1 1 1]、[1 0 ].7.在立方晶系中给出(1 1 1)面和(1 1 )面交棱的晶棱符号.8.找出正交晶系(斜方)(P点阵)宏观对称型.9.何谓布拉维点阵?举例论证为什么仅有14种?14种布拉维点阵分属的七个晶系名称?点阵常数特点?14种布拉维点阵分为几个类型?结点数计算?10.表示晶体的宏观对称性,其特点?如何表示晶体的微观对称性,其特点?11.划分单位平行六面体应遵循那些原则?何谓晶格常数?12.何谓晶胞、原胞、单位空间格子?13.试举例说明:晶体结构与空间点阵?晶胞与单位空间格子的关系?14.什么叫离子半径?有何实用意义?什么叫离子极化?极化对晶体结构有什么影响?15.解释原子,离子配位数. 根据半径比关系,说明下列离子与O2-配位时的配位数及配位多面体的类型.r =1.32 , r =0.39 ,r =0.57 ,r =0.78 ,r =1.10 .16.胞林规则有几条?其要点是什么?应用胞林规则有何局限性?17.试用胞林规则分析MgO晶体结构.(r =0.78 ,r =1.32 )18.运用胞林规则来解释在氧离子立方密堆体中,对于获得稳定结构各需要何种电价的离子,其中:①所有八面体间隙位置均填满.②所有四面体间隙位置均填满.③填满一半八面体间隙位置.④填满一半四面体间隙位置.19.已知:r =0.78 ,Mg的原子量为24.30,r =1.32计算:①MgO的点阵常数;②MgO的密度.20.画出闪锌矿、萤石晶胞结构在(0 0 1)面上的投影图.21.金红石的晶胞为什么不属于四方体心格子而是四方原始格子呢?而萤石的结构为什么不是立方原始格子而是立方面心格子?22.比较ThO2、TiO2、MgO结构中间隙的大小.23.简单说明下列名词的含义:反萤石结构,反尖晶石结构.24.指出下列化合物的结构类型,并改写成化学式:γ-Ca2[SiO4]、Ca2Al[AlSiO7]、CaMg[Si2O6]、Mg3[Si4O10](OH)2、K[AlSi3O8].25.高岭石、叶腊石和云母具有相似的结构,画出它们的结构草图,说明它们结构的区别及由此而引起的性质上的差异.26.下列物质的结构式,化学组成式写成相应的化学组成式和结构式:a) Al2O3·2SiO2·2H2O; ②2CaO·5MgO·8SiO2·H2O;③CaMg[Si206]; ④Na[AlSi3O8]27.说明高岭石、叶腊石和白云母结构区别及由此引起的性质上差异.28.在层状硅酸盐结构中,八面体层中的Al3+可以取代四面体层中的Si4+、而四面体层中的Si4+从来不会置换八面体层中的Al3+为什么?已知:r =1.40 , r =0.40 ,r =0.53 .29.青石2MgO·2Al2O3·5SiO2具有与绿柱石Be3Al2[Si6O8]类型结构,写出它的结构式,并指出它是由绿柱石进行怎样的离子置换而得来的?30.α—方石英属立方晶系,面心立方点阵,a=7.05 ,请a) 画出晶胞在(0 0 1)面上的投影图,注明各离子相对标高。
材料科学基础作业参考答案
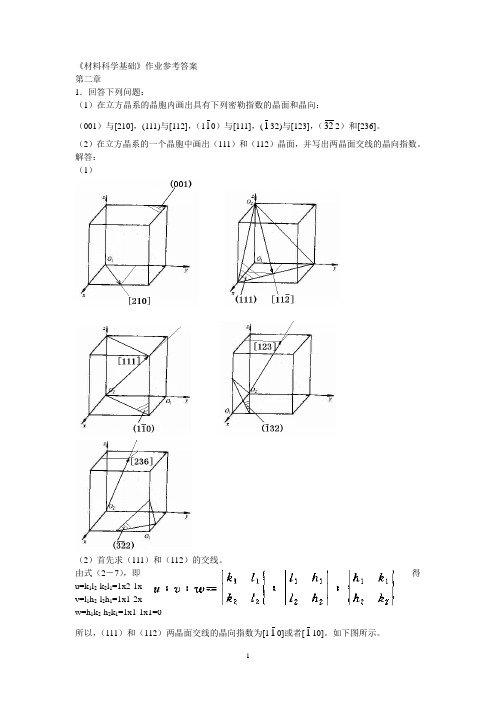
《材料科学基础》作业参考答案第二章1.回答下列问题:(1)在立方晶系的晶胞内画出具有下列密勒指数的晶面和晶向:(001)与[210],(111)与[112],(110)与[111],(132)与[123],(322)和[236]。
(2)在立方晶系的一个晶胞中画出(111)和(112)晶面,并写出两晶面交线的晶向指数。
解答:(1)(2)首先求(111)和(112)的交线。
由式(2-7),即得u=k1l2-k2l1=1x2-1x1=1v=l1h2-l2h1=1x1-2x1=-1w=h1k2-h2k1=1x1-1x1=0所以,(111)和(112)两晶面交线的晶向指数为[110]或者[110]。
如下图所示。
3 立方晶系的{111}、{110}、{123}晶面族各包括多少晶面?写出它们的密勒指数。
解答:++++++++=)213()231()321()132()312()321()231()123(}123{+++++++)312()132()213()123()132()312()231()132()123()213()321()231()213()123()312()321(++++++++注意:书中有重复的。
如(111)与(111)应为同一晶面,只是位于坐标原点的位置不同。
6.(略)7.(题略) (1)(2)用公式求。
(3) 用公式 求。
(1)d(100)=0.286nmd(110)=0.202nmd(123)=0.076nm显然,d(100)最大。
hkl d =(2) d(100)=0.365nmd(111)=0.211nmd(112)=0.149nm显然,d(100)最大。
(3) d(1120)=0.1605 nmd(1010)=0.278nmd(1012)=0.190nm显然,d(1010)最大。
由(1)、(2)、(3)得低指数的面间距较大,而高指数的晶面间距则较小8.回答下列问题:(1)通过计算判断(110)、(132)、(311)晶面是否属于同一晶带?(2)求(211)和(110)晶面的晶带轴,并列出五个属于该晶带的晶面的密勒指数。
《材料科学基础》作业-答案全

绪论一、填空题1、材料科学主要研究的核心问题是结构和性能的关系。
材料的结构是理解和控制性能的中心环节,结构的最微细水平是原子结构,第二个水平是原子排列方式,第三个水平是显微组织。
2. 根据材料的性能特点和用途,材料分为结构材料和功能材料两大类。
根据原子之间的键合特点,材料分为金属、陶瓷、高分子和复合材料四大类。
第一章材料的原子结构一、填空题1. 金属材料中原子结合以金属键为主,陶瓷材料(无机非金属材料)以共价键和离子键结合键为主,聚合物材料以共价键和氢键以及范德华键为主。
第二章材料的结构一、填空题1、晶体是基元(原子团)以周期性重复方式在三维空间作有规则的排列的固体。
2、晶体与非晶体的最根本区别是晶体原子排布长程有序,而非晶体是长程无序短程有序。
3、晶胞是晶体结构中的最小单位。
4、根据晶体的对称性,晶系有三大晶族,七大晶系,十四种布拉菲Bravais点阵,三十二种点群,230种空间群。
5、金属常见的晶格类型有体心立方、面心立方、密排六方。
6、fcc晶体的最密排方向为<110>,最密排面为{111},最密排面的堆垛顺序为ABCABCABCABC……。
7、fcc晶体的致密度为0.74,配位数为12,原子在(111)面上的原子配位数为6。
8、bcc晶体的最密排方向为<111>,最密排面为{110},致密度为0.68,配位数为8。
9、晶体的宏观对称要素有对称点、对称轴、对称面。
10、CsCl型结构属于简单立方格子,NaCl型结构属于面心立方格子,CaF2型结构属于面心立方格子。
11、MgO晶体具有NaCl型结构,其对称型是3 L44L36L29PC,晶族是高级晶族,晶系是立方晶系,晶体的键型是离子键。
12、硅酸盐晶体结构中的基本结构单元是硅氧四面体[SiO4]。
?13、几种硅酸盐晶体的络阴离子分别为[Si2O7]6-、[Si2O6]4-、[Si4O10]4-、[AlSi3O8]1-,它们的晶体结构类型分别为组群状,链状,层状,和架状。
(完整版)材料科学基础习题及答案

第一章材料的结构一、解释以下基本概念空间点阵、晶格、晶胞、配位数、致密度、共价键、离子键、金属键、组元、合金、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第二相强化.二、填空题1、材料的键合方式有四类,分别是(),( ),(),().2、金属原子的特点是最外层电子数(),且与原子核引力(),因此这些电子极容易脱离原子核的束缚而变成( )。
3、我们把原子在物质内部呈( )排列的固体物质称为晶体,晶体物质具有以下三个特点,分别是(),( ),( ).4、三种常见的金属晶格分别为(),( )和().5、体心立方晶格中,晶胞原子数为( ),原子半径与晶格常数的关系为( ),配位数是(),致密度是( ),密排晶向为(),密排晶面为( ),晶胞中八面体间隙个数为(),四面体间隙个数为( ),具有体心立方晶格的常见金属有()。
6、面心立方晶格中,晶胞原子数为( ),原子半径与晶格常数的关系为(),配位数是( ),致密度是(),密排晶向为( ),密排晶面为(),晶胞中八面体间隙个数为( ),四面体间隙个数为(),具有面心立方晶格的常见金属有()。
7、密排六方晶格中,晶胞原子数为(),原子半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为( ),密排晶面为(),具有密排六方晶格的常见金属有( )。
8、合金的相结构分为两大类,分别是()和( )。
9、固溶体按照溶质原子在晶格中所占的位置分为()和(),按照固溶度分为()和(),按照溶质原子与溶剂原子相对分布分为()和()。
10、影响固溶体结构形式和溶解度的因素主要有()、()、()、()。
11、金属化合物(中间相)分为以下四类,分别是( ),( ),( ),( )。
12、金属化合物(中间相)的性能特点是:熔点()、硬度( )、脆性(),因此在合金中不作为()相,而是少量存在起到第二相()作用。
13、CuZn、Cu5Zn8、Cu3Sn的电子浓度分别为(),( ),( ).14、如果用M表示金属,用X表示非金属,间隙相的分子式可以写成如下四种形式,分别是( ),(),( ),( ).15、Fe3C的铁、碳原子比为(),碳的重量百分数为(),它是( )的主要强化相。
材料科学基础章作业参考答案
作业参考答案第1章1. 结点数:7×2+3=17原子个数=1(底面中心)×0.5×2+6×1/6×2+3=1+2+3=6r=a/2配位数=1274.07401.02()660sin2221/[(6343≈=⨯⨯⨯︒⨯⨯⨯=rrrπ致密度2. α-Fe——BCC每个晶胞中有2个原子,质量=55.847×2/(6.02×1023)=18.554×10-23(g)体积=a3=(0.2866×10-7)=2.3541×10-23(cm3)872.7357.2554.18===体积质量ρ或直接用式(1.5)计算。
3.概念:晶面族、晶向族)101()011()110()101()011()110(}110{+++++={123}=(见教材P23)晶向族用上述同样的方法。
4. 晶面指数的倒数=截距如211)102(1)102(,,的截距∞==(102))211()312( [110] ]021[]213[5.晶向指数:]101[和]011[6.7.8. 9. (略,不要求) 10.设晶格常数为a22100a =)面密度( 785.048210022==⨯=ππr r )面致密度( 222110a=)面密度( 555.02428211022==⨯=ππrr )面致密度(2234321111a r ==)面密度( 906.03232111122==⨯=ππr r )面致密度( 11. (略,不要求)12. (略,不要求) 13. 6/2+12/4=614.立方晶系晶面间距计算公式: 222lk h na d ++=① )nm (143.0286.02100121222100=⨯=++=ad)011()110()112(]011[]212[]111[)nm (202.0286.021011222110=⨯=++=a d)nm (0764.0286.0141321222123=⨯=++=a d②)nm (1825.0365.02100121222100=⨯=++=ad)nm (2107.0365.031111222111=⨯=++=a d)nm (09125.0365.042121121222112=⨯=++=ad③(略,不要求)15. (略,不要求) 16. (略,不要求)一、 单项选择题。
材料科学基础作业
1.空位随温度升高而增加,在20℃和1020℃之间,由于热膨胀bcc铁的晶格常数增加0.51%,而密度减少2.0%,假设在20℃时,此金属中每1000个单位晶胞中有1个空位,试估计在1020℃时每1000个单位晶胞中有多少个空位?2.在500℃(773K)所做扩散实验指出,在1010个原子中有一个原子具有足够的激活能可以跳出其平衡位置而进入间隙位置,在600℃时,此比例会增加到109,问:(1)此跳跃所需要的激活能?(2)在700℃(973K)具有足够能量的原子所占的比例为多少?3.在金属中形成一个空位所需要的激活能为2.0eV(或0.32×10-18J)。
在800℃时,1×104个原子中有一个空位,问在何种温度下,1000个原子中含有1个空位?4.两个相同符合的的刃型位错,在同一滑移面相遇;它们会排斥还是会吸引?5.方形晶体中有两根刃型位错,如下图:(1)当周围晶体中:(a )空位多于平衡值;(b )空位少于平衡值;(c )间隙原子多于平衡值;(d )间隙原子少于平衡值时,位错易于向何种方向攀移?(2)加上怎样的外力,才能使这两根位错线通过纯攀移而相互靠拢?6. 简单立方晶体中(100)面上有一位错,b =[010],§// [001],问:(1)若在(001)面上有一个b =[010],§// [100]的位错与之相交割,结果如何?(2)若在(001)面上有一个b =[100],§// [001]的位移与之相交割,结果如何?(3)交割反应的结果对位错进一步运动有何影响?7. 判断下列位错反应能否进行:(1)]111[3]211[6]110[2a a a →+ (2)]110[2]101[2]100[a a a +→ (3)]111[6]111[2]112[3a a a →+ (4)]111[2]111[2]100[a a a +→。
材料科学基础习题及参考答案
材料科学基础参考答案材料科学基础第一次作业1.举例说明各种结合键的特点。
⑴金属键:电子共有化,无饱和性,无方向性,趋于形成低能量的密堆结构,金属受力变形时不会破坏金属键,良好的延展性,一般具有良好的导电和导热性。
⑵离子键:大多数盐类、碱类和金属氧化物主要以离子键的方式结合,以离子为结合单元,无方向性,无饱和性,正负离子静电引力强,熔点和硬度均较高。
常温时良好的绝缘性,高温熔融状态时,呈现离子导电性。
⑶共价键:有方向性和饱和性,原子共用电子对,配位数比较小,结合牢固,具有结构稳定、熔点高、质硬脆等特点,导电能力差。
⑷范德瓦耳斯力:无方向性,无饱和性,包括静电力、诱导力和色散力。
结合较弱。
⑸氢键:极性分子键,存在于HF,H2O,NF3有方向性和饱和性,键能介于化学键和范德瓦尔斯力之间。
2.在立方晶体系的晶胞图中画出以下晶面和晶向:(1 0 2)、(1 1 -2)、(-2 1 -3),[1 1 0],[1 1 -1],[1 -2 0]和[-3 2 1]。
3. 写出六方晶系的{1 1 -20},{1 0 -1 2}晶面族和<2 -1 -1 0>,<-1 0 1 1>晶向族中各等价晶面及等价晶向的具体指数。
的等价晶面:的等价晶面:的等价晶向:的等价晶向:4立方点阵的某一晶面(hkl)的面间距为M/,其中M为一正整数,为晶格常数。
该晶面的面法线与a,b,c轴的夹角分别为119.0、43.3和60.9度。
请据此确定晶面指数。
h:k:l=cosα:cosβ:cosγ5.Cu具有FCC结构,其密度为8.9g/cm3,相对原子质量为63.546,求铜的原子半径。
=> R=0.128nm。
6. 写出溶解在γ-Fe中碳原子所处的位置,若此类位置全部被碳原子占据,那么试问在这种情况下,γ-Fe能溶解多少重量百分数的碳?而实际上在γ-Fe中最大的溶解度是多少?两者在数值上有差异的原因是什么?固溶于γ-Fe中的碳原子均处于八面体间隙中,且γ-Fe中的八面体间隙有4个,与一个晶胞中Fe原子个数相等,所以:C wt%=12/(12+56)×100%=17.6%实际上C在γ-Fe中的最大溶解度为2.11%两者数值上有较大差异,是因为此固溶体中,碳原子尺寸比间隙尺寸大,会引起点阵晶格畸变,畸变能升高,限制了碳原子的进一步溶解。
材料科学基础1-8章例题、作业题及其解答
材料科学基础1-8章例题、作业题及其解答第2章例题(A )1. 在面心立方晶胞中画出[012]和[123]晶向。
2. 在面心立方晶胞中画出(012)和(123)晶面。
3. 右图中所画晶面的晶面指数是多少?4. 设晶面(152)和(034)属六方晶系的正交坐标表述,试给出其四轴坐标的表示。
反之,求(3121)及(2112)的正交坐标的表示。
5. (练习),上题中均改为相应晶向指数,求相互转换后结果。
答案:2. (2110) 4. (1562),(0334)5. [1322] [1214] (123)(212) [033] [302]第2章例题答案(A)4. (152))2615(6)51()(?-=+-=+-=v u t (034) )4303(3)30()(?-=+-=+-=v u t(1213) ? (123)(2112) ? (212)5. [152]]2231[22)51(31)(313)152(31)2(311)512(31)2(31==-=+-=+-==-?=-=-=-?=-=W w V U t U V v V U u [034]]4121[41)30(31)(312)032(31)2(311)302(31)2(31==-=+-=+-==-?=-=-=-?=-=W w V U t U V v V U u]3121[]033[33)1(20)1(1===--=-==---=-=w W t v V t u U[2112]]302[20)1(13)1(2===---=-==--=-=w W t v V t u U第2章例题(B )1. 已知Cu 的原子直径为2.56A ,求Cu 的晶格常数,并计算1mm 3Cu 的原子数。
2. 已知Al 相对原子质量Ar (Al )=26.97,原子半径γ=0.143nm ,求Al 晶体的密度。
3. bcc 铁的单位晶胞体积,在912℃时是0.02464nm 3;fcc 铁在相同温度时其单位晶胞体积是0.0486nm 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fundamentals of Materials Science 1. Determine the Miller indices for the planes shown in the following unit cell:A:(2 1 -1) B:(0 2 -1)2. Show that the atomic packing factor for HCP is 0.74.Solution:This problem calls for a demonstration that the APF for HCP is 0.74. Again, the APF is just the total sphere-unit cell volume ratio. For HCP, there are the equivalent of six spheres per unit cell, and thusNow, the unit cell volume is just the product of the base area times the cell height, c. This base area is just three times the area of the parallelepiped ACDE shown below.The area of ACDE is just the length of CD times the height BC. But CD is just a or 2R, and3. For both FCC and BCC crystal structures, the Burgers vector b may be expressed aswhere a is the unit cell edge length and [hkl] is the crystallographic direction having the greatest linear atomic density.(a) Compute and compare the linear densities of the [100], [110], and [111] directions for FCC and BCC.(b) What are the Burgers vector representations for FCC, BCC?(c) If the magnitude of the Burgers vector b isdetermine the values of b for aluminum, For Al which has an FCC crystal structure, R=0.1431nm.solutions:(a) In this problem we are to compute the linear densities of several crystallographic planes for the face-centered cubic crystal structure. For FCC the linear density of the [100] direction is computed as follows:The linear density, LD, is defined by the ratiowhere L l is the line length within the unit cell along the [100] direction, and Lc is line length passing through intersection circles. Now, L l is just the unit cell edge length, a which, for FCC is related to the atomic radius R according to a = 2R√2 [Equation (3.1)]. Also for this situation, Lc = 2R and therefore4. Show that the minimum cation-to-anion radius ratio for a coordination number of 6 is 0.414.solutions:In this problem we are asked to show that the minimum cation-to-anion radius ratio for a coordination number of six is 0.414. Below is shown one of the faces of the rock salt crystal structure in which anions and cations just touch along the edges, and also the face diagonals.5. The number-average molecular weight of a polypropylene is 1,000,000 g/mol. Compute the number-average degree of polymerization. Solution:We are asked to compute the number-average degree of polymerization for polypropylene, given that the number-average molecular weight is 1,000,000 g/mol.The mer molecular weight of polypropylene is justm = 3(A C) + 6(A H)= (3)(12.01 g/mol) + (6)(1.008 g/mol) = 42.08 g/molIf we let n n represent the number-average degree of polymerization, then from Equation (4.4a)6. A sheet of BCC iron 1mm thick was exposed to a carburizing gas atmosphere on one side and a decarburizing atmosphere on the other side at 725o C. After having reached steady state, the iron was quickly cooled to room temperature. The carbon concentrations at the two surfaces of the sheet were determined to be 0.012 and 0.0075 wt%. Compute the diffusion coefficient if the diffusion flux is 1.4 ×10-8 kg/m2-s. Hint: Use Equation 5.9 to convert the concentrations from weight percent to kilograms of carbon per cubic meter of iron.7. For a steel alloy it has been determined that a carburizing heat treatment of 10 h duration will raise the carbon concentration to 0.45 wt% at a point 2.5 mm from the surface. Estimate the time necessary to achieve the same concentration at a 5.0-mm position for an identical steel and at the same carburizing temperature.8. The diffusion coefficients for iron in nickel are given at two temperatures:(a) Determine the values of D0 and the activation energy Qd .(b) What is the magnitude of D at 1100 o C (1373 K)?9. A load of 44,500 N (10,000 lbf ) is applied to a cylindrical specimen of steel (displaying the stress–strain behavior shown in Figure 7.33) that has a cross-sectional diameter of 10 mm (0.40 in.).(a) Will the specimen experience elastic or plastic deformation? Why?(b) If the original specimen length is 500 mm (20 in.), how much will it increase in length when this load is applied?Solution:This problem asks us to determine the deformation characteristics of a steel specimen, the stress-strain behavior of which is shown in Figure7.33.(a)In order to ascertain whether the deformation is elastic or plastic, wemust first compute the stress, then locate it on the stress-strain curve, and, finally, note whether this point is on the elastic or plastic region.Thus,10. Consider a single crystal of silver oriented such that a tensile stress is applied along a [001] direction. If slip occurs on a (111) plane and in a[101] direction, and is initiated at an applied tensile stress of 1.1 MPa (160 psi), compute the critical resolved shear stress.Solution: λφστcos cos =11. For alloys of two hypothetical metals A and B, there exist an α, A-rich phase and a β, B-rich phase. From the mass fractions of both phases for two different alloys, which are at the same temperature,determine the composition of the phase boundary (or solubility limit) for both α and βphases at this temperature.12. What is the carbon concentration of an iron–carbon alloy for which the fraction of total ferrite is 0.94?Solution:This problem asks that we compute the carbon concentration of an iron-carbon alloy for which the fraction of total ferrite is 0.94. Application of the lever rule [of the form of Equation (10.12)] yields13. Is it possible to have an iron–carbon alloy for which the mass fractions of total ferrite and proeutectoid cementite are 0.846 and 0.049, respectively? Why or why not?Solution:This problem asks if it is possible to have an iron-carbon alloy for which Wα= 0.846 and W Fe3C = 0.049. In order to make this determination, it isnecessary to set up lever rule expressions for these two mass fractions in terms of the alloy composition, then to solve for the alloy composition of each; if both alloy composition values are equal, then such an alloy is possible. The expression for the mass fraction of total ferrite is14. The fatigue data for a brass alloy are given as follows:(a) Make an S–N plot (stress amplitude versus logarithm cycles to failure) using these data.(b) Determine the fatigue strength at 5×105 cycles.(c) Determine the fatigue life for 200 MPa.Solution:This problem first provides a tabulation of fatigue data (i.e., stress amplitude and cycles to failure) for a brass alloy.(a)These fatigue data are plotted below.(b) As indicated by one set of dashed lines on the plot, the fatigue strength at 5×105 cycles [log (5×105) = 5.7] is about 250 MPa.(c) As noted by the other set of dashed lines, the fatigue life for 200 MPa is about 2×106 cycles (i.e., the log of the lifetime is about 6.3).15. Is it possible to produce a continuous and oriented aramid fiber(芳香尼龙纤维)-epoxy matrix composite having longitudinal and transverse moduli of elasticity of 57.1 GPa and 4.12 GPa, respectively? Why or why not? Assume that the modulus of elasticity of the epoxy is 2.4 GPa. Solution:This problem asks for us to determine if it is possible to produce a continuous and oriented aramid fiber-epoxy matrix composite having longitudinal and transverse moduli of elasticity of 57.1 GPa and 4.12 GPa,respectively, given that the modulus of elasticity for the epoxy is 2.4 GPa. Also, from Table 15.4 the value of E for aramid fibers is 131 GPa. The approach to solving this problem is to calculate two values of Vf using the data and Equations (15.10b) and (15.16); if they are the same then this composite is possible.16. Below, weight gain-time data for the oxidation of copper at an elevated temperature are tabulated.(a) Determine whether the oxidation kinetics obey a linear, parabolic, or logarithmic rate expression.(b) Now compute W after a total time of 450 min.Solution:For this problem we are given weight gain-time data for the oxidation ofCu at an elevated temperature.(a)We are first asked to determine whether the oxidation kinetics obey aparabolic, linear, or logarithmic rate expression, expressions which are described by Equations (16.34), (16.35), and (16.36), respectively.One way to make this determination is by trial and error. Let us assume that the parabolic relationship is valid; that is, from Equation(16.34)which means that we may establish three simultaneous equations using the three sets of given W and t values, then using two combinations of two pairs of equations, solve for K1 and K2; if K1 and K2 have the same values for both solutions, then the kinetics are parabolic. If the values are not identical then the other kinetic relationships need to be explored. Thus, the three equations are。
