-初中数学竞赛——几何变换——旋转
初中数学竞赛辅导几何变换(旋转)
第2讲几何变换——旋转典型例题【例1】C是线段AE上的点，以AC、CE为边在线段AE的同侧作等边三角形ABC、CDE，△是等设AD的中点是M，BE的中点是N，连结MN、MC、NC，求证：CMN边三角形．Array【例2】如图，两个正方形ABCD和AKLM有一个公共点A．求证：这两个正方形的中心以及线段BM，DK的中点是某正方形的顶点．L【例3】 已知：如图，ABC △、CDE △、EHK △都在等边三角形，且A 、D 、K 共线，AD DK ．求证：HBD △也是等边三角形．ECHDBA【例4】 ABC △是等边三角形，P 是AB 边的中点，Q 是AC 边的中点，R 为BC 边的中点，M 为RC 上任意一点，且PMS △是等边三角形，S 与Q 在PM 的同侧，求证：RM QS =．【例5】 ABCD 是正方形，P 是ABCD 内一点，1PA =，3PB =，PD =求正方形ABCD的面积．Q⋅SMPCBAR D【例6】 P 是等边三角形ABC 内的一点，6PA =，8PB =，10PC =．求ABC △的边长．【例7】 设O 是等边ABC △内一点，已知115AOB ︒∠=，125BOC ︒∠=，求以线段OA 、OB、OC 为边所构成的三角形的各内角大小．【例8】 如图，在ABC △中，90ACB ︒∠=，AC BC =，P 是ABC △内一点，3PA =，1PB =，2PC =，求BPC ∠．APC【例9】 如图，已知ABC △中，90A =o ，AB AC =，D 为BC 上一点，求证：2222BD DC AD +=．【例10】 如图，在等腰直角ABC △中，90ACB ︒∠=，CA CB =，P 、Q 在斜边AB 上，且45PCQ ︒∠=，求证：222PQ AP BQ =+．ADCBAQBCP【例11】 在正方形ABCD 中，已知E 、F 分别是边BC 、CD 上的点，满足EF BE DF =+，AE 、AF 分别与对角线BD 交于M 、N ．求证：（1）45EAF ︒∠=； （2）222MN BM DN =+．【例12】 如图，在梯形ABCD 中，AD BC ∥，AD CD ⊥，2BC CD AD ==，E 是CD 上一点，且45ABE ︒∠=，AD α=．求CE 的长．EDCBADF【例13】 已知：ABC △中，120A ︒∠≥，P 是不与A 重合的定点，求证：PA PB PC AB AC +++＞．【例14】 已知：如图，ABD △是等边三角形，ABC △中，BC a =，CA b =．问：当ACB ∠为何值时，C 、D 两点的距离最大？最大值是多少？P CBA【例15】 已知ABC △，以其各边为底边，向ABC △的外部作等腰三角形ABD 、BCE 、CAF ，使顶角都等于120 ，求证：DEF △是正三角形．EBDAFC【例16】 已知：ABC △是锐角三角形，三边长分别是a 、b 、c ，O 是ABC △内的一点，120AOB BOC COA ︒∠=∠=∠=，OA u =，OB v =，OC w =，DEF △是等边三角形，P 是DEF △内一点，PD a =，PE b =，PF c =． 求证：DEF △的边长等于u v w ++．【例17】 已知：三条平行直线l 、m 、n ，求证：存在一个等边三角形ABC ，使顶点A 、B 、C 分别在l 、m 、n 上．作业1. 已知：ABCD 是正方形，O 是其中心，OEFG 也是正方形，两个正方形的边长都是a ，OG 、OE 分别交CD 、BC 于H 、K ．求证：214OKCH S a =．2. 已知：如图，ABCD 是正方形，12∠=∠．求证：BE DF AE +=．3.ABC △是等边三角形，P 是其内的一点，3PA =，4PB =，5PC =，求ABC △的面积．1FDEAC2B4.P 是等边ABC △内部一点，APB ∠、BPC ∠、CPA ∠的大小之比是5:6:7，求以PA 、PB 、PC 为边的三角形的三个角的大小之比．5. 等边ABC △的边长a =，点P 是ABC △内一点，且222PA PB PC +=，若5PC =，求PA 、PB 的长．6. 在梯形ABCD 中，AD BC ∥（BC AD ＞），90D ︒∠=，12BC CD ==，E 在CD 上，45ABE ︒∠=，若10AE =，求CE 的长．7. 如图，P 、Q 是边长为1的正方形ABCD 内两点，使得45PAQ PCQ ︒∠=∠=．求PAB PCQ QAD S S S ∆∆∆++的值．E DCBA。
九年级数学竞赛专题 旋转变换_答案
专题13 旋转变换例1 如图，连接OB 1，OB 2，B 1B 2，则OB 1＝OB 2，∠OB 1B 2＝∠OB 2B 1.又∠OB 1C ＝30°＝∠OB 2C ，∴∠CB 1B 2＝∠CB 2B 1，故CB 1＝CB 2.同理，B 2D ＝DC 1.设CB 1＝x ，则CB 2＝x ，CD＝x ，DC 1＝DB 2＝2x ，于是x ＋x ＋2x ＝1x ⇒=，故ABCDEF S 六边形＝22223A B C B CD SS －213324x x -⨯==.例2 ∵N ，M 分别为线段AB ，CB 的中点，∴MN ＝12AC .同理MQ ＝12BD ，PQ ＝12AC ，PN ＝12BD .∵AC ＝BD ，∴MN ＝MQ ＝PQ ＝PN ，∴四边形NMQP 为菱形.∵MN ∥AC ，MQ ∥BD ，∴AC ⊥BD ，∴∠NMQ ＝90°，∴菱形NMQP 为正方形.例3 APM AP C '≌，AP AP '＝，APB AP C '∠∠＝，P C PB '＝.连接PP '，由AP AP'＝得APP AP P ''∠∠＝，而APB APC ∠∠＜，即AP C APC '∠∠＜，∴PP C P PC ''∠∠＜，于是P C PC '＞，即PB PC ＞.例4 （1）60° 45° （2）90°－12α （3）∠AFB ＝90°－12α ∠AFB ＝90°＋12α对∠AFB ＝90°－12α证明如下：∵AB ＝AC ，EC ＝ED ，∠BAC ＝∠CED ，∴△ABC ∽△EDC ，得∠ACB ＝∠ECD ，BC ACDC EC=，∠BCD ＝∠ACE ，∴△BCD ∽△ACE ，得∠CBD ＝∠CAE .∵∠AQF ＝∠BQC ，∠CBD ＝∠CAF ，∴∠AFB ＝∠ACB ＝18019022BAC α︒-∠=︒-.例 5 ∵2EBE ABC DEB '∠∠∠＝＝，∴EBD E BD '∠∠＝.连接DE '.∵BD BD ＝，EBD E BD '∠∠＝，BE BE '＝，∴EBD E BD '≌，得ED E D CD CE ''＝＝＝，∴CDE '为正三角形，DCE '∠＝60°，又BC ＝CD ＝CE ’，则12E BD DCE ''∠∠＝＝30°.∴260ABC EBE E BD ''∠∠∠︒＝＝＝.例6 将△ABE 绕B 点逆时针旋转60°，得△FBG ，连接GE ，FC ，则△BEG 为等边三角形，GE ＝BE ，∴FC ≤FG ＋GE ＋EC ，即FC ≤EA ＋EB ＋EC ，∵FC 为定长，∴当E 点落在FC 上时，FC ＝EA ＋EB ＋EC 为最小值.∵∠FBC ＝150°，FB ＝BC ，∴∠BCF ＝∠BFC ＝15°，而∠GEB ＝60°，∴∠EBC ＝45°，即E 在正方形ABCD 的对角线BD 上.作FH ⊥BC 交CB 延长线于H ，设BC ＝x ，则FB ＝x ，FH ＝2x ，HB＝2x ，在Rt △FHC中，由222)()()2x x x =+，得x ＝2或x ＝－2（舍去），即正方形的边长为2.A 级1.1或52.6 150°3.1 4 . 80或120提示:如图,过B'作MN//AD ，分别AB,CD 于M,N,点B ’C ’交CD 于K ，则B ’M=AB ’sin60°’,AM=12,Rt △AKB ≌Rt △AKD,∠KAB ’=∠KAD=15°,∠ADB ’=75°,△ADK ∽△DN B ’,'DK AD NB DN =重叠部分面积=2S △AKD= 121(222⨯⨯⨯=6. 过P 作PM 丄AC 于M,PN 丄DF 于N ，可证明四边形PMGN 为正方形,PM=125,S 重叠=S 正方形PMGN=212144()525=. 7.D 8.A 9.B 提示:将△CPA 绕点A 逆时针旋转60°到△C ’AP ’, 连结PP ’, △APP ’ 为等边三角形.PB+PP ’+P ’C=PA+PB+PC ＞AB+AC ’=AB+AC.10.(1)AE ’=BF ’.(2) 证法较多，如取OE ’中点G,连结AG. 11.(1)AM=AN,∠MAN=α.(2) 第(1)问的结论仍成立，理由如下:由△ABE ≌△ACF 得BE=CF,∠ABM=∠CAN,进一步可以证明△ABM ≌△CAN.例6题图B 级1.2 提示:MN=BM+CN2.B 提示: △ACM ≌△BCD.∠ACM=∠BCD,CM=CD,∠MCN=∠NCD=45°,又CN=CN,则△MNC ≌△DNC,MN=ND=x ,AM=BD=m ,又∠DBN=45°+45°=90°,故m 2+n 2=x 2. 3.D 4.3 提示:将△ADF'绕点A 顺时针方向旋转90°,到△ABG.的位置, 则△AEF ≌△AEG. ∠AEF=∠AEG=∠FEC=60°1,1),S △AEF =S △ABG =12EG ·AB=3. 5. (1)提示:延长BC 至E,使CE=CD 连结DE,证明△ACD ≌△BED.(2)将△ABD 绕点A 旋转60°到△ACB ’,连结B ’D,B ’P ,则四边形AB ’DP 符合(1)的条件,于是B ’P=PA+PD 连结AC,则△ABD ≌△ACB ’.BD=B ’C,B ’C ≤PB ’+PC=PA+PD+PC,从而BD ≤PA+PD+PC.6. 直接解题有困难, △ABC 绕点A 逆时针旋转120°,240°拼成正△MBC(如图),则正△ADE 变为正△AD 1E 1和正△AD 2E 2易知,六边形DE D 1E 1 D 2E 2是正六边形, △DD 1D 2是正三角形, 其面积是△ADE 面积的3倍. .因此,设法由正△MBC 面积为150求出△DD 1D 2的面积, 问题就解决了.注意到BD:DC=CD 1:D 1M=MD 2:D 2B=2:3, 连结DM, 则S △ADE =13S △ABD =36cm 2,而122MD D DCD SS==36cm 2. 同理,可得12DD D S=150-3×36=42cm 2,故S △ADE =1312DD D S =14cm 2.7.如图,将BP ,BO,BC 绕点B 沿顺时针方向旋转60°，变为BP'，BO ’,BC ’ 连结OO ’,PP ’,则 △BOO ’, △BPP ’ 都是正三角形.因此OO ’=OB,PP ’=PB, 显然△BO ’C ’ ≌△BOC, △BP ’C ≌△BPC, 由于∠BO ’C=∠BOC=120°=180°-∠BO ’O,∴A,O,O ’,C ’ 四点共线.故AP+PP ’+P ’C ≥AC ’=AO+OO ’+O ’C, 即PA+PB+PC ≥OA+OB+OC.8.(1)提示:延长DM 交EF 于N,由△ADM ≌△ENM,得DM=MN,MF=12DN,FD=FN,故MD 丄MF.(2)延长DM 交CE 于N,连结DF,FN 先证明△ADM ≌△ENM,再证明△CDF ≌△ENF.第(1)问中的结论仍成立. (3)第(1)问中的结论仍成立,延长DM 至N,使MN=DM,连结DF,FN,证法同上.(9)提示:EG=CG,EG 丄CG,B, E,D 在一条直线上,(2)仍然成立，延长EG 交CD 于H 点△FEG ≌△DHG, △ECH,△ECG 为等腰直角三角形.(3) 仍然成立.10.(1)612(,)55D (2)α＝2β (3)如图1, △OAE ≌△DAE, △ABO ≌△ABD,B,D,C,三点共线.设D(a ,b ),则222222(3)3,(4)4,a b a b ⎧-+=⎨+-=⎩解得9672,2525a b ==,∴9672(,)2525D ,可得直线CD 的解析式为7424y x =-+.如图2,同理可得, 7424y x =+.11. 提示:易证∠ACB=90°,如图，将△APC 绕点A 顺时针旋转60°,得到△AQO,点D 为AB 的中点，连结PQ, 得到△APQ 为等边三角形.过点Q 作QE 丄AP ,垂足为E,则∠AQE=30°, QE=32,AE=PE 连结DE,则DE=12BP=52，于是DE 2=(52)2=QE 2+QD 2,从而∠DQE=90°, ∠AQD=∠AQE+∠EQD=120°=∠APC.过点C 作CF 丄AP 交AP 的延长线于点F ，得到∠CPF=60°,∵PC=2,∴于是AC 2=AF 2+CF 2=221)7+=+∴S △ABC =2S △ACD。
八年级数学竞赛例题专题讲解：几何变换
八年级数学竞赛例题专题讲解:几何变换阅读与思考几何变换是指把一个几何图形1F 变换成另一个几何图形2F 的方法，若仅改变图形的位置，而不改变图形的形状和大小，这种变换称为合同变换，平移、对称、旋转是常见的合同变换.l图3图2图1F 1F 21.平移变换如图1，如果把图形1F 上的各点都按一定方向移动一定距离得到图形2F 后，则由1F 到2F 的变换叫平移变换.平移变换前后的对应线段相等且平行，对应角的两边分别平行且方向一致. 2.对称变换如图2，将平面图形1F 变换到与它成轴对称的图形2F ，这样的几何变换就叫做关于直线l （对称轴）的对称变换.对称变换前后的对应线段相等，对应角相等，其对称轴是连结各对应点线段的垂直平分线. 3.旋转变换如图3，将平面图形1F 绕这一平面内一定点M 旋转一个定角α，得到图形2F ，这样的变换叫旋转变换，M 叫旋转中心，α叫旋转角.旋转变换前后的图形是全等的，对应点到旋转中心的距离相等，对应线段的夹角等于旋转角.例题与求解【例l 】如图，∠AOB =045，角内有点P ，PO =10，在角的两边上有两点Q ，R （均不同于O ），则△PQR 的周长的最小值为_______________. （黄冈市竞赛试题）解题思路:作P点关于OA，OB的对称点，确定Q，R的位置，化折线为直线，求△PQR的最小值.O【例2】如图，P是等边△ABC的内部一点，∠APB，∠BPC，∠CP A的大小之比是5:6:7，则以P A，PB，PC为边的三角形的三个角的大小之比（从小到大）是（）A. 2:3:4B. 3:4:5C. 4:5:6D.不能确定（全国通讯赛试题）B C解题思路:解本例的关键是如何构造以P A，PB，PC为边的三角形，若把△P AB，△PBC，△PCA60，就可以把P A，PB，PC有效地集中在一起.中的任一个，绕一个顶点旋转0【例3】如图，在△ABC中，AD⊥BC于D，∠B=2∠C，求证:AB+BD=CD.（天津市竞赛试题）解题思路:用截长法或补短法证明，实质都利用AD翻折造全等.C【例4】如图，六边形ABCDEF 中，AB ∥DE ，BC ∥FE ，CD ∥AF ，对边之差BC -FE=ED -AB=AF -CD ＞0，求证:该六边形的各角都相等.（全俄数学奥林匹克竞赛试题）解题思路:设法能将复杂的条件BC -FE=ED -AB=AF -CD ＞0，用一个基本图形表示，题设条件有平行条件，考虑实施平移变换.【例5】已知Rt △ABC 中，AC=BC ，∠ACB =090，∠MCN =045 （1） 如图1，当M 、N 在AB 上时，求证:222MN AM BN =+（2） 如图2，将∠MCN 绕C 点旋转，当M 在BA 的延长线时，上述结论是否成立？若成立，请证明；若不成立，请说明理由.（天津市中考试题）解题思路:222MN AM BN =+符合勾股定理的形式，需转化为直角三角形可将△ACM 沿直线图2图1MABBCM 对折，得△DCM . 连DN ，只需证DN=BN ，∠MDN =090；或将△ACM (或△BCM )旋转.【例6】如图，∠DAC=012，∠DBC=024，∠CAB=036，∠ABD=048，求∠DCA 的度数.（日本算术奥林匹克试题）解题思路:已知角的度数都是12的倍数，000362460+=，这使我们想到构作正三角形.A能力训练1.在如图所示的单位正方形网格中，将△ABC 向右平移3个单位后得到△A B C '''，则BA A '∠的度数是_______.（泰安市中考试题）B(第1题) （第2题）（第3题）2.如图，P是等边△ABC内一点，P A=6，PB=8，PC=10，则∠APB=_________.3.如图，直线143y x=与双曲线2(0)ky kx=>交于点A，将直线143y x=向右平移92个单位后，与双曲线2kyx=交于点B，与x轴交于点C. 若2AOBC=，则k=______________. （武汉市中考试题）4.如图，△ABC中，∠BAC=045，AD⊥BC，DB=3，DC=2，则△ABC的面积是___________.5.如图，P为正方形内一点，若::1:2:3PA PB PC=，则∠APB的度数是（）.A. 0120 B. 0135 C. 0145 D. 0150（第6题）（第5题）（第4题）AC BABD ABDA'6.如图，边长为2的正方形ABCD的对角线交于点O，把边BA、CD分别绕点B、C同时逆时针旋转060，得四边形A BCD'',下列结论:①四边形A BCD''为菱形；②12ABCDA BCDS S''=正方形四边形；③线段OD'1. 其中正确的结论有（）.A. 0个B. 1个C. 2个D. 3个7. 如图，A，B两个电话机离电话线l的距离分别是3米，5米，CD=6米，若由L上一点分别向A ，B 连电话线，最短为（ ）.A. 11米B. 10米C. 9米D. 8米8. 如图，在△ABC 中，∠BAC =0120，P 是△ABC 内一点，若记x PA PB PC =++，y AB AC =+，则（ ）.A. x y <B. x y =C. x y >D. x 与y 的大小关系不确定l第8题图第7题图CB9. 如图，已知D 是△ABC 中BC 边的中点，过D 作DE ⊥DF ，分别交AB 于E ，交AC 于F ，求证:BE CF EF +>.（天津市竞赛试题）B10.如图，△ABC ，△A B C '''其各边交成六边形DEFGHK ，且EF ∥KH ，GH ∥DE ，FG ∥KD ，0KH EF FG KD DE GH -=-=->. 求证:△ABC ，△A B C '''均为为正三角形.（“缙云杯”邀请赛试题）AB C A'11.如图，已知△ABC 中，AB=AC ，P ，Q 分别为AC ，AB 上的点，且AP=PQ=QB=BC ，求∠PCQ .（北京市竞赛试题）B12.如图，已知在平面直角坐标系中，A ，B 两点的坐标分别为(2,3)A -，(4,1)B -. (1) 若(,0)P x 是x 轴上的一个动点，当△P AB 的周长最短时，求x 的值；（2）若(,0),(3,0)C a D a +是x 轴上的两个动点，当四边形ABCD 的周长最短时，求a 的值； （3）设M ，N 分别为x 轴，y 轴上的动点，问:是否存在这样的点(,0)M m 和(0,)N n ，使四边形ABMN 的周长最短？若存在，求出,m n 的值；若不存在，请说明理由.（浙江省湖州市中考试题）13.如图，梯形ABCD 中，AD ∥BC ，分别以两腰AB ，CD 为边向两边作正方形ABGE 和正方形DCHF ，设线段AD 的垂直平分线l 交线段EF 于点M ，EP ⊥l 于P ，FQ ⊥l 于Q ，求证:EP=FQ.（全国初中数学联赛试题）14.如图所示，已知Rt △ABC 中，AB=BC ，在Rt △ADE 中，AD=DE ，连结EC ，取EC 中点M ，连结DM 和BM .（1）若点D 在边AC 上，点E 在边AB 上且与点B 不重合，如图1，求证:BM=DM ，且BM ⊥DM ；（2）如图2中的△ADE 绕点A 逆时针旋转小于045的角，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明.（广州市中考试题）图2图1ACBBCA45，AD⊥BC于D，若BD=3，CD=2，求△ABC的面积. 15.如图，在△ABC中，∠BAC=0（山东省竞赛试题）B。
最新初中数学竞赛辅导----几何变换(旋转)
第2讲几何变换——旋转典型例题【例1】C是线段AE上的点，以AC、CE为边在线段AE的同侧作等边三角形ABC、CDE，△是等设AD的中点是M，BE的中点是N，连结MN、MC、NC，求证：CMN边三角形．Array【例2】如图，两个正方形ABCD和AKLM有一个公共点A．求证：这两个正方形的中心以及线段BM，DK的中点是某正方形的顶点．L【例3】 已知：如图，ABC △、CDE △、EHK △都在等边三角形，且A 、D 、K 共线，AD DK =．求证：HBD △也是等边三角形．【例4】 ABC △是等边三角形，P 是AB 边的中点，Q 是AC 边的中点，R 为BC 边的中点，M 为RC 上任意一点，且PMS △是等边三角形，S 与Q 在PM 的同侧，求证：RM QS =．ECHDBAQ⋅S MPCBAR【例5】 ABCD 是正方形，P 是ABCD 内一点，1PA =，3PB =，PD =求正方形ABCD的面积．【例6】 P 是等边三角形ABC 内的一点，6PA =，8PB =，10PC =．求ABC △的边长．D【例7】 设O 是等边ABC △内一点，已知115AOB ︒∠=，125BOC ︒∠=，求以线段OA 、OB 、OC 为边所构成的三角形的各内角大小．【例8】 如图，在ABC △中，90ACB ︒∠=，AC BC =，P 是ABC △内一点，3PA =，1PB =，2PC =，求BPC ∠．【例9】 如图，已知ABC △中，90A =，AB AC =，D 为BC 上一点，求证：APCB2222BD DC AD +=．【例10】 如图，在等腰直角ABC △中，90ACB ︒∠=，CA CB =，P 、Q 在斜边AB 上，且45PCQ ︒∠=，求证：222PQ AP BQ =+．【例11】 在正方形ABCD 中，已知E 、F 分别是边BC 、CD 上的点，满足EF BE DF =+，ADCBAQBCPAE 、AF 分别与对角线BD 交于M 、N ．求证：（1）45EAF ︒∠=； （2）222MN BM DN =+．【例12】 如图，在梯形ABCD 中，AD BC ∥，AD CD ⊥，2BC CD AD ==，E 是CD 上一点，且45ABE ︒∠=，AD α=．求CE 的长．E DCBA DF【例13】 已知：ABC △中，120A ︒∠≥，P 是不与A 重合的定点，求证：PA PB PC AB AC +++＞．【例14】 已知：如图，ABD △是等边三角形，ABC △中，BC a =，CA b =．问：当ACB ∠为何值时，C 、D 两点的距离最大？最大值是多少？P CBA【例15】 已知ABC △，以其各边为底边，向ABC △的外部作等腰三角形ABD 、BCE 、CAF ，使顶角都等于120︒，求证：DEF △是正三角形．【例16】 已知：ABC △是锐角三角形，三边长分别是a 、b 、c ，O 是ABC △内的一点，120AOB BOC COA ︒∠=∠=∠=，OA u =，OB v =，OC w =，DEF △是等边三角形，P 是DEF △内一点，PD a =，PE b =，PF c =． 求证：DEF △的边长等于u v w ++． EBDAFC【例17】 已知：三条平行直线l 、m 、n ，求证：存在一个等边三角形ABC ，使顶点A 、B 、C 分别在l 、m 、n 上．作业1. 已知：ABCD 是正方形，O 是其中心，OEFG 也是正方形，两个正方形的边长都是a ，OG 、OE 分别交CD 、BC 于H 、K ．求证：214OKCH S a =．2. 已知：如图，ABCD 是正方形，12∠=∠．求证：BE DF AE +=．3. ABC △是等边三角形，P 是其内的一点，3PA =，4PB =，5PC =，求ABC △的面积．1FDEAC2B4.P 是等边ABC △内部一点，APB ∠、BPC ∠、CPA ∠的大小之比是5:6:7，求以PA 、PB 、PC 为边的三角形的三个角的大小之比．5. 等边ABC △的边长a =，点P 是ABC △内一点，且222PA PB PC +=，若5PC =，求PA 、PB 的长．6. 在梯形ABCD 中，AD BC ∥（BC AD ＞），90D ︒∠=，12BC CD ==，E 在CD 上，45ABE ︒∠=，若10AE =，求CE 的长．7. 如图，P 、Q 是边长为1的正方形ABCD 内两点，使得45PAQ PCQ ︒∠=∠=．求P A B P C Q Q A DS S S ∆∆∆++的值．CED。
初中竞赛数学旋转在初中数学竞赛中的应用
旋转在初中数学竞赛中的应用旋转是几何图形运动变化的基本形式之一。
所谓旋转，就是把一个图形绕着一个定点按一定方向旋转某个角度而得到另一个图形，这种变换叫做旋转变化，简称旋转。
旋转变化的基本性质性质1 经过旋转变化后，对应直线的交角等于旋转角。
性质2 经过旋转变化后，所得图形与原图形是全等形。
在初中数学各级各类竞赛中，我们常碰到的是旋转角等于60°、90°或180°。
一、60°的旋转例1 如图1，在凸四边形中，∠ABC=30°，∠ADC=60°，AD=DC 。
求证：BD 2=AB 2+BC 2 。
（2002年江苏省数学奥林匹克培训题）【分析】要证的结论中三条线段应该是一个直角三角形的三边长，因此，如何把BD ，AB ，BC 放在同一个直角三角形中内，是解答本题的关键，连结AC 之后，实际上ΔADC 是一个等边三角形，将ΔDCB 绕着点C 顺时针旋转60°，得到ΔACP ，由旋转性质2，得到ΔDCB ≌ΔACP ，∴ BC=CP ，DB=AP ，由旋转性质1，得出∠BCP=60°，即ΔBCP 是等边三角形， ∴BC=BP ，∠CBP=60°， ∵∠ABC=30°， ∴∠ABP=90°，由勾股定理得AP 2=AB 2+BP 2， 即BD 2=AB 2+BC 2。
【评注】 条件和结论的联系不明显，但是从结论上已经给我们暗示一条思路，而题中有一个等边三角形，我们习惯于绕着等边三角形某一个角的顶点旋转60°，使分散的条件其中起来，从而使辅助线的添加显得自然流畅，同时也使解题过程变得简捷而有趣。
【演变1】 如图2，已知ΔABC 是等边三角形，E 是AC 延长线上任意一点，选择一点D ，使得ΔCDE 是等边三角形，如果M 是线段AD 的中点，N 是线段BE 的中点。
求证：ΔCMN 是等边三角形。
初中数学重点梳理：旋转
旋转知识定位旋转在初中几何或者竞赛中占据非常大的地位，是解决平面几何中最重要的工具之一，它的有关知识是今后我们学习综合题目重要基础。
本节需要掌握旋转图形变换的特征；学会运用旋转的特征进行图形的求解换。
本节我们通过一些实例的求解，旨在介绍数学竞赛中旋转相关问题的常见题型及其求解方法本讲将通过例题来说明这些方法的运用。
知识梳理1、旋转的定义在平面内，把一个图形绕着某一个点O旋转一个角度的图形变换叫做旋转。
点O叫做旋转中心，转动的角叫做旋转角，如果图形上的点P经过旋转变为点P′，那么这两个点叫做对应点。
注意：①旋转是围绕一点旋转一定的角度的图形变换，因而旋转一定有旋转中心和旋转角，且旋转前后图形能够重合，这时判断旋转的关键．②旋转中心是点而不是线，旋转必须指出旋转方向．③旋转的范围是平面内的旋转，否则有可能旋转成立体图形，因而要注意此点。
2、旋转的基本特点（1）旋转的性质：①对应点到旋转中心的距离相等．②对应点与旋转中心所连线段的夹角等于旋转角．③旋转前、后的图形全等．（2）旋转三要素：①旋转中心；②旋转方向；③旋转角度．注意：三要素中只要任意改变一个，图形就会不一样．3、旋转对称图形如果某一个图形围绕某一点旋转一定的角度（小于360°）后能与原图形重合，那么这个图形就叫做旋转对称图形。
常见的旋转对称图形有：线段，正多边形，平行四边形，圆等．4、中心对称（1）中心对称的定义：把一个图形绕着某个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点。
（2）中心对称的性质：①关于中心对称的两个图形能够完全重合；②关于中心对称的两个图形，对应点的连线都经过对称中心，并且被对称中心平分．（3）中心对称图形：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心。
初中九年级数学竞赛培优讲义全套专题13 旋转变换
专题13 旋转变换阅读与思考在平面内，将一个图形绕一个定点沿某个方向转动一定的角度，这样的图形变换称为旋转，这个定点叫旋转中心，转动的角度叫旋转角．旋转变换不改变图形的形状和大小．通过旋转，图形上的每一点都绕旋转中心沿相同的方向转动同样大小的角度．旋转变换前后的图形有下列性质： （1）对应点到旋转中心的距离相等；（2）对应点与旋转中心的连线所成的角等于旋转角；（3）对应线段相等，对应线段的夹角等于旋转角，对应线段的垂直平分线都经过旋转中心．例题与求解【例1】如图，边长为1的正△A 1B 1C 1的中心为O ，将正△A 1B 1C 1绕中心O 旋转到△A 2B 2C 2，使得A 2B 2丄B 1C 1，则两个三角形的公共部分（即六边形ABCDEF ）的面积为＿＿．（“新知杯”上海市竞赛试题）解题思路：S 六边形ABCDEF ＝22223A B C B CD S S ∆∆-，解题的关键是寻找CB 1，CB 2，CD ，C 1D 之间的关系．【例2】如图，已知△AOB ，△COD 都是等腰直角三角形，∠AOB ＝∠CQD ＝90°，N ，M ，Q ，P 分别为AB ，CB ，CD ，AD 的中点． 求证：四边形NMQP 为正方形．解题思路：连结BD ，AC ，并延长AC 交于点E ，则△OAC 可以看作是由△OBD 绕点O 逆时针旋转90°得到的，且∠AED ＝90°，这是证明本例的关键．【例3】如图，巳知在△ABC 中，AB ＝AC ，P 为形内一点，且∠APB ＜∠APC ． 求证：PB ＞PC ． （北京市竞赛试题）解题思路：以A 为中心，将△APB 旋转一个∠BAC ，使AB 边与AC 边重合，这时△APB 到了△AP 'CQAB CDEM NOP1B 22的位置．【例4】点B ，C ，E 在同一直线上，点A ，D 在直线CE 的同侧，AB ＝AC ，EC ＝ED ，∠BAC ＝∠CED ，直线AE ，BD 交于点F ．（1）如图1，若∠BAC ＝60°，则∠AFB ＝＿＿＿＿；如图2，若∠BAC ＝90°，则∠AFB ＝＿＿＿＿； （2）如图3，若∠BAC ＝α，则∠AFB ＝＿＿＿＿（用含α的式子表示）；（3）将图3中的△ABC 绕点C 旋转（点F 不与点A ，B 重合），得图4或图5．在图4中，∠AFB 与∠α的数量关系是＿＿＿；在图5中，∠AFB 与∠α的数量关系是＿＿＿．请你任选其中一个结论证明． （武汉市中考试题）解题思路：从特殊到一般，在动态的旋转过程中，有两组不变的关系：△ABC ∽△EDC ，△BCD ∽△ACE ，这是解本例的关键．【例5】如图，已知凸五边形ABCDE 中，AB ＝BC ＝CD ＝DE ＝EA ，∠ABC ＝2∠DBE ．求证：∠ABC ＝60°． （北京市竞赛试题） 解题思路：将△ABE 以B 为旋转中心顺时针旋转∠ABC ，使得AB 与BC 重合，落在△CBE '位置，AB CDEF图1A BCDEF图2AB CDEF图3ABCDEF 图4ABCDEF图5Q AB C PP '则△ABE ≌△CBE ′，AE ＝CE ′，BE ＝BE ′，∠CBE ′＝∠ABE ．【例6】如图，已知正方形ABCD 内一动点E 到A ，B ，C方形的边长． （广东省竞赛试题）解题思路：本例是费马点相关的问题的变形，解题的关键是确定最小值时E 点的位置，通过旋转变换，把EA ，EB ，EC 连结起来．能力训练A 级1．如图，巳知正方形ABCD 中，点E 在边DC 上，DE ＝2，EC ＝1，把线段AE 绕点A 旋转，使点E 落在直线BC 上的点F 处，则F ，C 两点的距离为＿＿＿＿． （上海市中考试题）2．如图，P 是正△ABC 内的一点，且P A ＝6，PB ＝8，PC ＝10．若将△P AC 绕点A 逆时针旋转后，得到△P 'AB ，则点P 与点P '之间的距离为＿＿＿＿，∠APB ＝＿＿＿＿．（青岛市中考试题）3．如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD ＝2，BC ＝3，∠BCD ＝45°．将CD 以点D 为中心逆时针旋转90°至ED ，连结AE ，则△ADE 的面积是＿＿＿＿．4．如图，在Rt △ABC 中，已知∠C ＝90°，∠B ＝50°，点D 在边BC 上，BD ＝2CD ．把△ABC 绕着点D 逆时针旋转m （0＜m ＜180）度后，如果点B 恰好落在初始Rt △ABC 的边上，那么m ＝＿＿＿＿．（上海市中考试题）A BCD第1题ABCP P '第2题ABCDE第3题ABCDEE 'A B C DE5．如图，将边长为1的正方形ABCD 绕点A 按逆时针方向旋转60°至AB 'C 'D ′的位置，则这两个正方形重叠部分的面积是＿＿＿＿．（全国初中数学联赛试题）6．如图，在Rt △ABC 中，∠A ＝90°，AB ＝6cm ，AC ＝8cm ．以斜边BC 上距离点B 6cm 的点P 为中心，把这个三角形按逆时针方向旋转90°至△DEF ，则旋转前后两个三角形重叠部分的面积为＿＿＿．（黄冈市竞赛试题）7．如图，将△ABC 绕点C （0，-1）旋转180°得到△A 'B 'C ，设点A '的坐标为（a ，b ），则点A 的坐标为（ ）A ．（a -，b -）B ．（a -，1b --）C ．（a -，1b -+）D ．（a -，2b --）（河南省中考试题）8．如图，已知P 是等边△ABC 内部一点，∠APB ︰∠BPC ︰∠CP A ＝5︰6︰7．则以P A ，PB ，PC 为边的三角形的三个角的大小之比（从小到大）是（ ）A ．2︰3︰4B ．3︰4︰5C ．4︰5︰6D ．不能确定（全国初中数学通讯赛试题）9．如图，在△ABC 中，∠BAC ＝120°，P 是△ABC 内一点，则（ ） A ．P A ＋PB ＋PC ＜AB ＋AC B ．P A ＋PB ＋PC ＞AB ＋AC C ．P A ＋PB ＋PC ＝AB ＋ACD ．P A ＋R B ＋PC 与AB ＋AC 的大小关系不确定（武汉市竞赛试题）10．已知：如图1，O 为正方形ABCD 的中心，分别延长OA 到点F ，OD 到点E ，使OF ＝2OA ，OE ＝2OD ．连结EF ，将△FOE 绕点O 逆时针旋转α角得到△F ′OE ′（如图2）．BCD第4题A BCDB 'C 'D '第5题A BCDEF G H K P第6题第7题ABCP第8题ABCP第9题（1）探究A 'E 与BF ′的数量关系，并给予证明； （2）当α＝30°时，求证：△AOE '为直角三角形．（南通市中考试题）11．在△ABC 和△DEF 中，AB ＝AC ，DE ＝DF ，∠BAC ＝∠EDF ＝α，点M ，N 分别是BE ，CF 的中点．（1）若点A 与点D 重合，点E ，F 分别在AB ，AC 上（如图1），则AM 与AN 的数量关系是＿＿＿＿，∠MAN 与α的数量关系是＿＿＿＿；（2）将图1中的△DEF 绕点A （D ）旋转（如图2），第（1）问的两个结论是否仍成立？若成立，请证明；若不成立，请说明理由．B 级1．如图，△ABC 是边长为1的等边三角形，△BDC 是顶角∠BDC ＝120°的等腰三角形，∠MDN ＝ABCDE FO图1ABCDE 'F 'Oα图2A BC ()D EFMN 图1A BC()D EFMN图260°，则△AMN 的周长＝＿＿＿＿．（重庆市竞赛试题）2．如图，在等腰Rt △ABC 的斜边AB 上取两点M ，N ，使∠MCN ＝45°，记AM ＝m ，MN ＝x ，BN ＝n ，则以线段x ，m ，n 为边长的三角形的形状是（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．随x ，m ，n 的变化而变化（安徽省竞赛试题）3．如图，直线y ＝443x -+与x 轴，y 轴分别交于A ，B 两点，把△AOB 绕点A 顺时针旋转90°后得到△AO 'B '，则点B ′的坐标是（ ）A ．（3，4）B ．（4，5）C ．（7，4）D ．（7，3）（丽水市中考试题）4．如图，正方形ABCD 中，已知ABBC ，CD 上，且∠BAE ＝30°，∠DAF ＝15°，求△AEF 的面积．（“希望杯”邀请赛试题）5．（1）如图1，在四边形ABCD 中，AB ＝AD ，∠BAD ＝60°，∠BCD ＝120°． 求证：BC ＋DC ＝AC ；（2）如图2，在四边形ABCD 中，AB ＝BC ，∠ABC ＝60°，P 为四边形ABCD 内一点，且∠APD ＝120°，求证：P A ＋PD ＋PC ≥BD ．（江苏省竞赛试题）6．如图，在△ABC 中，AB ＝AC ，∠BAC ＝120°，△ADE 是正三角形，点D 在边BC 上，已知BD ︰DC ＝2︰3，当△ABC 的面积是50cm 2时，求△ADE 的面积．A BCDM N 第1题AB CMN 第2题第3题ABCD EF第4题ABCD图①A BCDP图②第5题（日本数学奥林匹克试题）7．如图，已知O 是锐角三角形ABC 内一点，∠AQB ＝∠BOC ＝∠COA ＝120°，P 是△ABC 内任一点．求证：P A ＋PB ＋PC ≥OA ＋OB ＋OC ．（杭州市竞赛试题）8．（1）如图1，已知正方形ABCD 和正方形CGEF （CG ＞BC ），B ，C ，G 在同一条直线上，M 为线段AE 的中点．探究：线段MD ，MF 的关系；（2）如图2，若将正方形CGEF 绕点C 顺时针旋转45°，使得正方形CGEF 的对角线CE 在正方形ABCD 的边BC 的延长线上，M 为AE 的中点．试问：（1）中探究的结论是否成立？若成立，请证明；若不成立，请说明理由．（3）如图3，若将正方形CGEF 绕点C 顺时针旋转 ，M 为AE 的中点．试问：第（1）问中探究的结论是否成立？（大连市竞赛试题）9．已知正方形ABCD 和等腰Rt △BEF ，BE ＝EF ，∠BEF ＝90°．按图1的位置，使点F 在BC 上，取DF 的中点G ，连结EG ，CG ．ABCDE第6题ABCOP第7题A BCDEF GM 图1A BCDEFGM 图2A BCDEFGM图3（1）探索EG ，CG 的数量关系和位置关系并证明；（2）将图中△BEF 绕点B 顺时针旋转45°，再连结DF ，取DF 中点G （如图2），第（1）问中的结论是否仍然成立？请你证明；（3）将图1中△BEF 绕点B 转动任意角度（在0°～90°之间），再连结DF ，取DF 的中点G （如图3），第（1）问中的结论是否仍成立？不必证明．10．在平面直角坐标系中，已知O 为坐标原点，点A （3，0），B （0，4）．以点A 为旋转中心，把△ABO 顺时针旋转，得△ACD ．记旋转角为α，∠ABO 为β．（1）如图1，当旋转后点D 恰好落在AB 边上时，求点D 的坐标； （2）如图2，当旋转后满足BC ∥x 轴时，求α与β之间的数量关系； （3）当旋转后满足∠AOD ＝β时，求直线CD 的解析式．（天津市中考试题）11．如图，在△ABC 中，∠BAC ＝60°，AB ＝2AD ，点P 在△ABC 内，且P APB ＝5，PC ＝2，求△ABC 的面积．（“《数学周报》杯”全国初中数学竞赛试题）ABCD E FG图3ABCDEFG图2图1ABCDE FG图1图2第10题ABCP第11题。
初中数学知识归纳空间几何体的几何变换
初中数学知识归纳空间几何体的几何变换初中数学知识归纳：空间几何体的几何变换在初中数学中，空间几何体是我们学习的一个重要内容。
它们在现实生活中随处可见，通过对空间几何体的几何变换的学习，我们可以更好地理解它们的性质和特点。
本文将对空间几何体的几何变换进行归纳总结，并分别介绍各个几何变换的定义和特点。
一、平移平移是指将一个物体沿着一定方向移动一定距离的操作。
在平面几何中，我们常常使用箭头表示平移的方向和距离。
而在空间几何中，我们需要指定一个平面作为平移面，并给出一个箭头表示平移的方向和距离。
通过平移，一个空间几何体在平移面上保持形状不变，只是位置发生了改变。
二、旋转旋转是指将一个物体绕某个点或某条轴线进行转动的操作。
我们可以通过指定旋转的中心和旋转的角度来描述一个旋转变换。
旋转可以使得一个空间几何体在旋转中心周围发生旋转，并保持其形状不变。
在旋转中，我们可以根据旋转的方向和角度来判断旋转是顺时针还是逆时针进行。
三、对称对称是指将一个物体关于某个点、线或面进行镜像的操作。
通过对称，一个空间几何体被映射到它的镜像位置，同时保持它的形状不变。
我们可以通过指定对称的中心和对称的轴线来描述一个对称变换。
在对称中，我们可以将对称视为特殊的旋转，旋转角度为180度。
四、放缩放缩是指将一个物体按照一定比例进行拉伸或压缩的操作。
放缩可以通过指定一个比例因子来描述，比例因子大于1时表示拉伸，比例因子小于1时表示压缩。
通过放缩，一个空间几何体的各个维度会按照相同的比例进行变化，保持其形状不变。
五、切变切变是指将一个物体沿某个方向进行倾斜的操作。
切变可以通过指定一个切变系数来描述，切变系数表示一个方向上的长度与另一个方向上的长度之间的比值。
通过切变，一个空间几何体在某个方向上会发生倾斜，但保持其形状不变。
在学习空间几何体的几何变换的过程中，我们需要掌握每种变换的定义和特点，了解它们的实际运用和意义。
同时，我们还需要通过大量的练习来提升对几何变换的理解和应用能力。
八年级数学竞赛专题训练29 几何变换(附答案)
例题与求解
【例l】如图，∠AOB= ，角内有点P，PO= ，在角的两边上有两点Q，R（均不同于O），则△PQR的周长的最小值为_______________.（黄冈市竞赛试题）
解题思路：作P点关于OA，OB的对称点，确定Q，R的位置，化折线为直线，求△PQR的最小值.
（北京市竞赛试题）
12.如图，已知在平面直角坐标系中，A，B两点的坐标分别为 ， .
(1)若 是 轴上的一个动点，当△PAB的周长最短时，求 的值；
（2）若 是 轴上的两个动点，当四边形ABCD的周长最短时，求 的值；
（3）设M，N分别为 轴， 轴上的动点，问：是否存在这样的点 和 ，使四边形ABMN的周长最短？若存在，求出 的值；若不存在，请说明理由.
【例3】如图，在△ABC中，AD⊥BC于D，∠B=2∠C，求证：AB+BD=CD.
（天津பைடு நூலகம்竞赛试题）
解题思路：用截长法或补短法证明，实质都利用AD翻折造全等.
【例4】如图，六边形ABCDEF中，AB∥DE，BC∥FE，CD∥AF，对边之差BC-FE=ED-AB=AF-CD＞ ，求证：该六边形的各角都相等.
（天津市中考试题）
解题思路： 符合勾股定理的形式，需转化为直角三角形可将△ACM沿直线CM对折，得△DCM.连DN，只需证DN=BN，∠MDN= ；或将△ACM(或△BCM)旋转.
【例6】如图，∠DAC= ，∠DBC= ，∠CAB= ，∠ABD= ，求∠DCA的度数.
（日本算术奥林匹克试题）
解题思路：已知角的度数都是 的倍数， ，这使我们想到构作正三角形.
（1）若点D在边AC上，点E在边AB上且与点B不重合，如图1，求证：BM=DM，且BM⊥DM；
初中数学竞赛中的图形旋转变换问题
图４
９ °得到 Ｒ ０ ｔ Ｅ Ｆ， △Ｄ ∴Ｅ Ｆ Ｆ⊥Ｂ Ｃ， Ｄ⊥Ｃ Ａ， 又 ∵Ａ 点 Ｐ 为Ｂ Ａ Ｂ＝３ ｃ ｍ， Ｃ＝４ ｃ ｍ， Ｃ 的中点 ，
２ ２ ＝５ Ｆ ∴Ｂ Ｃ＝Ｅ Ｆ＝ 槡 ３ ｃ ｍ， Ｐ＝Ｐ Ｃ＝２． ５ ｃ ｍ， ＋４
Ａ Ｂ ＡＨ ＝ＡＮ ， ＨＢ＝ＮＤ， Ｇ＝Ａ Ｆ， Ｇ＝Ｄ Ｆ，
Ｃ 的 延 长 线 上 的 Ｄ 点 处， Ａ 逆时针旋转 使 点 Ｂ 落 在 Ｂ
得到 △ＡＤ 则 ∠Ｂ Ｅ， Ｄ Ｅ 为 （ ） Ａ． ４ ０ ° Ｂ． ６ ０ ° ８ ０ ° ９ ０ ° Ｃ． Ｄ．
A
E B C D
ｘ ３ ５ （ ７ ８） ２ ： ， 则有 记 Ｓ△ＦＲＳ 为ｘ， Ｒ Ｓ Ｐ Ｓ ＝ Ｆ Ｃ ∽△ △ ２ １ ５ ３ ８
图 ８ 图 ９ 如 图 ９， 已 知 在 △Ａ ４． Ａ Ｂ Ｃ 中， Ｂ ＝Ａ Ｃ， Ａ Ｃ＝ ∠Ｂ 两边 Ｐ 直角 ∠Ｅ ９ ０ Ｐ Ｆ 的顶点 Ｐ 是 Ｂ Ｃ 的 中 点， Ｅ， Ｆ °， Ｐ 分别交 Ａ 给出以下四个结论 ： Ｂ， Ｃ 于点 Ｅ ， Ａ Ｆ，
°； Ｆ Ａ≌ △Ｐ Ｅ Ｂ； Ｆ Ｅ＝４ ５ Ｆ ＝Ａ Ｐ； ① △Ｐ ② ∠Ｐ ③Ｅ
由旋转的性质可得 ∠Ｂ Ｐ Ｃ＝ ∠Ａ Ｐ ′ Ｃ＝１ ５ ０ °． 【 使已知 方法小结 】本 题 主 要 是 通 过 旋 转 △Ｂ Ｐ Ｃ， 的三 边 正 好 组 成 △Ａ 由勾股定理的逆定理得 Ｐ Ｐ ′， 所 求 的 ∠Ｂ 且由两 °， Ｐ ′ Ｐ ＝９ ０ Ｐ Ｃ 与 ∠Ａ Ｐ ′ Ｃ 相 等， ∠Ａ 个特殊的角组成 ． 例 ２ 如图 ２， Ｐ 为正方形Ａ Ｂ Ｃ Ｄ 内 一 点， Ｐ Ａ ∠Ｂ 求Ｐ ＝１ °， Ａ Ｂ ３ ５ Ｐ＝３， Ｐ＝５， Ｃ 的长．
初中数学竞赛中考讲义之几何三大变换之旋转
第32讲几何三大变换之旋转旋转的性质【例题讲解】例题1．如图所示，将一副三角板的直角顶点重合摆放在桌面上，若145AOD ∠=︒，则BOC ∠=度．【解答】解：由图145AOD ∠=︒ ，1459055AOC AOD COD ∴∠=∠-∠=︒-︒=︒，则905535BOC ∠=︒-︒=度．故答案为：35．例题2．如图，ABC ∆中，90ACB ∠=︒，30A ∠=︒，将ABC ∆绕C 点按逆时针方向旋转α角(090)α︒<<︒得到DEC ∆，设CD 交AB 于F ，连接AD ，当旋转角α度数为，ADF ∆是等腰三角形．旋转中心：O旋转角：∠AOA'=∠BOB'=∠COC'性质：OA=OA'、OB=OB'、OC=OC'旋转中心：B旋转角：∠ABA'=∠CBC'性质：AB=A'B 、CB=C'B 连接AA'、CC'△ABA'∽△CBC'，且均为等腰三角形【解答】解：ABC ∆ 绕C 点按逆时针方向旋转α角(090)α︒<<︒得到DEC ∆，DCA α∴∠=，CD CA =，11(180)9022CDA CAD αα∴∠=∠=︒-=︒-，ADF ∆ 是等腰三角形，30DFA α∠=︒+，①CD CA =，则CDA CAD ∠=∠，当FD FA =，则FDA FAD ∠=∠，这不合题意舍去，②当AF AD =，ADF AFD ∴∠=∠，190302αα∴︒-=︒+，解得40α=︒；③当DF DA =，DFA DAF ∴∠=∠，13090302αα∴︒+=︒--︒，解得20α=︒．故答案为40︒或20︒．【旋转60°】得等边例题3.如图，在直角坐标系中，点A 在y 轴上，△AOE 是等边三角形，点P 为x 轴正半轴上任意一点，连接AP ，将线段AP 绕点A 逆时针60°得到线段AQ ，连接QE 并延长交x 轴于点F .（1）问∠QFP 角度是否发生变化，若不变，请说明理由；（2）若AO =，OP =x ，请表示出点Q 的坐标（用含x 的代数式表示）【解答】（1）不变（2）【旋转90°】构造全等例题4．如图，在平面直角坐标系中，点(,)A a b 为第一象限内一点，且a b <．连结OA ，并以点A 为旋转中心把OA 逆时针转90︒后得线段BA ．若点A 、B 恰好都在同一反比例函数的图象上，则b a的值等于多少？【解答】解：过A 作AE x ⊥轴，过B 作BD AE ⊥，90OAB ∠=︒ ，90OAE BAD ∴∠+∠=︒，90AOE OAE ∠+∠=︒ ，BAD AOE ∴∠=∠，在AOE ∆和BAD ∆中，90AOE BAD AEO BDA AO BA ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，()AOE BAD AAS ∴∆≅∆，AE BD b ∴==，OE AD a ==，DE AE AD b a ∴=-=-，OE BD a b +=+，则(,)B a b b a +-；A 与B 都在反比例图象上，得到()()ab a b b a =+-，整理得：22b a ab -=，即2(10b b a a--=， △145=+=，∴152b a ±=， 点(,)A a b 为第一象限内一点，0a ∴>，0b >，则152b a +=．故答案为152+．【旋转180°】由中心对称得平行四边形例题5．如图所示，抛物线2:(0,0)m y ax b a b =+<>与x 轴于点A 、B （点A 在点B 的左侧），与y 轴交于点C ．将抛物线m 绕点B 旋转180︒，得到新的抛物线n ，它的顶点为1C ，与x 轴的另一个交点为1A ．（1）四边形11AC A C 是什么特殊四边形，请写出结果并说明理由；（2）若四边形11AC A C 为矩形，请求出a ，b 应满足的关系式．【解答】解：（1）当1a =-，1b =时，抛物线m 的解析式为：21y x =-+．令0x =，得：1y =．(0,1)C ∴．令0y =，得：1x =±．(1,0)A ∴-，(1,0)B ，C 与1C 关于点B 中心对称，∴抛物线n 的解析式为：22(2)143y x x x =--=-+；四边形11AC A C 是平行四边形．理由：连接AC ，1AC ，11A C ，C 与1C 、A 与1A 都关于点B 中心对称，1AB BA ∴=，1BC BC =，∴四边形11AC A C 是平行四边形．（2）令0x =，得：y b =．(0,)C b ∴．令0y =，得：20ax b +=，∴x =∴(A B ，∴AB BC ===．要使平行四边形11AC A C 是矩形，必须满足AB BC =，∴=，∴24(b b b a a⨯-=-，3ab ∴=-．a ∴，b 应满足关系式3ab =-．例题6．如图1，抛物线23y ax ax b =-+经过(1,0)A -，(3,2)C 两点，与y 轴交于点D ，与x 轴交于另一点B ．（1）求此抛物线的解析式；（2）如图2，过点(1,1)E -作EF x ⊥轴于点F ，将AEF ∆绕平面内某点旋转180︒后得MNQ ∆（点M ，N ，Q 分别与点A ，E ，F 对应），使点M ，N 在抛物线上，求点M ，N 的坐标．【解答】解：（1） 抛物线23y ax ax b =-+过(1,0)A -、(3,2)C ，03a a b ∴=++，299a a b =-+．解得12a =-，2b =，∴抛物线解析式213222y x x =-++．（2）如图2，由题意知，AEF ∆ 绕平面内某点旋转180︒后得MNQ ∆，∴设绕点I 旋转，联结AI ，NI ，MI ，EI ，AI MI = ，NI EI =，∴四边形AEMN 为平行四边形，//AN EM ∴且AN EM =．(1,1)E - 、(1,0)A -，∴设(,)M m n ，则(2,1)N m n -+M 、N 在抛物线上，213222n m m ∴=-++，2131(2)(2)222n m m +=--+-+，解得3m =，2n =．(3,2)M ∴，(1,3)N ．【旋转过后落点问题】例题7．如图，Rt ABC ∆中，已知90C ∠=︒，48B ∠=︒，点D 在边BC 上，2BD CD =，把Rt ABC ∆绕点D 逆时针旋转(0180)m m ︒<<︒度后，如果点B 恰好落在初始Rt ABC ∆的边上，那么m =．【解答】解：当旋转后点B 的对应点B '落在AB 边上，如图1，Rt ABC ∆ 绕点D 逆时针旋转(0180)m m ︒<<︒度得到Rt △A B C '''，DB DB ∴'=，B DB m ∠'=，48DB B B ∴∠'=∠=︒，18084B DB DB B B ∴∠'=︒-∠'-∠=︒，即84m =︒；当点B 的对应点B '落在AB 边上，如图2，Rt ABC ∆ 绕点D 逆时针旋转(0180)m m ︒<<︒度得到Rt △A B C '''，DB DB ∴'=，B DB m ∠'=，2BD CD = ，2DB CD ∴'=，90C ∠=︒ ，30CB D ∴∠'=︒，60CDB ∴∠'=︒，18060120B DB ∴∠'=︒-︒=︒，即120m =︒，综上所述，m 的值为84︒或120︒．故答案为84︒或120︒．例题8．如图，在Rt ACB ∆中，90ACB ∠=︒，点O 在AB 上，且6CA CO ==，1cos 3CAB ∠=，若将ACB ∆绕点A 顺时针旋转得到Rt △AC B ''，且C '落在CO 的延长线上，连接BB '交CO 的延长线于点F ，则BF =．【解答】解：过C 作CD AB ⊥于点D ，CA CO = ，AD DO ∴=，在Rt ACB ∆中，16cos 3AC CAB AB AB∠===，318AB AC ∴==，在Rt ADC ∆中：1cos 3AD CAB AC ∠==，123AD AC ∴==，24AO AD ∴==，18414BO AB AO ∴=-=-=，△AC B ''是由ACB ∆旋转得到，AC AC ∴='，AB AB ='，CAC BAB ∠'=∠'，1(180)2ACC CAC ∠'=︒-∠' ，1(180)2ABB BAB ∠'=︒-∠'，ABB ACC ∴∠'=∠'，∴在CAO ∆和BFO ∆中，BFO CAO ∠=∠，CA CO = ，COA CAO ∴∠=∠，又COA BOF ∠=∠ （对顶角相等），BOF BFO ∴∠=∠，14BF BO ∴==．故答案为：14．例题9．在平面直角坐标系xOy 中，抛物线26(0)y mx mx n m =++>与x 轴交于A ，B 两点（点A 在点B 左侧），顶点为C ，抛物线与y 轴交于点D ，直线BC 交y 轴于E ，且ABC ∆与AEC ∆这两个三角形的面积之比为2:3．（1）求点A 的坐标；（2）将ACO ∆绕点C 顺时针旋转一定角度后，点A 与B 重合，此时点O 的对应点O '恰好也在y 轴上，求抛物线的解析式．【解答】解：（1）如图1，抛物线26(0)y mx mx n m =++>∴对称轴3x =-，当:2:3ABC AEC S S ∆∆=时，:2:1ABC AEB S S ∆∆∴=，过点C 作CF x ⊥轴于F ，:2:1CF OE ∴=易知，BFC BOE ∆∆∽，::2:1BF OB CF OE ∴==，1OB ∴=，2BF =，5OA ∴=，(5,0)A ∴-，(1,0)B -；（2）(1,0)B - ，06m m n ∴=-+，5n m ∴=，(3,4)C m ∴--，如图2，作CF AB ⊥于F ，CP OD ⊥于P ，则四边形CFOP 是矩形，4OP CF m ∴==，3CP OF ==，OP O P '=，28OO OP m'∴==由旋转知，5OA BO '==，在Rt BOO '∆中，1OB =，根据勾股定理得，2285126m =-=，64m ∴=263656424y x x ∴=++【旋转+“恰好”问题】例题10．如图，在直角坐标系中，直线4y =+分别与x 轴、y 轴交于点M 、N ，点A 、B 分别在y 轴、x 轴上，且30B ∠=︒，4AB =，将ABO ∆绕原点O 顺时针转动一周，当AB 与直线MN 平行时点A 的坐标．【另外再可思考，当“AB 所在直线与MN 垂直时点A 的坐标”】【解答】解：①4AB = ，30ABO ∠=︒，122OA AB ∴==，903060BAO ∠=︒-︒=︒，120OAD ∴∠=︒，直线MN 的解析式为43y x =-+，30NMO ∴∠=︒，//AB MN ，30ADO NMD ∴∠=∠=︒，30AOC ∴∠=︒，112AC OA ∴==，OC ∴==∴点A 的坐标为，1)；② 图②中的点A 与图①中的点A 关于原点对称，∴点A 的坐标为：(，1)-，故答案为：，1)、(1)-．例题11．在平面直角坐标系中，已知O 为坐标原点，点(3,0)A ，(0,4)B ，以点A 为旋转中心，把ABO ∆顺时针旋转，得ACD ∆．记旋转角为α．ABO ∠为β．（Ⅰ）如图①，当旋转后点D 恰好落在AB 边上时，求点D 的坐标；（Ⅱ）如图②，当旋转后满足//BC x 轴时，求α与β之间的数量关系：（Ⅲ）当旋转后满足AOD β∠=时，求直线CD 的解析式（直接写出结果即可）．【解答】解：（1） 点(3,0)A ，(0,4)B ，得3OA =，4OB =，∴在Rt AOB ∆中，由勾股定理，得225AB OA OB =+=，根据题意，有3DA OA ==．如图①，过点D 作DM x ⊥轴于点M ，则//MD OB ，ADM ABO ∴∆∆∽．有AD AM DM AB AO BO==，得39355AD AM AO AB ==⨯= ，65OM ∴=，∴125MD =，∴点D 的坐标为6(5，12)5．（2）如图②，由已知，得CAB α∠=，AC AB =，ABC ACB ∴∠=∠，∴在ABC ∆中，1802ABC α∴=︒-∠，//BC x 轴，得90OBC ∠=︒，9090ABC ABO β∴∠=︒-∠=︒-，2αβ∴=；（3）若顺时针旋转，如图，过点D 作DE OA ⊥于E ，过点C 作CF OA ⊥于F ，AOD ABO β∠=∠= ，3tan 4DE AOD OE ∴∠==，设3DE x =，4OE x =，则43AE x =-，在Rt ADE ∆中，222AD AE DE =+，2299(43)x x ∴=+-，2425x ∴=，96(25D ∴，72)25，∴直线AD 的解析式为：247277y x =-， 直线CD 与直线AD 垂直，且过点D ，∴设724y x b =-+，把96(25D ，72)25代入得，72796252425b =-⨯+，解得4b =，互相垂直的两条直线的斜率的积等于1-，∴直线CD 的解析式为7424y x =-+．同理可得直线CD的另一个解析式为7424y x=-．【巩固练习】1．如图，在等边ABC ∆中，D 是边AC 上一点，连接BD ．将BCD ∆绕点B 逆时针旋转60︒得到BAE ∆，连接ED ．若10BC =，9BD =，则AED ∆的周长是．2.如图一段抛物线：(3)(03)y x x x =--，记为1C ，它与x 轴交于点O 和1A ；将1C 绕1A 旋转180︒得到2C ，交x 轴于2A ；将2C 绕2A 旋转180︒得到3C ，交x 轴于3A ，如此进行下去，直至得到10C ，若点(28,)P m 在第10段抛物线10C 上，则m 的值为.3．如图，Rt ABC ∆中，90C ∠=︒，30ABC ∠=︒，2AC =，ABC ∆绕点C 顺时针旋转得△11A B C ，当1A 落在AB 边上时，连接1B B ，取1BB 的中点D ，连接1A D ，则1A D 的长度是．4．如图，AOB ∆中，90AOB ∠=︒，3AO =，6BO =，AOB ∆绕点O 逆时针旋转到△A OB ''处，此时线段A B ''与BO 的交点E 为BO 的中点，求线段B E '的值．5．如图，在直角坐标系中，直线14:83l y x =+与y 轴交于点A ，与x 轴交于点B ，将直线1l 绕着点A 顺时针旋转45︒得到2l ．求2l 的函数表达式．6．如图，四边形ABCO 是平行四边形，2OA =，6AB =，点C 在x 轴的负半轴上，将ABCO 绕点A 逆时针旋转得到ADEF ，AD 经过点O ，点F 恰好落在x 轴的正半轴上，若点D 在反比例函数(0)k y x x =<的图象上，则k 的值为．7.在平面直角坐标系中，O 为坐标原点，点A 的坐标为(8,0)-，直线BC 经过点(8,6)B -，(0,6)C ，将四边形OABC 绕点O 按顺时针方向旋转a 度得到四边形OA B C '''，此时直线OA '、直线B C ''分别与直线BC 相交于点P 、Q ．在四边形OABC 旋转过程中，若使12BP BQ =？则点P 的坐标为．8．如图，在BDE ∆中，90BDE ∠=︒，BD =，点D 的坐标为(5,0)，15BDO ∠=︒，将BDE∆旋转到ABC ∆的位置，点C 在BD 上，则旋转中心的坐标为．9．已知正方形ABCD 的边长为5，E 在BC 边上运动，DE 的中点G ，EG 绕E 顺时针旋转90︒得EF ，问CE =时，A 、C 、F 在一条直线上．10．如图，一次函数1(0)2y x m m =-+>的图象与x 轴、y 轴分别交于点A 、B ，点C 在线段OA 上，点C 的横坐标为n ，点D 在线段AB 上，且2AD BD =，将ACD ∆绕点D 旋转180︒后得到△11A C D ．（1）若点1C 恰好落在y 轴上，试求n m的值；（2）当4n =时，若△11A C D 被y 轴分得两部分图形的面积比为3:5，求该一次函数的解析式．11．在ABC ∆中，5AB AC ==，3cos 5ABC ∠=，将ABC ∆绕点C 顺时针旋转，得到△11A B C ．（1）如图①，当点1B 在线段BA 延长线上时．①求证：11//BB CA ；②求△1AB C 的面积；（2）如图②，点E 是BC 边的中点，点F 为线段AB 上的动点，在ABC 绕点C 顺时针旋转过程中，点F 的对应点是1F ，求线段1EF 长度的最大值与最小值的差．12．如图（1），在ABC=，动点P在线段AC上以5/cm s的速度从=，3BC cmAB cmC∆中，90∠=︒，5点A运动到点C，过点P作PD AB'，设点P的⊥于点D，将APD∆绕PD的中点旋转180︒得到△A DP 运动时间为()x s．（1）当点A'落在边BC上时，求x的值；（2）在动点P从点A运动到点C过程中，当x为何值时，△A BC'是以A B'为腰的等腰三角形；（3）如图（2），另有一动点Q与点P同时出发，在线段BC上以5/cm s的速度从点B运动到点C，过点Q 作QE AB⊥于点E，将BQE'，连结A B''，当直线A B''与ABC∆绕QE的中点旋转180︒得到△B EQ∆的一边垂直时，求线段A B''的长．13．如图，(0,2)A ，(1,0)B ，点C 为线段AB 的中点，将线段BA 绕点B 按顺时针方向旋转90︒得到线段BD ，抛物线2(0)y ax bx c a =++≠经过点D ．（1）若该抛物线经过原点O ，且13a =-，求该抛物线的解析式；（2）在（1）的条件下，点(,)P m n 在抛物线上，且POB ∠锐角，满足90POB BCD ∠+∠<︒，求m 的取值范围．14．如图1，抛物线210y ax ax c =-+经过ABC ∆的三个顶点，已知//BC x 轴，点A 在x 轴上，点C 在y 轴上35OA BC =，且AC BC =．（1）求抛物线的解析式；（2）如图2，将AOC ∆沿x 轴对折得到1AOC ∆，再将1AOC ∆绕平面内某点旋转180︒后得△112(A O C A ，O ，1C 分别与点1A ，1O ，2C 对应）使点1A 、2C 在抛物线_P 上，求点1A 、2C 的坐标；15．点P为图①中抛物线22m>上任一点，将抛物线绕顶点G逆时针旋转90︒=-+为常数，0)y x mx m m2(后得到的新图象与y轴交于A、B两点（点A在点B的上方），点Q为点P旋转后的对应点．（1）若点Q的坐标为(-，求该抛物线的函数关系式；（2）如图②，若原抛物线恰好也经过A点，点Q在第一象限内，是否存在这样的点P使得AGQ∆是以AG 为底的等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．参考答案1.【解答】解：ABC ∆ 是等边三角形，10AC AB BC ∴===，BAE ∆ 由BCD ∆逆时针旋旋转60︒得出，AE CD ∴=，BD BE =，60EBD ∠=︒，10AE AD AD CD AC ∴+=+==，60EBD ∠=︒ ，BE BD =，BDE ∴∆是等边三角形，9DE BD ∴==，AED ∴∆的周长19AE AD DE AC BD =++=+=．故答案为：19．2.【解答】解：令0y =，则(3)0x x --=，解得10x =，23x =，1(3,0)A ∴，由图可知，抛物线10C 在x 轴下方，相当于抛物线1C 向右平移3927⨯=个单位，再沿x 轴翻折得到，∴抛物线10C 的解析式为(27)(273)(27)(30)y x x x x =---=--，(28,)P m 在第10段抛物线10C 上，(2827)(2830)2m ∴=--=-．3.【解答】解：90ACB ∠=︒ ，30ABC ∠=︒，2AC =，9060A ABC ∴∠=︒-∠=︒，4AB =，BC =，1CA CA = ，1ACA ∴∆是等边三角形，112AA AC BA ===，1160BCB ACA ∴∠=∠=︒，1CB CB = ，1BCB ∴∆是等边三角形，1BB ∴=，12BA =，1190A BB ∠=︒，1BD DB ∴==，1A D ∴==，．4.【解答】解：90AOB ∠=︒ ，3AO =，6BO =，AB ∴==AOB ∆ 绕顶点O 逆时针旋转到△A OB ''处，3AO A O ∴='=，A B AB ''==，点E 为BO 的中点，116322OE BO ∴==⨯=，OE A O ∴='，过点O 作OF A B ⊥''于F ，1362A OB S OF ''=⨯=⨯⨯ ，解得655OF =，在Rt EOF ∆中，5EF ==，OE A O =' ，OF A B ⊥''，22A E EF ∴'==（等腰三角形三线合一），B E A B A E ∴'=''-'=5.【解答】解： 直线483y x =+与y 轴交于点A ，与x 轴交于点B ，(0,8)A ∴、(6,0)B -，如图2，过点B 做BC AB ⊥交直线2l 于点C ，过点C 作CD x ⊥轴，在BDC ∆和AOB ∆中，CBD BAO CDB AOB BC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩()BDC AOB AAS ∴∆≅∆，6CD BO ∴==，8BD AO ==，6814OD OB BD ∴=+=+=，C ∴点坐标为(14,6)-，设2l 的解析式为y kx b =+，将A ，C 点坐标代入，得1468k b b -+=⎧⎨=⎩，解得178k b ⎧=⎪⎨⎪=⎩，2l ∴的函数表达式为187y x =+；6.【解答】解：如图所示：过点D 作DM x ⊥轴于点M ，由题意可得：BAO OAF ∠=∠，AO AF =，//AB OC ，则BAO AOF AFO OAF ∠=∠=∠=∠，故60AOF DOM ∠=︒=∠，624OD AD OA AB OA =-=-=-= ，2MO ∴=，MD =，(2,D ∴--，2(k ∴=-⨯-=．故答案为：．7.【解答】解：存在这样的点P 和点Q ，使12BP BQ =．理由如下：过点Q 画QH OA ⊥'于H ，连接OQ ，则QH OC OC ='=，12POQ S PQ OC ∆= ，12POQ S OP QH ∆= ，PQ OP ∴=．设BP x =，12BP BQ =，2BQ x ∴=，如图4，当点P 在点B 左侧时，3OP PQ BQ BP x ==+=，在Rt PCO ∆中，222(8)6(3)x x ++=，解得13612x =+，23612x =-，（不符实际，舍去）．3692PC BC BP ∴=+=+，1(92P ∴--，6)，如图5，当点P 在点B 右侧时，OP PQ BQ BP x ∴==-=，8PC x =-．在Rt PCO ∆中，222(8)6x x -+=，解得254x =，257844PC BC BP ∴=-=-=，27(4P ∴-，6)，综上可知，存在点136(92P --，6)，27(4P -，6)使12BP BQ =．8.【解答】解：如图，AB 与BD 的垂直平分线的交点即为旋转中心P ，连接PD ，过P 作PF x ⊥轴于F ．点C 在BD 上，∴点P 到AB 、BD 的距离相等，都是12BD ，即12⨯=45PDB ∴∠=︒，4PD ==，15BDO ∠=︒ ，451560PDO ∴∠=︒+︒=︒，30DPF ∴∠=︒，114222DF PD ∴==⨯=， 点D 的坐标是(5,0)，523OF OD DF ∴=-=-=，由勾股定理得，PF ===∴旋转中心的坐标为(3，．故答案为：(3，．9.【解答】解：过F 作FN BC ⊥，交BC 延长线于N 点，连接AC ，90DCE ENF ∠=∠=︒ ，90DEC NEF ∠+∠=︒，90NEF EFN ∠+∠=︒，DEC EFN ∴∠=∠，Rt FNE Rt ECD ∴∆∆∽，DE 的中点G ，EG 绕E 顺时针旋转90︒得EF ，:2:1DE EF ∴=，:::2:1CE FN DE EF DC NE ∴===，2CE NF ∴=，1522NE CD ==．45ACB ∠=︒ ，∴当45NCF ∠=︒时，A 、C 、F 在一条直线上．则CNF ∆是等腰直角三角形，CN NF ∴=，2CE CN ∴=，22553323CE NE ∴==⨯=．53CE ∴=时，A 、C 、F 在一条直线上．故答案为：53．10.【解答】解：（1）由题意，得(0,)B m ，(2,0)A m ，如图，过点D 作x 轴的垂线，交x 轴于点E ，交直线11A C 于点F ，易知：23DE m =，2(3D m ，2)3m ，14(3C m n -，4)3m ，∴403m n -=，∴43n m =；（2）由（1）得，当3m >时，点1C 在y 轴右侧；当23m <<时，点1C 在y 轴左侧．①当3m >时，设11A C 与y 轴交于点P ，连接1C B ，由△11A C D 被y 轴分得两部分图形的面积比为3:5，S ∴△1:BA P S △13:1BC P =，11:3A P C P ∴=，∴，185m ∴=，11825y x ∴=-+；②当23m <<时，同理可得：11827y x =-+；综上所述，11827y x =-+或11825y x =-+．11.【解答】解：（1）①证明：AB AC = ，1B C BC =，1AB C B ∴∠=∠，B ACB ∠=∠，1AB C ACB ∠=∠ （旋转角相等），111B CA AB C ∴∠=∠，11//BB CA ∴；②过A 作AF BC ⊥于F ，过C 作CE AB ⊥于E ，如图①：AB AC = ，AF BC ⊥，BF CF ∴=，3cos 5ABC ∠=，5AB =，3BF ∴=，6BC ∴=，16B C BC ∴==，1318655BE B E ∴==⨯=，1365BB ∴=，424655CE =⨯=，13611555AB ∴=-=，∴△1AB C 的面积为：1112413225525⨯⨯=；（2）如图2，过C 作CF AB ⊥于F ，以C 为圆心CF 为半径画圆交BC 于1F ，1EF 有最小值，此时在Rt BFC ∆中，245CF =，1245CF ∴=，1EF ∴的最小值为249355-=；如图，以C 为圆心BC 为半径画圆交BC 的延长线于1F ，1EF 有最大值；此时11369EF EC CF =+=+=，∴线段1EF 的最大值与最小值的差为936955-=．12.【解答】解：（1）如图1， 在ABC ∆中，90C ∠=︒，5AB cm =，3BC cm =，4AC cm ∴=，当点A '落在边BC 上时，由题意得，四边形APA D '为平行四边形，PD AB ⊥ ，90ADP C ∴∠=∠=︒，APD ABC ∴∆∆∽，5AP x = ，4A P AD x ∴'==，45PC x =-，A PD ADP ∠'=∠ ，//A P AB ∴'，∴△A PC ABC '∆∽，∴PC A P AC AB '=，即45445x x -=，解得：2041x =，∴当点A '落在边BC 上时，2041x =；（2）当A B BC '=时，222(58)(3)3x x -+=，解得：4012373x ±=．45x ，∴4073x -=；当A B A C '='时，58x =．（3）Ⅰ、当A B AB ''⊥时，如图6，DH PA AD '∴==，HE B Q EB ='=，2224235AB AD EB x x =+=⨯+⨯= ，514x ∴=，514A B QE PD x ∴''=-==；Ⅱ、当A B BC ''⊥时，如图7，5B E x ∴'=，57DE x =-，53cos 575x B x ∴==-，1546x ∴=，2523A B B D A D ∴''='-'=；Ⅲ、当A B AC ''⊥时，如图8，由（1）有，2041x =，12sin 41A B PA A ∴''='=；当A B AB ''⊥时，514x =，514A B ''=；当A B BC ''⊥时，1546x =，2546A B ''=；当A B AC ''⊥时，2053x =，2553A B ''=．13.【解答】解：（1）过点D 作DF x ⊥轴，垂足为F ．90ABD ∠=︒ ，90DBF ABO ∴∠+∠=︒．又90OAB ABO ∠+∠=︒ ，DBF OAB ∴∠=∠．由旋转的性质可知AB BD =．在AOB ∆和BFD ∆中DBF OAB AOB BFD AB BD ∠=∠⎧⎪∠=∠⎨⎪=⎩，AOB BFD ∴∆≅∆．1DF OB ∴==，2AO BF ==．(3,1)D ∴．把点D 和点O 的坐标代入213y x bx c =-++得：1300b c c -++=⎧⎨=⎩，解得：43b =，0c =．∴抛物线的解析式为21433y x x =-+．（2）如图2所示：点(0,2)A ，(1,0)B ，C 为线段AB 的中点，1(2C ∴，1)．C 、D 两点的纵坐标为1，//CD x ∴轴．BCD ABD ∴∠=∠．∴当POB BAO ∠=∠时，恰好90POB BCD ∠+∠=︒．设点P 的坐标为214(,)33m m m -+．当点P 在x 轴上且POB BAO ∠=∠时，则1tan tan 2POB BAO ∠=∠=，即2141332m m m -+=，解得：52m =或0m =（舍去）．当点P 位于x 轴的下方，点P '处时，且POB BAO ∠=∠时，则1tan tan 2POB BAO ∠=∠=，即2141332m m m -=，解得：112m =或0m =（舍去）．POB ∠ 为锐角，4m ∴≠．由图形可知：当点P 在抛物线上P 与P '之间移动时，90POB BCD ∠+∠<︒．m ∴的取值范围是：51122m <<且4m ≠．14.【解答】解：（1）35OA BC = ，AC BC =∴设3OA k =，5(0)AC BC k k ==>4OC k∴= 当0x =时，210y ax ax c c=-+=(0,)C c ∴，即4OC c k==4c k ∴=3(4c A ∴-，50)(4c B ，)c 抛物线经过点A 、B ∴2233()10()04455(1044c c a a c c c a a c c ⎧---+=⎪⎪⎨⎪-+=⎪⎩解得：1128a c ⎧=-⎪⎨⎪=⎩∴抛物线解析式为：2158126y x x =-++（2）如图1，1AOC ∆旋转后得到△112A O C 的位置如图所示116O A OA ∴==，128O C OC ==，11//O A x 轴，12O C x ⊥轴设2C 坐标为215(,8)126t t t -++，则2115(6,)126A t t t +-+221515(6)(6)8126126t t t t ∴-++++=-+解得：10t =1A ∴坐标为(16,0)，2C 坐标为(10,8)．15.【解答】解：（1） 对于222y x mx m =-+，当0y =时，x m =，OG m ∴=，点Q 为点P 绕顶点G 逆时针旋转90︒后的对应点，P m ∴，2)m +，把P m +，2)m +代入222y x mx m =-+中，得222)2)m m m m m +=-+，4m ∴=，∴该抛物线的函数关系式为；2816y x x =-+；（2）存在，点Q 在第一象限内，AQ GQ =，如图2中，由题意可知OA OG =，∴m =，1m ∴=，∴点(0,1)A ，点A 的对应点(2,1)C ，(1,0)G ，∴直线CG 解析式为1y x =-，线段CG 的中垂线MN 解析式为2y x =-+，由2221y x y x x =-+⎧⎨=-+⎩解得15232x y ⎧=⎪⎪⎨⎪=⎪⎩或15232x y ⎧=⎪⎪⎨⎪=⎪⎩， 点P 在第一象限，∴点P坐标1(2+，32-．。
最新的初中数学竞赛——几何变换——旋转
第2讲 几何变换——旋转典型例题【例1】 C 是线段AE 上的点，以AC 、CE 为边在线段AE 的同侧作等边三角形ABC 、CDE ，设AD的中点是M ，BE 的中点是N ，连结MN 、MC 、NC ，求证：CMN △是等边三角形．【例2】 如图，两个正方形ABCD 和AKLM 有一个公共点A ．求证：这两个正方形的中心以及线段BM ，DK 的中点是某正方形的顶点．【例3】 已知：如图，ABC △、CDE △、EHK △都在等边三角形，且A 、D 、K 共线，AD DK ．求证：HBD △也是等边三角形．KECHDBAL【例4】 ABC △是等边三角形，P 是AB 边的中点，Q 是AC 边的中点，R 为BC 边的中点，M 为RC上任意一点，且PMS △是等边三角形，S 与Q 在PM 的同侧，求证：RM QS =．【例5】 ABCD 是正方形，P 是ABCD 内一点，1PA =，3PB =，PD =ABCD 的面积．【例6】 P 是等边三角形ABC 内的一点，6PA =，8PB =，10PC =．求ABC △的边长．Q ⋅SMPCBAR D【例7】 设O 是等边ABC △内一点，已知115AOB ︒∠=，125BOC ︒∠=，求以线段OA 、OB 、OC 为边所构成的三角形的各内角大小．【例8】 如图，在ABC △中，90ACB ︒∠=，AC BC =，P 是ABC △内一点，3PA =，1PB =，2PC =，求BPC ∠．【例9】 如图，已知ABC △中，90A = ，AB AC =，D 为BC 上一点，求证：2222BD DC AD +=．APCBADCB【例10】 如图，在等腰直角ABC △中，90ACB ︒∠=，CA CB =，P 、Q 在斜边AB 上，且45PCQ ︒∠=，求证：222PQ AP BQ =+．【例11】 在正方形ABCD 中，已知E 、F 分别是边BC 、CD 上的点，满足EF BE DF =+，AE 、AF分别与对角线BD 交于M 、N ．求证： （1）45EAF ︒∠=； （2）222MN BM DN =+．【例12】 如图，在梯形ABCD 中，AD BC ∥，AD CD ⊥，2BC CD AD ==，E 是CD 上一点，且45ABE ︒∠=，AD α=．求CE 的长．AQBCPE DCBADF【例13】 已知：ABC △中，120A ︒∠≥，P 是不与A 重合的定点，求证：PA PB PC AB AC +++＞．【例14】 已知：如图，ABD △是等边三角形，ABC △中，BC a =，CA b =．问：当ACB ∠为何值时，C 、D 两点的距离最大？最大值是多少？【例15】 已知ABC △，以其各边为底边，向ABC △的外部作等腰三角形ABD 、BCE 、CAF ，使顶角都等于120︒，求证：DEF △是正三角形．PCBAEBDAFC【例16】 已知：ABC △是锐角三角形，三边长分别是a 、b 、c ，O 是ABC △内的一点，120AOB BOC COA ︒∠=∠=∠=，OA u =，OB v =，OC w =，DEF △是等边三角形，P 是DEF△内一点，PD a =，PE b =，PF c =． 求证：DEF △的边长等于u v w ++．【例17】 已知：三条平行直线l 、m 、n ，求证：存在一个等边三角形ABC ，使顶点A 、B 、C 分别在l 、m 、n 上．作业1. 已知：ABCD 是正方形，O 是其中心，OEFG 也是正方形，两个正方形的边长都是a ，OG 、OE分别交CD 、BC 于H 、K ．求证：214OKCH S a =．2. 已知：如图，ABCD 是正方形，12∠=∠．求证：BE DF AE +=．3. ABC △是等边三角形，P 是其内的一点，3PA =，4PB =，5PC =，求ABC △的面积．4.P 是等边ABC △内部一点，APB ∠、BPC ∠、CPA ∠的大小之比是5:6:7，求以PA 、PB 、PC 为边的三角形的三个角的大小之比．1FDEAC2B5. 等边ABC △的边长a =点P 是ABC △内一点，且222PA PB PC +=，若5PC =，求PA 、PB 的长．6. 在梯形ABCD 中，AD BC ∥（BC AD ＞），90D ︒∠=，12BC CD ==，E 在CD 上，45ABE ︒∠=，若10AE =，求CE 的长．7. 如图，P 、Q 是边长为1的正方形ABCD 内两点，使得45PAQ PCQ ︒∠=∠=．求PAB PCQ QADS S S ∆∆∆++的值．E DCBA。
初中数学竞赛几何变换
几何变换一、 平移变换1． 定义 设是一条给定的有向线段，T 是平面上的一个变换，它把平面图形F 上任一点X 变到X'，使得=，则T 叫做沿有向线段的平移变换。
记为X −−→−)PQ (T X'，图形F −−→−)PQ (T F' 。
2． 主要性质 在平移变换下，对应线段平行且相等，直线变为直线，三角形变为三角形，圆变为圆。
两对应点连线段与给定的有向线段平行（共线）且相等。
二、 轴对称变换1． 定义 设l 是一条给定的直线，S 是平面上的一个变换，它把平面图形F 上任一点X 变到X'，使得X 与X'关于直线l 对称，则S 叫做以l 为对称轴的轴对称变换。
记为X −→−)l (SX'，图形F −→−)l (S F' 。
2． 主要性质 在轴对称变换下，对应线段相等，对应直线（段）或者平行，或者交于对称轴，且这两条直线的夹角被对称轴平分。
三、 旋转变换1． 定义 设α是一个定角，O 是一个定点，R 是平面上的一个变换，它把点O 仍变到O （不动点），而把平面图形F 上任一点X 变到X'，使得OX'=OX ，且∠XOX'=α，则R叫做绕中心O ，旋转角为α的旋转变换。
记为X −−−→−α),O (RX'，图形F −−−→−α),O (R F' 。
其中α<0时，表示∠XOX'的始边OX 到终边OX'的旋转方向为顺时针方向；α>0时，为逆时针方向。
2． 主要性质 在旋转变换下，对应线段相等，对应直线的夹角等于旋转角。
四、 位似变换1． 定义 设O 是一个定点，H 是平面上的一个变换，它把平面图形F 上任一点X 变到X'，使得 =k ·，则H 叫做以O 为位似中心，k 为位似比的位似变换。
记为X −−−→−)k ,O (HX'，图形F −−−→−)k ,O (H F' 。
初中几何旋转 知识点-概述说明以及解释
初中几何旋转知识点-概述说明以及解释1.引言1.1 概述在初中几何学习中，几何旋转是一个重要的知识点。
旋转是指围绕一个点旋转图形，将图形绕着旋转中心旋转一定的角度，但图形的大小和形状保持不变。
通过学习几何旋转，我们可以更好地理解平面几何中的基本概念和性质，同时也可以应用旋转的知识解决实际生活中的问题。
本文将详细介绍几何旋转的基本概念、性质以及应用实例，帮助读者更深入地理解和掌握这一知识点。
1.2 文章结构：本文主要包括引言、正文和结论三个部分。
- 引言部分将概述几何旋转的基本概念、重要性以及本文的研究目的和意义；- 正文部分将详细介绍几何旋转的定义、基本概念和性质，帮助读者全面了解几何旋转的相关知识；- 结论部分将总结几何旋转的重要知识点，并提供一些应用实例来帮助读者更好地理解和运用这些知识。
最后，展望几何旋转在未来的发展方向和可能的研究领域。
通过这三个部分的分析和探讨，读者将能够全面了解几何旋转的知识，并掌握其在实际生活和学术研究中的应用。
1.3 目的本文的目的主要是介绍和总结初中几何旋转的知识点，帮助读者全面了解几何旋转的基本概念和性质。
通过学习本文，读者将能够掌握几何旋转的相关概念，理解旋转的基本原理，并通过实例加深对几何旋转的理解。
此外，本文还旨在呼吁读者进一步关注几何旋转这一重要概念，在实际问题中灵活运用几何旋转的知识，提高解决问题的能力和几何思维。
通过深入学习和理解几何旋转，读者将能够更好地应用几何知识解决各类问题，拓展数学思维，提升数学素养。
愿本文能够为学习几何旋转的读者提供一定的帮助和指导，使其在数学学习中取得更好的成绩和收获。
2.正文2.1 什么是几何旋转几何旋转是指围绕一个定点按照特定的规则将图形沿着旋转轴旋转的一种操作。
在几何学中，旋转是一种常见的变换方式，它能够改变图形的位置和方向，但不改变其形状和大小。
在几何旋转中，旋转点即为旋转的中心点，旋转轴则是围绕旋转点进行旋转的线段。
【中考攻略】中考数学 专题11 几何三大变换之旋转探讨
轴对称、平移、旋转是平面几何的三大变换。
旋转变换是指在同一平面内，将一个图形（含点、线、面）整体绕一固定点旋转一个定角，这样的图形变换叫做图形的旋转变换，简称旋转。
旋转由旋转中心、旋转的方向和角度决定。
经过旋转，旋转前后图形的形状、大小不变，只是位置发生改变；旋转前、后图形的对应点到旋转中心的距离相等，即旋转中心在对应点所连线段的垂直平分线上； 旋转前、后的图形对应点与旋转中心所连线段的夹角等于旋转角。
把一个图形绕着某一定点旋转一个角度360°/n(n 为大于1的正整数)后，与初始的图形重合，这种图形就叫做旋转对称图形，这个定点就叫做旋转对称中心，旋转的角度叫做旋转角。
特别地，中心对称也是旋转对称的一种的特别形式。
把一个图形绕着某一点旋转180°，如果它能与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心，这两个图形的对应点叫做关于中心的对称点。
如果把一个图形绕某一点旋转180度后能与自身重合，这个图形是中心对称图形。
在初中数学以及日常生活中有着大量的旋转变换的知识，是中考数学的必考内容。
结合2011和2012年全国各地中考的实例，我们从下面九方面探讨旋转变换：（1）中心对称和中心对称图形；（2）构造旋转图形；（3）有关点的旋转；（4）有关直线（线段）的旋转；（5）有关等腰（边）三角形的旋转；（6）有关直角三角形的旋转；（7）有关平行四边形、矩形、菱形的旋转；（8）有关正方形的旋转；（9）有关其它图形的旋转。
一、中心对称和中心对称图形：典型例题：例1. （2012天津市3分）下列标志中，可以看作是中心对称图形的是【 】【答案】B 。
【考点】中心对称图形。
【分析】根据中心对称图形的概念：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，由此结合各图形的特点求解：A 、C 、D 都不符合中心对称的定义。
九年级数学竞赛题：图形的旋转
九年级数学竞赛题：图形的旋转一个图形绕着一个定点旋转一个角度后得到另一个图形，这样的运动称为旋转，这个定点称为旋转中心，转动的角称为旋转角．旋转不改变图形的大小和形状，有下列基本性质：旋转前后的对应线段相等，对应角相等，对应点判旋转中心的距离相等，任意一对对应点与旋转中心的连线所成的角都是旋转角．图形的旋转有以下方面的应用：1．在旋转中探索规律；2．在旋转中探寻图形性质的变化；3．在旋转中寻找变量之间的函数关系；4．利用旋转进行图案设计．例1 如图，P是正△ABC内的一点，且P A=6，PB=8，PC=10，若将△P AC绕点A逆时针旋转后，得到△P'AB，则点P与P'之间距离为___________，∠APB=___________．例2 如图，在等腰Rt△ABC的斜边AB上取两点M、N，使∠MCN=45°，记AM=m，MN=x，BN=n，则以线段x、m、n为边长的三角形的形状是（）．A．锐角三角形B．直角三角形C．钝角三角形D．随x、m、n的变化而改变例3 如图1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．（1）如图2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM、FN的长度，猜想BM、FN满足的数量关系，并证明你的猜想；（2）若三角尺GEF旋转到如图3所示的位置时，线段FE的延长线与AB的延长线交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．例4 把两个全等的等腰直角三角板ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点按顺时针方向旋转（旋转角α口满足条件：0°<α<90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图②）．（1）在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论；（2）连接HK，在上述旋转过程中，设BH=x，△GKH的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；（3）在（2）的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的516？若存在，求出此时x的值；若不存在，说明理由．例5 如图1，在平面直角坐标系中，两个全等直角三角形的直角顶点及一条直角边重合，点A在第二象限内，点B、点C在x轴的负半轴上，∠CAO=30°，OA=4．（1）求点C的坐标；（2）如图2，将△ACB绕点C按顺时针方向旋转30°到△A′CB ′的位置，其中A′C 交直线OA于点E，A′B ′分别交直线OA、CA于点F、G，则除△A′B ′C≌△AOC 外，还有哪几对全等的三角形，请直接写出答案．（不再另外添加辅助线）（3）在（2）的基础上，将△A′C B ′绕点C按顺时针方向继续旋转，当△COE的面积3时，求直线CE的函数表达式．1．如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF 交AD于点H，那么DH的长为_____________．2．如图，设P是等边△ABC内的一点，P A=3，PB=4，PC=5，则∠APB的度数是_________．3．如图，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBP′重合，若PB=3，则P P′=____________．4．如图，在正方形ABCD，E为DC边上的点，连接BE，将△BCE绕点C顺时针方向旋转90°得到△DCF，连结EF，若∠BEC=60°，则∠EFD的度数为（）．A．10°B．15°C．20°D．25°5．如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将腰DC绕点D逆时针方向旋转90°至DE，连结AE，则△ADE的面积是（）．A．1 B．2 C．3 D．46．如图，8×8方格纸上的两条对称轴EF、MN相交于中心点O，对△ABC分别作下列变换：①先以点A为中心顺时针方向旋转90°，再向右平移4格、向上平移4格；②先以点O为中心作中心对称图形，再以点A的对应点为中心逆时针方向旋转90°；③先以直线MN为轴作轴对称图形，再向上平移4格，再以点A的对应点为中心顺时针方向旋转90°．其中，能将△ABC变换成△PQR的是（）．。
数学培优竞赛新方法(九年级)-第13讲 旋转变换
第13讲 旋转变换知识纵横在平面内，将一个图形绕一个定点沿某个方向转动一定的角度，这样的图形变换称为旋转，这个定点叫旋转中心，旋转的角度叫旋转角。
旋转变换不改变图形的形状和大小，通过旋转，图形上的每一点都绕旋转中心沿相同的方向转动同样大小的角度，旋转变换前后的图形有下列性质： （1） 对应点到旋转中心的距离相等（2） 对应点与旋转中心的连线所成的角等于旋转角（3） 对应线段相等，对应线段的夹角等于旋转角，对应线段的垂直平分线都经过旋转中心。
例题求解【例1】如图，在ABC Rt ∆中，已知50,90=∠=∠B C ,点D 在边BC 上，BD=2CD,把ABC ∆绕着点D 逆时针旋转m （0<m<180）度后，如果点B 恰好落在初始ABC Rt ∆的边上，那么m= 。
(2011上海市中考题)思路点拨 因B 点所落得边未确定，故需分类讨论。
【例2】如图，P 是等边ABC ∆内部一点，CPA BPC APB ∠∠∠,,的大小之比是5:6:7，则PB.PA.PC 为边的三角形的三个角的大小（从小到大）之比是（ ） A 2：3：4 B 3：4：C 4：5：6D 不确定(全国初中数学竞赛题)思路点拨 由于PA.PB,PC 没有构成三角形，所以需要作辅助线构造以它们为边的三角形，不妨实施旋转变换。
【例3】点B,C,E 在同一直线上，点A,D 在直线CE 的同侧，AB=AC,EC=ED,CED BAC ∠=∠,直线AE,BD 交于点F ，（1）如图①，若=∠=∠AFB BAC 则,60 _____________;如图②，若=∠=∠AFB BAC 则,90__________________（2）如图③，若=∠=∠AFB BAC 则,α___________(用含α的式子表示)（3）将图③中的ABC ∆绕点C 旋转（点F 不与点A,B 重合），得图④或⑤，在图④中，α∠∠与AFB 的数量关系是_________;在图⑤中，α∠∠与AFB 的数量关系是__________请你任选其中一个结论证明。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第2讲 几何变换——旋转
典型例题
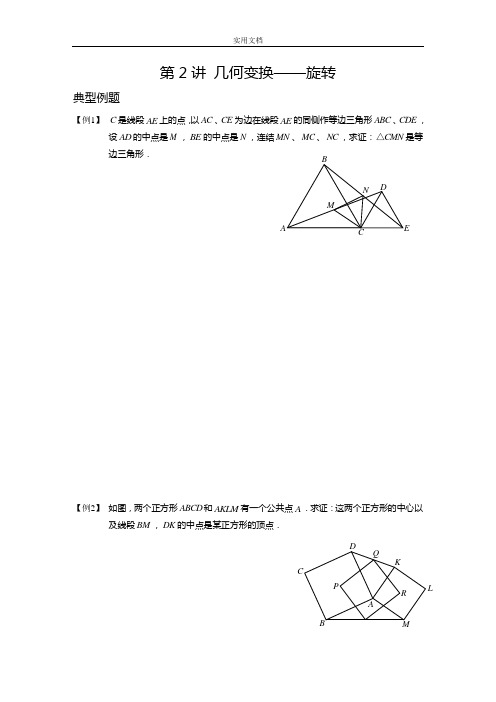
【例1】 C 是线段AE 上的点，以AC 、CE 为边在线段AE 的同侧作等边三角形ABC 、CDE ，设AD
的中点是M ，BE 的中点是N ，连结MN 、MC 、NC ，求证：CMN △是等边三角形．
【例2】 如图，两个正方形ABCD 和AKLM 有一个公共点A ．求证：这两个正方形的中心以及线段BM ，
DK 的中点是某正方形的顶点．
【例3】 已知：如图，ABC △、CDE △、EHK △都在等边三角形，且A 、D 、K 共线，AD DK ．
求证：HBD △也是等边三角形．
K
E
C
H
D
B
A
L
【例4】 ABC △是等边三角形，P 是AB 边的中点，Q 是AC 边的中点，R 为BC 边的中点，M 为RC
上任意一点，且PMS △是等边三角形，S 与Q 在PM 的同侧，求证：RM QS =．
【例5】 ABCD 是正方形，P 是ABCD 内一点，1PA =，3PB =
，PD =ABCD 的面积．
【例6】 P 是等边三角形ABC 内的一点，6PA =，8PB =，10PC =．求ABC △的边长．
Q ⋅
S
M
P
C
B
A
R D
【例7】 设O 是等边ABC △内一点，已知115AOB ︒∠=，125BOC ︒∠=，求以线段OA 、OB 、OC 为
边所构成的三角形的各内角大小．
【例8】 如图，在ABC △中，90ACB ︒∠=，AC BC =，P 是ABC △内一点，3PA =，1PB =，2PC =，
求BPC ∠．
【例9】 如图，已知ABC △中，90A = ，AB AC =，D 为BC 上一点，求证：2222BD DC AD +=．
A
P
C
B
A
D
C
B
【例10】 如图，在等腰直角ABC △中，90ACB ︒∠=，CA CB =，P 、Q 在斜边AB 上，且45PCQ ︒∠=，
求证：222PQ AP BQ =+．
【例11】 在正方形ABCD 中，已知E 、F 分别是边BC 、CD 上的点，满足EF BE DF =+，AE 、AF
分别与对角线BD 交于M 、N ．求证： （1）45EAF ︒∠=； （2）222MN BM DN =+．
【例12】 如图，在梯形ABCD 中，AD BC ∥，AD CD ⊥，2BC CD AD ==，E 是CD 上一点，且
45ABE ︒∠=，AD α=．求CE 的长．
A
Q
B
C
P
E D
C
B
A
D
F
【例13】 已知：ABC △中，120A ︒∠≥，P 是不与A 重合的定点，求证：PA PB PC AB AC +++＞．
【例14】 已知：如图，ABD △是等边三角形，ABC △中，BC a =，CA b =．问：当ACB ∠为何值时，
C 、
D 两点的距离最大？最大值是多少？
【例15】 已知ABC △，以其各边为底边，向ABC △的外部作等腰三角形ABD 、BCE 、CAF ，使顶角
都等于120︒，求证：DEF △是正三角形．
P
C
B
A
E
B
D
A
F
C
【例16】 已知：ABC △是锐角三角形，三边长分别是a 、b 、c ，O 是ABC △内的一点，
120AOB BOC COA ︒∠=∠=∠=，OA u =，OB v =，OC w =，DEF △是等边三角形，P 是DEF
△内一点，PD a =，PE b =，PF c =． 求证：DEF △的边长等于u v w ++．
【例17】 已知：三条平行直线l 、m 、n ，求证：存在一个等边三角形ABC ，使顶点A 、B 、C 分别
在l 、m 、n 上．
作业
1. 已知：ABCD 是正方形，O 是其中心，OEFG 也是正方形，两个正方形的边长都是a ，OG 、OE
分别交CD 、BC 于H 、K ．求证：21
4OKCH S a =．
2. 已知：如图，ABCD 是正方形，12∠=∠．求证：BE DF AE +=．
3. ABC △是等边三角形，P 是其内的一点，3PA =，4PB =，5PC =，求ABC △的面积．
4.
P 是等边ABC △内部一点，APB ∠、BPC ∠、CPA ∠的大小之比是5:6:7，求以PA 、PB 、PC 为
边的三角形的三个角的大小之比．
1
F
D
E
A
C
2
B
5. 等边ABC △
的边长a =点P 是ABC △内一点，且222PA PB PC +=，若5PC =，求PA 、
PB 的长．
6. 在梯形ABCD 中，AD BC ∥（BC AD ＞），90D ︒∠=，12BC CD ==，E 在CD 上，45ABE ︒∠=，
若10AE =，求CE 的长．
7. 如图，P 、Q 是边长为1的正方形ABCD 内两点，使得45PAQ PCQ ︒∠=∠=．求PAB PCQ QAD
S S S ∆∆∆++的值．
E D
C
B
A。