刚体动力学课件
刚体动力学

●
刚体基本动力学量
现在取 Axyz 坐标系为一个平动参考系 , 则刚体上的 R 点相对速度为 v r R =× R
dV
【定理】刚体相对动量为 p r =× mt R C
证明:pr =∫ v r R dV =∫ × R R dV
=×∫ R R dV =×m t RC(证毕)
⇒ L'A =∫ R2 I − R R ⋅ R dV =[∫ R2 I − R R R dV ]⋅
= J A⋅
(证毕)
1 1 ' 【定理】刚体相对动能为 T r = ⋅L A= ⋅J A⋅ 2 2
证明: T r=
1 1 2 v r R dV = ∫ v r⋅v r R dV ∫ 2 2 1 1 × R ⋅ v R dV = R × v r ⋅ R dV ∫ ∫ r 2 2
【推论】匀质刚体如果有一过 A 的镜像对称面,则过 A 且 与该镜像面垂直的轴是主轴;如果过 A 有两个正交的 镜像面,则两镜像面过 A 点的法线以及镜像面的交线 构成主轴系;匀质旋转体的旋转轴和任意与之正交的 两正交轴构成主轴系 . (请自己根据定义证明) 【定理】假定角速度在主轴坐标系下表示为
d d' J A⋅ 是矢量, J A⋅ = J A⋅× J A⋅ dt dt
⇒⋯⇒ J A⋅ = J XZ X J YZ Y J ZZ Z = ˙ Z ˙
d e ⋅M A ⇒ Z⋅ J A⋅= J ZZ = ≡M Z ¨ Z dt
2
J lk = J kl
(证毕)
因为:
lk =kl , Rl R k = Rk Rl
注:一般把 Jlk 称为惯量系数,由于对称性,只有 6 个是独立的 注:如果 AXYZ 不是固连在刚体上的坐标系,则 R 相对 AXYZ 有 转动,那么在 AXYZ 上看到的质量分布一般会随时间改变, 故在这个坐标系中惯量系数依赖于时间 . 注:如果 AXYZ 不是固连在刚体上的坐标系,在少数有良好对称性 的情况下 AXYZ 上看到的质量分布可能不随时间改变,此时在 这个坐标系中惯量系数是常数 .
第7.5节刚体平面运动的动力学

第7.5节 刚体平面运动的动力学7.5.1 10m 搞得烟筒因底部损坏而倒下来,求其上端到达地面时的线速度。
设倾倒时底部未移动。
可近似认为烟筒为均质杆。
解:烟筒的长度l =10m 。
设烟筒上端到达地面的瞬间,烟筒绕其底部的转动角速度为ω。
在倾倒过程中,只受重力作用,做的功为:mg ⋅½l 。
由刚体定轴转动的动能定理:lgmlI I l mg 323122121=∴==⋅ωω烟筒上端到达地面时的线速度为:s m gl l v /2.17108.933≈⨯⨯===ω7.5.2 用四根质量各为m 长度各为l 的均质细杆制成正方形框架,可围绕其中一边的中点在竖直平面内转动,支点O 是光滑的.最初,框架处于静止且AB 边沿竖直方向,释放后向下摆动,求当AB 边达到水平时,框架质心的线速度C v。
以及框架作用于支点的压力N .解:先求正方形框架对通过其质心且与其垂直的转轴(质心轴)的转动惯量:框架的质心位于框架的中心,即两条对角线的交点上。
每根细杆对其本身的质心轴的转动惯量:21210ml I =,细杆的质心与框架的质心的距离为l 21,由平行轴定理:2342210])([4ml l m I I c =⋅+⋅=再由平行轴定理,得框架对通过0点的转轴的转动惯量:237221)(4ml l m I I c =⋅+=(1)求框架质心的线速度v c框架在下摆过程中,只有重力做功,机械能守恒。
选取杆AB 达到水平时框架质心位置位势能零点,得:gll v l h m M I Mgh c lgc c 7321712212214===∴===ωωω(2)求框架对支点的压力N以框架为研究对象,它受到重力M g 和支点的支撑力N 的作用,由质心运动定理:c a M g M N =+取自然坐标系,τ沿水平方向,n 铅直向上,得投影方程:βτττc n c c n n Mh Ma N mgmg mg N mg l gl m h v M Ma Mg N n===+=⇒=⋅===-7372472421732744:ˆ:ˆ在铅直位置时,外力矩为0,故角加速度β=0,==〉N τ = 07.5.3 由长为l ,质量各为m 的均质细杆组成正方形框架,其中一角连于光滑水平转轴O ,转轴与框架所在平面垂直.最初,对角线OP 处于水平,然后从静止开始向下自由摆动.求OP 对角线与水平成450时P 点的速度,并求此时框架对支点的作用力.解:先求正方形框架对通过其质心且与其垂直的转轴(质心轴)的转动惯量:框架的质心位于框架的中心,即两条对角线的交点上。
《刚体动力学 》课件

牛顿第二定律
物体的加速度与作用在物 体上的力成正比,与物体 的质量成反比。
牛顿第三定律
对于任何两个相互作用的 物体,作用力和反作用力 总是大小相等,方向相反 ,作用在同一条直线上。
刚体的平动
刚体的平动是指刚体在空间中 的位置随时间的变化而变化, 而刚体的形状和大小保持不变
的运动。
刚体的平动具有三个自由度 ,即三个方向的平动。
05
刚体的动力学方程
刚体的动力学方程
牛顿第二定律
刚体的加速度与作用力成正比,与刚体质量 成反比。
刚体的转动定律
刚体的角加速度与作用力矩成正比,与刚体 对转动轴的转动惯量成反比。
刚体的动量方程
刚体的动量变化率等于作用力对时间的积分 。
刚体的自由度与约束
自由度
描述刚体运动的独立变量,如平动自由度和转动 自由度。
约束
限制刚体运动的条件,如固定约束、滑动约束等 。
约束方程
描述刚体运动受约束的数学表达式。
刚体的动力学方程的求解方法
解析法
通过代数运算求解动力学方程,适用于简单问 题。
数值法
通过迭代逼近求解动力学方程,适用于复杂问 题。
近似法
通过近似模型求解动力学方程,适用于实际问题。
06
刚体动力学中的问题与实例 分析
人工智能和机器学习的发展将为刚体 动力学的研究提供新的思路和方法, 有助于解决复杂动力学问题。
感谢您的观看
THANKS
船舶工程
在船舶工程中,刚体动力学 用于研究船舶的航行稳定性 、推进效率以及船舶结构的 安全性等。
兵器科学与技术
在兵器科学与技术领域,刚 体动力学用于研究弹药的发 射动力学、火炮的射击精度 和稳定性等。
刚体与流体

第三章 刚体和流体P.1§3-1刚体及其运动规律刚体:物体上任意两点 之间的距离保持不变 在力的作用下不发生形 变的物体。
P.23-1-1 刚体的运动平动: 刚体在运动过程 中,其上任意两点的 连线始终保持平行。
注:可以用质点动力学的方法来处理刚体的平 动问题。
P.3转动:刚体上所有质点都绕同一直线作圆周运动。
这种运动称为刚体的转动。
这条直线称为转轴。
定轴转动: 转轴固定不动的转动。
定点转动: 转轴上一点相对于参考系 静止,转轴方向随时间不 断变化。
例如陀螺和雷达天线。
P.4P.53-1-2刚体对定轴的角动量zv viv质元:组成物体的微颗粒元质元对O点的角动量为ωv v v Li = Ri × (mi vi )Li = mi Ri v iv Li 沿转轴Oz的投影为Liz = Li cos(v Lixv riγOmiv Riyπ2− γ ) = mi Ri vi sin γ = mi ri vi = mi ri 2ωP.6刚体对Oz轴的角动量为Lz = ∑ Liz = ∑ mi ri 2ω = (∑ mi ri 2 )ωi i i令J z = ∑mi rii2kg⋅ m2J z 为刚体对 Oz 轴的转动惯量比较:Lz = J z ωp = mvP.7转动惯量的定义式:J = ∑ mi rii2连续体的转动惯量:J = ∫ r dm2 V转动惯量的物理意义:反映刚体转动惯性的量度 转动惯量仅取决于刚体本身的性质,即与刚体 的质量、质量分布以及转轴的位置有关。
P.8转动惯量的计算J = ∑ m i ri 2i若质量连续分布 J = r 2 dm∫在(SI)中,J 的单位:kgm2dm为质量元,简称质元。
其计算方法如下:质量为线分布 质量为面分布 质量为体分布dm = λ dlλ为质量的线密度。
σ为质量的面密度。
ρ为质量的体密度。
dm = σ dsdm = ρ dV面分布线分布体分布P.9对于质量连续分布的刚体:J = ∫ r dm = ∫ r ρdV2 2 V V(体质量分布) (面质量分布) (线质量分布)J = ∫ r dm = ∫ r σdS2 2 S SJ = ∫ r dm = ∫ r λdl2 2 L LP.10例的细棒绕一端的转动惯量。
刚体动力学
n i 1
1 2
Δmi
vi2
o ri vi
mi
1 2
n i 1
Δmi ri 2
2
1
式中
n
mi
ri2
称为刚体对转轴的转动惯量
。
i 1
用J 表示:
n
J mi ri2
i 1
代入动能公式中, 得到刚体转动动能的一般表达式
Ek
1 2
J2
Ek
1 2
mv2
刚体转动动能与质点运动动能在表达形式上是相
3
若刚体的质量连续分布 , 转动惯量中的求和号 用积分号代替
J r 2dm r 2 dV
单位:kg.m2
讨论:1.质量越大,转动惯量越大。 2.在总质量一定的条件下,刚体的质元分布 离轴越远,转动惯量越大。和质量分布有关。 3.转轴位置不一样,转动惯量不同。
与转动惯量有关的因素:
0
R 2πr 3 d r
0
2π R r3 d r 1 mR2
0
2
9
三、力矩作的功
力 矩 (moment of force)
力矩
M
r
F
大小 M= F r sinθ= F d
方向 右手定则
力臂:从转轴Z与截面
的交点O到力F的作用
线的垂直距离d称为力
对转轴的力臂
M
i 1
矩的代数和, 也就是作用于刚体的外力对转轴的合外
力矩Mz 。14来自如果刚体在力矩Mz 的作用下绕固定轴从位置1转 到2 , 在此过程中力矩所作的功为
《刚体动力学 》课件

常用方法:拉格朗日方程、 哈密顿原理等
注意事项:需要熟练掌握 数学基础
数值法
定义:数值法 是一种通过数 值计算求解刚 体动力学问题
的方法
特点:精度高、 计算速度快、 适用于复杂问
题
常用算法:有 限元法、有限 差分法、有限
体积法等
应用领域:航 空航天、机械 制造、土木工
程等领域
近似法
近似法的定义和特点
刚体转动实例
风力发电机:利用风力驱动风车叶片旋转,通过变速器和齿轮装置将动力传递至发电机,最终 转化为电能。
搅拌机:利用电动机驱动搅拌器旋转,对物料进行搅拌、混合和输送等操作。
洗衣机:利用电动机驱动洗衣机的滚筒旋转,通过水和洗涤剂的作用将衣物清洗干净。
旋转木马:利用电动机驱动旋转木马旋转,使人们能够欣赏到各种美丽的景观和音乐。
物理教师
需要了解刚体 动力学知识的
相关人员
Part Three
刚体动力学概述
刚体定义
刚体:在运动过程中,其内部任意两点间的距离始终保持不变的物体 刚体运动:刚体的运动是相对于其他物体的位置和姿态的变化
刚体动力学:研究刚体运动过程中所受到的力、力矩以及运动状态变化规律的科学
刚体动力学的研究对象:各种工程实际中的刚体,如机械零件、构件、机构等
动能定理
定义:动能定理是描述物体动能变化的定理 表达式:动能定理的表达式为ΔE=W 应用范围:动能定理适用于一切具有动能变化的物理系统 注意事项:在使用动能定理时需要注意初始和终了状态的动能
Part Five
刚体动力学应用实 例
刚体平动实例
刚体平动定义 刚体平动应用实例1 刚体平动应用实例2 刚体平动应用实例3
刚体动力学在各领 域的应用
《刚体动力学》课件

单击此处输入你的项正文,文字是您思想的提炼。
应用场景:碰撞、打击、爆炸等 角动量定理 角动量定理
定义:角动量是物体转动惯量和角速度的乘积 单击此处输入你的项正文,文字是您思想的提炼。
角动量定理公式:L=Iω
单击此处输入你的项正文,文字是您思想的提炼。
应用场景:行星运动、陀螺仪等
刚体的滚动和滑动摩擦
刚体滚动:刚体在平面内绕固定点转动,滚动摩擦力产生的原因和影响
刚体滑动摩擦:刚体在平面内滑动时产生的摩擦力,滑动摩擦系数与接触面材料和粗糙度等因素 的关系
刚体滚动和滑动摩擦的应用实例:例如,汽车轮胎与地面之间的滚动摩擦力,以及机械零件之间 的滑动摩擦力等
刚体滚动和滑动摩擦的实验研究:通过实验研究刚体滚动和滑动摩擦力的影响因素和规律,为实 际应用提供理论支持
04
刚体动力学基本原理
牛顿第二定律
定义:物体加速度的大小跟作用 力成正比,跟物体的质量成反比
应用:解释物体运动状态变化的 原因
添加标题
添加标题
公式:F=ma
添加标题
添加标题
注意事项:只适用于宏观低速运 动的物体
动量定理和角动量定理
定义:动量是物体质量与速度的乘积
单击此处输入你的项正文,文字是您思想的提炼。
刚体动力学研究内容
刚体的定义和性质 刚体运动的基本形式 刚体动力学的基本方程 刚体动力学的研究方法
刚体动力学发展历程
早期发展:古代力学对刚体的研究 经典力学时期:牛顿、伽利略等经典力学大师对刚体动力学的研究 弹性力学时期:弹性力学的发展对刚体动力学的影响 现代发展:计算机技术和数值模拟方法在刚体动力学中的应用
课程内容:刚体 的平动、转动、 碰撞等动力、力学等相关专 业的本科生和研 究生
高等教育:刚体19952

注意:对同轴的转动惯量 才具有可加减性。
J
R
dJ
0
2mr 4dr R3
2 5
mR2
30
一些均匀刚体的转动惯量表
31
四:平行轴定理
J D JC md 2
d
m
D
C
32
练习 求长 L、质量 m 的均匀杆对 z 轴的转动惯量
z
A
mB
L4 o C
L
Jz
l 2dm 3L 4 m l 2dl 7 mL2
L 4 L
48
解二:
Jz
J oA
J oB
1 3
m 4
L 4
2
1 3
3m 4
3L 4
2
7 48
mL2
解三:
Jz
JC
m
L 4
2
1 12
mL2
m
L 4
2
7 48
mL2
33
§4-3 角动量 角动量守恒定律
一、质点的角动量定理和角动量守恒定律
数为 ,求 m1 下落的加速度和两段绳中的张力。
m2
ro m
m1
解:在地面参考系中,选取 m1 、m2 和滑轮为研究对
象,分别运用牛顿定律和刚体定轴转动定律得:
19
T1
m1
a
m1g
a
N
m2 g m2
T2
m2 g
T2
向里+
Ny
o
Nx
T1
列方程如下: 可求解
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
2 1
M z d
力矩的瞬时功率可以表示为
P
dA dt
Mz
d
dt
Mz
式中是刚体绕转轴的角速度。
20
四、动能定理 (theorem of kinetic energy )
根据功能原理, 外力和非保守内力对系统作的总功 等于系统机械能的增量。对于刚体一切内力所作的功 都为零。对定轴转动的刚体 , 外力所作的功即为外力 矩所作的功; 系统的机械能为刚体的转动动能。
Mzi 是外力Fi 对转轴Oz的力矩。
18
在整个刚体转过d角的过程中,n个外力所作的总功为
n
n
dA dAi ( M zi )d Mzd
i 1
i 1
n
式中 M zi 是作用于刚体的所有外力对Oz轴的力
i 1
矩的代数和, 也就是作用于刚体的外力对转轴的合外
力矩Mz 。
19
如果刚体在力矩Mz 的作用下绕固定轴从位置1转 到2 , 在此过程中力矩所作的功为
dA dEk
将转动动能的具体形式代入上式并积分, 得
A
1 2
J
2 2
1 2
J
2 1
定轴转动的刚体,外力矩作的功等于刚体转动动能
的增量,即作定轴转动刚体的动能定理。
21
或者利用
A 2 Md 1J d d 2 Jd
1
1 dt
1
A
2 1
Md
n i 1
1 2
Δmi
vi2
O ri vi
mi
1 2
n i1
Δmi ri 2
2
1
式中
n
mi
ri2
称为刚体对转轴的转动惯量
i 1
n
J mi ri2
i 1
若刚体的质量连续分布 , 形式变为
J r 2dm r 2 dV
SI制中,J的单位为kg·m2
则刚体转动动能的一般表达式
Ek
1 2
解: 方法一,盘的质量分布均匀, 盘的质量面密度为
m
R2
取半径为r、宽为 dr的圆环 如图所示,其质量为
y
R
dr
·r
O
x
dm 2 rdr
12
圆盘对Oz轴(过O点垂直于纸面)的转动惯量为
J z
R
0
r
2
d
m
R
0
2πr
3
d
r
2π
R
0
r3
dr
1 2
mR 2
根据垂直轴定理 J z J x J y
1 2
J 2
1 0.083 632 J 2
1.7 102J
7
方法二:
y
dx
O
x
x
J
0l ( x
l )2( m 2l
dx)
1 12
ml
2
8.3 102kg
m2
8
例 棒绕通过其左端点并与棒相垂直的转轴旋转, 求转动惯量。
y
dx
O
x
x
J左
0l
x2(m l
dx)
1 3
ml 2
9
两个定理:
1. 平行轴定理 J JC md 2
由于对称性, J J , 所以
x
y
Jz
2J x
1 2
mR 2
解得
Jx
1 mR 2 4
13
解: 方法二,
y
R
dr d
r
·
O
x
Jz
r 2 d m 2 0
R r 2(σrdrd ) 1 m R2
0
2
14
解: 方法三,
y
R
dr d
r
·
O
x
J x
y2dm 2 0
R
(rsin
)2 (σrdrd
§3-2,3 刚体动力学
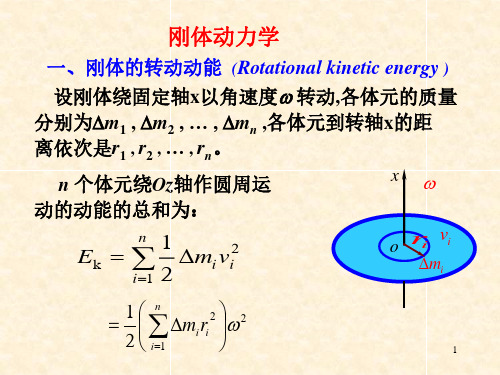
一、刚体的转动动能 (Rotational kinetic energy )
设刚体绕固定轴Oz以角速度 转动,各体元的质量
分别为m1 , m2 , … , mn ,各体元到转轴Oz的距离
依次是r1 , r2 , … , rn。 n 个体元绕Oz轴作圆周运动的
x
动能的总和为
Ek
点,建立坐标系Oxy,取y
Ox
l x
2
轴为转轴,如图所示。在距离转轴为x 处取棒元dx,
其质量为
m
dm dx
l
6
根据式 J r 2dm , 应有
J
x l/ 2 2
l/ 2
m dx
l
1 3
m l
3
x
l/ 2 l/ 2
1 ml 2 8.3 102 kg m 2 12
棒的转动动能为
Ek
式中JC 为刚体对通过质心的轴的转动惯量, m是刚 体的质量,d是两平行轴之间的距离 。
2. 垂直轴定理
若z 轴垂直于厚度为无限小的刚体薄板板面, xy 平 面与板面重合, 则此刚体薄板对三个坐标轴的转动惯
量有如下关系 J z J x J y
注意:对于厚度不是无限小的刚体板, 垂直轴定理不适用。
3
几 种 常 见 形 状 的 刚 体 的 转 动 惯 量
4
5
例1 一根质量为m=1.0kg、长为l=1.0m 的均匀细棒,
绕通过棒的中心并与棒相垂直的转轴以角速度=63
rads-1 旋转,求转动动能。 方法一:
解: 先求细棒对转轴的 转动惯量J,然后求转动动
y
dx
能Ek。
将棒的中点取为坐标原 l 2
10
例2 在上一例题中, 对于均匀细棒, 我们已求得对通 过棒心并与棒垂直的轴的转动惯量为
J 1 ml 2 12
求对通过棒端并与棒垂直的轴的J。
解:
两平行轴的距离
d
1 l
,
代入平行轴定理,
得
2
J J C md 2
1 ml 2 m( l )2 1 ml 2
12
23
11
例 3 求质量为m、半径为R 的均质薄圆盘对通过盘心 并处于盘面内的轴的转动惯量。
J2
2
二、刚体的转动惯量 (Moment of inertia )
转动惯量与质点的运动速度无关,影响的因素 有:刚体的质量、刚体的形状(质量分布)、转轴的 位置。
只有形状比较简单而密度又有规则地分布的物体 才能用数学方法求出它的转动惯量。对形状复杂而 密度又不均匀的物体,求转动惯量的最好办法是用 实验方法测定。
)
1
m R2
0
4
Jz
Jx
Jy
2J x
1 4
m R2
15
三、力矩作的功
力不在转动平面内时,
M rF
r (F1 F2 )
r F1 r F2
r F1
只能引起轴的变
形, 对定轴转动无贡献。
rr F1 F
r
转动
平面
r
F2
16
对定轴转动的刚体起作用的只是力矩沿转轴的分量 ,即若取转轴为z轴,则起作用的只是MZ。而提供MZ 的只是外力在转动平面内的投影,与外力沿转轴方向 的分量无关。所以,在讨论刚体定轴转动时,只需考 虑外力在转动平面内的分力即可。 约定:在定轴动问题中,如不加说明,所指的力矩均 指力在转动平面内的分力对转轴的力矩。
17
是假F设1 ,作F2用,于, 以Fnz。轴为转轴的刚体上的多个外力分别
在刚体转动中,外力 Fi 所作的元功为
d
Ai
Fi
d
ri
F d r cos
ii
i
d
Fi
O
r i
ds i
i
Pi
F d s cos
i
i
i
因为dsi = ri d,并且cosi = sini,所以
dAi Firi sini d Mzid
