(精品文献)PID控制算法的C语言实现设计论文
PID控制算法的C语言实现(完整版)

PID控制算法的C语言实现(完整版) 在现代工业生产中,为了实现对生产过程的精确控制,我们需要采用一种能够根据实际需求自动调整参数的控制算法。
PID(Proportional-Integral-Derivative)控制算法就是这样一种广泛应用于工业控制系统的算法。
本文将详细介绍PID控制算法的C语言实现,包括算法的基本原理、实现方法以及注意事项。
我们来了解一下PID控制算法的基本原理。
PID控制器由三个部分组成:比例(P)、积分(I)和微分(D)。
这三个部分分别对误差信号进行处理,然后将处理后的信号相加得到控制输出。
具体来说,比例部分根据误差信号的大小产生相应的控制作用;积分部分对误差信号进行累积,以消除系统的静差;微分部分对误差信号的变化趋势进行预测,以便及时调整控制策略。
通过这三个部分的综合作用,PID控制器能够实现对生产过程的精确控制。
接下来,我们来看一下如何用C语言实现PID控制算法。
我们需要定义一些变量来存储所需的参数和状态信息。
例如,我们需要定义比例系数Kp、积分系数Ki、微分系数Kd以及误差信号e等。
我们还需要定义一些变量来存储上一次的误差信号和积分项等。
这些变量的定义如下:```cdouble Kp, Ki, Kd; // 比例、积分、微分系数double e; // 当前误差信号double de; // 当前误差信号的导数double last_e; // 上一次的误差信号double integral; // 积分项有了这些变量之后,我们就可以开始实现PID控制器的计算过程了。
PID控制器的计算过程主要包括以下几个步骤:1. 计算误差信号:当前误差信号等于期望值与实际值之差。
2. 计算比例项:比例项等于当前误差信号乘以比例系数Kp;3. 计算积分项:积分项等于当前误差信号乘以积分系数Ki加上累积误差信号乘以积分系数Ki;4. 计算微分项:微分项等于当前误差信号的导数乘以微分系数Kd;5. 计算控制输出:控制输出等于比例项、积分项和微分项之和。
温度控制的PID算法 及C程序实现
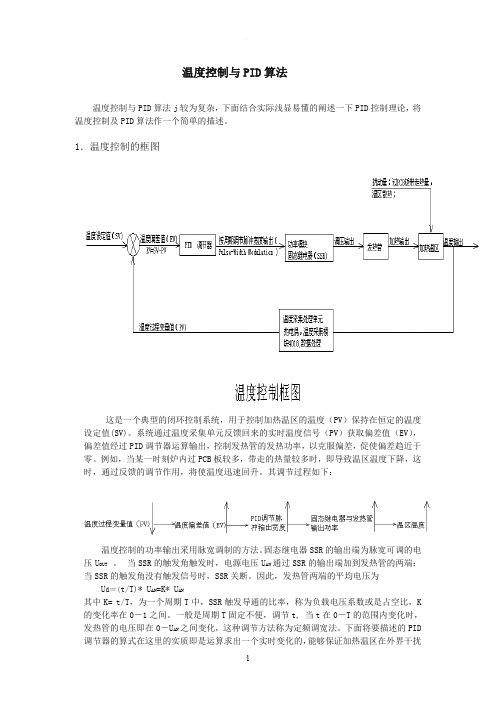
温度控制与PID算法温度控制与PID算法j较为复杂,下面结合实际浅显易懂的阐述一下PID控制理论,将温度控制及PID算法作一个简单的描述。
1.温度控制的框图这是一个典型的闭环控制系统,用于控制加热温区的温度(PV)保持在恒定的温度设定值(SV)。
系统通过温度采集单元反馈回来的实时温度信号(PV)获取偏差值(EV),偏差值经过PID调节器运算输出,控制发热管的发热功率,以克服偏差,促使偏差趋近于零。
例如,当某一时刻炉内过PCB板较多,带走的热量较多时,即导致温区温度下降,这时,通过反馈的调节作用,将使温度迅速回升。
其调节过程如下:温度控制的功率输出采用脉宽调制的方法。
固态继电器SSR的输出端为脉宽可调的电压U OUT 。
当SSR的触发角触发时,电源电压U AN通过SSR的输出端加到发热管的两端;当SSR的触发角没有触发信号时,SSR关断。
因此,发热管两端的平均电压为U d=(t/T)* U AN=K* U AN其中K=t/T,为一个周期T中,SSR触发导通的比率,称为负载电压系数或是占空比,K 的变化率在0-1之间。
一般是周期T固定不便,调节t, 当t在0-T的范围内变化时,发热管的电压即在0-U AN之间变化,这种调节方法称为定频调宽法。
下面将要描述的PID 调节器的算式在这里的实质即是运算求出一个实时变化的,能够保证加热温区在外界干扰的情况下仍能保持温度在一个较小的范围内变化的合理的负载电压系数K。
2.温度控制的两个阶段温度控制系统是一个惯性较大的系统,也就是说,当给温区开始加热之后,并不能立即观察得到温区温度的明显上升;同样的,当关闭加热之后,温区的温度仍然有一定程度的上升。
另外,热电偶对温度的检测,与实际的温区温度相比较,也存在一定的滞后效应。
这给温度的控制带来了困难。
因此,如果在温度检测值(PV)到达设定值时才关断输出,可能因温度的滞后效应而长时间超出设定值,需要较长时间才能回到设定值;如果在温度检测值(PV)未到设定值时即关断输出,则可能因关断较早而导致温度难以达到设定值。
基于C语言的数字PID控制算法及实现

参考文献
[1] 曹 书 生 , 等 . 网 络 业 务 流 模 型 综 述 [J]. 江 苏 通 信 技 术 ,2003,(05) [2] 刘 建 辉 , 等 . 基 于 离 散 MMDP 信 源 模 型 的 ATM 网 络 排 队 性 能 仿 真 [J]. 计 算 机 仿 真 . [3] 杨 敏 维 .ATM 突 发 模 型 MMDP 的 信 元 丢 失 率 估 计 [J]. 湖 南 大 学 学 报 ,1999,(02). [4] 陈 文 云 , 等 . 基 于 ON/OFF 信 源 模 型 的 信 元 丢 失 分 析 [J]. 数 字 通 信 ,2 000, (01 ). [5] 程 伟 明 . 基 于 ATM 网 络 的 多 媒 体 通 信 [J]. 现 代 电 信 科 技 ,1998, (07 ). [6] 过 莉 .ATM 网 络 实 时 通 信 系 统 的 响 应 时 间 分 析 [J]. 电 机 电 器 技 术 , 2 00 3 , ( 06 ) . [7] 张 如 娟 . 基 于 ATM 技 术 的 多 协 议 信 息 传 送 及 应 用 [J]. 甘肃科技 , 2001,(03). [8] A bdelnaser Adas.Traffic Models in Broadband Networks[J]. IEEE communications Magazine. Ju期 , 一 般 为 200ms, e ( k ) 为 系 统 第 k 次 采 样 时 刻 的 偏 差 值 , e ( k -l) 为 系 统 第 ( k -l) 次 采 样 时 刻 的 偏 差 值 , i 为 采 样 序 号 , i =0,1,2, … 。 将 上 面 的 (3) 式 和 (4) 式 代 入 (1) 式 , 则 可 以 得 到 离 散 的 PID 表 达 式 i T e( j ) + TD [ e ( k )- e ( k -1)]} u ( i )= K p { e ( i )+ T (5) T 1 j =0 如 果 采 样 周 期 T 足 够 小 (200ms), 该 算 式 可 以 很 好 的 逼 近 模 拟 PID 算式 , 因 而 使 被 控 过 程 与 连 续 控 制 过 程 十 分 接 近 。 通 常 把 (5) 式 称 为 PID 的 位 置 式 控 制 算 法 。 若 把 (5) 式 进 行 转 化 , 则 : 0.2 td u ( i )= k * e +k* e +k* (p v x -p v 1 ) (6 ) 0 .2 i ti i 式 (6) 即 为 数 字 PID 控 制 算 法 的 编 程 表 达 式 ,p vx 为 第 ( i -1) 次 测 量 值 ,p v1 为 第 i 次 测 量 值 。 其 程 序 流 程 图 如 图 1所 示 。 其 中 给 定 转 换 s v1 /25+1 是 要 把 设 定 值 数 模 转 化 , 比 如 要 求 给 定 液 位 100CM, 则 通 过 转 换 100/25+1=5, 代 表 的 是 最 高 液 位 所 测 量 的 电 压 为 5V 。 而 对 于 数 模 转 化 (O P1 +25)/ 6 .2 5 是 要 把 输 出 转 化 为 电 流 大 小 , 假 如 输 出 O P1 为 1 0 0% , 那 么 (100+25)/6.25=20, 代 表 输 出 为 最 大 电 流 20MA 。 对 于 输 入 输 出 量 ,要 注 意 内 部 的 数 模 /模 数 转 换 关 系 :经 过 变 送 器 输 出 (1 ~ 5v) 模 拟 量 , 送 入 A/D 模 块 转 化 为 (0 ~ 250) 数 字 量 , 数 字 量 要 与 给 定 量 进 行 比 较 , 就 必 须 要 数 模 转 化 , 把 0 ~ 250 十 进 制 数 转 换 为 1.00 ~ 5.00V, 数 据 处 理 公 式 参 考 下 面 程 序 。 反 之 ,同 样 可 把 (4 ~ 20mA) 进 行 模 数 转 化 , 得 出 0 ~ 250 十 进 制 数 , 再 经 过 D/A 模 块 , 把模拟量送给执行元件。 ( 图 1)
PID控制算法的C语言实现(完整版)

PID控制算法的C语言实现一 PID算法原理之欧侯瑞魂创作最近两天在考虑一般控制算法的C语言实现问题,发现网络上尚没有一套完整的比较体系的讲解。
于是总结了几天,整理一套思路分享给大家。
在工业应用中PID及其衍生算法是应用最广泛的算法之一,是当之无愧的万能算法,如果能够熟练掌握PID算法的设计与实现过程,对于一般的研发人员来讲,应该是足够应对一般研发问题了,而难能可贵的是,在我所接触的控制算法当中,PID控制算法又是最简单,最能体现反馈思想的控制算法,可谓经典中的经典。
经典的未必是复杂的,经典的东西经常是简单的,而且是最简单的,想想牛顿的力学三大定律吧,想想爱因斯坦的质能方程吧,何等的简单!简单的不是原始的,简单的也不是落后的,简单到了美的程度。
先看看PID算法的一般形式:PID的流程简单到了不克不及再简单的程度,通过误差信号控制被控量,而控制器自己就是比例、积分、微分三个环节的加和。
这里我们规定(在t时刻):1.输入量为rin(t);2.输出量为rout(t);3.偏差量为err(t)=rin(t)rout(t);pid的控制规律为理解一下这个公式,主要从下面几个问题着手,为了便于理解,把控制环境具体一下:1.规定这个流程是用来为直流电机调速的;2.输入量rin(t)为电机转速预定值;3.输出量rout(t)为电机转速实际值;4.执行器为直流电机;5.传感器为光电码盘,假设码盘为10线;6.直流电机采取PWM调速转速用单位转/min 暗示;不难看出以下结论:1.输入量rin(t)为电机转速预定值(转/min);2. 输出量rout(t)为电机转速实际值(转/min);3.偏差量为预定值和实际值之差(转/min);那么以下几个问题需要弄清楚:1.通过PID环节之后的U(t)是什么值呢?2.控制执行器(直流电机)转动转速应该为电压值(也就是PWM占空比)。
3.那么U(t)与PWM之间存在怎样的联系呢?/user1/3407/archives//33541.html(见附录1)这篇文章上给出了一种方法,即,每个电压对应一个转速,电压和转速之间呈现线性关系。
PID控制算法的c语言实现十二模糊PID的参数整定

PID控制算法的c语⾔实现⼗⼆模糊PID的参数整定这⼏天⼀直在考虑如何能够把这⼀节的内容说清楚,对于PID⽽⾔应⽤并没有多⼤难度,按照基本的算法设计思路和成熟的参数整定⽅法,就算是没有经过特殊训练和培训的⼈,也能够在较短的时间内容学会使⽤PID算法。
可问题是,如何能够透彻的理解PID算法,从⽽能够根据实际的情况设计出优秀的算法呢。
通过讲述公式和基本原理肯定是最能说明问题的,可是这样的话怕是犯了“专家”的错误了。
对于门槛⽐较低的技术⼈员来讲,依然不能透彻理解。
可是说的⼊⽿了,能不能透彻说明也是⼀个问题,所以斟酌了⼏天,整理了⼀下思路才开始完成PID系列⽂章的最后⼀篇。
我所说的最后⼀篇不代表PID的功能和发展就⽌步与此,仅仅是说明,透过这⼀些列的⽂章,基本上已经可以涵盖PID设计的要点,⾄于更深⼊的研究,就交给有需要的读者去做。
上⼀节中⼤致讲述了⼀下模糊算法。
实际上模糊算法的很多概念在上⼀节中并没有深⼊的解释。
举的例⼦也只是为了说明模糊算法的基本含义,真正的模糊算法是不能这么设计的,当然也不会这么简单。
模糊算法的核⼼是模糊规则,如果模糊规则制定的出⾊,那么模糊算法的控制效率就⾼。
其实这是智能算法的⼀般特性,规则是系统判断和处理的前提。
那么就说说PID的规则该怎么制定。
我们知道,模糊算法的本质是对PID的三个参数进⾏智能调节。
那么⾸先要提出的问题是如何对PID的参数进⾏调节?这个问题其实是参数整定的问题,现实当中有很多整定⽅法。
可是我们需要从根本上了解为什么这么整定,才能知道该如何建⽴数学模型进⾏分析。
那么要回答如何整定参数的问题,就需要先明⽩PID参数的作⽤都是什么?对系统有什么影响?我们从作⽤和副作⽤两个⽅⾯说明参数对系统的影响。
1.⽐例环节Kp,作⽤是加快系统的响应速度,提⾼系统的调节精度,副作⽤是会导致超调;2.积分环节Ki,作⽤是消除稳态误差,副作⽤是导致积分饱和现象;3.微分环节Kd,作⽤是改善系统的动态性能,副作⽤是延长系统的调节时间。
PID算法的C语言实现

PID算法的C语言实现PID(Proportional-Integral-Derivative)算法是一种常用的控制算法,被广泛应用于自动控制系统中。
它是通过计算系统当前的误差,来调整控制器的输出值,从而使得系统的输出与期望输出之间达到期望的关系。
以下是一个简单的PID算法的C语言实现示例:```c#include <stdio.h>//PID控制器参数float Kp = 1.0; // 比例系数float Ki = 0.5; // 积分系数float Kd = 0.2; // 微分系数//预设值float setpoint = 100.0;//PID控制器输出限制float outMin = 0.0;float outMax = 255.0;//PID控制器变量float integral = 0.0;float lastError = 0.0;//PID控制器计算函数//计算误差float error = setpoint - input;//计算比例项float proportional = Kp * error;//计算积分项integral += Ki * error;//计算微分项float derivative = Kd * (error - lastError);//保存上一次的误差lastError = error;//计算PID输出float output = proportional + integral + derivative; //限制输出值在指定范围内if (output > outMax)output = outMax;} else if (output < outMin)output = outMin;}return output;int maifloat processVariable = 0.0; // 进程变量,即被控制物理系统的输出值//模拟控制循环for (int i = 0; i < 100; i++)//获取控制器输出值//模拟物理系统processVariable += (output * 0.1);printf("Iteration: %d\tOutput: %.2f\tProcessVariable: %.2f\n", i, output, processVariable);}return 0;```上述代码中,首先定义了PID控制器的参数(比例系数Kp、积分系数Ki和微分系数Kd)、预设值(setpoint)以及PID控制器的输出限制(outMin和outMax)。
PID控制算法C语言

PID控制算法C语言PID控制算法是一种常用于工业控制系统的控制算法,用于调节和控制系统的输出,使其达到期望的目标值。
PID控制算法是由比例、积分和微分三个部分组成,通过对这三个部分的调节和组合,可以实现稳定、准确的控制。
1.比例(P)部分:比例控制器根据当前的误差,以比例系数乘以误差,产生一个控制量。
比例控制器的作用是根据误差的绝对值来调节控制量,其输出与误差成正比。
比例控制器的公式可以表示为:P=Kp*e(t),其中P为控制量,Kp为比例系数,e(t)为误差。
2. 积分(I)部分:积分控制器的作用是根据误差的累积值来调节控制量,主要对长期偏差进行修正。
积分控制器的公式可以表示为:I = Ki * ∫e(t)dt,其中I为控制量,Ki为积分系数,∫e(t)dt为误差的累积值。
3. 微分(D)部分:微分控制器的作用是根据误差的变化率来调节控制量,主要对瞬时变化进行修正。
微分控制器的公式可以表示为:D = Kd * de(t)/dt,其中D为控制量,Kd为微分系数,de(t)/dt为误差的变化率。
根据PID控制算法的公式,控制量可以表示为:PID=P+I+D。
通过对比例、积分、微分系数的调节,可以实现系统的稳定控制。
下面是一个用C语言实现的PID控制算法的示例代码:```c#include <stdio.h>float Kp = 0.5; // 比例系数float Ki = 0.2; // 积分系数float Kd = 0.1; // 微分系数float PID_Controller(float setpoint, float measured_value) static float last_error = 0; // 上次误差static float integral = 0; // 积分项//计算误差float error = setpoint - measured_value;//计算比例项float P = Kp * error;//计算积分项integral += error;float I = Ki * integral;//计算微分项float derivative = error - last_error;float D = Kd * derivative;//更新上次误差last_error = error;//计算控制量float control = P + I + D;return control;int mainfloat setpoint = 20; // 设定值float measured_value = 0; // 测量值for (int i = 0; i < 100; i++)//模拟测量值的变化measured_value += 0.1;//计算控制量float control = PID_Controller(setpoint, measured_value);printf("Measured value: %.1f, Control: %.1f\n",measured_value, control);}return 0;```以上是一个简单的PID控制算法的C语言实现示例。
PID控制算法的C语言实现(完整版)

PID控制算法的C语言实现(完整版) 嘿,伙计们!今天我们要聊聊一个非常实用的技能——PID控制算法。
PID是英文Proportional-Integral-Derivative的缩写,翻译过来就是“比例积分微分”。
这个算法在我们的日常生活中随处可见,比如空调、洗衣机等家电的温度调节,还有汽车的速度控制等等。
那么,这个看似高深莫测的算法到底是怎么实现的呢?别急,让我们一起揭开它的神秘面纱吧!我们来了解一下PID控制算法的基本概念。
PID控制算法主要包括三个部分:比例(P)、积分(I)和微分(D)。
这三个部分分别对误差进行处理,然后将处理后的结果相加,得到控制输出。
具体来说,比例部分主要负责消除误差的瞬时成分;积分部分主要负责消除误差的稳态成分;微分部分则负责预测误差的未来变化趋势。
通过这三个部分的综合作用,我们可以实现对系统的精确控制。
接下来,我们来看一下PID控制算法的具体实现。
我们需要定义一些变量和参数,比如比例系数Kp、积分系数Ki、微分系数Kd以及采样时间Ts等。
这些参数的选择对于算法的效果至关重要,需要根据实际应用场景进行调整。
然后,我们需要不断地对系统进行采样,计算出当前的状态值和期望值之间的误差e(t)。
误差e(t)可以通过以下公式计算得到:e(t) = 期望值实际值有了误差e(t),我们就可以开始计算PID控制器的输出了。
根据之前的介绍,PID控制器的输出由比例、积分和微分三个部分组成。
具体计算过程如下:1. 比例部分:计算比例系数Kp乘以误差e(t),得到比例输出u(t);2. 积分部分:计算积分系数Ki乘以误差e(t)的时间积分,得到积分输出u(t);3. 微分部分:计算微分系数Kd乘以误差e(t)的时间微分,得到微分输出u(t)。
将比例、积分和微分三个部分的输出相加,得到最终的控制输出u(t)。
这样,我们就完成了一次PID控制算法的计算过程。
这只是理论上的实现方法,实际上还需要考虑一些其他因素,比如控制器的稳定性、响应速度等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PID控制算法的C语言实现一 PID算法原理最近两天在考虑一般控制算法的C语言实现问题,发现网络上尚没有一套完整的比较体系的讲解。
于是总结了几天,整理一套思路分享给大家。
在工业应用中PID及其衍生算法是应用最广泛的算法之一,是当之无愧的万能算法,如果能够熟练掌握PID算法的设计与实现过程,对于一般的研发人员来讲,应该是足够应对一般研发问题了,而难能可贵的是,在我所接触的控制算法当中,PID控制算法又是最简单,最能体现反馈思想的控制算法,可谓经典中的经典。
经典的未必是复杂的,经典的东西常常是简单的,而且是最简单的,想想牛顿的力学三大定律吧,想想爱因斯坦的质能方程吧,何等的简单!简单的不是原始的,简单的也不是落后的,简单到了美的程度。
先看看PID算法的一般形式:PID的流程简单到了不能再简单的程度,通过误差信号控制被控量,而控制器本身就是比例、积分、微分三个环节的加和。
这里我们规定(在t时刻):1.输入量为rin(t);2.输出量为rout(t);3.偏差量为err(t)=rin(t)-rout(t);pid的控制规律为理解一下这个公式,主要从下面几个问题着手,为了便于理解,把控制环境具体一下:1.规定这个流程是用来为直流电机调速的;2.输入量rin(t)为电机转速预定值;3.输出量rout(t)为电机转速实际值;4.执行器为直流电机;5.传感器为光电码盘,假设码盘为10线;6.直流电机采用PWM调速转速用单位转/min表示;不难看出以下结论:1.输入量rin(t)为电机转速预定值(转/min);2. 输出量rout(t)为电机转速实际值(转/min);3.偏差量为预定值和实际值之差(转/min);那么以下几个问题需要弄清楚:1.通过PID环节之后的U(t)是什么值呢?2.控制执行器(直流电机)转动转速应该为电压值(也就是PWM占空比)。
3.那么U(t)与PWM之间存在怎样的联系呢?PID控制算法的C语言实现二 PID算法的离散化上一节中,我论述了PID算法的基本形式,并对其控制过程的实现有了一个简要的说明,通过上一节的总结,基本已经可以明白PID控制的过程。
这一节中先继续上一节内容补充说明一下。
1.说明一下反馈控制的原理,通过上一节的框图不难看出,PID控制其实是对偏差的控制过程;2.如果偏差为0,则比例环节不起作用,只有存在偏差时,比例环节才起作用。
3.积分环节主要是用来消除静差,所谓静差,就是系统稳定后输出值和设定值之间的差值,积分环节实际上就是偏差累计的过程,把累计的误差加到原有系统上以抵消系统造成的静差。
4.而微分信号则反应了偏差信号的变化规律,或者说是变化趋势,根据偏差信号的变化趋势来进行超前调节,从而增加了系统的快速性。
好了,关于PID的基本说明就补充到这里,下面将对PID连续系统离散化,从而方便在处理器上实现。
下面把连续状态的公式再贴一下:假设采样间隔为T,则在第K T时刻:偏差err(K)=rin(K)-rout(K);积分环节用加和的形式表示,即err(K)+err(K+1)+……;微分环节用斜率的形式表示,即[err(K)-err(K-1)]/T;从而形成如下PID离散表示形式:则u(K)可表示成为:至于说Kp、Ki、Kd三个参数的具体表达式,我想可以轻松的推出了,这里节省时间,不再详细表示了。
其实到这里为止,PID的基本离散表示形式已经出来了。
目前的这种表述形式属于位置型PID,另外一种表述方式为增量式PID,由U上述表达式可以轻易得到:那么:这就是离散化PID的增量式表示方式,由公式可以看出,增量式的表达结果和最近三次的偏差有关,这样就大大提高了系统的稳定性。
需要注意的是最终的输出结果应该为u(K)+增量调节值;PID的离散化过程基本思路就是这样,下面是将离散化的公式转换成为C语言,从而实现微控制器的控制作用。
PID控制算法的C语言实现三位置型PID的C语言实现上一节中已经抽象出了位置性PID和增量型PID的数学表达式,这一节,重点讲解C语言代码的实现过程,算法的C语言实现过程具有一般性,通过PID 算法的C语言实现,可以以此类推,设计其它算法的C语言实现。
第一步:定义PID变量结构体,代码如下:struct _pid{float SetSpeed; //定义设定值float ActualSpeed; //定义实际值float err; //定义偏差值float err_last; //定义上一个偏差值float Kp,Ki,Kd; //定义比例、积分、微分系数float voltage; //定义电压值(控制执行器的变量)float integral; //定义积分值}pid;控制算法中所需要用到的参数在一个结构体中统一定义,方便后面的使用。
第二部:初始化变量,代码如下:void PID_init(){printf("PID_init begin \n");pid.SetSpeed=0.0;pid.ActualSpeed=0.0;pid.err=0.0;pid.err_last=0.0;pid.voltage=0.0;pid.integral=0.0;pid.Kp=0.2;pid.Ki=0.015;pid.Kd=0.2;printf("PID_init end \n");}统一初始化变量,尤其是Kp,Ki,Kd三个参数,调试过程当中,对于要求的控制效果,可以通过调节这三个量直接进行调节。
第三步:编写控制算法,代码如下:float PID_realize(float speed){pid.SetSpeed=speed;pid.err=pid.SetSpeed-pid.ActualSpeed;pid.integral+=pid.err;pid.voltage=pid.Kp*pid.err+pid.Ki*pid.integral+pid.Kd*(pid.err -pid.err_last);pid.err_last=pid.err;pid.ActualSpeed=pid.voltage*1.0;return pid.ActualSpeed;}注意:这里用了最基本的算法实现形式,没有考虑死区问题,没有设定上下限,只是对公式的一种直接的实现,后面的介绍当中还会逐渐的对此改进。
到此为止,PID的基本实现部分就初步完成了。
下面是测试代码:int main(){printf("System begin \n");PID_init();int count=0;while(count<1000){float speed=PID_realize(200.0);printf("%f\n",speed);count++;}return 0;}下面是经过1000次的调节后输出的1000个数据(具体的参数整定过程就不说明了,网上这种说明非常多):83.000001 11.555000 59.559675 28.175408 52.907421 38.944152 51.891699 46.141651 53.339054 51.509998 55.908450 55.94463158.97068059.88293662.22500163.537254 65.52770767.01105868.810646 70.35531872.04204073.59565875.20762076.74544478.30152679.81213681.32192982.80030484.26890985.71310887.14345588.55300589.94696091.32207892.68099694.02223495.34718696.65524297.94718099.222808100.482601101.726572102.955049104.168125105.366066106.549019107.717187108.870756110.009898111.134811112.245652113.342615114.425860115.495564116.551897117.595029118.625116119.642331120.646826121.638767122.618307123.585603124.540813125.484079126.415549127.335383128.243715129.140691130.026459130.901149131.764909132.617870133.460162134.291942135.113308135.924419136.725382137.516332138.297401139.068697139.830352140.582499141.325237142.058701142.782985143.498218144.204509144.901969145.590726146.270843146.942486147.605718148.260674148.907425149.546109150.176794150.799612151.414626152.021959152.621696153.213951153.798781154.376315154.946626155.509812156.065958156.615146157.157471157.693012158.221871158.744097159.259826159.769078160.271991160.768588161.258996161.743264162.221494162.693737163.160075163.620593164.075347164.524422164.967877165.405795165.838235166.265257166.686967167.103377167.514610167.920681168.321682168.717670169.108719 169.494862 169.876198 170.252740 170.624605 170.991799 171.354406 171.712487 172.066080 172.415265 172.760077 173.100594 173.436838 173.768895 174.096796 174.420594 174.740352 175.056096 175.367915 175.675818 175.979886 176.280136 176.576656 176.869444 177.158600 177.444121 177.726087 178.004510 178.279458 178.550967 178.819094179.083860179.345315179.603504179.858466180.110241180.358866180.604388180.846849181.086262181.322699181.556172181.786733182.014396182.239222182.461226182.680475182.896971183.110768183.321881183.530369183.736239183.939545184.140301184.338555184.534321184.727651184.918558185.107080185.293243185.477080185.658625185.837886186.014930186.189745186.362382186.532859186.701207186.867437187.031605187.193713187.353802187.511884187.667997187.822151187.974384188.124700188.273148188.419728188.564488188.707429188.848592188.987995189.125644189.261576189.395801189.528364189.659258189.788528189.916170190.042233190.166702190.289633190.411007190.530867190.649236190.766119190.881544190.995531191.108087191.219243191.329005191.437382191.544428191.650111191.754504191.857565191.959350192.059857192.159119192.257135192.353919192.449511192.543890192.637105192.729137192.820032192.909776192.998410193.085920193.172360193.257700193.341993193.425214193.507408193.588568193.668715193.747847193.826004193.903175193.979391194.054643194.128963194.202349194.274828194.346393194.417073194.486854194.555777194.623820194.691027194.757390194.822919194.887626194.951536195.014633195.076965195.138496195.199273195.259270195.318547195.377060195.434856195.491918195.548283195.603919195.658886195.713145195.766734195.819654195.871912195.923517195.974472196.024791196.074478196.123558196.172016196.219859196.267115196.313778196.359851196.405363196.450296196.494672196.538492196.581753196.624494196.666678196.708363196.749493196.790138196.830267196.869889196.909019196.947656196.985803197.023493197.060701197.097449197.133733197.169558197.204940197.239872197.274378197.308436197.342089197.375309197.408125197.440523197.472520197.504114197.535309197.566127197.596546197.626594197.656258197.685546197.714486197.743047197.771265197.799113 197.826629 197.853799 197.880631 197.907131 197.933284 197.959122 197.984629 198.009823 198.034705 198.059275 198.083520 198.107481 198.131129 198.154493 198.177566 198.200349 198.222843 198.245062 198.267001 198.288662 198.310059 198.331178 198.352049 198.372645 198.392982 198.413066 198.432911 198.452499 198.471846 198.490953198.509819198.528439198.546842198.565003198.582945198.600648198.618147198.635415198.652474198.669313198.685955198.702378198.718611198.734625198.750448198.766067198.781497198.796736198.811776198.826628198.841303198.855788198.870087198.884218198.898162198.911943198.925538198.938970198.952229198.965320198.978257198.991033199.003643199.016092199.028390199.040542199.052536199.064373199.076067199.087617199.099019199.110280199.121407199.132381199.143240199.153940199.164511199.174957199.185270199.195457199.205514199.215440199.225262199.234930199.244503199.253928199.263275199.272468199.281571199.290541199.299421199.308165199.316815199.325345199.333789199.342115199.350336199.358462199.366479199.374396199.382228199.389943199.397586199.405110199.412555199.419891199.427152199.434307199.441389199.448363199.455264199.462073199.468802199.475442199.481995199.488475199.494857199.501183199.507404199.513578199.519639199.525656199.531579199.537437199.543230199.548936199.554583199.560149199.565647199.571073199.576436199.581730199.586961199.592118199.597220199.602260199.607218199.612132199.616974199.621764199.626486199.631156199.635757199.640316199.644808199.649249199.653636199.657959199.662246199.666457199.670635199.674752199.678815199.682833199.686798199.690715199.694583199.698409199.702177199.705905199.709582199.713209199.716788199.720339199.723826199.727276199.730690199.734054199.737378199.740657199.743901199.747111199.750260199.753393199.756474199.759526199.762524199.765490199.768422199.771314199.774169199.776992199.779775199.782527199.785247199.787938199.790590199.793204199.795787199.798338199.800860199.803343199.805802199.808225199.810624199.812986199.815326199.817642199.819915199.822175199.824388199.826587199.828755199.830902199.833006199.835097199.837155199.839194199.841210199.843191 199.845168 199.847096 199.849024 199.850905 199.852784 199.854621 199.856449 199.858238 199.860016 199.861757 199.863486 199.865199 199.866879 199.868549 199.870186 199.871813 199.873419 199.874997 199.876563 199.878109 199.879620 199.881136 199.882613 199.884088 199.885527 199.886971 199.888371 199.889783 199.891142 199.892518199.893845199.895180199.896485199.897783199.899057199.900322199.901562199.902797199.904010199.905222199.906392199.907576199.908720199.909875199.910985199.912108199.913193199.914287199.915352199.916423199.917459199.918505199.919527199.920526199.921513199.922496199.923452199.924415199.925348199.926275199.927198199.928108199.929019199.929903199.930788199.931653199.932509199.933353199.934187199.935002199.935816199.936617199.937420199.938195199.938971199.939733199.940477199.941228199.941961199.942685199.943392199.944111199.944804199.945491199.946181199.946854199.947518199.948165199.948824199.949456199.950083199.950714199.951326199.951930199.952532199.953125199.953714199.954290199.954863199.955424199.955979199.956538199.957073199.957623199.958146199.958671199.959189199.959693199.960203199.960689199.961191199.961665199.962156199.962619199.963098199.963543199.964014199.964448199.964907199.965330199.965772199.966201199.966625199.967046199.967458199.967868199.968263199.968664199.969047199.969437199.969817199.970193199.970565199.970943199.971297199.971668199.972011199.972363199.972712199.973047199.973388199.973726199.974049199.974379199.974699199.975014199.975326199.975645199.975939199.976249199.976546199.976832199.977125199.977414199.977688199.977969199.978247199.978525199.978782199.979061199.979312199.979576199.979825199.980077199.980335199.980569199.980812199.981053199.981300199.981522199.981755199.981984199.982213199.982427199.982648199.982860199.983080199.983298199.983501199.983704199.983914199.984114199.984309199.984500199.984698199.984887199.985079199.985262199.985442199.985623199.985803199.985984199.986170199.986327199.986508199.986668199.986846199.987006199.987169199.987321199.987481199.987633199.987800199.987948199.988094199.988237199.988386199.988526199.988675199.988815 199.988965 199.989090 199.989231 199.989359 199.989491 199.989629 199.989757 199.989889 199.990012 199.990133 199.990253 199.990373 199.990493 199.990614 199.990734 199.990854 199.990960 199.991072 199.991180 199.991289 199.991398 199.991507 199.991616 199.991718 199.991837 199.991922 199.992025 199.992123 199.992214 199.992314199.992412199.992503199.992604199.992701199.992792199.992878199.992967199.993047199.993136199.993216199.993305199.993385199.993474199.993554199.993637199.993726199.993806199.993881199.993952199.994024199.994101199.994170199.994241199.994313199.994391199.994459199.994531199.994602199.994680199.994748199.994805199.994868199.994928199.994989199.995049199.995109199.995175199.995226199.995295199.995346199.995416199.995466199.995536199.995593199.995653199.995713199.995759199.995811199.995859199.995902199.995960199.995999199.996051199.996100199.996148199.996191199.996249199.996288199.996340199.996389199.996438199.996480199.996538199.996578199.996629199.996678199.996712199.996746199.996787199.996824199.996855199.996896199.996927199.996967199.997005199.997036199.997076199.997113199.997145199.997185199.997216199.997256199.997294199.997325199.997365199.997403199.997434199.997474199.997512199.997543199.997583199.997614199.997640199.997669199.997689199.997711199.997740199.997760199.997789199.997809199.997838199.997858199.997880199.997909199.997929199.997958199.997978199.998007199.998027199.998049199.998078199.998098199.998127199.998147199.998170199.998199199.998218199.998247199.998267199.998296199.998316199.998339199.998368199.998387199.998416199.998436199.998459199.998488199.998508199.998537199.998556199.998585199.998590199.998605199.998616199.998634199.998642199.998654199.998665199.998676199.998694199.998702199.998714199.998725199.998743199.998745199.998766199.998774199.998785199.998803199.998805199.998826199.998834199.998845199.998863199.998871199.998883199.998894199.998905199.998923199.998931199.998943199.998954199.998972199.998974199.998995199.999003199.999014199.999032199.999034199.999055199.999063199.999074199.999092199.999094199.999115199.999123199.999135199.999152199.999161 199.999172 199.999183 199.999201 199.999203199.999224199.999232199.999243199.999261199.999263199.999284199.999292199.999304199.999321199.999323199.999344199.999352199.999364199.999381199.999390199.999401199.999412199.999430199.999432199.999453199.999461199.999473PID控制算法的C语言实现四增量型PID的C语言实现上一节中介绍了最简单的位置型PID的实现手段,这一节主要讲解增量式PID的实现方法,位置型和增量型PID的数学公式请参见我的系列文《PID控制算法的C语言实现二》中的讲解。
