共轴球面系统及其基点共16页
合集下载
第二章球面与共轴球面系统（ＰＤＦ）
第二章球面与共轴球面系统§2－1 光线光路计算与共轴光学系统共轴球面系统—光学系统一般由球面和平面组成，各球面球心在一条直线（光轴）上。
物象关系的研究方法—光线的光路计算。
逐面计算物象的大小、虚实、正倒、位置等特性。
子午面—包含物面与光轴的截面。
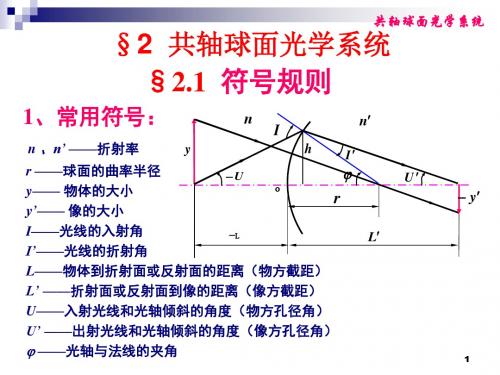
一、 光线经过单个折射面的折射OEAA ′II ′Cr-LL ′hnn ′-UU ′φ1.基本参量E －折射点 OE OE －折射球面 U U 、U ′－ 物象方孔径角O －顶点 h h －入射高度 n n 、n ′－物象方空间折射率C－球心 r－球面曲率半径 I 、I ′－入、折射角A 、A ′－物点、象点 L 、L ′－物距、象距φ －法线与光轴夹角2. 符号法则（便于统一计算）规定光线从左向右传播a）沿轴线段L、L′、r以O为原点，与光线传播方向相同，为“＋”与光线传播方向相反，为“－”b）垂轴线段h在光轴之上，为“＋”在光轴之下，为“－”c）光线与光轴夹角U、U′以光轴转向光线成的锐角来度量，顺时针为“＋”逆时针为“－”d）光线与法线夹角I、I′以光线转向法线成的锐角来度量，顺时针为“＋”逆时针为“－”e）光轴与法线的夹角φ以光轴转向法线成的锐角来度量，顺时针为“＋”逆时针为“－”f）折射面的间隔d，一般取“＋”g）所有参量是含符号的量，但图示标为参量的大小。
二、 远轴光的计算公式（实际光线光路计算） 给定n 、 n ′、r ，已知L 、U ，求解L ′、 U ′ 其中U 、 U ′较大，远轴光线成像（大光路）U I rr L I I U U In nI Ur r L I ′′+=′′−+=′′=′−=sin sin sin sin sin sin OEAA ′II ′Cr-LL ′hnn ′-UU ′φ3）物点位于物方无限远时，入射光线位置由高度h 决定。
rh I =sin 说明：1）L ′＝f (U 、L 、n 、n ′、r)2）当L 为定值时，L ′随U 变化而变化，象方光束失去同心性，成不完善象，形成球差。
3.9理想光具组的基点和基面
(例:两个会聚系统组成一个发散系统)
u
h F1 H1
u1 H1
F1
H 2 F2
h
u2 F2 H 2 h u2 F H
f1
f2
f 2
f1
d
d H1H2 f f2, 可正可负;
x 2 xH
f
F1F2,称为光学间隔可正可负,可为零.
当 n n时 有 1，所以在此情况下，主点与
节点重合. 利用两者重合的性质，并根据系统绕 节点作不大的转动时，平行光所生的像不发生 位移的特点，可确定主点和节点的位置，从而 确定任意复杂系统的焦距 .
确定节点，主点实验光路图
F
H N
F
利用主点和节点重合的性质，并根据系统绕节点作不大的转 动时,平行光所成的像不发生位移的特点，可确定主点的位置， 从而能确定任意复杂系统的焦距.
f f2 x2 . f1 f 2
因 F1和 F 关于子系统Ⅱ共轭,
按高斯公式应有:
（5）
f2 f2 1. f2 x2 ( f2 )
按牛顿公式 应有 x2 f2 f2,
或
x2
f 2 f 2 ,
（6） （7）
HF F N , H N FN,
证明
且有
HH NN.
证明
六个基点中，只有四个是独立的．但四个中必须至少有一 个是焦点.
F
平物 面方
焦
M
M
i
N N H H
R R
平物平像 面 方面 方
主主
F i
平像 面方
焦
共轴球面系统的物距 s HS, 像距 s H S,
u
h F1 H1
u1 H1
F1
H 2 F2
h
u2 F2 H 2 h u2 F H
f1
f2
f 2
f1
d
d H1H2 f f2, 可正可负;
x 2 xH
f
F1F2,称为光学间隔可正可负,可为零.
当 n n时 有 1，所以在此情况下，主点与
节点重合. 利用两者重合的性质，并根据系统绕 节点作不大的转动时，平行光所生的像不发生 位移的特点，可确定主点和节点的位置，从而 确定任意复杂系统的焦距 .
确定节点，主点实验光路图
F
H N
F
利用主点和节点重合的性质，并根据系统绕节点作不大的转 动时,平行光所成的像不发生位移的特点，可确定主点的位置， 从而能确定任意复杂系统的焦距.
f f2 x2 . f1 f 2
因 F1和 F 关于子系统Ⅱ共轭,
按高斯公式应有:
（5）
f2 f2 1. f2 x2 ( f2 )
按牛顿公式 应有 x2 f2 f2,
或
x2
f 2 f 2 ,
（6） （7）
HF F N , H N FN,
证明
且有
HH NN.
证明
六个基点中，只有四个是独立的．但四个中必须至少有一 个是焦点.
F
平物 面方
焦
M
M
i
N N H H
R R
平物平像 面 方面 方
主主
F i
平像 面方
焦
共轴球面系统的物距 s HS, 像距 s H S,
7.27.4共轴球面光学系统
点的位置有关。这个量在像差中有重要用途。
h
（2） n ' u ' nu (n ' n )
孔径变化式
r
表示近轴光经球面折射前后的孔径角 u 和 u ' 的关系 。
2020/9/27
7.3 单个折射球面近轴区成像
（3） n' n n'n “距度”（距离倒数）变化式或物像公式 l' l r
该式表示折射球面成像时，物像位置 l 和l ' 之间的关系。已
2020/9/27
7.2 单个折射球面的折射
➢ 单个折射球面的光路计算公式
如图，在ΔAEC中，应用正弦定律 ，得
sinAECsin(U)
Lr
r
又 sinIsin A E C
sin I (L r) sin U r
2020/9/27
7.2 单个折射球面的折射
➢ 单个折射球面的光路计算公式
在光线的入射点处应用折射定律
②当β>0，y’和y同号，成正像；l '和l 同号，物像位于球面的同
侧，实物成虚像，虚物成实像。 ③当∣β∣>1，为放大像；∣β∣<1，为缩小像。
2020/9/27
7.3 单个折射球面近轴区成像
➢ 轴向放大率
当物体在给定位置有一微量位移dl，其像也在像点位置处有一
微量位移dl′，定义dl′与dl 的比值为轴向放大率，用 表示.
➢ 高斯公式和牛顿公式
将r
/(n'
n)
乘以物象公式
n' l'
ห้องสมุดไป่ตู้
n l
(n
r '
n)，得
f' f 1
2-5共轴理想光学系统的基点
光学系统的成像性质可用这些基面和基点求得
最常用的是一对共轭面和轴上的两对共轭点。
应用光学讲稿
主平面性质： 任意一条入射光线与物方主平面的交点高度和出 射光线与像方主平面的交点高度相同
应用光学讲稿
二 .无限远轴上物点和它所对应的像点F’——像方焦点
n' n n' n l' l r
当轴上物点位于无限远时，它的像点位于F’处。 F’称为“像方焦点”。
应用光学讲稿
§2-6 单个折射球面的主平面和焦点 一. 球面的主点位置 主平面是垂轴放大率β =1的一对共轭面。 nl ' 1 或者 nl ' n' l n' l 同时，由于它是一对共轭面，主点位置应满足
n' n n' n l' l r
应用光学讲稿
, n n , , , 0 n l nl ll r
§2-5 共轴理想光学系统的基点 ——主平面和焦点 林硕
E-mail: linshuo_pv@
应用光学讲稿
近轴光学基本公式的缺点：物面位置改变时，需 重新计算，若要求知道整个空间的物像对应关系，势 必要计算许多不同的物平面。 已知两对共轭面的位置和放大率，或者一对共轭 面的位置和放大率，以及轴上的两对共轭点的位置， 则其任意物点的像点就可以根据这些已知的共轭面和 共轭点来求得。
n' n n' n l' l r
如果轴上某一物点F，和它共轭的像点位于轴上无限远， 则F称为物方焦点。 通过F垂直于光轴的平面称为物方焦平面 它和无限远的垂直于光轴的像平面共轭。
应用光学讲稿
物方焦点和物方焦平面性质： 1、过物方焦点入射的光线，通过光学系统后平 行于光轴出射 2、由物方焦平面上轴外任意一点下发出的所有 光线，通过光学系统以后，对应一束和光轴成一定 夹角的平行光线。
共轴球面系统及其基点
F -x -l -f
H
H'
F’
f’
x’ l’
主平面还可定义为：系统垂轴放大率为正1, 1的两个 共轭垂轴平面 物空间焦距HF: 物空间主点H到物空间主焦点F的距离 象空间焦距H’F’ : 象空间主点H’到物空间主焦点F’的距离
3．节点:
系统光轴角放大率 1 的两个共轭点
在物空间的折射率和象空间的折射率相同的共轴球面系统内
-h2
-u2’
l’2
d2
-u3
-l3
n2 n1' n3 n2' n k nk 1' 转面公式 u 2 u1' u3 u 2' u k u k 1' l l ' d l3 n 2' d 2 l k l k 1' -d k-1 1 2 1
1
∴在此情况下，主点和节点重合利用两者重合的性质并根据系 统绕节点作不大的转动时， 1 平行光生成的像不生位移的 特点，可确定系统主点位置，从而能确定任意复杂系统的焦距。
三、共轴系统的成像
F
-x -f f’
F’
-l
1．物像公式
x’ l’
f' f 1 l' l xx' ff '
上面公式与计算单球面的折射成像的高斯公式和牛顿公式 完全相同，但必须注意单球面的原点，为折射面与光轴交 点，而此处为组合系统的两主点。 4、轴向放大率 定义
dx ' dl ' dx dl
dx , dl
dx ' , dl '
为轴上物点A沿光轴移动的微小距离， 为当物点A移动距离时象点A’移动的相应距离。
第二章 共轴球面系统(二)
= l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
共轴球面系统的过渡公式（3-2）
lu l'u' h
l1u1 l'1 u'1 h1 ,l2u2 l'2 u'2 h2 ,
l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
拉格朗日- 赫姆霍兹恒等式
y' nl'
y n'l
lu l'u'
J为拉赫不变量 nuy n'u' y' J
题 例 1：在一直径为30cm的球形玻璃鱼缸内盛满水，鱼缸中
心处有一条小鱼，求缸外观察者看到鱼的位置及放大率！
解： n n n n l' l r
n' 4 ,l 15, r 15代入 3
定义：通过一定光学系统所成的像对光轴的 垂直高度与物本身对光轴的垂直高度的比。
公式：
y'
y
近轴区的放大率
-u
u’
近轴区的放大率----横向放大率
y'
y
y' l'r y l r
n(1 1) n'(1 1)
rl
r l'
物像位置关系式
n l r n' l' r
rl
rl'
l r l' r n' l nl'
n'k 2
共轴球面系统的过渡公式（3-2）
lu l'u' h
l1u1 l'1 u'1 h1 ,l2u2 l'2 u'2 h2 ,
l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
拉格朗日- 赫姆霍兹恒等式
y' nl'
y n'l
lu l'u'
J为拉赫不变量 nuy n'u' y' J
题 例 1：在一直径为30cm的球形玻璃鱼缸内盛满水，鱼缸中
心处有一条小鱼，求缸外观察者看到鱼的位置及放大率！
解： n n n n l' l r
n' 4 ,l 15, r 15代入 3
定义：通过一定光学系统所成的像对光轴的 垂直高度与物本身对光轴的垂直高度的比。
公式：
y'
y
近轴区的放大率
-u
u’
近轴区的放大率----横向放大率
y'
y
y' l'r y l r
n(1 1) n'(1 1)
rl
r l'
物像位置关系式
n l r n' l' r
rl
rl'
l r l' r n' l nl'
n'k 2
工程光学第2章 共轴球面光学系统
10
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , yk yk 1 y2 y1
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0，物体沿光轴移动时，像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
I
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U
o
U
r
l'
y
-l
7
共轴球面光学系统
结论：
1.
b是有符号数，具体表现为
成像正倒：当b>0时，表明y’、y同号，成正像；否则，成倒像。 成像大小：当|b|＝1时，表明|y’|=|y|，像、物大小一致；|b|>1时， 表明|y’|>|y|，成放大的像；反之，成缩小的像。 成像虚实：当b>0时，表明l’、l同号，物像同侧，虚实相反；否 则，物像异侧，虚实相同。
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , yk yk 1 y2 y1
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0，物体沿光轴移动时，像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
I
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U
o
U
r
l'
y
-l
7
共轴球面光学系统
结论：
1.
b是有符号数，具体表现为
成像正倒：当b>0时，表明y’、y同号，成正像；否则，成倒像。 成像大小：当|b|＝1时，表明|y’|=|y|，像、物大小一致；|b|>1时， 表明|y’|>|y|，成放大的像；反之，成缩小的像。 成像虚实：当b>0时，表明l’、l同号，物像同侧，虚实相反；否 则，物像异侧，虚实相同。
第3讲 共轴球面系统&球面反射镜
xx f 2
2 n r r f 2 r f 2 f 1 f
f n f n
横向放大率
ns ns
l l
例1 设有一半径为3cm的凹球面,球面两侧的折射率分别 为n = 1，n’ = 1.5，一会聚光束入射到界面上，光束的顶 点在球面右侧3cm处。求像的位置。
2)第一面：l1 ，r1 30, 1 1 2 l1 15 l1 30 物像位于反射系统异侧 l 15 1 0 l 物像虚实相反 虚像
1.5 l1 90 3)第一面：l1 , r1 30,n1 1, n1 第二面：d 60, l2 l1 d 30（虚物点）, , r2 30 n2 n2 1 1 2 10 l2 30 -30 l2
即： 通过球心的光线被反射镜原路反射回来， 球面反射镜对其曲率中心为等光程面。
r 2.当物在无穷远时，有： l l f 2
3. 对于平面反射镜，有：
1 1 0 l l r l 1 l
10
球面折射和球面反射公式对照表
1
B1 y1
2
u1 y1
3
4
M1
A1
u1
B2
A2
y2u2 M2
u2
y3 2y
B3
A3
M3
B4
y y3 4
l1 l2 l2
l3
A4
4
d12
d 23
1. 共轴球面系统的结构参量： 各球面半径：r1 , r2 …… rk-1 , rk 相邻球面顶点间隔：d1 , d2 …… dk-1 各球面间介质折射率：n1 , n2 …nk-1 , nk ,nk+1