矩形板塑性内力计算_李洪求
金属塑性成形原理第六章主应力法

第一节 概 述
研究不同形状和性能的坯料,在不同的工模 具和不同的外力作用下发生塑性变形时的应 力、应变和流动状态,是塑性成形理论的根 本任务之一。
知道了坯料塑性变形时的应力状态,即可 计算出变形力和功能消耗。
1
变形力:在塑性加工过程中,工具通过与坯料的接 触面,对坯料施加作用力,当此作用力达到一定值时, 坯料发生塑性变形,此时,工具作用在坯料上的作用 力称为变形力。
y ye
C
ye
2
h
xe
这时 x 0
自由表面
ye 2K
2S 3
y
2
h
( xe
x)
ye
2
h
( xe
x)
2S 3
17
5、确定单位流动压力(即单位面积的平均变形力)
变形力
xe
P ydF 2 l y dx
F
0
平均变形力 p P P 1 F l 2xe xe
ln( wb
we ) K1 y
2S 3
法
y
K2 K1
ln( wb
we ) K1 y
32
金 属
当y=0时,为挤压变形所需的单位流动压力值。
塑
性
成
形 原 理
p y
y0
K 2 ln we K1 wb
第 六 章 主 应 力 法
33
(三)轴对称变形的横向流动(镦粗型)
设有平行砧板间的轴对称镦粗。 摩擦条件为 s
4
1、空间问题:
塑性变形力学计算2Word版

杆件的塑性变形15. 1概 述工程问题中绝大部分构件必须在弹性范围内工作,不允许出现塑性变形。
但 有些问题确须考虑塑性变形。
15.2金属材料的塑性性质图15. 1是低碳钢拉伸的应力-应变曲线。
过屈服极限后,应力和应变的关系 是非线性的有£= £ + £图15.1低碳钢拉伸的应力-应变曲线弹性范围内,应力和应变之间是单值对应的。
塑性阶段却并非如此,应力和 应变不再是单值对应的关系(如图15.2)。
下面是儿种常见的塑性材料模型。
图15.2弹塑性应力-应变有时也把应力-应变关系近似地表为幕函数,幕强化材料的应力-应变关系曲线如 图15. 7所示。
b = cH15.3拉伸和压缩杆系的塑性分析现以图15. 8所示两端固定的杆件为例来说明静不定拉压杆系的塑性分析, 肖载荷P 逐渐增加时,杆件两端的反力是I5d 1Z O TH"出 I 比I 士fcT(a)1a +b fR 2 =Pa a +P 力作用点的位移是-R 、a Pab EA EA(a + b)如b>o 则&>仏。
随着P 的增加,■JAC- p>B%AC 段0 £m In. 3理根禅殖件材料槿型图15. 4刚塑性材料模型图15. 5线性强化材料模型图15. 6刚須性线性强化材料模型 图15. 7幕强化材料模型5 52(«)的应力将首先达到屈服极限。
若相应 的载荷为片,载荷作用点的位移为由(" )、3) 两式求得Aa s (a + b)b山平衡方程可知心"-2(0)载荷作用点C 的位移为EA (d)CB 段也进入塑性阶段时,心二人农,由(。
)式求出相应的载荷为图15. 9三杆桁架P? = 2/1乐载荷达到竹后,整个杆件都已进入塑性变形。
例18.1在图13.9"所示静不定结构中,设三杆的材料相同,横截面面积同 为A 。
试求使结构开始出现塑性变形的载荷片、极限载荷Pp 。
塑性计算方法及适用范围(精)

d 按弹性理论计算法计算时,支座弯矩总是远ቤተ መጻሕፍቲ ባይዱ于跨 中弯矩,支座配筋拥挤,构造复杂,施工不便。
塑性内力重分布的计算方法
对于均布荷载作用下,等跨连续板、次梁考虑塑性内力 重分布的弯矩,可按下列公式计算: (1)控制截面的弯矩 : M=am(g+q)l02 式中 am—弯矩系数,板和次梁按表6-4数据采用 。
式中 αm—弯矩系数,板和次梁按表 6-4 数据采用。
表 6-4 连续梁及连续单向板弯矩计算系数 m
截面位置
边
支承情况
端支
座
梁板搁置墙上
0
-
板
整浇刚性连
1/16
接
-
梁
1/24
- 梁与柱刚性连接
1/16
跨 边跨
中 1/11
1/14
1/14
第二跨
第二支座
第二跨 中
二跨连续-1/10 三跨以上连续- 1/16
外
内
侧
侧
0.55 0.55
钢筋混凝土连续梁板考虑塑性内力重分布的设计方法 按弹性理论计算法的缺陷: a 钢筋砼是两种材料组成的非匀质弹性体,在构件的截面 设计中己充分考虑了其塑性性能,按破坏阶段的构件截面计算 方法与按弹性理论计算的结构内力是互不协调的,材料强度未 能得到充分发挥。
b 弹性理论计算法是按活荷载的最不利位置时的内 力包络图来配筋的,但各跨中和各支座截面的最大内力实 际上并不能同时出现。
1/11
中间跨
中间支 中间跨
座
中
-1/14 1/16
(2) 控制截面的剪力
矩形板塑性内力计算

矩形板塑性内力计算
李洪求
【期刊名称】《建筑结构》
【年(卷),期】2002(32)4
【摘要】通过对分离式配筋矩形板内力塑性理论计算公式的推导 ,利用电算程序对现行结构手册中的塑性计算内力系数作了进一步的扩充 ,从而使设计应用中能更合理地计算板的内力及配筋 ,达到了安全经济的目的。
【总页数】3页(P25-26)
【关键词】矩形板;塑性计算;内力;计算;单向板;双向板;弹性计算
【作者】李洪求
【作者单位】北京市维拓时代建筑设计院
【正文语种】中文
【中图分类】TU323
【相关文献】
1.计入膜力塑性耗散效应的矩形板塑性动力响应 [J], 陈发良;余同希
2.局部均布荷载作用下四边支承矩形板的内力计算 [J], 杨成永;马文辉;韩薛果;程霖
3.关于矩形混凝土板内力的几种计算方法的比较 [J], 杜庆祖
4.矩形钢筋混凝土双向板板底塑性弯矩比设计取值研究 [J], 蒋秀根;剧锦三;庄金钊
5.框架结构中整体式单向板按塑性内力重分布理论的计算 [J], 栾曙光
因版权原因,仅展示原文概要,查看原文内容请购买。
弹塑性力学10-6梁模型计算圆板和环板的塑形极限载荷(精)
例题1:边长为 a 的正方形薄板,一边固支、两边简支,自由边中点A受集 中载荷 P 作用,板的塑性极限弯矩为: Mp ,求塑性极限载荷。 D
b
b
C
a
h
E A B
解:设A点的挠度为d
ABC与ACD的相对转角为q :
a
q
d
AC
cota cot b 5
j d
a
d
2 AC
j
d
ACD与CD的相对转角为j:
dr
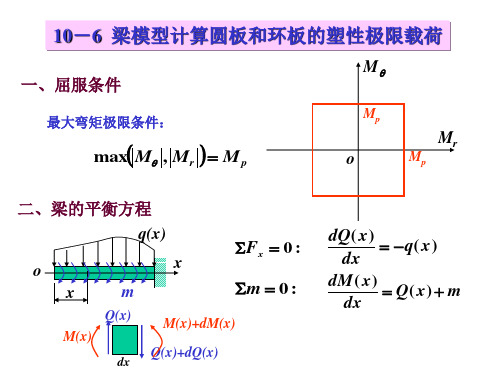
梁计算模型
板 x o r
q(r) r
o x
m
Mx Qx
m
q(x) 极限条件:
2rMr 2rQr 2Mq
2rq(r) Mmax Mp
若梁和圆板的边界条 件在形式上相同,可 通过求解变量转换后 梁的问题得到圆板的 解答。
四、 梁模型计算圆板和环板的塑性极限载荷的步骤
1. 结构转换 o
r
o
解:
o
z
r
r a
a
z
2rM r 2rM p r r 2rq 2 3
m= 2Mp
qr 2 Mr M p 6
Mr
r a
qa2 M p M p M p 6
ql 12
Mp a2
简支圆板:
Mr
r a
0
ql 6
Mp a2
例题2:半径为 a 的简支环板,内半径为 b ,受均布载荷 q 作用,圆板单 位塑性极限弯矩为: Mp ,求塑性极限载荷。 2rq q
i 1
ai bi
( n 2) 2n 2 n
Pl M P cota i cot b i
塑性力学第五章

或
在弹性状态时,上式右端等于零,可得 到弹性解。将它作为第一次近似解,代入上 式右端作为已知项,又可以解出第二次近似 解。重复以上过程,可得出所要求精度内接 近实际的解。在小变形情况下,可以证明解 能够很快收敛。在很多问题第二次近似解已 能给出较为满意的结果。
六、幂次强化材料 设梁的材料为幂次强化材料,其单向拉 压时的应力-应变关系服从幂规律 σ = B ε n signε 0 ≤ n ≤ 1 。单 式中 B 和 n 为常数,由实验测定, 拉时 n n σ = Φ(ε ) = Bε = B(κy )
M = 4∫ Φ(κy ) b( y ) ydy = 4 Bκ n ∫ b( y ) y n +1dy
§5-1 §5-2 §5-3
弹塑性力学中的边值问题 梁的纯弯曲 梁的横力弯曲
§5-1
弹塑性力学中的边值问题
塑性本构关系有全量和增量两种理论, 这两种理论的边值问题的提法及解法 全量理论的边值问题及解法 设在物体V内给定体力 f i ,在应力边界 ST 上 给定面力 f i ,在位移边界 Su 上给定 ui ,要求 物体内部各点的应力σ ij 、应变 ε ij 、位移 ui 。 确定这些未知量的基本方程组有: 1) σ ij ,i + f j = 0
d 2v ε ε x = ε = = − y 2 , ε y = ε z = − , γ xy = γ yz = γ zx = 0 dx ρ 2 y
满足应变协调方程 。 在弹性区的边界处 y = ys , σ = σ s ,由
d 2v σ x = Eε = − Ey 2 dx
所以梁轴的挠曲方程为 故
εs ys = κ
Eε s y y =σs Eε = Eκy == ys ys
弹塑性力学定理和公式

应力应变关系弹性模量 ||广义虎克定律1。
弹性模量对于应力分量与应变分量成线性关系的各向同性弹性体,常用的弹性常数包括:a 弹性模量单向拉伸或压缩时正应力与线应变之比,即b 切变模量切应力与相应的切应变之比,即c 体积弹性模量三向平均应力与体积应变θ(=εx+εy+εz)之比,即d 泊松比单向正应力引起的横向线应变ε1的绝对值与轴向线应变ε的绝对值之比,即此外还有拉梅常数λ。
对于各向同性材料,这五个常数中只有两个是独立的。
常用弹性常数之间的关系见表3-1 弹性常数间的关系。
室温下弹性常数的典型值见表3—2 弹性常数的典型值。
2。
广义虎克定律线弹性材料在复杂应力状态下的应力应变关系称为广义虎克定律。
它是由实验确定,通常称为物性方程,反映弹性体变形的物理本质.A 各向同性材料的广义虎克定律表达式(见表3—3 广义胡克定律表达式)对于圆柱坐标和球坐标,表中三向应力公式中的x 、y、z分别用r、θ、z和r、θ、φ代替。
对于平面极坐标,表中平面应力和平面应变公式中的x、y、z用r、θ、z代替。
B 用偏量形式和体积弹性定律表示的广义虎克定律应力和应变张量分解为球张量和偏张量两部分时,虎克定律可写成更简单的形式,即体积弹性定律应力偏量与应变偏量关系式在直角坐标中,i,j=x,y,z;在圆柱坐标中,i,j=r,θ,z,在球坐标中i,j=r,θ,φ。
弹性力学基本方程及其解法弹性力学基本方程|| 边界条件||按位移求解的弹性力学基本方法||按应力求解的弹性力学基本方程|| 平面问题的基本方程 || 基本方程的解法 || 二维和三维问题常用的应力、位移公式1.弹性力学基本方程在弹性力学一般问题中,需要确定15个未知量,即6个应力分量,6个应变分量和3个位移分量。
这15个未知量可由15个线性方程确定,即(1)3个平衡方程[式(2-1—22)],或用脚标形式简写为(2)6个变形几何方程[式(2—1—29)],或简写为(3)6个物性方程[式(3-5)或式(3—6)],简写为或2.边界条件弹性力学一般问题的解,在物体内部满足上述线性方程组,在边界上必须满足给定的边界条件。
计算力学4---加权残值法解矩形薄板的弹塑性问题

4.加权残值法解矩形薄板的弹塑性问题薄板理论的克希霍夫假设在板的弹塑性分析中仍可应用。
采用增量形式表示,板的本构方程的矩阵形式为:{}([][]{})e p e D D σβ∆=-∆ (4-7-1)式中{}[,,]{}[,,]T x y xy Tx y xy e σσστεεγ⎫∆=∆∆∆⎪⎬∆=∆∆∆⎪⎭(a ) 分别为应力增量分量和应变分量增量。
而弹性矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=210001011][2μμμμE D e (b ) 塑性矩阵[][][][]Te e e T ef f D D D f f H D σσσσ∂∂⎧⎫⎧⎫⎨⎬⎨⎬∂∂⎩⎭⎩⎭=∂∂⎧⎫⎧⎫'+⎨⎬⎨⎬∂∂⎩⎭⎩⎭(4-7-2) 这里/s p H d de σ'=为硬化参数;f 为屈服函数,对于密赛斯屈服条件0s f σσ=-= (4-7-3)式中2221/2(3)x y x y xy σσσστ=+-+ (c )式(4-7-1)中的β叫做塑性修正系数,在弹性区内β=0;在塑性区β=1;在弹塑性过渡区,取ba sa σσσσβ--= (d ) 上标b,a 分别表示加上载荷增量前后的值。
板的应力偏量)(31)(31y x y y y x x x S S σσσσσσ+-=+-= (4-7-4)将有关公式代入式(4-7-2)中,则得塑性矩阵:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-++++-+++-=xy xy x y xy y x xy x y x y x y y x xy y x x y y x y x p S S S S S S S S S S S S S S S S S S S S Q E D 2222)1())(1())(1())(1()())(())(1())(()()1(][τμτμμτμμτμμμμμτμμμμμμ(4-7-5)其中EH S S S S Q xyy x y x 9)1(4)1(222222--'+-+++=σμτμμ (e )分开应力增量{△σ}的弹性部分和塑性部分,沿板厚积分,即有}{}{}{P e M M M ∆+∆=∆ (f )式中T xy y x M M M M ],,[}{∆∆∆=∆ (g)弹性弯矩增量和挠度增量的关系⎪⎪⎪⎭⎪⎪⎪⎬⎫∆∂∂∂--=∆∆∂∂+∆∂∂-=∆∆∂∂+∆∂∂-=∆)()1()]()([)]()([222222222w y x D M w x w y D M w y w x D M exy ey exμμμ (4-7-6)式中,)1(1223μ-=Eh D 为板的抗弯刚度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第32卷第4期建筑结构2002年4月矩形板塑性内力计算李洪求(北京市维拓时代建筑设计院100025)[提要]通过对分离式配筋矩形板内力塑性理论计算公式的推导,利用电算程序对现行结构手册中的塑性计算内力系数作了进一步的扩充,从而使设计应用中能更合理地计算板的内力及配筋,达到了安全经济的目的。
[关键词]单向板双向板弹性计算塑性计算By inferring acc urate formula s of pla stic internal force for rectangle plate,the coefficient table s for plastic internal force are calculated.Internal force and reinforcing bars for plate can be calculated m ore precisely,so the plate can be designed safely and ec onomically.K eyword s:one-w ay plates;tw o-w ay plates;ela stic calculation;pla stic calculation一、问题的提出我国现行规范规程对于混凝土的基础底板、箱基顶板以及人防工程,均推荐采用塑性理论来计算板的内力[1]。
故在设计中常会遇到这样的情形:对于板边长比ly/l x在2附近的板块,尽管尺寸相近,支承条件、荷载均相同,由于当板边长比大于2时按单向弹性板计算,当板边长比小于2时按考虑塑性的双向板分析,会导致二者的内力结果相差极大,这显然是不合理的。
为了保证塑性内力计算的连续性,完全可以通过计算任意边长比的塑性内力计算系数或者计算表格,从而彻底地解决上述不合理的现象。
二、任意边界条件下薄板的塑性内力计算设m x,m y分别为板长边和短边单位宽度内的弯矩,m x c,m x d,m y c,m y d为对应于板长边和短边支座上的单位宽度弯矩。
根据板的弹性内力分析结果及控制弯矩调幅不宜过大的原则,先选定内力之间的比值,令m y=A m x,m x c=m x d=B m x,m y c=m y d=B m y=A B m x,式中A=1/n2,n为板长边与短边之比,B为支座与跨中弯矩之比,常取B=110~215,于是有:M x=l y m x=nl x m xM y=l x m y=A l x m xM x c=M x d=n B l x m xM y c=M y d=A B l x m x(1)式中Mx,M y,M x c ,M y c,M x d,M y d见图1,根据各塑性铰线上两个方向的极限弯矩总和与外荷载的平衡得[2]2M x+M x c+M x d+2M y+M y c+M y d=ql2x12(3l y-l x)(2)式中q为板上均布荷载。
采用的基本假定与前苏联学者格沃斯捷夫的方法[3]是一致的。
图1由式(2)可以很方便地求得各种边界支承条件下双向板塑性内力的计算公式。
应该注意的是,对于四边固定板,Mxc=Mxd,Myc=M y d,对于四边简支板,M x c=M x d=M y c=M y d=0。
对于其余的情形,可依此类推,据此可推导出各类边界支承条件下双向板的塑性内力公式。
(1)四边固定板(图2(a)):将式(1)代入式(2)得:m x=3n-124(n+A)(1+B)ql2x(3a)若令B=2,n y],有:limn y]m x=limn y]3n-124(n+A)(1+B)ql2x=124ql2x m x c=m x d=2m x=ql2x/12此时板跨中和支座弯矩与按单向板计算的内力结果相同。
这是由于mx,m x c的物理意义与单向弹性板中的定义完全一致,当n y]时,二者的结果必然相同,从另一个侧面验证了式(3a)的正确性。
按照同样的方法,我们可以推导出各种边界支承条件下板塑性内力弯矩的表达式:(2)三边固定一边简支(长边)(图2(b)):m x=3n-112[n(2+B)+2A(1+B)]ql2x(3b)(3)三边固定一边简支(短边)(图2(c)):m x=3n-112[2n(1+B)+A(2+B)]ql2x(3c)(4)两边固定两边简支(邻边)(图2(d)):25图2板的边界支承条件m x=3n-112(n+A)(2+B)ql2x(3d)(5)两边固定(长边)两边简支(短边)(图2(e)):m x=3n-124[n(1+B)+A]ql2x(3e)(6)两边固定(短边)两边简支(长边)(图2(f)):m x=3n-124[n+A(1+B)]ql2x(3f)(7)三边简支一边固定(长边)(图2(g)):m x=3n-112[n(2+B)+2A]ql2x(3g)(8)三边简支一边固定(短边)(图2(h)):m x=3n-112[2n+A(2+B)]ql2x(3h)(9)四边简支(图2(i)):m x=3n-124(n+A)ql2x(3i)三、几种边界条件下薄板的塑性内力系数在实际工程设计中,直接按式(3a)~(3i)计算各种边界条件下双向板的内力并不方便,为此,通过编制简易电算程序,可以很方便地计算出任意边界条件下的塑性内力系数。
这里将边长比n=210~310,B=110, 114,118,210,215时板的塑性内力系数编制成表1~5 (中间值可采用插值的方法确定),在实际应用中可以方便地由表中系数求得板块的塑性内力。
对于n<2的情况,可以从现行各类结构设计手册中查询,对于n >310的情况,可以由式(3a)~(3i)直接计算求解。
四、算例四边简支板,板边长比n=ly/l x=215,短边边长为3m,板的均布荷载q=10kN/m2;求该板的内力。
图2所示几种板的塑性内力系数(B=110)表1 n(a)(b)(c)(d)(e)(f)(g)(h)(i) 2100010460106001048010620104901083010640108801093 2110010470106101049010630105001086010650109101095 2120010480106301050010650105101089010670109301097 2130010490106401050010660105101092010680109501099 2140010500106501051010670105201094010680109701100 2150010510106701052010680105201096010690109901102 2160010520106801052010690105301098010700110001103 2170010520106801053010700105301099010710110201104 2180010530106901053010700105401101010710110301105 2190010530107001054010710105401102010720110401106 3100010540107101054010710105501103010720110501107图2所示几种板的塑性内力系数(B=114)表2 n(a)(b)(c)(d)(e)(f)(g)(h)(i) 2100010390105201040010540104101080010570108601093 2110010400105401041010560104201084010580108901095 2120010400105501041010570104301087010590109101097 2130010410105601042010580104301089010600109401099 2140010420105701043010590104401092010610109601100 2150010420105801043010600104401094010610109801102 2160010430105901044010610104401096010620109901103 2170010430106001044010610104501098010630110101104 2180010440106101044010620104501099010630110201105 2190010440106201045010630104501101010640110301106 3100010450106201045010630104601102010640110501107图2所示几种板的塑性内力系数(B=118)表3 n(a)(b)(c)(d)(e)(f)(g)(h)(i) 2100010330104601034010490103601077010510108401093 2110010340104801035010500103601081010520108701095 2120010350104901036010510103701084010530109001097 2130010350105001036010520103701087010540109201099 2140010360105101037010530103701090010550109501100 2150010360105201037010540103801092010550109701102 2160010370105301037010540103801094010560109801103 2170010370105401038010550103801096010560110001104 2180010380105401038010550103901098010570110101105 2190010380105501038010560103901099010570110301106 3100010380105501039010560103901101010570110401107图2所示几种板的塑性内力系数(B=210)表4 n(a)(b)(c)(d)(e)(f)(g)(h)(i) 2100010310104401032010460103301076010490108301093 2110010320104501033010470103401079010500108601095 2120010320104601033010480103401083010510108901097 2130010330104801034010490103501086010510109201099 2140010330104901034010500103501088010520109401100 2150010340104901035010510103501091010520109601102 2160010340105001035010520103601093010530109801103 2170010350105101035010520103601095010530109901104 2180010350105201036010530103601097010540110101105 2190010350105201036010530103601099010540110201106 3100010360105301036010540103701100010550110301107(下转第69页)26的安全质量标准。
