匀变速直线运动位移与时间和匀变速直线运动几个比例关系
高中物理新教材同步 必修第一册第2章 3 匀变速直线运动的位移与时间的关系

3 匀变速直线运动的位移与时间的关系[学习目标] 1.理解匀变速直线运动的位移与时间的关系,会用公式x =v 0t +12at 2解决匀变速直线运动的问题(重点)。
2.理解匀变速直线运动的速度与位移的关系式并会应用公式v 2-v 02=2ax 解题(难点)。
一、匀变速直线运动的位移1.物体做匀速直线运动,其v -t 图像与t 轴围成的矩形面积有什么意义?答案 做匀速直线运动的物体在时间t 内的位移大小对应着v -t 图线与t 轴围成的矩形面积,即v -t 图像与t 轴围成的矩形面积表示物体的位移大小。
2.如图是某物体以初速度v 0做匀变速直线运动的v -t 图像。
(1)如图甲所示,把物体的运动分成5段,每一段时间内,看成匀速直线运动,试着在图中画出这5小段的位移之和。
(2)如图乙所示,如果把过程分割为更多的小段,和甲图相比,哪种情形更接近整个过程的位移?(3)依次类推,如果把过程分割成无数个小段,能否用梯形的面积代表物体在这段时间的位移?(4)梯形面积为多少?试结合v =v 0+at 推导出位移x 与时间t 的关系。
答案 (1)位移为图中矩形面积之和,如图所示。
(2)图乙更接近整个过程中的位移。
(3)可以。
(4)S =v +v 02t =v 0+at +v 02t =v 0t +12at 2,则x =v 0t +12at 2。
1.匀变速直线运动位移与时间的关系式:x =v 0t +12at 2当v 0=0时,x =12at 2(由静止开始的匀加速直线运动),此时x ∝t 2。
2.适用范围:仅适用于匀变速直线运动。
3.公式的矢量性:公式中x 、v 0、a 都是矢量,应用时必须选取正方向。
一般选v 0的方向为正方向。
当物体做匀加速直线运动时,a 取正值。
当物体做匀减速直线运动时,a 取负值,计算结果中,位移x 的正、负表示其方向。
4.各物理量的单位都要使用国际单位制单位。
说明:推导匀变速直线运动的位移大小等于图像下方的面积时用到了微元法。
初速度为0的匀变速直线运动的几个比例关系

02
匀变速直线运动的加速度、速度、位移和时 间之间的比例关系;
03
通过实例分析和计算,掌握运用比例关系解 题的方法和技巧;
04
了解匀变速直线运动在实际生活中的应用和 意义。
学生对本次课程反馈和建议收集
01
学生普遍反映本次课程内容难 度适中,易于理解和掌握;
02
部分学生建议在讲解过程中可 以增加一些实例和练习题,以 加深对知识点的理解和记忆;
同时,中间时刻的速度也等于这 段时间内平均速度的大小,即 v_mid=(v_0+v)/2,其中v_0为 初速度(在这里为0)。
这个关系表明,在匀变速直线运 动中,中间时刻的速度具有特殊 的意义,它可以用来计算这段时 间内的平均速度。
2023
PART 03
匀变速直线运动中的推论 及应用
REPORTING
求解物体的加速度
可以通过测量物体在连续相等时间内的位移,然后 利用位移之差等于恒量的关系式求出加速度。
判断物体是否做匀变速直 线运动
可以通过测量物体在不同时间间隔内的位移 ,然后验证位移之差是否等于恒量来判断物 体是否做匀变速直线运动。
2023
PART 04
初速度为0的匀变速直线 运动特例分析
REPORTING
实验设计思路及步骤
01 3. 选择不同的初始高度,释放物体并同时开始计 时。
02 4. 通过光电门测量物体通过不同位置时的速度。 03 5. 记录实验数据,包括时间、位移、速度等。
数据采集和处理方法
数据采集
使用光电门测量物体通过不同位置时的速度,使用测量尺测量物体的位移,使用秒表记 录时间。
数据处理
2023
THANKS
感谢观看
高一物理必修课件二匀变速直线运动的六个比例关系

THANK YOU
感谢聆听
题型四
已知某段时间内的平均速度和 初速度(或末速度),求加速 度和时间等。这类问题可以通 过联立匀变速直线运动的平均 速度公式和速度公式进行求解 。
05
实验设计与操作指南
设计实验方案,验证六个比例关系
确定实验目的
验证匀变速直线运动中的六个 比例关系,包括初速度为零的 匀加速直线运动的比例关系。
设计实验步骤
挑战性问题:如何在实际生活中应用所学知识
在体育运动中的应用
在航天科技中的应用
通过分析运动员的运动轨迹和速度变 化,可以指导运动员进行更有效的训 练和提高竞技水平。
通过精确计算和控制卫星的轨道和速 度,可以实现卫星的精确导航和定位 。
在交通安全中的应用
了解汽车刹车距离和反应时间等因素 ,可以帮助驾驶员避免交通事故的发 生。
第二比例关系:末速度与时间成正比
02
01
03
在匀变速直线运动中,物体的末速度与时间成正比。
公式表示为:v = u + at,其中v为末速度,u为初速 度,a为加速度,t为时间。 当初速度为零时,末速度与时间成正比,即v = at。
第三比例关系:位移中点速度等于平均速度
公式表示为:v_mid = (v₀ + v) / 2,其中v_mid为位移中点 速度,v₀为初速度,v为末速 度。
$v = v_0 + at$,$x = v_0t + frac{1}{2}at^2$,$v^2 - v_0^2 = 2ax$。在解 题时,根据已知条件和所求物理量选择合适的公式进行计算。
中间时刻速度和中间位置速度的公式
$v_{frac{t}{2}} = frac{v_0 + v}{2}$,$v_{frac{x}{2}} = sqrt{frac{v_0^2 + v^2}{2}}$。在处理与中间时刻或中间位置有关的问题时,可以选用这两个公式 。
2.3匀变速直线运动的位移与时间的关系

变速 运动
抽象
匀速 运动
在很短一段时间内,化“变”为“不变”
化繁为简的思想方法
v/m·s-1
当 当△△tttt更11150小0tt时 时
V0
O
t
t/s
匀变速直线运动的v-t图象与时间轴所
围的面积表示位移。
v/m·s-1
v
S 1 (OA BC)OC 2
B
A
v0
C
O
t
梯形“面积”=位
1
1
x at 2 180m 1m / s2 (12s)2
v 2
2
9m / s
0
t
12s
在平直公路上,一汽车的速度为15m/s。 从某时刻开始刹车,在阻力作用下,汽车以 2m/s2的加速度运动,问刹车后10s末车离开 始刹车点多远?
注意刹车问题的陷阱!
结论:匀速直线
运动的位移就是
是V-t图线与t轴
t
t / s 所围矩形“面积”
v/m·s-1 10
16m
v/m·s-1
8 6
乙
4
甲0
t/s
2
-2 1 2 3 4 5 6
0 1 2 3 4 5 6 t/s -4
-16m
猜一猜
匀变速直线运动,它的位
移是不是也有类似的关系?
v
v
?…
v0
0
t
t
回顾
在初中时,我们 曾经用“以直代曲” 的方法,估测一段曲 线的长度。
伽利略相信,自然界是简单的,自然 规律也是简单的。我们研究问题,总是 从最简单的开始,通过对简单问题的研 究,认识了许多复杂的规律,这是科学 探究常用的一种方法。
高一物理匀变速直线运动的位移与时间的关系

一、匀速直线运动的位移
匀速直线运动,物体的位移对应着v-t图 像中的一块矩形的面积。
二、匀变速直线运动的位移
1、 匀变速直线运动,物体的位移对 应着v-t图像中图线与时间轴之间包围 公式 v=(v0+v)/2
课堂训练
1、一辆汽车以1m/s2的加速度加速行驶了 12s,驶过了180m,求汽车开始加速时的 速度是多少? 9m/s 2、骑自行车的人以5m/s的初速度匀减速上 一个斜坡,加速度的大小为0.4m/s2,斜坡 长30m,骑自行车的人通过斜坡需要多少 时间? 10s
3、以10m/s的速度匀速行驶的汽车刹车后 做匀减速运动。若汽车刹车后第2s内的 位移为6.25m(刹车时间超过2s),则 刹车后6s内汽车的位移是多大? a=-2.5m/s2 20m 4、以10m/s的速度行驶的汽车关闭油门后 后做匀减速运动,经过6s停下来,求汽 车刹车后的位移大小。 30m
小结
一、匀速直线运动的位移 1、匀速直线运动,物体的位移对应着v-t图像中 的一块矩形的面积。 2、公式:S = v t 二、匀变速直线运动的位移与时间的关系 1、 匀变速直线运动,物体的位移对应着v- t图 像 中图线与时间轴之间包围的梯形面积。 2、公式 3、平均速度公式
v=(v0+v)/2
[课堂探究]
三、匀变速直线运动的位移与 速度的关系
v2 - v02 = 2 a s
匀变速直线运动公式
1、速度公式 v = v0 + at
2、位移公式 S = v0 t+1/2 at2 3、推论
v2 - v02 = 2 a s
4、平均速度公式 v=(v0+v)/ 2
课堂训练
1、射击时,火药在枪筒里燃烧。燃气膨胀, 推动弹头加速运动。我们把子弹在枪筒里 的运动看做是匀加速直线运动,假设子弹 的加速度是a=5×105m/s,枪筒长 x= 0.64m,我们计算子弹射出枪口时的速度。
匀变速直线运动的位移与时间的关系
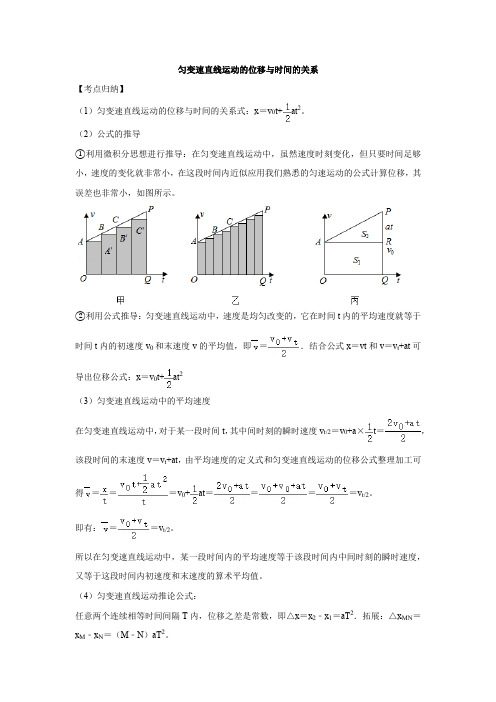
匀变速直线运动的位移与时间的关系【考点归纳】(1)匀变速直线运动的位移与时间的关系式:x=v0t+at2。
(2)公式的推导①利用微积分思想进行推导:在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,在这段时间内近似应用我们熟悉的匀速运动的公式计算位移,其误差也非常小,如图所示。
②利用公式推导:匀变速直线运动中,速度是均匀改变的,它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值,即=.结合公式x=vt和v=v t+at可导出位移公式:x=v0t+at2(3)匀变速直线运动中的平均速度在匀变速直线运动中,对于某一段时间t,其中间时刻的瞬时速度v t/2=v0+a×t=,该段时间的末速度v=v t+at,由平均速度的定义式和匀变速直线运动的位移公式整理加工可得===v0+at====v t/2。
即有:==v t/2。
所以在匀变速直线运动中,某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度,又等于这段时间内初速度和末速度的算术平均值。
(4)匀变速直线运动推论公式:任意两个连续相等时间间隔T内,位移之差是常数,即△x=x2﹣x1=aT2.拓展:△x MN=x M﹣x N=(M﹣N)aT2。
推导:如图所示,x1、x2为连续相等的时间T内的位移,加速度为a。
【命题方向】例1:对基本公式的理解汽车在平直的公路上以30m/s的速度行驶,当汽车遇到交通事故时就以7.5m/s2的加速度刹车,刹车2s内和6s内的位移之比()A.1:1B.5:9C.5:8D.3:4分析:求出汽车刹车到停止所需的时间,汽车刹车停止后不再运动,然后根据位移时间公式求出2s内和6s内的位移。
解:汽车刹车到停止所需的时间>2s所以刹车2s内的位移=45m。
t0<6s,所以刹车在6s内的位移等于在4s内的位移。
=60m。
所以刹车2s内和6s内的位移之比为3:4.故D正确,A、B、C错误。
匀变速直线运动的位移与时间的关系

选用 = 0 + 2 变形后求解
2
3.12s时的速度为多大?如果12s后以2/ 2 的加速度做减
速运动,经多长时间汽车停下来?减速的位移为多大?
12m/s
6s
36m
例 航空母舰的舰载机既要在航母上起飞,也要在航母上降落。
(1)某舰载机起飞时,采用弹射装置使飞机获得10 m/s的速度后,由机上发送机使飞机获得25 m/s2的
高中物理 必修第一册
第二章
第
3
匀变速直线运动的位
节
移与时间的关系
学习目标
任务1:匀速直线运动物体的位移.
任务2:匀变速直线运动的位移公式的推导.
任务3:应用位移公式解决生活中的实际问题.
任务4:匀变速直线运动的速度与位移关系公式的推导.
任务5:应用速度与位移公式解决生活中的实际问题.
任务6:初速度为0的匀加速直线运动的几个常用比例关系 .
等,平均速度不相等。
C错:两物体均做匀速运动,可知5 s末的加速度均为零。
B对:x-t图像的斜率表示速度,可知5 s末的速度vA>vB。
3.如图所示是A、B两个运动物体的x-t图像,下列说法正确的是( C )
A. A、B两个物体开始时相距100 m,同时同向运动
B. B物体做匀减速直线运动,加速度大小为5 m/s2
关系式求解,为什么?
02 + 2
=
2
2
不涉及时间,用速度和位移的关系求解
图2
任务5:应用速度与位移公式解决生活中的实际问题
问题情境:如图所示
问题
2.想一想:如果从A 到B 做匀减速直线运动,初速度为v0,
加速度为a,末速度为v,位移为x。那么结论仍然成立吗?
匀变速直线运动的四个基本公式

第二章 匀变速直线运动的研究 一、四个基本公式1、 匀变速直线运动速度随时间变化规律公式:at v v +=02、匀变速直线运动位移随时间变化规律公式:2021at t v x += 【例1】以10 m/s 的速度匀速行驶的汽车,刹车后做匀减速直线运动。
若汽车刹车后第2 s 内的位移为6.25 m(刹车时间超过2 s),则刹车后6 s 内汽车的位移是多大?3、匀变速直线运动位移与速度的关系:ax v v 2202=-【例2】身高为2 m 的宇航员,用背越式跳高,在地球上能跳2 m ,在另一星球上能跳5 m ,若只考虑重力因素影响,地球表面重力加速度为g ,则该星球表面重力加速度约为( ) A.52g B.25g C.15g D.14g 【例7】一辆车由静止开始作匀变速直线运动,在第8 s 末开始刹车,经4 s 停下来,汽车刹车过程也是匀变速直线运动,那么前后两段加速度的大小之比和位移之比x 1 ׃ x 2分别是( )A 、=1:4 ,x 1 ׃ x 2=1:4B 、=1:2,x 1 ׃ x 2=1:4C 、=1:2 ,x 1 ׃ x 2=2:1 C 、=4:1 ,x 1 ׃ x 2=2:1【例6】一只小球自屋檐自由下落,在Δt =0.25 s 内通过高度为Δh =2 m 的 窗口,求窗口的顶端距屋檐多高?(取g =10 m/s2)4、匀变速直线运动平均速度公式:(v0+v1)/2 通过图像关系证明二、 匀变速直线运动的三个推论1、 某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:试证明此结论:2、某段位移内中间位置的瞬时速度2x v 与这段位移的初、末速度0v 与t v 的关系为:()220221t x v v v +=试证明此结论:【例3】一列从车站开出的火车,在平直轨道上做匀加速直线运动,已知这列火车的长度为l , 火车头经过某路标时的速度为v 1,而车尾经过这个路标时的速度为v 2,求: (1)火车的加速度a ;(2)火车中点经过此路标时的速度v ; (3)整列火车通过此路标所用的时间t 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习2.一质点沿一直线运动,t=0时,位于坐标原点,
下图为质点做直线运动的
速度-时间图像。由图可知: ⑴该质点的位移随时间变化
v/(m·s-1) 4
的关系式是:x=_-_4_t_+_0__.2_t_2_。
⑵在时刻 t=___1_0__s时,
-4
质点距坐标原点最远。
10 20 t/s
vt
2
v
v0 v 2
你的能大比小较吗?vt / 2与vx/ 2
Байду номын сангаас 思考
一物体做匀变速直线运动,其相邻
相等时间间隔的位移有何特点?
v0 t
t
x1
x2
x1
v0t
1 2
at
2
x x2 x1 aT 2
x2
v0 (2t)
1 2
a(2t ) 2
(v0t
1 2
at2 )
v0t
3 2
三、时间比关系
例:物体由静止开始做匀加速直线运动,加速度 为a,求物体:
④在前X、前2X、前3X、前4X所用的时间之比,即 t1:t2:t3:t4;
推论四:初速度为零的匀加速直线运动,前nS米所
用之比t1 : t2 : t3 : ···: tn= 1 : 2 : 3 : ···: n ;
三、时间比关系
⑶从t=0到t=20s内质点的位移是___0___;
通过的路程是___4_0_m__。
m
• 1.在匀变速直线运动中,某段位移中间位 置的瞬时速度与这段位移的初、末速度有 什么样的关系?
vx
2
v02 v2 2
• 2.在匀变速直线运动中,某段时间中间时
刻的瞬时速度与全程的平均速度有什么样
的关系?
练习三:
一列车由等长的车厢连接而成。车厢之间 的间隙忽略不计,一人站在站台上与第一 节车厢的最前端相齐。当列车由静止开始 做匀加速直线运动时开始计时,测得第一 节车厢通过他的时间为1s,则从第5节至第 16节车厢通过他的时间为多少?
答案:t=2s
放映结束 感谢各位批评指导!
谢 谢!
让我们共同进步
练习二
1.一个做初速为零的匀加速直线运动的物体, 它在第1s内、第2s内、第3s内平均速度之 比是( ) D
A.1:1:1
B.1:2:3
C.12:22:32
D.1:3:5
2. 物体做自由落体运动,下落的时间为4s, 则物体在下落的最后2s时间内通过的位移 是( C )(g取10m/s2)
A.20m B.40m C.60m D.80m
A.1:1:1
B.1:2:3
C.12:22:32
D.1:3:5
2. 一自由下落物体,下落到地所需时间为5s, 在落地前1s末的速度为8m/s,问物体下落2s 末的速度为多少?
答案:v=4m/s
二、位移比关系
例:物体由静止开始做匀加速直线运动,加速度 为a,求物体:
②在前Ts内、前2Ts内、前3Ts内、前4Ts内的位移 之比,即X1:X2:X3:X4;
at 2
结论:
1.无论是匀加速直线运动还是匀减速直 线运动,都有
Vx Vt
2
2
2.匀变速直线运动的位移:
x
_
vt
v0
vt
t
2
思考
一物体做匀变速直线运动,其相邻 相等时间间隔的位移有何特点?
V
at
x aT 2
V0
0
t
t
t
t
初速度为零的匀加速直线运动的几个比例关系 以下比例关系对自由落体运动均适用
一、速度比关系
例:物体由静止开始做匀加速直线运动,加速度为a, 求物体:
①在Ts末、2Ts末、3Ts末、4Ts末的瞬时速度之比, 即V1:V2:V3:V4;
推论一:初速度为零的匀加速直线运动,nT秒末 瞬时速度之比 V1:V2:V3:···:Vn=1:2:3:···:n;
【练习一】
1. 一个做初速为零的匀加速直线运动的物体, 它在第1s末、第2s末、第3s末的瞬时速度之比 是( B)
推论二:初速度为零的匀加速直线运动,前nT秒 内位移之比X1:X2:X3:···:Xn=1:22:32:···:n2;
二、位移比关系
例:物体由静止开始做匀加速直线运动,加速度 为a,求物体:
③在第1个Ts内、第2个Ts内、第3个Ts内、第4个 Ts内的位移之比,即x1:x2:x3:x4。
推论三:初速度为零的匀加速直线运动,第n个T 秒内位移之比x1 :x2:x3 :···:xn =1:3:5:···:(2n1);
一、匀速直线运动的位移
1、匀速直线运动,物体的位移对应着v-t图像中的一
块矩形的面积。
2、公式:x=vt
二、匀变速直线运动的位移与时间的关系
1、匀变速直线运动,物体的位移对应着v-t图像 中图
线与时间轴之间包围的梯形面积。
2、公式
x
v0
t
1 2
at
2
例2.一质点以一定初速度沿竖直方向抛出,得到 它的速度一时间图像如图所示.试求出它在前2 s内的位移,后2 s内的位移,前4s内的位移.
例:物体由静止开始做匀加速直线运动,加速度 为a,求物体:
⑤在第一个X、第2个X、第3个X、第4个X所用的时 间之比,即t1:t2:t3:t4;
推论五:初速度为零的匀加速直线运动,第n个X米所
用之比t1:t2:t3:···:tn=1: 2 -1: 3 - 2 :···: n - n 1
;
综合练习:
1.关于自由落体运动,下列说法中正确的是(AC)D A.它是竖直向下v0=0,a=g的匀加速直线运动; B.在开始连续的三个1s内通过的位移之比是1:4:
9; C.在开始连续的三个1s末的速度大小之比是1:2:
3; D.从开始运动起下落4.9m,9.8m,14.7m所经历的
时间之比为 1: 2 : 3
