光课程设计平行平板多光束干涉的仿真
22平行平板的多光束干涉 15页

相位差为
其它无。
r 222nh cos
相邻两透射光之间的相位差为
t 24nh cos
设光从周围介质射入平板时的反射系数为r,透射系数为 t,光从平板射出时的反射系数为r′,透射系数为t′.
从平板反射出的各个光束的复振幅
9/20/2019
从平板反射出的各个光束的复振幅
22nhcos
也可以说干涉光强只与光束 倾角有关,这正是等倾干 涉条纹的特性。
9/20/2019
多光束干涉 装置示意图
实验装置中的透镜光轴 垂直于平板(T2-19)时
观察到的等倾条纹是一 组同心圆环。
9/20/2019
(3) 光强分布的极值条件
爱里公式
F sin2
2
It
1
1
Ii 1Fsin2m 2
4
Fsi2nFsi2n1
4
4
若F很大(即R较大),ε必定很小,有sinε/4≈ε/4,
F(ε/4) 2=1, 因而可得
4 2(1R)
ε是单色光照射下多光束干涉条纹
F R 的半值宽度,称为”仪器宽度“。
9/20/2019
反射率、透射率的关系
r 2 r'2 R
tt' 1 R T
9/20/2019
所有反射光在P点叠加,其合成场复振幅
E0r E01r E0lr l2
E0r1 t'tr'(2l3)E0iei(l1) l2
令 n l-2
E0r1t'tr'E0iei r'2nein
反映了能量守恒的普遍规律。即在不考虑吸收和其它损 耗的情况下,反射光强与透射光强之和等于入射光强。
2.2 平行平板的多光束干涉

概述
双光束干涉的不足与多光束干涉
2.2.1 2.2.2 2.2.3 2.2.4
平行平板多光束的光场分布 平行平板多光束的光强分布 多光束干涉图样特点 透射光的特点
1/4/2016
双光束干涉的不足与多光束干涉
平行平板双光束干涉,仅是在 表面反射率较小情况下的一种 近似处理。 实际上光束在平板内会不断地 反射和折射,如图所示
根据菲涅耳公式,可以证明
由平板表面反射系数、透射系数与 反射率、透射率的关系
r r ' tt ' 1 r 2
1/4/2016
r 2 r '2 R tt ' 1 R T
所有反射光在P点叠加,其合成场复振幅
E0 r E01r E0lr
l 2
E01r tt ' r '( 2l 3) E0i e i (l 1)
1/4/2016
在平板结构(n,h)给定,入射 光线方向()一定的情况下, 仅与波长有关。- -滤波 将改写
相邻透射光相位差处于 半宽度Δ内的光才能透 过平行平板。
4 nh cos c
4 nh cos c
1 2
滤波宽度
1/4/2016
滤波特性
It/Ii-曲线
l 2
n l - 2 令
E01r tt ' r ' E0i e i r ' 2 n e in
n 0 n 0
E0 r R E0i (1 R) R E0i e i ( Re i ) n
E0 r
22平行平板的多光束干涉

能够产生极明锐的透射光干涉条纹, 是多光束干涉的最显著和 最重要的特点。
11/8/2019
条纹宽度
It/Ii-曲线
若用条纹的半峰值全宽度
(简称半值宽度)ε=Δ表征
干涉条纹的锐度,则当
时 2m
11/8/2019
r 2 r'2 R
tt' 1 R T
11/8/2019
所有反射光在P点叠加,其合成场复振幅
E0r E01r E0lr l2
E0r1 t'tr'(2l3)E0iei(l1) l2
令 n l-2
E0r1t'tr'E0iei r'2nein
(3)频率特性
It/Ii-曲线
由t 4nhcos可知
在平板结构(n,h)给定,入射光 相邻透射光相位差处于
线方向()一定的情况下, 半宽度Δ内的光才能透
仅与波长有关。- -滤波
过平行平板。
将改写
4nhcos
c
1 2
ห้องสมุดไป่ตู้
4
nhcos
c
滤波宽度
22nhcos
也可以说干涉光强只与光束 倾角有关,这正是等倾干涉 条纹的特性。
11/8/2019
多光束干涉 装置示意图
实验装置中的透镜光轴垂 直于平板(T2-19)时
观察到的等倾条纹是一 组同心圆环。
11/8/2019
(3) 光强分布的极值条件
爱里公式
F sin2
透射光干涉条纹特点
(1)光强分布与反射率R有关
平行平板的多光束干涉及其应用1

2m和 2m+1 m=0,1, 2,
其相应旳透射光干涉光强为:
I
t M
I
(i
)和I
t m
1 1 F
I (i)
结论:不论对透射光还是反射光,形成亮纹和暗纹旳条件与 双光束完全相同,所以条纹旳位置相同。干涉场旳对比度由 界面旳反射比来拟定。
▪ 不同反射率下透射光强度与位相差关系
▪ 不同反射率下反射光与位相差旳关系
w A(i) n0 1 n
n0
2
r,t
h
r’ , t’
L’
p
tt' 1 r2 1
I
(t
P点光强为A:p(t )tt
) A(t) A(t)*
'r '
2( p1)
1 F
( A)(i)
1 • sin2
•
ei( p
I (i)
1)
其中
2
F
透镜焦平面上产生多光束干涉
4 1 2
透射光在P点旳光强:
▪ 设测量旳=22-和1,1旳=亮(纹2+级1数)/2为,m被2
e
和隔me,1,m2m和=mm1纹2- 旳m1间,隔条纹e 间
e
▪ 由到m=2h/(12)=e/e,得
➢ = e 2/(2he) ➢ e2=/(2eh时)—旳自由=光(谱范) S围.R=
二:激光谐振腔
多光束干涉原理在薄膜理论中旳应用
▪ 薄膜:在玻璃或金属等基片旳光滑表面上, 用物理、化学措施生成旳透明介质膜。
(三)干涉条纹锐度和精细度 对m级条纹,两个半强度点旳相位差分别是:
I (t) / I (i)
1
2 m 和 2 m -
2 2 0.5
2.2 平行平板的多光束干涉

若反射光因干涉加强,则透射光必因干涉而减弱,反之 亦然。即是说,反射光强分布与透射光强分布互补。
(2) 等倾性
由爱里公式可以看出,干涉光强随R和变化。
在特定的R条件下,仅随变化。
r
2
2nh cos
也可以说干涉光强只与光束 倾角有关,这正是等倾干涉 条纹的特性。
3/4/2020
R E0i (1 R) R E0i ei (Rei ) n n0
E0r
(1 ei ) 1 Re i
R
E0i
反射光在P点合成光场的复振幅
3/4/2020
2.2.2 平行平板多光束的光强分布
由I=E·E*, 得到反射光强与入射光强的关系为
F sin2
Ir
1
F
多光束干涉 装置示意图
实验装置中的透镜光轴垂 直于平板(T2-19)时
观察到的等倾条纹是一 组同心圆环。
3/4/2020
(3) 光强分布的极值条件
爱里公式
F sin2
Ir
1
F
2
sin2
Ii
2
反射光形成亮背景下线暗纹
反射光形成亮条纹条件及其光强
(2m 1) m 0,1,2,
能够产生极明锐的透射光干涉条纹, 是多光束干涉的最显著和 最重要的特点。
3/4/2020
条纹宽度
It/Ii-曲线
若用条纹的半峰值全宽度
(简称半值宽度)ε=Δ表征
干涉条纹的锐度,则当
时 2m
2
It
1
1
Ii 1 F sin 2 m 2
3.2 平行平板多光束干涉

该式反映了能量守恒的普遍规律, 该式反映了能量守恒的普遍规律,即反射光强与 透射光强之和等于入射光强。 透射光强之和等于入射光强。
It = 1 1+ F sin
2
ϕ
2
Ii
(43)
Ir =
F sin
2
ϕ
2 I i
2
1+ F sin
ϕ
(41)
2
(1)互补性 ) 若反射光因干涉加强,则透射光必因干涉而减弱, 若反射光因干涉加强,则透射光必因干涉而减弱, 反之亦然。即是说, 反之亦然。即是说,反射光强分布与透射光强分布 互补。 互补。
3.2 平行平板多光束干涉 (Parallel-plate multiple-beam
interference)
实际上平行平板的双光束干涉现象只是在表面反射 实际上平行平板的双光束干涉现象只是在表面反射 率较小情况下的一种近似处理。 率较小情况下的一种近似处理。
反射光干涉 4 100 96
0.96×3.84 =3.7
Irm = 0
F sin
2
(47)
ϕ
2 I i
Ir =
1+ F sin2
ϕ
(41)
2
(3)光强分布的极值条件 ) 对于透射光, 对于透射光,形成亮条纹和暗条纹的条件分别是
ϕ = 2mπ
和
m = 0,,, 1 2 L
( 48)
ϕ = (2m+1)π
m = 0,,, 1 2 L
() 49
It =
1 1+ F sin
n0 n
n0
θ0
t
1
2
3
平行平板的多光束干涉及其应用综述
n 1,2,3...
4
(3)反射光的和振幅与 A0 A1r A2 ... An ar 1 r 2 e i i i e 1 e 1 光强:I r Ar Ar * a 2 r 2 1 r 2 e i 1 r 2 e i
W
q1
P
~ A1r
~ ~ A2r A3r
h
no n no
(相邻光束之间)
=2nh cos q 2 , 4 nh cos q 2
q2
~ A1t
~t ~t A A2 3
L' L' P' 3P'
( 2) 反射率和透射率 设 r、t 、r 和t 是透射和反射系数
att'r ' expiδ
It Ii
1 1 F sin
2
2
对于透射光I t 亮条纹: 2m , 暗条纹: 2m 1 , F Kt 2 F
结论:反射光干涉场与透射光干涉场亮暗条纹互补。 反射场干涉条纹对比度好。 透射场的亮条纹亮。
8
I t max I i I t min I i (1 F )
27
四、光学薄膜
利用物理或化学方法涂镀在玻璃表面或金属光滑
表面上的透明介质膜,利于光波在薄膜中的反射、折
射和干涉达到增反或增透的作用,还可以起到分光、 滤光、调整振幅、位相和偏振态等作用。
1、单层膜
W
设n0-n面, t1, r1 n-nG面, t2, r2 n-n0面, t’1, r’1
no n nG
h1=2.73x10-7m h2=5.46x10-7m h3=8.19x10-7m
其中对应同一种波长,如5.46x10-7m,m1,m2, m3对应的h1,h2,h3分别称为1,2,3…级滤波片。
平行平板的多光束干涉

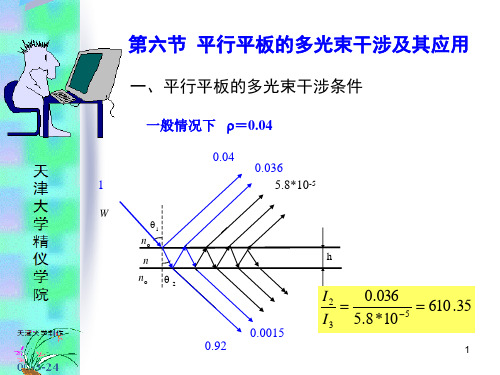
一、平行平板的多光束干涉
干涉条件 一般情况下,即没有镀反射膜在接近正入射时,反
射率为 0.04(4%), =0.04,
各反射光强度 分别是
设入射 光强为1
q1 no n no q 2
0.04 0.036
I2 I3
0.036 5.8*10 5
610 .35
5.8*10-5
两光波振幅相差很
大,610倍,因此
p1
p1
no
q 2
A~1t
A~2t A~3t
A(t ) p
tt'r'2( p1) A(i)
A~(t) A~p(t) tt 'r '2( e p1) i( p1) A(i)
p1
p1
LL' ' PP''
1.1 干涉场强度发布公式
平行平板透射光的振幅分布、光强发布
r' r(存在半波损失), r2, tt' 1 r2 1 , 1
I
(i)
/(1
F)
I (t)
1
F
1
sin(2
2)I (i)
条纹可见度
Kt
2
F F
注意:亮/ 暗条纹的
对于反射光I (r) ,存在半波损失
条件应具
亮条纹:=2m 1 ,
I
(r) max
F
I (i)
1 F
体而定。
暗条纹: 2m ,
I (r) m in
0
书P.358说明
条纹对比度:Kr Imax Imin Imax Imin 1
p1
p1
F精细度系数
F
(1
4 - )2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安邮电大学
光学报告
学院:电子工程
学生姓名:
专业名称:光信息科学与技术班级:光信1103班
1
2
平行平板多光束干涉的仿真
【一】实验目的
通过对平行平板多光束干涉的计算: 1.掌握等倾干涉的概念;
2.掌握干涉特点及条纹锐度,自由光谱范围及滤波特性等概念。
3.对单色光(600nm )与复色光(两种颜色,如600,620nm )进行多光束干涉(要求变化R 值,
如R=0.046,R=0. 27,R=0.64,R=0.87,R=0.99)的计算,绘出干涉条纹,观察条纹锐度;固定入射角(如0°,30°角),观察选频特性。
对复色光观察自由光谱范围。
对整个仿真进行总结归纳。
【二】实验原理
相邻两反射光之间的光程差为
相位差为
相邻两透射光之间的相位差为
设光从周围介质射入平板时的反射系数为r ,透射系数为t ,光从平板射出时的反射系数为r ′,透射系数为t ′. 从平板反射出的各个光束的复振幅
由平板表面反射系数、透射系数与反射率、透射率的关系
反射光在P 点合成光场的复振幅
由I=E ·E*, 得到反射光强与入射光强的关系为
反射光、透射光强与入射光强的关系式,常称为爱里公式 类似地,也可得到透射光强与入射光强的关系式: θ
cos 2nh =∆θ
λ
π
λπϕcos 222nh r =
∆=
θλπλπϕcos 42nh t =∆=
ϕϕϕ
)1(0)32(020*********''''''--====l i i l lr i i r i i
r
i r e E r tt E e E r tt E e E tt r E rE E 2
1''r tt r r -=-=T R tt R r r =-===1''22n
i n i i i r e R e E R R E R E )()1(0
000ϕϕ
∑∞=-+-=i
i i r E R
e E 00Re 1)1(ϕ
ϕ---=i r I F F I 2
sin 12sin 22ϕϕ+=i
t I F I 2
sin
112ϕ
+=
3
式中 精细度,描述干涉条纹的细锐程度 (1) 互补性
反映了能量守恒的普遍规律。
即在不考虑吸收和其它损耗的情况下,反射光强与透射光强之和等于入射光强。
若反射光因干涉加强,则透射光必因干涉而减弱,反之亦然。
即是说,反射光强分布与透射光强分布互补 (2) 等倾性
由爱里公式可以看出,干涉光强随R 和ϕ变化。
在特定的R 条件下,仅随ϕ变化。
也可以说干涉光强只与光束倾角θ有关,这正是等倾干涉条纹
的特性 (3) 光强分布的极值条件
爱里公式
反射光形成亮条纹条件及其光强
反射光形成暗条纹条件及其光强
2
)1(4R R
F -=
θλ
π
ϕcos 22nh r =i
r I
F F I 2
sin 12sin 2
2
ϕ
ϕ+=
,2,1,0)12(=+=m m πϕi
r I F
F
I +=1max
,2,1,02==m m πϕ0
min
=r I
透射光也可以由此得出类似的结果。
【三】程序框图
开始
已知入射光的入射角,反射率R,
入射光的波长
有光的干涉条件及光强的计算,由已知条件计
算出透射光的光强
计算出反射率与投射率与相位差的关系
用plot输出绘出反射率与投射率与相位
差的曲线图和投射光的干涉图样
结束
4
【四】实验结果及分析
i.
ii.
5
由透射光的相对光强图形和干涉条纹可以得出以下的规律:
首先第一幅图是在入射角一定的时候,改变反射率R所呈现不同的干涉条纹。
第二幅图依次是透射光的相对光强曲线、反射光的相对光强曲线(其中它们是光强随着相位差 和反射率R的变化而变化)、条纹锐度图形(透射的相对光强随相位差的变化而变化)。
1.光强分布与反射率R有关 R很小时,干涉光强的变化不大,即干涉条纹
的可见度很低。
R很大时,透射光强暗条纹的强度降低,条纹可见度提高。
控制R的大小,可以改变光强的分布;
2.条纹锐度与反射率R有关随着R增大,极小值下降,亮条纹宽度变窄。
但因相对透射光强的极大值与R无关,所以,在R很大时,透射光的干涉条纹是在暗背景上的细亮条纹。
与此相反,反射光的干涉条纹则是在亮背景上的细暗条纹,由于它不易辨别,故极少应用。
R愈大,条纹锐度愈小,条纹愈尖锐(由
一图可以看出)。
条纹锐度ε是单色光照射下多光束干涉条纹的半值宽度,称为”
6
7
仪器宽度“。
3.由条纹图可以看出其平行平板在透镜焦平面上产生的多光束干涉条纹是等倾干涉条纹,同时所观察到的等倾干涉条纹是一组同心圆环;这里由于光透过透镜是一个圆锥型,在屏幕上刚好是圆形;
4.频率特性 由图像可以看出,相邻透射光相位差ϕ处于半宽度Δϕ内的光才能透过平行平板,在平板结构(n,h)给定,入射光线方向(θ)一定的情况下,ϕ仅与波长λ有关;——滤波特性
滤波宽度
可见,R 愈大,滤波效果愈好。
- -高反膜F-P 可以用白光作光源,也可以得到细而亮的多光束干涉条纹。
也可作单色滤波器使用。
5.在有一个角度入射时,此时干涉图样只是一个圆;
【五】总结
这个实验在做之前,我先找到很多相关的资料和书籍在查看和翻阅,想更加深入的理解其中的原理,看过之后还是只知道透射率和反射率,进而得到相对光强,在询问别人之后才发现它就是通过透射率的相对光强的大小来衡量光的大小,进而绘制出图像,但这里加了色彩这部分,使得实验效果更佳。
不过需要懂得知识点很多。
程序中应用了很多新的函数,比如:hold on 和hold off ,是相对使用的前者的意
思是,你在当前图的轴(坐标系)中画了一幅图,再画另一幅图时,原来的图还在,与新图共存,都看得到;后者表达的是,你在当前图的轴(坐标系)中画了一幅图,此时,状态是hold off,则再画另一幅图时,原来的图就看不到了,在轴上绘制的是新图,原图被替换了。
程序中有很多要注意的语句,会使用它同时更注意的是知道它的功能用法。
在这些逐渐比较难的程序中,我们逐渐掌握了如何建立坐标,并给坐标上建立标注;如何给一幅图上加注标题等等。
感觉在程序上有很大的提高,也没有以前那么害怕。
在实验中不仅更加了解编程的思维,更重要的是对于平行平板多光束干涉的知识的巩固与复习,在实验中让我了解到:
1. 透射光的特点:具体为对光强分布、条纹锐度、频率特性的了解
2. 了解为什么干涉条纹是圆形,由于经过透镜光路为圆锥型;
3. 了解为什么实际中应用的是透射光而不是反射光,因为透射光的干涉条纹是在暗背
景上的细亮条纹。
与此相反,反射光的干涉条纹则是在亮背景上的细暗条
纹,由于它不易辨别,故极少应用
还有很多知识在老师的讲解下都有了清晰地获得,这里就不一一说明了。
θπϕ
νcos 421nh c
∆=
∆θπνcos R 2R)-c(121nh =∆。
