“隐圆”最值问题演示教学
专题18 隐形圆及最值问题

AB是 O 的直径,
ACB 90.
ABC 45 , AC 5 ,
ABC 45 ,
AB AC 5 5 2 , sin 45 2 2
MN最大
52 2
.
故答案为: 5 2 .
6.如图,在平面直角坐标系中,已知 C(3, 4) ,以点 C 为圆心的圆与 y 轴相切.点 A 、 B 在 x 轴上,且 OA OB .点 P 为 C 上的动点, APB 90 ,则 AB 长度的最大值为 .
1.如图,等边 ABC 的边长为 2, A 的半径为 1,D 是 BC 上的动点,DE 与 A 相切于 E , DE 的最小值是 ( )
A.1
B. 2
C. 3
D.2
【分析】连接 AE , AD ,作 AH BC 于 H ,因为 DE 与 A 相切于 E ,所以 AE DE , 可得 DE AD2 AE2 AD2 1 ,当 D 与 H 重合时, AD 最小,此时 DE 最小,求出 AH 的长,即可得出 DE 的最小值. 【解答】解:如图,连接 AE , AD ,作 AH BC 于 H ,
若平面上 A、B、C、D 四个点满足 ABC ADC , 则 A、B、C、D 四点共圆. 证明条件:1.四边形对角互补; 2.四边形外角等于内对角.
两条线段被一点分成(内分或外分)两段长的乘积相等,则这两条线段的四个端点共圆.
D
C
H
O
A
B
四边形 ABCD 的对角线 AC、BD 交于 H, 若 AH CH BH DH ,则 A、B、C、D 四点共圆.
作 AM⊥BP 于 M.当点 P 从点 C 运动到点 A 时,线段 BM 的中点 N 运动的路径长为(
)
A. 2 π 2
隐圆问题-利用圆的知识解决最值课件19张PPT

小是_______
练习:如图,已知AB=AC=AD,∠CBD=2∠BDC, ∠BAC=44°,则∠CAD的度数为__________
县民政局依法行政工作计划总结 2 0 * * 年,在县委、县政府的正确领导下, 在县法制办的直接指导下, 我局认真贯彻 落 实党的十八大精神和国务院《全面推 进依法 行政实 施纲要 》, 坚持“ 以人为本, 为民 解困、为民服务” 的工作理念, 认真履行“ 解决民生、落实民 权、维 护民利” 的工作 职 责, 以服务科学发展、创新体制机制、强化执 法队伍 建设, 全面推 进依法 行政工 作, 推动民政工作制度化、规范化, 充分发挥在社 会建设 和管理 中的职 能作用, 积极 实
施社会惠民保障工程。现将全年依法 行政工 作情况 汇报如 下: 一、齐抓共管, 加强对依法行政工作的组织领 导
为使依法行政理念真正落到实处, 我局成立了“ 一把 手” 局长、党组 书记为 组长, 分管 副局长为副组长和各职能业务科室负 责人为 成员的 依法行 政工作 领导小 组, 并明确 日常工作由办公室( 法制股) 组织实施。年初对全局 的依法 行政工 作排出 计划, 狠抓 落实, 切实把本单位的依法行政工作列入重要 议事日 程。建 立领导 责任制, 做到 有 部署、有检查、有总结, 逐步形成法制工作“ 一把手” 局长亲 自抓、 分管领 导分工 抓 、职能部门牵头抓、业务科室协同抓, 全局干 部职工 积极参 与的工 作格局, 并严 格
例1:等腰直角△ABC中,∠C=90°,AC=BC= 4,D为线段AC上一动点,连接BD,过点C作 CH⊥BD于H,连接AH,则AH的最小值.
练习:1、如图,在正方形ABCD中,动点E、F分 别从D、C两点同时出发,以相同的速度在边DC、 CB上移动,连接AE和DF交于点P,由于点E、F的 移动,使得点P也随之运动.若 ,线段CP的最小值 是_____________
模型23 隐圆系列之点圆最值模型(解析版)
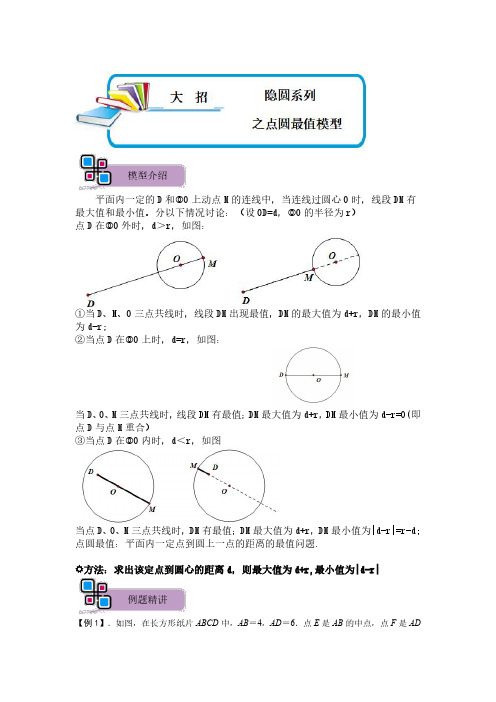
模型介绍平面内一定的D和⓪O上动点M的连线中,当连线过圆心O时,线段DM有最大值和最小值。
分以下情况讨论:(设OD=d,⓪O的半径为r)点D在⓪O外时,d>r,如图:①当D、M、O三点共线时,线段DM出现最值,DM的最大值为d+r,DM的最小值为d-r;②当点D在⓪O上时,d=r,如图:当D、O、M三点共线时,线段DM有最值;DM最大值为d+r,DM最小值为d-r=0(即点D与点M重合)③当点D在⓪O内时,d<r,如图当点D、O、M三点共线时,DM有最值;DM最大值为d+r,DM最小值为|d-r|=r-d;点圆最值:平面内一定点到圆上一点的距离的最值问题.方法:求出该定点到圆心的距离d,则最大值为d+r,最小值为|d-r|例题精讲【例1】.如图,在长方形纸片ABCD中,AB=4,AD=6.点E是AB的中点,点F是AD边上的一个动点.将△AEF沿EF所在直线翻折,得到△GEF.则GC长的最小值是()A.B.C.2D.2解:以点E为圆心,AE长度为半径作圆,连接CE,当点G在线段CE上时,GC的长取最小值,如图所示根据折叠可知:GE=AE=AB=2.在Rt△BCE中,BE=AB=2,BC=6,∠B=90°,∴CE==2,∴GC的最小值=CE﹣GE=2﹣2.故选:A.变式训练【变式1-1】.如图,在平行四边形ABCD中,AB=6,AD=2,∠A=45°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.解:如图,连接MC;过点M作ME⊥CD,交CD的延长线于点E.∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC=2,CD=AB=6,∵点M为AD的中点,∠A=45°,∴DM=MA=,∠MDE=∠A=45°,∴ME=DE=DM=1,∴CE=CD+DE=6+1=7,由勾股定理得:CM2=ME2+CE2,∴CM==5;由翻折变换的性质得:MA′=MA=,点A′在以M为圆心,为半径的圆上显然,当折线MA′C与线段MC重合时,线段A′C的长度最短,此时A′C=MC﹣MA′=5﹣=4,故答案为4.【变式1-2】.如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF=,则点F与点C的最小距离为.解:如图取AB的中点G,连接FG.FC.GC.∵∠EAF=90°,tan∠AEF=,∴=,∵AB=6,AG=GB,∴AG=GB=3,∵AD=9,∴==,∴=,∵四边形ABCD是矩形,∴∠BAD=∠B=∠EAF=90°,∴∠FAG=∠EAD,∴△FAG∽△EAD,∴FG:DE=AF:AE=1:3,∵DE=3,∴FG=1,∴点F的运动轨迹是以G为圆心1为半径的圆,∵GC==3,∴FC≥GC﹣FG,∴FC≥3﹣1,∴CF的最小值为3﹣1.故答案为3﹣1.【例2】.如图,△ABC中,AB=AC,BC=24,AD⊥BC于点D,AD=5,P是半径为3的⊙A上一动点,连结PC,若E PC的中点,连结DE,则DE长的最大值为_______解:如图,连接PB,∵AB=AC,AD⊥BC,∴CD=DB=BC=12,∵点E为AC的中点,∴DE是△PBC的中位线,∴DE=PB,∴当PB取最大值时,DE的长最∵P是半径为3的⊙A上一动点,∴当PB过圆心A时,PB最大,∵BD=12,AD=5,∴AB=,∵⊙A的半径为3,∴PB的最大值为13+3=16,∴DE长的最大值为8,故选:A.变式训练【变式2-1】.如图,在正方形ABCD中,AB=2,F是BD边上的一个动点,连接AF,过点B作BE⊥AF于E,在点F变化的过程中,线段DE的最小值是.解:如图,∵BE⊥AF于E,∴E在以AB为直径圆心为O的圆上,∴当O、E、D三点共线的时候线段DE最小,∵AB=2,四边形ABCD为正方形,∴AO=1=OE,AD=2,∴OD==,∴段DE最小值为OD﹣OF=﹣1.故答案为:﹣1.【变式2-2】.如图,AB是⊙O的直径,点C在半圆的中点,且BC=4cm,点D是上的一个动点,连接BD,过C点作CH⊥BD于H,连接AH,在点D的运动过程中,AH 长度的最小值是.解:连接AC,取BC的中点T,连接AT,TH.∵AB是直径,∴∠ACB=90°,∵点C在半圆的中点,∴=,∴AC=CB=4,∵CT=TB=2,∴AT===2,∵CH⊥BD,∴∠CHB=90°,∴点H在以BC为直径的圆上运动,∵CT=TB,∴HT=BC=2,∵AH≥AT﹣HT=2﹣2,∴AH的最小值为2﹣2,故答案为:2﹣2.1.如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为()A.B.C.﹣D.﹣2解:如图,取AD的中点O,连接OB,OM.∵四边形ABCD是矩形,∴∠BAD=90°,AD=BC=4,∴∠BAP+∠DAM=90°,∵∠ADM=∠BAP,∴∠ADM+∠DAM=90°,∴∠AMD=90°,∵AO=OD=2,∴OM=AD=2,∴点M在以O为圆心,2为半径的⊙O上,∵OB===,∴BM≥OB﹣OM=﹣2,∴BM的最小值为﹣2.故选:D.2.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为()A.1.5B.C.D.2解:∵△ABC是等边三角形,∴∠ABC=∠BAC=60°,AC=AB=3,∵∠PAB=∠ACP,∴∠PAC+∠ACP=60°,∴∠APC=120°,∴点P的运动轨迹是,设所在圆的圆心为O,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:此时PA=PC,OB⊥AC,则AD=CD=AC=,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,∴PD=,BD=,∴PB=BD﹣PD=﹣=.故选:B.3.如图,在Rt△ABC中,∠ACB=90°,AB=2,点D为线段AB的中点,将线段BC绕点B顺时针旋转90°,得到线段BE,连接DE,则DE最大值是.解:如图,将线段BD绕点B顺时针旋转90°,得到线段BP,连接PE,PD,则DB=PB,∠DBP=90°,∵将线段BC绕点B顺时针旋转90°,得到线段BE,∴BC=BE,∠CBE=90°,∴∠CBD=∠EBP,∴△CBD≌△EBP(SAS),∴PE=DC,∵在Rt△ABC中,∠ACB=90°,AB=2,点D为线段AB的中点,∴DB=CD=AB=1,∴PE=1,PB=1,∴DP=,∵PD+PE≥DE,∴DE≤+1,∴DE最大值为+1,故答案为:+1.4.如图,在边长为2的正方形ABCD中,E,F分别是边DC,CB上的动点,且始终满足DE=CF,AE,DF交于点P,则∠APD的度数为90°;连接CP,线段CP的最小值为﹣1.解:∵四边形ABCD是正方形,∴AD=CD,∠ADE=∠DCF=90°,在△ADE和△DCF中,,∴△ADE≌△DCF(SAS),∴∠DAE=∠CDF,∵∠CDF+∠ADF=∠ADC=90°,∴∠ADF+∠DAE=90°,∴∠APD=90°,取AD的中点O,连接OP,则OP=AD=×2=1(不变),根据两点之间线段最短得C、P、O三点共线时线段CP的值最小,在Rt△COD中,根据勾股定理得,CO===,所以,CP=CO﹣OP=﹣1.故答案为:90°,﹣1.5.如图,在△ABC中,∠BAC=90°,AC=8,BC=10,AD是BC边上的高,E、F分别为边DC,DA上的动点,且DE:DF=4:3,射线AE与BF相交于点M,若连接CM,则线段CM的最小值为.解:如图1,连接EF,并延长EF交边AB于点G,∵在△ABC中,∠BAC=90°,AC=8,BC=10,∴,∴AC:AB=4:3,∴AC:AB=DE:DF=4:3,∴,∵∠BAC=∠FDE=90°,∴△BAC∽△FDE,∴∠GBE=∠DFE,∵AD是BC边上的高,∴AD⊥BC,∴∠DFE+∠DEF=90°,∴∠GBE+∠DEF=90°,∴∠BGE=90°,∴EG是△ABE的高,∵AD是△ABE的BE边上的高,∴BM是△ABE的AE边上的高,∴BM⊥AM,∴∠AMB=90°,∴点M在线段AB为直径的上,如图2,作以线段AB为直径的,取圆心O,连接OC交于点N,则当点O、M、C 三点共线时,线段CM的最小值,如图3,∵AB=6,点O是圆心,∴OA=ON=3,∵∠BAC=90°,AC=8,∴,∴线段CM的最小值即,故答案为:.6.如图,直角梯形ABCD中,AB∥DC,∠B=90°,AB=1,BC=2,CD=3,以B为圆心,半径为1的弧交BC于M,E是线段CD上一动点,EG⊥AD,垂足为G,F是弧AM 上一动点,则EG+EF的最小值为.解:作AH⊥CD于点H是矩形.DH=CD﹣AB=3﹣1=2,AH=BC=2.则AH=DH,△ADH是等腰直角三角形.则∠ADC=45°.延长BC到M使CM=BC=2,作MN⊥AD于点N,交CD于点K.则当E到K时,EG+EF 取得最小值.∵∠ADC=90°,MN⊥AD,∴△DNK是等腰直角三角形,∠NKD=∠CKM=45°,同理△CMK是等腰直角三角形.则CK=CM=2,KM=CM=2,∴DK=CD﹣CK=3﹣2=1,∴NK=DK=.则MN=MK+NK=2+=,则EG+EF的最小值是﹣1=.故答案是:.7.如图,在△ABC中,∠ACB=90°,AB=4,点O是AB的中点,以BC为直角边向外作等腰Rt△BCD,连接OD,当OD取最大值时,则∠ODB的度数是.解:如图,将△ODB绕点B逆时针旋转90°,得到△ECB,连接CO,EO,∵将△ODB绕点B逆时针旋转90°,得到△ECB,∴OB=BE,OD=CE,∠BCE=∠BDO,∠OBE=90°∵CE≤OC+OE∴当点O在CE上时,CE有最大值,即OD取最大值,∵BE=OB,∠ABE=90°∴∠BOE=45°∵点O是AB中点,∠ACB=90°∴CO=BO∴∠ECB=∠CBO,∵∠EOB=∠ECB+∠OBC=45°∴∠ECB=22.5°=∠BDO故答案为:22.5°8.如图,正方形ABCD的边长为2,点E为正方形外一个动点,∠AED=45°,P为AB中点,线段PE的最大值是.解:如图,若点E在正方形右侧,连接AC,BD交于点O,连接PO,EO,∵∠AED=45°,∠ACD=45°,∴A,C,E,D四点共圆,∵正方形ABCD的边长为2,∴OE=OD=BD=,∵P为AB的中点,O是BD的中点,∴OP=AD=,∵PE≤OP+OE=+,∴当点O在线段PE上时,PE=OP+OE=+,即线段PE的最大值为+,如图,点E在正方形ABCD上方,作斜边为AD的等腰直角△AOD,∠AOD=90°,则点E在以O为圆心,OA为半径的圆上,∴当点P,点O,点E共线时,PE的值最大,过点O作ON⊥AB,交BA延长线于点N,∵AD=2,AO=DO,∠AOD=90°∴AO=,∠OAD=45°,∵ON⊥AB,AD⊥AB∴∠NAO=∠NOA=45°∴AN=NO=∴PO===∴PE最大值为+>+,故答案为:+9.如图,在矩形ABCD中,AB=4,BC=6.(1)如图①,点E是AB的中点,点F是BC边上一点,将△BEF沿EF折叠,点B的对应点为点P,求CP的最小值;(2)如图②,若点P是矩形ABCD内部一点,且∠BPC=90°,求PD取得最小值时,BP的长;(3)如图③,若点P是矩形ABCD内部一点,且∠PAD+∠PBC=60°,求AP+BP的最大值.解:(1)如图1,∵点E是AB的中点,∴BE=AB=2,由折叠知,PE=BE=2,∴点P是在以E为圆心,2为半径的半圆上运动,当点E,P,C共线时,CP最小,∵四边形ABCD时矩形,∴∠ABC=90°,∴CE===2,=CP′=CE﹣EP′=2﹣2;∴CP最小(2)如图2,∵∠BPC=90°,∴点P在以BC为直径的半圆O上运动,当点D,P,O共线时,PD最小,在Rt△COD中,CD=4,OC=BC=3,∴OD=5,∴P′D=OD﹣OP′=5﹣3=2,作P′Q⊥BC于Q,∵∠OQP′=∠BCD=90°,∠COD为公共角,∴△OQP′∽△OCD,∴,∴,∴OQ=,QP′=,在Rt△BQP′中,QP′=,BQ=OB+OQ=3+=,∴BP′==,∴当PD取得最小值时,BP的长为:;(3)如图3,∵四边形ABCD是矩形,∴∠CAB=∠BAD=90°,∴∠CAB+∠BAD=180°,∵∠PAD+∠PBC=60°,∴(∠CAB+∠BAD)﹣(∠PAD+∠PBC)=120°,∴∠PAB+∠PBA=120°,在△ABP中,∠APB=180°﹣120°=60°,延长BP至E,使PE=PA,∴∠E=∠PAE,∵∠E+∠PAE=∠APB=60°,∴∠E=30°,在AB的右侧作等边三角形ABO,以O为圆心,AB为半径作圆O,则点E优弧AEC上运动,当BE为直径时,即点P在点O处时,AP+BP最大,最大为直径BE′=2AB=8.10.如图,已知四边形ABCD为正方形,△AEF为等腰直角三角形,∠AEF=90°,连接FC,G为FC的中点,连接GD,ED.(1)如图①,当点E在AB边上时,请直接写出DE,DG的数量关系;(2)如图②,将图①中的△AEF绕点A逆时针旋转,其他条件不变.①探究(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;②若AD=4,AE=1,求DG的最大值和最小值.解:(1)DE=DG,理由如下:如图①,连接EG,延长EG交BC的延长线于M,连接DM.∵四边形ABCD是正方形,∴AD=CD,∠B=∠ADC=∠DAE=∠DCB=∠DCM=90°,∵∠AEF=∠B=90°,∴EF∥CM,∴∠CMG=∠FEG,∵∠CGM=∠EGF,GC=GF,∴△CMG≌△FEG(AAS),∴EF=CM,GM=GE,∵AE=EF,∴AE=CM,∴△DCM≌△DAE(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∴DG⊥EM,DG=GE=GM,∴△EGD是等腰直角三角形,∴DE=DG.(2)①结论成立,理由如下:如图②,连接EG,延长EG到M,使得GM=GE,连接CM,DM,延长EF交CD于R.∵EG=GM,FG=GC,∠EGF=∠CGM,∴△CGM≌△FGE(SAS),∴CM=EF,∠CMG=∠GEF,∴CM∥ER,∴∠DCM=∠ERC,∵∠AER+∠ADR=180°,∴∠EAD+∠ERD=180°,∵∠ERD+∠ERC=180°,∴∠DCM=∠EAD,∵AE=EF,∴AE=CM,∴△DAE≌△DCM(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∵EG=GM,∴DG=EG=GM,∴△EDG是等腰直角三角形,∴DE=DG;②∵AE=1,△AEF绕点A旋转,∴点E在以点A为圆心,1为半径的圆A上运动,如图③,当点A、E、D三点共线,且点E在点A的左侧时,DE最大,此时DE=AD+AE=4+1=5,由①可知,DE=DG,∴DG=DE=,即DG的最大值为;如图④,当点A、E、D三点共线,且点E在点A的右侧时,DE最小,此时DE=AD﹣AE=4﹣1=3,由①可知,DE=DG,∴DG=DE=,即DG的最小值为;综上所述,DG的最大值为,最小值为.11.(1)如图1,A、B是⨀O上的两个点,点P在⨀O上,且△APB是直角三角形,⨀O 的半径为1①请在图1中画出点P的位置;②当AB=1时,∠APB=30°;(2)如图2,⨀O的半径为5,A、B为⨀O外固定两点(O、A、B三点不在同一直线上),且OA=9,P为⊙O上的一个动点(点P不在直线AB上),以PA和AB为作平行四边形PABC,求BC的最小值并确定此时点P的位置;(3)如图3,A、B是⊙O上的两个点,过A点作射线AM⊥AB,AM交⨀O于点C,若AB=3,AC=4,点D是平面内的一个动点,且CD=2,E为BD的中点,在D的运动过程中,求线段AE长度的最大值与最小值.解:(1)①如图1,△APB、△AP′B是直角三角形;②在Rt△APB中,AB=AP,∴∠APB=30°,故答案为:30;(2)四边形PABC是平行四边形,∴BC=AP,∴BC的最小值即AP的最小值,∵当P为OA与⊙O的交点时,AP最小,∴AP的最小值为9﹣5=4,即BC的最小值为4;(3)连接BC,∵AM⊥AB,∴∠CAB=90°,∴BC是⊙O的直径,∵点D是平面内的一个动点,且CD=2,∴点D的运动路径为以C为圆心,以2为半径的圆,在直角△ABC中,BC===5,∵O是直角△ABC斜边BC上的中点,∴AO=BC=,∵E是BD的中点,O是BC的中点∴OE=CD=1,∴AE的最小值是AO﹣OE=,最大值是AO+OE=.12.【问题提出】(1)如图①,四边形ABCD为正方形,以BC边为直径在BC上方作半圆O,P是上一点,若AB=6,则DP的最小值为3﹣3;【问题探究】(2)如图②,在Rt△ABC中,∠ACB=90°,BC=4,AC=3,CD是中线,将△ACD 沿CD折叠,得到△ECD,点A的对应点为E,连接AE,求AE的长;【问题解决】(3)如图③是一块矩形ABCD的场地,AB=300m,AD=600m,D为场地的出人口,点E在AD边上,且AE=400m.按照规划,要在矩形内修建一个小型观光台P,且满足∠APE=90°,在BC上修建休息亭M,并要在观光台P、休息台M以及出入口D之间规划道路PM,DM,为了节约成本,要使得线段PM,DM之和最短,试求PM+DM的最小值,并说明理由.(道路的宽度忽略不计)解:(1)如图1,连接OD,交⊙O于点P,则DP最小,∵四边形ABCD是正方形,∴∠BCD=90°,CD=BC=AB=3,在Rt△COD中,OC==3,CD=6,∴OD==3,∴DP=OD﹣OP=3﹣3,故答案为:3﹣3;(2)设CD,AE交于点F,∵∠ACB=90°,AC=3,BC=4,∴AB=5,由折叠得:AE=2AF,CD⊥AE,∵∠ACB=90°,CD是中线,∴AD=CD,∴∠ACD=∠CAD,∵∠AFC=∠ACB=90°,∴△ACF∽△BAC,∴,∴=,∴AF=,∴AE=2AF=;(3)如图2,∵∠APE=90°,∴点P在以AE为直径的⊙O上运动,作点D关于BC的对称点G,连接OG,交BC于M,交⊙O于P,则PM+DM最小,最小值为PG的长,∵四边形ABCD是矩形,∴CG=CD=AB=300,∠ADC=90°,在Rt△ODG中,DG=CD+CG=600,OD=AD﹣OA=600﹣200=400,∴OG===200,∴PG=OG﹣OP=200﹣200,∴PM+DM的最小值为:200﹣200.。
2018中考专题复习 隐圆在几何最值问题中的应用 课件(共11张PPT) (1)

找线段,求张角; 定弦定角画隐圆 找路径,求最值; 圆的知识来帮忙
若∠ACB为锐角, 则C点在两段优弧AB上
若∠ACB为直角, 则C点在半圆AB上
C
若∠ACB为钝角, 则C点在两段劣弧AB上
如图,边长为3的等边△ABC,D、E分别为边BC、AC上 的两个动点,且BD=CE,AD、BE交于P点,求P点的运
探 究 隐 圆
在 几 何 最 值 问 题 中 的 作 用
已知线段AB=6,平面内一点C,满足∠AC能得到什么结论? 问题二:求C点的运动路径长? 问题三:求△ABC面积的最大值?
C
C
A
B
A
运动路径长:6π
Smax=9
∟
O
B
已知线段AB=6,平面内一点C,满足∠ACB=600,情况又如何?
动路径长?并求CP的最小值?
A
O P’
P B D C E
如图,E、F是正方形ABCD的边AD上两个动点,满足AE=DF,连接CF 交BD与点G, 连接BE交AG与点H,若正方形的边长为2,求线段DH长 度的最小值?
C
C1
600 ∟
A
B
600
C2
已知线段AB=4,线段外一点C,满足∠ACB=900 ,
问题四:若I点为△ABC的内心,求I点的运动路径长?
P
450
C1
I1 A
I2
O
B
A
1350
B
I2
C2
方法总结:AB为定线段,线段AB外一点C与A、B两端点形成的张角 固定(即∠ACB=θ),则点C在以AB为弦的圆上运动(不与A、B重合)
中考数学专题《隐形圆解析》

D
E O
C
B
取 CB 中点 M,所以 E 点轨迹是以 M 为圆心、CB 为直径的圆弧.
A
D
E O
CM
B
连接 AM,与圆弧交点即为所求 E 点,此时 AE 值最小, AE AM EM 102 22 2 2 26 2 .
A
E
C
M
B
【2019 园区一模】如图,正方形 ABCD 的边长为 4,动点 E、F 分别从点 A、C 同时出发,
C
M
E
A
O
B
【寻找定边与直角】如图,在 Rt△ABC 中,∠ACB =90°,BC=4,AC=10,点 D 是 AC 上的 一个动点,以 CD 为直径作圆 O,连接 BD 交圆 O 于点 E,则 AE 的最小值为_________.
A
D
O
E
C
B
【分析】连接 CE ,由于 CD 为直径,故∠CED=90°,考虑到 CD 是动线段,故可以将此 题看成定线段 CB 对直角∠CEB .
A
D
O
P
F
B
E
C
连接 OC,与圆的交点即为 P 点,再通过勾股定理即可求出 PC 长度. 思路概述:分析动点形 成原理,通常“ 非直即圆” (不是直线就 是圆),接下来可以 寻找与动 点相关有无定直线与定 角.
【2013 武汉中考】如图,E 、F 是正方形 ABCD 的边 AD 上的两个动点,满足 AE =DF,连 接 CF 交 BD 于点 G,连接 BE 交 AG 于点 H,若正方形边长为 2,则线段 DH 长度的最小 值是________.
A
O
B
【辅助圆+相切】如图,在 Rt△ABC 中,∠ACB =90°,∠B=30°,AB =4,D 是 BC 上一动点, CE ⊥AD 于 E ,EF⊥AB 交 BC 于点 F,则 CF 的最大值是_________.
隐圆问题-利用圆的知识解决最值课件19张PPT

例1:如图,若AB=OA=OB=OC,则∠ACB的大 小是_______
练习:如图,已知AB=AC=AD,∠CBD=2∠BDC, ∠BAC=44°,则∠CAD的度数为__________
例1:木杆AB斜靠在墙壁上,当木杆的上端A沿墙 壁NO竖直下滑时,木杆的底端B也随 之沿着射线OM方向滑动.下列图中用虚线画出木 杆中点P随之下落的路线,其中正确的是( )
2、(2016· 安徽)如图,Rt△ABC中,AB⊥BC, AB=6,BC=4,P是△ABC内部的一个动点,且满 足∠PAB=∠PBC,则线段CP长的最小值为 _________.
3、如图,在平面直角坐标系xOy中,A(﹣2, 0),B(0,2),⊙O的半径为1,点C为⊙O上一 动点,过点B作BP⊥直线AC,垂足为点P,则P点纵 坐标的最大值( )
4、如图,矩形OABC的边OA、OC分别在x轴、y 轴上,点B的坐标为(7,3),点E在边AB上,且 AE=1,已知点P为y轴上一动点,连接EP,过点O 作直线EP的垂线段,垂足为点H,在点P从点F (0, )运动到原点O的过程中,点H的运动路径 长为______.
5、如图,半圆的半径BC为2,O是圆心,A是半圆 上的一个动点,连接AB,M是AB的中点,连接CM 并延长交半圆于点D,连接BD,则BD的最大值为 ____________
练习、如图,AB为直径,AB=4,C、D为圆上两 个动点,N为CD中点,CM⊥AB于M,当C、D在 圆上运动时保持∠CMN=30°,则CD的长( ) A.随C、D的运动位置而变化,且最大值为4 B.随C、D的运动位置而变化,且最小值为2 C.随C、D的运动位置长度保持不变,等于2 D.随C、D的运动位置而变化,没有最值
模型 隐形圆问题梳理(附PPT)
例 2:已知圆C : x 32 y 42 1,点 A(m,0),
点 B(m,0) , m 0 , 若 圆 C 上 存 在 点 P , 使 得
APB 90o,则m的范围是___________. 解:由APB 90o可得点P在以 AB为直径的圆上,
其方程为 x2 y2 m2,且与圆 x 32 y 42 1有
2
2
所以2 2 m 2 2 .
变式 1:在平面直角坐标系中,已知点 A0,2,
B1,1, P 为圆 x2 y2 2上一动点,则 PB 的最大
PA 值是________.
解:设P x, y,则x2 y2 2,
PB
2
PA
x 12 y 12 x2 y 22
x2 y2 2x 2y 2 x2 y2 4y 4
直线l1与直线l2垂直,所以点P在以 AB为直径的圆上,
圆心C 1,1,半径r 2 ,其方程为 x 12 y 12 2
因为圆心C 到直线x y 4 0的距离为 d 4 2 2 ,所以点P到直线x y 4 0的距离的
2 最大值为2 2 2 3 2 .
变式 2:在直角坐标系中,已知点P(1,0),点Q(2,1), 直线l :ax by c 0,其中a ,b,c成等差数列, 点 P 在直线l 上的射影为 H ,则线段QH 的取值范围 是____________.
CD2 11 2sin2
P
C
D
Q O
CD2
1
1
2
1 CD2
CD2
2 CD2
3.
因为OD 2 3 ,所以CD 3,3 3 ,
所以CD2 3,27.
因为CD2
2 CD2
3在3,27上单调递增,
2024届新高考一轮复习人教A版 第八章 培优课(四) 隐圆问题 课件(27张)
,面积为π(
| -|
)2.
-
注意:使用阿波罗尼斯圆解题时,若已知条件中没有坐标系,则需要建立坐标系后求解.
[拓展演练 2] 若△ABC 满足条件|AB|=4,|AC|= |BC|,则△ABC 面积的最大值为
的 轨 迹 为 圆 C ′ , 圆 C ′ 上 的 点 到 直 线 l 的 最 短 距 离 为 t=
→
→
→
→
|+|=|2|=2||≥2t=2 -2.故选 A.
|-+|
-1= -1, 所 以
在平面内到定点的距离等于常数,则这个点的轨迹是一个圆.解决这类问题只
要抓住两个关键词:定点,定长.然后再化归为圆中的有关问题去解即可.
→
→
直线 l:x-y+3=0 上,则|+|的最小值为(
)
A.2 -2 B.2
C.2 +2 D.2 -
解析:设线段 MN 的中点为 D,圆 C:x2+y2-2x-4y=0 的圆心为 C(1,2),半径为
.C 到直线 MN
的距离为 ( ) -() =1,所以|CD|=1,故点 D 的轨迹是以 C 为圆心,半径为 1 的圆,设点 D
解析:建立如图所示的平面直角坐标系,则 A(-2,0),B(2,0).
设 C(x,y),
由|AC|= |BC|得 ( + ) + = · (-) + ,
化简整理可得(x-6)2+y2=32,
因此点 C 的轨迹是以(6,0)为圆心,4 为半径的圆(且去掉点(6+4 ,0)和(6-4 ,0)).
隐形圆_精品文档
隐形圆(引圆)最值问题:我们首先要知道圆上一动点到平面内一定点距离的何时取得最小值和最大值;1》当定点在圆外时,如图所示动点P是在圆o上运动,定点C在圆o外,连接CO并延长,连接OP;我们令OC=d,OP=r;(1)当P,O,C三点不共线时P,O,C三点围成三角形,OC-OP<PC<OC+OP;即d-r<PC<d+r;(2)当P,O,C三点共线时,①P在P’处时,OC-OP=PC,即d-r=PC;②P在P1处时,OC+OP=PC,即d+r=PC;综上可得d-r≤PC≤d+r,PC min=d-r,PC max=d+r.2》当定点在圆内时(不与圆心重合)如图所示:动点P是在圆o上运动,定点C在圆o内,连接CO并双向延长,连接OP;我们令OC=d,OP=r;(1)当P,O,C三点不共线时P,O,C三点围成三角形,OP-OC<PC<OC+OP;即r-d<PC<d+r;(2)当P,O,C三点共线时,①P在P’处时,OP-OC=PC,即r-d=PC;②P在P1处时,OC+OP=PC,即d+r=PC;综上可得r-d≤PC≤d+r,PC min=r-d,PC max=d+r.1.折叠引圆:如图所示在矩形ABCD中,AB=4,AD=6.点E为AB边中点,F为边BC上一动点,以EF为折痕将三角形BEF折叠点B落在B’处,求线段DB’最小值.解析:由题中条件可知折痕EF 满足一定一动的特点,所以满足折叠引圆,根据折叠的性质我们可得到EB=EB ’=21AB=2,根据圆的定义可知,动点B ’是以E 为圆心,2为半径的圆上运动,而B ’的运动又与动点F 有关,我们如果我们将F 看成是从点B →C 的运动可得到B ’的轨迹,如下图所示,B ’的运动并不是完整的圆,而是一部分圆弧。
根据圆上一动点到圆外一定点的最小值分析可知,B ’D 取得最小值时,B ’,D ,E 三点共线,B ’在G 处;所以B ’D min =DE-EG,在直角三角形ADE 中,DE=,因为EG=EB=2,所以B ’D min =-2例1. 如图所示,四边形ABCD 是菱形,∠A=60o,AB=6,点E 是边AD 中点,动点F 是在线段AB 上由A →B 运动,到达B 点停止运动,102AE AD 22=+102连接EF,以EF为折痕将△AEF折叠,点A落在A’处.(1)求A’C长度最小值.(2)求A’的路径长.例2.如图所示矩形ABCD中,AB=8,AD=6,点E是AD边上的中点,点F是AB边上的动点,连接EF,以EF为折痕将△AEF折叠,点A落在A’处,求△A’BC的面积最小值.定角定弦引圆(隐圆):如图所示,在平面内存在定点A,B.点P是平面内的一动点,且点∠P=a.像这类动点处存在一个角度恒为定角,且该角能放在一个三角形内,所对边为定边,那么该动点就是在圆上运动;这个定角就可以理解为圆周角,它所对的定边就是该圆周角所对的弦.(1)直角类型:如图1所示,在平面内存在定点A,B.点P是平面内的一动点,且点∠P=90o,根据上面定角定弦可知,∠P是圆周角,AB是它所对弦,因为∠P=90o,图1 图2(2)锐角类型:如图1所示,在平面内存在定点A,B.点P是平面内的一动点,且点∠P=a,且a<90o,根据上面定角定弦可知,∠P是圆周角,AB是它所对弦,此时的AB并不是直径,我们知道想要画出这个P所在的圆我们需要圆心和半径,或者找到直径;因为A,P,B三点都是圆上的点,∠A,∠B也是圆周角,点P在运动的时候∠A,∠B的大小是会发生改变的,,如图2所示.图1 图2(3)钝角类型:如图1所示,在平面内存在定点A,B.点P是平面内的一动点,且点∠P=a,且a>90o,根据上面定角定弦可知,∠P是圆周角,AB是它所对弦,此时我们发现钝角是无法构造到直角三角形中去的,那么我们就要想办法去转化,我们可以通过四点共圆的特点去转化,我们可以图1 图2图3例1. 如图所示,在矩形ABCD 中AB=8,AD=6,点Q 是边AD 边上一动点,连接CQ ,过点D 作DP ⊥CQ ,交CQ 于点P .(1) 求线段BP 最小值.(2) 如图2所示,点M 也是边AD 上的动点,求BM+PM 最小值.(3) 如图2所示,点M 是边AD 上的动点,求AM+PM 最小值21图1 图2例2.在三角形ABP中,AB=6,∠P=60o,求AP+BP最大值.例3.在等边三角形ABC中,D、E分别为边AC,AB上的动点,且AD=BE;BC=6,连接CE、BD交于点F.(1).求∠CFD.(2).求AF最小值.2.瓜豆原理引圆:瓜豆原理:从动点的运动状态与主动点吻合(主动点在直线上运动,从动点就会在直线上运动;主动点在圆上运动,从动点就会在圆上运动)(1)如图所示点A 、B 都是定点,点D 是圆B 上一动点,连接AD ,取AD 上一点E ,使=k ,此时点D 在圆B 上运动的时候就会带着点E 一起运动,那么点D 就是主动点,点E 就是从动点;(圆B 大小不变,k 为定值)∵=k (主动点与从动点之间的关联所在)∵点A 是定点∴我们可以将点E 所在图形是点D 所在图形关于点A 位似得到的如下图:圆的位似可以对其半径进行位似,即取AB 上一点C ,使=k ∵∠A=∠A ,==k ,∴△ABD ∽△ACE ,∴==k∴CE=kBD 为定值;所以点E 就是以点C 为圆心CE 为半径的圆上运动AD AEAD AEAB ACAD AE AB AC BD CE ABAC(2).如图所示,点A 、B 是平面内定点,点D 是圆B 上一动点,∠DAE=a ,=k ,此时点D 在圆B 上运动的时候就会带着点E 一起运动,那么点D 就是主动点,点E 就是从动点;(圆B 大小不变,k 为定值,a 角度为定值)这个可以看成(1)中图形旋转得到的;取AB 上一点C ,使=k ,将AC 以点A 为旋转中心逆时针旋转a得到C ’,易证△ACE ’∽△ABD ,所以==k ,即C ’E=kBD 所以点E 为C ’为圆心C ’E 为半径的圆上运动例1.如图,点A ,B 的坐标分别为(60)(06)A B C ,,,,为坐标平面内一点,BC M 为线段AC 的中点,连接OM ,当OM 取最大值时,点M 的坐标为__________________. AD AEAB ACBD E C'ABAC2.如图,△ACB中,CA=CB=4,∠ACB=90°,点P为CA上的动点,连BP,过点A作AM⊥BP于M.当点P从点C运动到点A 时,线段BM的中点N运动的路径长为。
中考数学复习指导:发现“隐形”圆巧求最小值
发现发现““隐形隐形””圆 巧求最小值在近几年的中考数学试题中,常有一些涉及到求线段最小值的问题.这些题目入手较难,得分率很低,分析其原因不难发现,学生对题目中运动变化的本质没有搞清楚.在这些蕴含运动变化的问题中,并没有显性的圆,但是仔细分析题目的条件,如果能发现某个点的运动路径是一个圆(或是一段弧),可谓是“山重水复疑无路,柳暗花明又一村”,将会对问题的解决起着重要的作用.下面举例说明.一、翻折中的“隐形”圆例1 如图1,在Rt ABC ∆中,90,6,8C AC BC ∠=°==,点F在边AC 上,并且2CF =,点E 为边BC 上的动点,将CEF ∆沿直线EF 翻折,点C 落在点P 处,则点P 到边AB 距离的最小值是 .解 如图2,当点E 在BC 上运动时, PF 的长固定不变,即2PF CF ==.所以点P 在 以点F 为圆心,以2为半径的圆上运动.过点F 作FH AB ⊥交⊙F 于点P ,垂足为H ,此时PH 最短.由AFH ABC ∆∆:,得FH FA BC AB=.又由已知易得4,10AF AB ==.所以4810FH =,即165FH =.所以P 到AB 距离的最小值166255PH FH FP =−=−=.点评 本题关键的地方在于抓住无论点E 的位置在哪,翻折,FCE PF ∆的长度始终等 于FC 的长度,即2PF =.也就是说动点P 到定点F 的距离是定值2,所以点F 的运动路径是以点F 为圆心,2为半径的圆(或部分).如此,这个问题就最终转化为在圆上找一个到定直线距离最短的点.我们可以利用图3的模型1来作出直观解释.模型1 如图3,直线m 与⊙O 相离,过D 点O 作直线m 的垂线,垂足为点H ,交⊙O 与点P 、点Q ,则⊙O 上点P 到直线m 的距离最短,点Q 到直线m 的距离最长理由简述 在⊙O 上任意找一点P ′,过P ′作P H ′′⊥直线m ,垂足为点H ′.由三角形三边关系及直角三角形斜边大于直角边可得:OP P H OH OH ′′′′+>>,而OH OP PH =+,OP OP ′=,所以P H PH ′′>,所以点P 到直线m 的距离最短.类似的方法可以说明点P 到直线m 的距离最长.例2如图4,在边长为2的菱形ABCD 中,60,A M ∠=°对是AD 边的中点,N 是AB 边上一动点.将AMN ∆沿MN 所在的直线翻折得到A MN ′∆,连结A C ′,则A C ′长度的最小值是 .解 当点N 在AB 边上运动时,MA ′的长度固定不变,即1MA MA ′==,所以点A ′在以点M 为圆心,1为半径的圆上运动,如图5,连接CM ,与⊙M 交于点A ′,此时CA ′最短.过点C 作CG AD ⊥交AD 的延长线于点G .因为2,60CD CDG A =∠=∠=°,所以1,DG CG ==,在Rt CMG ∆中,由勾股定理,得CM == 点评 同例1,无论N 点在何处,沿MN 翻折后,线段MA ′的长度(1MA MA ′==)保持不变,而且点M 是定点,所以点A ′的运动轨迹是以M 为圆心,1为半径的圆(部分).要求A C ′的最小值,回归到模型1中,连结圆外定点C 与圆心M 与圆M 交于点A ′,此时A C ′的长度即为最小值.我们可以借助图6利用模型2来作出直观解释.模型2 如图6,点P 为⊙O 外一定点,连结PO 交⊙O 于点A ,延长线与⊙O 交于另一点B ,则PA 的长度为⊙O 外一点P 到⊙O 的最短距离,PB 的长度为⊙O 外一点P 到⊙O 的最长距离.理由简述 在⊙O 上再任意找一点A ′ ,连接PA ′,由三角形三边关系,可得OA PA OP ′′+>.又,OP OA AP OA OA ′=+=,所以PA PA ′>.类似的方法可以说明PB 的长度为⊙O 外一点P 到⊙O 的最长距离.例3 如图7,菱形ABCD 的边8,60AB B =∠=°,P 是AB 上一点,3,BP Q =是CD 边上一动点,将梯形APQD 沿直线PQ 折叠, A 的对应点为A ′.当 CA ′的长度最小时,CQ 的长为 .解 如图8,过C 作CE AB ⊥,连结AC .因为ABCD 是菱形,60B ∠=°,所以ABC ∆为等边三角形,所以84,3,12AE EB BP EP =====.要使CA ′的长度最小,则梯形APQD 沿直线PQ 折叠后A 的对应点A ′应落在CP 上,且对称轴PQ 应满足//PQ DE .由作图知,DEPQ 为平行四边形,所以1,817DQ EP CQ CD DQ ===−=−=.点评 点Q 在线段CD 上无论运动到何处,梯形APQD 沿直线PQ 折叠后PA ′的长度始终保持不变,因此A ′点的运动路径就是以点P 为圆心,PA 长为半径的圆.借助模型2,可知,当点A ′落在线段CP 与⊙P 的交点时,CA ′的长度最小.由PQ 平分,//APC CD AB ∠,可得CQ CP =.作CE AB ⊥,构造Rt CEP ∆,从而可以求出CP 的长.二、直角中的“隐形”圆例4 如图9,在正方形ABCD 中,动点,E F 分别从,D C 两点同时出发,以相同的速度在直线,DC CB 上移动.连结AE 和DF 交于点P ,由于点,E F 的移动,使得点P 也随之运动,请你画出点P 运动路径的草图.若2AD =,试求出线段CP 的最小值.解 由题意,可得DE CF =.又因为,90AD CD ADC DCB =∠=∠=°,所以ADE DCF ∆≅∆,所以DAE CDF ∠=∠.因为90ADP CDF ∠+∠=°,所以90DAE ADP ∠+∠=°.由于点P 在运动中保持90APD ∠=°.听以点P 的路径是一段以AD 为直径的弧.设AD 的中点为O ,连结OC 交弧于点P ,此时CP 的长度最小.在Rt ODC ∆中,OC ===,所以1CP OC OP =−=−. 点评 此题的本质是抓住动点,E F 在运动过程中,始终保持AE DF ⊥,即90APD ∠=°,这样点P 的运动路径就确定了,即点P 在以AD 为直径的圆弧上,再根据模型2求解即可.例5如图10, Rt ABC ∆中,,6,4,AB BC AB BC P ⊥==是ABC ∆内部的一个动点,且满足PAB PBC ∠=∠,则线段CP 长的最小值为 .解 因为90ABC ∠=°,所以90ABP PBC ∠+∠=°.又因为PAB PBC ∠=∠,所以90BAP ABP ∠+∠=°,即90APB ∠=°,所以点P 在以AB 为直径的⊙O 上.连结OC 交⊙O 于点P ,此时PC 最小,在Rt BCO ∆中,90,4,3OBC BC OB ∠=°==,可得5OC =,所以532PC OC OP =−=−=,即PC 最小值为2.点评 首先,根据题目的条件不难得出90APB ∠=°,从而可以证明点P 在以AB 直径的⊙O 上.利用模型2,连结OC ,与⊙O 交于点P ,此时PC 最小,利用勾股定理求出OC即可解决问题.以上例题说明,在求一类线段最值问题中,如果遇到动点的运动路径是圆时,只需利用上面提到的模型1或模型2就可以解决.然而难点在于如何知道动点的运动路径是圆,如何将这个隐身“圆”找出来?从以上例子中可以得出以下两种方法:①观察到定点的距离,即圆是到定点距离等于定长的点的集合;②“定弦对定张角”,如例5中线段AB是定值,当动点P在运动过程中,APB∠的大小不变等于90°(当然不一定为直角),点P的运动路径也是圆(或弧).因此,教师在教学时,要让学生理解概念的本质,还要培养学生对常见模型的敏感性,从而在有限的考试时间内,能快速获得破解难题的策略.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
隐圆”最值问题
隐圆”最值问题
分析题目条件发现题目中的隐藏圆,并利用一般的几何最值求解方法来解
决问题
【例1】在平面直角坐标系中,直线y = - x + 6分别与x轴、y轴交于点A、B两点,点C在
A y轴的左边,且/ AC
B = 90 ,则点C的横坐标x c的取值范围是
c
【练】(201$ 2014六中周练16)如图,已知Rt△ ABC中,/ ACB =
90° AC = 3,BC = 4,点D是AB的中点,E、F分别是直线AC、Bf
上的动点,/ EDF = 90,贝U EF长度的最小值是_________ .
【例2】如图,在Rt△ ABC中,/ ACB = 90 : D是AC的中点,
M是BD的中点,将线段AD绕A点任意旋转(旋转过程中始
终保持点M是BD的中点),若AC = 4,BC = 3,那么在旋转
过程中,线段CM长度的取值范围是________________ :
【练】已知△ ABC和△ ADE都是等腰直角三角形,/ ACB =Z
ADE
=90,AC = 2 2 : AD = 1,F是BE的中点,若将△ ADE绕点A
旋转一周,则线段AF长度的取值范围是 ________ .
A
E
【例3】如图,已知边长为2的等边△ ABC,两顶点A、B分别在平面直角 C 坐标系的x轴、y轴的正半轴上滑动,点
长的最大值是()
B. 1
C. 1 + 3
【练1】如图,在矩形ABCD中,AB = 2
直角坐标系的x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则OC
【练2】(2013武汉中考16)如图,E 、F 是正方形ABCD 的边AD 上两个
动点,
满足AE = DF ,连接CF 交BD 于点G ,连接BE 交AG 于点H ,若正方形的 长为2,则线段DH 长度的最小值是
【例4】如图,/ XOY = 45 : 一把直角三角尺ABC 的两个顶点A 、B 分别在
OX 、OY 上移动,其中AB = 10,那么点O 到AB 的距离的最大值为
【练】(20102014二中、七一九上期中16)已知线段AB = 4,在线段AB 上取一点P ,在 AB 的同侧作等边△ APC 和等边△ BPD ,则线段CD 的最小值为 __________ .
【例5】已知A (2, 0), B (4, 0)是x 轴上的两点,点C 是y 轴上的动点,当/ ACB 最 大时,则点C 的坐标为 ___________ .
【练】当你站在博物馆的展厅中时,你知道站在何处观赏最理想吗? 如图,设墙壁上的展品最高点 P 距底面2.5米,最低点Q 距底面 2米,观察者的眼睛E 距底面1.6米,当视角/ PEQ 最大时,站 在此处观赏最理想,则此时E 到墙壁的距离为() A . 1 米 B . 0.6米 C . 0.5米 D . 0.4
米
o s
c
E F
X
s y
【课外提升】
1. (2010 河南)如图,Rt △ ABC 中,/ C = 90,° / ABC = 30 , AB = 6, 点D 在AB 边上,点E 是BC 边上一点(不与点 B 、C 重合),且DA = DE ,则AD 的取值范围是()
4.已知点A 、B 的坐标分别是(0, 1)、( 0,3),点C 是x 轴正半轴上一动点,当 / ACB
2 < AD < 3
D 1 W AD < 2
2. (2012济南)如图,矩形 ABCD 中,AB =
分别在x 轴正半轴和y 轴正半轴上移动时,矩形 OD 的最大值为()
A .
2
+ 1 B . 5 C .书
3. (2013-2014 黄陂区九上期中 10)在厶ABC 中,/ ACB = 90,/ ABC p =30 °将厶ABC 绕顶点C 顺时针旋转,旋转角为 (0° < X 180 °,得
C
到厶MNC , P 、Q 分别是AC 、MN 的中点,AC = 2t ,连接PQ ,则旋转时
PQ 长度的最大值是()
A . 2 6t
B. 2 3t
C . 6t
D . 3t
M
Q
N。
