2018-2019-初等数学研究李长明-推荐word版 (9页)
2018-2019-杂志文案范例-推荐word版 (16页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==杂志文案范例篇一:实用杂志广告文案范文实用杂志广告文案范文广告文案查阅次数:470次发布人:范文网编辑推荐阅读:下面关于广告文案范文的文章由查字典范文大全小编统一整理,希望对您有帮助。
摘要:杂志广告文案范文在传统媒体广告发展受到阻碍的...下面关于广告文案范文的文章由查字典范文大全小编统一整理,希望对您有帮助。
摘要:杂志广告文案范文在传统媒体广告发展受到阻碍的今天备受关注,杂志广告刊登在杂志上的广告.杂志可分为专业性杂志、行业性杂志、消费者杂志等.杂志广告文案范文在传统媒体广告发展受到阻碍的今天备受关注,杂志广告刊登在杂志上的广告.杂志可分为专业性杂志、行业性杂志、消费者杂志等.杂志广告文案范文就是对杂志广告文案策划的一个经典案例,助力企业分析广告后进行的报告撰写,对广告行业有着非凡意义。
1992年创刊的《健康与美容》杂志,是一本由卫生部主管的时尚类健康杂志,已走过了19年的历程。
HEALTH 健康与美容深受广大读者的喜爱,因此也吸引广大广告业主的关注,HEALTH 健康与美容广告价格与广告收益是成正比的,这也是广告业主选择其的原因。
具有固定的读者层面是杂志广告的特色,可以使广告宣传深入某一专业行业.杂志种类繁多,从出版时间上看,有周刊、旬刊、半月刊、双月刊、季刊;从内容上看,有政治、军事、娱乐、文化、经济、生活、教育等.专业性杂志针对不同的读者对象,安排相应的阅读内容,因而就能受到不同的读者对象的欢迎.杂志的专业化倾向也发展得很快,如医学杂志、科普杂志、各种技术杂志等,其发行对象是特定的社会阶层或群体.杂志的读者虽然广泛,但也是相对固定的.因此,对特定消费阶层的商品而言,在专业杂志上做广告具有突出的针对性,适于广告对象的理解力,能产生深入的宣传效果,而很少有广告浪费.从广告传播上来说,这种特点有利于明确传播对象,广告可以有的放矢.用较多的篇幅来传递关于商品的详尽信息是杂志广告的优势所在,既利于消费者理解和记忆,也有更高的保存价值. 杂志广告的缺点是:影响范围较窄.因杂志出版周期长,经济信息不易及时我们知道,杂志和报纸相同,它也是一种传播媒体,它的形式是以印刷符号传递信息的连续性出版物.因此借鉴杂志广告文案范文有利于杂志广告在同类竞争中力度增加。
大学数学之初等数学研究 李长明 周焕山版

大学数学之初等数学研究李长明 周焕山版高等教育出版社习题一1、答:原则:(1)A ⊂B(2)A 的元素间所定义的一些运算或基本关系,在B 中被重新定义。
而且对于A 的元素来说,重新定义的运算和关系与A 中原来的意义完全一致。
(3)在A 中不是总能施行的某种运算,在B 中总能施行。
(4) 在同构的意义下,B 应当是A 满足上述三原则的最小扩展,而且由A 唯一确定。
方式:(1)添加元素法;(2)构造法2证明:(1)设命题能成立的所有c 组成集合M 。
Θa=b ,M 11b 1a ∈∴⋅=⋅∴,假设bc ac M c =∈,即,则M c c b b bc a ac c a ∈'∴'=+=+=',由归纳公理知M=N ,所以命题对任意自然数c 成立。
(2)若a <b ,则bc kc ac bc,k)c (a )1(b k a N k =+=+=+∈∃即,,由,使得 则ac<bc 。
(3)若a>b ,则ac m c bc ac,m )c (b )1(a m b N m =+=+=+∈∃即,,由,使得 则ac>bc 。
3证明:(1)用反证法:若b a b,a b a <>≠或者,则由三分性知。
当a >b 时,由乘法单调性知ac >bc. 当a <b 时,由乘法单调性知ac<bc.这与ac=bc 矛盾。
则a=b 。
(2)用反证法:若b a b,a b a =>或者,则由三分性知不小于。
当a >b 时,由乘法单调性知ac >bc. 当a=b 时,由乘法单调性知ac=bc.这与ac<bc 矛盾。
则a <b 。
(3)用反证法:若b a b,a b a =<或者,则由三分性知不大于。
当a<b 时,由乘法单调性知ac<bc. 当a=b 时,由乘法单调性知ac=bc.这与ac>bc 矛盾。
初等几何研究习题2(李长明版)

汕头职业技术学院初等几何研究习题课数学教育(师范类)1. I是△ABC的内心,AI、BI、CI的延长线分别交△ABC的外接圆于D、E、F求证:EF⊥AD。
D AB C EFI 五、关于平行与垂直2. A、B、C、D在圆周上相继的四点,P、Q、R、S分别是弧AB、BC、、CD、DA的中点,求证:PR⊥QS。
ACBP QDRS3. 凸四边形ABCD的每条对角线皆平分它的面积,求证:ABCD是平行四边形。
A BDC4. 已知:△BCX 和△DAY 是□ABCD 外的等边三角形,E 、F 、G 、H 是YA 、AB 、XC 、CD 的中点。
求证:EFGH 是平行四边形。
ABXD C YE F GH5. 在△ABC的各边上向外作正方形BCDE、CAFG、ABHI,其中心依次为O1、O2、O3求证:AO1⊥O2O3。
AO1O2BCO36. 在正方形ABCD 内任取一点E ,连接AE 、BE ,在△ABE 外以AE 、BE 为边作正方形AEMN 和EBFG ,连NC 、AF 。
求证:NC∥AF 。
A BCD E MNFG7. 以□ABCD的对角线AC为一边的两侧各作一个正三角形ACP、ACQ。
求证:BPDQ是□。
ABPDCQ8. 已知:凸五边形的四条边平行于所对的对角线。
求证:第五边也平行于所对的对角线。
CA B DE9.在△ABC中,∠B≠90°,BC边的垂直平分线交AB于D,△ABC的外接圆在A、C两点之切线交于E.求证:DE∥BC.AD EB C10.P 是正方形ABCD 的边CD 上的一点,过D 作AP 的垂线分别交AP 、BC 于Q 、R ,O 是正方形的中心.求证:OP ⊥OR.ABCDOPR12. 给定正方形ABCD ,P 、Q 分别人为AB 、BC 上的点,满足BP=BQ ,自B 作BH ⊥PC 于H ,求证:∠DHQ=900.ABCDO PHQ13. 在△ABC中,AB=AC,O为外心,D为AB的中点,E是△ACD的重心。
初等数学研究答案 李长明 周焕山编习题4(1)答案

24.⎪⎪⎩⎪⎪⎨⎧=+=+31111222y x x y y x 解:方程组的定义域(){}0,0,≠≠y x y x原方程组变形为: ⎪⎪⎩⎪⎪⎨⎧=+=+311233xyy x xy y x 即()⎩⎨⎧=+=+)2.......(....................3)1.(....................1233xy y x xy y x ())(3333y x xy y x y x +++=+ ()⎩⎨⎧=+=+++∴)2.(........................................)(3)3.(....................12)(3x 3xy y x xy y x xy y 令x+y=u,xy=v,有:⎩⎨⎧==+)5........(..............................3)4.......(....................123u 23v u v v u 由(5)代入(4)得:0369u 23=-+u()0369u 2=-+u u0u =∴或036-u 9u 2=+,即3u 12u -==,将u=0代入(5),得v=0 ⎩⎨⎧==+∴00y x xy 解得⎩⎨⎧==00y x 不在定义域内 将U=-12代入(5)得:v=36⎩⎨⎧==+∴3612x xy y ,解得:6,0)6(,0361222==-=+-x x x x ⎩⎨⎧==∴66y x 将u=-3代入(5)得。
v=-9⎩⎨⎧-=-=+∴93y x xy ,解得:⎪⎪⎩⎪⎪⎨⎧--=+-=2532325323y x ⎪⎪⎩⎪⎪⎨⎧+-=--=2532325323y x x y 9-= 故原方程的解为:()⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+25323253-23-253-23-25323-6,6,,,, (3)()⎩⎨⎧=+=+++xyy x x y x 71232y 22原方程可化为:()()()⎩⎨⎧=+=++-+)(2.....................................712)1..(....................3222xy y x y x xy y x 令x+y=u,xy=v,代入上方程组,有:⎩⎨⎧==+-)4......(..............................712)3......(....................3222v u u v u 由(4)得:u 712v =代入(3),并整理得:.(5)....................0.........224-u 17-u 72= 解(5)的得:732,7u 21-==u 将u=7代入(4),得v=12,故⎩⎨⎧==+127xy y x 解得⎩⎨⎧==43y x 或⎩⎨⎧==34y x 将732-=u 代入(4)得:49384v -= 故⎪⎩⎪⎨⎧-==+49384732-y x xy 得:0384224492=-+x x 解:987526450176224983844942242242+±-=⨯⨯+±-=x 9871022249812544022428⨯⨯±-=±-= 9810722244⨯±-=9810112224±-= 7108716±-= 故解得:()()⎪⎪⎩⎪⎪⎨⎧+-=-=2107872108y x ()()⎪⎪⎩⎪⎪⎨⎧-=+-=2107872108y x 故原方程组的解为:()()()()()()⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+2-107821078,21078-2-10783,44,3,,,, 26.(1)⎩⎨⎧==++)(2 (2464))1.......(....................12646422y X y x 解:令v u y x ==64,64,则原方程组可化为:⎩⎨⎧==+)(4.........................24)3....(....................12u 22uv v (3)+2(4),得:28122u 22+=++uv v即()()22222v u +=+ 222+=+∴v u⎩⎨⎧==∴22v 2u 或⎩⎨⎧==2v 22u ()⎩⎨⎧==∴2264264I y x 或()⎩⎨⎧==2642264II y x 解(I)得:⎪⎩⎪⎨⎧==4161y x 解(II )得:⎪⎩⎪⎨⎧==6141y x 故原方程组的解为:⎪⎭⎫⎝⎛41,61,或⎪⎭⎫ ⎝⎛61,41,(2)()⎪⎩⎪⎨⎧=+-=⎪⎪⎭⎫ ⎝⎛+-)(2.....................25)1.......(..........21log log 2225.0y x y x y 解:方程(1)左边取以2为底的对数,得:()22log 1log 5.0log log 2222-=⎪⎪⎭⎫ ⎝⎛+-y x y 即: ()2log log -22-=--y x y()2.log 2=-y x y()4x -y =∴y 即)(3........................42=-xy y 解(2),(3)联立方程组得:⎩⎨⎧=+=-)2..(....................25)3..(....................4222y x xy y 令y=tx,分别代入(2),(3)得: ()()⎩⎨⎧=+=-))5.(..............................2514.....(....................41222t x t t x 由(4),(5)解出2x 的表达式得:())6( (1)25142+=-t t t 由(6)变形整理得:0425212=--t t ()()0174-t 3=+t71,3421-==t t 由34=t ,有x y 34=,代入(3)得:3±=x 由71-=t ,有x y 71-=,代入(3)得:227±=x ⎩⎨⎧==∴43y x ,⎩⎨⎧-=-=43y x (舍),⎪⎪⎩⎪⎪⎨⎧-==22227y x (舍),⎪⎪⎩⎪⎪⎨⎧==22227-y x 所以原方程组的根为()⎪⎪⎭⎫ ⎝⎛22,227-4,3,,27.(1)⎪⎩⎪⎨⎧=+=+)2.......(..............................125)1....(..............................43sin sin 22πy x y x 解:利用降次公式,(1)即:4322cos 122cos -1=-+y x 212cos 2cos =+y x ()21cos 2=+y x ()())3....(.. (2)1cos cos 2=-+y x y x (2)代入(3),化简得:()21cos .125cos 2=-⎪⎭⎫ ⎝⎛y x π ()426261cos +=-=-y x ⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+=42664cos 125cos πππ )4........(2426cos πk acr y x ++±=-∴ (2)(4)联立解得:⎪⎪⎩⎪⎪⎨⎧Z ∈-+±=Z ∈++±=k k acr y k k acr x ,426cos 21245,426cos 21245ππππ 4.(1)()()()()()())1.......(..........131321212--=--+--x x x x x x x 解:方程定义域为}{3,2,1,M ≠∈=x R x x 且将(1)式左边通分, ()()()()()()()1313212123--=----+-x x x x x x x x 即()()()()()131321222--=-----x x x x x x x 左边分子因式分解:()()()()()()()13-x 132121x 2-x -=---+x x x x左边约分()()()())2......(....................1313121--=--+x x x x x 两边同乘以(x-1)(x-3)得:1,21,121==+=+∴x x x 但x=1不在定义域内,为增根,原方程无解解法2:方程定义域为}{3,2,1,M ≠∈=x R x x 且将方程右边的分式移到左边: ()()()()()()0131321212=-----+--x x x x x x x 左边通分整理得:()()()()()()0321222123=------+-x x x x x x x 即:()()()()()()()()0321212,0321-x 2232=-----=--+-x x x x x x x x x 约去公因式()()021-x ≠-x ,将方程左边化成最简因式:()0321=-x 上式的分子为非零常数,显然无解。
《初等数学研究》教学大纲

本章教学要求:要求学生掌握数系的扩充过程,深刻掌握式的变形基础,式的变形技巧
函数的理论(8课时)
函数的定义
函数的变量说定义与对应说定义,
函数的表示方法
表达式,图表,图象,方程等
函数的基本性质
定义域,值域,单调性、奇偶性与对称性,周期性
复合函数的性质
复合函数的定义域,值域,单调性等
开语句,真值集,开语句的复合,全称量词,存在量词,量词的否定,假言命题的四种形式,充分条件与必要条件
集合与逻辑的关系
本章重点:复合命题的真值定义,等价命题,假言命题的四种形式
本章难点:假言命题的四种形式
本章教学要求:要求学生掌握假言命题命题的四种形式(逆、否、逆否),开语句的复合,判断命题真假。
第三章数与式的理论(8课时)
2.葛军涂荣豹编著,《初等数学研究教程》,2009年7月第一版,江苏教育出版社, 2009
3.李长明周焕山编著,《初等数学研究》,1995年6月第一版,高等教育出版社,1995
4.叶立军编著,《初等数学研究》,2008年5月第一版,华东师范大学出版社,2008
5. Klaus Hulek著,胥鸣伟译,《初等代数几何》,2014年10月第一版,高等教育出版社,2014
初等数学研究是专业选修课,系主干课程。一般情况下第七---八学期开设,安排32周,有条件时可安排36周,共64课时。
二、教学内容与学时分配
序号
章节名称
学时分配
1
第一章绪论
2
2
第二章集合与逻辑
6
3
第三章数与式的理论
8
4
第四章函数的理论
8
5
第五章方程、不等式86ຫໍສະໝຸດ 公理化方法与演绎推理6
在“初等数学研究”中开展研究性学习的探索与实践

维普资讯
第 8 第 3期 卷
20 0 6年 5月
石家庄学院学报 Ju a o h izun nvr t or l f iah agU i sy n Sj e i
Vo . N . 1 8. o 3 Ma .0 6 y2 0
在“ 初等数学研究" 中开展研究性学习的探索与实践
课程内容、 教学 目标的改革必然会对教师和学生提出新要求. 要改变教师单~的传授者的角色 。 确立教
学活动组织者 、 引导者、 参与者的地位. 积极开发课程资源 , 充分发挥图书馆 、 网络的作用 , 拓宽学生学习范
围, 扩大学生学习视野 ; 改变学生被动接受性学习 , 倡导主动参与、 乐于探究 、 勤于思考的学习风范 , 培养学
生主动发现问题 , 以问题为导向 , 并 搜集和整理信息 , 从而解决问题的能力 , 并在此过程中, 提高学生对问题 的研究意识和能力 , 合作和交流的能力.
刘学军 , 魏喜凤 , 孙庆利
( 石家庄学院 数学系, 河北 石家庄 0 03 ) 5 05
摘 要: “ 在 初等数学研 究” 课程 中开展研 究性学习, 是课程和教 学改革的需要. 通过对课程
目标、 内容、 学和学习方式、 教 学习评价的改革, 可以达到提 高学生的学 习主体性 、 更新教 学观和 学 习观 、 扩大学习的知识 面、 高学生的科研意识和初步的科研能力、 提 获得 良好的情感体验的 多元教
初等几何研究试题答案(3)李长明版
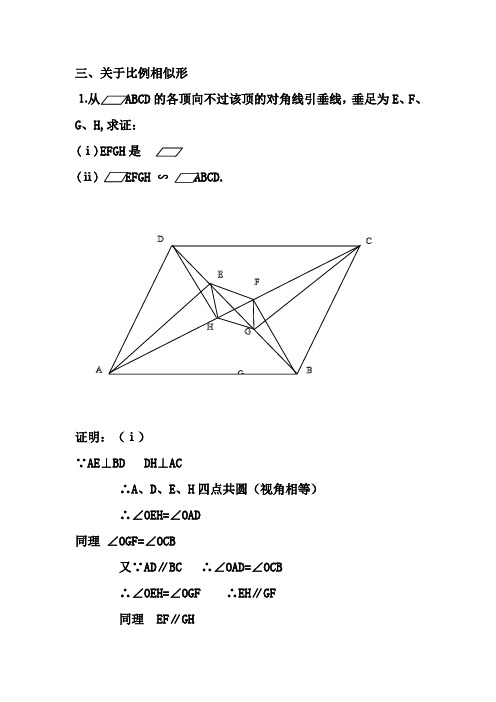
三、关于比例相似形⒈从 ABCD 的各顶向不过该顶的对角线引垂线,垂足为E 、F 、G 、H,求证: (ⅰ)EFGH 是 ; (ⅱ) EFGH ∽ ABCD.证明:(ⅰ) ∵AE ⊥BD DH ⊥AC∴A 、D 、E 、H 四点共圆(视角相等) ∴∠OEH=∠OAD 同理 ∠OGF=∠OCB又∵AD ∥BC ∴∠OAD=∠OCB ∴∠OEH=∠OGF ∴EH ∥GF 同理 EF ∥GHDACBEFGGH∴四边形EFGH 为平行四边形 (ⅱ)∵△OEH ∽△OAD∴.OD OHOA OE = ∴BD FHACEG =EFGH 与 ABCD 对角线夹角相等且对角线又成比例 ∴ EFGH ∽ ABCD 2.3.已知:AD 是△ABC 的中线,过C 的一直线分别交AD 、AB 与E 、F 。
求证:A E ·BF=2AF ·ED证明:延长CF 至点H ,使得CE=EH 连结BH ∵点D 是BC 上的中点 ∴DE 是△CBH 的中位线即D E ∥BH 且DE= 21BH∵DE ∥BH∴∠CED=∠CHB=∠AEF ∠AFE=∠BFH ∴△AFE ∽△BFH ∴BFAFBH AE =,且BH=2ED ∴AE ·BF=2AF ·ED4.直线l 与□ABCD 的边AB 、AD 和对角线AC 依次相交于E 、F 和G 。
求证:AGACAF AD AE AB =+证明:连结BF 、BE 、CF 和CE , ∵SS SS AEFACF AEFABF AEAB==S S SS AEFACE AEFADE AFAD==∴AGACAG GC AG AFAD AE AB SS SSS SAEFCEFAEFAEFACEACF=+=+=+=+ABC DE F G5.AB 、CD 是等腰梯形ABCD 的二底,求证:DC AB AD AC ∙+=22证明:(如上图)作CD 的延长线到点H ,使得AH 垂直CH作点C 的延长线,使得CP 垂直ABABCP AD AC DH CH CP AD AC AB BP AP DH CH BP DH AP CH CPB AHD CBPDAC APH CB AD CPB AHD DH CH CP AD DH CH DH CH AD DH CH AD CH DH AD CH AH AC ⋅+=+⋅+==+=+==∆≅∆∴∠=∠=∠==∠=∠+⋅+=-++=-+=+-=+=222222222222222 )( 90)( ))(( )( )( 故有又6.AD 是Rt △ABC 斜边上的高,作DE ⊥AB 于E,DF ⊥AC于F.求证:AD 3=BC ∙BE ∙CFHDCA B证明:∵AD2=BD∙DC,BD2=BE∙BA,CD2=CF∙CA,∴AD4=BE∙CF∙AB∙AC=BE∙CF∙BC∙AD约去AD,得AD3=BC∙BE∙CF7 .在△ABC中,∠A=60°,∠B=80°。
初等数学研究答案第一章到第六章

大学数学之初等数学研究,李长明,周焕山版,高等教育出版社 习题一1答:原则:(1)A ⊂B(2)A 的元素间所定义的一些运算或基本关系,在B 中被重新定义。
而且对于A 的元素来说,重新定义的运算和关系与A 中原来的意义完全一致。
(3)在A 中不是总能施行的某种运算,在B 中总能施行。
(4) 在同构的意义下,B 应当是A 满足上述三原则的最小扩展,而且由A 唯一确定。
方式:(1)添加元素法;(2)构造法2证明:(1)设命题能成立的所有c 组成集合M 。
a=b ,M 11b 1a ∈∴⋅=⋅∴, 假设bc ac M c =∈,即,则M c c b b bc a ac c a ∈'∴'=+=+=',由归纳公理知M=N ,所以命题对任意自然数c 成立。
(2)若a <b ,则bc kc ac bc,k)c (a )1(b k a N k =+=+=+∈∃即,,由,使得 则ac<bc 。
(3)若a>b ,则ac mc bc ac,m)c (b )1(a m b N m =+=+=+∈∃即,,由,使得 则ac>bc 。
3证明:(1)用反证法:若b a b,a b a <>≠或者,则由三分性知。
当a >b 时,由乘法单调性知ac >bc. 当a <b 时,由乘法单调性知ac<bc.这与ac=bc 矛盾。
则a=b 。
(2)用反证法:若b a b,a b a =>或者,则由三分性知不小于。
当a >b 时,由乘法单调性知ac >bc. 当a=b 时,由乘法单调性知ac=bc.这与ac<bc 矛盾。
则a <b 。
(3)用反证法:若b a b,a b a =<或者,则由三分性知不大于。
当a<b 时,由乘法单调性知ac<bc. 当a=b 时,由乘法单调性知ac=bc.这与ac>bc 矛盾。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!
== 本文为word格式,下载后可方便编辑和修改! ==
初等数学研究李长明
篇一:初等数学研究(李长明周焕山编) p494第7题,p497第3题,p498第
9题答案
初等数学研究(李长明周焕山编) p494第7题,p497第3题,p498第9题答
案
7.在直角梯形
ABCD中,AB是垂直二底的腰,另一腰切以AB为直径之圆于E,过E作底的平行线交AB于F,求证:AC平分EF.
证明: ∠DAB=∠ABC=90°, 圆O以AB为直径, ∴
AD,BC均与圆O相切; 又圆O与CD相切于E, ∴AD=ED;EC=BC;
又AD∥EF∥BC,∴FG/BC=AF/AB=DE/DC=AD/DC=EG/EC=EG/BC.
∴EG=FG .即AC平分EF.
3.凸四边形ABCD的每条对角线皆平分它的面积.
求证:ABCD是平行四边形
证明:作AE⊥BD于E,CF⊥BD于F,BM⊥AC于M,DN⊥AC于N.
BD平分凸四边形ABCD的面积,∴1
2BD?AE=1
2BD?CF?AE=CF.
又∠AEO=∠CFO=90?,∠AOE=COF(对顶角相等).??AEO??CFO
∴AO=CO,同理易证得:BO=DO.?凸四边形ABCD是平行四边形.(对角线互相平分)
9.在?
ABC中,∠B≠90,BC边的垂直平分线交求证:DE//BC.?AB于D,?ABC的外接圆
在A,C两点之切线交于E.
证明:连结OA,OC,CD. AE,CE是圆O的切线,∴∠OAE=∠OCE=90?.
∴BD=CD.∴∠DBC=∠DCB.
2倍),∠BDC=180?-∠DCB-∠DBC.=∠ACE.(同弧弦切角等于圆周角
∴∠AOC+∠AEC=180?. DM是BC的垂直平分线又∠AOC=2∠ABC.(同弧圆心角是
圆周角的∴∠ACE=∠ADE.(同弧圆周角相等
∴∠ADE=∠ABC.∴DE//BC∴∠BDC=180?-2∠DBC=180?-∠AOC=∠AEC.∴A,D,C,E
四点共圆.),∠ABC)
篇二:初等几何研究试题答案(1)(李长明版)
初等几何研究试题答案(I)
一、线段与角的相等
1. ⊙O1、⊙O2相交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F, 求证: (1)若∠DBA=∠CBA,则DF=CE; (2) 若DF=CE,则∠DBA=∠CBA.
证明:(1)连接AC、AE、AF、AD
在⊙O1中,由∠CBA=∠DBA得AC=AF在⊙O2中,由∠CBA=∠DBA得AE=AD由A、C、B、E四点共圆得∠1=∠2由A、D、B、E四点共圆得∠3=∠4所以
△ACE≌△AFD∴DF=CE
(2)由(1)得∠1=∠2,∠3=∠4∵DF=CE
∴△ACE≌△AFD
∴AD=AE
在⊙O2中,由AD=AE可得∠DBA=∠CBA
2. 在△ABC中,AC=BC,∠ACB=90O ,D是AC上的一点,AE⊥BD的延长线于E,又
AE=BD, 求证:BD平分∠ABC.
1
2
证明:延长AE,BC交于点F
∠AED=∠BCA=90? ∠ADE=∠BDC∴∠CBD=∠CAF
又∠ACF=∠BCA=90? AC=BC∴?ACF??BCD∴AF=BD
11BD∴AE=AF22
又ABEE⊥BE又AE=∴BE平分∠ABF即BD平分∠ABC
3. 已知在凸五边形ABCDE中,∠BAE=3α,BC=CD=DE,且∠BCD=∠CDE=180o-2α,
求证:∠BAC=∠CAD=∠DAE.
证明:连接BD,得ΔCBD是等腰三角形
且底角是∠CDB=[180o-(180o-2α)]÷2=α. ∴∠BDE=(180°-2α)-α=180o -3α ∴A、B、D、E共圆同理A、C、D、E共圆∴∠BAC=∠CAD=∠DAE
4. 设H为锐角△ABC的垂心,若AH等于外接圆的半径. 求证:∠BAC=60o
证明:过点B作BD⊥BC,交圆周于点D,连结CD、AD
C ∵∠DBC=90o, ∴CD是直径,则∠CAD=90o
由题,可得AH⊥BC, BH⊥AC
∴BD∥AH, AD∥BH∴四边形ADBH是□ ∴AH=BD
又∵AH等于外接圆的半径(R) ∴BD=R,而CD=2R ∴在Rt△BCD中,CD=2BD,即
∠BCD=30o ∴∠BDC=60o
又∵∠BAC=∠BDC∴∠BAC=∠BDC=60o
5. 在△ABC中,∠C=90o,BE是∠B的平分线,CD是斜边上的高,过BE、CD之交点O且平行于AB的直线分别交AC、BC于F、G,求证AF=CE.
证明:如图∵∠1=∠3,∠1=∠2.∴∠2=∠3,∴GB = GO, ∵ ∠5=∠4=∠6,∴CO =CE,
∵ FG∥AB,∴AF/CF=BG/CG=GO/CG, 又∵△FCO∽△COG,∴CO/CF=GO/CG=AF /CF, ∴CO=AF,∵CO=CE,∴AF=CE.
6. 在△ABC中,先作角A、B的平分线,再从点C作上二角的平分线值平行线,并连结它们的交点D、E,若DE∥BA,求证:△ABC等腰.
证:如图所示设AC、ED的交点为F。
