捷联惯导与组合导航.30页PPT
捷联惯导／天文导航／合成孔径雷达组合导航系统
捷 联 惯 导／ 天 文 导 航／ 合 成 孔径 雷达 组合 导 航 系统 术
李群生 ， 赵 剡 ， 鲁
（ １ ．北京航 空航天大学仪器科学与光 电工程学 院 北京
浩ቤተ መጻሕፍቲ ባይዱ ， 徐 剑 芸
１ ０ ０ １ ９ １ ； ２ ． 中国空空导 弹研究 院 洛阳 ４ ７ １ ０ ０ ９ ）
摘
要： 设计 了适 用于巡航 导弹的捷联惯性／ 天文导航／ 合成孔径雷达 （ Ｓ Ｉ Ｎ Ｓ ／ Ｃ Ｎ Ｓ ／ Ｓ Ａ Ｒ） 组合 导航 系统 ， 针对 巡航导 弹对导航 系
ｃ ｒ ｕ ｉ ｓ ｅ ｍｉ ｓ ｓ ｉ ｌ ｅ ， ｔ ｈ ｅ ｅ ｎ ｇ ｉ ｎ ｅ ｅ ｒ ｉ ｎ ｇ ｐ ｒ ａ ｃ ｔ ｉ ｃ ａ ｂ ｉ ｌ ｉ ｔ ｙ ｏ ｆ ｔ ｈ ｅ ｐ ｒ ｏ ｊ ｅ ｃ ｔ ｉ ｓ ｈ ｉ ｇ ｈ ｌ ｉ ｇ ｈ ｔ ｅ ｄ ．Ｔ ｈ ｅ ｎ ｏ ｎ ｌ ｉ ｎ ｅ ａ ｒ ｍ ｏ ｄ ｅ ｌ ｉ ｎ ｇ ｉ ｓ ａ ｄ ｏ ｐ ｔ ｅ ｄ ｆ ｏ ｒ ｔ ｈ ｅ Ｓ Ｉ Ｎ Ｓ ／ Ｃ Ｎ Ｓ ／ Ｓ Ａ Ｒ
ｒ ｅ ｑ ｕ ｉ ｒ ｅ ｍｅ ｎ ｔ ｓ ｏ ｆ ｈ ｉ ｇ ｈ ｐ ｒ ｅ ｃ ｉ ｓ ｉ ｏ ｎ ａ ｎ ｄ ａ ｕ ｔ ｏ ｎ ｏ ｍｙ ｏ ｆ ｔ ｈ ｅ ｎ ａ ｖ ｉ ｇ ａ ｔ ｉ ｏ ｎ ｓ ｙ ｓ ｔ ｅ ｍ ａ ｎ ｄ ｔ ｈ ｅ ｃ ｈ ａ ｒ ａ ｃ ｔ ｅ ｒ ｉ ｓ ｔ ｉ ｃ ｓ ｏ ｆ ｕ ｎ ｉ ｆ ｏ ｒ ｍ ｓ ｐ ｅ ｅ ｄ ａ ｎ ｄ ｃ ｏ ｎ ｓ ｔ ａ ｎ ｔ ｈ ｅ ｉ ｇ ｈ ｔ ｌ ｆ ｉ ｇ ｈ ｔ ｏ ｆ
捷联惯性导航系统的解算方法ppt课件
的 分量构成的矩阵，则
r rnT n r nT Cnb n rnT r nT Cbn
由于坐标系不动而是矢量转动，它 相应于矢量固定时坐标系方向转动
rn
n
C
n b
r
2010-03-19
方向余弦矩阵微分方程
由矢量相对导数和绝对导数的关系式
dr dt
n
dr dt
b
ω nb r
假定地理坐标系为参考坐标系，作为参考 坐标系认为它在空间是不动的，即
如把OXbYbZb作为动坐标系， ENU作为参考坐标系，则航向 角H，纵摇角（俯仰角）P和横 摇角（横滚角、倾斜角）R。就 是一组欧拉角。
Zb Zb'' U Zb' P
欧拉角没有严格的定义，根 据
需要，可以选用不同的欧拉 角
组。第一次转动，可以绕三 个
轴中的任一个转动，故有3种 可
能，第二次有2种可能，第三 次
启动
自检 测
初始 化
返回9
姿态
迭 数
代
次阵计 算
N O
YES
导 航 计 控 制 信 息算提 取
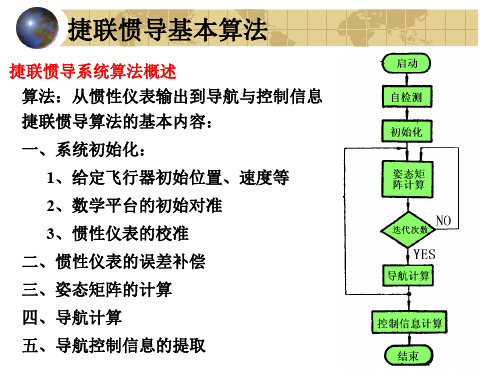
3.2 姿态矩阵的计算
捷联式惯导中，载体地理位置就是地理坐标系相对 地球坐标系的方位。而载体的姿态和航向则是载体 坐标系相对于地理坐标系的方位关系。确定两个坐 标系的方位关系问题，是力学中的刚体定点转到理 论。在刚体定点转动理论中，描述动坐标系相对参 考坐标系方位关系的方法有多种。
求解方程可以直接得到航向和姿态信息，
欧 拉角法得到的姿态阵永远是正交阵，用这
个矩 阵将比力fb→fn信息的坐标变换时，变换后的信 息
中不存在非正交误差。因此，用欧拉角法得 到的姿态矩阵无
捷联惯导系统算法.ppt
cos
b Ebz
注意事项：当 θ= 90 度时，方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度，所以：
CbE
b ib
E iE
C
E b
或四元数微分方程：
q(t)
(
b ib
b iE
)q(t)
注意事项： 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小，计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量：陀螺仪数字脉冲输出，每个脉冲代表一个角增量
一个采样周期内，陀螺输出脉冲数对应的角增量为：
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述：
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序：
Ψ →θ →γ
捷联惯性导航系统的解算方法课件
02
CATALOGUE
捷联惯性导航系统组成及工作 原理
主要组成部分介绍
惯性测量单元
包括加速度计和陀螺仪，用于测量载体在三个正交轴上的加速度 和角速度。
导航计算机
用于处理惯性测量单元的测量数据，解算出载体的姿态、速度和 位置信息。
控制与显示单元
用于实现人机交互，包括设置导航参数、显示导航信息等。
工作原理简述
学生自我评价报告
知识掌握情况
学生对捷联惯性导航系统的基本原理、解算 方法和实现技术有了深入的理解和掌握。
实践能力提升
通过实验和仿真，学生的动手实践能力得到了提升 ，能够独立完成相关的实验和仿真验证。
团队协作能力
在课程项目中，学生之间的团队协作能力得 到了锻炼和提升，能够相互协作完成项目任 务。
对未来发展趋势的预测和建议
捷联惯性导航系统的解算 方法课件
CATALOGUE
目 录
• 捷联惯性导航系统概述 • 捷联惯性导航系统组成及工作原理 • 捷联惯性导航系统解算方法 • 误差分析及补偿策略 • 实验验证与结果展示 • 总结与展望
01
CATALOGUE
捷联惯性导航系统概述
定义与基本原理
定义
捷联惯性导航系统是一种基于惯性测量元件（加速度计和陀螺仪）来测量载体（如飞机、导弹等）的加速度和角 速度，并通过积分运算得到载体位置、速度和姿态信息的自主导航系统。
01
高精度、高可靠性
02
多传感器融合技术
随着科技的发展和应用需求的提高， 捷联惯性导航系统需要进一步提高精 度和可靠性，以满足更高层次的应用 需求。
为了克服单一传感器的局限性，可以 采用多传感器融合技术，将捷联惯性 导航系统与其他传感器进行融合，提 高导航系统的性能和鲁棒性。
导航原理组合导航ppt课件
.
60年代以前，综合导航一般都采用频率滤波的方法 或古典控制中校正的方法，具体的形式是环节的校 正。60年代以来，滤波技术更加成熟，尤其是计算 机技术迅猛发展，使得综合方式转变为以Kalman （卡尔曼）滤波为主，即在两个（或两个以上）导 航系统输出的基础上，利用卡尔曼滤波去估计系统 的各种误差（称为误差状态），再用误差状态的估 值去校正系统，达到综合的目的。
组合导航
.
1
4.1 概述
一般而言，较理想的导航系统应具有以下性能：
①自主性强：不依赖天气、气候及其它外部条件；
②功能完备：可实时输出载体的全部运动参数，包 括位置、速度、姿态、角速度和加速度甚至角加速 度。
③精度高：提供足够精确的导航与控制参数；
④环境适应性好：在大的温度范围、恶劣的冲击、 振动及化学污染、烟尘等环境中能可靠工作；
.
7
下面以外部位置信息阻尼方案为例予以说明。
利用天文导航系统得到的外部位置信息实现对 惯导系统阻尼的一种方案如图6.2所示：
r 为外部位置信息， c 为惯导系统的位置信息。
.
8
图中， r为外部位置信息, 可由天文导航系统给出，
其和惯导系统输出的纬度信息相比较，以其差值
信号，通过k1,k2,k3环节反馈到系统中去。
.
16
.
9
.
10
由上式可见，系统成为三阶系统，可通 过适当选择参数K1、K2和K3，使原来无 阻尼的惯导系统变成阻尼综合导航系统 （也可通过引入外部速度信息来实现）。 此外，还可通过适当选择参数来改变自 振周期以得到所需的动态特性。
惯性导航原理ppt课件
Ve ' x'i y' j z' k q 1 P1i P2 j P3k
x'i y' j z'k
( P1i P2 j P3k) (xi yj zk) ( P1i P2 j P3k)
进行四元数乘法运算，整理运算结果可得
20
四元数表示转动 方向余弦
或简单表示为
q M v, P
12
四元数基本性质 乘法
2．四元数乘法
q M ( P1i P2 j P3k)(v 1i 2 j 3k)
(v P11 P2 2 P33 )
( 1 P1v P2 3 P32 )i
( 2 P2v P31 P13 ) j
( 3 P3v P12 P2 1 )k
7
6. 机体坐标系——
Oxb yb zb
机体坐标系是固连在机体上的坐标系。机 体坐标系的坐标原点o位于飞行器的重心处， x沿机体横轴指向右，y沿机体纵轴指向前， z垂直于oxy，并沿飞行器的竖轴指向上。
8
3.2四元数理论
9
四元数 表示
四元数：描述刚体角运动的数学工具 (quaternions) 针对捷联惯导系统，可弥补欧拉参数在描述和解算方面的不足。
四元数 映象图解
V xi yj zk
V x'i' y' j'z'k'
Ve xi yj zk Ve ' x'i y' j z' k
19
四元数表示转动 方向余弦
Ve ' q 1Ve q 将该投影变换式展开，也就是把
Ve xi yj zk q P1i P2 j P3k
捷联惯导算法与组合导航原理讲义
捷联惯导算法与组合导航原理讲义严恭敏，翁浚编著西北工业大学2016-9前言近年来，惯性技术不论在军事上、工业上，还是在民用上，特别是消费电子产品领域,都获得了广泛的应用,大到潜艇、舰船、高铁、客机、导弹和人造卫星，小到医疗器械、电动独轮车、小型四旋翼无人机、空中鼠标和手机，都有惯性技术存在甚至大显身手的身影。
相应地，惯性技术的研究和开发也获得前所未有的蓬勃发展，越来越多的高校学生、爱好者和工程技术人员加入到惯性技术的研发队伍中来。
惯性技术涉及面广，涵盖元器件技术、测试设备和测试方法、系统集成技术和应用开发技术等方面，囿于篇幅和作者知识面限制，本书主要讨论捷联惯导系统算法方面的有关问题，包括姿态算法基本理论、捷联惯导更新算法与误差分析、组合导航卡尔曼滤波原理、捷联惯导系统的初始对准技术、组合导航系统建模以及算法仿真等内容。
希望读者参阅之后能够对捷联惯导算法有个系统而深入的理解，并能快速而有效地将基本算法应用于解决实际问题。
本书在编写和定稿过程中得到以下同行的热心支持，指出了不少错误之处或提出了许多宝贵的修改建议,深表谢意:西北工业大学自动化学院：梅春波、赵彦明、刘洋、沈彦超、肖迅、牟夏、郑江涛、刘士明、金竹、冯理成、赵雪华；航天科工第九总体设计部：王亚军；辽宁工程技术大学：丁伟；北京腾盛科技有限公司：刘兴华；东南大学：童金武；中国农业大学:包建华；南京航空航天大学：赵宣懿；武汉大学：董翠军;网友：Zoro；山东科技大学:王云鹏。
书中缺点和错误在所难免，望读者不吝批评指正.作者2016年9月目录第1章概述 (6)1.1捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)第2章捷联惯导姿态解算基础 (10)2。
1反对称阵及其矩阵指数函数 (10)2。
1。
1 反对称阵 (10)2。
1.2 反对称阵的矩阵指数函数 (12)2。
2方向余弦阵与等效旋转矢量 (13)2.2.1 方向余弦阵 (13)2。
捷联惯导算法与组合导航原理讲义(20210220)
捷联惯导算法与组合导航原理讲义严恭敏，翁浚编著西北工业大学2021-9前言近年来，惯性技术不管在军事上、工业上，还是在民用上，特别是消费电子产品领域，都获得了广泛的应用，大到潜艇、舰船、高铁、客机、导弹和人造卫星，小到医疗器械、电动独轮车、小型四旋翼无人机、空中鼠标和手机，都有惯性技术存在甚至大显身手的身影。
相应地，惯性技术的研究和开发也获得前所未有的蓬勃开展，越来越多的高校学生、爱好者和工程技术人员参加到惯性技术的研发队伍中来。
惯性技术涉及面广，涵盖元器件技术、测试设备和测试方法、系统集成技术和应用开发技术等方面，囿于篇幅和作者知识面限制，本书主要讨论捷联惯导系统算法方面的有关问题，包括姿态算法根本理论、捷联惯导更新算法与误差分析、组合导航卡尔曼滤波原理、捷联惯导系统的初始对准技术、组合导航系统建模以及算法仿真等内容。
希望读者参阅之后可以对捷联惯导算法有个系统而深化的理解，并能快速而有效地将根本算法应用于解决实际问题。
本书在编写和定稿过程中得到以下同行的热心支持，指出了不少错误之处或提出了许多珍贵的修改建议，深表谢意：西北工业大学自动化学院：梅春波、赵彦明、刘洋、沈彦超、肖迅、牟夏、郑江涛、刘士明、金竹、冯理成、赵雪华；航天科工第九总体设计部：王亚军；辽宁工程技术大学：丁伟；北京腾盛科技：刘兴华；东南大学：童金武；中国农业大学：包建华；南京航空航天大学：赵宣懿；武汉大学：董翠军；网友：Zoro；山东科技大学：王云鹏。
书中缺点和错误在所难免，望读者不吝批评指正。
作者2021年9月目录第1章概述 (6)捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)第2章捷联惯导姿态解算根底 (10)反对称阵及其矩阵指数函数 (10)2.1.1 反对称阵 (10)2.1.2 反对称阵的矩阵指数函数 (12)方向余弦阵与等效旋转矢量 (13)2.2.1 方向余弦阵 (13)2.2.2 等效旋转矢量 (14)方向余弦阵微分方程及其求解 (16)2.3.1 方向余弦阵微分方程 (16)2.3.2 方向余弦阵微分方程的求解 (17)姿态更新的四元数表示 (19)2.4.1 四元数的根本概念 (19)2.4.2 四元数微分方程 (23)2.4.3 四元数微分方程的求解 (24)等效旋转矢量微分方程及其泰勒级数解 (26)2.5.1 等效旋转矢量微分方程 (26)2.5.2 等效旋转矢量微分方程的泰勒级数解 (29)圆锥运动条件下的等效旋转矢量算法 (31)2.6.1 圆锥运动的描绘 (31)2.6.2 圆锥误差补偿算法 (33)第3章地球形状与重力场根底 (40)地球的形状描绘 (40)地球的正常重力场 (46)地球重力场的球谐函数模型 (50)3.3.1 球谐函数的根本概念 (50)3.3.2 地球引力位函数 (58)3.3.3 重力位及重力计算 (63)第4章捷联惯导更新算法及误差分析 (69)4.1捷联惯导数值更新算法 (69)4.1.1 姿态更新算法 (69)4.1.2 速度更新算法 (70)4.1.3 位置更新算法 (76)捷联惯导误差方程 (76)惯性传感器测量误差 (76)姿态误差方程 (78)速度误差方程 (79)位置误差方程 (79)误差方程的整理 (80)静基座误差特性分析 (82)4.3.1 静基座误差方程 (82)4.3.2 高度通道 (83)4.3.3 程度通道 (83)4.3.4 程度通道的简化 (88)4.3.5 程度通道误差方程的仿真 (90)第5章卡尔曼滤波根本理论 (92)递推最小二乘法 (92)5.2 Kalman滤波方程的推导 (94)连续时间随机系统的离散化与连续时间Kalman滤波 (101)噪声相关条件下的Kalman滤波 (107)序贯滤波 (111)信息滤波与信息交融 (113)平方根滤波 (116)遗忘滤波 (123)5.9 Sage-Husa自适应滤波 (125)最优平滑算法 (126)非线性系统的EKF滤波、二阶滤波与迭代滤波 (129)间接滤波与滤波校正 (135)联邦滤波〔待完善〕 (135)滤波的稳定性与可观测度分析 (140)第6章初始对准及组合导航技术 (146)捷联惯导粗对准 (146)矢量定姿原理 (146)解析粗对准方法 (148)间接粗对准方法 (151)捷联惯导精对准 (152)惯性/卫星组合导航 (156)空间杆臂误差 (156)时间不同步误差 (157)状态空间模型 (157)车载惯性/里程仪组合导航 (158)航位推算算法 (158)航位推算误差分析 (160)6.惯性/里程仪组合 (163)低本钱姿态航向参考系统〔AHRS〕 (166)简化的惯导算法及误差方程 (166)6地磁场测量及误差方程 (168)低本钱组合导航系统模型 (169)低本钱惯导的姿态初始化 (170).5捷联式地平仪的工作原理 (172)第7章捷联惯导与组合导航仿真 (175)飞行轨迹和惯性器件信息仿真 (175)飞行轨迹设计 (175)7.1.2 捷联惯导反演算法 (176)7.1.3 仿真 (177)捷联惯导仿真 (179)7.2.1 Matlab子函数 (179)捷联惯导仿真主程序 (184)惯导/卫星组合导航仿真 (184)子函数 (184)组合导航仿真主程序 (186)附录 (188)A一些重要的三维矢量运算关系 (188)B 运载体姿态的欧拉角描绘 (190)C 姿态更新的毕卡算法、龙格—库塔算法及准确数值解法 (197)D 从非直角坐标系到直角坐标系的矩阵变换 (205)E 线性系统根本理论 (209)F 加权最小二乘估计 (214)G 矩阵求逆引理 (215)H 几种矩阵分解方法〔QR、Cholesky与UD〕 (217)I 二阶滤波中的引理证明 (221)J 方差阵上界的证明 (223)K 三阶非奇异方阵的奇异值分解 (224)L Matlab仿真程序 (229)M 练习题 (235)参考文献 (239)第1章概述第1章概述 (6)捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)1.1捷联惯导算法简介在捷联惯导系统〔SINS〕中惯性测量器件〔陀螺和加速度计〕直接与运载体固联，通过导航计算机采集惯性器件的输出信息并进展数值积分求解运载体的姿态、速度和位置等导航参数，这三组参数的求解过程即所谓的姿态更新算法、速度更新算法和位置更新算法。