残差自相关的修正
实验四--自相关性的检验及修正

实验四 -- 自相关性的检验及修正实验四自相关性的检验及修正一、实验目的掌握自相关性的检验与处理方法。
二、实验学时: 2三、实验内容及操作步骤建立我国城乡居民储蓄存款模型,并检验模型的自相关性。
1.回归模型的筛选2.自相关的检验3.自相关的调整四、实验要求利用表 5-1 资料,试建立我国城乡居民储蓄存款模型,并检验模型的自相关性。
我国城乡居民储蓄存款与GDP统计资料( 1978 年= 100)存款GDP 年份存款余额Y GDP指数X年份余额指数Y X19919241.6 199211759.4 199315203.5 199421518.8 199529662.3 199638520.8 199746279.8 199853407.5 199959621.8 200064332.4308.2200286910.6888.5 351.52003103617.7981.6 399.62004119555.41084.5 452.020051410511201.7 494.22006161587.31361.2 544.520071725341560.5 596.920082178851717.8 640.620092607721861.1 691.520103033022050.0 750.62011343635.92228.9 811.12410.3200173762.43995512012【实验步骤】(一)回归模型的筛选⒈相关图分析SCAT X Y相关图表明, GDP指数与居民储蓄存款二者的曲线相关关系较为明显。
现将函数初步设定为线性、双对数、对数、指数、二次多项式等不同形式,进而加以比较分析。
⒉估计模型,利用LS命令分别建立以下模型⑴线性模型: LS Y C Xy?62251.79175.4516 xt (-9.5629) (33.3308)R2= 0.9823 F=1110.940S.E=15601.32⑵双对数模型: GENR LNY=LOG(Y)GENR LNX=LOG(X)LS LNY C LNX?0.59996 1.7452 ln xln yt(-1.6069) (31.8572)R2= 0.9807 F= 1014.878 S.E=0.1567⑶对数模型: LS YCLNX?y1035947170915.4 ln xt(-10.2355)(11.5094)R2=0.8688 F =132.4672 S.E =42490.60⑷指数模型: LS LNY C Xln y? 9.5657 0.001581xt (55.0657) (11.2557)2R = 0.8637 F=126.6908 S.E=0.4163LS Y CXX2?16271.5477.8476x0.0378x2yt(-2.4325)(6.1317) (7.8569)R2= 0.9958F=2274.040 S.E= 7765.275⒊选择模型比较以上模型,可见各模型回归系数的符号及数值较为合理。
多重共线性、异方差及自相关的检验和修正

计量经济学实验报告多重共线性、异方差及自相关的检验和修正——以财政收入模型为例经济学 1班一、引言财政收入是一国政府实现政府职能的基本保障,对国民经济的运行及社会的发展起着非凡的作用。
首先,它是一个国家各项收入得以实现的物质保证。
一个国家财政收入规模的大小通常是衡量其经济实力的重要标志。
其次,财政收入是国家对经济实行宏观调控的重要经济杠杆。
财政收入的增长情况关系着一个国家的经济的发展和社会的进步。
因此,研究财政收入的增长显得尤为重要。
二、数据及模型说明研究财政收入的影响因素离不开一些基本的经济变量。
回归变量的选择是建立回归模型的一个极为重要的问题。
如果遗漏了某些重要变量,回归方程的效果肯定不会好;而考虑过多的变量,不仅计算量增大许多,而且得到的回归方程稳定性也很差,直接影响到回归方程的应用。
通过经济理论对财政收入的解释以及对实践的观察,对财政收入影响的因素主要有农业增加值、工业增加值、建筑业增加值、总人口数、最终消费、受灾面积等等。
全部数据均来源于中华人民共和国国家统计局网站/具体数据见附录一。
为分析被解释变量财政收入(Y)和解释变量农业增加值(X1)、工业增加值(X2)、建筑业增加值(X3)、总人口(X4)、最终消费(X5)、受灾面积(X6)的关系。
作如下线性图(图1)。
图1可以看出Y、X1、X2、X3、X5基本都呈逐年增长的趋势,仅增长速率有所变动,而X4和X6在多数年份呈现水平波动,可能这两个自变量和因变量间不一定是线性关系。
可以初步建立回归模型如下:Y=α+β1*X1+β2*X2+β3*X3+β4*X4 +β5*X5+β6*X6 +U i 其中,U i为随机干扰项。
三、模型的检验及验证(一)多重共线性检验及修正利用Eviews5.0,做Y对X1、X2、X3、X4、X5和X6的回归,Eviews的最小二乘估计的回归结果如下表(表1)所示:表1Dependent Variable: YMethod: Least SquaresDate: 11/16/13 Time: 20:54Sample: 1990 2011Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C 145188.0 26652.27 5.447488 0.0001X1 -0.972478 0.222703 -4.366701 0.0006X2 0.210089 0.068192 3.080851 0.0076X3 -0.100412 0.569465 -0.176327 0.8624X4 -1.268320 0.247725 -5.119870 0.0001X5 0.600205 0.130089 4.613794 0.0003X6 -0.007430 0.044233 -0.167964 0.8689R-squared 0.999306 Mean dependent var 27186.86Adjusted R-squared 0.999029 S.D. dependent var 28848.33S.E. of regression 899.0866 Akaike info criterion 16.69401Sum squared resid 12125351 Schwarz criterion 17.04116Log likelihood -176.6341 F-statistic 3600.848Durbin-Watson stat 1.825260 Prob(F-statistic) 0.000000 由上表的回归结果可见,,该模型可决系数R2=0.9993很高,F检验值3601,明显显著。
自相关的检验与修正

实验2自相关的检验与修正一、实验目的:
掌握自相关模型的检验方法与处理方法.。
二、实验内容及要求:
表1列出了1985-2007年中国农村居民人均纯收入与人均消费性支出的统计数据。
(1)利用OLS法建立中国农村居民人均消费性支出与人均纯收入的线性模型。
(2)检验模型是否存在自相关。
(3)如果存在自相关,试采用适当的方法加以消除。
实验如下:
首先对数据进行调整,将全年人均纯收入和全年人均消费性支出相应调整为全年实际人均纯收入和全年实际人均消费性支出。
图1
1、用OLS估计法估计参数
图2
图3
图形分析:
图4
从图4中可以看出,中国农村居民人均消费性支出与人均纯收入存在着显着的正相关关系。
估计回归方程:。
从图8中可以得出此时的D.W.=1.324681,在取显着水平为5%,n=23,k=2,d L=1.26, d U=1.44,模型中d L<DW<d U,此时不能确定是否存在自相关。
在广义差分法无法完成修正的情况下,现建立对对数模型:
图9
对双对数模型进行调整:
图10
图11
从图11中可以得出此时的D.W.=1.985950,在取显着水平为5%,n=23,k=2,d L=1.26,
d U=1.44,模型中d U<DW<4-d U,此时不存在自相关。
由此完成对自相关的修正。
异方差、自相关检验及修正

异方差、自相关的检验与修正实验目的:通过对模型的检验掌握异方差性问题和自相关问题的检验方法及修正的原理,以及相关的Eviews 操作方法。
模型设定:εβββ+++=23121i i i X X YYi----人均消费支出X1--从事农业经营的纯收入X2--其他来源的纯收入 中国内地2006年各地区农村居民家庭人均纯收入与消费支出 单位:元 城市 y x1 x2 城市 y x1 x2 北京 5724.5 958.3 7317.2 湖北 2732.5 1934.6 1484.8 天津 3341.1 1738.9 4489 湖南 3013.3 1342.6 2047 河北 2495.3 1607.1 2194.7 广东 3886 1313.9 3765.9 山西 2253.3 1188.2 1992.7 广西 2413.9 1596.9 1173.6 内蒙古 2772 2560.8 781.1 海南 2232.2 2213.2 1042.3 辽宁 3066.9 2026.1 2064.3 重庆 2205.2 1234.1 1639.7 吉林 2700.7 2623.2 1017.9 四川 2395 1405 1597.4 黑龙江 2618.2 2622.9 929.5 贵州 1627.1 961.4 1023.2 上海 8006 532 8606.7 云南 2195.6 1570.3 680.2 江苏 4135.2 1497.9 4315.3 西藏 2002.2 1399.1 1035.9 浙江 6057.2 1403.1 5931.7 陕西 2181 1070.4 1189.8 安徽 2420.9 1472.8 1496.3 甘肃 1855.5 1167.9 966.2 福建 3591.4 1691.4 3143.4 青海 2179 1274.3 1084.1 江西 2676.6 1609.2 1850.3 宁夏 2247 1535.7 1224.4 山东 3143.8 1948.2 2420.1 新疆 2032.4 2267.4 469.9 河南 2229.3 1844.6 1416.4 数据来源:《中国农村住户调查年鉴(2007)》、《中国统计年鉴(2007)》参数估计:估计结果如下:2709030.01402097.01402.728X X Y ++=Λ(2.218) (2.438) (16.999) 922173.02=R D.W.=1.4289 F=165.8853 SE=395.2538实验步骤:一、检查模型是否存在异方差1.图形分析检验(1)散点相关图分析分别做出X1和Y 、X2和Y 的散点相关图,观察相关图可以看出,随着X1、X2的增加,Y 也增加,但离散程度逐步扩大,尤其表现在X1和Y .这说明变量之间可能存在递增的异方差性。
自相关的检验与修正

实验2自相关的检验与修正、实验目的:掌握自相关模型的检验方法与处理方法.。
、实验内容及要求:表1列出了1985—2007年中国农村居民人均纯收入与人均消费性支出的统计数据。
(1)利用OLS法建立中国农村居民人均消费性支出与人均纯收入的线性模型。
(2)检验模型是否存在自相关。
(3)如果存在自相关,试采用适当的方法加以消除。
表1 1985 —2007年中国农村居民人均纯收入与人均消费性支出(单位:元)年份全年人均纯收入(现价)全年人均消费性支出(现价)消费价格指数(1985=100)1985397.6317.42100 1986423.8357106.1 1987462.6398.3112.7 1988544.9476.7132.4 1989601.5535.4157.9 1990686.3584.63165.1 1991708.6619.8168.9 1992784659.8176.8 1993921.6769.7201 199412211016.81248 19951577.71310.36291.4 19961923.11572.1314.4 19972090.11617.15322.3 199821621590.33319.1 19992214.31577.42314.3 20002253.41670314 20012366.41741316.5 20022475.61834315.2 20032622.241943.3320.2 20042936.42185335.6 20053254.932555343 200635872829348.1实验如下:首先对数据进行调整,将全年人均纯收入和全年人均消费性支出相应调整为全年实际人均纯收入和全年实际人均消费性支出。
LIL I. .一.... U h ―................ H全年人沟地收入全年人均泊箜低立出J泊费桥特描旷全年人均实际地收/全年人枸实加寸抵性女出tMM1昭W7…6J17.4Z m35^.60 31X42恤(山妙1441斯石Mid JMJ m.T41M7ma«44J J-L7JJ2.44IL5636*05MU UU期M45W.A8州IMJ nus ltf.1Uf矽»ill14^1TlV.b他E I4B.9m到W:71417*4⑷話珊肿1W3Kl.«THL73D1 4SU1M1M喻i*ii toirn3JS49*14』I・M157TJ IJ1IU4^1.4:出紺阳阳J157!4314J«1.«750•巧2000J3t:J 5OL75[潮2U3159U331S,1491^8L9M2114J isn«314J■04J1S0LJB32WI22S3J L6TO314 71T..U531.852«1UWJ P4I JMJ卿AS1W2倔ud)m31SJ■SS.I1繩US:621.21ifl-jjj irsij UU4乂MU wn困口6.4sits»71.97izM.yj皿會埠HLN T I4.W 加?n«HU 1W負建tUMSW741 4055T43M 8iraj^171711用OLS 估计法估计参数<-□ Group; UN1TTUD Wcrldilft UNTTTLED;;UMtided\[UMr][fi&£|[Oto[jKt |ftjrtt£narrtfeJprMafe]匚][Sart|Eart£pflgj&]旦fc#^[Sapli4j 』T 程]色3y?.弓13S$ [1936 VT1937 1920 193919^?19931934 1935 1936 1037 1939 2»J0 2001 20 J 2 205J 20342035G3E?017397 5000 317.42M1399 43DO 330,«Q0 410 47DO 353.420C 411 56D0 36D.050C SSOEWDO333.0 30C416.690041^ 54J0443 44DU 375 190C 45S5100 382.340C 492.34 DO 410.0000 541 4200 443.680C 611.6700 501030C 648 50 DO 50L75M 677 53DO 4DL3SO0 704 52 DO 501 aaoo J17MOO 531 B500 747 68DO 550.080C 75541D0 M1.350C G10 94DO GO5.930C C74 97D0 esijD7oo 阳⑹0 71J.030C 1033.4S0 81Z7DOO 112R170 Q7B 71 nr也 E\ie\;&zi e Edit Object View Proc Qui:k Options Window Heipdaw Uy ciO Eq uatio n: U NTTTLED Worlcflvc UMTTTLEI>:U 般―、3. frx| JDEU |f i rure I UEUE ihstma 世 心已工竄 '曲ts KKdtCoefficientSU Error t SkteticProa.G 50.21B7S 14 548SB 3.E642100.(]0Q9KC 6969260.02134231 99373 C 0000R-gquan&10S7QQ34dep^nd&ntvarjqu Q013-etiusted R-squar?d C.978947&D, ciependeTitvar15E.3tZ3 3.El ofreer&ssion 22.97705 4<aike info cnteilori 9.1B9B13 Sun squared resic 1105B.87 Sshwa-irz. cnUnon9.2ft Log hka || hood -1026826 Hannar^Oiilrin cfit&r. 9214646 h-S^tlStlC1023.933 □urciin Batson sealU4 码rroa(r-statistic) 0.000030-i e Edit Otwect Viav Proc Quick Options 州nticm 卜口 dacg iy图2DeDerKfentA ;an3ti«: T LlEtnnd: LEastSqijarss Dats: 04/24^5 Tria: 12:32 fianph 1Q95200?ricuaec ooser/atcns 、u图4从图4中可以看出,中国农村居民人均消费性支出与人均纯收入存在着显著的正相关关系。
处理自相关问题的两种简单方法(一)

处理自相关问题的两种简单方法(一)处理自相关问题的两种简单方法什么是自相关问题自相关问题是统计学中的重要问题之一。
在分析时间序列等数据时,经常会出现自相关问题。
自相关问题指的是一个变量与其自身在不同时间点上的相关性。
自相关问题给数据分析带来的挑战自相关问题会导致数据分析结果出现偏差,进而影响决策的准确性。
因此,解决自相关问题是保证数据分析准确性的重要步骤。
处理自相关问题的两种简单方法方法一:差分法差分法是一种简单的处理自相关问题的方法。
差分法通过对数据进行一阶或二阶差分,将原数据转变为不具有自相关性的新数据,从而保证数据分析的准确性。
方法二:滑动平均法滑动平均法也是一种常用的处理自相关问题的方法。
滑动平均法通过计算一定时间窗口内的平均值,来平滑数据的波动。
滑动平均法不需要对原始数据进行差分,因此更加简单易用。
总结自相关问题是数据分析中的一个重要问题,不处理好自相关问题可能导致数据分析结果出现偏差,进而影响决策的准确性。
差分法和滑动平均法是两种处理自相关问题的简单方法,具体使用根据实际情况选择。
•差分法和滑动平均法的缺点–差分法差分法虽然能够有效地处理自相关问题,但会使得数据的均值和方差发生变化,从而影响部分数据分析方法的特性。
–滑动平均法滑动平均法会使得数据出现平滑的趋势,但同时也会使得数据的波动性降低,从而可能影响观察到的真实变化。
•差分法和滑动平均法的应用–差分法差分法常用于金融领域的时间序列分析中,如股票收益率的差分处理。
–滑动平均法滑动平均法常用于气象、经济和股票等领域的数据分析中,如股票均线的计算和天气预测中的平滑处理。
•总结处理自相关问题是数据分析中重要的一步,差分法和滑动平均法是两种简单易用的方法。
使用时需要考虑数据的特性和具体分析需求,选择合适的方法进行处理。
序列自相关检验及修正

R2=0.9913 D.W.=2.31
序列自相关检验及修正
第二步,作差分变换:点对象窗口工具栏上的 genr按钮,在对话框中输入等式1[mnew=m0.938*m(-1)+0.469*m(-2)]和等式 2[gdpnew=gdp-0.938*gdp(-1)+0.469*gdp(2)],再对新得到的mnew关于gdpnew进行OLS估 计,其结果见图六:
d1=1.27,du=1.45,D.W.=0.628<d1,故存在 正自相关。
序列自相关检验及修正
三、G-B检验(拉格朗日乘数检验) 点击View\Residual Test\Serial Correlation LM
Test,Lag取2,得到(见图三):
序列自相关检验及修正
含2阶滞后残差项的辅助回归为: et=6.593-0.0003*GDP+1.094*et-1-0.786et-2
序列自相关检验及修正
辅助回归方程为: et=6.692-0.0003*GDP+1.108*et-1(0.228)(-0.497)(4.541)
0.819et-2+0.032et-3 (-1.842)(0.087)
R2=0.6615 LM=13.89,大于显著性水平为5%,自由度为3的临界
值x20.05(3)=7.815,原模型仍存在序列相关性,但 由于et-3的参数不显著,说明不存在3阶序列相关性。
(0.231)(-0.504)(6.231)(-3.692) R2=0.6614
LM=22*0.6614=14.55,该值大于显著性水平为 5%,自由度为2的x2分布的临界值x20.05(2) =5.991,由此判断原模型存在2阶序列自相关。
自相关的检验与修正
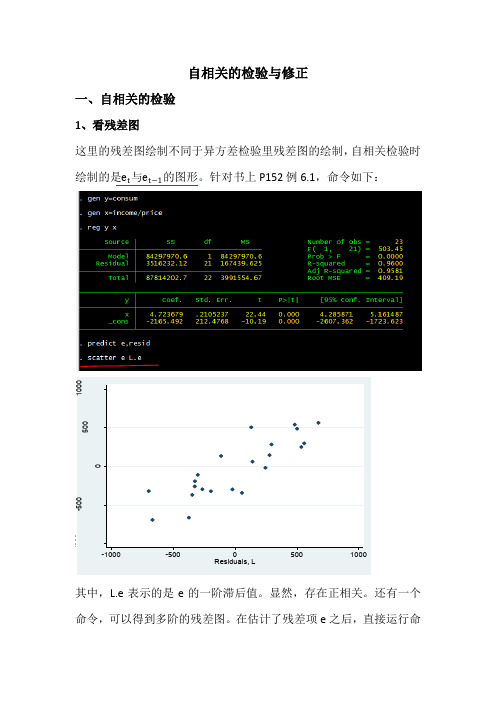
自相关的检验与修正一、自相关的检验1、看残差图这里的残差图绘制不同于异方差检验里残差图的绘制,自相关检验时绘制的是e t 与e t −1的图形。
针对书上P152例6.1,命令如下:其中,L.e 表示的是e 的一阶滞后值。
显然,存在正相关。
还有一个命令,可以得到多阶的残差图。
在估计了残差项e之后,直接运行命R e s i d u a l s令ac e 就可得到下图(ac 为autocorrelation 的缩写):横轴表示的是滞后阶数,阴影部分表示的是相应的置信区间,在上图中,显然一阶滞后是自相关的。
补充:滞后算子L 。
L.x 表示x 的一阶滞后值,L2.x 表示二阶滞后值。
差分算子D 。
D.x 表示x 的一阶差分,D2.x 表示二阶差分。
LD.x 表示一阶差分的一阶滞后值。
需要注意的是,在使用之后算子和差分算子时,一定要事先设定时间变量。
2、DW 检验该方法出现较早,现在已经过时,主要是因为该方法只能检验一阶自相关。
命令:estat dwatson 。
经验上DW 值在1.8---2.2之间接受原假设,不存在一阶自相关。
DW 值接近于0或者接近于4,拒绝原假设,存在一阶自相关。
3、LM检验(BG检验)命令:estat bgodfrey 一阶滞后自相关检验estat bgodfrey,lags(p) P阶滞后自相关检验滞后阶数P的选取最简单的方法就是看自相关图,阴影部分以外的自相关阶数为显著。
二、自相关的处理—广义最小二乘法FGLS命令:prais y x1 x2 x3 该命令对应的是书上P147的(6.33)方法prais y x1 x2 x3,corc 该命令对应的是书上P147的(6.32)方法在自相关检验及处理上,还有比较常用的稳健标准差命令newey以及Q-Test命令,感兴趣的同学可以去查阅相关书籍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用回归分析·上机作业二学号:200930980106 姓名:何斌年级专业: 10级统计1班指导老师:丁仕虹思考与练习 4.91.用普通最小二乘法建立回归方程,并画出残差散点图。
1.1首先录入数据,sas程序如下:proc import out=aa /*使用import过程导入数据,并输出到数据集aa*/datafile="d:\xt4.09.xls"dbms=excel2000 replace;getnames=yes; /*首行为变量名*/run;proc print data=aa noobs;run;1.2建立回归方程,画残差散点图,sas程序如下:proc reg data=aa;model y=x;output out=out r=residual;/*把回归的结果输出在文件out里,残差给变量名residual */ run;proc gplot data=out;plot residual*x;/*做残差图,检验是否存在异方差*/symbol v=star i=none;run;1.3得到结果如下:图1.3.1方差分析以及参数估计1.4结果分析: 1.4.1由方差分析可知:p 值小于0.05,所以该回归方程显著有效。
1.4.2 R-Square=0.7046,Adj R-Sq=0.6988,可见回归方程的拟合度较高。
1.4.3由参数估计可得,常数项的检验P 值为0.0655大于0.05,故常数项不显著。
1.5除去常数项,重新拟合方程。
1.5.1 sas 程序如下: proc reg data=aa; model y=x/noint; run; 1.5.2得到结果如下: 图1.5.1方差分析以及参数估计 1.5.3结果分析: (1)由方差分析可知:P 值小于0.05,所以该回归方程显著有效,且F 值较有常数项时明显变大,故拟合方程较有常数项时更好。
(2) R-Square=0.8704,Adj R-Sq=0.8679,可见回归方程的拟合度有较大幅度提高。
(3)由参数估计可得,所有参数的检验P 值均小于0.05,参数显著有效。
(4)拟合的回归方程为:x y 0.00314=∧ (1.5.3.4) 1.6得到残差散点图如下:图1.6.1残差散点图2.判断是否存在异方差。
2.1残差图分析:由图1.6.1残差散点图可以直观地看到,残差散点图上的点的分布是有一定规律的,即误差随着x的增加而波动幅度增加,呈大喇叭的形状,因此可以认为误差项存在异方差。
2.2利用等级相关系数法判断,sas程序如下:proc reg data=aa;model y=x/r noint;/*r是残差,noint无常数项*/output out=out r=residual;/*把回归的结果输出在文件out里,残差给变量名residual */ run;/*下面利用残差的绝对值和X间的 spearman的相关系数检验异方差*/data out1 ;set out; /*调用数据集out*/z=abs(residual); /*求残差的绝对值*/run;proc corr data=out1 outs=out2;/*corr指做相关分析 outs=out2表示将等级相关检验的结果输出到out2*/var x z;run;2.2.1得到结果如下:图2.2.1等级相关系数2.2.2结果分析:由2.2.1的输出结果可知,残差绝对值||ie与ix的等级相关系数0.21271sr,对应的P值=0.1262,故认为残差绝对值||ie与自变量ix显著相关,存在异方差。
3.用幂指数型的权函数建立加权最小二乘回归方程。
3.1 sas程序如下:title"wls method";data w1;/*建立新的数据集w1,以便计算权重*/set out1;keep y x;run;data w2;/*建立新的数据集w,以保留权重*/set w1;array row{10} w1-w10;/* w1-w10为不同m时的权数值*/ array p{10}(-2,-1.5,-1,-0.5,0,0.5,1,1.5,2,2.5);do i=1 to 10;row(i)=1/x**p{i};end;run;proc print data=w2;run;proc reg data=w2;model y=x/r;weight w1;output out=test r=residual;run;proc gplot data=test;plot residual*x;symbol v=dot i=none color=red;run;3.2结果如下图所示:图3.2.1方差分析图3.2.1拟合优度以及参数估计 3.3结果分析:(1)由方差分析可知:P 值小于0.05,所以该回归方程显著有效。
(2) R-Square=0.8175,Adj R-Sq=0.8139,可见回归方程的拟合度较高。
(3)由参数估计可得,所有参数的检验P 值均小于0.05,参数显著有效。
(4)加权最小二乘的回归方程为:x y 0.0046-2.40038+=∧ (3.3.4) 3.4.1残差散点图:3.4.2残差散点图分析:由3.4.1残差散点图可以直观地看到,残差图上的点仍是有规律的,即误差随着x 的增加而波动幅度增加,呈大喇叭的形状,因此可以认为误差项仍存在异方差。
4. 作变换:y=sqrt(y) 。
4.1得到结果如下:图4.1.1方差分析以及参数估计4.2结果分析:由图4.1.1可知,回归方程通过了显著性检验,调整2R为0.6520,回归方程的系数都通过了显著性检验,方差稳定变换'y y=后,回归方程为:'0.582230.00095286*y x=+(4.2.1)思考与练习 4.131.用普通最小二乘法建立y关于x的回归方程。
1.1首先录入数据,sas程序如下:proc import out=aa2 /*使用import过程导入数据,并输出到数据集aa2*/datafile="d:\xt_4.13.xls"dbms=excel2000 replace;getnames=yes; /*首行为变量名*/run;1.2建立回归方程,sas程序如下:proc reg data=aa2;model y=x/clb p r spec DW ;/*其中p是预测值,r是残差,clb是给出回归系数的区间估计,spec 可以给出怀特检验(检验异方差)的结果,DW给出一阶线性自相关检验*/output out=out r=residual;/*把回归的结果输出在文件out里,残差给变量名residual */ run;1.3得到结果如下: 图1.3.1方差分析以及参数估计 1.4结果分析: (1)由方差分析可知:p 值小于0.05,所以该回归方程显著有效。
(2)R-Square=0.9982,Adj R-Sq=0.9981,可见回归方程的拟合度较高。
(3)由参数估计可得,所有参数的检验P 值均小于0.05,参数显著有效。
(4)拟合的回归方程为:x y 17565.035145.1+-=∧ (1.4.1) 2.残差图以及DW 检验诊断序列的相关性。
2.1残差图如下:残差图分析:该图存在一定的锯齿形,故可判断残差项存在相关。
2.2DW检验:查DW分布表可得临界值d L和d U分别为1.20和1.41,由于DW值=0.771<d L=1.20,故模型存在序列正自相关。
3.迭代法处理序列相关,建立回归方程。
3.1 sas程序如下:/*迭代法处理序列相关*/data bb;set out;ro=1-(1/2)*0.771;/*求自相关系数的估计值ro,DW值=0.771*/y_t_1=y-ro*lag1(y);x_t_1=x-ro*lag1(x);/*lagn(n自定)函数可把一变量的各观测值移后n位;*/proc reg data=bb;model y_t_1=x_t_1/clb p r spec DW ;run;3.2结果如下所示:图3.2.1方差分析以及参数估计图3.2.2 DW 检验 3.3结果分析: 由图3.2.1可知,迭代法所得的回归模型通过了显著性检验,调整2R 为0.9922,回归方程为: 't 't 37x 17.040801.0y +-= (3.3.1) 其中,''11,t t t t t t y y py x x px --=-=- 由图3.2.2可知,DW=1.60。
查DW 表,n=19,k=2,显著水平a=0.05,得d L =1.18,d U =1.40。
由于1.40<1.60<4-1.40,所以迭代法得到的回归方程的误差项间无自相关。
4. 用一阶差分法处理数据,建立回归方程。
4.1 sas 程序如下: /*一阶差分法处理序列相关*/ data bb2; set aa2; difx=x-lag1(x);/*lagn (n 自定)函数可把一变量的各观测值移后n 位;对x 各观测值作一阶差分*/dify=y-lag1(y);/*lagn (n 自定)函数可把一变量的各观测值移后n 位;对y 各观测值作一阶差分*/run; proc reg data=bb2;/*对bb2运行回归分析过程*/ model dify=difx/p r dw; run; 4.2结果如下所示:图4.2.1方差分析以及参数估计图4.2.2 DW 检验 4.3结果分析: 由图 4.2.1可见,一阶差分法处理数据后建立的回归模型通过了显著性检验,调整2R 为0.9346,回归方程为: t x ∆+=∆16248.002827.0y t (4.3.1) 其中,1t t t y y y -∆=-,1t t t x x x -∆=-由图4.2.2可知,DW=1.828。
查DW 表,n=19,k=2,显著水平a=0.05,得dL=1.18,dU=1.40。
由于1.40<1.828<4-1.40,所以迭代法得到的回归方程的误差项间无自相关。
5. 三种方法的优良性比较。
在回归模型不存在序列相关时,普通最小二乘法比迭代法和一阶差分法操作起来更简便,但是,当一个回归模型存在序列相关性时,普通最小二乘法所建立的回归方程就不适用了,这时需要使用迭代法或一阶差分法。
由于一阶差分法的应用条件是自相关系数P=1,当P 接近1时,一阶差分法比迭代法好,当原模型存在较高程度的一阶自相关的情况时,一般使用一阶差分法而不用迭代法,因为一阶差分法比迭代法简单而且迭代法需要用样本估计自相关系数P ,对P 的估计误差会影响迭代法的使用效率,同时迭代法的算法时间复杂度比一阶差分的高,在效率上不如一阶差分好。
