经典线性回归模型的诊断与修正
标准线性回归模型

可以通过对自变量进行变换(如对数 转换、幂转换等)或使用多项式回归 等方法处理非线性关系,提高模型拟 合效果。
时间序列数据的处理
时间序列数据的特点
时间序列数据具有时序依赖性和动态 变化性,不同时间点的数据之间存在 相关性。
处理方法
通过差分、季节性差分、指数化等方 法消除时间序列数据的趋势和季节性 影响,或者使用ARIMA、SARIMA等 时间序列模型对数据进行拟合和预测。
可以通过剔除相关性较高的自变量、使用主成分分析等方法处
理多重共线性问题。
无异方差性
异方差性的定义
异方差性是指误差项的方差不恒定,即随着自变量的变化,误差 项的方差也会发生变化。
异方差性的检验
可以通过图形方法(如残差图)或统计方法(如White检验)来 检验异方差性。
处理异方差性的方法
可以通过使用稳健的标准误、对数变换等方法处理异方差性问题。
准线性回归模型
• 引言 • 模型假设 • 标准线性回归模型的参数估计 • 模型的评估与诊断 • 线性回归模型的扩展 • 案例分析
01
引言
目的和背景
探索自变量与因变量 之间的非线性关系
为复杂数据提供更准 确的预测和解释
弥补标准线性回归模 型的局限性,处理非 线性数据
标准线性回归模型的定义
线性关系
检验残差是否服从正态分布。
详细描述
正态性检验是用来检验回归模型的残差是否服从正态分布的一种方法。如果残差服从正态分布,那么 我们可以认为模型满足经典假设之一,这有助于我们更好地理解和解释模型的结果。
异方差性检验
总结词
检验残差是否具有异方差性。
详细描述
异方差性检验是用来检验回归模型的残差是否具有异方差性的一种方法。如果残差具有 异方差性,那么模型的估计参数可能会受到影响,导致模型的结果不准确。因此,进行
第二章_经典线性回归模型

(3)
2
(4)
此二式称为正规方程。解此二方程,得:
( X t X )(Yt Y ) n X t Yt X t Yt xt yt ˆ (5) 2 2 2 2 n X t ( X t ) (X t X ) xt ˆX ˆ Y (6)
21
二、最小二乘法估计
(1)最小二乘原理 为了便于理解最小二乘法的原理,我们用双
变量线性回归模型作出说明。
对于双变量线性回归模型Y = α+βX + u, 我们
的任务是,在给定X和Y的一组观测值 (X1 , Y1), (X2 , Y2) , ..., (Xn , Yn) 的情况下, 如何求出 和 , Yt = α + βXt + ut 中 α 和 β 的估计值 使得拟合的直线为“最佳”。
et
E( )
真实的回归直线
估计的回归直线
拟合的回归线
Y Yt *
残差
** * *
X Y
拟合方程或估 计方程
ˆ Y t
et
*
*
*
* *
* *
Y
*
* *
ˆ Y * t
*
Yt
Xt 图2
X
残差
拟合的直线 称为拟合的回归线。 对于任何数据点 (Xt, Yt), 此直线将Yt 的总值 分成两部分。
第二章 经典线性 回归模型
(Classical Linear Regression Model)
第一节 线性回归模型的概念
第二节 线性回归模型的估计
第三节
拟合优度
第四节 非线性关系的处理 第五节 假设检验
第六节 预测
第七节 虚拟变量
经典线性回归模型的Eviews操作

经典线性回归模型经典回归模型在涉及到时间序列时,通常存在以下三个问题:1)非平稳性→ ADF单位根检验→ n阶单整→取原数据序列的n阶差分(化为平稳序列)2)序列相关性→D.W.检验/相关图/Q检验/LM检验→n阶自相关→自回归ar(p)模型修正3)多重共线性→相关系数矩阵→逐步回归修正注:以上三个问题中,前两个比较重要。
整体回归模型的思路:1)确定解释变量和被解释变量,找到相关数据。
数据选择的时候样本量最好多一点,做出来的模型结果也精确一些。
2)把EXCEL里的数据组导入到Eviews里。
3)对每个数据序列做ADF单位根检验。
4)对回归的数据组做序列相关性检验。
5)对所有解释变量做多重共线性检验。
6)根据上述结果,修正原先的回归模型。
7)进行模型回归,得到结论。
Eviews具体步骤和操作如下。
一、数据导入1)在EXCEL中输入数据,如下:除去第一行,一共2394个样本。
2)Eviews中创建数据库:File\new\workfile, 接下来就是这个界面(2394就是根据EXCEL里的样本数据来),OK3)建立子数据序列程序:Data x1再enter键就出来一个序列,空的,把EXCEL里对应的序列复制过来,一个子集就建立好了。
X1是回归方程中的一个解释变量,也可以取原来的名字,比如lnFDI,把方程中所有的解释变量、被解释变量都建立起子序列。
二、ADF单位根检验1)趋势。
打开一个子数据序列,先判断趋势:view\graph,出现一个界面,OK。
得到类似的图,下图就是有趋势的时间序列。
X1.4.2.0-.2-.4-.6-.8100020003000400050002)ADF检验。
直接在图形的界面上进行操作,view\unit root test,出现如下界面。
在第二个方框内根据时序的趋势选择,Intercept指截距,Trend为趋势,有趋势的时序选择第二个,OK,得到结果。
上述结果中,ADF值为-3.657113,t统计值小于5%,即拒绝原假设,故不存在单位根。
线性回归模型的建模与分析方法

线性回归模型的建模与分析方法线性回归模型是一种常用的统计学方法,用于研究自变量与因变量之间的关系。
在本文中,我们将探讨线性回归模型的建模与分析方法,以及如何使用这些方法来解决实际问题。
一、线性回归模型的基本原理线性回归模型假设自变量与因变量之间存在线性关系,即因变量可以通过自变量的线性组合来预测。
其基本形式可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中,Y表示因变量,X1、X2、...、Xn表示自变量,β0、β1、β2、...、βn表示回归系数,ε表示误差项。
二、线性回归模型的建模步骤1. 收集数据:首先需要收集自变量和因变量的相关数据,确保数据的准确性和完整性。
2. 数据预处理:对数据进行清洗、缺失值处理、异常值处理等预处理步骤,以确保数据的可靠性。
3. 模型选择:根据实际问题和数据特点,选择适合的线性回归模型,如简单线性回归模型、多元线性回归模型等。
4. 模型拟合:使用最小二乘法等方法,拟合回归模型,得到回归系数的估计值。
5. 模型评估:通过统计指标如R方值、调整R方值、残差分析等,评估模型的拟合优度和预测能力。
6. 模型应用:利用已建立的模型进行预测、推断或决策,为实际问题提供解决方案。
三、线性回归模型的分析方法1. 回归系数的显著性检验:通过假设检验,判断回归系数是否显著不为零,进一步判断自变量对因变量的影响是否显著。
2. 多重共线性检验:通过计算自变量之间的相关系数矩阵,判断是否存在多重共线性问题。
若存在多重共线性,需要进行相应处理,如剔除相关性较高的自变量。
3. 残差分析:通过观察残差的分布情况,判断模型是否符合线性回归的基本假设,如误差项的独立性、正态性和方差齐性等。
4. 模型诊断:通过观察残差图、QQ图、杠杆值等,判断是否存在异常值、离群点或高杠杆观测点,并采取相应措施进行修正。
5. 模型优化:根据模型评估结果,对模型进行优化,如引入交互项、非线性变换等,以提高模型的拟合效果和预测准确性。
经典线性回归模型

·β的OLS估计量:在假定2.3成立时
( ) å å b =
XTX
-1 X T Y
= çæ 1 èn
n i=1
xi xiT
Hale Waihona Puke -1ö æ1 ÷ç ø èn
n i=1
xi yi
÷ö ø
( ) ·估计量的抽样误差(sampling error): b - b = X T X -1 X Te
·第i次观测的拟合值(fitted value): yˆi = xiTb
且自变量的回归系数和 y 与 x 的样本相关系数之间的关系为
b1 == corr(Y , X )
å( 1 n
n - 1 i=1
yi
- y)2
º r sy
å( ) 1 n
n - 1 i=1
xi - x 2
sx
·修正决定系数(adjusted coefficient of determination, adjusted R square)
4.假定我们观测到上述这些变量的n组值: (y i , x i1 , L , ) x ip (i=1,…,n)。称
这n组值为样本(sample)或数据(data)。
§2.2 经典线性回归模型的假定
假定 2.1(线性性(linearity))
yi = b0 + b1xi1 + L + b p xip + e i (i=1,…,n)。
( ) ( ) E ~x jei
çæ E x j1e i =ç M
÷ö ÷=0
(i=1,…,n ; j=1,…,n )。
( ) ç
è
E
x jp e i
÷ ø
·不相关条件(zerocorrelation conditions)
线性回归(异方差的诊断、检验和修补)—SPSS操作
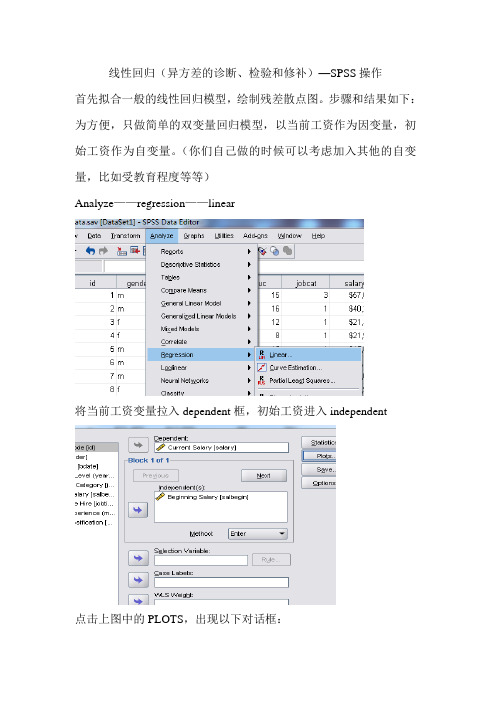
线性回归(异方差的诊断、检验和修补)—SPSS操作首先拟合一般的线性回归模型,绘制残差散点图。
步骤和结果如下:为方便,只做简单的双变量回归模型,以当前工资作为因变量,初始工资作为自变量。
(你们自己做的时候可以考虑加入其他的自变量,比如受教育程度等等)Analyze——regression——linear将当前工资变量拉入dependent框,初始工资进入independent点击上图中的PLOTS,出现以下对话框:以标准化残差作为Y轴,标准化预测值作为X轴,点击continue,再点击OK第一个表格输出的是模型拟合优度2R,为0.775。
调整后的拟合优度为0.774.第二个是方差分析,可以说是模型整体的显著性检验。
F统计量为1622.1,P值远小于0.05,故拒绝原假设,认为模型是显著的。
第三个是模型的系数,constant代表常数项,初始工资前的系数为1.909,t检验的统计量为40.276,通过P值,发现拒绝原假设,认为系数显著异于0。
以上是输出的残差对预测值的散点图,发现存在喇叭口形状,暗示着异方差的存在,故接下来进行诊断,一般需要诊断异方差是由哪个自变量引起的,由于这里我们只选用一个变量作为自变量,故认为异方差由唯一的自变量“初始工资”引起。
接下来做加权的最小二乘法,首先计算权数。
Analyze——regression——weight estimation再点击options,点击continue,再点击OK,输出如下结果:由于结果比较长,只贴出一部分,第二栏的值越大越好。
所以挑出来的权重变量的次数为2.7。
得出最佳的权重侯,即可进行回归。
Analyze——regression——linear继续点击save,在上面两处打勾,点击continue,点击ok这是输出结果,和之前同样的分析方法。
接下需要绘制残差对预测值的散点图,首先通过transform里的compute计算考虑权重后的预测值和残差。
回归诊断

-1.05
3
140
5.3
4.27143 1.02857
4
120
4
3.40179 0.59821
5
180
6.55
6.01071 0.53929
6
100
2.15
2.53214 -0.38214
7
200
6.6
6.88036 -0.28036
8
160
5.75
5.14107 0.60893
由上述数据,可得 y 关于 x 的一元线性回归方程
n
hii hi2j hi2i hi2j hi2j 0
j 1
ji
ji
故有: hii hi2i ,由此可得。
n
(2) hii tr(I H ) tr( X ( X X )1 X ) tr(( X X )1 X X ) t 1
i 1
一般情况下:
hii
1 n
(xi
x)' L1(xi
• 其次,必须确定“度量影响的尺度是什么?”为了定量 地刻划影响的大小,迄今为止已提出多种尺度,基于置 信域的尺度,基于似然函数的尺度等等。在每一种类型 中又可能有不同的统计量,例如基于影响函数就已提出 多种“距离”来度量影响,有Cook距离、Welsch Kuh距离、Welsch距离等等。每一种度量都是着眼于某 一方面的影响,并在某种具体场合下较为有效。这一方 面反映了度量影响问题的复杂性,另一方面也说明了影 响分析的研究在统计诊断中是一个甚为活跃的方向,还 有大量有待解决的问题。
置。
M,c 常用的选择: M X X , c (t 1)s 2 ,此时,有:
Di
(M ,c)
ri2
回归分析回归诊断

0.925064 0.855744
0.814528
0.192504 19
方差分析
回归分析 残差 总计
df 4
14 18
SS 3.077652 0.518811 3.596463
Intercept X Variable 1 X Variable 2 X Variable 3 X Variable 4
还有模型的设定
标准的回归假定:
1,关于模型设定的假定 2,关于误差的假定 3,关于预测变量的假定
非随机的 其取值是误差取得的,但几乎不可能。测量误差将 影响到误差方差,相关系数,复相关系数及回归系数 的估计,其影响程度的大小取决于多个因素。 是线性无关的
4,关于观测的假定 所有观测是同样可靠性
数据的诊断 异常值 强影响点 假定是否满足
y
12
10
8
6
4
2
0
0
10
20
30
x 40
存在一个有影响观测值的散点图
有影响的观测值 (图示)
y
12
10
8
6
4
存在影响值的趋势
2
有影响的观
测值
0
0
10
20
30
x 40
存在一个有影响观测值的散点图
有影响的观测值 (图示)
y
12
10
不存在影响
8
值的趋势
6
4
存在影响值的趋势
2
有影响的观
测值
0
0
10
20
其次,必须确定“度量影响的尺度是什么?”为 了定量地刻划影响的大小,迄今为止已提出多种 尺度,基于置信域的尺度,基于似然函数的尺度 等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典线性回归模型的诊断与修正下表为最近20年我国全社会固定资产投资与GDP的统计数据:1
年份国内生产总值(亿元)GDP 全社会固定资产投资(亿元)PI
1996 71813.6 22913.5
1997 79715 24941.1
1998 85195.5 28406.2
1999 90564.4 29854.7
2000 100280.1 32917.7
2001 110863.1 37213.49
2002 121717.4 43499.91
2003 137422 55566.61
2004 161840.2 70477.43
2005 187318.9 88773.61
2006 219438.5 109998.16
2007 270232.3 137323.94
2008 319515.5 172828.4
2009 349081.4 224598.77
2010 413030.3 251683.77
2011 489300.6 311485.13
2012 540367.4 374694.74
2013 595244.4 446294.09 1数据来源于国家统计局网站年度数据
1、普通最小二乘法回归结果如下:
方程初步估计为:
GDP=75906.54+1.1754PI
(32.351)
R2=0.9822F=1046.599 DW=0.3653
2、异方差的检验与修正
首先,用图示检验法,生成残差平方和与解释变量PI的散点图如下:
从上图可以看出,残差平方和与解释变量的散点图主要分布在图形的下半部分,有随PI的变动增大的趋势,因此,模型可能存在异方差。
但是否确定存在异方差,还需作进一步的验证。
G-Q检验如下:
去除序列中间约1/4的部分后,1996-2003年的OLS估计结果如下所示:
残差平方和RSS1=4274.201.
2008-2015年的OLS估计结果如下:
残差平方和RSS2=2.39E+09.
根据G-Q检验,F统计量为
=2.39∗109/4274.201=559168.836>F0.057,7=3.79 F=RSS2
RSS1
因此,在5%的显著性水平下拒绝两组子样本方差相同的假设,即存在异方差。
Gleiser检验结果如下
参数的估计值显著地不为0,则可以认定模型存在着异方差。
异方差的修正:
运用加权最小二乘法对异方差进行修正
对加权后的模型进行异方差检验,结果如下:
已知White统计量n R2=3.682,由于χ20.052=5.991>3.682,因此,可以判断在给定
显著性水平0.05的情况下,加权后的模型不再存在异方差,说明异方差性已经消除。
3、序列相关性的检验与修正
序列相关性的检验如下:
做残差与残差滞后一期的散点图:
可以看出,E与E(-1)逐渐合拢,因此残差与其滞后一期的残差存在序列相关性。
D-W检验:
从OLS估计结果中可直接得到DW值为0.3653,给定α=0.05,已知n=20,k=2,查DW检验临界值表可得,d l=1.20,d u=1.41,由0.3653<1.20可知模型存在正自相关。
序列相关性的修正:
利用广义差分法,由于ρ=1−DW
2=1−0.3653
2
=0.8174,有估计结果如下:
在新序列估计结果下,d u=1.41<DW=1.577<4-d u=4−1.41=2.59,故不再存在序列相关性,自相关已经得到消除。
运用Cochrane-Orcutt迭代法进行自相关的修正:
根据结果可知,d u=1.41<DW=1.7687<4-d u=4−1.41=2.59,故不再存在自相关。
