二阶倒立摆实验报告材料
直线两级倒立摆实验指导
∂f 2 | . . . .. ∂x x =0,θ1 =0,θ 2 =0, x =0,θ1 =0,θ 2 =0, x =0 ∂f 2 | . . . .. ∂θ 2 x = 0,θ1 =0,θ 2 =0, x =0,θ1 =0,θ 2 =0, x =0
k 22 =
∂f 2 | . . . .. ∂θ1 x =0,θ1 =0,θ 2 =0, x =0,θ1 =0,θ 2 =0, x =0
' '' ' '
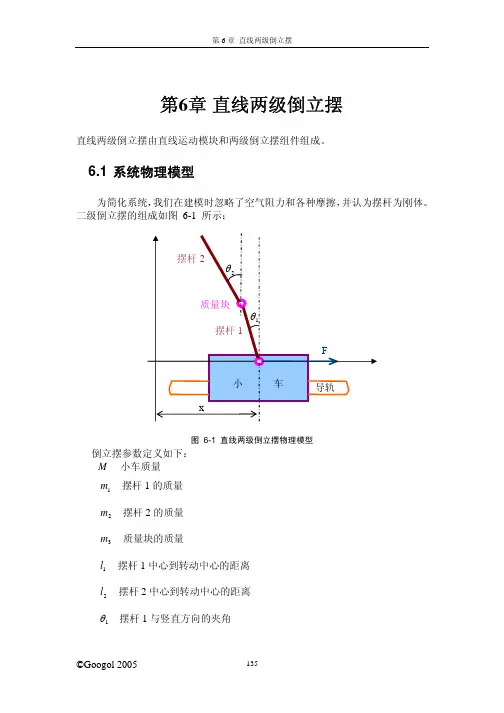
对于系统，设以下变量： xpend1 摆杆 1 质心横坐标； yangle1 摆杆 1 质心纵坐标； xpend2 摆杆 2 质心横坐标； yangle2 摆杆 2 质心纵坐标； xmass 质量块质心横坐标； ymass 质量块质心纵坐标； 又有：
©Googol 2005
136
第 6 章 直线两级倒立摆
L( q, q ) = T ( q, q ) − V ( q , q )
. . .
其中 L 为拉格朗日算子，q 为系统的广义坐标，T 为系统的动能，V 为系统的 势能。
d ∂L ∂L − = fi dt ∂ q. ∂qi i
其中 i＝1,2,3……n， f i 为系统在第 i 个广义坐标上的外力，在二级倒立摆系统 中，系统的广义坐标有三个广义坐标，分别为 x, θ 1 , θ 2 。 首先计算系统的动能：
©Googol 2005
139
第 6 章 直线两级倒立摆
k11 = ∂x@tD a dd ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k12 = ∂θ1@tD add ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k13 = ∂θ2@tD add ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k14 = ∂x'@tD add ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. a'@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k15 = ∂θ1'@tD add ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k16 = ∂θ2'@tD add ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k17 = ∂x''@tD add ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k21 = ∂x@tD bdd ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k22 = ∂θ1@tD bdd ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k23 = ∂θ2@tD bdd ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k24 = ∂x'@tD bdd ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k25 = ∂θ1'@tD bdd ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k26 = ∂θ2'@tD bdd ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; k27 = ∂x''@tD bdd ê. x@tD → 0 ê. θ1@tD → 0 ê. θ2@tD → 0 ê. x'@tD → 0 ê. θ1 '@tD → 0 ê. θ2'@tD → 0 ê. x''@tD → 0; Simplify@k12D Simplify@k13D Simplify@k17D Simplify@k22D Simplify@k23D Simplify@k27D m1 = 0.05 ; m2 = 0.13; m3 = 0.236; l1 = 0.0775; l2 = 0.25; g = 9.8 ; k12 k13 k17 k22 k23 k27
倒立摆实验报告建筑结构抗震研究
倒立摆实验报告：建筑结构抗震研究一、引言随着我国经济的快速发展，高层建筑日益增多，建筑结构的抗震性能成为社会关注的焦点。
为了提高建筑物的抗震能力，保障人民生命财产安全，我国政府及相关部门对建筑结构抗震研究给予了高度重视。
本实验报告针对倒立摆实验在建筑结构抗震研究中的应用，分析了倒立摆实验的基本原理、实验方法、实验结果及其在建筑结构抗震研究中的应用前景。
二、倒立摆实验原理倒立摆实验是一种研究建筑结构抗震性能的有效方法。
它利用倒立摆的稳定性原理，模拟地震作用下的建筑物振动响应，从而评估建筑结构的抗震能力。
倒立摆实验系统由摆杆、质量块、基础和支撑装置组成。
当摆杆在一定角度范围内摆动时，质量块产生的惯性力使摆杆保持倒立状态。
通过调整摆杆长度、质量块质量和基础刚度等参数，可以模拟不同建筑结构的抗震性能。
三、实验方法本实验采用数值模拟与实验相结合的方法，研究倒立摆实验在建筑结构抗震研究中的应用。
首先，建立倒立摆实验的数值模型，分析摆杆长度、质量块质量和基础刚度等参数对建筑结构抗震性能的影响。
然后，设计并实施倒立摆实验，验证数值模型的准确性。
最后，根据实验结果，提出提高建筑结构抗震能力的措施。
四、实验结果与分析1.数值模拟结果通过数值模拟，得到了不同参数下建筑结构的抗震性能。
结果表明，摆杆长度、质量块质量和基础刚度对建筑结构的抗震性能有显著影响。
摆杆长度越长，建筑结构的抗震能力越强；质量块质量越大，建筑结构的抗震能力越弱；基础刚度越大，建筑结构的抗震能力越强。
2.实验结果根据实验方案，进行了倒立摆实验。
实验结果表明，倒立摆实验可以有效地模拟建筑结构在地震作用下的振动响应。
通过对比实验结果与数值模拟结果，验证了数值模型的准确性。
同时，实验结果也表明，倒立摆实验可以评估建筑结构的抗震能力，为建筑结构设计提供依据。
五、建筑结构抗震研究展望倒立摆实验作为一种有效的建筑结构抗震研究方法，具有广泛的应用前景。
未来研究方向主要包括：1.进一步优化倒立摆实验系统，提高实验精度和可靠性。
倒立摆实验报告
实验报告姓名：王琳学号：12030078一、控制对象描述本实验的控制对象是二级倒立摆系统，它主要由机电装置和控制装置两部分组成，机电装置的结构主要由小车、两根摆杆及连接轴构成。
假设系统中的每一根摆杆都是匀质刚体，忽略实验中的摩擦力，驱动力与放大器的输入成正比且无延迟地直接作用于小车上。
设定摆杆竖直向上时，下摆杆角位移、上摆杆角位移均为零，摆杆顺时针旋转为正。
下图为二级倒立摆模型。
二、系统建模设x为小车质量，下摆杆质量为M1l1，上摆杆质量为M2，转动惯量为J1，上摆杆重心到转轴b 间的长度l2，小车与地面摩擦力系数f ，下摆杆转轴a 与b 间的长度L ，重力加速度g 。
运用牛顿力学定律建立方程：2212112211222222()()cos ()sin cos sin F f x m M M x M l M l M l M l M l M l ααααββββ∙∙∙∙∙∙∙=+++++-++-222222222222222222222222222sin cos sin sin sin 2sin cos sin cos sin cos cos cos cos J M gl M Ll M Ll M l M l M l x M Ll M Ll M l ββαβααβαββββββαβααβαββ∙∙∙∙∙∙∙∙∙∙=+∙+∙+∙+∙-+∙-∙-∙222221111122222222221111222222222sin sin sin 2sin sin sin sin cos sin sin cos cos cos cos cos sin cos cos J M gl M l M gL M L M L M Ll M Ll M l x M l M L x M L M Ll M Ll ααααααβααααββαββαααααααββαββ∙∙∙∙∙∙∙∙∙∙∙∙∙∙=+∙++∙+∙+∙+∙--∙-∙-∙+∙-∙经过线性化得到如下式子：12112222()()F f x m M M x M l M l M l αβ∙∙∙∙∙∙∙=++++++ 2222222222J M gl M l x M Ll M l ββαβ∙∙∙∙∙∙=---22111211211222()()()J M gl M gL M l M L x M l M L M Ll αααβ∙∙=+-+-+-参数取值：g=9.8；m=1.328；M1=0.22；M2=0.187；l1=0.303；l2=0.2261122334455660100000016.7 1.300.100.70001000039.118.107.90 1.70000010068.514.4025.900.3x x x x x x F x x x x x x ∙∙∙∙∙∙⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ 123456100000001000000010000000100000001000000010x x x x x Y F x x x ααββ∙∙∙⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦可以得到A 、B 、C 、D ：10000016.7 1.300.10000100039.118.107.90000001068.514.425.90A ⎡⎤⎢⎥--⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦00.701.700.3B ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦100000010000001000000100000010000001C ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦000000D ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦三、系统分析与控制器设计采用线性二次型最优控制器(linearquadraticregulator —LQR)对系统进行控制。
倒立摆实验报告(现代控制理论)
现代控制理论实验报告——倒立摆小组成员：指导老师：2013.5实验一建立一级倒立摆的数学模型一、实验目的学习建立一级倒立摆系统的数学模型，并进行Matlab仿真。
二、实验内容写出系统传递函数和状态空间方程，用Matlab进行仿真。
三、Matlab源程序及程序运行的结果（1）Matlab源程序见附页（2）给出系统的传递函数和状态方程（a）传递函数gs为摆杆的角度：>> gsTransfer function:2.054 s-----------------------------------s^3 + 0.07391 s^2 - 29.23 s - 2.013（b）传递函数gspo为小车的位移传递函数：>> gspoTransfer function:0.7391 s^2 - 20.13---------------------------------------s^4 + 0.07391 s^3 - 29.23 s^2 - 2.013 s（c）状态矩阵A,B,C,D：>> sysa =x1 x2 x3 x4x1 0 1 0 0x2 0 -0.07391 0.7175 0x3 0 0 0 1x4 0 -0.2054 29.23 0b =u1x1 0x2 0.7391x3 0x4 2.054c =x1 x2 x3 x4y1 1 0 0 0y2 0 0 1 0d =u1y1 0y2 0Continuous-time model.（3）给出传递函数极点和系统状态矩阵A的特征值（a）传递函数gs的极点>> PP =5.4042-5.4093-0.0689（b）传递函数gspo的极点>> PoPo =5.4042-5.4093-0.0689（c）状态矩阵A的特征值>> EE =-0.06895.4042-5.4093（4）给出系统开环脉冲响应和阶跃响应的曲线（a）开环脉冲响应曲线（b）阶跃响应曲线四、思考题（1）由状态空间方程转化为传递函数，是否与直接计算传递函数相等？答：由状态空间方程转化为传递函数：>> gso=tf(sys)Transfer function from input to output...0.7391 s^2 - 6.565e-016 s - 20.13#1: ---------------------------------------s^4 + 0.07391 s^3 - 29.23 s^2 - 2.013 s2.054 s + 4.587e-016#2: -----------------------------------s^3 + 0.07391 s^2 - 29.23 s - 2.013#1为gspo传递函数，#2为gs的传递函数而直接得到的传递函数为：>> gspoTransfer function:0.7391 s^2 - 20.13---------------------------------------s^4 + 0.07391 s^3 - 29.23 s^2 - 2.013 s>> gsTransfer function:2.054 s-----------------------------------s^3 + 0.07391 s^2 - 29.23 s - 2.013通过比较可以看到，gspo由状态空间方程转化的传递函数比直接得到的传递函数多了s的一次项，而6.565e-016非常小几乎可以忽略不计，因此可以认为两种方法得到的传递函数式相同的，同理传递函数gs也可以认为是相同的。
倒立摆实验报告
直线二级倒立摆实验报告目录第1章倒立摆简介 (1)1.1倒立摆设备介绍 (1)第2章直线二级倒立摆的建模及仿真 (2)2.1直线二级倒立摆的数学模型 (2)2.2.1拉格朗日方法建模 (2)2.1.2系统的阶跃响应分析 (4)第3章相关极点设计的MATLAB仿真 (6)3.1远距离的闭环极点仿真 (6)3.2近距离极点的仿真 (6)第4章不同RQ值的MATLAB仿真 (7)4.1不同RQ值仿真 (7)结论 (10)直线二级倒立摆实验报告第1章倒立摆简介1.1 倒立摆设备介绍倒立摆是进行控制理论研究的典型实验平台。
由于倒立摆系统的控制策略和杂技运动员顶杆平衡表演的技巧有异曲同工之处，极富趣味性，而且许多抽象的控制理论概念如系统稳定性、可控性和系统抗干扰能力等等，都可以通过倒立摆系统实验直观的表现出来，因此在欧美发达国家的高等院校，它已成为必备的控制理论教学实验设备。
学习自动控制理论的学生通过倒立摆系统实验来验证所学的控制理论和算法，非常的直观、简便，在轻松的实验中对所学课程加深了理解。
倒立摆不仅仅是一种优秀的教学实验仪器，同时也是进行控制理论研究的理想实验平台。
由于倒立摆系统本身所具有的高阶次、不稳定、多变量、非线性和强耦合特性，许多现代控制理论的研究人员一直将它视为典型的研究对象，不断从中发掘出新的控制策略和控制方法，相关的科研成果在航天科技和机器人学方面获得了广阔的应用。
二十世纪九十年代以来，更加复杂多种形式的倒立摆系统成为控制理论研究领域的热点，每年在专业杂志上都会有大量的优秀论文出现。
深圳市元创兴科技有限公司为高等院校的自动控制教学提供了整套基于倒立摆系统的实验解决方案。
包括各种摆的开发生产、实验内容的安排和配置，以及对应的自动控制理论教学内容和相关经典教材的推荐。
元创兴科技开发生产的倒立摆系列包括直线运动型、圆周运动型和复合倒立摆三个大系列，主要特点包括：开放性：采用四轴运动控制板卡，机械部分和电气部分非常容易扩展，可以根据用户需要进行配置。
线性系统倒立摆实验（5篇材料）
线性系统倒立摆实验（5篇材料）第一篇：线性系统倒立摆实验直线倒立摆控制及一级正摆位移和角度控制一、实验目的（1）在Matlab Simulink环境下实现控制伺服电机；（2）完成直线倒立摆建模、仿真与分析；（3）通过控制器设计使倒立摆系统稳定运行（摆角保持零度附近）：二、实验内容及要求（1）状态空间极点配置控制实验（一组极点为书上指定，任选另一组，但保证控制效果要好于前者）具体记录要求：在稳定后（先截一张图），叠加一扰动（仅角度扰动），记录消除扰动的过程（再截一张图），同时记录你所选择的期望极点组。
（2）线性二次最优控制LQR 控制实验（R,Q选择为书上指定，任选另一组，但保证控制效果要好于前者）具体记录要求：在稳定后（先截一张图），叠加一扰动（仅角度扰动），记录消除扰动的过程（再截一张图），同时记录你所选择的R，Q取值。
（3）一级正摆位移和角度控制借助于正摆实验平台，构思、设计控制策略和控制算法，并编程实现，通过实验设备将物体快速、准确地运输到指定的位置，且在吊运的整个过程（起吊，运输，到达目的地）保持较小的摆动角。
要求：系统启动后，在当前位置给正摆施加一角度扰动，当平衡（摆角为零）后，让小车直线运行30厘米，并快速保证平衡(摆角为零)。
三、实验过程1.实验方法（1）Matlab Simulink仿真环境下精确控制电机在MATLAB Simulink仿真环境中，建立模型，然后进行仿真并分析结果。
（2）直线倒立摆建模、仿真与分析利用牛顿力学进行受力分析，然后建立直线一级倒立摆系统的数学模型；进行仿真分析。
（3）状态空间极点配置控制实验进入MATLAB Simulink 实时控制工具箱“Googol Education Products”打开“Inverted PendulumLinear Inverted PendulumLinear 1-Stage IP Experiment PolesExperiments”中的“Poles Control M File1”。
倒立摆实验报告
《线性系统理论》课程——倒立摆实验报告基本情况实验完成了基本要求，通过pid、极点配置、根轨迹、和ldr方法调试运行一级倒立摆，设计新的pid参数，调试运行状态，逐渐使一级倒立摆稳定，完成了实验的基本要求。
在对一级倒立摆完成实验的基础上，进一步对二级倒立摆进行了分析研究。
这其中的工作主要包括针对LDR方法运行demo，观察系统稳定性，快速性，调整系统参数，查看有什么问题，并且针对问题提出修改意见。
在多次试验后，对系统有了进一步的了解，便开始着手二级倒立摆极点配置方法的实现问题。
这部分继续学习了极点配置的方法，通过编写m文件，计算K，仿真运行系统，查看系统图像，查看调节时间，超调量等。
逐渐调试参数，使系统指标顺利达到。
最后是进行试验，进一步调整系统参数。
在这一个过程中，经验很重要，同时偶然因素也起到了重要的作用。
所以调试一个系统真的不容易。
这一部分的内容在第六节中进行了较为详细的介绍收获对倒立摆的系统原理有了更深层次的了解掌握了pid、极点配置、根轨迹、ldr方法设计系统学会了一些调试运行系统的经验加强了和同学之间的交流，锻炼了软件实现编程能力改进意见这里我有一个小小的建议，这是我在做实验的时候遇到了问题总结。
系统参数含义还不是很清楚。
在这个方面尤其是参数对应着系统的具体实际含义不明确，只能在尝试凑参数，有时出现了一个问题，不知道是哪个参数引起的，所以影响了效率，结果也不是很明显。
改进意见：共有四次实验，第一次实验安排不变但是试验后，负责人要收集问题，主要是要老师来解决的，在第二次实验前针对上一次的问题进行集体讲解一下，尤其是与物理的联系，不要仅仅是自己做实验吧，第三次和第一次相同，第四次与第二次相同。
在这个完成后，如果课堂有时间，可以进行了一个小小的试验心得介绍，和大家交流心得体会。
或者是老师统一解决一下这个总体过程中的问题，我觉得这样结果会更好一点。
下面是具体的详细报告一、倒立摆系统介绍倒立摆是机器人技术、控制理论、计算机控制等多个领域、多种技术的有机结合，其被控系统本身又是一个绝对不稳定、高阶次、多变量、强耦合的非线性系统，可以作为一个典型的控制对象对其进行研究。
倒立摆仿真报告
计算机控制系统课题报告1.倒立摆基本背景：倒立摆，Inverted Pendulum ，是典型的多变量、高阶次，非线性、强耦合、自然不稳定系统。
倒立摆系统的稳定控制是控制理论中的典型问题，在倒立摆的控制过程中能有效反映控制理论中的许多关键问题，如非线性问题、鲁棒性问题、随动问题、镇定、跟踪问题等。
因此倒立摆系统作为控制理论教学与科研中典型的物理模型，常被用来检验新的控制理论和算法的正确性及其在实际应用中的有效性。
从 20 世纪 60 年代开始，各国的专家学者对倒立摆系统进行了不懈的研究和探索。
倒立摆系统按摆杆数量的不同，可分为一级，二级，三级倒立摆等，多级摆的摆杆之间属于自由连接（即无电动机或其他驱动设备）。
由中国的大连理工大学李洪兴教授领导的“模糊系统与模糊信息研究中心”暨复杂系统智能控制实验室采用变论域自适应模糊控制成功地实现了四级倒立摆。
因此，中国是世界上第一个成功完成四级倒立摆实验的国家。
倒立摆的控制问题就是使摆杆尽快地达到一个平衡位置，并且使之没有大的振荡和过大的角度和速度。
当摆杆到达期望的位置后，系统能克服随机扰动而保持稳定的位置。
2.倒立摆模型分析倒立摆系统的输入为小车的位移（即位置）和摆杆的倾斜角度期望值，计算机在每一个采样周期中采集来自传感器的小车与摆杆的实际位置信号，与期望值进行比较后，通过控制算法得到控制量，再经数模转换驱动直流电机实现倒立摆的实时控制。
直流电机通过皮带带动小车在固定的轨道上运动，摆杆的一端安装在小车上，能以此点为轴心使摆杆能在垂直的平面上自由地摆动。
作用力F平行于铁轨的方向作用于小车，使杆绕小车上的轴在竖直平面内旋转，小车沿着水平铁轨运动。
当没有作用力时，摆杆处于垂直的稳定的平衡位置（竖直向下）。
为了使杆子摆动或者达到竖直向上的稳定，需要给小车一个控制力，使其在轨道上被往前或朝后拉动。
我们的分析对象是一阶倒立摆。
很多国内实验都说可以合理的假设空气阻力为0，但查阅了更多的文献和真正仿真做出模型并在网络上开源的一些实验后，我认为这是不正确的。
毕业设计 二级倒立摆建模
四川理工学院毕业设计（论文）二级倒立摆系统建模与仿真学生：学号：专业：自动化班级：自动化指导教师：四川理工学院自动化与电子信息学院二O一一年六月摘要常规的PID控制从理论上可以控制二级倒立摆，但在实际中对PID控制器参数的整定为一难点。
本文针对二级倒立摆系统单输入三输出的不稳定系统，通过三回路PID 控制方案，来完成对倒立摆的控制。
利用状态反馈极点配置的方法来对参数进行整定，解决PID参数整定的难点。
然后借助于MATLAB中的Simulink模块对所得的参数进行仿真，结果表明三回路PID控制是成功的，参数的有效性，也证实了这种参数整定方法简单实用。
并通过配置不同位置的极点，对其结果进行分析得到极点配置的最佳配置方案。
关键词：倒立摆；PID；状态反馈； MATLABABSTRACTDouble Inverted Pendulum System Modeling and SimulationConventional PID control theory to control the inverted pendulum, but in practice the parameters of PID controller tuning is a difficult. In this paper, double inverted pendulum system, the instability of single-input three-output system, through the three-loop PID control program to complete the inverted pendulum control.Pole placement using state feedback approach to setting the parameters to resolve the difficulties PID parameter tuning. With MATLAB and Simulink in the module parameters obtained from simulation results show that the three-loop PID control is successful, the effectiveness of the parameters, but also confirms this tuning method is simple and practical.Different locations through the pole configuration, the results were too extreme configuration of the best configuration.Key words:pendulum；PID control ；state feedback；MATLAB目录摘要............................................................... ABSTRACT (I)第1章引言 01.1 倒立摆研究的目的及意义 01.2 倒立摆的发展史和研究现状 01.3本文的主要工作 (3)第2章倒立摆的建模 (3)2.1 二级倒立摆的简介及物理模型 (3)2.2 二级倒立摆计算机控制系统结构 (4)2.3 二级倒立摆的数学模型 (5)2.4根据牛顿力学、刚体动力学列写二级倒立摆的数学模型 (6)第3章控制策略的选择 (11)3.1 MATLAB简介 (11)3.2该系统的能控、能观及稳定性的分析 (14)3.2.1系统的能控性 (14)3.2.2系统能观性 (16)3.2.3系统的稳定性 (16)3.3 确定控制策略 (17)3.4 控制器参数整定方法 (17)3.5 通过状态反馈极点配置法来整定参数 (19)第4章计算机仿真及结果分析 (22)4.1 Matlab下Simulink模块简介 (22)4.2 在Simulink下的仿真 (23)4.3对仿真结果的分析 (31)第5章结束语 (32)致谢 (33)参考文献 (34)第1章引言1.1 倒立摆研究的目的及意义在控制理论发展的过程中, 一种理论的正确性及在实际应用中的可行性，往往需要一个典型对象来验证, 并比较各种控制理论之间的优劣, 倒立摆系统就是这样的一个可以将理论应用于实际的理想实验平台。
二级倒立摆系统
新疆大学实验报告(设计)题目: 《线性系统理论》实验报告****: **学生姓名：***学生学号： ************ 所属院系：电气工程学院专业：控制科学与工程班级：控制工程2018级完成日期：2018年12月19日二级倒立摆系统一、实验目的1. 掌握能控性和能观测性的概念，学会用MATLAB判断能控能观测性；2. 掌握稳定性的概念，学会用MATLAB判断稳定性；3. 掌握线性系统状态方程解的结构，学会用MATLAB求解线性时不变系统的状态方程和输出响方程的解，并绘制相应曲线；4. 对于给定对象的性能指标，掌握对系统进行综合方法。
二、主要实验设备及仪器1．计算机一台2．MATLAB软件三、实验内容1.系统的模型本次实验的系统的实物模型如下所示：图1-1 系统模型其中部分参数解释如下：x代表小车位移;θ1代表摆杆1与竖直方向的夹角；θ2代表摆杆2与竖直方向的夹角；l1代表摆杆1的长度；l2代表摆杆2的长度；m1代表摆杆1的质量；m2代表摆杆2的质量；m3代表摆杆1和摆杆2之间连接的质量；M代表小车的质量；经查文献，得到系统的状态空间模型如下所示：[ ẋθ1θ2ẍθ1θ2] =⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0.5335- 0.9825 21.6317- 102.0255 123.5638- 00.3119 0.7292- 70.7948 44.3562- 114.8425 00.02- 0.0624 20.2945 - 1.2821 11.689- 01 0 0 0 0 00 1 0 0 0 00 0 1 0 0 0[ x θ1θ2ẋθ1θ2] +Buy=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000100000010000001[ xθ1θ2ẋθ1θ2]+u 其中：B=[0 0 0 1.6236 −5.6636 1.7305]T2.系统的模型分析2.1 能控性分析根据秩判据定理，在n 维连续时间线性时不变系统中，构造的能控性矩阵M 的秩等于n 时，系统完全能控，否则，系统不能控。
哈工大倒立摆实验报告
研究生自动控制专业实验地点：A区主楼518房间平面二级倒立摆系统实验报告主编：钱玉恒，杨亚非哈工大航天学院控制科学实验室平面二级倒立摆控制系统实验报告一、实验内容1、熟悉平面二级倒立摆控制系统的结构和原理；2、了解平面二级倒立摆物理模型建模与控制器设计；3、掌握LQR控制器仿真与实验；二、实验设备1、平面二级倒立摆控制系统一套平面二级倒立摆控制系统包括平面二级倒立摆控制器、平面二级倒立摆本体实验装置等组成。
在平面二级倒立摆本体上有起动/停止电源开关，螺旋浆起动/停止开关。
2、平面二级倒立摆控制系统计算机部分平面二级倒立摆控制系统计算机部分主要有计算机、SV-400控制卡等；三、实验步骤1、系统实验的线路连接平面二级倒立摆本体与计算机全部采用标准线连接，电源部分有标准电源线，在试验前，实验装置的线路已经连接完毕。
2、启动实验装置通电之前，请详细检察电源等连线是否正确，确认无误后，可接平面二级倒立摆本体电源，随后起动计算机和控制器。
3、系统实验的参数调试根据仿真的数据及控制规则进行参数调试，直到获得较理想参数为止。
四、实验要求1、学生上机前要求学生在实际上机调试之前，必须用自己的计算机，对系统的仿真全部做完，并且经过老师的检查许可后，才能申请上机调试。
2、学生上机要求上机的同学要按照要求进行实验，不得有违反操作规程的现象，严格遵守实验室的有关规定。
五、实验结果与分析 经过实际调试，实验结果如下：当LQR 控制参数为：14.142x K =， 15.722a K =， 74.93b K = ,29.49x K =， ,196.29a K =， ,34.83b K =系统的时间运行曲线如图1、图2所示。
图1 第一组参数X 方向实际运动曲线图2 第二组参数Y 方向实际运动曲线从图1、图2中可以看出，X 方向控制较好，但Y 方向控制的波动幅度比较大，为此，需要进一步调整LQR 控制参数。
经过多次试验，得到如下一组比较好的控制参数：14.142x K =， 15.892a K =， 77.71b K = ,30.018x K =， ,193.73a K =， ,33.355b K =该组参数下，系统的实际运行曲线如下图3、图4所示。
倒立摆线性二次型控制实验报告
（3）
x 0 0 Q11 x 0 0 1 ，x ，令 Q ,B 0 0 0 0 0 0 29.4 0 3 0
0 0 ，R=4， 0 Q22 0 0 0 0
设系统的状态方程为
: y Cx
x Ax Bu
x 0 x 0 x ， A 0 0
tf
1 0
0 0 1 0 ， B ， C 1 0 0 0 ， 其 性 能 指 标 为 0 0 0 0 0 29.4 0 3 0 0
0
-0.02
-0.04 0
0.5
1
1.5 t(s)
2
2.5
3
图 9
从这两张结果中可以看出， 仿真的效果和上面类比分析的结果不太吻合。 其实， 仔细分析可以发现，Q11 和 Q22 变化时，如果按照严格对应的规则,即 Q11 为小车 的位置权系数，Q22 为摆杆角度的权系数，对应的仿真初始扰动也应该分别为位置
0.3
0.25
0.2 Q11= 100
position(m)
0.15
Q11= 200 Q11= 500 Q11= 1000 Q11= 2000
0.1
0.05
0
-0.05 0
0.5
1
1.5 t(s)
2
2.5
3
图 4
0.1 0.08 0.06 0.04
theta(rad)
0.02 0 -0.02 -0.04 -0.06 0
图 0-1 一级倒立摆的物理模型
其中， M —小车质量， m —摆杆质量， b —小车摩擦系数， l —摆杆转动轴心 到杆质心的长度， I —摆杆惯量， F —加在小车上的力， x —小车位置， —摆杆 与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下）。 小车和摆杆的动能分别为
二阶倒立摆实验报告
研究生课程报告二阶倒立摆的控制二阶倒立摆的控制指导老师：屈桢深问题描述小车质量0.8kg，摆杆1质量0.3kg, 摆杆长度1.0m；摆杆2质量0.1kg, 摆杆长度0.5m。
要求：设计NN控制器，满足指标要求：0.2Hz正弦信号幅值裕度<10%, 相角裕度<15度。
同时系统具备抗噪声和干扰性，控制输入合理步骤：1阶倒立摆->2阶倒立摆。
一阶倒立摆建模小车由电机通过同步带驱动在滑杆上来回运动，保持摆杆平衡。
电机编码器和角编码器向运动卡反馈小车和摆杆位置（线位移和角位移）。
小车在轨道上可以自由滑动。
单级倒立摆系统数学模型N 和P 分别为小车与摆杆相互作用力的水平和垂直方向的分量。
分析小车水平方向所受的合力，可得到方程为：N x b F x M --=&&&由摆杆水平方向的受力进行分析可以得到下面等式：()θθθθθsin cos sin 222&&&&&ml ml x m N l x dtd m N -+=+= 把这个等式代入式中，得到系统的第一个运动方程：()F ml ml x b x m M =-+++θθθθsin cos 2&&&&为了推出系统的第二个运动方程，对摆杆垂直方向的合力进行分析，得到下面的方程：()θcos 22l dtd m mg P =-θθθθcos sin 2&&ml ml mg P --=-力矩平衡方程如下：θθ&&I Nl Pl =--cos sin方程中力矩的方向，θφθφsin sin ,cos cos -=-=，故等式前面有负号。
合并这两个方程，约去P 和N ，得到第二个运动方程：()θθθcos sin 2x ml mgl ml I &&&&-=++假设φ与1（单位是弧度）相比很小，即1〈〈φ，则可进行近似处理：0,sin ,1cos 2=⎪⎭⎫⎝⎛-=-=dt d θφθθ用u 代表被控对象的输入力，线性化后两个运动方程如下：()()⎪⎩⎪⎨⎧=-++=-+u ml x b x m M x ml mgl ml I φφφ&&&&&&&&&2 对方程（7）进行拉普拉斯变换，得到：()()⎪⎩⎪⎨⎧=-++=-+)()()()()()()(22222s U s s ml s s bX s s X m M s s mlX s mgl s s ml I φφφ 推导时假设初始条件为0则摆杆角度和小车位移的传递函数为：mgls ml I mls s X s -+=222)()()(φ 摆杆角度和小车加速度之间的传递函数为：()mgls ml I mls A s -+=22)()(φ摆杆角度和小车所受外界作用力的传递函数：22432222()()()()()()ml ss qb I ml M m mgl bmgl F s s s s sq q qq M m I ml m l φ=+++--⎡⎤=++-⎣⎦以外界作用力作为输入的系统状态空间表达式为：22222222220100()00()()0001()00()()0()0()x x I ml b m gl x x I M m Mml I M m Mml mlb mgl M m I M m Mml I M m Mml I ml I M m Mml uml I M m Mml φφφφ⎡⎤⎢⎥⎡⎤⎡⎤-+⎢⎥⎢⎥⎢⎥⎢⎥++++⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+⎣⎦⎣⎦⎢⎥++++⎣⎦⎡⎤⎢⎥+⎢⎥⎢⎥+++⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦&&&&&&&&1000000100x x x y u φφφ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦&& 以小车加速度作为输入的系统系统状态空间表达式：'010000000100010330044x x x x u g ll φφφφ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦&&&&&&'1000000100x x x y u φφφ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦&& 2系统的可控性、可观测性分析 对于连续时间系统：Bu AX X+=& Du CX y +=系统状态完全可控的条件为：当且仅当向量组BA AB B n 1,...,,-是线性无关的，或n ×n 维矩阵[]BA AB B n 1-M ΛM M的秩为n 。
二阶倒立摆实验报告.doc
ml2(s) s2
mgl (s)
mlX ( s)s2
M
m X (s)s2
bX (s) s
ml ( s)s2
U (s)
推导时假设初始条件为0则摆杆角度和小车位移的传递函数
为：
(s)mls2
X (s)(Iml2) s2mgl
摆杆角度和小车加速度之间的传递函数为：
( s)ml
A(s)Iml2s2mgl
摆杆角度和小车所受外界作用力的传递函数：
Mml2
I (M
m)
Mml2
I ( M
0
I
ml2
I (M
m)
Mml2
0
u
ml
I (M
m)
Mml2
x
x
1
0
0
&
0
y
0 x
u
0
0
1
0
0
&
以小车加速度 作为输入的系统系统状态空间表达式：
&
0
1
0
0
x
0
x
0
0
0
0
1
&&x
x&
u'
0
0
0
1
0
&
0
0
3g
0
&
3
4l
4l
x
x
1
0
0
0
&
0
y
x
u'
0
0
1
0
0
&
2系统的可控性、可观测性分析
2cos2
x
倒立摆实验报告建筑起重机械稳定性分析
建筑起重机械稳定性分析——倒立摆实验报告一、引言随着我国经济的快速发展，建筑行业取得了举世瞩目的成就。
在高层建筑、大型基础设施等项目中，起重机械发挥着举足轻重的作用。
然而，起重机械在施工现场的安全事故时有发生，其中稳定性问题尤为突出。
为了提高起重机械的稳定性，降低事故风险，本文以倒立摆实验为研究对象，分析建筑起重机械的稳定性问题，并提出相应的改进措施。
二、实验原理与方法1.实验原理倒立摆实验是一种研究物体在重力作用下保持稳定的实验方法。
在本实验中，将起重机械简化为倒立摆模型，通过改变摆长、摆重等参数，研究起重机械在受到外部扰动时的稳定性。
2.实验方法（1）搭建实验装置：采用一根细杆作为摆杆，一端固定，另一端悬挂重物，模拟起重机械的吊臂和吊重。
（2）测量摆长：通过测量摆杆长度，确定摆长参数。
（3）施加外部扰动：在摆杆上施加不同大小的横向力，模拟施工现场的外部扰动。
（4）观察摆动情况：记录摆杆在受到外部扰动时的摆动幅度和摆动周期，分析稳定性变化。
三、实验结果与分析1.摆长对稳定性的影响实验结果显示，摆长越长，起重机械的稳定性越差。
这是因为摆长越长，摆动周期越长，抵抗外部扰动的能力减弱。
因此，在设计起重机械时，应合理选择吊臂长度，以提高稳定性。
2.摆重对稳定性的影响实验结果显示，摆重越大，起重机械的稳定性越好。
这是因为摆重越大，摆杆受到的外部扰动产生的摆动幅度越小。
因此，在施工现场，应合理配置吊重，提高起重机械的稳定性。
3.外部扰动对稳定性的影响实验结果显示，外部扰动越大，起重机械的稳定性越差。
这是因为外部扰动会破坏起重机械的平衡状态，导致摆动幅度增大。
因此，在施工现场，应尽量减少外部扰动，确保起重机械的稳定性。
四、改进措施与建议1.优化设计参数根据实验结果，合理选择吊臂长度和吊重，以提高起重机械的稳定性。
在设计过程中，可以采用现代设计方法，如有限元分析、优化算法等，寻找最佳设计参数。
2.提高制造质量加强起重机械制造过程的质量控制，确保零部件的精度和强度。
倒立摆仿真及实验报告
最优控制实验报告二零一五年一月目录第1章一级倒立摆实验 (3)1.1 一级倒立摆动力学建模 (3)1.1.1 一级倒立摆非线性模型建立 (3)1.1.2 一级倒立摆线性模型建立 (5)1.2 一级倒立摆t∞状态调节器仿真 (5)1.3 一级倒立摆t∞状态调节器实验 (10)1.4 一级倒立摆t∞输出调节器仿真 (12)1.5 一级倒立摆t∞输出调节器实验 (14)1.6 一级倒立摆非零给定调节器仿真 (16)1.7 一级倒立摆非零给定调节器实验 (17)第2章二级倒立摆实验 (18)2.1 二级倒立摆动力学模型 (18)2.1.1 二级倒立摆非线性模型建立 (18)2.1.2 二级倒立摆线性模型建立 (19)2.2 二级倒立摆t∞状态调节器仿真 (20)2.3 二级倒立摆t∞状态调节器实验 (23)2.4 二级倒立摆t∞输出调节器仿真 (24)2.5 二级倒立摆t∞输出调节器实验 (24)2.6 二级倒立摆非零给定调节器仿真 (25)2.7 二级倒立摆非零给定调节器实验 (26)第1章一级倒立摆实验1.1一级倒立摆动力学建模在忽略了空气阻力和各种摩擦之后，可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统，如图所示图1-1 直线一级倒立摆模型M小车质量1.096 kg；m 摆杆质量0.109 kg；b 小车摩擦系数0 .1N/m/sec；l 摆杆转动轴心到杆质心的长度0.25m；I 摆杆惯量0.0034 kg·m2；φ摆杆与垂直向上方向的夹角，规定角度逆时针方向为正；x 小车运动位移，规定向右为正。
1.1.1一级倒立摆非线性模型建立采用拉格朗日方法，系统的拉格朗日方程为：()()()&&&(1.1)=-L q q T q q V q q,,,其中，L 为拉格朗日算子，q 为系统的广义坐标，T 为系统的动能，V 为系统的势能。
拉格朗日方程由广义坐标i q 和L 表示为：i i id L Lf dt q q ∂∂-=∂∂& (1.2)i f 为系统沿该广义坐标方向上的外力，在本系统中，系统的两个广义坐标分别为φ和x 。
倒立摆实验报告
《线性系统理论》课程——倒立摆实验报告基本情况实验完成了基本要求，通过pid、极点配置、根轨迹、和ldr方法调试运行一级倒立摆，设计新的pid参数，调试运行状态，逐渐使一级倒立摆稳定，完成了实验的基本要求。
在对一级倒立摆完成实验的基础上，进一步对二级倒立摆进行了分析研究。
这其中的工作主要包括针对LDR方法运行demo，观察系统稳定性，快速性，调整系统参数，查看有什么问题，并且针对问题提出修改意见。
在多次试验后，对系统有了进一步的了解，便开始着手二级倒立摆极点配置方法的实现问题。
这部分继续学习了极点配置的方法，通过编写m文件，计算K，仿真运行系统，查看系统图像，查看调节时间，超调量等。
逐渐调试参数，使系统指标顺利达到。
最后是进行试验，进一步调整系统参数。
在这一个过程中，经验很重要，同时偶然因素也起到了重要的作用。
所以调试一个系统真的不容易。
这一部分的内容在第六节中进行了较为详细的介绍收获对倒立摆的系统原理有了更深层次的了解掌握了pid、极点配置、根轨迹、ldr方法设计系统学会了一些调试运行系统的经验加强了和同学之间的交流，锻炼了软件实现编程能力改进意见这里我有一个小小的建议，这是我在做实验的时候遇到了问题总结。
系统参数含义还不是很清楚。
在这个方面尤其是参数对应着系统的具体实际含义不明确，只能在尝试凑参数，有时出现了一个问题，不知道是哪个参数引起的，所以影响了效率，结果也不是很明显。
改进意见：共有四次实验，第一次实验安排不变但是试验后，负责人要收集问题，主要是要老师来解决的，在第二次实验前针对上一次的问题进行集体讲解一下，尤其是与物理的联系，不要仅仅是自己做实验吧，第三次和第一次相同，第四次与第二次相同。
在这个完成后，如果课堂有时间，可以进行了一个小小的试验心得介绍，和大家交流心得体会。
或者是老师统一解决一下这个总体过程中的问题，我觉得这样结果会更好一点。
下面是具体的详细报告一、倒立摆系统介绍倒立摆是机器人技术、控制理论、计算机控制等多个领域、多种技术的有机结合，其被控系统本身又是一个绝对不稳定、高阶次、多变量、强耦合的非线性系统，可以作为一个典型的控制对象对其进行研究。
(完整版)倒立摆实验报告
机械综合设计与创新实验（实验项目一）二自由度平面机械臂三级倒立摆班级：姓名：学号：指导教师：时间：综述倒立摆装置是机器人技术、控制理论、计算机控制等多个领域、多种技术的有结合，被公认为自动控制理论中的典型实验设备，也是控制理论教学和科研中不可多得的典型物理模型。
倒立摆的典型性在于：作为实验装置，它本身具有成本低廉、结构简单、便于模拟、形象直观的特点；作为被控对象，它是一个高阶次、不稳定、多变量、非线性、强耦合的复杂被控系统，可以有效地反映出控制中的许多问题；作为检测模型，该系统的特点与机器人、飞行器、起重机稳钩装置等的控制有很大的相似性[1]。
倒立摆系统深刻揭示了自然界一种基本规律，即一个自然不稳定的被控对象，运用控制手段可使之具有良好的稳定性。
通过对倒立摆系统的研究，不仅可以解决控制中的理论问题，还能将控制理论所涉及的三个基础学科，即力学、数学和电学（含计算机）有机的结合起来，在倒立摆系统中进行综合应用。
在多种控制理论与方法的研究和应用中，特别是在工程实践中，也存在一种可行性的试验问题，将其理论和方法得到有效的经验，倒立摆为此提供一个从控制理论通往实践的桥梁[2]。
因此对倒立摆的研究具有重要的工程背景和实际意义。
从驱动方式上看，倒立摆模型大致可分为直线倒立摆模型、旋转倒立摆模型和平面倒立摆模型。
对于每种模型，从摆杆的级数上又可细分为一级倒立摆、二级倒立摆和多级倒立摆[3]。
目前，国内针对倒立摆的研究主要集中在运用倒立摆系统进行控制方法的研究与验证，特别是针对利用倒立摆系统进行针对于非线性系统的控制方法及理论的研究。
而倒立摆系统与工程实践的结合主要体现在欠驱动机构控制方法的验证之中。
此外，倒立摆作为一个典型的非线性动力系统，也被用于研究各类非线性动力学问题。
在倒立摆系统中成功运用的控制方法主要有线性控制方法，预测控制方法及智能控制方法三大类。
其中，线性控制方法包括PID控制、状态反馈控和LQR 控制等；预测控制方法包括预测控制、分阶段起摆、变结构控制和自适应神经模糊推理系统等，也有文献将这些控制方法归类为非线性控制方法；智能控制方法主要包括神经网络控制、模糊控制、遗传算法、拟人智能控制、云模型控制和泛逻辑控制法等。
倒立摆带降维观测器实验报告
一、实验目的和要求（1）了解倒立摆控制系统的原理和系统组成（2）加深对实际控制系统物理组成部分的认识和理解（3）掌握线性系统控制器的设计、软件算法编制与实现要求针对直线型一级或二级倒立摆系统，设计状态反馈控制器和状态观测器，完成对小车倒立摆的稳定控制。
二、实验内容和原理以直线一级或二级倒立摆为研究对象，开展以下实验内容：（1）系统数学模型建模与分析（2）倒立摆经典控制设计（3）倒立摆状态反馈控制与状态观测器设计（4）倒立摆实物控制调试三、实验项目（1）倒立摆前馈控制起摆研究（2）能量控制起摆研究（3）倒立摆经典控制器设计及调试（4）倒立摆状态反馈控制器设计及调试四、实验器材倒立摆实验系统GLIP 一套计算机（MA TLAB）一台五、操作方法与实验步骤第一种起摆控制（一）模型建立一级倒立摆的模型示意图如下：图1 直线倒立摆一级模型由[1]可得到运动方程：222(cos (cos )()sin cos ()cos ()()()sin ml bx ml ml M m ml u I ml M m M m ml θθθθθθθθθ⋅+-⋅=+⋅+++++222222()()()()sin ()sin cos ()()(cos )I ml M m x I ml bx I ml ml ml g I ml M m u ml xθθθθθ++++-+-⋅=+++可以写成关于θ和x 的微分方程：222()cos ()sin cos ()sin cos (cos )()()M m ml u m M ml mlb x ml ml I ml M m θθθθθθθθ+⋅++-+⋅-++=222222()()()sin ()()sin cos (cos )()()M m I ml u I ml ml I ml bx ml gml I ml M m x θθθθθ-++⋅-+++-⋅-++=由[2]可得到运动方程：2()sin cos I ml mg b ml u θθθθ+=-+⋅根据本次试验对两种模型分别进行了输入输出观察，以[1]中的模型为主进行计算。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实用文档研究生课程实验报告课程名称：线性系统实验名称：平面二级倒立摆实验班级： 12S0441学号：12S104057姓名：白俊林实验时间： 2012 年12 月 21 日控制科学与工程教学实验中心1.实验目的1)熟悉Matlab/Simulink仿真；2)掌握LQR控制器设计和调节；3)理解控制理论在实际中的应用。
倒立摆研究的意义是，作为一个实验装置，它形象直观，简单，而且参数和形状易于改变；但它又是一个高阶次、多变量、非线性、强耦合、不确定的绝对不稳定系统的被控系统，必须采用十分有效的控制手段才能使之稳定。
因此，许多新的控制理论，都通过倒立摆试验对理论加以实物验证，然后在应用到实际工程中去。
因此，倒立摆成为控制理论中经久不衰的研究课题，是验证各种控制算法的一个优秀平台，故通过设计倒立摆的控制器，可以对控制学科中的控制理论有一个学习和实践机会。
2.实验内容1）建立直线二级倒立摆数学模型对直线二级倒立摆进行数学建模，并将非线性数学模型在一定条件下化简成线性数学模型。
对于倒立摆系统，由于其本身是自不稳定的系统，实验建立模型存在一定的困难，但是经过小心的假设忽略掉一些次要的因素后，倒立摆系统就是一个典型的运动的刚体系统，可以在惯性坐标系内应用经典力学理论建立系统的动力学方程。
对于直线二级倒立摆，由于其复杂程度，在这里利用拉格朗日方程推导运动学方程。
由于模型的动力学方程中存在三角函数，因此方程是非线性的，通过小角度线性化处理，将动力学非线性方程变成线性方程，便于后续的工作的进行。
2）系统的MATLAB仿真依据建立的数学模型，通过MATLAB仿真得出系统的开环特性，采取相应的控制策略，设计控制器，再加入到系统的闭环中，验证控制器的作用，并进一步调试。
控制系统设计过程中需要分析内容主要包括得出原未加控制器时系统的极点分布，系统的能观性，能控性。
3）LQR 控制器设计与调节实验利用线性二次型最优（LQR ）调节器MATLAB 仿真设计的参数结果对平面二阶倒立摆进行实际控制实验，参数微调得到较好的控制效果，记录实验曲线。
4）改变控制对象的模型参数实验调整摆杆位置，将摆杆1朝下，摆杆2朝上修改模型参数、起摆条件和控制参数，重复3的内容。
3. 实验步骤1）倒立摆系统模型在忽略了空气流动，各种摩擦之后，可将倒立摆系统抽象成小车、匀质杆和质量块组成的系统，如图1所示。
图1 直线两级倒立摆物理模型下面利用拉格朗日方程推导运动学方程 。
拉格朗日方程为： ()()(),,,L q q T q q V q q =-(1)i d L Lf dt q qδδδδ-= (2)123M m m m T T T T T =+++(3)111m mm T T T '''=+ (4) 222m mm T T T '''=+ (5)212M T Mx =(6)()()2211111122211111111sin sin 1211cos 22m d x l d l T m dt dt m x m l x m l θθθθθ⎛⎫-⎛⎫⎛⎫ ⎪'=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-+ (7)222221111111111112236mp T J m l m l ωθθ⎛⎫''=== ⎪⎝⎭(8)则'''2221111111111112cos 23m m m T T T m x m l x m l θθθ=+=-+ (9)同样可以求出()()22'112211222222221112222111222(2sin sin (2cos cos )1122112cos cos 2sin sin 22m d x l l d l l T m m dt dt m x l l m l l θθθθθθθθθθθθ--+⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭=--++(10)''2222222222222211112236m T J m l m l ωωθ⎛⎫=== ⎪⎝⎭(11)()()()'''22222111222222221122121221122cos cos 21444cos 23m m m T T T m x x l l m l l l l θθθθθθθθθθ=+=-+⎛⎫+++- ⎪⎝⎭(12)2211113322233111311(2sin )(2cos )1212cos 22m d x l d l T m dt dt m x m l x m l θθθθθ⎛⎫-⎛⎫⎛⎫=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-+ (13)因此，可以得到系统的总动能为：()()()1232222111111112211122222222112212122122233111311112cos 223122cos cos 21444cos 2312cos 22M m m m T T T T T Mx m x m l x m l m x x l l m l l l l m x m l x m l θθθθθθθθθθθθθθθθ=+++=+-++-+⎛⎫+++- ⎪⎝⎭+-+ (14)系统的总势能为：()12311131121122cos 2cos 2cos cos m m m V V V V m gl m gl m g l l θθθθ=++=+++ (15)从而拉格朗日算子：()()()2222111111112211122222222112212122122233111311111311211112cos 223122cos cos 21444cos 2312cos 2cos 22cos 2cos L T VMx m x m l x m l m x x l l m l l l l m x m l x m l m gl m gl m g l θθθθθθθθθθθθθθθθθθθ=-=+-++-+⎛⎫+++- ⎪⎝⎭+-+---()22cos l θ+(16)由于因为在广义坐标 21,θθ上均无外力作用，有以下等式成立：110d L Ldt θθ⎛⎫∂∂-= ⎪∂∂⎝⎭ (17)220d L Ldt θθ⎛⎫∂∂-= ⎪∂∂⎝⎭ (18)展开（17），（18）式，分别得到（19），（20）式2222121231122221123116sin()4(3())3(2cos()(2())(sin cos ))0m l m m m l m l m m m g x θθθθθθθθθ-+++---++++=(19)22111222112123sin 6sin()46cos()3cos 0g l l l x θθθθθθθθθ---++--=(20)将（19），（20）式对21,θθ 求解代数方程，得到以下两式111213122122221121212212211213121222112321(3(2sin 4sin 4sin 3cos()sin 6cos()sin()4sin()2cos 4cos 4cos 3cos()cos ))/(2(412129cos (gm gm m g m g m l m l m x m x m x m x l m m m m θθθθθθθθθθθθθθθθθθθθθθ=---+-+--+----+----+-2)))θ(21)22221231221112222212122221212311222222212312212124((3())(3sin 6sin()3cos )92cos()(6sin()3(2())(sin cos )))/316((3())4cos ())9m m m m l l g l x m l l m l m m m g x m m m m l l m l l θθθθθθθθθθθθθθθ=--++----+---+++-+++-(22)表示成以下形式：111212(,,,,,,)f x x x θθθθθ= (23)221212(,,,,,,)f x x x θθθθθ=(24)取平衡位置时各变量的初值为零，1212(,,,,,,)(0,0,0,0,0,0,0)0A x x x θθθθ===(25)将（23）式在平衡位置进行泰勒级数展开，并线性化，令:11100A f K x=∂==∂ (26)1231120112313(244)2(4312)A gm gm gm f K m m m l θ=---∂==∂---(27)121302123192(4312)A f m gK m m m l θ=∂==∂---(28)11400A f K x=∂==∂ (29)115010A f K θ=∂==∂ (30)116020A f K θ=∂==∂ (31)123117012313(24)2(4312)A m m m f K xm m m l =---∂==∂---(32)带入（21）式，得到线性化之后的公式112113217K K K x θθθ=++(33)将（24）式在平衡位置进行泰勒级数展开，并线性化，令22100A f K x=∂==∂ (34)123222012212322(2())164(3())9A g m m m f K m l m m m l θ=++∂==∂-++ (35)123223022212324(3())163(4(3()))9A g m m m fK m l m m m l θ=++∂==-∂-++(36)22400A f K x=∂==∂ (37)225010A f K θ=∂==∂ (38)226020A f K θ=∂==∂ (39)123123227022123242(2())(3()3164(3())9A m m m m m m f K x m l m m m l =++-++∂==∂-++ (40)带入（22）式，得到222123227K K K x θθθ=++(41)即：112113217K K K x θθθ=++ (42)222123227K K K x θθθ=++(43)现在得到了两个线性微分方程，由于我们采用加速度作为输入，因此还需加上一个方程u x = (44) 取状态变量如下：1213245162x x x x x x x x θθθθ=⎧⎪=⎪⎪=⎪⎨=⎪⎪=⎪=⎪⎩ (45)由（33），（41），（42）式得到状态空间方程如下：112233445121351762223627000100000001000000010000000100000000x x x x x x u x x x K K x K x K K x K ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦(46)其中直线两级倒立摆系统参数为：M小车质量 2.32kg 1m 摆杆1质量 0.04kg 2m摆杆2质量 0.132kg 3m质量块质量 0.208kg1θ 摆杆1与垂直向上方向的夹角 2θ摆杆2与垂直向上方向的夹角 1l 摆杆1到转动中心质心的距离 0.09m 2l摆杆1到转动中心质心的距离 0.27m F作用在系统上的外力由以上方程，将以下参数代入123121.320.040.1320.2089.80.090.27M m m m g l l =⎧⎪=⎪⎪=⎪=⎨⎪=⎪=⎪⎪=⎩ (47)求出各个K 值：12221323172777.0642-38.5321-21.192737.81865.7012-0.0728K K K K K K ====== (48)得到状态矩阵为： A =0 0 0 1.0000 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 0 86.6907 -21.6172 0 0 0 0 -40.3112 39.4500 0 0 0 B = 0 0 0 1.0000 6.6402 -0.0877 C =1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 00 0 0 0 0 1D=[0 0 0 0 0 0]'2）根据建模结果仔细计算并寻找合适的理论控制器参数。