第4讲异方差与自相关解析
异方差与自相关问题

a
与 b 。 a 与 b 的线性相关系数,称为
q
z
的等级相关系数 。
(ai a )(bi b ) rs (ai a ) 2 (bi b ) 2
6 (ai bi ) 2 rs 1 n(n 2 1)
§5.2
等级相关检验
异方差问题
(a) 完成模型的OLS估计,获取残差数据
X 11 f ( X j1 ) X 12 f ( X j2 ) X 1n f ( X jn )
X k1 f ( X j1 ) X k2 f ( X j2 ) X kn f ( X jn )
~ Y
Y f (X j )
~ Xi
Xi f (X j )
1 1 1
X 11 X 12 X 1n
Y1 X k 1 f ( X j1 ) Y2 X k2 f ( X j2 ) Y n X kn f ( X jn )
1 f ( X j1 ) 1 f ( X j2 ) 1 f ( X jn )
第五章
异方差与自相关问题
除了本章讨论所涉及的同方差性与不自相关性以外,
关于线性回归模型的其它假定在本章中都成立。 ——广义最小平方估计; ——异方差模型及其估计; ——自相关模型及其估计; ——异方差模型、自相关模型的预测。
§5.1
广义最小平方法
同方差且不自相关
cov(U ) 2 I cov(U ) 2
ei ;
(b) 选择可能与异方差有关的解释变量 rs ( j ),计算变量 X j与变
量
e 的等级相关系数
(c) 计算统计量
徐芳燕-计量经济学软件Stata15.0应用教程:从基础到前沿-第四章

三 、B-P检验
( 1) 命令
help bpagan //查询bpagan指令 use crime1.dta, clear //打开数据 gen avgsensq = avgsen^2 //生成平方项 方 式 一 ( estat):
regress consumption income price temp100 //回归 predict e,r //将回归的残差部分保存为变量e
gen le=l.e1 //用滞后一期残差生成新变量le
scatter e le //对残差和残差的滞后一期做散点图 ac e //查看残差e自相关图 pac e //查看残差e偏自相关图 //pa即patial , c即correlation corrgram e // 残差的相关系数矩阵
wntestq e //Q检验 estat dwatson //DW检验 , 只能用来检验一阶自相关
二 、处理自相关 1 第一种处理方式:OLS+HAC 即Newey-West方法,指令如下: 先取Newey-West滞后阶数为3。 newey consumption temp price income,lag (3) //HAC(异方差自相关稳健标准误) newey consumption temp price income,lag (5) //改变滞后阶数看稳定性如何
、数据介绍
变量名 tcost output plabor lnpfuel pcapital lntcost lntoutput lnplabor lnpf lnpfuel lnpk lnpcapital lntc lntcost
异方差自相关豪斯曼检验

异方差自相关豪斯曼检验异方差性(Heteroscedasticity)是指数据的方差不是常数,而是随着自变量的变化而变化。
当数据呈现异方差性时,固定效应模型可能会产生无偏但不一致的估计,而随机效应模型通常能够更好地处理异方差性。
因此,豪斯曼检验可以帮助确定在存在异方差性时应该选择哪种模型。
同时,时间序列数据中还可能存在自相关性(Autocorrelation),即误差项之间存在相关性。
如果数据中存在自相关性,那么OLS估计量可能不再是最佳线性无偏估计。
通过进行豪斯曼检验,可以确定在存在自相关性时是否需要使用修正的OLS估计方法。
要进行豪斯曼检验,首先需要建立两个模型:一个固定效应模型和一个随机效应模型。
然后通过计算两个模型的估计值的差异来进行检验。
在检验中,我们感兴趣的是这个差异是否由异方差性或自相关性引起的。
具体来说,豪斯曼检验的原假设是两个模型没有系统性的差异。
如果原假设被拒绝,说明两个模型之间存在显著差异,这可能是由于异方差性或自相关性导致的。
为了说明豪斯曼检验的方法和步骤,我们将考虑一个实际的研究示例。
假设我们对一个国家的 GDP 进行研究,我们想分析GDP 与劳动力投入之间的关系。
我们建立了一个固定效应模型和一个随机效应模型,用来估计 GDP 对劳动力投入的影响。
在固定效应模型中,我们假设不同国家之间的劳动力投入是不同的,即随着时间的推移,劳动力投入在各国之间也可能存在差异。
而在随机效应模型中,我们假设劳动力投入在各国之间是同质的,即不同的劳动力投入只是由于随机误差所致。
接下来,我们用豪斯曼检验来检验这两个模型之间的差异。
我们首先估计这两个模型,并计算它们之间的差异。
接着,我们对这些差异进行统计检验,以确定差异是否显著。
如果实证结果表明固定效应模型比随机效应模型更好,那么我们可以得出结论,数据中存在异方差性和自相关性。
在这种情况下,我们可能需要对模型进行修正,以更准确地描述数据。
总的来说,豪斯曼检验是一种在经济学和其他社会科学研究中经常使用的方法,用于检验两个模型之间的差异。
异方差与自相关
1.5 假定条件的不成立用OLS 法得到的估计模型通过统计检验后,还要检验摸型是否满足假定条件。
由1.3 节知,只有模型的4个假定条件都满足时,用OLS 法得到的估计量才具有最佳线性无偏特性。
当一个或多个假定条件不成立时,OLS 估计量将丧失上述特性。
本节讨论当假定条件不成立时,对参数估计带来的影响以及相应的补救措施。
以下讨论都是在某一个假定条件被违反,而其他假定条件都成立的情况下进行。
分为5个步骤。
(1)回顾假定条件。
(2)假定条件不成立对模型参数估计带来的影响。
(3)定性分析假定条件是否成立。
(4)假定条件是否成立的检验(定量判断)。
(5)假定条件不成立时的补救措施。
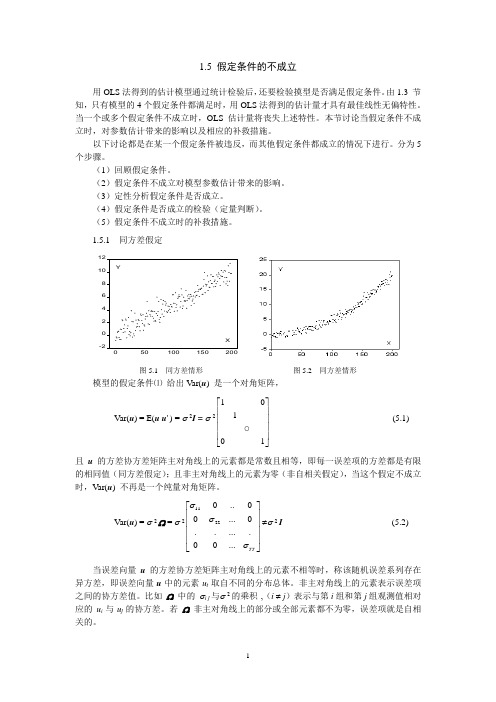
1.5.1 同方差假定-224681012050100150200XY图5.1 同方差情形 图5.2 同方差情形模型的假定条件⑴ 给出V ar(u ) 是一个对角矩阵, Var(u ) = E(u u ' ) = σ 2I = σ 21011⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(5.1) 且u 的方差协方差矩阵主对角线上的元素都是常数且相等,即每一误差项的方差都是有限的相同值(同方差假定);且非主对角线上的元素为零(非自相关假定),当这个假定不成立时,Var(u ) 不再是一个纯量对角矩阵。
Var(u ) = σ 2 Ω = σ 211220..00...0 00...TT σσσ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦≠σ 2 I (5.2)当误差向量u 的方差协方差矩阵主对角线上的元素不相等时,称该随机误差系列存在异方差,即误差向量u 中的元素u t 取自不同的分布总体。
非主对角线上的元素表示误差项之间的协方差值。
比如 Ω 中的 σi j 与σ 2的乘积 ,(i ≠ j )表示与第i 组和第j 组观测值相对应的u i 与 u j 的协方差。
若 Ω 非主对角线上的部分或全部元素都不为零,误差项就是自相关的。
本节讨论异方差。
下一节讨论自相关问题。
异方差自相关共线性

检验解释变量之间是否存在多重共线性的 常见方法有以下几种: (1)相关系数检验法 (2)辅助回归模型检验 (3)方差膨胀因子检验 (4)特征值检验 下面介绍如何利用Eviews6.0软件进行 相关系数检验和方差膨胀因子检验。
①相关系数检验 下面分析我国居民家庭电力消耗量(单位:千瓦 小时)与居住面积x1(单位:平方米)及可支配 收入x2(1978=100)的关系,以预测居民家庭电 力的需求量,原始数据如下图:
这里n R2的值明显变小了
3、自相关
自相关违背了经典线性回归假设中对随 机误差项无序列相关的要求。即随机误差项 之间存在着自相关性或者序列相关。 自相关的影响有:模型参数估计值不具有 最优性;随机误差的方差一般会低估;模型 的统计检验失效;区间估计和预测区间的精 度降低。
自相关性的检验方法主要有以下几种: (1)图示法; (2)德宾—沃森(DW)检验; (3)高阶自相关性检验; (4)回归检验法。 下面将介绍如何利用Eviews6.0软件进 行DW检验与高阶自相关性检验。
异方差的解决方法有: (1)模型变换法; (2)加权最小二乘法; (3)模型的对数变换; (4)广义最小二乘法。 其中最常见的是加权最小二乘法。下面 就介绍如何用Eviews6.0进行加权最小二乘 法的实现。
加权最小二乘法估计 模型的方法为:在方 程窗口中单击 Quick→Estimate Equation→Options, 并在权数变量栏输入 加权变量,这里选取 1/x为权数,点击确定, 就可以得到估计结果。
滞后阶数的选择, 一般会根据样本选 择默认的滞后阶数
检验的进入步骤
得到的检验结果表示残差与滞后各期的 相关系数与偏相关系数。(这里在时间序 列ARMA模型里面会介绍)。通过自相关系 数和偏自相关系数图,可以得到,残差序 列存在一阶和二阶自相关。
【总结】计量经济学异方差性、多重共线性、自相关的联系与区别知识总结

《计量经济学》中多重共线性、异方差性、自相关三者之间的联系与区别首先我们先来回顾一下经典线性回归模型的基本假设:1、为什么会出现异方差性我们可以从一下两方面来分析:第一,因为随即误差项包括了测量误差和模型中被省略的一些因素对因变量的影响;第二,来自不同抽样单元的因变量观察值之间可能差别很大。
因此,异方差性多出现在截面样本之中。
至于时间序列,则由于因变量观察值来自不同时期的同一样本单元,通常因变量的不同观察值之间的差别不是很大,所以异方差性一般不明显。
含义及影响:y=X β+ε,var(εi )var(εj ), ij ,E(ε)=0,或者记为212200['|]0000n E X σεεσσ⎛⎫⎪=Ω= ⎪ ⎪⎝⎭即违背假设3。
用OLS 估计,所得b 是无偏的,但不是有效的。
111(')'(')'()(')'b X X X y X X X X X X X βεβε---==+=+由于E(ε)=0,所以有E(b )=β。
即满足无偏性。
但是,b 的方差为1111121var(|)[()()'][(')''(')|] (')'['|](') (')'()(')b X E b b E X X X X X X X X X X E X X X X X X X X X X ββεεεεσ------=--===Ω其中212200['|]0000n E X σεεσσ⎛⎫⎪=Ω= ⎪ ⎪⎝⎭2、自相关产生的原因:(1)、经济数据的固有的惯性带来的相关 (2)、模型设定误差带来的相关 (3)、数据的加工带来的相关 含义及影响:cov(,)0,i j i j εε≠≠影响:和异方差一样,系数的ls 估计是无偏的,但不是有效的。
D -W 检验(Durbin -Watson )221212222121212222112112122211221122121()()()2()()222222(1)n i i i n i i n n n i i i i i i i n i i n n n i i i i i i i n n i i n i i i nn n i i i i nn i ie e d e e e e e e e e e e e e e e e e e e e e e e ρρ=-===-=-====-==-===∑-=∑∑+∑-∑=∑∑+∑-∑--=∑∑+=--∑∑+=--∑≈-其中2121n i i i n i ie e e ρ=-=∑=∑是样本一阶自相关函数。
自相关和异方差处理顺序

自相关和异方差处理顺序自相关和异方差是时间序列分析中常见的问题,处理它们的顺序对结果有很大的影响。
在处理时间序列数据时,我们通常需要对数据进行平稳性检验,以确保数据的稳定性和可靠性。
其中,自相关和异方差是两个常见的非平稳性问题。
自相关是指时间序列中的数据点之间存在相关性,即当前数据点与之前的数据点之间存在一定的关联性。
在时间序列分析中,我们通常使用自相关函数(ACF)来检测数据的自相关性。
如果数据存在自相关性,则需要对其进行处理,以消除这种相关性。
异方差是指时间序列中的方差不稳定,即方差随时间变化而变化。
在时间序列分析中,我们通常使用异方差函数(HCF)来检测数据的异方差性。
如果数据存在异方差性,则需要对其进行处理,以消除这种方差不稳定性。
在处理自相关和异方差时,处理的顺序对结果有很大的影响。
通常情况下,我们应该先处理自相关,再处理异方差。
这是因为自相关可能会导致模型的误差项不独立,从而影响模型的准确性。
而异方差则可能会导致模型的方差不稳定,从而影响模型的可靠性。
在处理自相关时,我们通常使用差分法或滑动平均法来消除自相关性。
差分法是指对时间序列进行差分,即将当前数据点与之前的数据点相减,以消除自相关性。
滑动平均法是指对时间序列进行平滑处理,即将当前数据点与之前的若干个数据点的平均值作为当前数据点的值,以消除自相关性。
在处理异方差时,我们通常使用对数变换或方差稳定化方法来消除异方差性。
对数变换是指对时间序列取对数,以消除方差不稳定性。
方差稳定化方法是指对时间序列进行加权处理,以使方差稳定。
总之,处理自相关和异方差时,处理的顺序对结果有很大的影响。
通常情况下,我们应该先处理自相关,再处理异方差。
在处理自相关时,我们可以使用差分法或滑动平均法来消除自相关性;在处理异方差时,我们可以使用对数变换或方差稳定化方法来消除异方差性。
通过合理的处理顺序和方法,我们可以有效地消除时间序列数据中的非平稳性问题,提高模型的准确性和可靠性。
自相关和异方差处理顺序

自相关和异方差处理顺序引言自相关和异方差是时间序列分析中常见的两种问题,它们影响了模型的准确性和可靠性。
在进行时间序列建模时,需要处理这些问题,以确保模型的有效性。
本文将深入探讨自相关和异方差处理的顺序,并讨论不同处理顺序的影响。
什么是自相关和异方差自相关自相关是指时间序列中当前观测值与之前观测值之间的相关性。
它衡量的是时间序列中各个观测值之间的依赖关系。
自相关可以用自相关函数(ACF)图来表示,通过观察ACF图,可以判断时间序列是否存在自相关。
异方差异方差是指时间序列中方差不稳定的特征。
在时间序列中,方差可能随着时间的推移发生变化,这会导致模型的拟合不准确。
异方差可以用方差函数(VCF)图来表示,通过观察VCF图,可以判断时间序列是否存在异方差。
自相关和异方差处理的重要性自相关和异方差对时间序列建模的准确性和可靠性有重要影响,它们需要被处理以获得可靠的模型结果。
•自相关的存在会导致参数估计不准确,预测结果失真。
如果存在自相关,模型会无法捕捉到序列的真实动态,导致预测结果不准确。
•异方差使得模型的残差不符合正态分布,违背了建模的基本假设。
这会使得模型的显著性检验和置信区间估计不可靠,影响模型的有效性。
因此,为了获得可靠的模型结果,需要对自相关和异方差进行处理。
自相关和异方差处理顺序的影响自相关和异方差的处理顺序会对最终的模型结果产生影响。
不同的处理顺序可能导致不同的模型结构和参数估计。
先处理自相关后处理异方差如果先处理自相关再处理异方差,可能会导致如下影响:1.自相关处理可能会改变时间序列的动态特征。
当我们去除自相关时,可能会削弱序列中的一些重要信息,导致模型无法准确捕捉到序列的动态变化。
2.异方差处理可能会影响自相关的结构。
当我们对残差进行异方差处理时,可能会改变残差序列的结构,从而使得自相关的估计失真。
先处理异方差后处理自相关如果先处理异方差再处理自相关,可能会产生如下影响:1.异方差处理可能改变原始序列的动态特征。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、实验操作指导
这就是实验模型。显然模型将一个非线性模型转化成了线性 模型,在运用计量经济学进行模型研究时,将非线性模型 化为线性模型来简化分析一直是计量经济学的指导准则。
2.打开文件,进行回归
(1)打开文件命令 use c:\data\nerlove,clear 或者直接从菜单栏中“file”选择“open”找到需要打开的数据 文件nerlove
通过绘制残差图可以直观地观察到是否存在异方 差,但是观察残差图的方法标准较为模糊,会遇 到模型残差图很难判断的情形。所以只采用残差 图的方式判定模型的方差形式是不够严谨的,必 须配合下面几种正规的检验方法才有信服力。 (2)怀特检验法 根据本章节介绍的该方法的原理,Stata可以直接 得到检验结果。对模型基本回归结束后,需要在 命令窗口输入如下命令:
3.异方差检验 对模型进行回归并不是本章的知识,然而回归是一个基础, 即做异方差检验之前必须做回归,下面将会详细介绍异方 差检验的基本方法。 (1)残差图观察法 做完模型的基本回归后,运用Stata绘制残差图来观察异 方差是否存在。 在命令窗口中输入如下两个命令中的任意一个即可 rvfplot (residual-versus-fitted plot) rvpplot varname (residual-versus-predictor plot) 第一个命令语句的作用是绘制默认形式的残差图,第二个 命令语句的作用是绘制残差与某个解释变量的散点图, varname可以换做认为合理的解释变量。
二、实验内容和数据来源 数据来自Nerlove 1963年的一篇文章,数据内容是美国1955 年145家电力企业的横截面数据,变量主要有TC(企业总 成本)、Q(产量)、PL(工资率)、PF(燃料价格)及 PK(资本租赁价格)。完整的数据在本书附带光盘里的 data文件夹的“nerlove.dta”工作文件夹中。 根据cobb-douglas生产函数:,在企业追求成本最小化的 的合理假设下,可证明其成本函数也为cobb-douglas函数, 可显示如下: 本实验中,运用nerlove数据分析各个解释变量对总成本 TC的影响,并运用多种方法检验是否存在异方差,如果 存在异方差则对模型进行合理的修正,最终得到一个效果 较好的模型。
Байду номын сангаас
estat imtest, white
读怀特检验结果图: 可见怀特检验的原假设是模型是同方差,备择假 设是无约束异方差。怀特检验结果显示,模型以 p值为0的检验结果显著地拒绝了原假设。结论与 前面的残差图结果是一致的,但更具有说服力。 此外,该检验还对异方差的的形式(skewness (偏斜)、kurtosis(峰度))进行了检验,结 果显示偏斜的程度在统计上更加显著。
(2)对回归方程进行估计 在stata命令窗口中输入如下命令:
根据实验结果图回归方程具体化为:lntc=3.57+0.72lnq+0.46lnpl-0.22lnpk + 0.43lnpf;根 据结果图中给出的p值看出,在10%和5%的置信 度下模型都只有lnq和lnpf的系数和常数项通过了t 检验。
在前面的章节中,已经介绍过作残差图的各种命令,所作 出的各种图形虽然有些差异,但是所展示的信息是基本一 致的。图8.2中显示残差的方差是变化的,从一开始时分 散程度很大(方差大),然后逐渐变得紧凑(方差变小), 这样一来很显然的否定了球形扰动项的假设。即通过残差 图观察法,得出的结论是此模型存在异方差问题。 在stata中分别输入: rvpplot lnq rvpplot lnpf rvpplot lnpl rvpplot lnpk 通过rvpplot varname命令的残差预测图知道异方差存在主 要的决定变量是lnq,因为它与残差形成的散点图与被解 释变量的拟合值形成的残差图形状最相似,但是其他变量 也或多或少的影响了异方差的形成。
第4讲 异方差与自相关
主要内容
1-异方差检验与处理 2-自相关和可行广义最小二乘法
第1节:异方差检验与处理
一、基本原理
要解决模型中存在的异方差问题,分为两个步骤:第一, 要准确的检测出异方差的存在;第二,解决异方差带来的 副作用,使模型估计量具有很好的性质。下面将会详细介 绍异方差检验和处理的原理。
4、异方差的处理
若检测结果是存在异方差,就要对异方差的问题进行处理, 下面将会介绍Stata中常用的修正存在异方差的模型的方 法。 (1)稳健标准差加OLS法 此方法适用于大样本的情况,Stata中所使用的命令语句 是: reg y x1 x2 …, robust 显然从命令语句上看,与普通最小二乘法区别就是后面加 上“robust”,表示在模型估计中采用的是稳健标准差。在 实验中,以nerlove数据为例,来看此种修正的操作结果。 在命令窗口中输入: reg lntc lnq lnpl lnpf lnpk, robust 与图8.1异方差处理之前的回归结果比较,系数的估计量 没有发生变化,而估计量的置信区间和标准差发生了变化。 在稳健标准差这种方法估计下,各估计量的t检验p值发生 了很大变化,在10%的置信度下,只有lnpk的系数未通过 检验。
(一)异方差检验的方法
(1)残差图观察法。由于异方差就是模型 扰动项的方差是变化的,根据这个原理就 可以观察模型残差拟合值的图形,根据图 形的形状变化判断异方差是否存在。但是 这种方法的严谨性稍差,并不是主流的检 验方法。
(2)怀特检验方法。由于模型扰动项的稳健标准差在同 方差的情况下还原为普通标准差,所以怀特检验的原理简 单来说就是看扰动项的稳健标准差与普通标准差的差距大 小。 White在1980年基于这一思想提出了怀特检验。
(二) 异方差的处理方法
(1)稳健标准差加OLS法 只要样本容量足够大,在模型出现异方差的情况 下,使用稳健标准差时参数估计、假设检验等均 可正常进行,即可以很大程度上消除异方差带来 的副作用。
(2)广义最小二乘法
(3)加权最小二乘法(WLS)
(4)可行广义最小二乘法 该方法是先用样本数据一致的估计出V(X),然后使用GLS法对模型进行估计。 (此方法克服了GLS和WLS要求扰动项协方差已知的缺点)
