2021-2022年高一数学下学期第二次间周考试题
北京师范大学附属中学2021-2022学年高一下学期期中考试数学试题
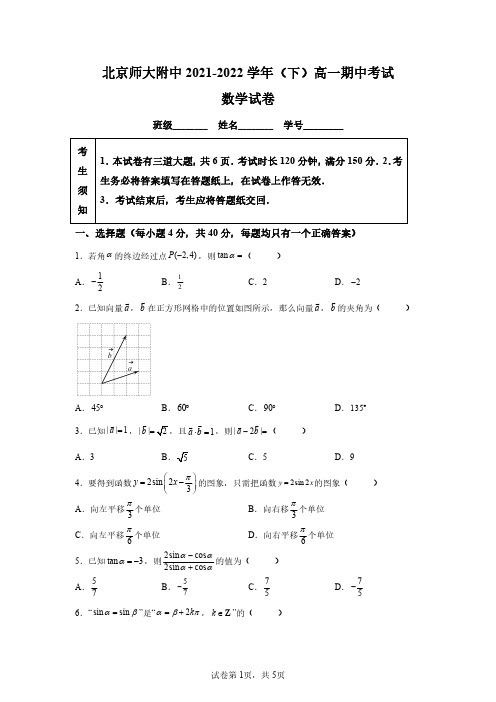
北京师大附中2021-2022学年(下)高一期中考试数学试卷班级________姓名________学号________考生须知1.本试卷有三道大题,共6页.考试时长120分钟,满分150分.2.考生务必将答案填写在答题纸上,在试卷上作答无效.3.考试结束后,考生应将答题纸交回.一、选择题(每小题4分,共40分,每题均只有一个正确答案)1.若角α的终边经过点(2,4)P-,则tanα=()A.12-B.12C.2D.2-2.已知向量a ,b 在正方形网格中的位置如图所示,那么向量a ,b 的夹角为()A.45︒B.60︒C.90︒D.135︒3.已知||1a=,||b=,且1ab⋅=,则|2|a b-=()A.3B C.5D.94.要得到函数2sin23y xπ⎛⎫=-⎪⎝⎭的图象,只需把函数2sin2y x=的图象()A.向左平移3π个单位B.向右移3π个单位C.向左平移6π个单位D.向右平移6π个单位5.已知tan3α=-,则2sin cos2sin cosαααα-+的值为()A.57B.57-C.75D.75-6.“sin sinαβ=”是“2kαβπ=+,k∈Z”的()A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件7.化简cos(2)sin()sin 2πααπα--⎛⎫+ ⎪⎝⎭的结果为()A .tan αB .cos αC .sin αD .sin α-8.在锐角中,设sin sin ,cos cos x A B y A B =⋅=⋅,则,x y 的大小关系为A .x y≤B .x y≥C .x y>D .x y <9.设函数()sin(cos )f x x x =,下列命题中真命题的个数为()①()f x 是奇函数;②当0,2x π⎛⎫∈ ⎪⎝⎭时,()0f x >;③()f x 是周期函数;④()f x 在无数个零点;⑤()f x 在0,2π⎛⎫⎪⎝⎭上单调递增A .1个B .2个C .3个D .4个10.在矩形ABCD 中,22AB BC ==,动点M 在以点C 为圆心且与BD 相切的圆上,则AM BD ⋅的取值范围为()A .[5,1]--B .[5,1]-C.[31]-+-D.[3-+-二、填空题(每小题5分,共25分)11.已知扇形的圆心角为120°,扇形的面积为3π,则该扇形所在圆的半径为________.12.已知5sin cos 4αα-=,则sin 2α=________.13.23sin 502cos 20-︒=-︒_______.14.如图,正方形ABCD 的边长为3,点E 是线段AB 的靠近点B 的一个三等分点,若边DC上存在点F ,使得EA EF λ⋅=成立,则λ的一个符合题意的值为________.15.声音是由物体振动而产生的声波通过介质(空气、固体或液体)传播并能被人的听觉器官所感知的波动现象.在现实生活中经常需要把两个不同的声波进行合成,这种技术被广泛运用在乐器的调音和耳机的主动降噪技术方面.技术人员获取某种声波,其数学模型记为()H t ,其部分图象如图所示,对该声波进行逆向分析,发现它是由1S ,2S 两种不同的声波合成得到的,1S ,2S 的数学模型分别记为()f t 和()g t ,满足()()()H t f t g t =+.已知1S ,2S 两种声波的数学模型源自于下列四个函数中的两个:①sin2y t π=;②sin 2t y π=;③y sin 3t π=;④y 2sin 3t π=.则1S ,2S 两种声波的数学模型分别是________.(填写序号)三、解答题(共6小题,共85分.解答时写出文字说明,演算步骤或证明过程)16.已知向量a →=(1,2),b →=(-3,k ).(1)若a →∥b →,求b →的值;(2)若a →⊥(a →+2b →),求实数k 的值;(3)若a →与b →的夹角是钝角,求实数k 的取值范围.17.函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示,其中712π是()f x 的一个零点.(1)求()f x 的最小正周期及解析式;(2)求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最值.18.据市场调查,某种商品一年内每月的价格满足函数关系式:f (x )=A sin(ωx +φ)+B 0,0,2A πωϕ⎛⎫>>< ⎪⎝⎭,x 为月份.已知3月份该商品的价格首次达到最高,为9万元,7月份该商品的价格首次达到最低,为5万元.(1)求f (x )的解析式;(2)求此商品的价格超过8万元的月份.19.设函数()4cos sin 3f x x x π⎛⎫=-+ ⎪⎝⎭,x ∈R .(1)求()f x 的单调递减区间;(2)若曲线()y f x =的对称轴只有一条落在区间[0,]m 上,求m 的取值范围.20.已知函数()4sincos (0)223xx f x m ωωπω⎛⎫=++> ⎪⎝⎭.在下列条件①、条件②、条件③这三个条件中,选择可以确定ω和m 值的两个条件作为已知.(1)求6f π⎛⎫⎪⎝⎭的值;(2)若函数()f x 在区间[0,]a 上是增函数,求实数a 的最大值.条件①:()f x 最小正周期为π;条件②:()f x 最大值与最小值之和为0;条件③:(0)2f =.21.已知集合{1,2,,}S n =⋅⋅⋅(3n ≥且*n ∈N ),{}12,,,m A a a a =⋅⋅⋅,且A S ⊆.若对任意i a A ∈,(1)j a A i j m ∈≤≤≤,当i j a a n +≤时,存在(1)k a A k m ∈≤≤,使得i j k a a a +=,则称A 是S的m 元完美子集.(1)判断下列集合是否是{1,2,3,4,5}S =的3元完美子集,并说明理由;①1{1,2,4}A =;②2{2,4,5}A =;(2)若{}123,,A a a a =是{1,2,,7}S =⋅⋅⋅的3元完美子集,求123a a a ++的最小值;(3)若{}12,,,m A a a a =⋅⋅⋅是{1,2,,}S n = (3n ≥且*n ∈N )的m 元完美子集,求证:12(1)2m m n a a a ≥+++⋅⋅⋅+.。
甘肃省兰州第一中学2021-2022学年高一下学期期中考试数学试题

兰州一中2021-2022-2学期期中考试试题高一数学说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.总分150分,考试时间120分钟.第Ⅰ卷(选择题共60分)一.单选题(共8小题,每小题5分)1.已知向量a ,b ,且AB =a +2b ,BC =-5a +6b ,CD =7a -2b ,则一定共线的三点是()A .A ,B ,DB .A ,B ,CC .B ,C ,DD .A ,C ,D2.已知sin α-sin β=1,cos α-cos β=-22,α,β∈(0,π),则α-β=()A.-π3B.-π32C .πD .±π36333.下列命题中是真命题的有()A.一组数据2,1,4,3,5,3的平均数、众数、中位数相同;B.有A 、B 、C 三种个体按3:1:2的比例分层抽样调查,如果抽取的A 个体数为9,则样本容量为30;C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是甲;D .一组数1,2,2,2,3,3,3,4,5,6的80%分位数为4.4.已知向量a ,b 满足a =4,b =(1,22),且(a +2b )⊥(3a -b ).则向量a 与向量b 的夹角是()A .πB .πC .2πD .5π63365.从2,3,5,7这四个数中任取三个数组成无重复数字的三位数,则这个三位数是奇数的概率为()A.13B.23C.34D.566.2cos20︒-cos40︒=()2sin 40︒A.32B.12C .D .137.已知i ,j 为互相垂直的单位向量,a =-i +2j ,b =3i -(λ-4)j ,且a 与a -b 的夹角为锐角,则λ的取值范围为()3⎝A .(0,+∞)B .(0,10) (10,+∞)C .(-∞,0)D .(-∞,-2) (-2,0)8.函数f (x )=sin ωx +cos ωx (ω>0)在区间⎡π,π⎤上单调递减,则实数ω的取值范围是()A .⎡1,1⎤B .⎛0,1⎤⎢⎣2⎥⎦C .⎡1,5⎤D .(0,1]⎢⎣2⎥⎦2⎥⎦⎢⎣24⎥⎦二.多选题(共4小题,每小题5分,有漏选得3分,有错选得0分)9.已知事件A ,B ,且P (A )=0.4,P (B )=0.3,则()A .如果B ⊆A ,那么P (A B )=0.4,P (AB )=0.3B.如果A 与B 互斥,那么P (A B )=0.7,P (AB )=0C.如果A 与B 相互独立,那么P (A B )=0.7,P (AB )=0.12D.如果A 与B 相互独立,那么P (AB )=0.42,P (AB )=0.1810.已知某地区有小学生120000人,初中生75000人,高中生55000人,当地教育部门为了了解本地区中小学生的近视率,按小学生、初中生、高中生进行分层抽样,抽取一个容量为2000的样本,得到小学生,初中生,高中生的近视率分别为30%,70%,80%.下列说法中正确的有()A .从高中生中抽取了440人B .每名学生被抽到的概率为1150C .估计该地区中小学生总体的平均近视率为53%D.估计高中学生的近视人数约为4400011.下列命题中是真命题的有()A.存在α,β,使tan (α-β)=tan α-tan βB.在∆ABC 中,若sin2A =sin 2B ,则∆ABC 是等腰三角形C.在∆ABC 中,“A >B ”是“sin A >sin B ”的充要条件D.在∆ABC 中,若cos A =5,cos B =3则cos C 的值为631356512.在∆ABC 中,角A ,B ,C 所对的对边分别为a ,b ,c ,下列命题中正确的是()A.若A >B >C ,则sin A >sin B >sin CB.若a =40,b =20,B =25︒,则满足条件的∆ABC 有且仅有一个C.若a =b cos C ,则∆ABC 是直角三角形D.若∆ABC 为锐角三角形,且cos 2A -3sin A +2=0.若b +c =6,则∆ABC 外接圆面积的最小值为9π363第Ⅱ卷(非选择题)三.填空题(共4小题,每小题5分)13.已知数据x ,x ,x , ,x 的方差为8,则数据1x +5,1x +5,1x +5, ,1x +5的方123n差为.2122232n14.已知sin ⎛π+α⎫=2,则cos ⎛2π-2α⎫= .⎪ ⎝⎭⎝3⎪⎭⎡π⎤15.关于x 的方程3sin x cos x +cos 2x =k +1在x ∈⎢⎣0,2⎥⎦上有两个解,则实数k 的取值范围为.16.设|AB |=20,若平面上点P 满足,对于任意t ∈R ,有|AP -t AB |5,则PA ⋅PB 的最小值为.四、解答题17.(10分)如图,在∆ABC 中,AD =1AB =1,AC =2,∠BAC =60︒,点E 是CD 的中点,3记AB =a ,AC =b .(1)用a ,b 表示CD ,AE ;(2)求∠AED 的余弦值.18.甲、乙两所学校之间进行排球比赛,采用五局三胜制(先赢3局的学校获胜,比赛结束).约定比赛规则如下:先进行两局男生排球比赛,后进行女生排球比赛.按照以往比赛经验,在21男生排球比赛中,每局甲校获胜的概率为3,乙校获胜的概率为3,在女生排球比赛中,每12局甲校获胜的概率为3,乙校获胜的概率为3,设各局比赛相互之间没有影响且无平局.(1)求恰好比赛3局,比赛结束的概率;(2)求甲校以3:1获胜的概率.19.2021年秋季学期,某省在高一推进新教材,为此该省某市教育部门组织该市全体高中教师在暑假期间进行相关学科培训,培训后举行测试(满分100分),从该市参加测试的数3学老师中抽取了100名老师并统计他们的测试分数,将成绩分成五组,第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90],得到如图所示的频率分布直方图.(1)求a 的值以及这100人中测试成绩在[80,85)的人数;(2)估计全市老师测试成绩的平均数(同组中的每个数据都用该组区间中点值代替)和中位数(保留两位小数);(3)若要从第三、四、五组老师中用分层抽样的方法抽取6人作学习心得交流分享,并在这6人中再抽取2人担当分享交流活动的主持人,求第四组至少有1名老师被抽到的概率.20.已知函数f (x )=-1+23sin x cos x +2cos 2x .(1)求函数f (x )的单调减区间;(2)当x ∈⎡-7π,5π⎤时,求函数f (x )的值域.⎣⎢1212⎥⎦21.如图所示,在海岸A 处发现北偏东45°方向,距A 处-1海里的B 处有一艘走私船,在A 处北偏西75°方向,距A 处2海里的C 处的我方缉私船,奉命以20海里/小时的速度追截走私船,此时走私船正以20海里/小时的速度,从B 处向北偏东30°方向逃窜.问:缉私船应沿什么方向行驶才能最快截获走私船?并求出所需时间.22.已知∆ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且(2a -b )cos C =c cos B (1)求角C ;(2)若a =2,b =3,CD 为角C 的平线,求CD 的长;(3)若a cos B +b cos A =4,求锐角∆ABC 面积的取值范围.3高一期中考试数学答案参考答案与试题解析一.选择题(共8小题)题号12345678答案ACACCABC二.多选题(共4小题)题号9101112答案ABDACDACACD三.填空题(共4小题)13.2.114.9-.115.0,2⎡⎫⎪⎢⎣⎭.16.-75.四.解答题(共6小题)17.【答案】(1)13CD b a =-+ ,A E 1126b a =+ .217【解析】(1)根据题意,利用向量的加法的线性运算,直接计算即可.(2)根据题意,得3AB a == ,2AC b == ,且cos 603a b a b ⋅=⋅⋅︒= ,由(1)得,13CD b a =-+ ,A E 1126b a =+,所以,可以分别求出,,CD AE AD ,然后,直接利用余弦定理即可求出AED ∠的余弦值(1)因为E 是CD 的中点,113AD AB ==,所以,13AD AB = ,∴CD CA AD =+1133AC AB b a =-+=-+ .111()226AE AC AD AC AB =+=+ 1126b a =+.(2)在ADC 中,113AD AB ==,2AC =,60BAC ∠=︒,所以,3AB a == ,2AC b == ,且cos 603a b a b ⋅=⋅⋅︒=,所以,211()33CD b a b a =-+=-+ 12943393=⨯+-⨯,21111111117()493126264366422AE b a b a =++=⨯+⨯+⨯=++= E 是CD 的中点,所以,32DE =.因此,在ADE 中,32DE 72AE =,1AD =,利用余弦定理得,2227c 731os 21442212AE DE AD AED AE DE +-+-==⋅∠⋅18.【答案】(1)29(2)427【解析】(1)分甲校获胜和乙校获胜两种情况讨论,利用独立事件和互斥事件的概率公式可求得所求事件的概率;(2)分两种情况讨论:①前两局男排比赛中甲全胜,第三局比赛甲负,第四局比赛甲胜;②前两局男排比赛中甲1胜1负,第三局比赛甲胜,第四局比赛甲胜,利用独立事件与互斥事件的概率公式可求得所求事件的概率.(1)解:恰好比赛3局,比赛结束的情况有:甲校获胜,概率为1221433327P =⨯⨯=,乙校获胜,概率为2112233327P =⨯⨯=,∴恰好比赛3局,比赛结束的概率1242227279P P P =+=+=.(2)解:甲校以3:1获胜的情况有:①前两局男排比赛中甲全胜,第三局比赛甲负,第四局比赛甲胜,概率为:23221833381P ⎛⎫=⨯⨯= ⎪⎝⎭;②前两局男排比赛中甲1胜1负,第三局比赛甲胜,第四局比赛甲胜,概率为14221114C 333381P =⨯⨯⨯⨯=,∴甲校以3:1获胜的概率34844818127P P P '=+=+=.19.【答案】(1)0.04a =;20;(2)77.25分,76.67分(3)35【解析】(1)根据频率之和为1,可求得a 的值,根据频数的计算可求得测试成绩在[80,85)的人数;(2)根据频率分布直方图可计算中位数,即可求得第50%分数位;(3)列举出所有可能的抽法,再列出第四组至少有1名老师被抽到可能情况,根据古典概型的概率公式求得答案.(1)由题意得:5(0.010.020.060.07)1a ⨯++++=,解得0.04a =;这100人中测试成绩在[80,85)的人数为1000.04520⨯⨯=(人);(2)平均数为:(67.50.0172.50.0777.50.0682.50.0487.50.02)577.25⨯+⨯+⨯+⨯+⨯⨯=(分),设中位数为m ,且7580m ≤≤,则0.050.35(75)0.060.5m ++-⨯=,解得76.67m ≈,故第50%分数位76.67分;(3)第三组频率为50.060.3⨯=,第四组频率为50.040.2⨯=,第五组频率为50.020.1⨯=,故从第三、四、五组老师中用分层抽样的方法抽取6人作学习心得交流分享,三组人数为3人,2人和1人,记第三组抽取的人为123,A A A ,,第四组抽取的人为12B B ,,第五组抽取的人为1C ,则抽取2人的所有情况如下:121311121123212221313231121121,,,,,,,,,,,A A A A A B A B A C A A A B A B A C A B A B A C B B B C B C ,,,共15种,其中第四组至少有1名老师被抽到的抽法有111221223132121121,,,,,,,,A B A B A B A B A B A B B B B C B C 共9种,故第四组至少有1名老师被抽到的概率为93155P ==.20.【【答案】(1)单调减区间是2,63k k ππππ⎡⎤++⎢⎥⎣⎦,k Z∈(2)[]22-,【解析】(1)先对函数化简变形得()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,由3222262k x k πππππ+≤+≤+,k Z ∈可求出函数的减区间,(2)由75,1212x ππ⎡⎤∈-⎢⎥⎣⎦,得[]2,6x πππ+∈-,再利用正弦函数的性质可求出函数的值域(1)()2123cos 2cos f x x x x =-++,cos 232x x =,2sin 26x π⎛⎫=+ ⎪⎝⎭,令3222262k x k πππππ+≤+≤+,k Z ∈,解得263k x k ππππ+≤≤+,k Z ∈,所以函数的单调减区间是2,63k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈;(2由75,1212x ππ⎡⎤∈-⎢⎥⎣⎦,得[]2,6x πππ+∈-,所以1sin 216x π⎛⎫-≤+≤ ⎪⎝⎭,所以22sin 226x π⎛⎫-≤+≤ ⎪⎝⎭,所以函数的值域为[]22-,21.【答案】缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要620小时.【解析】在ABC 中,由余弦定理求得BC ,由正弦定理求得ABC ∠,在BCD △中,由正弦定理求得∠BCD ,得BD ,由速度公式可得时间.【详解】设缉私船应沿CD 方向行驶t 小时,才能最快截获(在D 点)走私船,则3CD t =海里,BD =20t 海里.在ABC 中,由余弦定理,有222222cos (31)22(31)BC AB AC AB AC A =+-⋅⋅=-+--1262⎛⎫⨯⨯-= ⎪⎝⎭则6=BC 又sin sin BC AC BAC ABC =∠∠,2sin 26ABC ∴∠=,∴∠ABC =45°,故B 点在C 点的正东方向上.∴∠CBD =90°+30°=120°,在BCD △中,由正弦定理得,sin sin BD CDBCD CBD=∠∠,sin 1sin 2203BD CBD BCD CD t⋅∠∴∠===,∴∠BCD =30°,则缉私船应沿北偏东60°的方向行驶.又在BCD △中,∠CBD =120,∠DCB =30°,∴∠CDB =30,6BD CB ==.206BD t ==620t =故缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要620小时.22.【答案】(1)3π(2)635(3)83,433⎛⎝(1)解:由()2cos cos a b C c B -=及正弦定理得()2sin sin cos sin cos A B C C B -=所以()2sin cos sin sin A C B C A =+=∴sin 0A ≠,∴1cos 2C =∵0C π<<,∴3C π=(2)解:设CD x =由+= ACD BCD ABC S S S 得111113326222222x x ⋅⋅+⋅⋅=⨯⨯.解得635x =CD 的长度为635(3)解:设ABC 外接圆半径为R ,由cos cos 4a Bb A +=2sin cos 2sin cos 4R A B R B A +=,即2sin 4R C =,即42sin sin cR C C==,∴4c =所以ABC 的面积13sin 24S ab C ab==∵4sin sin 32b a B A =83sin 3a A =,83sin 3b B =∴1632sin 33S A A π⎛⎫=- ⎪⎝⎭16322sin cos sin 333A A A ππ⎛⎫=- ⎪⎝⎭16331sin 322A A A ⎫=+⎪⎪⎝⎭216331cos sin 322A A A ⎫=+⎪⎪⎝⎭163311cos23444A A ⎫=-+⎪⎪⎝⎭8343sin 2363A π⎛⎫=-+ ⎪⎝⎭∵02A π<<,02B π<<,23A B π+=,∴2032A <-<ππ,∴62A ππ<<,∴52666A πππ<-<,∴1sin 2126A π⎛⎫<-≤ ⎪⎝⎭,∴8333S ⎛∈ ⎝。
四川省成都市新都一中2021-2022学年高一下学期期中联考模拟数学试卷(二)

四川省成都市新都一中高2021级第二期期中联考模拟02数学试卷一、单选题1.已知04πα<<,且1sin ,cos ,tan a b c ααα===,则()A .a b c>>B .b a c>>C .c b a>>D .c a b>>2.在ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,若10b =,6A π=,且ABC 有唯一解,则a 的取值情况是()A .5a =B .5a =或者10a ≥C .510a ≤≤D .不确定3.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积12=(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与其实际面积之间存在误差,现有圆心角为23π,弧长等于8m 3π的弧田,按照上述经验公式计算所得弧田面积约是(参考数据3 1.73≈)()A .26m B .29m C .212m D .215m 4.用分期付款的方式购买一件电器,价格为1150元,购买当天先付150元,以后每月这一天都交付50元及欠款的利息,月利率为1%,则买这件电器实际花().A .1105元B .1255元C .1305元D .1405元5.数列{}n a 中,12a =,21n n a a +=,则下列结论中正确的是()A .数列{}n a 的通项公式为2n n a =B .数列{}n a 为等比数列C .数列{}ln n a 为等比数列D .数列{}ln n a 为等差数列6.已知向量a ,b 的夹角为120︒,1a b ==r r ,c 与a b +同向,则a c - 的最小值为()A .1B .12C .34D .327.如图,在ABC 中,2AD DB =,AE EC =,CD 交BE 于F ,设AB a =,AC b = ,则AF =()A .1133a b+ B .1255a b+C .2355a b+ D .1134a b+ 8.在ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,若()()()sin sin sin a b A B b c C +-=+,7a =,则该三角形的外接圆直径为()A .14B .7CD9.已知数列{}n a 的前n 项和为n S,满足121,3,2)a a n ===≥,则2022a =()A .4043B .4042C .4041D .404010.在数列{}n a 中,11a =,142n n S a +=+,则2019a 的值为()A .20207572⨯B .20197572⨯C .20187572⨯D .无法确定11.数列{}n a 中,11a =,10(2)n n a a n n ---=≥,12111222n n S a a a =+++ .当99100n S =时,n 等于()A .98B .99C .100D .10112.设数列{}n a 满足15a =,213a =,2126n n n na a a +++=,则下列说法不正确的是()A .2156n n na a a ++=-B .n a 都是整数C .4nn a >D .{}n a 中与2019最接近的项是7a 二、填空题13.非零向量(sin ,2)a θ= ,(cos ,1)b θ= ,若a 与b 共线,则tan 4πθ⎛⎫-= ⎪⎝⎭_________.14.已知数列{}n a的通项公式为n a n =n a 的最小值为___________.15.已知等差数列{}n a 的前n 项和为n S ,若222S =,5100S =,则10S =______.16.已知A ,B ,C ,D 是平面内四点,且(2,1),(2,1)AC BD ==- ,则AB CD ⋅的最小值为___________.三、解答题17.已知cos 410x π⎛⎫-=⎪⎝⎭,3,24x ππ⎛⎫∈ ⎪⎝⎭(1)求sin x 的值;(2)求tan 24x π⎛⎫+ ⎪⎝⎭的值.18.已知等差数列{}n a 为递减数列,且132a a +=-,133a a =-.(1)求数列{}n a 的通项公式;(2)若数列{}n a 的前k 项和35k S =-,求k 的值.19.某台商到大陆一创业园投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年比上一年增加4万美元,每年销售蔬菜收入50万美元,设()f n 表示前n 年的纯利润(()f n =前n 年的总收入-前n 年的总支出-投资额).(1)从第几年开始获得纯利润?(2)若五年后,该台商为开发新项目,决定出售该厂,现有两种方案:①年平均利润最大时,以48万美元出售该厂;②纯利润总和最大时,以16万美元出售该厂.问哪种方案较合算?20.已知等差数列{}n a 为3,7,11,15,….(1)求{}n a 的通项公式;(2)135,()*419N m m +∈是数列{}n a 中的项吗?为什么?(3)若m a ,()*N ,t a m t ∈是{}n a 中的项,那么23m t a a +,是数列{}n a 中的项吗?请说明理由.21.已知函数()()()()cos 0,0,f x A x A ωϕϕπ=+>∈,同时满足下列四个条件中的三个:①最小正周期T π=;②()f x 的图像可以由sin cos y x x =+的图像平移得到;③函数()f x 的最大值为2;④()0f =(1)请选出这三个条件并说明理由,再求出函数()f x 的解析式;(2)若曲线()y f x =的图像只有一个对称中心落在区间[]0,a 内,求a 的取值范围.22.如图,在ABC 中,1CA =,2CB =,60ACB ∠=︒.(1)求||AB uu u r ;(2)已知点D 是AB 上一点,满足AD AB λ=uuu r uu u r,点E 是边CB 上一点,满足BE BC λ= .①当12λ=,求AE CD ⋅ ;②是否存在非零实数λ,使得AE CD ⊥?若存在,求出λ的值;若不存在,请说明理由.四川省成都市新都一中高2021级第二期期中联考模拟02数学参考答案1.C∵04πα<<,1cos sin 0∴>>>αα,∴1cos 1tan sin c ==>ααα,∴c b a >>,故选:C 2.B由正弦定理得,sin 5sin sin b A a B B==,由ABC 有唯一解,当sin 1B =时,即90B = ∠,ABC 唯一,符合条件,可得5a =;当1sin ,12B ⎛⎫∈ ⎪⎝⎭时,B Ð有两个值,ABC 不唯一,不符合条件;当1sin 0,2B ⎛⎤∈ ⎥⎝⎦时,5sin a b B =≥,故B A ∠≤∠,ABC 唯一,符合条件,可得10a ≥,故选:B 3.B如图,由题意可得:823=43AOB ππ∠=,4OA =,在Rt AOD 中,可得:3AOD π∠=,6DAO π∠=,114222OD AO ==⨯=,可得:矢422=-=,由sin43AD AO π=== 可得:弦2AD ==所以:弧田面积12=(弦⨯矢+矢221)22)292=⨯+=+≈平方米.故选:B4.B购买时付150元,欠1000元,每月付50元,分20次付清.设每月付款数构成数列{}n a ,则15010001%60a =+⨯=,()2501000501%59.5600.51a =+-⨯==-⨯,()35010005021%59600.52a =+-⨯⨯==-⨯,…∴()()600.510.560.5120n a n n n =--=-+≤≤,∴{}n a 是以60为首项,0.5-为公差的等差数列,∴()20201915020600.515012552S ⨯+=⨯+⨯-+=,∴买这件电器实际花1255元.故选:B 5.C数列{}n a 中,12a =,21n n a a +=,则22212a a ==,222432(2)2a a ===,显然123,,a a a 不成等比数列,A ,B都不正确;依题意,1ln ln 20a =>,由21n n a a +=两边取对数得:1ln 2ln n n a a +=,因此,数列{}ln n a 是首项为ln 2,公比为2的等比数列,C 正确,D 不正确.故选:C 6.D1a b ==r r Q ,向量a ,b 的夹角为120︒,c 与a b +同向,a ∴r 与c的夹角为60︒.又a c -=故mina c-=.故选;D 7.B因为2AD DB =,AE EC =,所以11,32AD AB AE AC == ,因为,,D F C 三点共线,所以1(1)(1)3AF AD AC AB AC λλλλ=+-=+- ,因为,,E F B 三点共线,所以1(1)(1)2AF AB AE AB AC μμμμ=+-=+- ,所以1311(1)2λμλμ⎧=⎪⎪⎨⎪-=-⎪⎩,解得31,55λμ==,所以1255AF AB AC =+,故选:B8.D由已知,()()()sin sin sin a b A B b c C +-=+,由正弦定理可得:()()()a b a b b c c +-=+,化简得:222b c a bc +-=-,所以2221cos 222b c a bc A bc bc +--===-,又因为ABC 中,(0,π)A ∈,所以2π3A =,所以2πsin sin3A =设三角形的外接圆半径为r ,由正弦定理可得:2sin 3a r A ==,故选:D.9.A由2)n =≥知:为等差数列,1==2==,则公差1d =,n =,故2n S n =,则21(1)n S n -=-(2)n ≥,可得221(1)21n n n a S S n n n -=-=--=-,而11a =也满足,所以21n a n =-,则20222202214043a =⨯-=.故选:A 10.A∵11a =,142n n S a +=+,∴212142S a a a =+=+,解得25a =.∵142n n S a +=+,∴2142n n S a ++=+,两式相减得,2144n n n a a a ++=-,∴()211222n n n n a a a a +++-=-,∴{}12n n a a +-是以212a a -=3为首项,2为公比的等比数列,∴11232n n n a a -+-=⨯,两边同除以12n +,则113224n n n n a a ++-=,∴2n n a ⎧⎫⎨⎬⎩⎭是以34为公差,11122a =为首项的等差数列,∴()133112244n n a n n -=+-⨯=,∴()23123124nn n n a n --=⨯=-⨯,∴()20172020201932019127572a =⨯-⨯=⨯.故选:A.11.B由10(2)n n a a n n ---=≥,得1(2)n n a a n n --=≥,()()()()n n n a a a a a a a a a a -=+-+-+-++-21213431 ()n n n =+++++=+1123412.当1n =时,此式也满足1a ,故数列{}n a 的通项公式为:()n a n n =+112.()n a n n n n ∴==-+⨯+1111121212121111111112222231n n S a a a n n ⎛⎫⎛⎫⎛⎫=+++=-+-++- ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭1111nn n =-=++.又因为99100n S =,所以991100n n =+,解得99n =.故选:B.12.C易知当2n =时,22134a =<,可知C 不正确.依题意,可得2216nn n n a a a ++-=,则335a =.所以2312+++-n n n a a a ()122166+++==-n n n n a a a ,223112266n n n n n n a a a a a a ++++++=+,()()1312266++++++=+n n n n n n a a a a a a ,又0n a ≠,所以3122166n n n nn n a a a a a a +++++++=,令216n nn n a a b a +++=,所以{}n b 为常数列,又31265a a a +=,即2156n n n a a a ++=-,所以A ,B 正确.由2156n n n a a a ++=-,()211232n n n n a a a a +++-=-或()211323n n n n a a a a +++=--,又2123a a -=,2132a a -=-,所以{}12n n a a +-是首项为3,公比为3的等比数列,{}13n n a a +-是首项为2-,公比为2的等比数列.故123n n n a a +-=,132+-=-nn n a a ,所以两式相减得23n nn a =+,所以6793a =,72315a =,D 正确.故选:C.13.13解:∵非零向量a 与b共线,∴sin 2cos θθ=,显然cos 0θ≠,所以tan 2θ=,∴tan 11tan()41tan 3πθθθ--==+.故答案为:1314.1因为n n n a n+===易知数列{}n a为递增数列,所以数列{}n a 的最小项为1a,即最小值为1故答案为:115.350方法一:设等差数列{}n a 的公差为d ,则2151222,510100,S a d S a d =+=⎧⎨=+=⎩解得18,6,a d =⎧⎨=⎩所以10110810963502S =⨯+⨯⨯⨯=.方法二:设2n S An Bn =+,则254222,255100,S A B S A B =+=⎧⎨=+=⎩解得3,5,A B =⎧⎨=⎩所以210310510350S =⨯+⨯=.故答案为:350.16.4-设(,)A x y ,(,)B m n ,则(2,1)C x y ++,(2,1)D m n -+,所以(,)AB m x n y =-- ,(4,)CD m x n y =---,则2222()4()()(2)()4AB CD m x m x n y m x n y ⋅=---+-=--+--,当2m x -=,n y =时AB CD ⋅的最小值为4-.故答案为:4-17.(1)因为x ∈(π2,3π4),所以x -π4∈(π4,π2),于是sin(x -π4),则sin x =sin[(x -π4)+π4]=sin(x -π4)cos π4+cos(x-π4)sin π4=10×2+10×2=45.(2)由(1)知,4sin 5x =,因为x ∈(π2,3π4),所以cos x35,所以tan x =43-,则22tan 24tan 21tan 7x x x ==-,所以tan 2tan314tan(24171tan 2tan 4x x x πππ++==--⋅.18.(1)设等差数列{}n a 的公差为d ,则()11n a a n d +-=,且0d <.由132a a +=-,133a a =-,解得11a =,33a =-(13a =-,31a =不合题意,舍去).由3123a d =+=-,解得2d =-.从而()()11232n a n n =+-⨯-=-.(2)由(1)可知32n a n =-,所以()213222n n n S n n +-⎡⎤⎣⎦==-.由35k S =-,可得2235k k -=-,即22350k k --=,解得7k =或5k =-.又*k N ∈,故7k =.19.(1)由题意,知每年的经费构成了以12为首项,4为公差的等差数列,则()()215012472240722n n f n n n n n -⎡⎤=-+⨯-=-+-⎢⎥⎣⎦,获得纯利润就是要求()0f n >,即2240700n n -+->,解得218n <<.又*n N ∈,故从第三年开始获得纯利润;(2)①年平均利润为()23640216216f n n n n ⎛⎫=-+=-≤ ⎪⎝⎭,当且仅当6n =时取等号,故此方案获利61648144⨯+=(万美元),此时6n =.②()()2224072210128f n n n n =-+-=--+,当10n =时,()max 128f n =.故此方案共获利12816144+=(万美元).比较两种方案,在获利相同的前提下,第①种方案只需六年,第②种方案需要十年,故选择第①种方案.20.(1)设数列{}n a 的公差为d ,依题意有13a =,734d =-=,∴()34141n a n n =+-=-.(2)令41135n a n =-=,得34n =,∴135是数列{}n a 的第34项;∵()419451m m +=+-,且*N m ∈,∴419m +是数列{}n a 的第()5m +项.(3)∵m a ,t a 是数列{}n a 中的项,∴41m a m =-,41t a t =-,∴()()()2324134142311m t a a m t m t +=-+-=+--,∵*231N m t +-∈,∴23m t a a +是数列{}n a 的第()231m t +-项.21.(1)由题意知条件②:sin cos )4y x x x π=+=+,与③矛盾,故②③不能同时成立,则①④必满足,所以T π=,所以22πωπ==,故排除②,所以()cos()(0,2f x A x A πωϕϕ=+><同时满足①③④.所以2A =,2ω=,此时()2cos(2)f x x ϕ=+,因为(0)f =,所以2cos ϕ=即cos 2ϕ=,因为(0,)ϕπ∈,所以6π=ϕ,所以()2cos(2)6f x x π=+;(2)令262x k πππ+=+,k Z ∈,解得26k x ππ=+,所以()f x 的对称中心是(,0),26k k Z ππ+∈,因为曲线()y f x =只有一个对称中心落在区间[0,]a 内,所以263a ππ< ,所以a 的取值范围是2[,)63ππ.22.(1)解:∵AB CB CA =- ,且24CB = ,21CA = ,21cos 601CB CA ⋅=⨯⨯︒= ,∴||||AB CB CA =-=(2)解:①12λ=时,12AD AB = ,12BE BC = ,∴D 、E 分别是边AB 、BC 的中点,∴12AE AC CE AC CB =+=+ ,1()2CD CA CB =+ ,∴11()22AE CD AC CB CA CB ⎛⎫⋅=+⋅+ ⎪⎝⎭ 211112244AC CA AC CB CB CA CB =⋅+⋅+⋅+ 211112cos12022=-⨯+⨯⨯⨯︒211121cos602444+⨯⨯⨯︒+⨯=;②存在.理由如下:假设存在非零实数λ,使得AE CD ⊥ ,由AD AB λ=uuu r uu u r ,得()AD CB CA λ=- ,∴()CD CA AD CA CB CA λ=+=+- (1)CB CA λλ=+- .又BE BC λ= ,∴()AE AB BE CB CA BC λ=+=-+ (1)CB CA λ=-- ,∴AE CD ⋅= 2(1)CB CB CA λλλ--⋅+ 22(1)(1)CB CA CA λλ-⋅-- 24(1)(1)(1)λλλλλ=--+---2320λλ=-+=,解得23λ=或0λ=(不合题意,舍去),所以存在非零实数23λ=,使得AE CD ⊥ .。
2021-2022学年广东省江门市高一下学期期末调研测试(二)数学试题

2021-2022学年广东省江门市高一下学期期末调研测试(二)数学试题1.实数满足条件:,(其中为i虚数单位),则()A.B.2 C.3 D.2.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为A.6 B.8 C.10 D.123.抛掷两枚质地均匀的硬币,设事件“第一枚硬币正面向上”,事件“第二枚硬币反面向上”,下列结论中正确的是()A.A与B为相互独立事件B.A与B互为对立事件C.A与B为互斥事件D.4.把函数的图像上所有的点向左平行移动个单位长度,再把所得图像上所有点的横坐标缩短到原来的(纵坐标不变),得到的图像所表示的函数是A.B.C.D.5.已知,,且,则()A.1 B.C.2 D.6. 2021年江苏进入新高考模式,数学增加了多选题,已知在多项选择题的四个选项A、B、C、D中,有多项符合题目要求.规定:全部选对得5分,部分选对得2分,有选错得0分.若某题的正确答案是ABC,某考生随机选了一些选项(选项个数大于或等于1),则其得分的概率为().A.B.C.D.7.已知为异面直线,平面平面.直线满足,则( )A.,且B.,且C.与相交,且交线垂直于D.与相交,且交线平行于8.向量旋转具有反映点与点之间特殊对应关系的特征,在电子信息传导方面有重要应用.平面向量旋转公式在中学数学中用于求旋转相关点的轨迹方程具有明显优势,已知对任意平面向量,把绕其起点沿逆时针方向旋转角得到向量,叫做把点B绕点A沿逆时针方向旋转角得到点P.已知平面内点,点,把点B绕点A沿顺时针方向旋转后得到点P,则点P的坐标为()A.B.C.D.9.下列式子正确的是()A.B.C.D.10.已知某班10名男生引体向上的测试成绩统计如表所示,则下列说法正确的是()A.这10名男生引体向上测试成绩的平均数为8.4B.这10名男生引体向上测试成绩的第25百分位数为7.5C.这10名男生引体向上测试成绩的中位数为8.5D.这10名男生引体向上的测试成绩众数为911.在水流速度为的河水中,一艘船以的实际航行速度垂直于对岸行驶,则下列关于这艘船的航行速度的大小和方向的说法中,正确的是()A.这艘船航行速度的大小为B.这艘船航行速度的大小为C.这艘船航行速度的方向与水流方向的夹角为D.这艘船航行速度的方向与水流方向的夹角为12.如图,在三棱锥中,D,E,F分别是侧棱,,的中点.则下列结论中,其中正确的有()A.∥平面B.平面∥平面C.三棱锥与三棱锥的体积比为1∶4D.异面直线与所成角为60°13.已知复数,是z的共轭复数,则___________.14.已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为______.15.甲、乙二人做射击游戏,甲、乙射击击中与否是相互独立事件.规则如下:若射击一次击中,则原射击人继续射击;若射击一次不中,就由对方接替射击.已知甲、乙二人射击一次击中的概率均为,且第一次由甲开始射击,则第4次由甲射击的概率___________.16.已知函数,若函数的最小正周期为,则__________,若,则函数的最小正周期为__________.17.如图,在正方体中,点E为的中点.(1)求证:平面;(2)若,从正方体中截去三棱锥后,求剩下的几何体的体积.18.江门市某中学高一年级举行了一次数学竞赛,从中随机抽取了一批学生的成绩.经统计,这批学生的成绩全部介于50至100之间,将数据按照,,,,的分组作出频率分布直方图如图所示.(1)求频率分布直方图中a的值,并估计本次竞赛成绩的第80百分位数:(2)若按照分层随机抽样的方法从成绩在,的两组中抽取5人,再从这5人中随机抽取3人,求至少有2人的成绩在内的概率.19.已知,,,,求的值.20.甲乙两人组成“星队”参加猜谜语活动,每轮活动由甲乙各猜一个谜语,已知甲每轮猜对的概率为,乙每轮猜对的概率为,.在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响.甲和乙在第一轮都猜错的概率为,“星队”在第二轮中只猜对一个谜语的概率为.(1)求,;(2)求“星队”在前两轮活动中猜对3个谜语的概率.21.如图,四棱锥的底面是矩形,E为侧棱的中点,侧面是正三角形,且侧面底面.(1)求证:平面;(2)当为何值时,使得?22.在①;②;③,这三个条件中任选一个,补充在下面的横线上,并加以解答.在中,角A,B,C的对边分别是a,b,C,S为的面积,若__________(填条件序号)(1)求角C的大小;(2)若边长,求的周长的最大值.。
辽宁省沈阳市第二中学2021-2022学年高一下学期期中考试数学试题

沈阳二中2021-2022学年度下学期期中考试高一(24届)数学试题第Ⅰ卷一、单项选择题:本题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.若(12)5i z i -=(i 是虚数单位),则z 的值为A .3B .5CD 2.若sin10sin100a ︒=︒,则sin 20︒=()A .21aa +B .21a a -+C .221a a +D .221a a -+3.若z C ∈且221z i +-=,则12z i --的最小值是()A .2B .3C .4D .54.已知()()tan ,1,1,2a b θ=-=- ,其中θ为锐角,若a b +与a b - 夹角为90 ,则212sin cos cos θθθ=+()A .1B .1-C .5D .155.ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若2cos sin sin B A C =,则ABC 的形状为()A .直角三角形B .等腰三角形C .等边三角形D .等腰直角三角形6.由于潮汐,某港口一天24h 的海水深度H (单位:m )随时间t (单位:h ,024t ≤<)的变化近似满足关系式()2124sin 123H t t ππ⎛⎫=+- ⎪⎝⎭,则该港口一天内水深不小于10m 的时长为()A .12hB .14hC .16hD .18h717sinsin 918π-=()A .3B .4C D .38.我国南宋著名数学家秦九韶提出了由三角形三边求三角形面积的“三斜求积”公式,设ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,面积为S ,“三斜求积”公式表示为S =在ABC 中,若2sin 6sin a C A =,()2216a c b +=+,则用“三斜求积”公式求得ABC 的面积为()A .2B C .D .二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列说法正确的是()A .如果α是第一象限的角,则α-是第四象限的角B .如果α,β是第一象限的角,且αβ<,则sin sin αβ<C .若圆心角为3π的扇形的弧长为π,则该扇形面积为23πD .若圆心角为23π的扇形的弦长为83π10.已知平面向量()0,1a =,()2b = ,则下列说法正确的有()A .36a b +=B .()()30a b a b +⋅-=-C .向量a b + 在a上的投影向量为3aD .向量a b + 与a 的夹角为3π11.已知不相等的复数1z ,2z ,则下列说法正确的是()A .若20z <,则z 是纯虚数B .若12=z z ,则2212z z =C .若21z =z ,则1z ,2z 在复平面内对应的点关于实轴对称D .若22120z z ->,则2212z z >12.已知函数()()cos 206f x x πωω⎛⎫=-> ⎝⎭的最小正周期为2π,将()f x 的图象向左平移6π个单位长度,再把得到的曲线上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数()g x 的图象,则下列结论正确的是()A .()00g =B .()g x 在0,4⎡⎤⎢⎥⎣⎦π单调递增C .()g x 的图象关于4x π=-对称D .()g x 在,123ππ⎡⎤-⎢⎣⎦上的最大值是1第Ⅱ卷三、填空题:本题共4小题,每小题5分,共计20分.13.已知0θπ<<,向量2sin ,2cos 2a θθ⎛⎫= ⎪⎝⎭ ,()1,sin θ= b ,且a b ∥ ,则θ=______________.14.一艘轮船向正东方向航行,在A 处看,灯塔B 在船的北偏东60 方向上,航行30千米后到达C 处,在C 处看,灯塔B 在船的北偏西75 方向上,则此时船与灯塔B 之间的距离是______千米.15.设复数1z ,2z 满足122z z ==,且12z z +=,其中i 为虚数单位,则12z z -=________.16.设函数()66sincos 55kx kxf x =+,其中k 是一个正整数,若对任意实数a ,均有(){}(){}1f x a x a f x x R <<+=∈,则k 的最小值为______.四、解答题:本题共6小题,共计70分.解答时应写出文字说明、证明过程或演算步骤.17.已知平面向量a ,b 满足()1,3a =,2b = .(1)若//b a,求b 的坐标;(2)若()()25a b a b +⊥- ,求32a b - 的值.18.已知1sin cos 8αα=,且ππ42α<<.(1)求cos sin αα-的值;(2)求()()()()()π11πsin 2πcos πcos cos 229πcos πsin 3π2sin πsin 2αααααααα⎛⎫⎛⎫-+++- ⎪ ⎪⎝⎭⎝⎭⎛⎫--+--+ ⎪⎝⎭的值.19.在ABC 中,a ,b ,c 分别是内角A ,B ,C 所对的边,向量()m b = 与()cos ,sin n B A =r共线.(1)求角B 的大小;(2)若a +c =5,ABC 外接圆面积为16π3,求ABC 内切圆的半径.20.已知()1sin cos sin 23234f x x x x ππ⎛⎫=++⎛⎫⎪⎝⎭+- ⎪⎝⎭.(1)求()f x 的单调递增区间;(2)若122612x af x f ππ--⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭+≥对任意的5,66x ππ⎡⎤∈⎢⎥⎣⎦恒成立,求a 的取值范围.21.已知函数()()sin 0,0,02f x A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭的图象如图所示.(1)求()f x 的解析式;(2)若函数()()sin 4g x f x x =+,当,62x ππ⎡⎤∈⎢⎥⎣⎦时,求()g x 的值域.22.如图,风景区的形状是如图所示的扇形OAB 区域,其半径为4千米,圆心角为60°,点C 在弧AB 上.现在风景区中规划三条商业街道DE 、CD 、CE ,要求街道DC 与OA 平行,交OB 于点D ,街道DE 与OA 垂直(垂足E 在OA 上).(1)如果弧BC 的长为弧CA 长的三分之一,求三条商业街道围成的△CDE 的面积;(2)试求街道CE 长度的最小值.1.D 【分析】直接利用复数的模的求法的运算法则求解即可.【详解】() 125i z i -=(i 是虚数单位)可得()125i z i -=解得z =本题正确选项:D 【点睛】本题考查复数的模的运算法则的应用,复数的模的求法,考查计算能力.2.C 【分析】利用诱导公式,同角三角函数的平方关系以及二倍角公式化简求解【详解】由题0a >,()sin10sin100sin 9010cos10a a a ︒=︒=+=,又因为22sin 10cos 101+= 解得sin10==又因为21sin 202sin10cos102a a ︒==+=故选:C 3.A 【分析】设z x yi =+,得到()()22221x y ++-=,化简得到12z i --何意义计算得到答案.【详解】设z x yi =+,则()()22221z i x y i +-=++-==,即()()22221x y ++-=,表示圆心为()2,2-,半径为1r =的圆.()()1212z i x y i --=-+-=,表示点(),x y 和()1,2之间的距离,故()()min 12122z i r --=---=.故选:A.【点睛】本题考查了复数的模,与圆相关距离的最值问题,意在考查学生的计算能力和转化能力.4.A 【分析】由向量夹角为90 ,可得22()()0a b a b a b +⋅-=-=,进而求得tan 2θ=,由222221sin cos tan 12sin cos cos 2sin cos cos 2tan 1θθθθθθθθθθ++==+++代入求解即可.【详解】由()()tan ,1,1,2a b θ=-=- ,a b + 与a b - 夹角为90 ,则22()()0a b a b a b +⋅-=-=,所以2tan 150θ+-=,θ为锐角,解得tan 2θ=.222221sin cos tan 14112sin cos cos 2sin cos cos 2tan 141θθθθθθθθθθ+++====++++.故选A.【点睛】本题主要考查了向量的数量积的坐标运算及三角函数的基本关系,考查了利用三角齐次式进行弦化切的转化,属于中档题.5.B 【分析】利用正弦定理、余弦定理将角化为边,即可得到,a b 之间的关系,从而确定出三角形的形状.【详解】因为2cos sin sin B A C =,所以22222a c b a c ac+-⋅⋅=,所以22a b =,所以a b =,所以三角形是等腰三角形,故选:B.【点睛】本题考查利用正、余弦定理判断三角形的形状,难度一般.本例还可以直接利用()sin sin C A B =+,通过三角函数值找到角之间的联系从而判断三角形形状.6.C 【分析】由题意列出不等式,根据正弦函数的图象与性质求解即可.【详解】由题意,可知()2124sin 10123H t t ⎛⎫=+-≥ ⎪⎝⎭ππ,即21sin 1232t ⎛⎫-≥- ⎝⎭ππ,因为024t ≤<,所以22431233t -≤-<ππππ,由正弦函数图象与性质可知,2761236t -≤-≤ππππ,解得622t ≤≤,所以该港口一天内水深不小于10m 的时长为22616-=小时,故选:C 7.B 【分析】根据三角函数诱导公式及三角恒等变换公式化简即可.【详解】17sin sin 918π9sin1sin cos sincos99999πππππ-===49995sin)4cos()4cos 18225sinsin cos99186ππππππππ-+===.故选:B .8.C 【分析】根据若2sin 6sin a C A =,()2216a c b +=+,得到ac 和222a c b +-,代入S =.【详解】解:因为2sin 6sin a C A =,所以26=a c a ,即6ac =,又()2216a c b +=+,所以2224a c b +-=,所以=S ,故选:C 9.AD 【分析】由象限角的概念判断A ;举反例判断B ;由扇形弧长、面积公式计算判断C ,D 作答.【详解】对于A ,α是第一象限的角,即22,Z 2k k k ππαπ<<+Î,则22,Z 2k k k ππαπ--<<-Î,α-是第四象限的角,A 正确;对于B ,令11,66ππαβ=-=,α,β是第一象限的角,且αβ<,而sin sin αβ=,B 不正确;对于C ,设扇形所在圆半径为r ,则有3r ππ=,解得3r =,扇形面积13322S ππ=⨯⨯=,C不正确;对于D ,设圆心角为23π的扇形所在圆半径为r ',依题意,4sin3r '==,扇形弧长2833l r ππ'==,D 正确.故选:AD 10.BCD 【分析】根据向量的模的坐标公式即可判断A ;根据根据数量积的坐标运算即可判断B ;根据,向量a b + 在a上的投影向量为()a b a a a a+⋅⋅ ,即可判断C ;根据向量夹角的计算公式即可判断D.【详解】解:对于A ,()a b +=,则6a b +=,故A 错;对于B,()1a b -=-- ,则()()27330a b a b +⋅-=--=- ,故B 正确;对于C ,向量a b + 在a上的投影向量为()3a b a a a a a+⋅⋅=,故C 正确;对于D,()31cos ,62a b a a b a a ba+⋅+===+,又0,a b a π≤+≤,所以向量a b + 与a 的夹角为3π,故D 正确.故选:BCD.11.AC 【分析】由题意设(),z a bi a b R =+∈,由复数的乘法运算及性质可得0,0a b =≠,即可判断A ;举出反例即可判断B 、D ;由复数的几何意义可判断C ,即可得解.【详解】对于A ,设(),z a bi a b R =+∈,则22220z a b abi =-+<,则0ab =且220a b -<,所以0,0a b =≠,所以z 是纯虚数,故A 正确;对于B ,若11z =,2z i =,此时121z z ==,但221211z z =≠=-,故B 错误;对于C ,若()2,z a bi a b R =+∈,在复平面对应的点为(),a b ,则()21z =z ,a bi a b R =-∈,在复平面对应的点为(),a b -,所以1z 、2z 在复平面内对应的点关于实轴对称,故C 正确;对于D ,若12z i =+,212z i =+,则2134z i =+,2234z i =-+,此时22120z z ->,但21z 、22z 的大小无法比较,故D 错误.故选:AC.【点睛】本题考查了复数的分类、运算、几何意义的应用,考查了复数模的求解与应用,牢记知识点、举出合理反例是解题关键,属于中档题.12.AC 【分析】由周期求出ω,由图象变换求得()g x 的解析式并化简,然后由正弦函数的性质判断各选项.【详解】由题意222ππω=,2ω=,所以()cos(46f x x π=-,1()cos[4(]cos(4sin 4662g x x x x πππ=+-=+=-,()sin 2=-g x x ,(0)0g =,A 正确;0,4x π⎡⎤∈⎢⎣⎦时,220,x π⎡⎤∈⎢⎥⎣⎦,sin 2y x =递增,()g x 递减,B 错;()sin(142g ππ-=--=是最大值,C 正确;,123x ππ⎡⎤∈-⎢⎥⎣⎦时,22,63x ππ⎡⎤∈-⎢⎥⎣⎦,sin 2y x =的最小值是12-,()g x 的最大值是12,D 错;故选:AC .13.2π【分析】由向量共线的坐标运算可得答案.【详解】因为∥ a b ,所以22sin 2cos 2θθ=,所以2224sincos 2cos 222θθθ=,因为0θπ<<,cos 02θ≠,所以21sin ,sin 222θθ==,因为0θπ<<,所以24θπ=,2πθ=.故答案为:2π.14.【分析】确定三角形ABC ∠的内角度数,根据正弦定理求得答案.【详解】由题意可知AC =30千米,30135BAC ABC ∠=∠=, ,由正弦定理可得sin sin BC AC BAC ABC=∠∠,则130sin 2sin AC BAC BC ABC ⨯∠==∠千米,故答案为:15.【解析】令1,(,)z a bi a R b R =+∈∈,2,(,)z c di c R d R =+∈∈,根据复数的相等可求得2ac bd +=-,代入复数模长的公式中即可得到结果.【详解】设1,(,)z a bi a R b R =+∈∈,2,(,)z c di c R d R =+∈∈,12()z z a c b d i i ∴+=+++=+,1a cb d ⎧+=⎪∴⎨+=⎪⎩12||=||=2z z ,所以224a b +=,224cd +=,222222()()2()4a c b d a c b d ac bd ∴+++=+++++=,2ac bd ∴+=-,12()()z z a c b d i ∴-=-+-===.故答案为:16.8【分析】首先化简函数,()224224345(sin cos )(sin sin cos cos cos 555555858kx kx kx kx kx kx kx f x =+-⋅+=+,根据题意最小正周期1T <,可得52k π>,即可得解.【详解】()66224224sin cos (sin cos sin cos cos )55555555kx kx kx kx kx kx kx kx f x =+=+-⋅+22222(sin cos )3sin cos 5555kx kx kx kx =+-⋅2323451sin cos 45858kx kx =-=+,若对任意实数a ,均有(){}(){}1f x a x a f x x R <<+=∈,则最小正周期1T <,即2145k π<,即52k π>,由Z k ∈,所以8k ≥,所以则k 的最小值为8.故答案为:817.(1)13,22b ⎛⎫= ⎪⎝⎭或13,22b ⎛⎫=-- ⎪⎝⎭ (2)【分析】(1)运用向量的共线定理表示出b ,再根据模长公式建立方程求解即可;(2)根据向量垂直的等价形式求出a b ,再根据模与向量的关系式求解即可.(1)由题意设()1,3b λ= ,b λ== 12λ=±,即13,22b ⎛⎫= ⎪⎝⎭或13,22b ⎛⎫=-- ⎪⎝⎭ ,(2)∵()()25a b a b +⊥- ,∴()()250a b a b +-= ,即222950a b a b --= ,即()22102139504a b ⨯+--⨯= ,故56a b = ,又a ==所以32a b -===18.(1)(2)5【分析】(1)先求()2cos sin αα-,再根据象限判断正负,即可求解。
2021-2022学年山东省聊城市聊城第一中学高一下学期数学检测试题(解析版)

2021-2022学年山东省聊城市聊城第一中学高一下学期数学检测试题一、单选题 1.若复数21iz =-+,则z =( )A .2BC .1D 【答案】B【分析】根据复数的除法运算法则,结合复数模的计算公式进行求解即可. 【详解】因为22(1)11(1)(1)i z i i i i ⋅--===---+-+--,所以z ==故选:B2.在ABC 中,已知6a =,4b =,c =C =( ) A .30︒ B .45︒ C .60︒ D .120︒【答案】C【分析】利用余弦定理的推论计算cos C 的值,进而求出C 的值.【详解】因为6a =,4b =,c = 所以2223616281cos 22642a b c C ab +-+-===⨯⨯, 又()0,180C ︒∈,所以60C ︒=.故选:C .3.已知向量(1,2)a =,(1,0)b =,(3,4)c =.若λ为实数,(a λb +)∥c ,则λ=( ). A .14B .12C .1D .2【答案】B【分析】先求出a λb +的坐标,再由(a λb +)∥c ,,列方程可求得结果 【详解】因为向量(1,2)a =,(1,0)b =, 所以(1,2)(1,0)(1,2)a b λλλ+=+=+, 因为(a λb +)∥c ,(3,4)c =, 所以1234λ+=,解得12λ=,4.已知用斜二测画法画得的正方形的直观图的面积为182,那么原正方形的面积为( ) A .36 B .362C .72D .722【答案】C【分析】根据斜二测画法的原则得到直观图的对应边长关系,即可求出相应的面积. 【详解】解:设原正方形的边长为a ,根据斜二测画法的原则可知O C a ''=,1122O A OA a ''==,高122sin 452A D O A a '''=︒==, ∴对应直观图的面积为222182a ==即272a =,故原正方形的面积为72. 故选:C.5.已知点D 是ABC 所在平面上一点,且满足12BD BC =-,则AD =( )A .1122AB AC -B .1122AB AC +C .1322AB AC -+D .3122AB AC -【答案】D【分析】根据向量的加法、减法法则运算即可得到答案. 【详解】解:由题意:D 为ABC 所在平面内的一点, 12BD BC =-,所以32CD CB =所以()33312222AD AC CD AC CB AC AB AC AB AC =+=+=+-=-故选:D .6.瑞士著名数学家欧拉发现公式i cos isin x x x e =+(i 为虚数单位),它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位.被誉为数学中的“天桥”.根据欧拉公式可知,2021i4πe 表示的复数在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【分析】由欧拉公式并结合三角函数的诱导公式进行计算,并结合复数的几何意义进行判断即可. 【详解】∵2021i 420212021cossin i cos 505sin 505i 4444πππππe ππ⎛⎫⎛⎫=+=+++ ⎪ ⎪⎝⎭⎝⎭ 22cossin i i 4422ππ=--=--, ∴2021i4πe表示的复数在复平面内对应的点22,22⎛⎫-- ⎪ ⎪⎝⎭,位于第三象限. 故选:C.7.已知点G 是三角形ABC 所在平面内一点,满足0GA GB GC ++=,则G 点是三角形ABC 的( ) A .垂心 B .内心C .外心D .重心【答案】D【分析】直接利用平面向量的线性运算和三角形重心的定义,即可判断点G 是△ABC 的重心. 【详解】因为0GA GB GC ++=,所以 GA GB GC CG +=-=.以GA 、GB 为邻边作平行四边形GADB ,连接GD 交AB 于点O .如图所示:则CG GD =,所以13GO CO =,CO 是AB 边上的中线,所以G 点是△ABC 的重心.故选:D8.在棱长为a 的正方体1111ABCD A B C D -中,E 为1AA 的中点,则过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面面积为( )A 2310 B .298aC 232 D 210 【答案】B【分析】取11A D 中点F ,连接BE 、EF 、1C F 、1BC 、1AD ,证明出1//EF BC ,故四点B 、1C 、E 、F 共面,所以过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面为等腰梯形1EFC B ,根据已知,即可求解.【详解】取11A D 中点F ,连接BE 、EF 、1C F 、1BC 、1AD ,因为11//AB C D 且11AB C D =,所以,四边形11ABC D 为平行四边形,所以,11//AD BC ,E 、F 分别为1AA 、11A D 的中点,所以,1//EF AD 且11222EF AD a ==, 所以,1//EF BC ,故B 、1C 、E 、F 四点共面,所以过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面为等腰梯形1EFC B , 其中22EF a =,12BC a =,22152BE C F AB AE a ==+=, 过点E 、F 在平面1BC FE 内分别作1BC 的垂线,垂足点分别为G 、H ,因为1BE C F =,1EBG FC H ∠=∠,12EGB FHC π∠=∠=,所以,1Rt EBG Rt FHC ≅△△,故1BG C H =,在平面1BC FE 内,因为1EG BC ⊥,1FH BC ⊥,1//EF BC , 所以,四边形EFHG 为矩形,则2GH EF ==, 所以,1122BC EF BG C H -==, 所以,梯形1BC FE 的高22225232244a a h BE BG ⎛⎫⎛⎫=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 梯形1B CFE 的面积223219228a S a ⎫=⨯=⎪⎪⎭.故选:B.9.已知非零向量a ,b ,下列说法正确的是( )A .若a b =,则a b =B .若a ,b 为单位向量,则a b =C .若a b >且a 与b 同向,则a b >D .a b a b +≥+【答案】A【分析】根据平面向量的定义依次判断选项即可得到答案.【详解】对于A ,若a b =,则两向量的大小相等,方向相同,故a b =成立,故A 对, 对于B ,若a ,b 都是单位向量,两向量的方向不定,故a b =不成立,故B 错, 对C ,因为两向量不能比较大小,故C 错,对于D ,根据平面向量的三角形法则a b a b +≤+成立,故D 错, 故选:A二、多选题10.下列命题正确的是( )A .如果一条直线上有两个点在一个平面上,那么这条直线不一定在这个平面内B .如果两个不重合的平面有一个公共点,那么他们有且只有一条过该点的公共直线C .过直线外一点,可以作无数个平面与这条直线平行D .如果一条直线平行于平面内的无数条直线,则该直线与平面平行 【答案】BC【分析】由公理1判断A ,由公理3判断B ,由空间中点、线、面的位置关系判断C 和D .【详解】由公理1可知,如果一条直线上有两个点在一个平面上,那么这条直线一定在这个平面内,故A 错误;由公理3知,如果两个不重合的平面有一个公共点,那么他们有且只有一条过该点的公共直线,故B 正确;因为过直线外一点可以作一条直线与已知直线平行,所以经过这条直线且不经过已知直线的平面都与已知直线平行,即过直线外一点,可以作无数个平面与这条直线平行,故C 正确; 一条直线平行于平面内的无数条直线,该直线与平面平行或直线在平面内,故D 错误. 故选:BC .11.已知△ABC 中,D 是BC 上的点,AD 平分BAC ∠,2BD DC =,下列结论正确的是( ) A .sin 2sin C B =B .若30B ∠=︒,则△ABC 为直角三角形C .若60BAC ∠=︒,则△ADC 为等边三角形D .若30BAD ∠=︒,则△ABD 为等腰三角形【答案】ABD【分析】由已知设22BD DC x ==,BAD CAD α∠=∠=,利用正弦定理即可判断A ; 若30B =︒,结合已知得sin 2sin 1C B ==,可求得角C ,即可判断B ;若30BAD ∠=︒,则60BAC ∠=︒,结合sin 2sin C B =,求得△ABC 的内角,即可判断CD. 【详解】解:做出图形:由已知设22BD DC x ==,BAD CAD α∠=∠=, 在△ABD ,△CAD 中,由正弦定理得sin sin AD BDB α=,sin sin AD CDC α=, 两式相除得sin 2sin C BDB CD==,所以sin 2sin C B =. 对于A ,由以上可知,A 正确;对于B ,若30B =︒,结合已知得sin 2sin 1C B ==,故90C =︒,故B 正确; 对于D ,若30BAD ∠=︒,则60BAC ∠=︒,所以120C B =︒-,代入sin 2sin C B =得()sin 1202sin B B ︒-=,即sin120cos cos120sin 2sin B B B ︒-︒=,即33cos sin 22B B =,所以3tan 3B =,所以30B =︒,90C =︒,故△ABD 为等腰三角形,△ADC 为直角三角形,故C 错误,D 正确. 故选:ABD.12.如图,在透明塑料制成的长方体1111ABCD A B C D -容器内灌进一些水,将容器底面一边BC 固定于地面上,再将容器倾斜,随着倾斜度的不同,下列说法中正确的是( )A .水的部分始终呈棱柱状,没水的部分也始终成棱柱状B .水面四边形EFGH 的面积不改变C .棱11AD 始终与水面EFGH 平行 D .当1E AA ∈时,AE BF +是定值 【答案】ACD【分析】从棱柱的特征平面可判断A ;由水面四边形EFGH 的面积是改变的可判断B ;由11//////A D AD CB EH ,11A D ⊄水面EFGH ,EH ⊂水面EFGH ,可判断C ;由体积是定值,高BC 为定值,则底面积EABF 为定值,可判断D .【详解】根据面面平行性质定理,可得BC 固定时,在倾斜的过程中,始终有//////AD EH FG BC , 且平面//AEFB 平面DHGC ,故水的形状成棱柱状,没水的部分也始终成棱柱状,故A 正确; 水面四边形EFGH 的面积是改变的,故B 错误;因为11//////A D AD CB EH ,11A D ⊄水面EFGH ,EH ⊂水面EFGH , 所以11//A D 水面EFGH 正确,故C 正确;由于水的体积是定值,高不变,所以底面ABFE 面积不变, 即当E 在1AA 时,AE BF +是定值.故D 正确. 故选:ACD .三、填空题13.已知复数z 满足2z =,则34z i +-的最小值是______. 【答案】3【分析】根据绝对值不等式a b a b a b -≤+≤+,求出34z i +-的最小值即可. 【详解】∵复数z 满足2z =, ∴3434523z i i z +-≥--=-=, ∴34z i +-的最小值是3. 故答案为3.【点睛】本题主要考查了不等式的应用问题,也考查了复数的运算问题,是基础题目. 14.已知向量(),1a x =,()1,2b =-,且a b ⊥,则a b -=___________.【答案】10【分析】由垂直的坐标表示求得x ,再由模的坐标运算求解. 【详解】由a b ⊥得20a b x ⋅=-=,2x =,则(1,3)a b -=,所以221310a b -=+=.故答案为:10.15.如图所示,位于A 处的信息中心获悉:在其正东方向相距40海里的B 处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30、相距20海里的C 处的乙船,现乙船朝北偏东θ的方向沿直线CB 前往B 处救援,则cos θ=__________.21. 【分析】利用余弦定理求出BC 的数值,正弦定理推出ACB ∠的余弦值,利用()cos cos 30ACB θ=∠+︒展开求出cos θ的值.【详解】解:如图所示,在ABC 中,40AB =,20AC =,120BAC ∠=︒, 由余弦定理得2222cos1202800BC AB AC AB AC =+-⋅⋅︒=, 所以7.BC =由正弦定理得21sin sin AB ACB BAC BC ∠∠=⋅=. 由120BAC ∠=知ACB ∠为锐角,故227cos 1sin ACB ACB ∠=-∠ 故()21cos cos 30cos cos30sin sin3014ACB ACB ACB θ∠∠∠=+=-=. 21.四、双空题16.球面几何是几何学的一个重要分支,在刚海、航空、卫星定位等方面都有广泛的应用.如图,A ,B ,C 是球而上不在同一大圆(大圆是过球心的平面与球面的交线)上的三点,经过这三点中任意两点的大圆的劣弧分别为AB ,BC ,CA ,由这三条劣弧组成的图形称为球面△ABC .已知地球半径为R ,北极为点N ,P 、Q 是地球表面上的两点.①若P ,Q 在赤道上,且经度分别为东经40°和东经100°,则球面△NPQ 的面积为___________.②若26NP NQ PQ ===,则球面NPQ △的面积___________. 【答案】23R π 2R π【分析】利用PQ 所在的经度求出球面三角形PNQ 面积,再利用已知可得三角形PNQ 为等边三角形,进而可以求解.【详解】解:PQ 在赤道上,且经度分别为40︒和100︒,上半球面面积为221422R R ππ⨯⨯=,球面PNQ 面积为226023603R R ππ︒⨯=︒, 当26RNP NQ PQ ==PNQ 为等边三角形, 根据题意构造一个正四面体N PQS -,如图所示: 其中心为O ,O 是高NH 的靠近H 的四等分点, 则1cos cos 3OH OH NOP HOP OP ON ∠=-∠=-=-=-, 由余弦定理可得:22222221cos 223ON OP PN R PN NOP ON OP R +--∠===-⋅, 解得26PN ,正好为题目所给的长度, 所以球面PNQ 的面积为22144PNQS R R ππ=⨯=, 故答案为:23R π;2R π.五、解答题17.如图所示,在三棱柱111ABC A B C -中,E ,F ,G ,H 分别是AB ,AC ,11A B ,11A C 的中点,求证:(1)B ,C ,H ,G 四点共面; (2)平面1EFA ∥平面BCHG . 【答案】(1)证明详见解析 (2)证明详见解析【分析】(1)通过证明//BC GH 来证得,,,B C H G 四点共面. (2)通过面面平行的判定定理来证得平面1EFA ∥平面BCHG . 【详解】(1)由于,G H 分别是1111,A B AC 的中点,所以11//GH B C , 根据三棱柱的性质可知,11//BC B C , 所以//BC GH ,所以,,,B C H G 四点共面.(2)由于,E F 分别是,AB AC 的中点,所以//BC EF ,由于EF ⊂/平面BCHG ,BC ⊂平面BCHG ,所以//EF 平面BCHG .根据三棱柱的性质可知11//,AG BE AG BE =, 所以四边形1BEA G 是平行四边形,所以1//A E BG ,由于1A E ⊂/平面BCHG ,BG ⊂平面BCHG ,所以1//A E 平面BCHG . 由于11,,EF A E E EF A E ⋂=⊂平面1EFA ,所以平面1EFA ∥平面BCHG .18.已知复数()()2204332i z a a a a =-++-+(i 为虚数单位,a R ∈)为纯虚数,0z 和实数b 是关于x 的方程()232i 6i 0x x -++=的两个根.(1)求a ,b 的值;(2)若复数z 满足i z a b =+,说明在复平面内z 对应的点Z 的集合是什么图形?并求该图形的面积.【答案】(1)3a =,3b =;(2)在复平面内z 对应的点Z的集合是以原点为圆心,以为圆,18S π=.【分析】(1)根据纯虚数的定义求得a ,再根据0z 和实数b 是关于x 的方程()232i 6i 0x x -++=的两个根结合韦达定理即可求得b ;(2)设()i,,z x y x y R =+∈,根据i z a b =+,即可求得在复平面内z 对应的点Z 的轨迹,从而得出答案.【详解】解:(1)∵复数()()2204332i z a a a a =-++-+(i 为虚数单位,a R ∈)为纯虚数,∴22430320a a a a ⎧-+=⎨-+≠⎩,解得3a =, ∴02i z =,由韦达定理可得,0032i 6i z b z b +=+⎧⎨=⎩,解得3b =; (2)∵复数z 满足i z a b =+,∴z =设()i,,z x y x y R =+∈,则有2218x y +=,∴在复平面内z 对应的点Z的集合是以原点为圆心,以为∴218S πr π==.19.已知ABC的面积为①、条件②这两个条件中选择一个作为已知,求:条件①6a =,1cos 3=-C ;条件②:A C =,7cos 9B =-. (1)b 和c 的值.(2)sin()A B -的值.【答案】(1)若选①:2b =,c =②:8b =,c =(2)若选①;若选②:2327-.【分析】若选择条件①:(1)利用同角三角函数基本关系式可求sin C 的值,利用三角形的面积公式可求a ,b 的值,进而根据余弦定理可求c 的值.(2)由正弦定理可求sin A ,sin B 的值,利用同角三角函数基本关系式可求cos A ,cos B 的值,进而根据两角差的正弦公式即可求解sin()A B -的值.若选择条件②:(1)由题意可得a c =,利用同角三角函数基本关系式可求sin B ,利用三角形的面积公式可求a ,c 的值,根据余弦定理可求b 的值.(2)由正弦定理可求sin A ,利用同角三角函数基本关系式可求cos A ,利用两角差的正弦公式即可求解sin()A B -的值.【详解】(1)若选择条件①:在ABC 中,∵1cos 3=-C ,∴(,)2C ππ∈,sin C∵1sin 2S ab C ==6a =,∴2b =,由余弦定理,2222cos 48c a b ab C =+-=, ∴c =若选择条件②:在ABC 中,∵A C =,∴a c =.∵7cos 9B =-,∴(,)2B ππ∈,sin B ==,∵211sin 22S ac B c ===∴a c ==由余弦定理,2222cos 64b a c ac B =+-=,∴8b =;(2)若选择条件①:由正弦定理sin sin sin a b c A B C ==,可得62sin sin A B =,∴sin A =sin B , ∵,(0,)2A B π∈,∴cos Acos B ,∴sin()sin cos cos sin A B A B A B -=-. 若选择条件②: 由正弦定理得sin sin a b A B =,∴1sin sin 3aA B b ==, ∵(0,)2A π∈,∴cos 3A ==∴1723sin()sin cos cos sin ()3927A B A B A B -=-=⨯-=-. 20.已知向量a 与b 的夹角为34πθ=,且3a =,22b =. (1)若2ka b +与34a b +共线,求k ;(2)求a 与a b +的夹角的余弦值.【答案】(1)32;(2. 【分析】(1)可设()234ka b a b λ+=+,可得出关于λ、k 的方程组,解出这两个未知数即可得解;(2)计算出()a a b ⋅+、a b +的值,利用平面向量的数量积可求得a 与a b +的夹角的余弦值.【详解】(1)若2ka b +与34a b +共线,则存在λ,使得()234ka b a b λ+=+即()()3240k a b λλ-+-=, 又因为向量a 与b 不共线,所以30240k λλ-=⎧⎨-=⎩,解得1232k λ⎧=⎪⎪⎨⎪=⎪⎩,所以32k =; (2)cos 36a b a b θ⎛⋅=⋅=⨯=- ⎝⎭, 222912a b a a b b +=+⋅+=- ()296cos ,35a ab a a ba ab a a b a a b ⋅++⋅-<+>====⋅++21.如图一个透明的球形装饰品内放置了两个具有公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知大圆锥轴截面是等边三角形,设球的半径为R ,圆锥底面半径为r .(1)试确定R 与r 的关系;(2)若小圆锥、大圆锥的侧面积为1S 、2S ,球的表面积为3S ,求123::S S S ;(3)求出两个圆锥的总体积(即体积之和)与球的体积之比.【答案】(1)3R r =;(2)123::3S S S =;(3)3:8. 【分析】(1)根据题意分析出△ABC 为直角三角形,及30ABC ∠=︒,进而得到答案;(2)由题意,求出大小圆锥的母线长,进而算出它们的侧面积,再求出球的表面积,最后得到答案;(3)根据(1),求出圆锥体积之和与球的体积,进而得到答案.【详解】(1)由几何体的特征,得到△ABC 为直角三角形,由于大圆锥的轴截面为等边三角形, 故30ABC ∠=︒,所以:AC R =,3BC R ,所以32BC R r == (2)球心到圆锥底面的距离12R OO =,所以小圆锥的高为22R R R -=, 故小圆锥的母线长为R 3R ,所以213πS R =,2232πS R =⋅,234S πR =⋅,故123::3S S S .(3)由(1)得:两个圆锥的体积和为321232R r R ππ⋅⋅⋅=,球的体积为343R π. 故两个圆锥的体积和为32πR ;体积之比为:334:3:823R R ππ=. 22.如图,某市政府计划在长为1km 的道路AB 一侧的一片区域内搭建一个传染病预防措施宣传区.该区域由直角三角形区域ABC (ACB ∠为直角)和以BC 为直径的半圆形区域拼接而成.点P 为半圆弧上的一点(异于B 、C ),CH AB ⊥.设,62ππA θ⎛⎫∠=∈ ⎪⎝⎭.(1)为了让更多的市民看到宣传内容,达到最佳宣传效果,需满足CAB PBC ∠=∠,且CA CP +达到最大值.求θ为何值时,CA CP +最大,最大值为多少?(2)为了让宣传栏达到最佳稳定性,更加耐用,需满足π3PBA ∠=,且CH CP +达到最大值.问当θ为何值时,CH CP +取得最大值.【答案】(1)3πθ=时,AC CP +的最大值为54;(2)512πθ=. 【分析】(1)由题意得BAC PBC θ∠=∠=,则cos AC θ=,2sin PC θ=,再结合平方关系及二次函数的最值即可出答案;(2)在直角△ABC 中,由1122ABC S CA CB AB CH =⋅⋅=⋅,得sin cos CH θθ=,在直角△PBC 中,sin sin 6πPC θθ⎛⎫=- ⎪⎝⎭,再利用三角恒等变换结合正弦函数的性质即可得出答案. 【详解】解:(1)由题意得BAC PBC θ∠=∠=,1AB =千米,则在直角△ABC 中,cos AC θ=,sin BC θ=,在直角△PBC 中,2sin sin PC BC θθ=⋅=,2cos cos 1AC CP θθ+=-++,,62ππθ⎛⎫∈ ⎪⎝⎭, 所以当1cos 2θ=,即3πθ=时,AC CP +的最大值为54; (2)在直角△ABC 中,由1122ABC SCA CB AB CH =⋅⋅=⋅, 解得sin cos sin cos 1θθCH θθ==, 在直角△PBC 中,sin sin sin 326πππPC BC θθθ⎡⎤⎛⎫⎛⎫=⋅--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 所以31sin cos sin cos 2CH CP θθθθθ⎫+=+-⎪⎪⎝⎭,,62ππθ⎛⎫∈ ⎪⎝⎭, 故23131cos 21sin cos sin cos 222θCH CP θθθθθ-++=+11sin 22sin 2423πθθθ⎛⎫==- ⎪⎝⎭,所以当512πθ=时,CH CP +.。
2021-2022学年江苏省盐城市响水中学高一年级下册学期第二次学情分析考试数学试题【含答案】

2021-2022学年江苏省盐城市响水中学高一下学期第二次学情分析数学试题一、单选题1.设复数z 满足(其中i 为虚数单位),则( )2i z =-z =ABC .5DA【分析】利用复数求模长公式进行计算.=故选:A2.已知样本9,10,11,x ,y 的平均数是10xy =( )A .93B .94C .95D .96D【分析】根据平均数和标准差列方程即可求解.【详解】由题意 ,91011105x y++++=,解得 或 ,()()222010108x y x y +=⎧⎪∴⎨-+-=⎪⎩812x y =⎧⎨=⎩128x y =⎧⎨=⎩∴ ;96xy=故选:D.3.设, ,)1cos 662a =22tan131tan 13b =-c =A .B .C.D .a b c >>a b c <<a c b<<b c a<<C【分析】利用和差公式,二倍角公式等化简,再利用正弦函数的单调性比较大小.,,a b c 【详解】,1cos 66sin 30cos 6cos30sin 6sin(306)sin 242a ==-=-= ,,22tan13tan 261tan 13b ==-sin 25c == 因为函数在上是增函数,,sin y x =()0,90 242526<<所以sin 24sin 25sin 26<<由三角函数线知:,,因为,sin 26MP = tan 26AT =MP AT <所以,所以sin 26tan 26<a c b<<故选:C.4.已知平面平面,直线平面,直线平面,,在下列说法α⊥βm ⊂αn ⊂βl αβ= 中,①若,则;②若,则;③若,则.m n ⊥m l ⊥m l ⊥m β⊥m β⊥m n ⊥正确结论的序号为( )A .①②③B .①②C .①③D .②③D【分析】由面面垂直的性质和线线的位置关系可判断①;由面面垂直的性质定理可判断②;由线面垂直的性质定理可判断③.【详解】平面平面.直线平面,直线平面,,α⊥βm ⊂αn ⊂βl αβ= ①若,可得,可能平行,故①错误;m n ⊥m l ②若,由面面垂直的性质定理可得,故②正确;m l ⊥m β⊥③若,可得,故③正确.m β⊥m n ⊥故选:D .本题考查空间线线和线面、面面的位置关系,主要是平行和垂直的判断和性质,考查推理能力,属于基础题.5.在中,内角A ,B ,C 的对边分别为a ,b ,c .若,则的形ABC 1cos cos b B a A -=ABC 状是( )A .锐角三角形B .直角三角形C .等腰三角形D .等腰直角三角形C【分析】通过正弦定理将边化为角,化简即可得结果.【详解】由正弦定理得,即,sin cos sin sin cos B A A A B =-sin sin C A =由于为三角形内角,所以.,A C C A =故选:C.6.如图正方体中,M ,N 分别是,的中点,则正确的是1111ABCD A B C D -1AD 1BD ( )A .且平面ABCD 11A D BD ⊥MN ∥B .且平面11A D BD ⊥MN ∥11BDD B C .与相交且平面ABCD 1A D 1BD MN ∥D .与异面且平面1A D 1BD MN ∥11BDD B A【分析】结合线线垂直、线面平行和直线相交、异面等知识正确答案.【详解】由于平面,所以与平交,由此排除BD 选项.1N BD ∈⊂11BDD B MN 11BDD B 由于平面,平面,且,1BD ⊂11BDD B 1A D ⋂11BDD B D =1D BD ∉根据异面直线的知识可知:与是异面直线.由此排除C 选项.1A D 1BD 对于A 选项,根据正方体的性质可知,1111,,A D AD A D AB AD AB A ⊥⊥= 所以平面,所以.1A D ⊥1ABD 11A D BD ⊥由于分别是的中点,所以,,M N 11,AD BD //MN AB由于平面平面,所以平面,所以A 选项正确.MN ⊂,ABCD AB ⊂ABCD //MN ABCD 故选:A7.在△中,,E 是上一点.若,则( )ABC 2BD DC =AD 12λ=+ CE CA CB λ=A .B .C .D .16121413A【分析】根据图形可设,从而得到,根据已知条件= AE m AD (1)3m CE m CA CB =-+,即可求出的值.12λ=+ CE CA CBλ【详解】如图所示,设,=AE m AD 则1()3⎛⎫=+=+=+-=+- ⎪⎝⎭CE CA AE CA mAD CA m CD CA CA m CB CA ,(1)3=-+m m CA CB又∵,∴,∴,12λ=+CE CA CB 12m =136λ==m 故选:.A 8.如图,在平行六面体中,点是棱上靠近的三等分点,点1111ABCD A B C D -E 1BB B 是棱的中点,且三棱锥的体积为2,则平行六面体的F 1CC 1A AEF -1111ABCD A B C D -体积为( )A .8B .12C .18D .20B【分析】首先设点到的距离为,点到平面的距离为,得到E 1AA dF 11ABB A h,11112△=A AE ABB A S S 再计算平行六面体的体积即可.1111ABCD A B C D -【详解】如图设点到的距离为,点到平面的距离为,E 1AA dF 11ABB A h 则,,1112△=⋅⋅A AE S AA d ,1=⋅ABB A S AA d 所以11112△=A AE ABB A S S ,111,1263△△-=⋅⋅=⇒⋅=A AEF A AE A AEV S h Sh 平行六面体的体积为1111ABCD A B C D -111111-=⋅ABCD A B C D ABB A S V h所以.11111212△-==⋅ABCD A A D AE B C S h V 故选:B本题主要考查几何体的体积,同时考查了三棱锥的体积,属于简单题.二、多选题9.为了了解参加运动会的名运动员的年龄情况,从中抽取了名运动员的年龄200020进行统计分析.就这个问题,下列说法中正确的有( )A .名运动员是总体;B .所抽取的名运动员是一个样本;200020C .样本容量为;D .每个运动员被抽到的机会相等.20CD【分析】根据总体、样本、总体容量、样本容量等概念及在整个抽样过程中每个个体被抽到的机会均等即可求解.【详解】由已知可得,名运动员的年龄是总体,名运动员的年龄是样本,总200020体容量为,样本容量为,在整个抽样过程中每个运动员被抽到的机会均为,2000201100所以A 、 B 错误,C 、D 正确.故选:CD.本题主要考查总体、样本、总体容量、样本容量等概念及抽样的公平性问题,属基础题.10.已知复数的实部为,则下列说法正确的是( )()()()32=-+∈z a i i a R 1-A .复数的虚部为B .复数的共轭复数z 5-z 15=-z iC .D .在复平面内对应的点位于第三象限z =z ACD首先化简复数,根据实部为-1,求,再根据复数的概念,判断选项.z a 【详解】,()()()()23232323223z a i i a ai i i a a i=-+=+--=++-因为复数的实部是-1,所以,解得:,321a +=-1a =-所以,15z i =--A.复数 的虚部是-5,正确;B.复数的共轭复数,不正确;z z 15z i =-+,正确;D.在复平面内对应的点是,位于第三象=z ()1,5--限,正确.故选:ACD11.下列命题中是真命题的是( )A .在四边形ABCD 中,若,且,则四边形ABCD 是菱形0AB CD +=0AC BD ⋅= B .若点G 为的外心,则ABC 0GA GB GC ++=C .向量,能作为平面内的一组基底1(2,3)e =-213,24e ⎛⎫=- ⎪⎝⎭ D .若O 为△所在平面内任一点,且满足,则△ABC ()(2)0OB OC OB OC OA -⋅+-=为等腰三角形ABC AD【分析】A 由相反向量的定义及向量数量积的垂直表示知ABCD 是菱形,B 根据钝角三角形外心即可判断命题的真假,C 由平面内基底的性质判断真假,D 利用向量加减法的几何含义及向量数量积的垂直表示即可判断真假.【详解】A :四边形ABCD 中,由知:线段、平行且相等,由0AB CD +=AB CD 知:对角线相互垂直,即ABCD 是菱形,真命题;0AC BD ⋅=B :以钝角△的外心为例,显然若点G 为外心时,,假命题;ABC 0GA GB GC ++≠C :由已知有,显然共线,所以不能作为平面内的一组基底,假命题;124e e =D : ,,若为中点,则,OB OC CB -=OB OA OC OA AB AC -+-=+ D BC 2AB AC AD += 由有,所以垂直平分,即,()(2)0OB OC OB OC OA -⋅+-= 0CB AD ⋅= AD BC AB AC =故△为等腰三角形.ABC 故选:AD.关键点点睛:利用相反向量的定义、向量数量积的垂直表示、平面中基底的性质、几何图形中向量加减法表示判断各选项所描述命题的真假.12.在正方体中,分别为的中点,则下列结论中1111ABCD A B C D -,,E F G 11,,BC CC BB 正确的是( )A .1D D AF⊥B .二面角F AEC --C .异面直线与1A G EFD .点到平面的距离是点到平面的距离的2倍G AEF C AEF BCD【分析】由于在正方体中,,与不垂直,故与不垂直,判11//D D A A 1A A AF 1D D AF 断选项A ;过点作,交的延长线于,连接,设正方体的棱长为C CM AE ⊥AE M FM 2,,判断选项B ;取的中点,连接,则,tan FCFMC CM ∴∠=11B C H 1,A H GH //GH EF 与所成角即为直线与所成角,在中用余弦定理,判断1A GEF 1A G GH 1A GH ∠11AC G △选项C ;连接交于点,则点到平面的距离与点到平面的距离CG EF N G AEF C AEF 之比为,而∽,判断选项D.GNCN GNF △CNE 【详解】在正方体中,显然有,且在正方体1111ABCD A B C D -11//D D A A中,与不垂直,1111ABCD A B C D -1A A AF 故与不垂直,选项A 错误;1D DAF 过点作,交的延长线于,连接,由二面角的定义可知,C CM AE ⊥AE M FM 即为二面角的平面角,不妨设正方体的棱长为2,则FMC ∠F AE C --1,CF CM === ,选项B 正确;tan FC FMC CM ∴∠===取的中点,连接,则,11B C H 1,A H GH //GH EF 故异面直线与所成角即为直线与所成角1A G EF 1A G GH 1A GH∠而,1A H =1A G ==GH ==故在中,由余弦定理可得11AC G △,选项C 正确;2221111cos 2A G GH A H A GH A G GH +-∠===⋅⋅连接交于点,则点到平面的距离与点到平面的距离之比为CG EF N G AEF C AEF ,而∽ GNCN GNF △CNE 故, 选项D 正确.2GN GFCN CE ==故选:BCD.三、填空题13.一组数据从小到大排列,依次为,若它们的中位数与平均数相等,则2,3,4,,9,10x______.x =8【分析】先计算平均数和中位数,根据题意得出关于x 的方程,解方程得到x 的值.【详解】因为数据2,3,4,,9,10的中位数与平均数相等,所以x ,解得.423491026x x ++++++=8x =主要考查了平均数,中位数的概念和方程求解的方法.要掌握这些基本概念才能熟练解题.14.如图,某人在高出海平面方米的山上P 处,测得海平面上航标A 在正东方向,俯角为,航标B 在南偏东,俯角,且两个航标间的距离为200米,则30°60︒45︒__________米.h =200【分析】根据题意利用方向坐标,根据三角形边角关系,利用余弦定理列方程求出的值.h 【详解】航标在正东方向,俯角为,由题意得,.A 30°60APC ∠=︒30PAC ∠=︒航标在南偏东,俯角为,则有,.B 60︒45︒30ACB ∠=︒45CPB ∠=︒所以,;BC PC h ==tan 30PCAC ==︒由余弦定理知,2222cos AB BC AC BC AC ACB =+-∠即,224000032h h h =+-可求得(米.200h =)故200.本题考查方向坐标以及三角形边角关系的应用问题,考查余弦定理应用问题,是中档题.15.在 中.已知,为线段上的一点,且满ABC ∆2CD DB =P AD足.若的面积为,则的最小值为12CP CA mCB =+ ABC ∆3ACB π∠=CP_______.2【分析】利用A ,P ,D 三点共线可求出m ,并得到.再利用平面13=1123CP CA CB =+ 向量的基本性质和基本不等式即可求出的最小值.CP【详解】解∵12CP CA mCB=+13(2)22CA m CD CD DB=+⋅=∵A ,P ,D 三点共线,∴,即m .13122m +=13=∴131223CP CA CD=+⨯ 1122CA CD=+ 112223CA CB =+⨯,1123CA CB =+又∵.3ABC S ACB π=∠=∴,即CA •CB =8.12CA CBsin ACB ⋅∠=∴8ab =∴CP ==)CA b CB a ===令,=≥.2==故答案为2.本题考查平面向量共线定理,是中档题,解题时要认真审题,注意平面向量线性运算的运用.四、双空题16.若正三棱台中上底的边长为1,下底的边长为2,侧棱长为1,则它111ABC A B C -的表面积为_________,与所成角的余弦值为_______________.1AA 1BC【分析】根据题目所给边长,直接求表面积即可得解,延长交于点,111,,AA BB CC P 作中点,中点,连接, ,则与1PC N AB M 11,,MN B N MB 1111//,//MB AA B N BC 1AA 所成角即为和所成角,在中解三角形,即可得解.1BC 1MB 1B N1MB N【详解】根据题意正三棱台的上下底面为等边三角形,111ABC A B C -上底面为边长为1的等边三级形,下底为边长为2的等边三角形,侧面为等腰梯形上底边长为1,下底边长为2,腰长为1,所以高h=所以面积,111122322S =⨯⨯⨯⨯延长交于点,111,,AA BB CC P 由上底的边长为1,下底的边长为2,所以分别为中点,111,,A B C ,,PA PB PC 作中点,中点,连接,1PC N AB M 11,,MN B N MB ,则与所成角即为和所成角,1111//,//MB AA B N BC 1AA 1BC 1MB 1B N 连接,在底面的投影为,为底面的中心且在上,MC P O O MC 作于,显然NH MC ⊥H //NH PO 由,23CO ==2PC=所以PO ===所以,34NHPO ==MH MOOH =+==所以,,32MN ==212APMB ==在等腰梯形上底边长为1,下底边长为2,腰长为1,11BCC B 所以,1BC =1B N =在中,,1MB N222111211cos 2MB B N MN MB N MB B N +-∠===⋅根据线线所成角的范围,则与1AA 1BC 故.本题考查了求空间几何体的表面积,考查了异面直线所成角,计算量较大,属于较难题.本题的关键点为:(1)通过平移把异面直线平移到同一平面中;(2)通过空间线面关系进行计算,是本题的核心能力.五、解答题17.已知复数满足(a >0,a ∈R ),且,其中为虚数单位.z i 1i ⋅=-+z a 2z z +∈R i (1)求复数;z (2)若复数,,在复平面内对应的点分别为A ,B ,C ,求cos ∠ABC .z 2z 2z z -(1)1iz =+【分析】(1)根据,得到,进而得到为实数求解.i 1i ⋅=-+z a i z a =+2z z +(2)化简得到复数所对应的点,进而得到向量 和的坐标,然后利用向量的夹BA BC 角公式求解.【详解】(1)解:因为,i 1i ⋅=-+z a 所以,()i 1i i=--+=+z a a 则,22i i +=+++z a z a ,()22i i 1-=+++a a a ,22221i 11⎛⎫=++-∈ ⎪++⎝⎭a a Ra a 所以,22101a -=+所以,21a =又,所以,0a >1a =所以.1i z =+(2),,()221i 2iz =+=21i z z -=-所以,,,()1,1A ()0,2B ()1,1C -所以,,()1,1BA =-()1,3BC =-.cos cos ,BA BC ABC BA BC BA BC⋅∠=<>==18.某企业员工人参加“抗疫”宣传活动,按年龄分组:第组,第组x 1[)25,302,第组,第组,第组,得到的频率分布直方图如图[)30,353[)35,404[)40,455[]45,50所示.区间[)25,30[)30,35[)35,40[)40,45[]45,50频数5050a 150b(1)上表是年龄的频数分布表,结合此表与频率分布直方图,求正整数、、的值;x a b (2)现在要从年龄较小的第、、组中用分层抽样的方法抽取人,问:这三组应各12330取多少人?(3)若同组中的每个数据用该组区间的右端点值代替,根据频率分布直方图估计该企业员工的平均年龄.(1),,500x =200a =50b =(2)这三组中抽取的人数分别为、、5520(3)41【分析】(1)计算出第组的频率,结合频率、频率和总人数之间的关系可求得的值,1x 再利用频率、频率和总人数之间的关系可求得、的值;a b (2)计算出第、、组的人数之比,结合分层抽样可计算出这三组所抽取的人数;123(3)将每个矩形底边的右端点值乘以对应矩形的面积,将所得结果全加可得结果.【详解】(1)解:第组的频率为,所以,,150.020.1⨯=505000.1x ==,50050.08200a =⨯⨯=.5000.02550b =⨯⨯=(2)解:第、、组的人数之比为,12350:50:2001:1:4=现在要从年龄较小的第、、组中用分层抽样的方法抽取人,12330第组抽取的人数为人,第组所抽取的人数为人,113056⨯=213056⨯=第组所抽取的人数为人.3430206⨯=(3)解:,300.025350.025400.085450.065500.02541x =⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=所以估计该企业员工的平均年龄为.4119.在中,角 ,,所对边分别为,,,且.ABC A B C a b c ()tan 2tan b A c b B=-(1)求角;A (2)若向量,,求的取值范围.()cos ,2cos m B A =20,cos 2C n ⎛⎫= ⎪⎝⎭ 2m n -(1);(2).60︒【分析】(1)首先,利用正弦定理,正切化为正弦和余弦,化简得,求角;1cos 2A =(2)根据(1)的结果,得的坐标,再化简,根据角2m n - 121sin 226m n B π⎛⎫-=-- ⎪⎝⎭ 的范围求模的范围.B 【详解】解:(1)由,及正弦定理,()tan 2tan b A c b B=-得,()sin sin sin 2sin sin cos cos A BBC B A B =-即,sin cos cos sin 2sin cos A B A B C A +=即,()sin 2sin cos A B C A+=所以,.1cos 2A =3A π=(2),()222cos ,12cos cos ,cos cos ,cos 23C m n B B C B B π⎛⎫⎛⎫⎛⎫-=-==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 所以,22241cos 221cos 232cos cos 322B B m n B B ππ⎛⎫+- ⎪+⎛⎫⎝⎭-=+-=+⎪⎝⎭ 11sin 226B π⎛⎫=-- ⎪⎝⎭由于,得,203B π<<1sin 2,162B π⎛⎫⎛⎤-∈- ⎪ ⎥⎝⎭⎝⎦所以.2m n -∈ 20.如图,四棱锥P -ABCD 中,底面ABCD 为菱形,PA ⊥底面ABCD ,PA =2,E 是线段PC 上的一点,.PC =()RPE EC λλ=∈(1)试确定实数,使平面BED ,并给出证明;λ//PA (2)当时,证明:PC ⊥平面BED .2λ=(1),证明见解析1λ=(2)证明见解析【分析】(1)作辅助线,连接AC ,可证明当E 为PC 中点时,使平面BED ,即//PA 得答案.(2)证明平面PAC ,即证明,再通过证明△PAC 与△OEC 相似,证明BD ⊥BD PC ⊥,根据线面垂直的判定定理,即可证明PC ⊥平面BED .PC OE ⊥【详解】(1)连接AC ,且,AC BD O =若平面BED ,因为平面PAC ,平面平面,PA ∥PA ⊂PAC BED EO =所以,又因为O 为AC 中点,PA EO ∥所以E 为PC 中点,即.1λ=当时,E 为PC 中点,又因为O 为AC 中点,1λ=所以,平面BED ,平面BED ,PA OE ∥PA ⊂OE ⊂所以平面BED .PA ∥(2)连接OE ,因为平面ABCD ,平面ABCD ,PA ⊥BD ⊂所以,在菱形ABCD 中,,PA BD ⊥AC BD ⊥又因为,PA AC A = 所以平面PAC ,平面PAC ,BD ⊥PA ⊂所以,BD PC ⊥在直角三角形PCA 中,,2PA =PC =AC =所以OC =因为,所以,所以2λ=CE =CE OC=又,故△PAC 与△OEC 相似,AC PC=CE AC OC PC =所以,PC OE ⊥又因为,,OE ,平面BED ,PC BD ⊥OE BD O = BD ⊂所以平面BED .PC ⊥21.如图,四棱锥P -ABCD 的底面ABCD 是平行四边形,BA =BD ,AD =2,PA =PD E ,F 分别是棱AD ,PC 的中点.(1)证明:EF ∥平面PAB ;(2)若二面角P -AD -B 为60°.①证明:平面PBC ⊥平面ABCD ;②求直线EF 与平面PBC 所成角的正弦值.(1)证明见解析;(2)①证明见解析;.【详解】试题分析:(1)要证明平面,可以先证明平面,利用线//EF PAB //EF MA 面平行的判定定理,即可证明平面;(2)①要证明平面平面//EF PAB PBC ⊥,可用面面垂直的判定定理,即只需证明平面即可;②由①ABCD PB ⊥ABCD平面,所以为直线与平面所成的角,由BE ⊥PBC FEB ∠EF PBC PB 为直角,即可计算的长度,在中,即计算直线与平面ABP ∠,AM EF Rt EBF ∆EF 所成的角的正弦值.PBC 试题解析:(1)证明:如图,取PB 中点M ,连接MF ,AM .因为F 为PC 中点,故MF ∥BC 且MF =BC .由已知有BC ∥AD ,BC =AD .12又由于E 为AD 中点,因而MF ∥AE 且MF =AE ,故四边形AMFE 为平行四边形,所以EF ∥AM .又AM ⊂平面PAB ,而EF ⊄平面PAB ,所以EF ∥平面PAB .(2)①证明:如图,连接PE ,BE .因为PA =PD ,BA =BD ,而E 为AD 中点,故PE ⊥AD ,BE ⊥AD ,所以∠PEB 为二面角P -AD -B 的平面角.在△PAD 中,由PA =PD AD =2,可解得PE =2.在△ABD 中,由BA =BD AD =2,可解得BE =1.在△PEB 中,PE =2,BE =1,∠PEB =60°,由余弦定理,可解得PB 从而∠PBE =90°,即BE ⊥PB .又BC ∥AD ,BE ⊥AD ,从而BE ⊥BC ,因此BE ⊥平面PBC .又BE ⊂平面ABCD ,所以平面PBC ⊥平面ABCD .②连接BF .由①知,BE ⊥平面PBC ,所以∠EFB 为直线EF 与平面PBC 所成的角.由PB∠ABP 为直角.而MB =PBAMEF12又BE =1,故在Rt △EBF 中,sin ∠EFB =.BE EF 所以直线EF 与平面PBC 直线与平面平行的判定及直线与平面垂直的判定与性质;直线与平面所成角的求解.【方法点晴】本题主要考查了直线与平面平行的判定及直线与平面垂直的判定与性质,直线与平面所成角的求解,熟练掌握线面位置关系的判定定理与性质定理是解答基础,同时根据题设条件确定直线与平面所成的角是解答的关键,本题的第二问的解答中,根据平面,可以确定为直线与平面所成的角,可放置在BE ⊥PBC FEB ∠EF PBC 中,即计算直线与平面所成的角的正弦值.Rt EBF ∆EF PBC 22.如图所示,四边形OAPB 中,OA ⊥OB ,PA +PB =10,∠PAO =∠PBO ,∠APB =,56π设∠POA =α,△AOB 的面积为.S (1)用α表示OA 和OB ;(2)求△AOB 面积S 的最大值.(1),;,;(2)π10sin()3sin cos OA ααα+=+π(0,)2α∈π10sin()6sin cos OB ααα+=+π(0,)2α∈【分析】(1)在和中分别利用正弦定理可求得,从而AOP BOP △10sin sin cos AP ααα=+得,在和中再一次分别利用正弦定理可求得OA 和10cos sin cos BP ααα=+AOP BOP △OB ;(2)由(1)表示出,50AOB S = sin cos t αα=+将上式转化为可求出结果25AOB S=π4t α=+∈【详解】解:(1)在中,由正弦定理得.AOP sin sin AP OPPAO α=∠在中,由正弦定理得.BOP △πsin sin()2BP OPPBOα=∠-因为∠PAO =∠PBO ,PA +PB =10,所以,10sin cos AP APαα-=则,.10sin sin cos AP ααα=+10sin 10cos 10sin cos sin cos BP αααααα=-=++因为四边形OAPB 内角和为2,可得∠PAO =∠PBO =,π3π在中,由正弦定理得,AOP sin sin AP OAAPO α=∠即,10πsin cos sin()3OAααα=++所以,π10sin()3sin cos OA ααα+=+π(0,)2α∈在中,由正弦定理得即,BOP △sin sin BP OBBOP BPO =∠∠cos sin BP OB BPO α=∠则,10πsin cos sin()6OBααα=++所以,.π10sin()6sin cos OB ααα+=+π(0,2α∈(2)的面积AOB ππ10sin()10sin()113622sin cos sin cos S OA OB αααααα++=⋅=⋅⋅++=.50=设,.sin cos t αα=+π)4t α+∈则50S ==150(252=当时,即时,t =π4α=S 25=所以AOB。
海南省海口市第一中学2021-2022学年高一下学期期中考试数学试题(A)

海口市第一中学2021-2022学年度第二学期高一年级数学科期中考试试题(A)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|4}A x x =<,{0,1,2,3,4}B =,则A ∩B =()A.{0,1,2} B.{1,2,3}C.{2,3}D.{0,1,2,3}2.1b a >+是33b a >的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.若一个平面图形的直观图是边长为2的正三角形,则该平面图形的面积为()A.64 B. C.24 D.4.已知()f x 为定义在R 上的偶函数,当0x ≤时,()2x f x =,则()f x 的值域为()A.[1,+∞) B.(0,1) C.(0,1] D.(-∞,1]5.函数2()2f x x a x =--的一个零点在区间(1,2)内,则实数a 的取值范围是()A.(1,3)B.(1,2)C.(0,3)D.(0,2) 6.已知3sin()63πα+=-,则2cos(2)3πα-=()A.23- B.13- C.23 D.137.圣·索菲亚教堂(英语:SAINT SOPHIA CATHEDRAL)坐落于中国黑龙江省,是一座始建于1907年拜占庭风格的东正教教堂,距今已有114年的历史,为哈尔滨的标志性建筑.1996年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点.其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美.小明同学为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物AB ,高为15)-m,在它们之间的地面上的点M (,,B M D 三点共线)处测得楼顶A ,教堂顶C 的仰角分别是15︒和60 ,在楼顶A 处测得塔顶C 的仰角为30,则小明估算索菲亚教堂的高度为()A.20mB.30mC.3mD.303m8.已知函数()2sin()(0)6f x x πωω=+>,若方程|()|1f x =在区间(0,2)π上恰有5个实根,则ω的取值范围是()A.75,63⎛⎤ ⎥⎝⎦ B.513,36⎛⎤ ⎥⎝⎦ C.41,3⎛⎤ ⎥⎝⎦ D.43,32⎛⎤ ⎥⎝⎦二、多项选择题:本题共4小题,每小题5分,共20分在每小题给出的四个选项中,有多项符合题目要求全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知复数z 的共轭复数为z ,若1iz i =+,则()A.z 的实部是1 B.z 的虚部是i - C.1z i=+ D.||2z =10.设函数2log (1),2()23,2x x x f x x ->⎧=⎨-≤⎩,则以下结论正确的为()A.()f x 为R 上的增函数B.()f x 有唯一零点0x ,且012x <<C.若()5f m =,则33m =D.()f x 的值城为R11.已知0,0a b >>,且2a b +=,则()A.24a b -<B.22112a b ≥+C.lg lg a b +≤0D.23b a b +≥12.有下列4个关于三角函数的命题,其中是真命题的是()A.0003cos 1x R x x ∃∈+=B.函数44()cos sin 22x x f x =-的图象关于y 轴对称C.若,αβ都是第一象限角,且αβ>,则tan tan αβ>D.当()2sin cos f x x x =+取最大值时,5cos 5x =三、填空题:本题共4个小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021-2022年高一数学下学期第二次间周考试题
一.选择题:(60分)
1.是().
A.第一象限角B.第二象限角
C.第三象限角 D.第四象限角
2.执行如图所示的程序框图,输出的S值为( )
A.2 B.4 C.8 D.16
3.已知为第三象限角,则所在的象限是()
A.第一或第二象限B.第二或第三象限
C.第一或第三象限 D.第二或第四象限角
4.某市共有400所学校,现要用系统抽样的方法抽取20所学校作为样本,调
查学生课外阅读的情况.把这400所学校编上1~400的号码,再从1~20中
随机抽取一个号码,如果此时抽得的号码是6,则在编号为21到40的学校中,
应抽取的学校的编号为( )
A.25 B.26 C.27 D.以上都不是
5.在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是( )
A. B. C. D.
6.已知是第四象限角,,则()
A. B. C.D.
7.若角的终边在第二象限且经过点,则等于
A. B. C. D.
8. 如果一扇形的弧长为,半径等于,则扇形所对圆心角为().A.B. C. D.
9.1001101
(2)
与下列哪个值相等( )
A.115
(8)B.113
(8)
C.114
(8)
D.116
(8)
10.已知件产品中有件次品,其余为合格品.现从这件产品中任取件,恰有一件次品的概率为()
A.B. C. D.
11.从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是()
A.至少有1个白球,都是白球 B.至少有1个白球,至少有1个红球
C.恰有1个白球,恰有2个白球 D.至少有1个白球,都是红球
13.为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示.若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,并决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,则第4组至少有一名志愿者被
抽中的概率为()
A. B. C. D.
二.填空题:(20分)
13.某校高一年级有900名学生,其中女生400名,按男女比例用
分层抽样的方法,从该年级学生中抽取一个容量为45的样本,则
应抽取的男生人数为_______.
14.点在角的终边上,则
15.已知样本数据,,,的均值,则样本数据,,,的均值为.
16.执行如图所示的程序框图,则输出的S值是 .
三.解答题:(60分)
17.对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:
通过计算平均值和方差,回答:甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?18.同时抛掷1角、5角和1元的三枚硬币,计算:
(1)恰有一枚出现正面的概率;
(2)至少有两枚出现正面的概率.
19.某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球和1个白球的甲箱与装有2个红球和2个白球的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(I)用球的标号列出所有可能的摸出结果;
(II)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
20.随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
(Ⅰ)求y 关于t 的回归方程
(Ⅱ)用所求回归方程预测该地区xx 年()的人民币储蓄存款. 附:回归方程中
1
12
2
21
1
()(),
()
.
n n
i
i
i i
i i n
n
i
i
i i x x y y x y nx y
b x x x
nx
a y bx ====⎧---⎪⎪==
⎪⎨--⎪⎪=-⎪⎩
∑∑∑∑
延津县高级中学间周考考试卷
数学参考答案
1~12:BCBBC DABAB CC 13. 14. 15. 16. 17. 解()1
=
6080709070745
x ++++=甲 ()1
=
8060708075735x ++++=乙 ()2222221
=14641641045s ++++=甲
()2222221
=713372565
s ++++=甲
从以上数据可知:,
所以,甲的平均成绩较好,乙的各门功课发展较为均衡。
18. (1)用A 表示“恰有一枚出现正面”这一事件:
则A ={(正,反,反),(反,反,正),(反,正,反)}.因此P(A)=38.
(2)用B 表示“至少有两枚出现正面”这一事件,
则B ={(正,正,反),(正,反,正),(反,正,正),(正,正,正)}, 因此P(B)=48=1
2
.
19. 解:(I )所有可能摸出的结果是:
111211122122{,},{,},{,},{,},{,},{,},A a A a A b A b A a A a 21221212{,},{,},{,},{,},{,},{,},A b A b B a B a B b B b
20. 解:(1)()11234535t =
++++=;()1
5678107.25
y =++++=
5
1
15263748510120i i
i t y
==⨯+⨯+⨯+⨯+⨯=∑
5
21
149162555i
i t
==++++=∑
所以1
2
21
120108
=
=1.25545
n
i i
i n
i i t y nx y
b t nx
==--=
--∑∑
ˆˆ7.2 1.23 3.6a
y bt =-=-⨯= 故所求回归方程为.
(2)将代入回归方程可预测该地区xx 年的人民币储蓄存款为
ˆ 1.26 3.610.8().y
千亿元20316 4F5C 作34882 8842 衂39262 995E 饞20232 4F08 伈#838538 968A 隊 29970 7512 甒31310 7A4E 穎22464 57C0 埀37561 92B9 銹U29523 7353 獓27291 6A9B 檛。
