初中学业水平考试(数学)试卷及答案

合集下载

2023-2024学年北京市6月初中模拟学业水平考试数学试题+答案解析

2023-2024学年北京市6月初中模拟学业水平考试数学试题一、选择题：本题共8小题，每小题3分，共24分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.下列各数中，比的相反数大的是()A.3B.C.2D.12.中国“二十四节气”已被正式列入联合国救科文组织人类非物质文化遗产代表作品录.下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是()A. B. C. D.3.新能源汽车已经成为全球汽车产业转型发展的主要方向，根据中国乘用车协会的统计数据，2023年第一季度，中国新能源汽车销量为159万辆，同比增长，其中159万用科学记数法表示为()A. B. C. D.4.在某月的月历中圈出相邻的3个数，其和为这3个数的位置可能是()A. B. C. D.5.一元二次方程的根的情况为()A.无实数根B.有两个不相等的实数根C.有两个相等的实数根D.不能判定6.如图，在中，，以B为圆心，适当长为半径画弧交BA于点M，交BC于点N，分别以为圆心，大于的长为半径画弧，两弧相交于点D，射线BD交AC于点E，点F为BC的中点，连接EF，若，则的周长是()A.12B.C.D.7.《九章算术》是人类科学史上应用数学的“算经之首”，其书中卷八方程[七]中记载：“今有牛五、羊二，直金十两．牛二、羊五，直金八两．牛、羊各直金几何？”题目大意是：“5头牛、2只羊共值金10两．2头牛、5只羊共值金8两，每头牛、每只羊各值金多少两？”设每头牛值金x两，每只羊值金y两，那么下面列出的方程组中正确的是()A. B. C. D.8.构建几何图形解决代数问题是“数形结合”思想的重要性，在计算时，如图．在中，，，延长CB使，连接AD，得，所以类比这种方法，计算的值为()A. B. C. D.二、填空题：本题共8小题，每小题3分，共24分。

9.因式分解：_______.10.如图，数轴上点M，N表示两个连续整数，点A表示的数是，则点N表示的数是__________.11.甲口袋中装有两个相同的小球，它们上面分别写有数字1和2，乙口袋中装有三个相同的小球，它们上面分别写有数字3，4和5，从两个口袋中各随机摸一个小球，两个小球上的数字都是偶数的概率是__________.12.如图，在A、B两地间修一条笔直的公路，从A地测得公路的走向为北偏东，如果A、B两地同时开工，那么为__________时，才能使公路准确接通．13.已知点，都在反比例函数图象上，则__________.14.方程的解为__________15.如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，P为切点，如果，小圆直径径为6cm，那么大圆半径为______________16.如图是某停车场的平面示意图，停车场外围的长为30米，宽为18米．停车场内车道的宽都相等．停车位总占地面积为288平方米．设车道的宽为x米，可列方程为__________.三、解答题：本题共12小题，共96分。

2024年江西省初中学考数学参考答案

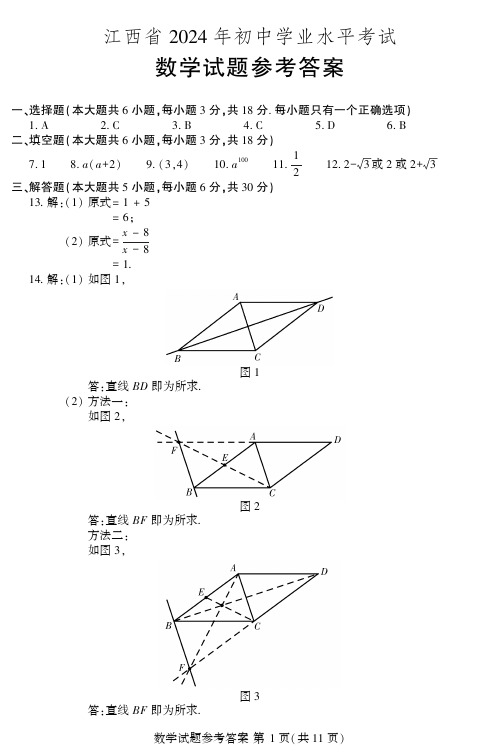
江西省2024年初中学业水平考试数学试题参考答案一㊁选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项) 1.A 2.C 3.B 4.C 5.D 6.B二㊁填空题(本大题共6小题,每小题3分,共18分)7.1㊀㊀8.a(a+2)㊀㊀9.(3,4)㊀㊀10.a100㊀㊀11.12㊀㊀12.2-3或2或2+3三㊁解答题(本大题共5小题,每小题6分,共30分)13.解:(1)原式=1+5=6;(2)原式=x-8x-8=1.14.解:(1)如图1,图1答:直线BD即为所求.(2)方法一:如图2,图2答:直线BF即为所求.方法二:如图3,图3答:直线BF即为所求.15.解:(1)13;(2)解法一:根据题意,列表如下:乙㊀㊀甲A B CA(A,A)(B,A)(C,A)B(A,B)(B,B)(C,B)C(A,C)(B,C)(C,C)总共有9种结果,每种结果出现的可能性相同,而甲㊁乙分到同一个班的结果有3种:(A,A),(B,B),(C,C),()=39=13.所以P甲㊁乙分到同一个班解法二:根据题意,画树状图如下:总共有9种结果,每种结果出现的可能性相同,而甲㊁乙分到同一个班的结果有3种:(A,A),(B,B),(C,C),()=39=13.所以P甲㊁乙分到同一个班16.解:(1)B(2,2);(2)ȵ双曲线y=k x经过点B(2,2),ʑ2=k2.解得k=4.ʑ双曲线的解析式为y=4x.ȵACʅx轴,A(4,0),ʑ点C的横坐标为4.将x=4代入y=4x,得y=44=1.ʑ点C的坐标为(4,1).设BC所在直线的解析式为y=ax+b,则2a+b=2,{解得a =-12,b =3.ìîíïïïʑBC 所在直线的解析式为y =-12x +3.17.解:(1)方法一:ȵAB 是半圆O 的直径,ʑøACB =90ʎ.ȵøABC =60ʎ,ʑøBAD =30ʎ.ȵøD =60ʎ,ʑøABD =90ʎ.ʑBD ʅOB.ȵ点B 是半径OB 的外端点,ʑBD 是半圆O 的切线.方法二:ȵAB 是半圆O 的直径,ʑøACB =90ʎ.ʑøCAB +øABC =90ʎ.ȵøD =øABC ,ʑøCAB +øD =90ʎ.ʑøABD =90ʎ.ʑBD ʅOB.ȵ点B 是半径OB 的外端点,ʑBD 是半圆O 的切线.(2)连接OC.在RtәABC 中,ȵøABC =60ʎ,ʑøBAD =30ʎ.ȵBC =3,ʑAB =2BC =6.ʑOA =OC =3.ʑøACO =øBAD =30ʎ.ʑøAOC =120ʎ.ʑAC (的长=120ˑπˑ3180=2π.因此,AC (的长为2π.四㊁解答题(本大题共3小题,每小题8分,共24分)18.解:(1)方法一:设该书架上有数学书x本,则有语文书(90-x)本.依题意,得0.8x+1.290-x()=84.解得㊀x=60.㊀㊀㊀90-60=30.答:该书架上有数学书60本,语文书30本.方法二:设该书架上有数学书m本,语文书n本.依题意,得m+n=90, 0.8m+1.2n=84.{解得m=60, n=30. {答:该书架上有数学书60本,语文书30本.(2)设在该书架上还可以摆数学书y本.依题意,得0.8y+1.2ˑ10ɤ84.解得㊀㊀㊀㊀㊀㊀㊀㊀yɤ90.答:数学书最多还可以摆90本.19.解:(1)ȵADʊEF,AMʊDN,ʑ四边形AMND是平行四边形.ʑAD=MN.ȵME=FN=20.0m,EF=40.0m,ʑMN=ME+EF+FN=80.0m.ʑAD=80.0m.即大碗的口径为80.0m.(2)作BGʅAM于点G,则øAGB=øBGM=90ʎ.ȵ四边形BEFC是矩形,ʑøBEF=90ʎ.ʑøBEM=90ʎ.ȵAMʅMN,ʑøAME=90ʎ.ʑ四边形GMEB是矩形.ʑGB=ME=20.0m,GM=BE=2.4m.ȵøABE=152ʎ,ʑøABG=øABE-øGBE=152ʎ-90ʎ=62ʎ.ʑAG=GB㊃tanøABG=20㊃tan62ʎʈ37.6(m).ʑAM=AG+GM=37.6+2.4=40.0(m).即大碗的高度约为40.020.解:(1)әBDE是等腰三角形.理由如下:ȵBD平分øABC,ʑøABD=øDBC.ȵDEʊBC,ʑøEDB=øDBC.ʑøEDB=øEBD.ʑEB=ED.ʑәBDE是等腰三角形.(2)①B;②方法一:ȵ四边形ABCD是平行四边形,ʑABʊCD,AB=CD,ADʊBC,AD=BC.ʑøAEB=øEBC,øBAF=øAFD.ȵBE平分øABC,ʑøABE=øEBC.ʑøABE=øAEB.ʑAB=AE.ȵAFʅBE,ʑøBAF=øDAF.ʑøDAF=øAFD.ʑDF=AD=BC.ȵAB=3,BC=5,ʑCF=DF-CD=AD-AB=BC-AB=5-3=2.方法二:连接BF,EF.ȵ四边形ABCD是平行四边形,ʑABʊCD,AB=CD,ADʊBC,AD=BC.ʑøAEB=øEBC,øEDF=øFCB,øABF+øCFB=180ʎ.ȵBE平分øABC,ʑøABE=øEBC.ʑøABE=øAEB.ʑAB=AE.ȵAFʅBE,AF垂直平分BE.ʑEF =BF.ʑәABF ɸәAEF.ʑøABF =øAEF.ȵøDEF +øAEF =180ʎ.ʑøDEF +øABF =180ʎ.ʑøDEF =øCFB.ʑәDEF ɸәCFB.ʑDE =CF.ȵED =AD -AE =BC -AB =5-3=2.ʑCF =2.五㊁解答题(本大题共2小题,每小题9分,共18分)21.解:(1)s =22,t =2,α=72ʎ;(2)①260ˑ210=52(人).答:估计该校七年级男生偏胖的人数为52人.②260ˑ2+110+240ˑ210=126(人).答:估计该校七年级学生BMI ȡ24的人数为126人.(3)建议一:偏胖青少年要加强体育锻炼,注意科学饮食;建议二:BMI 正常的青少年应保持良好的生活习惯;建议三:偏瘦青少年需要加强营养,增强体质.22.解:(1)①m =3,n =6;②方法一:把x =1,y =72ìîíïïï和x =2,y =6{分别代入y =ax 2+bx ,得a +b =72,4a +2b =6.ìîíïïï解得a =-12,b =4.ìîíïïïʑy =-12x 2+4x.将y =14x 代入y =-12x 2+4x ,得1x =-1x 2+4x.解得x 1=0(舍),x 2=152.将x =152代入y =14x ,得y =158.ʑ点A 的坐标是(152,158).方法二:设y =a x -4()2+8,将(2,6)代入,得a 2-4()2+8=6,解得a =-12.ʑy =-12x -4()2+8.即㊀y =-12x 2+4x.将y =14x 代入y =-12x 2+4x ,得14x =-12x 2+4x.解得x 1=0(舍),x 2=152.将x =152代入y =14x ,得y =158.ʑ点A 的坐标是(152,158).(2)①8;(填 v 220亦可)②方法一:ȵy =-5t 2+vt =-5t -v10()2+v 220,ʑv 220=8.ʑv 1=410,v 2=-410.ȵy =-5t 2+vt =-5t -v10()2+v 220的对称轴为t =v 10,ʑv10>0.ʑv >0.v =410.(答案写 410米/秒亦可)方法二:ȵy =-5t 2+vt 的顶点纵坐标为8,ʑ4ˑ-5()ˑ0-v 24ˑ-5()=8.ʑv 1=410,v 2=-410.当v =-410时,y =-5t 2+vt =-5t 2-410t ,ȵt ȡ0,ʑy ɤ0.ʑv =-410不成立.ʑv =410.(答案写 410米/秒亦可)六㊁解答题(本大题共12分)23.解:(1)BE ʅAD ,BE =AD.(或填垂直 , 相等 )(2)BE ʅAD ,BE =mAD ;图1如图1,ȵøACB =90ʎ,øDCE =90ʎ,ʑøACD =øBCE.ȵCE CD =CBCA,ʑәBCE ʐәACD.ʑBE AD =CBCA=m ,øEBC =øDAC.ʑBE =mAD.ȵøBAC +øABC =90ʎ,ʑøEBC +øABC =90ʎ.即øABE =90ʎ.ʑBE ʅAD.图2(3)①方法一:如图2,由(1)知:当m =1时,BE =AD =x ,BE ʅAD.ʑCB =CA =6,CD =CE.ȵøACB =øDCE =90ʎ,ʑAB =CA 2+CB 2=62+62=62.ʑBD =AB -AD =62-x.ʑDE 2=BE 2+BD 2=x 2+(62-x )2=2x 2-122x +72.ȵ点C 与点F 关于DE 对称,ʑCD =CE =EF =DF.ʑ四边形CDFE 是正方形.ʑy =12DE 2=x 2-62x +36.ʑy =x -32()2+18.ʑ当x =32时,y 的最小值为18.图3方法二:如图3,作DG ʅAC 于点G ,ʑøDGA =90ʎ.ȵ在RtәABC 和RtәCDE 中,CE CD =CBCA=1,ʑCD =CE ,CB =CA.ʑøA =45ʎ.ʑDG =AG.ȵ点C 与点F 关于DE 对称,ʑ四边形CDFE 是正方形.ʑAG =DG =22AD =22x.在RtәCDG 中,CD 2=CG 2+DG 2.ʑCD 2=6-22x()2+22x ()2.ʑy =x 2-62x +36.ʑy =x -32()2+18.ʑ当x =32时,y 的最小值为18.方法三:图4如图4,作CG ʅAB 交AB 于点G ,连接CF.ȵ在RtәABC 和RtәCDE 中,CE CD =CBCA=1,ʑCD =CE ,CB =C A.ʑøA =45ʎ.ʑCG =AG.ȵ点C 与点F 关于DE 对称,ʑ四边形CDFE 是正方形.ȵAC =6,ʑCG =AG =32.ʑDG =32-x 或DG =x -32.在RtәCGD 中,CD 2=CG 2+DG 2,ʑCD 2=32-x ()2+32()2.ʑy =x 2-62x +36.ʑy =x -32()2+18.ʑ当x =32时,y 的最小值为18.②22或42.图5方法一:如图5,作CG ʅAB 于点G ,连接CF ,则әCBG 和әCFD 都是等腰直角三角形,ʑCB CG =CFCD=2,øBCG =øFCD =45ʎ,ʑøFCB =øDCG.ʑәCFB ʐәCDG.ʑBF DG =BCCG .图6ʑ232-x =632.ʑx =22.如图6,同理可得:BF DG =BCCG.ʑ2x -32=632.ʑx =42.即AD =22或42.方法二:如图7,连接CF 交DE 于点O ,连接OB.图7ȵәCDE 是等腰直角三角形,点C 与点F 关于DE 对称,ʑCD =CE =FE =FD.ʑ四边形CDFE 是正方形.ʑOF =OC =OD.ȵøCBE =øCAD =45ʎ,øCBA =45ʎ,ʑøEBA =90ʎ.ȵ点O 是DE 的中点,ʑOB =OD.ʑOB =OC =OD =OF.ʑ点B ,C ,D ,F 在以O 为圆心,以OB 为半径的圆上.ʑøCBF +øCDF =180ʎ.ʑøCBF =90ʎ.ȵBC =AC =6,BF =2,ʑCF =BC 2+BF 2=62+22=210.ʑy =210ˑ210ˑ12=20.ʑx 2-62x +36=20.ʑx 1=22,x 2=42.即AD =22或42.方法三:如图8,作CG ʅAB 于点G ,连接CF 交DE 于点O ,连接OB.ȵәCDE 是等腰直角三角形,点C 与点F 关于DE 对称,图8ʑCD =CE =FE =FD.ʑ四边形CDFE 是正方形.ʑOF =OC =OD.ȵøCBE =øCAD =45ʎ,øCBA =45ʎ,ʑøEBA =90ʎ.ȵ点O 是DE 的中点,ʑOB =OD.ʑOB =OC =OD =OF.ʑ点B ,C ,D ,F 在以O 为圆心,以OB 为半径的圆上.ʑøCBF +øCDF =180ʎ.ȵøCDF =90ʎ,ʑøCBF =90ʎ.ȵBC =AC =6,BF =2,图9ʑCF =BC 2+BF 2=62+22=210.ʑCD =25.ȵAC =6,ʑCG =AG =32.ʑDG 2=25()2-32()2=2.ʑDG =2ʑAD =AG -DG =22.如图9,同理可得:AD =AG +DG =32+2=42.即AD =22或42.数学试题参考答案第11页(共11页)。

2024年广东省初中学业水平考试数学(含详解)

2024年广东省初中学业水平考试数学本试卷共4页，23小题，满分120分．考试用时120分钟．注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名、考场号和座位号填写在答题卡上．用2B 铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号．将条形码粘贴在答题卡“条形码粘贴处”．2．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑：如需改动，用橡皮擦干净后，再选涂其他答案、答案不能答在试卷上．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回．一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．的绝对值等于（）A ．B ．3C ．D．2．据教育部统计，2024届全国普通高校毕业生规模预计达1179万人．数据1179万用科学记数法表示为（）A ．B ．C ．D ．3．如题3图是一个由5个相同的正方体组成的立体图形，它的俯视图是（）题3图A ．B ．C ．D ．4．不等式组的解集在数轴上表示为（）A ．B ．C ．D ．3-3-13-1380.117910⨯81.17910⨯611.7910⨯71.17910⨯22343x xx +≥⎧⎨+<⎩5．勾股定理在《九章算术》中的表述是：“勾股各自乘，并而开方除之，即弦．”即为勾，为股，为弦），若“勾”为2，“股”为3，则“弦”最接近的整数是（）A ．2B ．3C ．4D ．56．若关于的方程有实数根，则的值可能是（）A ．4B ．5C ．6D ．77．正方形与的位置如题7图所示，已知，则的度数为（）题7图A ．B ．C ．D ．8．某校运动会的接力赛中，甲、乙两名同学都是第一棒，这两名同学各自随机从四个赛道中抽取一个赛道，则甲、乙两名同学恰好抽中相邻赛道的概率为（）A．B ．C ．D ．9．关于反比例函数，下列说法错误的是（）A ．反比例函数图象经过点B ．当时，C．该反比例函数图象与函数的图象没有交点D ．若点在该反比例函数的图象上，则点也在其图象上10．如题10图，已知菱形的顶点，若菱形绕点逆时针旋转，每秒旋转，则第20秒时，菱形的对角线交点的坐标为（）题10图c a =b c x 240x x c -+=c ABCO Rt DEO △AOD COE α∠+∠=DOC ∠90α︒-90α︒+902α︒-902α︒+4400m ⨯121416182y x=1x >02y <<y x =-(),P m n (),Q m n -OABC ()()0,0,2,2O B O 45︒DA ．B ．C ．D ．二、填空题：本大题共5小题，每小题3分，共15分．11．因式分解：______．12．一个多边形的内角和比外角和多，这个多边形的边数是______．13．代数式与代数式的值相等，则______．14．如题14图，是的直径，是上一点，过点作的切线交的延长线于点，连接，且，若的长为______．题14图15．北宋数学家贾宪提出一个定理“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所得两长方形面积相等（如题15—1图中）”．问题解决：如题15—2图，是矩形的对角线上一点，过点作分别交于点，连接．若，则______．题15—1图题15—2图三、解答题（一）：本大题共3小题，第16题10分，第17、18题各7分，共24分．16．（1）计算：；（2）先化简，再求值：其中．17．漏刻是我国古代的一种计时工具．小轩依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现其水位与时间之间成一次函数关系．小轩通过多次计时并测量水位的高度，得到如下表数据：()1,1-()1,1--)(0,269x x -+=180︒31x -4xx =AB O e C O e A O e BC D AC BAC CAD ∠=∠AC =BD AEOM CFON S S =矩形矩形M ABCD AC M EF BC ∥,AB CD ,E F ,BM DM 4,3,2CF EM DF ===MF =()1012024sin452-⎛⎫-+-︒ ⎪⎝⎭21,11x x x x ⎛⎫÷+ ⎪--⎝⎭3x =()cm h ()min t…1235……2.42.83.24.0…（1）求关于的函数关系式；（2）若小轩开始测量的时间为早上9：30，当水位读数为14cm 时，求此时的时间．18．如题18图，在等边中，为边上的高．题18图（1）实践与操作：利用尺规，以为边在下方作等边，延长交于点；（要求：尺规作图并保留作图痕迹、不写作法，标明字母）（2）应用与证明：在（1）的条件下，证明．四、解答题（二）：本大题共3小题，每小题9分，共27分．19．测速仪是协助道路安全工作必不可少的装置，如题19图．为保障学生安全，某中学入口处的街道安装了车辆自动测速仪，测速仪置于路面上方横杆的点位置，点到路面的距离米．已知，点，在同一平面内．求测速区间的距离．（结果保留整数，参考数据：，）题19图20．某市教育部启动“书香校园”的读书行动，鼓励学生多读书、读好书，好读书．现从某校八、九年级中各随机抽取20名学生的阅读时间．并分为五个类别：（6小时及以下），（7小时），（8小时），（9小时），（10小时），整理分析后绘制了如下统计图表：抽取的八年级学生阅读时间条形统计图抽取的九年级学生阅读时间扇形统计图题20图抽取的八、九年级学生阅读时间统计表()min t ()cm h h t ABC △AD BC CD CD CDE △ED AB M CE BM =C C 6CD =12,33CAD CBD ∠=︒∠=︒A ,,B C D AB sin120.21,cos120.98,tan120.21︒=︒≈︒≈sin330.54,cos330.84,tan330.65︒=︒≈︒≈A B C D E年级平均数中位数众数八年级7.58九年级8.210根据以上信息，解答下列问题：（1），．（2）该校八年级共有400名学生、九年级共有500名学生参加此次读书行动，若该校计划给阅读时间不低于9小时的学生颁发荣誉证书，请估计该校需准备多少份证书；（3）根据分析的数据，请从一个方面评价该校八、九年级中哪个年级抽取的学生阅读时间更好，并说明理由．21．综合与实践“转化”是一种重要的数学思想，将空间问题转化为平面问题是转化思想的一个重要方面．为了让同学们探究“转化”思想在数学中的应用，在数学活动课上，老师带领学生研究几何体的最短路线问题：问题情境：如题21—1图，一只蚂蚁从点出发沿圆柱侧面爬行到点C ，其最短路线正是侧面展开图中的线段，若圆柱的高为．底面直径为．问题解决：（1）判断最短路线的依据是______；（2）求出蚂蚁沿圆柱侧面爬行的最短路线的长（结果保留根号和）；拓展迁移：如题21—2图，为圆锥的顶点，为底面圆周上一点，点是的中点，母线，底面圆半径为2，粗线为蚂蚁从点出发绕圆锥侧面爬行回到点时所经过的路径的痕迹．（3）请求出蚂蚁爬行的最短距离．题21—1图题21—2图五、解答题（三）：本大题共2小题，每小题12分，共24分．22．综合探究如题22图，在平面直角坐标系中．直线与抛物线交于两点，点的横坐标为．ab______a =______b =A AC AB 2cm BC 8cm AC πO M P OM 8OM =P P ()0y kx k =≠()20y ax c a =+≠()8,6,A B B 2-题22图（1）求抛物线的解析式；（2）点是直线下方抛物线上一动点，过点作轴的平行线，与直线交于点C ．连接，设点的横坐标为．①若点在轴上方，当为何值时，；②若点在轴下方，求周长的最大值．23．综合运用如题23—1图，在平面直角坐标系中，点为，点为，连接．提出问题：（1）如题23—2图，以为边在右侧构成正方形，且正方形的边与轴相交于点，用含的代数式表示此时点的坐标；问题探究：（2）如题23—3图，以为对角线构成正方形，且正方形的边与轴相交于点，当时，求线段的值；问题深化：（3）若以为边在右侧构成正方形，过点作轴于点，连接，令的面积为，求关于的函数关系式．题23—1图图题23—2图题23—3图P AB P x AB PO P m P x m OC CP =P x POC △A ()0,4B (),0n AB AB AB ABCD ABCD y E n E AB ACBD ACBD y E 2n =-:BE CE AB AB ABCD D DF x ⊥F CF CDF △S S n数学快速对答案一、选择题：共10小题，每小题3分，共30分。

2025年河北省初中学业水平考试数学试题(样卷)参考答案

第1页（共4页）2025年河北省初中学业水平考试数学试题（样卷）参考答案一、选择题题号123456789101112答案CADBACBDBCAC二、填空题13．14．2-15．32916三、解答题17．解：（1）列式为：(21)(2)3-+⨯--，原式1=-.（2）设这个数为x ，(3)(2)1x -⨯-+27x =-+.∵3x >，∴26x -<-，∴271x -+<.18．解：（1）第1题第一步，第2题第二步.（2）（任选其中一道作答）习题1：2111x x x +-+1(1)(1)(1)(1)(1)x x x x x x -=++-+-21(1)(1)x x x x -+=+-.习题2：解：方程两边同乘2(1)-x ，得21(1)1x x x +-=-.解得2x =．经检验2x =是原分式方程的解．19．解：（1）90520360n =÷=；20135336014420α-+++=⨯︒=︒（）．补全条形统计图(略)．（2）中位数为10.0kg ，众数为10.0kg ．（3）平均数：9.819.9310.0810.1510.23200.610.03kg 2020⨯+⨯+⨯+⨯+⨯==．总产量：g 100.03550501k 0000⨯=．第2页（共4页）20．解：（1）∵OE ⊥AB ，AB ∥CD ，∴OE ⊥CD ．∵CD =cm，∴DF =cm ．如图1，连接OD ，设⊙O 的半径OD r =，则30OF OM FM r =-=-．在Rt △ODF中，222(30)r r =+-．解得r =60，即⊙O 的半径为60cm ．（2）∵△OAB 为等边三角形，∴∠OBE =60°．在Rt △BOE 中，OE=60+20=80cm ，2s n 3i OBE ∠=．∴sin O OE OB BE =∠S △OAB =12AB OE=180233⨯⨯=．∴260π60600π360POQS ⨯==扇形．∴264003600π (cm )3S =-阴影．21．解：（1）由题意，得B (4，0)．设直线AB 解析式为y kx b =+，则有604.k b k b =+⎧⎨=+⎩，解得2.8k b =-⎧⎨=⎩，∴直线AB 的解析式为28y x =-+．（2）①当2a =时，点P 坐标为(2，5)，将2x =代入28y x =-+得45y =≠，∴点P 不在直线AB 上．②当53=a 时，点P 在线段AB 上，AP BP +最小，最小值为=．（3）3553a <<．22．解：（1）30°，48m ．（2）如图2，作OH ⊥AB 于点H ，EG ⊥AB 于点G ，则四边形HOEG 为矩形．由题意可知：sin ∠EFB =45．∴OH =EG=EF ·sin ∠EFB =4205⨯=16．∵OH ⊥AB ，∠ABO =30°．∴16321sin 2∠===OH OB ABO ．∴点B 到地面DF 的最小距离为16m OD OB -=．G 图2EFBACDO H 图1CDOMlABP Q E F第3页（共4页）23．解：（1）∵点A （0，2），点B （6，0.5）在抛物线218y x bx c =-++上，∴210.53668c b c =⎧⎪⎨=-⨯++⎪⎩，．解得122b c ⎧=⎪⎨⎪=⎩，．∴211282y x x =-++．抛物线的顶点坐标为（2，52）．（2）∵点B （6，0.5），BC ⊥OC ，点C 在x 轴上，∴点C 的坐标为（6，0）．∴直线AC 的解析式为123y x =-+．∵点M 在直线AC 上，∴点M 的坐标可设为（m ，123m -+）．∵MA = NA ，MN ⊥x 轴，点A （0，2），∴点N 的坐标可以表示为（m ，123m +）．∵点N 在抛物线上，∴211122382m m m +=-++．解得143m =，20m =（舍去）．∴点M 的坐标为（43，149）．（3）①令)231()22181(2+--++-=x x x d ．化简得x x d 65812+-=．∵ 1.25==DE MN ，∴当 1.25=d 时， 1.2565812=+-x x ．解得110103-=x ，210103+=x ．∵MN 在DE左侧，∴=M x=D x ．∴20cos 9-==∠D E x x DM ACO ．②23＜m ＜103．第4页（共4页）24．解：（1）9，365．（2）∵AB =20，BC =15，DE =12，EF =9，∴53AB BC DE EF ==，又有∠B =∠DEF =90°，∴Rt △ABC ∽Rt △DEF ，∴∠A =∠EDF ．又∵∠APD =∠DPE ，∴△ADP ∽△DEP .∴AP ADDP DE=．当DP =12时，DP =DE ，∴AP =AD ．（3）①尺规作图如图3，AN 即为所求．②∵AM 垂直平分DE ，∴AE =AD ．又∵AN ⊥DF ，∴∠MAN +∠MDN =180°．∴∠MAN =∠EDF =∠BAC ．∴∠EAM =∠DAN ．又∵AE =AD ，∠AME =∠AND ，∴△AME ≌△AND ．∴AN =AM ．如图4，延长ED 交AN 延长线于点G ，在Rt △DNG 中，DN =DM =6．又∵cos ∠GDN =45，∴DG =152．∴MG =DG +DM =6+152=272．在Rt △DNG 中，∵tan ∠MAG =34，MG =272．∴AM =18．∴AN =18．（4）10+．FC BDE A图3MN CFBDEA图4M NG。

2024年山东济南初中学业水平考试数学试卷真题(含答案详解)

秘密★启用前济南市2024年九年级学业水平考试数学试题本试卷共8页，满分150分.考试时间为120分钟注意事项：1.答卷前，考生务必将自己的姓名、准考证号、座号等填写在答题卡和试卷指定位置上.2.回答选择题时，选出每小题答案，用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时,用0.5mm黑色签字笔将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.一、选择题：本题共10小题，每小题4分，共40分.每小题只有一个选项符合题目要求.1.9的相反数是（）11A.—B.——C.9D.-9992.黑陶是继彩陶之后中国新石器时代制陶工艺的又一个高峰，被誉为“土与火的艺术，力与美的结晶”.如图是山东博物馆收藏的蛋壳黑陶高柄杯.关于它的三视图，下列说法正确的是（）A.主视图与左视图相同B.主视图与俯视图相同C.左视图与俯视图相同D.三种视图都相同3.截止2023年底，我国森林面积约为3465000000亩，森林覆盖率达到24.02%，将数字3465000000用科学记数法表示为（）A.0.3465xlO9B. 3.465xl09C. 3.465xl08D.34.65xl084. 一个正多边形，它的每一个外角都等于45。

，则该正多边形是（）A.正六边形B.正七边形C.正八边形D.正九边形5.如图，已知 △DEC ,ZA = 60。

,ZB = 4。

,则 NQCE 的度数为（）.DA. 40°C. 80°D. 100°6. 下列运算正确的是（）A. 3x + 3y = 6xy B. = xy 6 C. 3（x + 8）= 3x + 8 D.疽泌二 j7. 若关于x 的方程x 2-x-m^ 0有两个不相等的实数根，则实数川的取值范围是（）m <——4 B. m > ——4 C. m<-4 D. m>-48. 3月14日是国际数学节、某学校在今年国际数学节策划了“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个挑战活动，如果小红和小丽每人随机选择参力口其中一个活动，则她们恰好选到同一个活动的概率是（）1112A. — B . — C. — D .—9 6 3 39. 如图，在正方形刃与CD 中，分别以点力和8为圆心，以大于」，8的长为半径作弧，两弧2相交于点E 和E ,作直线EE ,再以点力为圆心，以刀。

数学学普试卷答案初三

一、选择题（每题2分，共20分）1. 下列各数中，是正数的是（）A. -1B. 0C. 1/2D. -1/2答案：C解析：正数是指大于0的数，故选C。

2. 下列各数中，有理数是（）A. √2B. πC. -1/3D. 无理数答案：C解析：有理数包括整数和分数，故选C。

3. 下列各式中，正确的是（）A. a^2 = b^2，则a = bB. a^2 = b^2，则a = -bC. a^2 = b^2，则a = ±bD. a^2 = b^2，则a ≠ b答案：C解析：当a^2 = b^2时，a可以等于b，也可以等于-b，故选C。

4. 下列各式中，绝对值最大的是（）A. |-2|B. |3|C. |-1|D. |0|答案：B解析：绝对值表示一个数与0的距离，故|3|的绝对值最大。

5. 下列各式中，等式成立的是（）A. 2x + 3 = 5x + 1B. 2x + 3 = 5x - 1C. 2x + 3 = 5x + 2D. 2x + 3 = 5x答案：A解析：将等式两边的x项移项，常数项合并，可得2x + 3 = 5x + 1，故选A。

6. 下列各式中，不等式成立的是（）A. 2x > 3xB. 2x < 3xC. 2x = 3xD. 2x ≠ 3x答案：B解析：将不等式两边的x项移项，可得2x < 3x，故选B。

7. 下列各式中，函数的定义域是（）A. y = √xB. y = 1/xC. y = x^2D. y = √(-x)答案：C解析：函数的定义域是指使函数有意义的自变量的取值范围。

C选项中，x^2的定义域为全体实数，故选C。

8. 下列各式中，函数的值域是（）A. y = √xB. y = 1/xC. y = x^2D. y = √(-x)答案：A解析：函数的值域是指函数的输出值构成的集合。

A选项中，√x的值域为[0,+∞)，故选A。

9. 下列各式中，平行四边形的面积是（）A. 2B. 4C. 6D. 8答案：B解析：平行四边形的面积等于底乘以高，根据题意，底为2，高为2，故面积为4，故选B。

2024年陕西省初中学业水平考试数学真题试卷(含答案)

2024年陕西省初中学业水平考试数学真题试卷注意事项：1．本试卷分为第一部分（选择题）和第二部分（非选择题），全卷共8页，，考试时间120分钟2．领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡上填写姓名和准考证号，同时用2B 铅笔在答题卡上填涂对应的试卷类型信息点（A 或B ）3．请在答题卡上各题的指定区域内作答，否则作答无效4．作图时，先用铅笔作图，再用规定签字笔描黑5．考试结束，本试卷和答题卡一并交回第一部分（选择题共24分）一、选择题（共8小题，每小题3分，计24分，每小题只有一个选项是符合题意的）1. 的倒数是（）3-A. B. C. D. 31313-3-2. 如图，将半圆绕直径所在的虚线旋转一周，得到的立体图形是（）A. B.C. D.3. 如图，，，，则的度数为（）AB DC ∥BC DE ∥145B ∠=︒D ∠A. B. C. D. 25︒35︒45︒55︒4. 不等式的解集是（）()216x -≥A. B. C. D. 2x ≤2x ≥4x ≤4x ≥5. 如图，在中，，是边上的高，E 是的中点，连接，ABC 90BAC ∠=︒AD BC DC AE 则图中的直角三角形有（）A. 2个B. 3个C. 4个D. 5个6. 一个正比例函数的图象经过点和点，若点A 与点B 关于原点对称，则()2,A m (),6B n -这个正比例函数的表达式为（）A. B. C.D.3y x =3y x=-13y x =13y x=-7.如图，正方形的顶点G 在正方形的边上，与交于点H ，若CEFG ABCD CD AFDC ，，则的长为（）6AB =2CE =DH A. 2 B. 3C. D. 52838. 已知一个二次函数的自变量x 与函数y 的几组对应值如下表，2y ax bx c =++x (4)-2-035…y…24-8-03-15-…则下列关于这个二次函数的结论正确的是（）A. 图象的开口向上B. 当时，y 的值随x 的值增大而0x >增大C. 图象经过第二、三、四象限D. 图象的对称轴是直线1x =第二部分（非选择题共96分）二、填空题（共5小题，每小题3分，计15分）9. 分解因式：=_______________．2a ab -10. 小华探究“幻方”时，提出了一个问题：如图，将0，，，1，2这五个数分别填在五2-1-个小正方形内，使横向三个数之和与纵向三个数之和相等，则填入中间位置的小正方形内的数可以是________．（写出一个符合题意的数即可）11.如图，是的弦，连接，，是所对的圆周角，则与BC O OB OC A ∠BC A ∠的和的度数是________．OBC ∠12. 已知点和点均在反比例函数的图象上，若，则()12,A y -()2,B m y 5y x =-01m <<________0．12y y +13.如图，在中，，E 是边上一点，连接，在右侧作ABC AB AC =AB CE BC ，且，连接．若，，则四边形的面积为BF AC ∥BF AE =CF 13AC =10BC =EBFC ________．三、解答题（共13小题，计81分。

2024年天津市初中学业水平考试数学试卷及参考答案

（B ）（A ）（C ）（D ）第（2）题机密★启用前2024年天津市初中学业水平考试试卷数学本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分。

第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页。

试卷满分120分。

考试时间100分钟。

答卷前，请务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝你考试顺利!第Ⅰ卷注意事项：1．每题选出答案后，用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。

2．本卷共12题，共36分。

一、选择题（本大题共12小题，每小题3分，共36分. 在每小题给出的四个选项中，只有一项是符合题目要求的）（1）计算33--（）的结果等于（A ）6- （B ）0（C ）3（D ）6（2）右图是一个由5个相同的正方体组成的立体图形，它的主视图是（3（A ）1和2之间（B ）2和3之间（C ）3和4之间（D ）4和5之间（4）在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（5）据2024年4月18日《天津日报》报道，天津市组织开展了第43届“爱鸟周”大型主题宣传活动．据统计，今春过境我市候鸟总数已超过800000只．将数据800000用科学记数法表示应为（A ）70.0810⨯ （B ）60.810⨯ （C ）5810⨯（D ）48010⨯（61︒-的值等于（A ）0 （B ）1（C1- （D1-（7）计算3311---xx x 的结果等于（A ）3 （B ）x （C ）1-x x （D ）231-x （8）若点11-，（）A x ，21B x ，（），35，（）C x 都在反比例函数5=y x的图象上，则1x ，2x ， 3x 的大小关系是（A ）123<<x x x （B ）132x x x << （C ）321x x x <<（D ）213x x x <<（A ）（B ）（C ）（D ）EABCF DP第（10）题第（11）题ABCFE（9）《孙子算经》是我国古代著名的数学典籍，其中有一道题：“今有木，不知长短．引绳度之，余绳四尺五寸；屈绳度之，不足一尺．木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺．问木长多少尺？设木长x 尺，绳子长y 尺，则可以列出的方程组为（A ） 4.50.51-=⎧⎨-=⎩，y x x y（B ） 4.50.51-=⎧⎨+=⎩，y x x y（C ） 4.51+=⎧⎨-=⎩，x y x y（D ） 4.51+=⎧⎨-=⎩，x y y x（10）如图，Rt △ABC 中，90∠=︒C ，40∠=︒B ，以点A 为圆心，适当长为半径画弧，交AB 于点E ，交AC 于点F ；再分别以点E ，F 为圆心，大于12EF 的长为半径画弧，两弧（所在圆的半径相等）在∠BAC 的内部相交于点P ；画射线AP ，与BC相交于点D ，则∠ADC 的大小为（A ）60︒ （B ）65︒（C ）70︒（D ）75︒（11）如图，ABC △中，30∠=︒B ，将ABC △绕点C 顺时针旋转60︒得到DEC △，点A ，B 的对应点分别为D ，E ，延长BA 交DE 于点F ，下列结论一定正确的是（A ）∠=∠ACB ACD （B ）//AC DE （C ）=AB EF（D ）⊥BF CE（12）从地面竖直向上抛出一小球，小球的高度h （单位：m ）与小球的运动时间t（单位：s ）之间的关系式是2305=-h t t （06≤≤t ）．有下列结论： ① 小球从抛出到落地需要6s ； ② 小球运动中的高度可以是30m ；③ 小球运动2s 时的高度小于运动5s 时的高度．其中，正确结论的个数是（A ）0 （B ）1 （C ）2（D ）3C第（17）题AFBOED第（18）题机密★启用前2024年天津市初中学业水平考试试卷数学第Ⅱ卷注意事项：1．用黑色字迹的签字笔将答案写在“答题卡”上（作图可用2B 铅笔）。

初中学业水平考试数学试卷-带答案

初中学业水平考试数学试卷-带答案学校:___________班级：___________姓名：___________考号：___________注意事项：1. 本试卷共6页. 全卷满分 120分. 考试时间为120分钟. 考生答题全部答在答题卡上，答在本试卷上无效.2. 请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、考试证号用0.5 毫米黑色墨水签字笔填写在答题卡及本试卷上. 3. 答选择题必须用 2B 铅笔将答题卡上对应的答案标号涂黑. 如需改动，请用橡皮擦干净后，再选涂其他答案. 答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效.4. 作图必须用2B 铅笔作答，并请加黑加粗，描写清楚.一、选择题(本大题共6小题，每小题2 分，共 12分. 在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置．．．．．．．上) 1.全国深入践行习近平生态文明思想，科学开展大规模国土绿化行动，厚植美丽中国亮丽底色, 去年完成造林约 3 830 000 公顷. 用科学记数法表示3830000 是 A. 3.83×10⁶ B. 0.383×10⁶ C. 3.83×10⁷ D.0.383×10⁷ 2. 整数a 满足 √19<a <√29,则a 的值为A. 3B. 4C. 5D. 6 3. 若一个等腰三角形的腰长为3，则它的周长可能是A. 5B. 10C. 15D. 204.甲、乙两地相距100km ，汽车从甲地匀速行驶到乙地，则汽车行驶的时间t(单位：h)与行驶速度 v(单位：km/h) 之间的函数图像是5. 我国南宋数学家秦九韶的著作《数书九章》中有一道问题：“问沙田一段，有三斜，其小斜一十三里，中斜一十四里，大斜一十五里. 里法三百步，欲知为田几何? ”问题大意：如图, 在△ABC 中, AB=13里, BC=14里, AC=15里, 则 △ABC 的面积是 A. 80 平方里 B. 82平方里 C. 84平方里 D. 86平方里6.如图，不等臂跷跷板 AB 的一端A 碰到地面时，另一端B 到地面的高度为60cm ；当AB 的一端B 碰到地面时，另一端A 到地面的高度为 90cm ，则跷跷板 AB 的支撑点 O 到地面的高度 OH 是A. 36cmB. 40cmC. 42cmD. 45cm 二、填空题(本大题共 10 小题，每小题2 分，共20分. 请把答案填写在答题卡相应位置．．．．．．．上)7. 计算: |−2|=¯;√(−2)2=¯.8. 若式子 1x−2在实数范围内有意义，则x 的取值范围是 ▲ . 9. 计算 √12×√6−√18的结果是 ▲ . 10. 分解因式 3a²−6a +3的结果是 ▲ . 11. 计算 23×44×(18)5的结果是 ▲ .12. 某校九年级有8个班级, 人数分别为37, a, 32, 36, 37, 32, 38, 34. 若这组数据的众数为32，则这组数据的中位数为 ▲ .13. 甲车从 A 地出发匀速行驶，它行驶的路程y(单位：km) 与行驶的时间x(单位：min)之间的函数关系如图所示. 甲车出发20 min 后，乙车从A 地出发沿同一路线匀速行驶. 若乙车经过 20min~30min 追上甲车,则乙车的速度 v(单位:km/min)的取值范围是 ▲ .14. 在平面直角坐标系中，点O 为原点，点A 在第一象限，且OA=3. 若反比例函数 y =kx的图像经过点A ，则k 的取值范围是 ▲ .15. 如图, ⊙O 与正六边形ABCDEF 的边CD, EF 分别相切于点C, F. 若AB=2, 则⊙O 的半径长为 ▲ .16. 如图, 在菱形纸片ABCD 中, 点E 在边 AB 上,将纸片沿CE 折叠, 点 B 落在 B'处,CB'⊥AD, 垂足为F 若 CF=4cm, FB'=1cm, 则BE= ▲ cm三、解答题(本大题共11 小题，共88分. 请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤)17.(7分) 计算 (1−9x 2)÷x−3x.18.(8分) 解不等式组 {2x −1<0,x−14<x 3, 并写出它的整数解.19.(7分) 如图,在▱．ABCD 中, 点 M, N 分别在边 BC, AD 上, 且AM∥CN, 对角线BD 分别交 AM,CN 于点E, F. 求证BE=DF.20.(8分) 社会运转和日常生活离不开物流行业的发展，阅读以下统计图并回答问题.2011~2022年中国社会物流总费用及占GDP 比重统计图(1) 下列结论中，所有正确结论的序号是 ▲ .①2011~2022年社会物流总费用占 GDP 比重总体呈先下降后稳定的趋势： ②2011~2016年社会物流总费用的波动比2017~2022年社会物流总费用的波动大； ③2012~2022 年社会物流总费用逐年增加，其中增加的幅度最大的一年是 2021年 (2) 请结合上图提供的信息，从不同角度写出两个与我国GDP 相关的结论.21.(8分) 某旅游团从甲、乙、丙、丁4个景点中随机选取景点游览.(1) 选取2个景点，求恰好是甲、乙的概率；(2) 选取3个景点，则甲、乙在其中的概率为▲ .22.(8分) 如图，某校的饮水机有温水、开水两个按钮，温水和开水共用一个出水口. 温水的温度为30℃,流速为20ml/s; 开水的温度为100℃,流速为 15ml/s. 某学生先接了一会儿温水，又接了一会儿开水，得到一杯280ml温度为60℃的水(不计热损失)，求该学生分别接温水和开水的时间.物理常识开水和温水混合时会发生热传递，开水放出的热量等于温水吸收的热量，可以转化为开水的体积X开水降低的温度=温水的体积×温水升高的温度.23.(8分) 如图，为了测量无人机的飞行高度，在水平地面上选择观测点A，B. 无人机悬停在C处，此时在A 处测得 C的仰角为36°52′;：无人机垂直上升5m悬停在D处，此时在B 处测得 D的仰角为(63°26′.AB=10m,点A, B, C, D在同一平面内, A, B两点在 CD的同侧. 求无人机在 C 处时离地面的高度.(参考数据：tan36°52′≈0.75,tan63°26′≈2.00.)24.(8分) 如图，玻璃桌面与地面平行，桌面上有一盏台灯和一支铅笔，点光源O与铅笔AB所确定的平面垂直于桌面. 在灯光照射下，AB 在地面上形成的影子为 CD(不计折射)，AB∥CD.(1) 在桌面上沿着 AB 方向平移铅笔，试说明CD的长度不变.(2) 桌面上一点P恰在点O的正下方，且(OP=36cm,PA=18cm,AB=18cm,桌面的高度为 60cm.在点O 与AB 所确定的平面内，将AB绕点A 旋转，使得CD的长度最大.①画出此时AB所在位置的示意图；②CD的长度的最大值为▲ cm.25.(8分) 已知二次函数y=ax²−2ax+3(a为常数, a≠0).(1) 若a<0，求证：该函数的图像与x轴有两个公共点.(2) 若a=-1, 求证: 当-1<x<0时, y>0.(3) 若该函数的图像与x轴有两个公共点(x₁, 0), (x₂, 0), 且-−1<x₁<x₂<4,则a的取值范围是▲ .26.(9分) 如图, 在△ABC中, AB=AC, ⊙O 是△ABC的外接圆, 过点 O作 AC的垂线,垂足为 D，分别交直线BC, AC于点E, F, 射线AF 交直线 BC 于点G.(1) 求证AC=CG.(2) 若点 E 在 CB 的延长线上, 且EB=CG, 求∠BAC的度数.(3) 当BC=6时，随着CG 的长度的增大，EB 的长度如何变化? 请描述变化过程，并说明理由.27.(9分) 在平面内，将一个多边形先绕自身的顶点 A 旋转一个角度(θ(0°<θ<180°),再将旋转后的多边形以点 A 为位似中心放大或缩小，使所得多边形与原多边形对应线段的比为 k ，称这种变换为自旋转位似变换. 若顺时针旋转，记作 T(A ，顺θ，k)；若逆时针旋转, 记作T(A, 逆θ, k).例如：如图①，先将 △ABC 绕点B 逆时针旋转. 50°,得到 △A₁BC₁,再将 △A₁BC₁以点 B 为位似中心缩小到原来的 12,得到 △A₂BC₂,这个变换记作T(B ，逆 50∘,12).(1) 如图②, △ABC 经过 T(C, 顺60°, 2) 得到 △A ′B ′C,用尺规作出 △A ′B ′C.(保留作图痕迹)(2) 如图③, △ABC 经过 T(B, 逆α, k ₁) 得到 △EBD,△ABC 经过 T(C, 顺β, k ₂) 得到 △FDC,连接AE,AF. 求证: 四边形AFDE 是平行四边形.(3) 如图④, 在 △ABC 中 ∠A =150°,AB =2,AC =1.若 △ABC 经过(2) 中的变换得到的四边形AFDE 是正方形.Ⅰ. 用尺规作出点D(保留作图痕迹，写出必要的文字说明)； Ⅱ. 直接写出AE 的长.参考答案题号 1 2 3 4 5 6 答案ACBDCA1.【解析】科学记数法的表示为a×10" (1≤a<10, n为整数), 故3830 000可表示为33.83×10°..故选 A.2.【解析】:√19<√25<√29,∴a=5.故选 C.3.【解析】根据三边关系可得0<x<6，则周长的取值范围为6<C<12.故选 B.4.【解析】根据路程=速度×时间，可得t=100v(v⟩0,t>0),所以t与v成反比例. 故选 D.5.【解析】本题考察双勾股定理，过点 A 作AD⊥BC交BC于点D.在Rt△ABD中,AD²=AB²−BD²,在Rt△ACD中,AD²=AC²−CD².∴AB²−BD²=AC²−CD².设BD=x, 则可列方程: 13²−x²=15²−(14−x)²,求得x=5.则AD=12, 所以三角形ABC的面积为14×12×12=84.故选 C.6.【解析】设长边OA=a, 短边(OB=b,， O离地面的距离为h，根据相似得：{ℎ90=ba+b,ℎ60=ba+b解得h=36二、解答题题号 7 8 9 10 11 12 答案 2; 2 x≠2 3 3(a-1)² 1135题号 13 14 1516答案1.5≤v≤1.80<k≤4.57. 【解答】解: 2; 2.8. 【解答】解: x≠2.9.【解答】解:√12×√6−√18 =√72−√18 =6√2−3√2 =3√2故答案为 3√210.【解答】解:3a²−6a +3=3(a²−2a +1) =3(a −1)²故答案为 3(a −1)²11.【解答】解: 23×44×|18)5=23×28×(12)15=211×(12)15=211×(12)11×(12)4=(2×12)11×(12)4=(12)4=116故答案为： 116.12. 【解答】解: 由题可知a=32将这组数从小到大排列，由中位数概念可知，中位数为中间两个数34和36 的平均数 35. 故答案为：35.13.【解答】解:由函数图像可知甲的速度为18÷20=0.9 (km/min) 追及的路程为0.9×20=18(km)x=20min 时, 甲乙两车速度差为18÷20=0.9(km/min), 此时乙车速度为0.9+0.9=1.8(km/min)x=30min 时, 甲乙两车速度差为18÷30=0.6(km/min), 此时乙车速度为0.9+0.6=1.5(km/min)所以乙车的速度v 的取值范围是1.5≤．v ≤．1.814. 【解答】解:反比例函数如图所示，因为函数经过第一象限，所以k>0，因为反比例函数关于直线y=x 对称所以直线 y=x 与反比例函数的交点是到原点的距离最小值点，k 的值最小，由k 的几何意义可知，k 为图像上的点与坐标轴围成的正方形的面积，此时k=3×3÷2=4.5 所以k 的取值范围是0<k≤4.5.15.【解答】解：如图由正六边形的内角和和对称性可知 CF=4且CF 平分∠BCD 和∠AFE 每个内角都为120° ∴∠QCD=60°过点O 作OQ⊥CF, ∴CQ=2 ∵OC 与圆O 相切∴∠OCD=90°, ∴∠OCQ=30°∴．在直角三角形OCQ 中，由三边比例关系可知 CO =2÷√3×2=43√3∴半径OC 的长为 43√316.【解析】由翻折得: BC=CD=B'C=5, ∠BCE=∠B'CE=45°,∵CD=5, CF=4, ∠CFD=90°∴FD=3, 过点E 作EG⊥BC, 设 CG=x, 则EG=x,BC=5-x, ∵△EGB∽△CFD,∴．EG=GB解得 x =207,∴BE =257.三、解答题17. 解: x 2−9x 2÷x−3x=x 2−9x 2⋅xx−3=(x+3)(x−3)x 2.x x−3=x+3x18. 解: {2x −1<0circle1x−14<x 3circle2解不等式①得： x <12解不等式②得:x>-3∴−3<x <12∵x 取整数 ∴x 取-2,-1,0.19.【解析】连接AC 交BD 于点O ∵□ABCD 为平行四边形 ∴AO=CO, BO=DO ∵AM ∥CN ∴∠EAC=∠FCA在△AEO 和△CFO 中{∠EAC =∠FCAAO =CO∠AOE =∠COF∴△AOE≌．△COF∴BE=DF20.【解析】(1) 比重总体呈先下降后稳定的趋势，故①正确；2011 ~2016 年社会物流总费用的波动范围为2.7,2017 ~2022年社会物流总费用的波动范围为5.7,故2011 ~2016 年社会物流总费用的波动比2017 ~2022年社会物流总费用的波动小，故②错误；2012~2022年社会物流总费用逐年增加，其中增加的幅度最大的一年是 2021年，故③正确. 故答案为: ①③. (2) 根据统计图可得①从2012年到2017年社会物流总费用平稳增长，占GDP 的比重却逐年递减；说明我国GDP 总量在逐年增长; ②从2017年到2022年社会物流总费用逐年增加，占GDP 的比重却趋于稳定，变化不大。

2024年贵州省初中学业水平考试数学试卷真题(含答案详解)

贵州省2024年初中学业水平考试（中考）试题卷数学同学你好！答题前请认真阅读以下内容：1．全卷共6页，三个大题，共25小题，满分150分．考试时长120分钟．考试形式为闭卷．2．请在答题卡相应位置作答，在试题卷上答题无效．3．不能使用计算器．一、选择题（本大题共12题，每题3分，共36分．每小题均有A 、B 、C 、D 四个选项，其中只有一个选项正确，请用2B 铅笔在答题卡相应位置填涂）1．下列有理数中最小的数是（）A ．2-B ．0C ．2D ．42．“黔山秀水”写成下列字体，可以看作是轴对称图形的是（）A ．B ．C ．D ．3．计算23a a +的结果正确的是（）A ．5aB ．6aC ．25a D ．26a 4．不等式1x <的解集在数轴上的表示，正确的是（）A ．B ．C ．D ．5．一元二次方程220x x -=的解是（）A ．13x =，21x =B ．12x =，20x =C ．13x =，22x =-D ．12x =-，21x =-6．为培养青少年的科学态度和科学思维，某校创建了“科技创新”社团．小红将“科”“技”“创”“新”写在如图所示的方格纸中，若建立平面直角坐标系，使“创”“新”的坐标分别为()2,0-，()0,0，则“技”所在的象限为（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限7．为了解学生的阅读情况，某校在4月23日世界读书日，随机抽取100名学生进行阅读情况调查，每月阅读两本以上经典作品的有20名学生，估计该校800名学生中每月阅读经典作品两本以上的人数为（）A ．100人B ．120人C ．150人D ．160人8．如图，ABCD Y 的对角线AC 与BD 相交于点O ，则下列结论一定正确的是（）A ．AB BC =B ．AD BC =C ．OA OB =D ．AC BD⊥9．小星同学通过大量重复的定点投篮练习，用频率估计他投中的概率为0.4，下列说法正确的是（）A ．小星定点投篮1次，不一定能投中B ．小星定点投篮1次，一定可以投中C ．小星定点投篮10次，一定投中4次D ．小星定点投篮4次，一定投中1次10．如图，在扇形纸扇中，若150AOB ∠=︒，24OA =，则 AB 的长为（）A ．30πB ．25πC ．20πD ．10π11．小红学习了等式的性质后，在甲、乙两台天平的左右两边分别放入“■”“●”“▲”三种物体，如图所示，天平都保持平衡．若设“■”与“●”的质量分别为x ，y ，则下列关系式正确的是（）A ．x y =B ．2x y =C ．4x y =D ．5x y=12．如图，二次函数2y ax bx c =++的部分图象与x 轴的一个交点的横坐标是3-，顶点坐标为()1,4-，则下列说法正确的是（）A ．二次函数图象的对称轴是直线1x =B ．二次函数图象与x 轴的另一个交点的横坐标是2C ．当1x <-时，y 随x 的增大而减小D ．二次函数图象与y 轴的交点的纵坐标是3二、填空题（本大题共4题，每题4分，共16分）13的结果是．14．如图，在ABC 中，以点A 为圆心，线段AB 的长为半径画弧，交BC 于点D ，连接AD ．若5AB =，则AD 的长为．15．在元朝朱世杰所著的《算术启蒙》中，记载了一道题，大意是：快马每天行240里，慢马每天行150里，慢马先行12天，则快马追上慢马需要的天数是．16．如图，在菱形ABCD 中，点E ，F 分别是BC ，CD 的中点，连接AE ，AF ．若4sin 5EAF ∠=，5AE =，则AB 的长为．三、解答题（本大题共9题，共98分．解答应写出必要的文字说明、证明过程或演算步骤）17．（1）在①22，②2-，③()01-，④122⨯中任选3个代数式求和；（2）先化简，再求值：()21122x x -⋅+，其中3x =．18．已知点()1,3在反比例函数ky x=的图象上．(1)求反比例函数的表达式；(2)点()3,a -，()1,b ，()3,c 都在反比例函数的图象上，比较a ，b ，c 的大小，并说明理由．19．根据《国家体质健康标准》规定，七年级男生、女生50米短跑时间分别不超过7.7秒、8.3秒为优秀等次．某校在七年级学生中挑选男生、女生各5人进行集训，经多次测试得到10名学生的平均成绩（单位：秒）记录如下：男生成绩：7.61，7.38，7.65，7.38，7.38女生成绩：8.23，8.27，8.16，8.26，8.32根据以上信息，解答下列问题：(1)男生成绩的众数为______，女生成绩的中位数为______；(2)判断下列两位同学的说法是否正确．(3)教练从成绩最好的3名男生（设为甲，乙，丙）中，随机抽取2名学生代表学校参加比赛，请用画树状图或列表的方法求甲被抽中的概率．20．如图，四边形ABCD 的对角线AC 与BD 相交于点O ，AD BC ∥，90ABC ∠=︒，有下列条件：①AB CD ∥，②AD BC =．(1)请从以上①②中任选1个作为条件，求证：四边形ABCD 是矩形；(2)在（1）的条件下，若3AB =，5AC =，求四边形ABCD 的面积．21．为增强学生的劳动意识，养成劳动的习惯和品质，某校组织学生参加劳动实践．经学校与劳动基地联系，计划组织学生参加种植甲、乙两种作物．如果种植3亩甲作物和2亩乙作物需要27名学生，种植2亩甲作物和2亩乙作物需要22名学生．根据以上信息，解答下列问题：(1)种植1亩甲作物和1亩乙作物分别需要多少名学生？(2)种植甲、乙两种作物共10亩，所需学生人数不超过55人，至少种植甲作物多少亩？22．综合与实践：小星学习解直角三角形知识后，结合光的折射规律进行了如下综合性学习．【实验操作】第一步：将长方体空水槽放置在水平桌面上，一束光线从水槽边沿A 处投射到底部B 处，入射光线与水槽内壁AC 的夹角为A ∠；第二步：向水槽注水，水面上升到AC 的中点E 处时，停止注水．（直线NN '为法线，AO 为入射光线，OD 为折射光线．）【测量数据】如图，点A ，B ，C ，D ，E ，F ，O ，N ，N '在同一平面内，测得20cm AC =，45A ∠=︒，折射角32DON ∠=︒．【问题解决】根据以上实验操作和测量的数据，解答下列问题：(1)求BC 的长；(2)求B ，D 之间的距离（结果精确到0.1cm ）．（参考数据：sin 320.52︒≈，cos320.84︒≈，tan 320.62︒≈）23．如图，AB 为半圆O 的直径，点F 在半圆上，点P 在AB 的延长线上，PC 与半圆相切于点C ，与OF 的延长线相交于点D ，AC 与OF 相交于点E ，DC DE =．(1)写出图中一个与DEC ∠相等的角：______；(2)求证：OD AB ⊥；(3)若2OA OE =，2DF =，求PB 的长．24．某超市购入一批进价为10元/盒的糖果进行销售，经市场调查发现：销售单价不低于进价时，日销售量y （盒）与销售单价x （元）是一次函数关系，下表是y 与x 的几组对应值．销售单价x /元…1214161820…销售量y /盒…5652484440…(1)求y 与x 的函数表达式；(2)糖果销售单价定为多少元时，所获日销售利润最大，最大利润是多少？(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m 元的礼品，赠送礼品后，为确保该种糖果日销售获得的最大利润为392元，求m 的值．25．综合与探究：如图，90AOB ∠=︒，点P 在AOB ∠的平分线上，PA OA ⊥于点A ．(1)【操作判断】如图①，过点P 作PC OB ⊥于点C ，根据题意在图①中画出PC ，图中APC ∠的度数为______度；(2)【问题探究】如图②，点M 在线段AO 上，连接PM ，过点P 作PN PM ⊥交射线OB 于点N ，求证：2OM ON PA +=；(3)【拓展延伸】点M 在射线AO 上，连接PM ，过点P 作PN PM ⊥交射线OB 于点N ，射线NM 与射线PO 相交于点F ，若3ON OM =，求OPOF的值．1．A【分析】本题考查有理数的大小比较，解题的关键是掌握比较有理数大小的方法．根据有理数的大小比较选出最小的数．【详解】解：∵2024-<<<，∴最小的数是2-，故选：A ．2．B【分析】本题考查了轴对称图形概念，一个图形沿着某条直线折叠后直线两旁的部分能够完全重合，这个图形就叫轴对称图形．根据轴对称图形概念，结合所给图形即可得出答案．【详解】解：A ．不是轴对称图形，不符合题意；B ．是轴对称图形，符合题意；C ．不是轴对称图形，不符合题意；D ．不是轴对称图形，不符合题意；故选：B ．3．A【分析】本题主要考查合并同类项，根据合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变即可得．【详解】解：235a a a +=，故选：A ．4．C【分析】根据小于向左，无等号为空心圆圈，即可得出答案．本题考查在数轴上表示不等式的解集，熟知“小于向左，大于向右”是解题的关键．【详解】不等式1x <的解集在数轴上的表示如下：．故选：C ．5．B【分析】本题考查了解一元二次方程，利用因式分解法求解即可．【详解】解∶220x x -=，∴()20x x -=，∴0x =或20x -=，∴12x =，20x =，故选∶B ．6．A【分析】本题考查坐标与图形，先根据题意确定平面直角坐标系，然后确定点的位置．【详解】解：如图建立直角坐标系，则“技”在第一象限，故选A ．7．D【分析】本题考查用样本反映总体，利用样本百分比乘以总人数计算即可解题．【详解】解：20800160100⨯=（人），故选D ．8．B【分析】本题主要考查平行四边形的性质，掌握平行四边形的对边平行且相等，对角线互相平分是解题的关键．【详解】解：∵ABCD 是平行四边形，∴AB CD AD BC AO OC BO OD ====，，，，故选B ．9．A【分析】本题主要考查了概率的意义，概率是反映事件发生机会的大小的概念，只是表示发生的机会的大小，机会大也不一定发生，据此求解即可．【详解】解：小星同学通过大量重复的定点投篮练习，用频率估计他投中的概率为0.4，则由概率的意义可知，小星定点投篮1次，不一定能投中，故选项A 正确，选项B 错误；小星定点投篮10次，不一定投中4次，故选项C 错误；小星定点投篮4次，不一定投中1次，故选项D 错误故选；A ．10．C【分析】本题考查了弧长，根据弧长公式∶π180n rl =求解即可．【详解】解∵150AOB ∠=︒，24OA =，∴ AB 的长为150π2420π180⨯=，故选∶C ．11．C【分析】本题考查等式的性质，设“▲”的质量为a ，根据题意列出等式2x y y a +=+，2x a x y +=+，然后化简代入即可解题．【详解】解：设“▲”的质量为a ，由甲图可得2x y y a +=+，即2x a =，由乙图可得2x a x y +=+，即2a y =，∴4x y =，故选C ．12．D【分析】本题考查了二次函数的性质，待定系数法求二次函数解析式，利用二次函数的性质，对称性，增减性判断选项A 、B 、C ，利用待定系数法求出二次函数的解析式，再求出与y 轴的交点坐标即可判定选项D ．【详解】解∶∵二次函数2y ax bx c =++的顶点坐标为()1,4-，∴二次函数图象的对称轴是直线=1x -，故选项A 错误；∵二次函数2y ax bx c =++的图象与x 轴的一个交点的横坐标是3-，对称轴是直线=1x -，∴二次函数图象与x 轴的另一个交点的横坐标是1，故选项B 错误；∵抛物线开口向下，对称轴是直线=1x -，∴当1x <-时，y 随x 的增大而增大，故选项C 错误；设二次函数解析式为()214y a x =++，把()3,0-代入，得()20314a =-++，解得1a =-，∴()214y x =-++，当0x =时，()20143y =-++=，∴二次函数图象与y 轴的交点的纵坐标是3，故选项D 正确，故选D ．13【分析】利用二次根式的乘法运算法则进行计算．【详解】解：原式，．【点睛】本题考查二次根式的乘法运算，a ≥0，b ＞0）是解题关键．14．5【分析】本题考查了尺规作图，根据作一条线段等于已知线段的作法可得出AD AB =，即可求解．【详解】解∶由作图可知∶AD AB =，∵5AB =，∴5AD =，故答案为∶5．15．20【分析】本题考查了一元一次方程的应用，设快马追上慢马需要x 天，根据快马走的路程等于慢马走的总路程，列方程求解即可．【详解】解∶设快马追上慢马需要x 天，根据题意，得()24015012x x =+，解得20x =，故答案为：20．16##3【分析】延长BC ，AF 交于点M ，根据菱形的性质和中点性质证明ABE ADF ≌，ADF MCF ≌，过E 点作EN AF ⊥交N 点，根据三角函数求出EN ，AN ，NF ，MN ，在Rt ENM △中利用勾股定理求出EM ，根据菱形的性质即可得出答案．【详解】延长BC ，AF 交于点M，在菱形ABCD 中，点E ，F 分别是BC ，CD 的中点，AB BC CD AD ∴===，BE EC CF DF ===，AD BC ，D FCM ∠=∠，B D ∠=∠在ABE 和ADF △中AB AD B D BE DF =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABE ADF ≌，∴AE AF =，在ADF △和MCF △中D FCM DF CF AFD MFC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ASA ADF MCF ≌，∴CM AD =，AF MF =，5AE = ，5AE AF MF ∴===，过E 点作EN AF ⊥于N 点，90ANE ∴∠=︒ 4sin 5EAF ∠=，5AE =，4EN ∴=，3AN =，∴2NF AF AN =-=，527MN ∴=+=，在Rt ENM △中EM ===，即12EM EC CM BC BC =+=+=AB BC CD AD === ，AB BC ∴==．【点睛】本题考查了菱形的性质，全等三角形的判定和性质，运用三角函数解直角三角形，勾股定理等，正确添加辅助线构造直角三角形是解本题的关键．17．（1）见解析（2）12x -，1【分析】本题考查分式的化简求值和实数的混合运算，掌握运算法则是解题的关键．（1）利用实数的混合运算的法则和运算顺序解题即可；（2）先把分式的分子、分母分解因式，然后约分化为最简分式，最后代入数值解题即可．【详解】（1）解：选择①，②，③，2022(1)+-+-421=++7=；选择①，②，④，212222+-+⨯421=++7=；选择①，③，④，()0212122+-+⨯411=++6=；选择②，③，④，()012122-+-+⨯211=++4=；（2）解：()21122x x -⋅+()()11(1)21x x x =-+⋅+12x -=；当3x =时，原式3112-==．18．(1)3y x=(2)a c b <<，理由见解析【分析】本题主要考查了反比例函数的性质，以及函数图象上点的坐标特点，待定系数法求反比例函数解析式，关键是掌握凡是函数图象经过的点必能满足解析式．（1）把点()1,3代入k y x=可得k 的值，进而可得函数的解析式；（2）根据反比例函数表达式可得函数图象位于第一、三象限，再根据点A 、点B 和点C 的横坐标即可比较大小．【详解】（1）解：把()1,3代入k y x =，得31k =，∴3k =，∴反比例函数的表达式为3y x =；（2）解：∵30k =>，∴函数图象位于第一、三象限，∵点()3,a -，()1,b ，()3,c 都在反比例函数的图象上，3013-<<<，∴0a c b <<<，∴a c b <<．19．(1)7.38，8.26(2)小星的说法正确，小红的说法错误(3)23【分析】本题考查用树状图或列表法求概率，众数和中位数的定义，掌握列表法或树状图求概率是解题的关键．（1）利用中位数和众数的定义解题即可；（2）根据优秀等次的要求进行比较解题即可；（3）列表格得到所有可能的结果数n ，找出符合要求的数量m ，根据概率公式计算即可．【详解】（1）解：男生成绩7.38出现的次数最多，即众数为7.38，女生成绩排列为：8.16，8.23，8.26，8.27，8.32，居于中间的数为8.26，故中位数为8.26，故答案为：7.38，8.26；（2）解：∵用时越少，成绩越好，∴7.38是男生中成绩最好的，故小星的说法正确；∵女生8.3秒为优秀成绩，8.328.3>，∴有一人成绩达不到优秀，故小红的说法错误；（3）列表为：甲乙丙甲甲，乙甲，丙乙乙，甲乙，丙丙丙，甲丙，乙由表格可知共有6种等可能结果，其中抽中甲的有4种，故甲被抽中的概率为4263=．20．(1)见解析(2)12【分析】本题考查矩形的判定，勾股定理，掌握矩形的判定定理是解题的关键．（1）先根据条件利用两组对边平行或一组对边平行且相等证明ABCD 是平行四边形，然后根据矩形的定义得到结论即可；（2）利用勾股定理得到BC 长，然后利用矩形的面积公式计算即可．【详解】（1）选择①，证明：∵AB CD ∥，AD BC ∥，∴ABCD 是平行四边形，又∵90ABC ∠=︒，∴四边形ABCD 是矩形；选择②，证明：∵AD BC =，AD BC ∥，∴ABCD 是平行四边形，又∵90ABC ∠=︒，∴四边形ABCD 是矩形；（2）解：∵90ABC ∠=︒，∴4BC ===，∴矩形ABCD 的面积为3412⨯=．21．(1)种植1亩甲作物和1亩乙作物分别需要5、6名学生(2)至少种植甲作物5亩【分析】本题考查了二元一次方程组的应用，一元一次不等式的应用，（1）设种植1亩甲作物和1亩乙作物分别需要x 、y 名学生，根据“种植3亩甲作物和2亩乙作物需要27名学生，种植2亩甲作物和2亩乙作物需要22名”列方程组求解即可；（2）设种植甲作物a 亩，则种植乙作物()10a -亩，根据“所需学生人数不超过55人”列不等式求解即可．【详解】（1）解：设种植1亩甲作物和1亩乙作物分别需要x 、y 名学生，根据题意，得32272222x y x y +=⎧⎨+=⎩，解得56x y =⎧⎨=⎩，答：种植1亩甲作物和1亩乙作物分别需要5、6名学生；（2）解：设种植甲作物a 亩，则种植乙作物()10a -亩，根据题意，得：()561055a a +-≤，解得5a ≥，答：至少种植甲作物5亩．22．(1)20cm(2)3.8cm【分析】本题考查解直角三角形的应用，解答本题的关键是明确题意，利用数形结合的思想解答．（1）根据等腰三角形的性质计算出的值；（2）利用锐角三角函数求出DN 长，然后根据BD BN DN =-计算即可．【详解】（1）解：在Rt ABC 中，45A ∠=︒，∴45B ∠=︒，∴20cm BC AC ==，（2）解：由题可知110cm 2ON EC AC ===，∴10cm NB ON ==，又∵32DON ∠=︒，∴tan 10tan 32100.62 6.2cm DN ON DON =⋅∠=⨯︒≈⨯=，∴10 6.2 3.8cm BD BN DN =-=-=．23．(1)DCE ∠（答案不唯一）(2)163(3)163【分析】（1）利用等边对等角可得出DCE DEC ∠=∠，即可求解；（2）连接OC ，利用切线的性质可得出90DCE ACO ∠+∠=︒，利用等边对等角和对顶角的性质可得出AOE DCE ∠=∠，等量代换得出90AEO CAO ∠+∠=︒，然后利用三角形内角和定理求出90AOE ∠=︒，即可得证；（3）设2OE =，则可求2AO OF BO x ===，EF x =，22OD x =+，2DC DE x ==+，在Rt ODC△中，利用勾股定理得出()()()2222222x x x +=++，求出x 的值，利用tan OP OC D OD CD ==可求出OP ，即可求解．【详解】（1）解：∵DC DE =，∴DCE DEC ∠=∠，故答案为：DCE ∠（答案不唯一）；（2）证明：连接OC ，，∵PC 是切线，∴OC CD ⊥，即90DCE ACO ∠+∠=︒，∵OA OC =，∴OAC ACO ∠=∠，∵DCE DEC ∠=∠，AEO DEC ∠=∠，∴90AEO CAO ∠+∠=︒，∴90AOE ∠=︒，∴OD AB ⊥；（3）解：设OE x =，则2AO OF BO x ===，∴EF OF OE x =-=，22OD OF DF x =+=+，∴2DC DE DF EF x ==+=+，在Rt ODC △中，222OD CD OC =+，∴()()()2222222x x x +=++，解得14x =，20x =（舍去）∴10OD =，6CD =，8OC =，∵tan OP OC D OD CD ==，∴8106OP =，解得403OP =，∴163BP OP OB =-=．【点睛】本题考查了等腰三角形的性质，切线的性质，勾股定理，解直角三角形的应用等知识，灵活运用以上知识是解题的关键．24．(1)280y x =-+(2)糖果销售单价定为25元时，所获日销售利润最大，最大利润是450元(3)2【分析】本题考查了二次函数的应用，解题的关键是：（1）利用待定系数法求解即可；（2）设日销售利润为w 元，根据利润=单件利润×销售量求出w 关于x 的函数表达式，然后利用二次函数的性质求解即可；（3）设日销售利润为w 元，根据利润=单件利润×销售量-m ×销售量求出w 关于x 的函数表达式，然后利用二次函数的性质求解即可．【详解】（1）解∶设y 与x 的函数表达式为y kx b =+，把12x =，56y =；20x =，40y =代入，得12562040k b k b +=⎧⎨+=⎩，解得280k b =-⎧⎨=⎩，∴y 与x 的函数表达式为280y x =-+；（2）解：设日销售利润为w 元，根据题意，得()10w x y=-⋅()()10280x x =--+22100800x x =-+-()2225450x =--+，∴当25x =时，w 有最大值为450，∴糖果销售单价定为25元时，所获日销售利润最大，最大利润是450元；（3）解：设日销售利润为w 元，根据题意，得()10w x m y=--⋅()()10280x m x =---+()22100280080x m x m =-++--，∴当()100250222m m x ++=-=⨯-时，w 有最大值为()25050210028008022m m m m ++⎛⎫⎛⎫-++-- ⎪ ⎪⎝⎭⎝⎭，∵糖果日销售获得的最大利润为392元，∴()25050210028008039222m m m m ++⎛⎫⎛⎫-++--= ⎪ ⎪⎝⎭⎝⎭，化简得2601160m m -+=解得12m =，258m =当58m =时，542b x a=-=,则每盒的利润为：5410580--<,舍去，∴m 的值为2．25．(1)画图见解析，90(2)见解析(3)23或83【分析】（1）依题意画出图形即可，证明四边形OAPC 是矩形，即可求解；（2）过P 作PC OB ⊥于C ，证明矩形OAPC 是正方形，得出OA AP PC OC ===，利用ASA 证明APM CPN △≌△，得出AM CN =，然后利用线段的和差关系以及等量代换即可得证；（3）分M 在线段AO ，线段AO 的延长线讨论，利用相似三角形的判定与性质求解即可；【详解】（1）解：如图，PC 即为所求，∵90AOB ∠=︒，PA OA ⊥，PC OB ⊥，∴四边形OAPC 是矩形，∴90APC ∠=︒，故答案为：90；（2）证明：过P 作PC OB ⊥于C ，由（1）知：四边形OAPC 是矩形，∵点P 在AOB ∠的平分线上，PA OA ⊥，PC OB ⊥，∴PA PC =，∴矩形OAPC 是正方形，∴OA AP PC OC ===，90APC ∠=︒，∵PN PM ⊥，∴90APM CPN MPC ∠=∠=︒-∠，又90A PCN ∠=∠=︒，AP CP =，∴APM CPN △≌△，∴AM CN =，∴OM ON OM CN OC +=++OM AM AP=++OA AP=+2AP =；（3）解：①当M 在线段AO 上时，如图，延长NM 、PA 相交于点G ，由（2）知2OM ON PA +=，设OM x =，则3ON x =，2AO PA x ==，∴AM AO OM x OM =-==，∵90AOB MAG ︒∠=∠=，AMG OMN ∠=∠，∴()ASA AMG OMN ≌，∴3AG ON x ==，∵90AOB ∠=︒，PA OA ⊥，∴AP OB ∥，∴ONF PGF ∽ ，∴33325OF ON x PF PG x x ===+，∴53PF OF =，∴53833OP OF +==；②当M 在AO 的延长线上时，如图，过P 作PC OB ⊥于C ，并延长交MN 于G由（2）知：四边形OAPC 是正方形，∴OA AP PC OC ===，90APC ∠=︒，PC AO ∥，∵PN PM ⊥，∴90APM CPN MPC ∠=∠=︒-∠，又90A PCN ∠=∠=︒，AP CP =，∴APM CPN △≌△，∴AM CN =，∴ON OM-OC CN OM=+-AO AM OM=+-AO AO=+2AO =，∵33ON OM x==∴AO x =，2CN AM x ==，∵PC AO ∥，∴CGN OMN ∽，∴CG CN OM ON=，即23CG x x x =，∴23CG x =，∵PC AO ∥，∴OMF PGF∽，∴3253OF OM xPF PG x x===+，∴53 PFOF=，∴53233 OPOF-==；综上，OPOF的值为23或83．【点睛】本题考查了矩形的判定与性质，正方形的判定与性质，角平分线的性质，全等三角形的判断与性质，相似三角形的判断与性质等知识，明确题意，添加合适辅助线，构造全等三角形、相似三角形，合理分类讨论是解题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Evaluation Warning: The document was created with Spire.Doc for JAVA.2019年广东省初中学业水平考试数学说明：1．全卷共4页，满分为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B 铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑． 1．-2的绝对值是（A ） A ．2B ．-2C ．12D ．±22．某网店2019年母亲节这天的营业额为221000元，将数221000用科学记数法表示为（B ） A ．2.21×106B ．2.21×105C ．221×103D ．0.221×1063．如图，由4个相同正方体组合而成的几何体，它的左视图是（A ）4．下列计算正确的是（C ） A ．632b b b ÷=B ．339b b b ⋅=C ．2222a a a +=D ．()363a a =5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（C ）6．数据3、3、5、8、11的中位数是（C ）A ．3B ．4C ．5D ．67．实数a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是（D ）A ．a b >B ．a b <C ．0a b +>D ．0ab<8（B ） A ．-4B ．4C ．±4D ．29．已知1x 、2x 是一元二次方程220x x -=的两个实数根，下列结论错误．．的是（D ） A ．12x x ≠ B ．2112=0x x - C ．12=2x x +D ．12=2x x ⋅10．如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K ．则下列结论：ANH GNF ①≌△△ ；AFN HFG ∠=∠② ；2FN NK =③；:1:4AFN ADM S S =④△△．其中正确的结论有（C ）A ．1个B ．2个C ．3个D ．4个二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上． 11．计算：1120193-⎛⎫+ ⎪⎝⎭= ．答案：4解析：本题考查了零次幂和负指数幂的运算12．如图，已知a b ，175∠=°，则∠2＝．答案：105︒解析：本题考查了平行线的性质，互为补角的计算13．一个多边形的内角和是1080︒，这个多边形的边数是．答案：8解析：本题考查了多边形内角和的计算公式14．已知23-+的值是．x yx y=+，则代数式489答案：21解析：整体思想，考查了整式的运算15．如图，某校教学楼AC与实验楼BD的水平间距CD=米，在实验楼顶部B点测得教学楼顶部A点的仰角是30°，底部C点的俯角是45°，则教学楼AC的高度是米（结果保留根号）．答案：(15+解析：本题利用了特殊三角函数值解决实际问题16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（题16-1图）拼出来的图形的总长度是（结果用含a、b代数式表示）．答案：8a b+解析：本题考查了轴对称图形的性质，根据题目找规律三、解答题（一）（本大题3小题，每小题6分，共18分） 17．解不等式组：()12214x x ->⎧⎨+>⎩①②解 ①21>-x x >3 ②4)1(2>+x 422>+x 22>x 1>x∴该不等式组的解集是x >318．先化简，再求值：221224x x x x x x -⎛⎫-÷ ⎪---⎝⎭，其中x 解原式=)1()2)(2(21--+⋅--x x x x x x =xx 2+ 当2=x 原式=222+ =2222+ =21+19．如图，在ABC △中，点D 是AB 边上的一点．（1）请用尺规作图法，在ABC △内，求作∠ADE ，使∠ADE =∠B ，DE 交AC 于E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若2AD DB =，求AEEC的值．解（1）如图（2）A A B ADE ∠=∠∠=∠,ADE ∆∴∽ABC ∆2==∴DB AD EC AE四、解答题（二）（本大题3小题，每小题7分，共21分）20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A 、B 、C 、D 四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答下列问题：（1）x = ，y = ，扇形图中表示C 的圆心角的度数为度；（2）甲、乙、丙是A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．解 (1) 4x = ； 40y = ; 36(2)解：由题意可知树状图为由树状图可知，同时抽到甲、乙两名学生的概率为21=63答：同时抽到甲、乙两名学生的概率为13。

21．某校为了开展“阳光体育运动”，计划购买篮球、足球共60个，已知每个篮球的价格为70元，每个足球的价格为80元．（1）若购买这两类球的总金额为4600元，求篮球、足球各买了多少个？（2）若购买篮球的总金额不超过购买足球的总金额，求最多可购买多少个篮球？解 (1)方法一：解：设计划购买篮球x 个，足球y 个由题意得， 6070804600x y x y +=⎧⎨+=⎩解得： 2040x y =⎧⎨=⎩答：计划购买篮球20个，足球40个.方法二：解：设计划购买篮球x 个，则购买足球(60)x -个由题意得， 7080(60)4600x x +-= 解得： 20x =则60602040x -=-=答：计划购买篮球20个，足球40个. (2)解：设计划购买篮球a 个，则购买足球(60)a -个则有 7080(60),(060)a a a ≤-≤≤ 解得：032a ≤≤答：最多可购买32个篮球。

22．在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫格点，ABC △的三个顶点均在格点上，以点A 为圆心的EF 与BC 相切于点D ，分别交AB 、AC 于点E 、F ．（1）求ABC △三边的长；（2）求图中由线段EB 、BC 、CF 及FE 所围成的阴影部分的面积．解（1）由图可知102406222==+=AB102406222==+=AC 54808422==+=BC（2）由（1）可知102=AB ，102=AC ，54=BC222BC AC AB =+∴︒=∠∴90BAC又D BC A 相切于点为圆心的圆与以点∵ 5221==∴=∴⊥∴BC AD BD CD BC AD ，2010210221=⨯⨯=∴∆ABC S2)52(4120⋅⋅-=∴π阴Sπ⨯⨯-=204120π520-=五、解答题（三）（本大题3小题，每小题9分，共27分） 23．如图，一次函数y =k 1x +b 的图象与反比例函数2k y x=的图象相交于A 、B 两点，其中点A 的坐标为（-1，4），点B 的坐标为（4，n ）．（1）根据图象，直接写出满足21k k x b x+>的x 的取值范围；（2）求这两个函数的表达式；（3）点P 在线段AB 上，且:1:2AOP BOP S S ∆∆=，求点P 的坐标．解（1）由已知得：1-<x 或40<<x（2） xk y 2=经点)4,1(-A 24k -=∴，解得42-=kxy 4-=∴当4=x 时，得144-=-=y )1,4(-∴B将)1,4(),4,1(--B A 代入b x k y +=1得⎩⎨⎧+=-+-=b k bk 11414 解得⎩⎨⎧=-=311b k3+-=∴x y ∴反比例函数为xy 4-=一次函数为3+-=x y（3）∵S △AOP ：S △BOP =1：2， ∴AP:BP =1:2； ∵A （-1，4），B （4，-1），∴AB =√（4+1）2+（−1−4）2=5√2； ∴AP =13AB =5√23设点P （t ，-t+3）∵P 在线段AB 上，∴−1＜t ＜4； ∴AP =√（t +1）2+（−t +3−4）2=√2t 2+4t +2 =5√23解得：t 1=23；t 2=−83（舍去）； ∴P （23，73）；∴当S △AOP ：S △BOP =1：2时，P （23，73）24．如题24-1图，在ABC 中，AB =AC ，⊙O 是ABC △的外接圆，过点C 作∠BCD =∠ACB 交⊙O 于点D ，连接AD 交BC 于点E ，延长DC 至点F ，使CF =AC ，连接AF ．（1）求证：ED =EC ；（2）求证：AF 是⊙O 的切线；（3）如题24-2图，若点G 是ACD 的内心，25BC BE ⋅=，求BG 的长．解（1） ∵AB=AC∴弧AB=弧AC,∠B=∠ACB ∴∠D=∠B又∵∠BCD=∠ACB ∴∠D=∠BCD ∴ED=EC （2）证明：连接AO,交BC 于点H ∵AB=AC∴A 为弧BC 中点 ∴OA ⊥BC∵∠ACD=∠F ＋∠FAC又∵∠ACB=∠BCD,∠F=∠CAF ∴∠CAF=∠ACB ∴AF ∥BC∴∠FAO=∠CHO=90° 即AO ⊥AF又∵A 在圆上， ∴AF 为⊙O 的切线（3）连接AG由（2）知AF ∥BC ∴∠FAG=∠AGB ∵G 为△ACD 的内心 ∴AG 平分∠DAC ∴∠EAG=∠CAG又∵∠BAE=∠BCD=∠CAF∴∠FAC+∠CAG=∠BAE+∠EAG ∴∠BAG=∠BGA ∴AB=BG∵∠B=∠B,∠BAE=∠ACB ∴△AEB ∽△CAB ∴BC AB AB EB = 即BC BE AB ⋅=2 ∵EB ·BC=25,AB=BG ∴BG=AB=525．如题25-1图，在平面直角坐标系中，抛物线2y 与x 轴交于点A 、B （点A 在点B 右侧），点D 为抛物线的顶点．点C 在y 轴的正半轴上，CD 交x 轴于点F ，CAD △绕点C 顺时针旋转得到CFE △，点A 恰好旋转到点F ，连接BE ．（1）求点A 、B 、D 的坐标；（2）求证：四边形BFCE 是平行四边形；（3）如题25-2图，过顶点D 作1DD x ⊥轴于点D 1，点P 是抛物线上一动点，过点P 作PM x ⊥轴，点M 为垂足，使得PAM △与1DD A △相似（不含全等）．①求出一个满足以上条件的点P 的横坐标；②直接回答．．．．这样的点P 共有几个？解（1）依题意837433832-+=x x y 令0=y 得： 0837433832=-+x x ........① 解得：71-=x ，12=x∴)0,7(-B ,)0,1(A 把3832433-=⨯-=x 代入①得：32-=y ∴)32,3(--D（2）由（1）得：B （-7，0） A （1，0），D(-3,-32) 由题意可知，△CAD ≌△CFE∴CF=AC又CO ⊥AF∴0A=0F∴F(-1,0)∴AF=2∴设DF 解析式为y=kx ＋b⎩⎨⎧+-=-+-=bk b k 3320 所以：k=3b=3∴y=3x ＋3令x=0 得 y=3∴C(0,3)∴AC=22)3(1+=2∴AC=AF=CF∴△ACF 为等边三角形∴∠CAF=60°∵△CAD ≌△CFE∴∠ACF=∠FCE=60°，CD=CE又∠ECA+∠CAF=180°∴CE ∥AB又BF=6 CD=22)323(3++=6∴BF=CE∴四边形BFCE 为平行四边形（3）①当P 在下方时，∵1190DAD PAM A DD ∠≠∠︒=∠且当A DD 1∆∽AMP ∆时； ∴AD MA DD PM 11= 由（1）可知：A （1，0） D （-3，-23） )0,3(1-D 设)83743383,(2-+m m m P ；则M （m,0） ∴83743383)83743383(022+--=-+-=m m m m PM 32)32(01=--=DDmMA A D -==--=1;4)3(11 根据AD MA DD PM 11=得： 3214837433832m m m -=+-- 整理得：05232=-+m m∴（3m+5）（m -1）=0 ∴1,35=-=m m （舍）∴P 的横坐标为35-②P 共有3个．。