高三文科数学三角函数数列与导数试卷
高三数学第一轮复习 阶段测试卷 三角函数、向量、数列、导数、立体、解析 文 试题

高三文科数学阶段测试卷制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日[测试范围:三角函数、向量、数列、导数、立体、解析]一、选择题:〔10×5=50分〕1、设复数θθsin cos i z +=,],[πθ0∈,i +-=1ω,那么||ω-z 的最大值是 A.12+B.5C.2D.12-2、假设函数)(),(x g x f 的定义域都是R ,那么)()()(R x x g x f ∈>成立的充要条件是 A. 有一个R x ∈,使)()(x g x f >B. 有无数多个R x ∈,使)()(x g x f >C. 对R 中任意的x ,使1+>)()(x g x fD. 在R 中不存在x ,使)()(x g x f ≤ 3、b a ,是非零向量且满足a b a ⊥-)(2,b a b ⊥-)(2,那么a 与b 的夹角是 A.6π B.3π C.32π D.65π 4、函数R x x x x f ∈+=,cos 3sin )(ωω,又02=-=)(,)(βαf f ,且βα-的最小值为43π,那么正数ω的值是 A. 31 B. 32 C.34 D.235、假设c b a ,,为常数,那么“0402<->ac b a 且〞是“对任意02>++∈c bx ax R x 有〞的6、命题甲:22,2,211x x x-⎪⎭⎫⎝⎛成等比数列;命题乙:)3lg(,)1lg(,lg ++x x x 成等差数列;那么甲是乙的7、设函数⎩⎨⎧<+≥+-=0,60,64)(2x x x x x x f 那么不等式)1()(f x f >的解集是A .),3()1,3(+∞⋃-B .),2()1,3(+∞⋃-C .),3()1,1(+∞⋃-D .)3,1()3,(⋃--∞ 8、π4cos sin 365αα⎛⎫-+= ⎪⎝⎭,那么7πsin 6α⎛⎫+ ⎪⎝⎭的值是A .235-B .235C .45-D .459、正四棱台的上、下底面边长分别为3和6,其侧面积等于两底面积之和,那么该正四棱台的高是A .2B .25 C .3 D .27 10、一个正方体的展开图如下图,A 、B 、C 、D 为原正方体的顶点,那么在原来的正方体中A .AB∥CDB .AB 与CD 相交C .AB ⊥CD D .AB 与CD 所成的角为60°题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题:〔5×5=25分〕11、数列{}n a 中,)2,(122,511≥∈-+==*-n N n a a a n n n ,假设存在实数λ,使得数列⎭⎬⎫⎩⎨⎧+n n a 2λ为等差数列,那么λ= 12、定义域为R 的函数)(x f 为奇函数,且满足)()2(x f x f -=+,当]1,0[∈x 时,12)(-=x x f ,那么)24(log 21f =13、关于x 的实系数方程022=++b ax x 的一根在),(10内,另一根在),(21内,那么点),(b a 所在区域的面积为14、关于x 的二次方程210x mx ++=在区间[]0,2上有解,那么实数m 的范围是 15、如下列图所示,棱长为a 的正方体沿阴影面将它切割成两块,拼成右图所示的几何体,那么拼成的几何体的全面积为三、解答题:〔55分〕 16、〔本小题满分是13分〕ABC ∆的面积S 满足2323≤≤S ,且3=⋅BC AB ,AB 与BC 的夹角为θ. 〔1〕求θ的取值范围;〔2〕求函数θθθθθ22323cos cos sin sin )(+⋅+=f 的最大值及最小值.17、〔此题满分是为14分〕函数⎩⎨⎧≥<+++-=1,ln 1,)(23x x a x c bx x x x f 的图像过坐标原点O ,且在点))1(,1(--f 处的切线的斜率是5-.〔1〕务实数c b ,的值;〔2〕求()x f 在区间[]2,1-上的最大值.18、〔本小题满分是14分〕设n T 为数列{}n a 的前n 项的积,即12n n T a a a =⋅⋅⋅.⑴假设2n T n =,求345a a a 的值;⑵假设数列{}n a 各项都是正数,且满足()2*4n n a T n =∈N ,证明数列{}2log n a 为等比数列,并求{}n a 的通项公式;19、(本小题满分是14分)如图(1)所示,在直角梯形ABCP 中,BC∥AP ,AB ⊥BC ,CD ⊥AP ,AD =DC =PD =2,E 、F 、G 分别为线段PC 、PD 、BC 的中点,现将△PDC 折起,使平面PDC ⊥平面ABCD (图(2)).(1)求证:AP∥平面EFG ;(2)假设点Q 是线段PB 的中点,求证:PC ⊥平面ADQ ; (3)求三棱锥C -EFG 的体积. 参考答案一、选择题:〔12×5=60分〕题号 1 2 3 4 5 6 7 8 9 10 答案BDBBBAACAD二、填空题:〔5×5=25分〕 11、-1;12、2-;13、2;14、m ≤-2;15、()2224a +。
2020-2021高三数学统练试卷-8-导数、三角函数、向量、数列(教师版)

sinxcos
π 12
+
cosxsin
π 12
+
cos
π 12
cosx
+
sinxsin
π 12
=
(sinx
+
cosx)sin1π2+cos1π2= 26× 2sinx+π4≤ 26× 2= 3,故选 C.
6.(2019·全国卷Ⅰ)△ABC 的内角 A,B,C 的对边分别为 a,b,
c.已知 asinA-bsinB=4csinC,cosA=-14,则bc=( A )
c 的位置关系可能是相交、平行或异面,故选 D.
5.函数 f(x)=sinx+1π2+sinx+51π2的最大值是( C )
A.2
B.23
C. 3
D.2 3
解析:sin1π2+cos1π2= sin1π2+cos1π22
= 1+sinπ6= 1+12= 26,
所 以 f(x) = sin x+1π2 + sin x+51π2 = sin x+1π2 + cos 1π2-x =
解析:因为长方体 ABCDA1B1C1D1 的体积是 120, 所以 CC1·S 四边形 ABCD=120,又 E 是 CC1 的中点, 所以三棱锥 EBCD 的体积 VEBCD=31EC·S△BCD =13×12CC1×12S 四边形 ABCD=112×120=10. 8.一个六棱锥的体积为 2 3,其底面是边长为 2 的正六边形, 侧棱长都相等,则该六棱锥的侧面积为 12. 解析:设六棱锥的高为 h,则 V=13Sh, 所以13× 43×4×6h=2 3,解得 h=1. 设六棱锥的斜高为 h′,则 h2+( 3)2=h′2,故 h′=2. 所以该六棱锥的侧面积为12×2×2×6=12. 9.将函数 f(x)=asinx+bcosx(a,b∈R 且 a≠0)的图象向左平移π6 个单位长度后,得到一个偶函数图象,则ba= 3. 解析:解法 1:将 f(x)=asinx+bcosx(a,b∈R 且 a≠0)的图象向
函数、导数、三角函数、数列、极坐标与参数方程考试试卷

,若
A
、
B
都在曲线
C1
上,
求
1 12
+
1 22
的值.
17、已知函数 f x ax2 a 2 x lnx ,其中 a R .
(Ⅰ)当 a 1时,求曲线 y f x 的点 1, f 1 处的切线方程;
(Ⅱ)当 a 0 时,若 f x 在区间1,e 上的最小值为-2,求 a 的取值范围.
…………○…………外…………○…………装…………○…………订…………○…………线…………○………… 学校:___________姓名:___________班级:___________考号:___________
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
又 c 2a ,
∴ b2 2a2 ,故得 b 2a .
cosB a2 c2 b2 a2 (2a )2 ( 2a )2 3
∴
2ac
2 a (2a)
4.
故选 B. 【点睛】 本题考查余弦定理的应用,解题的关键是根据题意得到三角形中三边间的关系,并用统 一的参数表示,属于基础题. 6、【答案】A
若
S99
1 50
,则
k
__________.
12、在
ABC
中,角
A,B,C
的对边分别为
a,
b,
c
,若
b
cos
C
2a
c
sin
B
2
,
且 b 3 ,记 h 为 AC 边上的高,则 h 的取值范围为
最新三角函数、数列、导数试题及详解

三角函数、数列导数测试题及详解一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是 符合题目要求的. 1.已知点A (-1,1),点B (2,y ),向量a=(l ,2),若//AB a ,则实数y 的值为 A .5B .6C .7D .82.已知等比数列123456{},40,20,n a a a a a a a ++=++=中则前9项之和等于 A .50B .70C .80D .903.2(sin cos )1y x x =+-是A .最小正周期为2π的偶函数B .最小正周期为2π的奇函数C .最小正周期为π的偶函数D .最小正周期为π的奇函数 4.在右图的表格中,如果每格填上一个数后,每一横行成等差数列,每一纵列成等比数列,那么x+y+z 的值为 A .1 B .2 C .3 D .4 5.已知各项均不为零的数列{}n a ,定义向量*1(,),(,1),n n n n c a a b n n n N +==+∈,下列命题中真命题是A .若*,//n n n N c b ∀∈总有成立,则数列{}n a 是等差数列 B .若*,//n n n N c b ∀∈总有成立,则数列{}n a 是等比数列 C .若*,n n n N c b ∀∈⊥总有成立,则数列{}n a 是等差数列 D .若*,n n n N c b ∀∈⊥总有成立,则数列{}n a 是等比数列6.若sin2x 、sinx 分别是sin θ与cos θ的等差中项和等比中项,则cos2x 的值为A .18+ B .18C .18± D .14-7.如图是函数sin()y x ωϕ=+的图象的一部分,A ,B 是图象上的一个最高点和一个最低点,O 为坐标原点,则OA OB ⋅的值为 A .12π B .2119π+C .2119π-D .2113π-8.已知函数()cos ((0,2))f x x x π=∈有两个不同的零点x 1,x 2,且方程()f x m =有两个不同的实根x 3,x 4.若把这四个数按从小到大排列构成等差数列,则实数m 的值为A .12B .12-C.2D.—29.设函数f (x ) =e x (sinx —cosx ),若0≤x ≤2012π,则函数f (x )的各极大值之和为A .1006(1)1e e e πππ--B .20122(1)1e e e πππ-- C .10062(1)1e e e πππ-- D .2012(1)1e e eπππ-- 10.设函数011()(),21xf x x A x =++为坐标原点,A 为函数()y f x =图象上横坐标为*()n n N ∈ 的点,向量11,(1,0),nn k k n n k a A A i a i θ-===∑向量设为向量与向量的夹角,满足15tan 3nkk θ=<∑的最大整数n 是 A .2 B .3 C .4 D .5二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上,题两空的题,其答案按先后次序填写,填错位置,书写不清,模棱两可均不得分. 11.设1(sin cos )sin 2,()3f f ααα+=则的值为 . 12.已知曲线1*()()n f x xn N +=∈与直线1x =交于点P ,若设曲线y=f (x )在点P 处的切线与x 轴交点的横坐标为201212012220122011,log log log n x x x x +++则的值为____.13.已知22sin sin ,cos cos ,33x y x y -=--=且x ,y 为锐角,则tan (x -y )= . 14.如图放置的正方形ABCD ,AB =1.A ,D 分别在x 轴、y 轴的正半轴(含原点)上滑动,则OC OB ⋅的最大值是____.15.由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项,按图中多边形的边数依次称 这些数列为“三角形数列”、“四边形数列”…,将构图边数增加到n 可 得到“n 边形数列”,记它的第r 项为P (n ,r ),则(1)使得P (3,r )>36的最 小r 的取值是 ;(2)试推导P (n ,r )关于,n 、r 的解析式是____.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)已知2(2sin ,),(1,cos 1)OA a x a OB x x ==-+,O 为坐标原点,0,a ≠设(),.f x OA OB b b a =⋅+>(I )若0a >,写出函数()y f x =的单调速增区间; (Ⅱ)若函数y=f (x )的定义域为[,2ππ],值域为[2,5],求实数a 与b 的值,17.(本小题满分12分)如图,某测量人员,为了测量西江北岸不能到达的两点A ,B 之间的距离,她在西江南岸找到一个点C ,从C 点可以观察到点A ,B ;找到一个点D,从D 点可以观察到点A ,C ;到一个点E ,从E 点可以观察到点B ,C ;并测量得到数据:∠ACD=90°,∠ADC= 60°,∠ACB =15°,∠BCE =105°,∠CEB =45°,DC=CE =1(百米). (I )求△CDE 的面积; (Ⅱ)求A ,B 之间的距离.18.(本小题满分12分)国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生李顺在本科期间共申请了24000元助学贷款,并承诺在毕业后3年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第13个月开始,每月工资比前一个月增加5%直到4000元.李顺同学计划前12个月每个月还款额为500元,第13个月开始,每月还款额比前一月多x 元.(I )若李顺恰好在第36个月(即毕业后三年)还清贷款,求x 的值;(II )当x=50时,李顺同学将在第几个月还清最后一笔贷款?他还清贷款的那一个月的工资余额是多少?(参考数据:1.0518 =2.406,1.0519=2.526,1.0520 =2.653,1.0521=2.786) 19.(本小题满分12分)已知函数()sin .f x x x =+ (I )当[0,],()x f x π∈时求的值域;(II )设2()()1,()1[0,)g x f x g x ax '=-≥++∞若在恒成立,求实数a 的取值范围.20.(本小题满分13分)已知211()(1),()10(1),{}2,()()()0,n n n n n f x x g x x a a a a g a f a +=-=-=-+=数列满足9(2)(1).10n n b n a =+- (I )求证:数列{a n ,-1)是等比数列;(Ⅱ)当n 取何值时,b n 取最大值,并求出最大值;(Ⅲ)若1*1m m m m t t m N b b ++<∈对任意恒成立,求实数t 的取值范围.21.(本小题满分14分)设曲线C :()ln ( 2.71828),()()f x x ex e f x f x '=-=表示导函数.(I )求函数f (x )的极值;(Ⅱ)数列{a n }满足111,2(3)n na e a f e a +'==+.求证:数列{a n }中不存在成等差数列的三项;(Ⅲ)对于曲线C 上的不同两点A (x 1,y 1),B (x 2,y 2),x 1<x 2,求证:存在唯一的012(,)x x x ∈,使直线AB 的斜率等于0().f x '参考答案一、选择题: 1.【考点分析】本题主要考查平面向量的运算和向量平行充要条件的基本运用.【参考答案】 C【解题思路】AB →=(3,y -1),∵AB →∥a ,∴31=y -12,∴y =7.2. 【考点分析】本题主要考查等比数列的基本运算性质.【参考答案】 B .【解题思路】3321654)(q a a a a a a ++=++,∴213=q ,3654987)(q a a a a a a ++=++=10,即9s =70.3.【考点分析】本题考查三角函数的性质和同角三角函数的基本关系式的运用,考查基本运算能力. 【参考答案】D【解题思路】2(sin cos )12sin cos sin 2y x x x x x =+-==,所以函数2(sin cos )1y x x =+-是最小正周期为π的奇函数。
高三数学三角函数与函数导数专题训练(含解析)
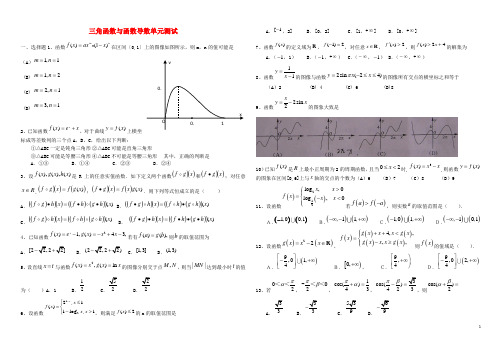
三角函数与函数导数单元测试一、选择题1、函数()()m nf x ax x =1-在区间〔0,1〕上的图像如图所示,则m ,n 的值可能是(A )1,1m n == (B) 1,2m n == (C) 2,1m n == (D) 3,1m n ==2、已知函数()xf x e x =+,对于曲线()y f x =上横坐标成等差数列的三个点A ,B ,C ,给出以下判断:①△ABC 一定是钝角三角形 ②△ABC 可能是直角三角形③△ABC 可能是等腰三角形 ④△ABC 不可能是等腰三角形 其中,正确的判断是A .①③B .①④C .②③D .②④ 3、设)(),(),(x h x g x f 是R 上的任意实值函数.如下定义两个函数()()x g f 和()()x g f •;对任意R x ∈,()()())(x g f x g f = ;()()())(x g x f x g f =•.则下列等式恒成立的是( )A .()()()()()())(x h g h f x h g f ••=•B .()()()()()())(x h g h f x h g f •=•C .()()()()()())(x h g h f x h g f =D . ()()()()()())(x h g h f x h g f •••=••4、已知函数2()1,()43,x f x e g x x x =-=-+-若有()(),f a g b =则b 的取值范围为 A .[22,22]-+ B .(22,22)-+ C .[1,3] D .(1,3)5、设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为( )A .1 B .12 C .52 D .226、设函数⎩⎨⎧>-≤=-1,log 11,2)(21x x x x f x ,则满足2)(≤x f 的x 的取值范围是A .1[-,2]B .[0,2]C .[1,+∞]D .[0,+∞]7、函数)(x f 的定义域为R ,2)1(=-f ,对任意R ∈x ,2)(>'x f ,则42)(+>x x f 的解集为A .(1-,1)B .(1-,+∞)C .(∞-,1-)D .(∞-,+∞)8、函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于(A )2 (B) 4 (C) 6 (D)89、函数2sin 2xy x =-的图象大致是10)已知()f x 是R 上最小正周期为2的周期函数,且当02x ≤<时,3()f x x x =-,则函数()y f x =的图象在区间[0,6]上与x 轴的交点的个数为(A )6 (B )7 (C )8 (D )911、设函数()()212log ,0log ,0x x f x x x >⎧⎪=⎨-<⎪⎩若()()f a f a >-,则实数a 的取值范围是( ).A.()()1001,,-B.()()11,,-∞-+∞C.()()101,,-+∞D.()()101,,-∞-12、设函数()22g x x =-()x ∈R ,()()()()()4,,,,g x x x g x f x g x x x g x ++<⎧⎪=⎨-≥⎪⎩则()f x 的值域是( ). A.()9,01,4⎡⎤-+∞⎢⎥⎣⎦B.[)0,+∞, C.9,4⎡⎫+∞⎪⎢⎣⎭ D.()9,02,4⎡⎤-+∞⎢⎥⎣⎦13、若02πα<<,02πβ-<<,1cos()43πα+=,3cos()423πβ-=,则cos()2βα+=A .33B .33-C .39D .69-y0.1xO0.14已知函数()sin(2)f x x ϕ=+,其中ϕ为实数,若()()6f x f π≤对x R ∈恒成立,且()()2f f ππ>,则()f x 的单调递增区间是(A ),()36k k k Z ππππ⎧⎫-+∈⎨⎬⎩⎭ (B ),()2k k k Z πππ⎧⎫+∈⎨⎬⎩⎭(C )2,()63k k k Z ππππ⎧⎫++∈⎨⎬⎩⎭ (D ),()2k k k Z πππ⎧⎫-∈⎨⎬⎩⎭15)设函数()sin()cos()f x x x ωϕωϕ=+++(0,||)2πωϕ><的最小正周期为π,且()()f x f x -=则(A )()y f x =在(0,)2π单调递减 (B )()y f x =在3(,)44ππ单调递减 (C )()y f x =在(0,)2π单调递增 (D )()y f x =在3(,)44ππ单调递增 二、填空题16\如图,△ABC 中,AB=AC=2,BC=23,点D 在BC 边上,∠ADC=45°,则AD 的长度等于______。
高三文科数学三角函数数列与导数试卷

高三文科数学三角函数数列与导数试卷(完卷时间:120分钟,满分:150分)命题及审题:周建梅一、选择题(每小题5分,共60分): 1.sin15cos75cos15sin105+等于( )A.0B.12D.12.在数列{a n }中,a 1=1,a n +1=a n 2-1(n ≥1),则a 1+a 2+a 3+a 4+a 5等于( )A .-1B .1C .0D .23.{a n }是等差数列,且a 1+a 4+a 7=45,a 2+a 5+a 8=39,则a 3+a 6+a 9的值是( )A .24B .27C .30D .33 4.函数y =Asin(ωx +φ) (A >0,ω>0,|φ|<2π=的图象如图所示,则y 的表达式为( ) A .y =2sin(611x 10π+) B .y =2sin(611x 10π-)C .y =2sin(2x +6π)D .y =2sin(2x -6π)5.函数y =f(x)的图象在点P (1,f(1))处的切线方程为y =-2x +10, 导函数为()f x ',则f(1)+(1)f '的值为 ( )A. -2B.2 C .6 D. 86.已知等差数列{a n }的公差为正数,且a 3·a 7=-12,a 4+a 6=-4,则S 20为( )A .180B .-180C .90D .-90 7.函数13)(23+-=x x x f 是减函数的区间为( )A .),2(+∞B .)2,(-∞C .)0,(-∞D .(0,2)8.由公差为d 的等差数列a 1、a 2、a 3…重新组成的数列a 1+a 4, a 2+a 5, a 3+a 6…是( )A .公差为d 的等差数列B .公差为2d 的等差数列C .公差为3d 的等差数列D .非等差数列 9. 曲线3231y x x =-+在点(1,-1)处的切线方程为(A .34y x =- B.32y x =-+ C.43y x =-+ 10.设函数f(x)在定义域内可导,y =f(x)的图象如图1可能为( )11.函数,93)(23-++=x ax x x f 已知3)(-=x x f 在时取得极值,则a = ( )A .2B .3C .4D .5A B C D12. 要得到)42sin(3π+=x y 的图象只需将y =3sin2x 的图象( )A .向左平移4π个单位 B .向右平移4π个单位C .向左平移8π个单位D .向右平移8π个单位二、填空题(每小题4分,共16分):13.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为________. 14.首项是125,从第10项开始比1大,则该等差数列的公差d 的取值范围是__________. 15.若函数y =x 3+ax 2+bx +27在x =-1时有极大值,在x =3时有极小值,则a =____,b =____. 16.等差数列{}n a 中,30216131074=++++a a a a a ,则其前19项和19S =_________. 三、解答题(共74分): 17.(本小题共12分)(1)在等差数列}{n a 中,已知94=a ,69-=a ,求满足63=n S 的所有的n 的值。
高中高三第三次月考文科函数导数立体几何逻辑用语三角函数向量数列附含答案汇总

高三数学周周练(十九)一、选择题(每题5 分,共 12×5 分= 60 分,每题只有一个正确答案)1、复数i (i 是虚数单位 ) 的实部是( )1 iA .2B . -2C . -1D .1222、设 { a n } 是等差数列,若a 2 3, a 7 13 ,则数列 { a n } 的公差为()A . 2B . 2C . 3D . 33、设等比数列a n 的公比 q=2,前 n 项和为 S n ,则S 3=()a 2A .3B . 47D .13C .224、若直线 ax 2 y2 0 与直线 x ( a 1) y 1 0 相互平行,则 a 的值为()A .-1B . 2C . -1 或 2D .不存在、已知会合Ax y log 2 ( x 1) ,By y 2 x1, x A ,则 AB ()5A .B . (1, 3)C .(3,)D .(1,)、已知 p :x 2 3 是q : 0 x a 建立的必需非充足条件,则实数a 的取值范围是()6A . (0,5]B . ( 1, 0)C . (5,)D . ( 1,5)7、若 , 为锐角, sin2 5) 4(), cos(,则 cos55A . 2 5B .2 5C . 2 5 或 2 5D .2 552552558、已知数列 { a n } 为等差数列,且a 1 a 7a134 ,则 tan(a 2a 12 ) =()A .3B . 3C .3D .339、已知等比数列a n 的前 n 项和为 S n ,且 S 5 2,S 10 6,则 a 16 a 17 a 18a 19 a 20 ()A .54B . 48C . 30D . 1612x y 4,10、设 x, y 知足 xy 1, 则 z( x 5) 2y 2 的最小值为()x 2 y 2,93C .6 D . 3 5A .B .555511、已知函数 yf ( x)(x R) 的 图像如右图所示,y则不等式 xf / (x)0 的解集为()A . (, 1) ( 1, 2) 1O1123 x222B . (,0)( 1, 2)2[C . (, 1 ) ( 1, )2 2D . (, 1) (2, )212、已知函数 f ( x) 是 ( , ) 上的偶函数,若对于x 0 ,都有 f ( x2) f (x) ,且当 x [0, 2) 时,f ( x) log 2 (x1),则 f2009 f2010 的值为()A . 2B . 1C . 2D . 1二、填空题(每题4 分,共 4×4 分= 16 分)13、已知向量 a(4,2) , b ( x ,3) ,若 a ∥ b ,则 x =.14、过点 p ( 3, -4)且在两坐标轴上截距相等的直线方程为 .15、数列a n 知足: a 1 2,a n 11( n 2,3,4, ) ,则 a 15 =.an 116、对于函数 f (x) 23cos 2 x 2sin xcos x 3 ( x R) 有以下命题:①由 f ( x 1 ) f ( x 2 ) 0可得x 1 x 2必是 的整数倍;② yf ( x) 的图象可由 y 2cos2 x 的图象向右平移个单位获得;6③ yf ( x) 的图象对于直线 x6 对称;2④ y f ( x) 在区间 [ , ] 上是减函数.6 3此中是假命题的序号有.三、解答题(本大题共 6 小题,共 74 分.解答应写出文字说明,证明过程或演算步骤.)17、(本小题满分12 分 )在ABC 中, a, b, c 分别是A, B, C 的对边长,已知a, b, c 成等比数列,且 a 2 c2 ac bc ,求 A 的大小及bsin B的值.c18、 (本小题满分12 分 ) 已知等比数列a n中, a1a310,a4a680(n N * ).(Ⅰ)求数列 { a n } 的通项公式;(Ⅱ)求数列 {( 2n1) a n}的前n项的和S n.19、(本小题满分12 分)已知函数 f ( x) A sin( x)( x R, A 0,0,| |) 的图象(部2分)如下图.( 1)试确立 f ( x) 的分析式;( 2)若x[0,1] ,求函数f ( x) 的值域.20、(此题满分 12 分)如图组合体中,三棱柱ABC A1 B1C1的侧面 ABB1 A1是圆柱的轴截面(过圆柱的轴截圆柱所获得的截面), C是圆柱底面圆周上不与 A 、 B 重合的一个点.(1)求证:不论点 C 怎样运动,平面A1BC 平面 A1 AC ;(2)当点C是弧AB的中点时,求四棱锥A1 BCC1 B1与圆柱的体积比.第 20 题图21、(本小题满分12 分)已知数列{ a n } 的前 n 项和 S n知足 S n- S n 1=S n+S n 1(n2 ),a11.3(1)证明:数列{ S n } 是等差数列,并求数列{ a n} 的通项公式;1, T n b1 b2 b n ,求证: T n 1(2)若b n .an an 1 21 3 2(a 2 b( a,b R )22、(本小题满分 14 分)已知函数 f (x) x ax 1)x3(1)若 x 1 为 f (x) 的极值点,求a的值;(2)若 y f ( x) 的图象在点 (1,f (1)) 处的切线方程为x y 3 0 ,求 f (x) 在区间 [ 2,4] 上的最大值;(3)当 a 0 时,若 f (x) 在区间 ( 11),上不但一,求 a 的取值范围.简要答案:1-12 DBCACADADDBD13、614、4 x 3 y 0 或 x y 1 015、-116、①②③17、解:(1)a,b,c 成等比数列b2 ac 又 a2 c2 ac bcb2 c 2 a 2 bc ,在ABC 中,由余弦定理得4b 2c 2 a 2bc 1 cos A2bc 2bc2A 60b sin A ( 2)在ABC 中,由正弦定理得 sin Bab 2ac , A60b sin B b 2 sin 60 sin 603cca218、解:(1)∵ a 1a 3 10,a 4 a 6 80 ,∴ a 1 a 3 10 q 2,a 1 q 3 a 3q 3 80又a 1a 3 a 1q a 1q 2 10 a 1 2∴ a na 1q n 1 2 2n 1 2n(2)S n1 23 225 23(2n 1) 2n2S n 1 22 3 23 5 24 (2 n 1) 2n 1①②① -②得 - S n 2 2 222 232 24... 2 2n (2n 1)2n 12 2 22 (1 2n 1 )(2n n 11 21)22 8n 1 (2n 1)2 n 12 26 (2n 3)2n 1∴ Sn (2n 3)2n 1619、解:(Ⅰ)由 象可知 A=2且T5 1146 32∴T=2 ∴2 ,将点 P ( 1 ,2) 代入 y2sin( x ) 得 sin() =1T33又 | |,因此,26故所求分析式 f ( x) 2sin( x), x R ⋯⋯6分6(Ⅱ)∵ x [0,1] ∴ x6 [ , 7]6 6∴ sin( x) [ 1,1]6 2∴ f ( x) 的 域 [ -1,2]⋯⋯ 12 分20、( 12 分) (1)因 面 ABB 1 A 1 是 柱的 截面,故 AB 是底面的直径,又C 是 柱底面 周上不与A 、B 重合一个点,因此5第18 题图AC BC⋯⋯⋯⋯2 分又 柱母 AA 1 平面 ABC , BC平面 ABC ,因此 AA 1BC ,又 AA 1 AC A ,因此 BC 平面 A 1AC ,因 BC平面 A 1BC ,因此平面 A 1 BC 平面 A 1AC ;⋯6分 (2)法 1: 柱的底面半径 r ,母 度 h , A 1C 1 B 1 C 12r A 1B 1是底面 的直径AC 1 1 B 1C 1又在 柱中 CC 1 面A 1B 1C 1AC 11 面 A 1 B 1C 1CC 1 AC 11, 又B 1C 1CC 1 C 1AC 1 1 面 B 1C 1 BC故 AC 11是四棱 A 1 B 1C 1 BC 的高 , AC 11hVA B C BC1SB C BCh2 hr 211 13 113V圆柱r 2h故四棱 A 1 BCC 1B 1 与 柱的体 比2 :3 .(2)法 2: 柱的底面半径 r ,母 度 h ,[ 根源 :学,科 ,网] 当点 C 是弧 AB 的中点 ,三角形 ABC 的面 r 2 , 三棱柱 ABC A 1B 1C 1 的体 r 2h ,三棱 A 1ABC 的体 1r 2 h ,3四棱 A 1BCC 1 B 1 的体 r 2h1 r 2h 2r 2h ,r 2h ,3 3柱的体四棱 A 1 BCC 1 B 1 与 柱的体 比 2: 3 .21、解:(1) S nSn 1S nSn 1S nSn 1S nSn 1, n 2易知 S n 0 ,S nS n11,⋯⋯⋯⋯ 2 分又 S 1a 1 1,因此数列S n是一个首1 公差 1 的等差数列. ⋯⋯⋯⋯ 3 分 S 1 n 1 1 n , S n 2.⋯⋯⋯⋯ 4 分nn当 n2, a n S nSn 1n 2 (n 1)2 2n 1 ;a 1 1 合适上式,a n2n 1 ( n N * ).⋯⋯⋯⋯ 7 分 1= 1111, ⋯⋯⋯⋯ 9 分( 2) b na nan 12n 1 2n 1 2 2n 1 2n 1T nb 1 b 2b n1 1 1 1 1 11 1 1 K1 1 1 1 ;232 3 52 5 72 2n 2n 16= 11 1 1 1 1111 23 3 5 5 72n 1 2n 1=1111⋯⋯⋯⋯ 12 分22nn N *,1 1 0 ,1 1 1 1 , 11 11,即 T n 1.⋯⋯⋯⋯ 13 分[ 根源 :2n2n 22n 12222、解: (1) f ( x) x 2 2ax a 21⋯⋯⋯⋯1 分∵ x 1 是 f ( x) 的极 点,∴f (1)0 ,即 a 22a 0,解得 a 0 或 2.⋯⋯⋯⋯2分(2)∵ (1, f (1))在 x y 3 0 上∴ f (1) 2∵ (1,2) 在 y f (x) 上∴ 2 12①a a 1 ba 23又 f (1)1∴ 1 2 a 11②立①、②式,解得 a1,b8 ⋯⋯5分318, f (x)∴ f ( x) x3x2x 2 2x3 3令 f (x) 0 可知: x 0 或 x 2x2( 2,0)0 (0,2)2(2,4)4f ( x)0 0f ( x)48 4 833∴ f ( x) 在区 [ 2,4] 上的最大 8.⋯⋯⋯⋯8 分( 3)因 函数 f ( x) 在区 ( 1,1) 不 ,因此函数 f ( x) 在 ( 1,1) 上存在零点.而 f (x) 0 的两根 a 1 , a 1 ,区 2∴在区 ( 1,1)上不行能有 2 个零点.因此 f ( 1) f (1) 0 ,即 a 2 (a 2)(a 2)0 .∵ a 2 0 ,∴ ( a 2)( a 2) 0, 2 a 2 .又∵ a 0 ,∴ a ( 2,0) (0,2) . ⋯⋯⋯⋯ 12分7。
高三数学三角函数试题答案及解析

高三数学三角函数试题答案及解析1.在中,已知,若分别是角所对的边,则的最大值为.【答案】【解析】由正余弦定理得:,化简得因此即最大值为.【考点】正余弦定理,基本不等式2. sin7°cos37°﹣sin83°cos53°的值为()A.﹣B.C.D.﹣【答案】A【解析】sin7°cos37°﹣sin83°cos53°=cos83°cos37°﹣sin83°sin37°=cos(83°+37°)=cos120°=﹣,故选A.3.三角形ABC是锐角三角形,若角θ终边上一点P的坐标为(sin A-cos B,cos A-sin C),则的值是( )A.1B.-1C.3D.4【答案】B【解析】因为三角形ABC是锐角三角形,所以A+B>90°,即A>90°-B,则sin A>sin(90°-B)=cos B,sin A-cos B>0,同理cos A-sin C<0,所以点P在第四象限,=-1+1-1=-1,故选B.4.已知函数则=【答案】【解析】因为函数由需要求的x都是整数,所以当x为奇数时的解析式为,当x为偶数时的解析式为.所以.所以.【考点】1.分段函数的性质.2.归纳推理的思想.3.三角函数的运算.4.等差数列的求和公式.5.若方程有实根,则实数的取值范围为【答案】【解析】由方程得,,即,因为,所以,若方程有实根,则,解得.【考点】方程的根.6.设,将函数在区间内的全部极值点按从小到大的顺序排成数列.(1)求数列的通项公式;(2)设,数列的前项和为,求.【答案】(1);(2).【解析】(1)先根据三角函数的恒等变换化简,得,再根据三角函数的性质找到极值点,利用等差数列的性质写出数列的通项公式;(2)先根据(1)中的结果写出的通项公式,然后写出的解析式,在构造出,利用错位相减法求,计算量比较大,要细心.试题解析:(1),其极值点为, 2分它在内的全部极值点构成以为首项,为公差的等差数列, 4分所以; 6分(2), 8分所以,,相减,得,所以. 12分【考点】1、三角函数的恒等变换及化简;2、三角函数的性质的应用;3、等差数列的通项公式;4、错位相减法求数列的前项和;5、等比数列的前项和.7.已知函数d的最大值为2,是集合中的任意两个元素,且的最小值为.(1)求函数的解析式及其对称轴;(2)若,求的值.【答案】(1),;(2).【解析】本题主要考查两角和与差的正弦公式、二倍角的余弦公式、诱导公式、三角函数的最小正周期、单调性等基础知识,考查运算能力.第一问,利用倍角公式化简表达式,先利用周期求出,再求最值,通过解方程求出,确定了解析式后求正弦函数的对称轴;第二问,通过角之间的关系转化角,考查诱导公式和倍角公式.试题解析:(1),由题意知:的周期为,由,知 2分由最大值为2,故,又, 4分∴ 5分令,解得的对称轴为 7分(2)由知,即, 8分∴ 10分12分【考点】1.倍角公式;2.两角和与差的三角函数;3.函数的周期;4.函数的对称轴.8.是偶函数,,则 .【答案】【解析】,,所以,因为为偶函数,所以对任意的,都有即成立,又,所以.【考点】三角函数的恒等变换,偶函数.9.已知方程在上有两个不同的解、,则下列结论正确的是()A.B.C.D.【答案】C【解析】由于方程在上有两个不同的解、,即方程在上有两个不同的解、,也就是说,直线与函数在轴右侧的图象有且仅有两个交点,由图象可知,当时,直线与曲线相切,且切点的横坐标为,当时,,则,故,在切点处有,即,,两边同时乘以得,,故选C.【考点】1.函数的零点;2.函数的图象;3.利用导数求切线的斜率10.将函数图像上各点的横坐标缩短到原来的倍(纵坐标不变),再向右平移个单位,那么所得图像的一条对称轴方程为()A.B.C.D.【答案】B【解析】将函数的图像按题中要求变换后得到函数的图像,令,则,当时,.【考点】1.三角函数的变换;2.三角函数图象的对称轴.11.函数f(x)=sin+ACos(>0)的图像关于M(,0)对称,且在处函数有最小值,则的一个可能取值是( )A.0B.3C.6D.9【答案】D【解析】根据题意:相邻对称点与最小值之间可以相差也可以是不妨设为:=,可以为9,故选D.【考点】三角函数的最值;正弦函数的对称性.12.已知函数,(1)求的值;(2)若,且,求.【答案】(1);(2).【解析】(1)直接将代入计算即可;(2)用二倍角的正弦、余弦公式化简,再将正弦、余弦合为同一个的三角函数;根据已知条件,求出的值.试题解析:(1)(2)因为,且,所以,所以【考点】1、三角恒等变换;2、三角函数的基本运算.13.已知函数的最小正周期为.(Ⅰ)求的值;(Ⅱ)讨论在区间上的单调性.【答案】(Ⅰ)(Ⅱ)当,即时,单调递增;当,即,单调递减.【解析】(1)由题意,所以由(1)知若,则当,即时,单调递增;当,即,单调递减.第(1)题根据三角函数的和差化简,二倍角公式以及辅助角公式,最后化成的形式,利用确定的值;第(2)题用整体法的思想确定的单调性,再反求出在指定范围内的单调性.本题属简单题.【考点】本题主要考查三角恒等变形、三角函数的图像及性质与三角函数图像的变换.考查逻辑推理和运算求解能力,中等难度.14.已知函数若方程有三个不同的实根,且从小到大依次成等比数列,则m的值为 .【答案】【解析】设三个根由小到大依次为,结合余弦函数图像可知关于直线对称,关于直线对称,代入计算得【考点】三角函数图像及性质点评:题目中主要结合三角函数图像的轴对称性找到三根之间的联系15.已知,则的值为()A.B.C.D.【答案】B【解析】因为,,即,,所以,=,故选B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
文科数学三角函数数列与导数一、选择题(每小题5分,共60分): 1.sin15cos75cos15sin105+等于( )A.0B.12D.12.在数列{a n }中,a 1=1,a n +1=a n 2-1(n ≥1),则a 1+a 2+a 3+a 4+a 5等于( )A .-1B .1C .0D .23.{a n }是等差数列,且a 1+a 4+a 7=45,a 2+a 5+a 8=39,则a 3+a 6+a 9的值是( )A .24B .27C .30D .334.函数y =Asin(ωx +φ) (A >0,ω>0,|φ|<2π=的图象如图所示,则y 的表达式为( )A .y =2sin(611x 10π+)B .y =2sin(611x 10π-)C .y =2sin(2x +6π)D .y =2sin(2x -6π)5.函数y =f(x)的图象在点P (1,f(1))处的切线方程为y =-2x +10, 导函数为()f x ',则f(1)+(1)f '的值为 ( )A. -2B.2 C .6 D. 86.已知等差数列{a n }的公差为正数,且a 3·a 7=-12,a 4+a 6=-4,则S 20为( )A .180B .-180C .90D .-90 7.函数13)(23+-=x x x f 是减函数的区间为 ( ) A .),2(+∞ B .)2,(-∞ C .)0,(-∞ D .(0,2)8.由公差为d 的等差数列a 1、a 2、a 3…重新组成的数列a 1+a 4, a 2+a 5, a 3+a 6…是( )A .公差为d 的等差数列B .公差为2d 的等差数列C .公差为3d 的等差数列D .非等差数列 9. 曲线3231y x x =-+在点(1,-1)处的切线方程为(A .34y x =- B.32y x =-+ C.43y x =-+ 10.设函数f(x)在定义域内可导,y =f(x)的图象如图1可能为( )11.函数,93)(23-++=x ax x x f 已知3)(-=x x f 在时取得极值,则a = ( )A .2B .3C .4D .5 12. 要得到)42sin(3π+=x y 的图象只需将y =3sin2x 的图象( )A .向左平移4π个单位 B .向右平移4π个单位C .向左平移8π个单位D .向右平移8π个单位二、填空题(每小题4分,共16分):13.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为________.A B C D14.首项是125,从第10项开始比1大,则该等差数列的公差d 的取值范围是__________. 15.若函数y =x 3+ax 2+bx +27在x =-1时有极大值,在x =3时有极小值,则a =____,b =____. 16.等差数列{}n a 中,30216131074=++++a a a a a ,则其前19项和19S =_________. 三、解答题(共74分): 17.(本小题共12分)(1)在等差数列}{n a 中,已知94=a ,69-=a ,求满足63=n S 的所有的n 的值。
(2)在等比数列}{n b 中,813=-b b ,21646=-b b ,40=n S ,求公比q 、1b 及n 。
18.(本小题12分)设{}n a 是一个公差为)0(≠d d 的等差数列,它的前10项和11010=S 且1a ,2a ,4a 成等比数列。
(1)证明d a =1;(2)求公差d 的值和数列{}n a 的通项公式. 19.(本小题12分)求下列数列的前n 项和n S : (1))1(1+=n n a n(2)求数列}2{nn ⋅的前n 项和n S20.(本小题12分)等差数列}{n a 中,已知251=a ,917S S =,则该数列前多少项和最大?并求此最大值。
21.(本小题12分)已知:a R a a x x x f ,.(2sin 3cos 2)(2∈++=为常数) (1)若R x ∈,求)(x f 的最小正周期;(2)若)(x f 在[]6,6ππ-上最大值与最小值之和为3,求a 的值.22.(本小题14分)已知函数d cx bx x x f +++=23)(的图象过点P (0,2),且在点))1(,1(--f M 处的切线方程为076=+-y x .(Ⅰ)求函数)(x f y =的解析式;(Ⅱ)求函数)(x f y =的单调区间.参考答案一、选择题(每小题5分,共60分):DADCC ADBBD DC 二、填空题(每小题4分,共16分):13.3;14. 83,7525⎛⎤⎥⎝⎦;15. -3 ,–9; 16. 95 三、解答题(本大题共74分): 17.(本小题共12分)解:(1)由已知34949-=--=a a d -------------------2分18)3()3(9)41(41=-⋅-+=--=d a a-------------------3分 又63)3(2)1(182)1(1=-⋅-+=-+=n n n d n n na S n -------------------4分 整理得042132=+-n n -------------------5分76或=∴n -------------------6分(2)由已知可得⎩⎨⎧=-=-21683151121q b q b b q b -------------------8分 则⎩⎨⎧==311q b------------------10分又4031311)1(1=--=--=nn n q q b S 得813=n4=∴n------------------12分 18. (本小题共12分)解:(1)证明:因1a ,2a ,4a 成等比数列,故4122a a a ⋅=-------------2分 而{}n a 是等差数列,有d a a +=12,d a a 314+=,于是 21)(d a +)3(11d a a +=,-------------4分 即d a a d d a a 121212132+=++,化简得 d a =1-------------6分 (2)解:由条件11010=S 和d a S 291010110⨯+=, -------------8分 得到11045101=+d a , -------------9分 由(1),d a =1,代入上式得11055=d ,故 2=d ,-------------10分 n d n a a n 2)1(1=-+=∴-------------12分19.(本小题共12分) 解:(1) 111+-=n n a n --------------------2分 )111()4131()3121()211(+-++-+-+-=∴n n S n --------------------4分1111+=+-=n n n -------------------6分(2) nn n S 223222132⋅++⋅+⋅+⋅= ①13222)1(22212+⋅+⋅-++⋅+⋅=n n n n n S ②两式相减得13222222+⋅-++++=-n n n n S-------------------8分111222221)21(2+++⋅--=⋅---⋅=n n n n n n-------------------10分22)2(2221+⋅-=+⋅+-=∴+n n n n n n S-------------------12分20.(本小题12分) 解法一: 由917S S =得d a d a 2899216171711⋅+=⋅+--------------------2分 则02521=+d a --------------------4分 251=a 代入可得 2-=d --------------------6分 272)2()1(25+-=-⋅-+=∴n n a n--------------------8分由0272>+-=n a n 得5.13227=<n ∴数列}{n a 前13项均为正,从第14项开始为负故前13项和最大--------------------10分 16913)2(212132513213==-⨯⨯+⨯=S--------------------12分解法二: 由917S S =d a d a 2899216171711⋅+=⋅+得 --------------------2分 则02521=+d a --------------------4分251=a 代入可得 2-=d--------------------6分 n n d n n na S n 262)1(21+-=⋅-+=∴--------------------8分169)13(2+--=n--------------------10分 故前13项和最大,且最大值为169--------------------12分21.(本小题12分)解:1)62sin(22sin 32cos 1)(+++=+++=a x a x x x f π---------------------4分(1)最小正周期ππ==22T----------------------6分(2)]2,6[62]3,3[2]6,6[πππππππ-∈+⇒-∈⇒-∈x x x----------------------8分 1)62s i n (21≤+≤-∴πx ---------------------10分 即033211)(12)(min max =⇒=+∴⎩⎨⎧++-=++=a a a x f a x f ---------------------12分22.(本小题14分) 解:(Ⅰ)由)(x f 的图象经过P (0,2),知d =2,---------------1分所以,2)(23+++=cx bx x x f.23)(2c bx x x f ++=' ---------------2分由在))1(,1(--f M 处的切线方程是076=+-y x ,知.6)1(,1)1(,07)1(6=-'=-=+---f f f 即 ---------------4分 .3,0,32.121,623-==⎩⎨⎧=--=-⎩⎨⎧=+-+-=+-∴c b c b c b c b c b 解得即 ---------------6分故所求的解析式是 .233)(23+--=x x x x f ---------------7分(Ⅱ).012,0363.363)(222=--=----='x x x x x x x f 即令 ---------9分解得 .21,2121+=-=x x 当;0)(,21,21>'+>-<x f x x 时或当.0)(,2121<'+<<-x f x 时----------------12分故)21,(233)(23--∞+--=在x x x x f 内是增函数,在)21,21(+-内是减函数,在),21(+∞+内是增函数. ------------14分。
