计算方法 常微分方程初值问题(欧拉和改进欧拉)源代码
数值分析课程设计代码_常微分方程组的初值问题

scanf("%d",&i); switch(i) { case 1:xianshi();break; case 2:yinshi();break; case 3:gaijin();break; case 4:tixing();break; case 5:RK();break; case 6:youxianchafen();break; case 7:exit(0); }}while(i!=7); }
a[1][2]=1; for(i=2;i<n-1;i++) {a[i][i-1]=1; a[i][i]=-2-q(x[i])*pow(h,2); a[i][i+1]=1; } a[n-1][n-1]=-2-q(x[n-1])*pow(h,2); a[n-1][n-2]=1; b[1]=r(x[1])*pow(h,2)-y[0]; for(i=2;i<n-1;i++) {b[i]=r(x[i])*pow(h,2); } b[n-1]=r(x[n-1])*pow(h,2)-y[n]; m[1]=a[1][2]/a[1][1]; for(i=2;i<n-1;i++) {m[i]=a[i][i+1]/(a[i][i]-a[i][i-1]*m[i-1]); } y1[1]=b[1]/a[1][1]; for(i=2;i<n;i++) {y1[i]=(b[i]-a[i][i-1]*y1[i-1])/(a[i][i]-a[i][i-1]*m[i-1]); } y[n-1]=y1[n-1]; for(i=n-2;i>0;i--) {y[i]=y1[i]-m[i]*y[i+1]; } printf(" x\t\t\ty\n\n"); for(i=0;i<=n;i++) {printf("%lf\t\t%lf\n",x[i],y[i]); }} void main() {
微分方程的MATLAB实现与欧拉算法

微分方程的MATLAB实现与欧拉算法微分方程是数学中的重要概念,由于数值计算的发展,人们开始使用计算机来求解微分方程。
MATLAB作为一款强大的数学计算软件,提供了丰富的工具和函数来求解微分方程。
本文将介绍MATLAB如何实现微分方程的求解,并详细讨论了欧拉算法的原理和实现。
MATLAB中求解微分方程的函数主要有ode45、ode23、ode15s、ode23s和ode113等。
其中,ode45是最常用的函数,其基本用法如下:```[t,y] = ode45(fun,tspan,y0)```其中,fun是代表微分方程函数的句柄,tspan是时间范围,y0是初始条件。
返回的t是时间向量,y是对应时间的函数值。
例如,我们要求解一个简单的一阶常微分方程dy/dt = -2y,初始条件为y(0) = 1,在MATLAB中的代码如下:```tspan = [0 10];y0=1;[t,y] = ode45(fun,tspan,y0);```运行上述代码,我们得到了在时间范围[0,10]内的y的值,并且存储在数组y中。
欧拉算法是一种简单而粗糙的求解微分方程的方法,其基本原理是利用初始条件和微分方程的定义式逐步逼近所要求解的函数。
欧拉算法的迭代公式为y(n+1)=y(n)+h*f(t(n),y(n)),其中h为步长,f为微分方程的函数。
我们可以用MATLAB实现欧拉算法来求解微分方程。
以下是一个简单的例子,求解一阶常微分方程dy/dt = -2y,初始条件为y(0) = 1,步长为0.1,时间范围为[0,10]:```h=0.1;t=0:h:10;y(1)=1;for i = 1:length(t)-1y(i+1)=y(i)+h*(-2*y(i));end```在上述代码中,我们首先定义了步长h和时间范围t,然后初始化初始值y(1),接下来通过循环计算每个时间点的函数值。
通过以上的示例,我们可以看到,虽然欧拉算法是一种较为简单的求解微分方程的方法,但是当步长较大时,结果往往不够精确,因此在实际应用中,通常会使用更为高阶的方法,如ode45函数。
课题10常微分方程初值问题的数值方法

课题10. 常微分方程初值问题的数值方法一.问题提出(1)利用欧拉方法和改进的欧拉方法求解初值问题:dy/dx=4*x/y-x*y; y(0)=3; 其中0<x<=2二.问题算法、c语言编程和上机运算结果1.欧拉法算法:输入微分方程f(x,y);输入积分部数n;输入初值x0,y0;输入步长h;利用k1=f(xn,yn)y(n+1)=yn+k1*h;n=0,1,2……采取不断循环计算;输出x1,x2,……xn.程序:/*微分方程*/float f(x,y)float x,y;{float z;z=4*x/y-x*y;return(z);}/* 欧拉法*/float EULAR(f)float (*f)();{int i,n;float x0,y0,x,y,k1,h;printf("\n请输入积分步数n:");scanf("%d",&n);printf("\n请输入初值x(0) y(0):");scanf("%f%f",&x0,&y0);printf("\n请输入步长h:");scanf("%f",&h);printf("\n x y"); printf("\n %f %f",x0,y0); for(i=1;i<=n;i++){x=x0+h;k1=(*f)(x0,y0);y=y0+h*k1;printf("\n %f %f",x,y); x0=x;y0=y;}}main(){EULAR(f);}结果:(1)h=0.1时(2)h=0.2时(3)h=0.4时2.改进的欧拉法算法:输入微分方程f(x,y);输入积分部数n;输入初值x0,y0;输入步长h;利用k1=f(xn,yn)k2=f(xn+h,yn+h*k1)y(n+1)=yn+(k1+k2)/2;n=0,1,2……采取不断循环计算;输出x1,x2,……xn.程序:/*微分方程*/float f(x,y)float x,y;{float z;z=y-2.0*x/y;return(z);}/* 改进欧拉法*/float EULAR(f)float (*f)();{int i,n;float x0,y0,x,y,k1,k2,h;printf("\n请输入积分步数n:");scanf("%d",&n);printf("\n请输入初值x(0) y(0):");scanf("%f%f",&x0,&y0);printf("\n请输入步长h:");scanf("%f",&h);printf("\n x y"); printf("\n %f %f",x0,y0); for(i=1;i<=n;i++){x=x0+h;k1=(*f)(x0,y0);k2=(*f)(x,y0+h*k1);y=y0+h*(k1+k2)/2.0;printf("\n %f %f",x,y); x0=x;y0=y;}}main(){EULAR(f);}结果:(1)当h=0.1时(2)当h=0.2时(3)当h=0.4时三.结果分析讨论1.对比欧拉法,改进的欧拉法和精确解的结果可知,改进的欧拉法所得到结果的精度比欧拉法的大,这是因为改进的欧拉法融入了属于隐式公式的梯形公式,它的计算数值解的精度要比欧拉公式好。
欧拉法解常微分方程代码

}
}
void main()
{
float x0,y0,h; //x0:自变量初值,y0:y(x0),h:步长
int n; //步数
char FxyString[200]; //存放C表达式格式的f(x,y)
printf("\nInput function,x0,y0,h,n: ");
void Euler(char FxyString[],float x0,float y0,float h,int n)
{
int i;
float yi;
if(CreateFxy(FxyString)) return;
yi=y0;
for(i=1;i<n;++i)
{
yi=yi+h*f(x0+(i-1)*h,yi);
//§4常微分方程的差分方法
//程序4.1 —欧拉方法
#include <stdlib.h>
#include <stdio.h>
#include <conio.h>
#include <string.h>
#include <graphics.h>
#include <math.h>
#include "expressi.cpp"
欧拉法解常微分方程代码.doc 欧拉方法#include <stdlib.h> #include <stdio.h> #include <conio.h> #include <string.h> #include <graphics.h> #include <math.h> #include "expressi.cpp" void euler(char fxystring[],float x0,float y0,float h,int floatyi; if(createfxy(fxystring)) return; yi=y0; yi=yi+h*f(x0+(i-1)*h,yi);printf("\ny%d=%f",i,yi); voidmain() floatx0,y0,h; //x0:自变量初值,y0:y(x0),h:步长 int charfxystring[200]; //存放c表达式格式的f(x,y) printf("\ninput function,x0,y0,h,n: %d",fxystring,&x0,&y0,&h,&n);euler(fxystring,x0,y0,h,n); getch();运行实例input function,x0,y0,h,n: y-2*x/y 0.111 y1=1.100000 y2=1.191818 y3=1.277438 y4=1.358213 y5=1.435133 y6=1.508966 y7=1.580338 y8=1.649784 y9=1.717780 y10=1.784771 2012-11-16 15:12:9.8
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
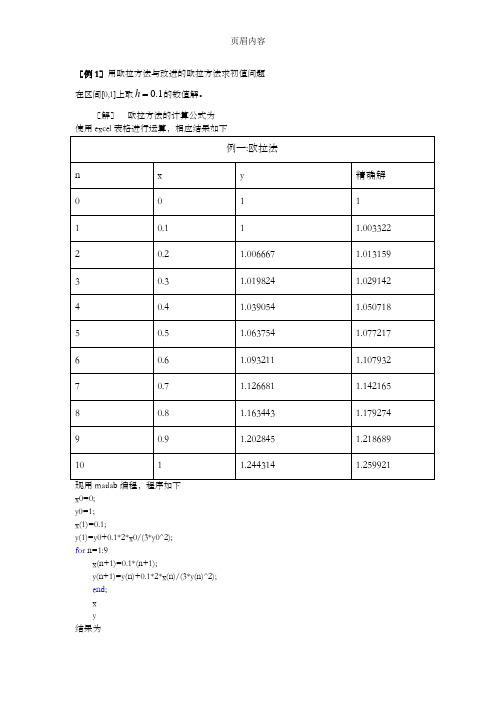
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
MATLAB Euler法解常微分方程

Euler 法解常微分方程Euler 法解常微分方程算法:Step 1 分别取积分上限、积分下限、步长Step 2计算h n n +=判断b n ≤是否成立,成立转到Step 3,否则继续进行Step 4 Step 3 计算),(1n n n n y x hf y y +=+Step 4 ),(1n n n n y x hf y y +=+Euler 法解常微分方程算程序:function euler2(fun,y0,A,h)%fun--y'%y0---初值%A----x 取值范围%a----x 左区间端点值%b----x 右区间端点值%h----给定步长x=min(A);b=max(A);y=y0;while x<b-hb=y;y=y+h*feval(fun,x,b)x=x+h;end例:用Euler 法计算下列初值问题(取步长h=0.2))6.00(1)0('2≤≤⎩⎨⎧=--=x y xy y y输入:fun=inline('-y-x*y^2')euler2(fun,1,[0 0.6],0.2)得到:y =0.8000y =0.6144y =0.4613指导教师: 年 月 日改进Euelr 法解常微分方程改进Euler 法解常微分方程算法:Step 1 分别取积分上限、积分下限、步长Step 2 取一个以h 为步长,a ,b 分别为左右端点的矩阵Step 3 (1)做显性Euler 预测),(1n n i i y x hf y y +=+(2)将1+i y 带入)],(),([2h 111+++++=i i i i i i y x f y x f y y Step 4计算h n n +=判断b n ≤是否成立,成立返回Step 3,否则继续进行Step 5 Step 5 )],(),([2h 111+++++=i i i i i i y x f y x f y y 改进Euler 法解常微分方程算程序:function gaijineuler2(fun,y0,A,h)%fun--y'%y0---初值%A----x 取值范围%a----x 左区间端点值%b----x 右区间端点值%h----给定步长a=min(A);b=max(A);x=a:h:b;y(1)=y0;for i=1:length(x)-1w1=feval(fun,x(i),y(i));y(i+1)=y(i)+h*w1;w2=feval(fun,x(i+1),y(i+1));y(i+1)=y(i)+h*(w1+w2)/2;endx=x'y=y'例:用改进Euler 法计算下列初值问题(取步长h=0.25) )50(2)0('2≤≤⎩⎨⎧=-=x y xy y 输入:fun=inline('-x*y^2')gaijineuler2(fun,2,[0 5],0.25)得到:x =0.25000.50000.75001.00001.25001.50001.75002.00002.25002.50002.75003.00003.25003.50003.75004.00004.25004.50004.75005.0000y =2.00001.87501.59391.28241.00960.79320.62820.50370.40970.33790.28240.23890.20430.17650.15380.13520.11960.10660.09550.08610.0779指导教师:年月日。
matlab实例讲解欧拉法求解微分方程

欧拉法是数值分析中常用的一种方法,用于求解常微分方程的数值解。
在MATLAB中,可以通过编写相应的代码来实现欧拉法求解微分方程。
下面我们将通过具体的实例来讲解MATLAB中如何使用欧拉法求解微分方程。
我们要了解欧拉法的基本原理。
欧拉法是一种通过迭代逼近微分方程解的方法,它基于微分方程的定义,通过离散化的方法逼近微分方程的解。
其基本思想是利用微分方程的导数定义,将微分方程以差分形式进行逼近。
具体而言,欧拉法通过将微分方程转化为差分方程的形式,然后通过迭代逼近得到微分方程的数值解。
接下来,我们通过一个具体的实例来讲解MATLAB中如何使用欧拉法求解微分方程。
假设我们要求解以下的一阶常微分方程:(1) dy/dx = x + y(2) y(0) = 1现在我们来编写MATLAB代码来实现欧拉法求解这个微分方程。
我们需要确定微分方程的迭代步长和迭代范围。
假设我们将x的范围取为0到10,步长为0.1。
接下来,我们可以编写MATLAB代码如下:```matlab欧拉法求解微分方程 dy/dx = x + y定义迭代步长和范围h = 0.1;x = 0:h:10;初始化y值y = zeros(1,length(x));y(1) = 1;使用欧拉法迭代求解for i = 1:(length(x)-1)y(i+1) = y(i) + h * (x(i) + y(i));end绘制图像plot(x,y,'-o');xlabel('x');ylabel('y');title('欧拉法求解微分方程 dy/dx = x + y');```在这段MATLAB代码中,我们首先定义了迭代的步长和范围,并初始化了微分方程的初始值y(0) = 1。
然后通过for循环使用欧拉法进行迭代求解微分方程,最后绘制出了微分方程的数值解的图像。
通过以上的实例讲解,我们可以看到,在MATLAB中使用欧拉法求解微分方程是非常简单而直观的。
用欧拉方法求初值问题matlab

欧拉方法是一种常用的数值求解方法,可以用于解决微分方程初值问题。
在MATLAB中,我们可以利用欧拉方法对初值问题进行求解,得到数值解的近似值。
在本文中,我将深入探讨欧拉方法在MATLAB中的应用,从简单的原理和基本操作开始,逐步深入讨论其在不同情况下的适用性和局限性。
1. 欧拉方法的基本原理欧拉方法是一种数值逼近方法,用于求解微分方程的初值问题。
它基于微分方程的定义,通过将微分方程进行离散化处理,然后利用迭代的方式逐步逼近真实解。
欧拉方法的基本原理是利用微分方程的导数来估计下一个时间步长的值,从而逼近微分方程的解。
2. 在MATLAB中应用欧拉方法在MATLAB中,我们可以编写脚本或函数来实现欧拉方法对初值问题的求解。
我们需要将微分方程离散化,得到差分方程的形式。
然后利用循环结构和递推关系,逐步计算出微分方程在离散时间点上的近似解。
我们可以将这些近似解绘制成图表,以便更直观地了解微分方程的行为。
3. 欧拉方法的适用性和局限性尽管欧拉方法是一个简单易用的数值求解方法,但它也有其适用性和局限性。
在某些情况下,欧拉方法可能会产生较大的误差,特别是在微分方程的解具有较大变化率或非线性特性时。
此时,我们需要考虑其他高阶的数值求解方法,如改进的欧拉方法或Runge-Kutta方法。
4. 个人观点和理解在我看来,欧拉方法是一个非常好的入门级数值求解方法,能够帮助我们快速了解和掌握微分方程的数值求解技巧。
通过在MATLAB中实际应用欧拉方法,我们可以更深入地理解微分方程的求解过程,以及数值方法的适用性和局限性。
在实际工程和科学计算中,我们需要根据具体情况选择合适的数值求解方法,以确保结果的准确性和稳定性。
回顾总结通过本文的讨论,我们全面地了解了欧拉方法在MATLAB中的应用。
从基本原理到具体操作,再到其适用性和局限性,我们都对欧拉方法有了深入的认识。
在以后的学习和工作中,我将更加灵活地运用欧拉方法,并根据需求选择合适的数值求解方法。
