学而思培优之圆和扇形的周长与面积(二)

合集下载

第2讲圆、扇形的面积与周长(二)

第2讲圆形、扇形的面积与周长（二）重点摘要本讲主要讲授利用等积变形，重叠等方法求解圆形、扇形的面积与周长。

以及求解圆形、扇形与其他平面图形所组成的平面组合图形的面积。

精讲精练例题1、有七根直径5cm 的塑料管，用一根橡皮筋把它们勒成一捆（如图所示），此时橡皮筋的长度是多少？(π取3.14)练习1、如下图所示,圆的周长为15.7分米,圆的面积是长方形面积的32,问图中阴影部分的周长是多少分米?(π=3.14)例题2、如图，图①和图②是两个相同的正方形，图①中阴影部分是4个圆，图②中阴影部分是9个圆。

那么图中阴影部分的面积大？为什么？练习2、下左图是一个圆环，L 是圆环内最长的线段，下右图是以L 为直径的圆。

问：下左图的圆环与下右图的圆相比，谁的面积大？L L例题3、如下图，等边三角形边长是10厘米，那么阴影部分的周长是厘米？(π取3.14)练习3、如图所示，图中圆的直径AB是4厘米，平行四边形ABCD的面积是7平方厘米，∠ABC＝30度，求阴影部分的面积（π取3.14，得数保留两位小数）。

例题4、如图所示,阴影部分的面积是200平方厘米，求两个圆之间的圆环面积。

(π取3.14)练习4、在正方形ABCD中，AC＝6厘米。

求阴影部分的面积。

例题5、如图所示，求图中阴影部分的面积（π取3.14）。

练习5、图中阴影部分的面积是多少平方厘米?（π取3.14）例题6、求图中阴影部分的面积（π取3.14）。

练习6、等腰直角三角形的一腰的长是8厘米，以它的两腰为直径分别画了两个半圆，那么阴影部分的面积共有多少平方厘米?(π取3.14)【拓展题】如图正方形边长为1,则阴影部分面积为多少？。

（结果保留π）【课堂练习】1、求图形中阴影部分的面积（π取3.14）。

2、右图是由五个圆所构成的，其中总共有3种不同长度的直径，且有部分的圆彼此相切，如图所示。

若最大圆内白色部分的总面积是20cm2，则其中阴影部分的面积是多少平方厘米？3、三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米.AB长40厘米,BC长多少厘米？（π取3.14）4、下图三个圆的半径都是5厘米，三个圆两两相交于圆心。

五年级奥数圆和扇形的周长与面积二

加油站
C B
答案：1
【例6】（★★★★）（北大附中“资优博雅杯”数学竞赛）（2）如图，阴影正方形的顶点分别是大正方形
各边的中点，分别以大正方形各边的一半为直径向外
各边的中点分别以大正方形各边的一半为直径向外
做半圆，再分别以阴影正方形的各边为直径向外作半
圆，形成个月牙形个月牙形
圆，形成8个“月牙形”。

这8个“月牙形”的总面积
为32平方厘米，问大正方形EFGH的面积是多少？
A
H
D
加加点睛
三个转化：化未知为已知；
化不规则为规则；为不可求为可求
四个基本方法：割补、变换、
差不变、整体、
重点例题：例1，例2，例3，例4，例5。

扇形周长和面积公式弧度制

扇形周长和面积公式弧度制
以《扇形周长和面积公式弧度制》为标题，本文旨在讨论扇形在弧度制中的周长和面积的计算公式。

扇形是椭圆的一种特殊形式，其定义常以弧度制来表示，即一个有指定半径和弧段的圆形。

它与圆形在概念上具有相似性，但是比圆形有更多的功能，因此有许多应用。

例如，扇形经常用于制图和地理教学，并且经常用于建筑领域，如天花板或扇形墙等。

因此，如何以弧度制计算扇形的周长和面积对专业人士具有重要的意义。

首先，让我们以弧度制讨论扇形的周长。

计算扇形周长的公式是2πr，其中r是指扇形的半径，θ(弧度)是指扇形的弧度。

因此，当计算扇形周长时，我们首先需要计算扇形的半径和弧度值，然后将这两个数字相乘，结果就是扇形的周长。

例如，如果一个扇形的半径为5，其弧度为2π，则该扇形的周长为2π*5=10π。

其次，让我们以弧度制讨论扇形的面积。

计算扇形面积的公式为r2θ，其中r是指扇形的半径，θ(弧度)是指扇形的弧度。

因此，当计算一个扇形的面积时，我们需要先计算出该扇形的半径和弧度，然后将这两个数字相乘，结果就是该扇形的面积。

例如，如果一个扇形的半径是5，其弧度值为2π，则该扇形的面积为5×5×2π=50π。

最后，弧度制是一种常见的坐标系统，它的应用非常广泛，而扇形的周长和面积也是在弧度制下计算的。

以上是有关以弧度制计算扇形周长和面积的简要介绍，期望对读者有所帮助。

- 1 -。

第二讲圆和扇形的周长与面积学案及详解[六年级秋]

第二讲图形问题(二)————圆的周长与面积知识导航一、概念。

圆：到定点等于定长的点的集合叫做圆，其中定点叫做圆心，圆心用字母O表示。

圆的半径：从圆心到圆上任意一点之间的线段叫做圆的半径，用字母r表示。

在同一个圆中有无数条半径，所有半径长度都相等。

圆的直径：通过圆心并且两端都在圆上的线段叫做圆的直径，直径用字母d表示。

在同一个圆里有无数条直径，所有直径长度都相等。

圆周率：圆的周长与它的直径的比值叫做圆周率，用字母π表示。

它是一个固定的数，是一个无限不循环小数（即无理数）。

圆的周长：围成圆的曲线的长叫做圆的周长。

圆的面积：圆所占平面的大小叫做圆的面积。

圆是轴对称图形，圆的直径所在的直线就是圆的对称轴，它有无数条对称轴。

二、常用公式。

用字母C、S分别表示圆的周长与面积，计算公式可以表示为：C=πd或C=2πr S=πr²三、解题策略数形结合、代换……精典例题例1：把一个圆切拼成一个宽等于半径的近似长方形后，周长增加12cm，那么这个圆的面积与周长各是多少？(2007年成都七中育才学校东区衔接班招生考试题1)思路点拨想一想：你能画出切拼图吗？并在图上标出切拼图与圆的关系吗？模仿练习把一个圆切拼成一个宽等于半径的近似长方形后，这个长方形的周长是33.12cm，那么这个圆的面积与周长各是多少？例2：在一个面积为20cm²的正方形中画一个最大的圆，这个圆的面积是多少？思路点拨想一想：在一个正方形中画一个最大的圆，这个圆与正方形有什么关系？如果从另一个角度想：要求圆的面积必须知道的最直接的条件是什么？友情提示：所谓的最直接的条件，就是指知道后可以只用一步计算就能回答问题的。

模仿练习在一个正方形中画一个最大的圆，这个最大圆的面积是15.7cm²，那么这个正方形的面积是多少？例3：图中阴影部分的面积是4cm²，环形面积是多少？(2004年成都七中育才东区初中招生考试题)思路点拨想一想：难吧！其实不难，把问题想简单一点儿！什么叫做圆环，圆环的面积怎么计算？想清楚后，你会发现这道题格外的简单！模仿练习如图，阴影部分的面积是60cm²，那么圆环的面积是多少？例4：如图所示，已知正方形的边长是3cm，那么阴影部分的面积是多少？思路点拨想一想，计算阴影部分面积的基本方法是什么？你认为关键是要先求出什么？现在你可以计算了吗？再想一想，还有没有更巧的方法呢？模仿练习已知下图长方形的长宽分别是6cm、4cm，分别以长、宽为半径作了两个直角扇形，计算阴影部分的面积。

六年级上奥数第7讲圆与扇形(二)

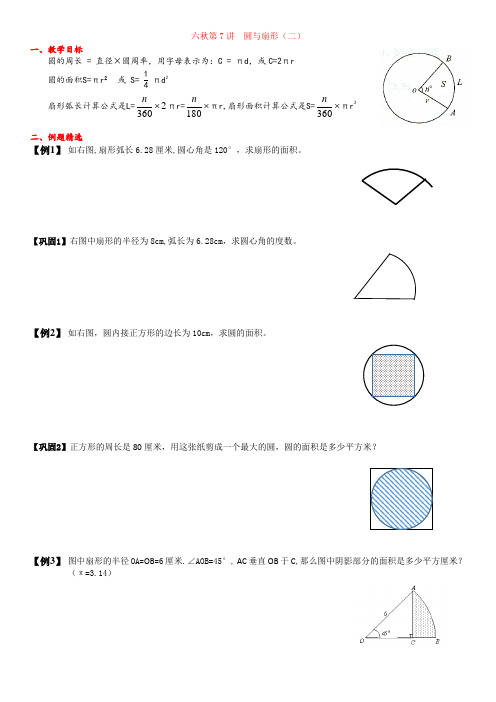
六秋第7讲圆与扇形（二）
一、教学目标
圆的周长 = 直径×圆周率，用字母表示为：C = πd ，或C=2πr
圆的面积S=πr ² 或 S= 14 πd 2 扇形弧长计算公式是L=2360⨯n πr=⨯180n πr,扇形面积计算公式是S=⨯360
n πr 2
二、例题精选【例1】如右图,扇形弧长6.28厘米,圆心角是120°，求扇形的面积。

【巩固1】右图中扇形的半径为8cm,弧长为6.28cm ，求圆心角的度数。

【例2】如右图，圆内接正方形的边长为10cm ，求圆的面积。

【巩固2】正方形的周长是80厘米，用这张纸剪成一个最大的圆，圆的面积是多少平方米？
【例3】图中扇形的半径OA =OB=6厘米.∠AOB=45°, AC 垂直OB 于C ,那么图中阴影部分的面积是多少平方厘米？
（π=3.14）
【巩固3】如图O是圆心，圆中直角三角形的面积是25平方厘米，求阴影部分的面积？
O
【例4】直经均为2米的四根管子被一根金属带紧紧地捆在一起,试求金属带的长度和阴影部分的面积。

【巩固4】右图中每个小圆的半径是10厘米，外围被一条金属带捆在一起。

求金属带长度和阴影部分的面积是多少？
【例5】如图所示,阴影部分的面积是200平方厘米，求两个圆之间的圆环面积。

【例6】牧场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊。

问：这只羊能够活动的范围有多大？。

学而思-----第二讲圆和扇形的周长与面积

D
E
D
E
A
A
B
C
F
B
C
F
4、旋转法（例 6）旋转法是本讲的重点与难点，对于“羊吃草”的问题还是比较简单的。关键是直线型旋转面积，学员无法想到
直线旋转后所扫发到过的面积，其实，由教师讲解后你会发现，一般情况下直线所扫过一周的面积（有特例，如：钝
角三角形的长边绕钝角顶点旋转时）就是一个圆环的面积。所以旋转多少度就再乘以即可。
够活动的最大范围是多少？（
）
分析：如图，羊活动的范围是受绳子的牵制的，所以羊活动的最大范围即绳子 AE 所扫过的总面积。（三部分）
（1）红色部分为按绳长 30 米所能达到的最大范围（绳子不受任何牵制），此图形为半径 30，
圆心角 270 度的扇形。
（2）黄色部分为按绳长 10 米所能达到的最大范围（绳子受点 D 牵制），所以之后只能按半径
由第三个图可知：所求面积已转化为扇环的面积，圆心角度数为 120 度。所以阴影=
（
）
S=
E
E
E
C
C
G
C
G
A
B
D
A
F
B
D
A
F
B
D
第二讲圆和扇形的周长和面积 2.2
五年级秋季班第二讲圆和扇形的周长与面积
曹威
拓展练习：“羊吃草 ”问题
草场上有一个长 20 米，宽 10 米的关闭着的羊圈，在羊圈外的一角，用长 30 米的绳子拴着一只羊，问这只羊能
B
C
C
B
O
A
O
A
分析：与丄题同理 A 点移到 O 点，阴影面积变为扇形 OBC 的面积，注意：圆心角 COB=60 度。

2013学而思五年级春季下学期超长123班讲义学案试题813讲

第八讲圆与扇形进阶圆的面积＝π2r ；扇形的面积＝π2r ×360n ；圆的周长＝2πr ；扇形的弧长＝2πr ×360n。

二5.传说古老的天竺国有一座钟楼，钟楼上有一座大钟，这座大钟的钟面有10平方米。

每当太阳西下，钟面就会出现奇妙的阴影(如图)。

那么，阴影部分的面积是_______平方米。

作业4，图中正方形的边长为5厘米，则图中阴影部分的面积是多少？作业5.在图中所示的正方形ABCD 中，对角线AC 长2厘米，扇形ADC 是以D 为圆心，以AD 为半径的圆的一部分，求阴影部分的面积？π=3.14作业6.图中正方形的边长为20厘米，中间的三段圆弧分别以为圆心，求阴影部分的面积？第九讲比较与估算一.大小比较1.通分2.化成小数3.倒数法4.参考值法5.交叉相乘 6、糖水原理 1.ab ＜c a db ++＜cd 7.糖水原理 2.a b＜m a m b ++二.估算1、整体放缩2、部分放缩3、中项放缩4、分组放缩一1.把32、53、75、1915按照从小到大的顺序排列。

一2.将250131、4021、0.5、0.52、0.5 从小到大排列，第三个数是_______。

一3.比较大小：2713和5728；1111111和111111111。

交叉相乘若ab ＞cd (a 、b 、c 、d 为正整数)，则bc ＞ad 。

一5.下式中五个分数都是最简真分数，要使不等式成立，这些分母的和最小是多少？ (__)1＞(__)2＞(__)3＞(__)4＞(__)5一.7设321311301++=a ，521511501491481++++=b ，则在a 与b 中，较大的数是______。

参考值法二6.将178、2413、3518、5931按从小到大的顺序排列。

糖水原理－结论1 若0＜ab ＜cd ＜1，则ab ＜ca db ++＜cd导问4.如果一个班的女生人数占全班人数的31和83之间，这个班至少有多少人？补充.54＜?25＜65糖水原理－结论2 若0＜ab ＜1，m ＞0，则ab ＜ma mb ++原理解读：(1)横向看：分子分母同时“+”一个常数，分数值变大；(2)纵向看：每个分数的“分母－分子”差是相同的，也就是说这个糖水原理的应用条件是：如果“分母－分子”差不同，可以通过扩倍变成差相同，之后就可以应用糖水原理二2(2).比较75、2320、3329、161149的大小。

圆与扇形进阶培优奥数课件小学数学六年级

知识精讲捆绳问题的秘密
捆绳问题总结基本方法确定圆心，连点作答，应用公式。规律总结绳子的长度＝外圈圆的个数×直径+圆的周长
知识精讲旋转与轨迹
若线段绕某个点顺时针或逆时针进行旋转，旋转的线段的长度即圆的半径，旋转360º所形成的图形是圆形，旋转其他较小的度数，所形成的图形是扇形。
做此类题型时，千万要注意避开单位坑，注意已知条件与问题单位的异同，计算后，进行单位换算，单位变小，数要变大。单位变大，数要变小。
10×10＝100 3.14×10²÷4＝78.5 100－78.5＝21.5
例题8 下面3幅图中互相垂直的两条线段的长度均为10，求各图阴影部分的面积。
3.14×10² ÷4＝78.5 78.5×2＝157 10×10＝100 157－100＝57
例题9
下图中圆的周长是20厘米，圆的面积与长方形的面积正好相等，则图中阴影部分的周长是多少厘米？设长方形的长为a,则πr² ＝ar，由此可得，a＝πr。由此得，阴影部分周长由四分之一圆+一个圆的周长组成，列式可得。 20÷4+20＝5+20＝25(厘米 )
每份的面积 (16π )÷(2π ) ＝8 正方形面积 8×4＝32 小圆面积 8π
答正方形的面积是32，里面小圆的面积是8π。
例题6 一根绳子将三根圆形的木头紧密地捆在了一起，已知一根木头的横截面是半径为4的圆，求绳子的长度。圆的周长 3.14×2×4＝25.12
圆的六条半径 4×6＝24
知识精讲解几何问题的解题技巧
1.转化思想。也就是复杂转化为简单，不熟悉的转化为熟悉的。 2.等积变形。割补，平移，旋转，平行线间进行等积变形。 3.借来还去。加减法。 4.外围入手，曲线救国。从会求的图形或者能求的图形入手，看与要求的部分之间的关系。 5.容斥原理。实际上这种思想是贯穿于加减法始终的。我们把两部分面积加起来，去掉总面积，剩下的就是重叠部分面积。 6.差不变原理。同加同减差不变。 7.整体减空白，用大图形的面积减去小图形的面积。

学而思培优之圆(二) (2)

n
【今日讲题】例5，例6，例7, 【讲题心得】 _________________________________________________ ____________________________________. 【家长评价】 ________________________________________________ ________________________________________________ ________________________________.
【例7】(★★★★) 如图，正方形ABCD的边长为4厘米，分别以B、D为圆心以4厘米为半径在正方形内画圆．求阴影部分面积．( 取3.14)
A DLeabharlann 5BC3
知识大总结 1. 两个公式： ⑴ 周长, C＝π×d ⑵ 面积, S＝π×r2 2. 扇形公式: ⑴ 周长，不要忘记2个半径 ⑵ 在圆的基础上× 360 3. 圆环面积，大圆－小圆. 4. 求面积：割补法.
）））
【例3】(★★) 左图涂色部分是个环形。它的内圆半径是10厘米，外圆半径是15厘米。它的面积是多少？
【例4】(★★☆)求下图阴影部分的面积.
100
10
【例5】(★★★) 大圆半径为R，小圆半径为r，两个同心圆构成一个环形．以圆心O为顶点，半径R为边长作一个正方形：再以O为顶点，以r为边长作一个小正方形．图中阴影部分的面积为50平方厘米，求环形面积．(π取 3.14) 10
圆的认识（二）
本讲主线 1、圆的面积公式 2、圆环和扇形
r
O
【例1】(★★) 街心花园中圆形花坛的周长是18.84米。花坛的面积是多少平方米？ 1、圆的面积＝π×r2

学而思五年级春季下学期超长123班讲义学案试题(8-13讲)

第八讲圆与扇形进阶圆的面积＝π2r ;扇形的面积＝π2r ×360n ；圆的周长＝2πr ;扇形的弧长＝2πr ×360n。

二5．传说古老的天竺国有一座钟楼，钟楼上有一座大钟，这座大钟的钟面有10平方米。

每当太阳西下，钟面就会出现奇妙的阴影（如图)。

那么,阴影部分的面积是＿_＿____平方米。

作业4，图中正方形的边长为５厘米，则图中阴影部分的面积是多少?作业5.在图中所示的正方形ABCD 中，对角线AC 长2厘米,扇形ADC 是以D 为圆心,以AD 为半径的圆的一部分,求阴影部分的面积？π=3.１４作业6.图中正方形的边长为2０厘米，中间的三段圆弧分别以为圆心，求阴影部分的面积?第九讲比较与估算一.大小比较1．通分２.化成小数 3.倒数法 4.参考值法 5.交叉相乘6、糖水原理 1．a b <c a d b ++＜cd 7.糖水原理２.a b <m a m b ++ 二.估算１、整体放缩 2、部分放缩 3、中项放缩４、分组放缩一１．把32、53、75、1915按照从小到大的顺序排列。

一2．将250131、4021、0．５2o3o、0．523o、０.52o从小到大排列，第三个数是＿＿＿___＿。

一3.比较大小：2713和5728;1111111和111111111。

交叉相乘若ab >cd (ａ、b 、c 、d 为正整数)，则bc>ad 。

一5.下式中五个分数都是最简真分数,要使不等式成立,这些分母的和最小是多少? (__)1＞(__)2＞(__)3>(__)4＞(__)5一．7设321311301++=a ,521511501491481++++=b ,则在a 与b 中,较大的数是_＿_＿＿_。

参考值法二6．将178、2413、3518、5931按从小到大的顺序排列。

糖水原理－结论1 若０<ab <cd ＜1，则ab ＜ca db ++<cd导问4.如果一个班的女生人数占全班人数的31和83之间，这个班至少有多少人?补充.54<?25＜65糖水原理－结论2 若０<ab <1,m ＞0，则ab ＜ma mb ++原理解读：(１)横向看:分子分母同时“＋”一个常数，分数值变大；(2)纵向看：每个分数的“分母-分子”差是相同的，也就是说这个糖水原理的应用条件是:如果“分母-分子”差不同，可以通过扩倍变成差相同,之后就可以应用糖水原理二2（2)．比较75、2320、3329、161149的大小。

六年级圆和扇形培优

（选做）例题5.如图，阴影部分的周长为多少厘米？
（半径r=4厘米，π取3.14）
（选做）例题6.如图，大小两圆的相交部分(即阴影区域)的面积是大圆面积的，是小圆面积的．如果量得小圆的半径是5厘米，那么大圆半径是多少厘米?
练习5：用圆规画一个周长是25.12厘米的圆，圆规两脚间的距离应是多少厘米？
【热点考题讲析】
例题1：求图中阴影部分的周长。
例题2：图中圆的周长是18.84厘米，圆的面积与长方形的面积正好相等，图中阴影部分的周长是多少？
例题3：计算图中阴影部分的面积和周长。
例题4：下图正方形的边长是1圆半径是10厘米，内圆半径是6厘米。这个胶垫的面积是多少平方厘米？
练习3：有一个运动场，它的的两头是半圆形，中间是长方形。围绕这个运动场跑两圈是多少米？这个运动场的面积是多少平方米？
练习4：一种中国圆形指针式手表，分针长3厘米，分针从12走到9，扫过的面积是多少？针尖走过的路程是多少厘米？
圆和扇形
【知识点梳理】
1、圆的周长：
2、弧长：l＝其中r为半径，n为圆心角度数。
3、扇形的周长：其中r为半径，n为圆心角度数。
4、圆环的周长：其中R为外圆半径，r为内圆半径。
5、圆的面积：
6、圆环面积：其中R为外圆半径，r为内圆半径。
7、扇形的面积：其中r为扇形的半径，n为圆心角度数。
【课前速练】
练习1：如图，求半圆的面积和周长。

圆和扇形学而思讲义

“谷子”的面积＝弓形面积×2
常用的思想方法：
１．转化思想（复杂转化为简单，不熟悉的转化为熟悉的）
２．等积变形（割补、平移、旋转等）
３．借来还去（加减法）
４．外围入手（从会求的图形或者能求的图形入手，看与要求的部分之间的“关系”。就是我们暑期学
习的“求反面”）
５．容斥（实际上容斥思想是贯穿于加减法始终的。我们把两部分面积加起来，去掉总面积，剩下的
就是重叠部分面积）
内容提要
圆形
周长和面积
扇形
认识一些概念：
面积
周长
半径
直径
圆周率无限不循环小数（通常取3或3.14）
公式总结:
圆的面积圆的周长 =
扇形的面积 = 扇形的弧长：
扇形的周长： =一些特殊的图 Nhomakorabea：１．弓形：
弓形通常只求面积
弓形面积＝扇形面积－三角形面积（除了半圆）
２．“弯角”：
弯角的面积＝正方形－扇形
３．“谷子”：

爱提分圆和扇形的周长及面积公式

一：周长与面积公式知识精讲在同一平面内，到定点的距离等于定长的点的集合叫做圆．点O就称为该圆的圆心；圆心与圆周上任意一点的连线（例如线段OA）叫做半径；通过圆心，并且两端都在圆上的线段叫做直径．直径长恰好是半径长的两倍．圆心确定了圆所在的位置，半径长度确定了圆的大小．一个圆只要确定了“圆心”和“半径”，就能完全确定下来．圆周长与直径的比值是一个固定不变的数，我们称之为圆周率，用希腊字母表示．圆周率是一个无限不循环小数，无法写成分数的形式．在实际问题的计算中，常常取近似值．一．圆的周长与面积公式1．直径长度通常用字母d表示，半径长度通常用r表示，圆周长通常用C 表示，圆面积通常用字母S表示．2．圆周长公式：蜜蜂飞行：无论小圆有多少个，大小是否相等，只要所有小圆的直径之和等于大圆的直径，那么它们的周长之和也等于大圆的周长．3．圆面积公式：?二．扇形的周长与面积公式扇形是指圆上被两条半径和半径之间的弧所包围的部分．其中，圆的半径也称为扇形的半径，而两条半径所成的夹角称为扇形的圆心角．扇形是圆的一部分．要想知道扇形的弧长与面积，只要知道它是所在圆的几分之几就可以了．它是圆的几分之几，它的弧长就是圆周长的几分之几，它的面积也同样就是圆面积的几分之几．1．扇形弧长公式：2．扇形面积公式：3．温馨提示：扇形的弧长不是它的周长，扇形的周长还必须加上两条半径．三点剖析重难点：扇形周长公式，需要加上两条半径题模精讲题模一?圆的周长与面积公式例、已知一个圆的直径为2厘米，那么这个圆的周长为_________厘米，面积为_________平方厘米．答案：；解析：周长为厘米，面积为平方厘米．?例、已知一个圆的周长为厘米，那么这个圆的直径为_________厘米．答案：16解析：直径为厘米．?例、有一个圆形花坛，直径为20米，一只小蜜蜂沿着花坛外周飞了一圈，请问它飞了多少米？如果小蜜蜂沿着图中的虚线，飞一个“8”字，路线构成过花坛圆心的两个小圆，那么这次它飞了多少米？（取）答案：（1）米（2）米解析：小圆半径是5米，飞行路线为两个小圆周长，所以是米．无论小圆有多少个，大小是否相等，只要所有小圆的直径之和等于大圆，那么它们的周长之和也等于大圆．?例、如图，已知长方形的面积是12，则图中阴影部分的面积是多少？（取）答案：解析：长方形可以分成两个面积相等的正方形，面积都是6．方中圆，方和圆的面积比为，可求出小圆的面积是，那么阴影部分的面积是．?例、如图，在一块面积为平方厘米的圆形铝板中，裁出了7个同样大小的圆铝板．问：余下的边角料的总面积是多少平方厘米？（取）答案：平方厘米解析：，大圆半径是3厘米．小圆半径是1厘米，所以边角料面积为平方厘米．?例、已知大圆的直径为10厘米，有四个大小不等的圆，圆心都在大圆的一条直径上，并且它们的直径之和与大圆相等．那么4个小圆的周长之和是________厘米．（取）答案：解析：假设中间4个小圆的直径分别为a、b、c、d，则有，4个小圆的周长之和为厘米．?例、如图，直角三角形的面积是40平方厘米，圆的面积是________平方厘米（π取3）．答案：240解析：直角三角形的直角边即为圆的半径，所以，，圆的面积是平方厘米．?题模二?扇形的周长与面积公式例、如图3，圆P的直径OA是圆O的半径，，，则阴影部分的面积是__________．（π取3）答案：75解析：阴影部分的面积等于大圆面积的一半减去小圆的面积，即．?例、一个扇形的半径为6平方厘米，圆心角为60°，这个扇形的周长是__________厘米．（?取）答案：解析：这个扇形是它所在圆的，所以这个扇形的弧长是cm，扇形的周长是厘米．?例、一个扇形的面积为平方厘米，圆心角为45°，这个扇形的周长是_______厘米．（取）答案：解析：这个扇形是它所在圆的，所以这个圆的半径的平方是，所以这个圆的半径是4厘米，所以扇形的半径是4厘米，扇形的周长是厘米．?例、在荷兰的小镇卡茨赫弗尔，2013年6月建成了一个由三个半圆组成的城市雕塑，三个半圆的直径分别为，，．这个雕塑的原始图形来自于阿基米德《引理集》中的鞋匠刀形（Arbelos），即下图中阴影部分所示的图形．那么，该城市雕塑中的鞋匠刀形的周长为__________（圆周率用π表示）答案：πm解析：鞋匠刀形的周长是由3条半圆形弧线组成，所以周长为m．?例、如图，等边三角形ABC的边长是1，依次以A、C、B为圆心，以BA、CD、BE 为半径画扇形，那么三个扇形的面积和是多少？（结果保留π）答案：解析：各扇形圆心角均为，半径分别为1、2、3，因此三个扇形的面积和是．?例、一个半径为3分米的扇形，面积为平方分米，那么它的圆心角是__________，它的弧长又是__________分米．答案：80°，解析：根据题意得，，所以，所以圆心角是度．弧长为．?例、如图，边长为3cm与5cm的两个正方形并排放在一起，在大正方形中画一个以它的顶点B为圆心，边长为半径的圆弧，则阴影部分的面积是________（结果保留π）．答案：解析：?连结AC、FB．易知，故，．?例、如图，有三个同心半圆，它们的直径分别为2，6，10，用线段分割成9块，如果每块字母代表这一块的面积并且相同的字母代表相同的面积，那么(A＋B)：C ＝_______答案：55：48解析：设A的半径为，B的半径为，C的半径为A的面积：B的面积：3B=，．C的面积：5C=，．．?题模三?捆圆的周长和面积例、已知下图中的每个小圆的半径均为1，这个图形的面积是__________．（取）答案：解析：如图，对图形进行分割后可知这个图形的面积相当于8个边长为2的正方形和一个半径为1的圆的面积的和．面积为．?例、如图，有8个半径为1的小圆，用它们圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心．那么花瓣图形的周长和面积分别是多少？答案：周长，面积解析：如图，做辅助线后可以看出周长为4个的圆弧加上4个半圆弧，所以周长为；而面积为正方形减去4个半圆加上4个圆，即．?例、如图，每个圆的面积都为，求该图形的外周长．答案：解析：圆半径为2．图形外周长可以分为三段长为4的线段和三段120°角的圆弧，则外周长为．?例、如图，有七根直径为5厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米？答案：解析：如图，作辅助线后可以发现外周长是由6段长度为5的线段和6个60°角的圆弧组成，所以皮筋长度为．?随堂练习随练、已知一个圆的直径是12厘米，那么这个圆的面积为__________平方厘米？（取）答案：解析：直径为12厘米，那么半径为6厘米，面积是平方厘米．?随练、已知一个圆的面积为314平方厘米，那么这个圆的直径为_______厘米？（取）答案：20解析：这个圆的半径为平方是，所以这个圆的半径是10厘米，直径是20厘米．?随练、半径分别为1、2、3、4厘米的四个圆的周长之和是多少厘米？（取）答案：厘米解析：圆的周长公式为，周长之和为厘米．?随练、如图，在一块面积为平方厘米的纸板中，裁出了2个同样大小的圆纸板．问：余下的纸板的总面积是多少平方厘米？（取）答案：平方厘米解析：大圆的面积是平方厘米，可求出大圆的半径是2厘米，那么小圆的半径是1厘米，面积是平方厘米．阴影部分的面积是平方厘米．?随练、已知三个小圆的圆心在大圆同一直径上，周长分别为3、1、2厘米，则大圆周长为多少厘米？（π取近似值）答案：6解析：大圆的直径等于三个小圆的直径之和，周长也恰为3个小圆周长之和．?随练、如图，边长为3cm与5cm的两个正方形并排放在一起，在大正方形中画一个以它的顶点B为圆心，边长为半径的圆弧，则阴影部分的面积是__________（结果保留π）．答案：解析：阴影部分面积为梯形ABFE与扇形ABC的面积之和减去三角形FEC的面积，易得为．?随练、已知一个扇形的半径是10厘米，圆心角是，那么：（1）这个扇形所在圆的周长是_________厘米，扇形的圆心角占圆周角的_________，它的弧长占圆周长的_________，这个扇形的弧长是_________厘米，周长是_________厘米．（2）这个扇形面积占它所在圆的面积的_________，是_________平方厘米．答案：（1）；；；；（2）；解析：（1）这个扇形所在圆的周长是厘米，扇形的圆心角占圆周角的，它的弧长占圆周长的，这个扇形的弧长是厘米，周长是．（2）这个扇形面积占它所在圆的面积的，面积是平方厘米．?随练、半径为10、20、30的三个扇形如下图放置，是的__________倍．答案：5解析：为，为，所以是的5倍．?随练、根据图中所给的数值，求这个图形的面积．（π取近似值）答案：解析：平方厘米．4个直角扇形的面积之和是4，因此整个圆角矩形的面积就是．?随练、如图，有七根直径为4厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米？（π取近似值）答案：解析：把圆角六边形的周长分为12个部分，由6条直线段和6段圆弧组成．6条直线段中，每段的长度都是5厘米，它们的长度和是厘米6段圆弧中，每段所对应的圆心角都是60°，每段的弧长都是圆周长的，6段圆弧恰好能拼成一个完整的圆周．它们的弧长之和就是圆周长，即厘米．圆角六边形的周长就是这两部分长度之和，即厘米．?课后作业作业1、已知圆的直径为20米，那这个圆的周长为多少米？（π取近似值）答案：解析：圆周长的计算公式为：C=π×D．?作业2、把两根横截面半径都是10厘米的钢管用铁丝紧紧捆在一起，如果捆绑处不计，至少要用铁丝____________厘米．答案：解析：厘米．?作业3、一辆压路机的前轮是圆柱形，轮宽米，直径是米．前轮转动一周，压路的面积是______平方米．答案：平方米解析：轮子压一周，周长为米，即压在路面上的长是米，压路的面积=长×宽平方米．?作业4、已知圆的面积是314平方米，那圆的周长是多少米？（π取近似值）答案：解析：由圆的面积可以求出半径的平方，算出半径后可由公式计算圆的周长，为．?作业5、已知三个小圆的圆心在大圆同一直径上，周长分别为1、2、3厘米，则大圆周长为多少厘米？（π取近似值）答案：6解析：大圆的直径等于三个小圆的直径之和，周长也恰为3个小圆周长之和．?作业6、如图，在一块面积为36平方厘米的圆形铝板中，裁出了7个同样大小的圆铝板．问：余下的边角料的总面积是多少平方厘米？答案：8平方厘米解析：小圆的半径是整个大圆半径的，因此小圆的面积是大圆面积的，为平方厘米；大圆去掉7个小圆后剩下的面积是平方厘米．?作业7、已知一个扇形的圆心角为120°，半径为2，这个扇形的面积是________，周长是________（π取）．答案：面积，周长解析：扇形的面积；周长．?作业8、如图，求各图中阴影部分的面积．（取）答案：解析：阴影部分面积为半径为4的半圆面积减去对角线为8的等腰直角三角形面积．阴影部分面积为．?作业9、已知扇形的半径为3米，面积为米，那扇形的圆心角为多少度？（π取近似值）答案：180解析：扇形所在圆的面积≈×3=平方米，由此可知该扇形是它所在圆的．那么圆心角应该是360°的二分之一．?作业10、已知一个扇形的半径为5厘米，弧长为厘米，这个扇形的面积是多少？答案：解析：因为扇形的弧长为厘米，所以，可得．扇形面积为平方厘米．作业11、根据图中所给的数值，求这个图形的面积．（π取近似值）答案：解析：平方厘米．4个直角扇形的面积之和是，因此整个圆角矩形的面积就是．?作业12、如图，三个圆的半径都是4，那整个图形的外周长是多少？（π取近似值）答案：解析：整个外周长可以分为3段直线和3段弧形．作业13、如图，有七根直径为10厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米？（π取近似值）答案：解析：把圆角六边形的周长分为12个部分，由6条直线段和6段圆弧组成．6条直线段中，每段的长度都是5厘米，它们的长度和是厘米6段圆弧中，每段所对应的圆心角都是60°，每段的弧长都是圆周长的，6段圆弧恰好能拼成一个完整的圆周．它们的弧长之和就是圆周长，即厘米．圆角六边形的周长就是这两部分长度之和，即厘米．。

五年级奥数思维训练圆与扇形的周长与面积计算

练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2 3 4
直径（d） 2 4 6 8
周长（C） 2π 4π 6π 8π
面积（S） 1π 4π 9π
25π
通过观察此表，回答：圆的半径扩大n倍，周长和面积分别扩大几倍？
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
直径（d） 2 4 6
周长（C） 2π 4π 6π 8π
面积（S） 1π 4π
25π
通过观察此表，回答：圆的半径扩大n倍，周长和面积分别扩大几倍？
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2 3
直径（d） 2 4 6
周长（C） 2π 4π 6π 8π
面积（S） 1π 4π 9π
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2
直径（d） 2 4 6
周长（C） 2π
8π
面积（S） 1π
25π
通过观察此表，回答：圆的半径扩大n倍，周长和面积分别扩大几倍？
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2
直径（d） 2 4 6
ห้องสมุดไป่ตู้
半径（r） 1 2
直径（d） 2
6
周长（C） 2π
8π
面积（S） 25π
通过观察此表，回答：圆的半径扩大n倍，周长和面积分别扩大几倍？
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2
直径（d） 2

六年级奥数：圆与扇形

学习好资料欢迎下载
学而思奥数网奥数专题 (几何) 2010年12月13日
1、6年级几何：圆与扇形
难度：高难度
答：
学而思奥数网奥数专题 (
几何) 2010年12月14日
2、6年级几何：圆与扇形
难度：高难度
答：
在4×7的方格纸板上面有如阴影所示的”6”字，阴影边缘是线段或圆弧．问阴影面积占纸板面积的几分之几？
先做一个边长为2cm 的等边三角形，再以三个顶点为圆心，2cm 为半径作弧，形成曲边三角形(如左图)．再准备两个这样的图形，把一个固定住(右图中的阴影)，另一个围绕着它滚动，如右图那样，从顶点相接的状态下开始滚动．请问此图形滚动时经过的面积是多少平方厘米？(π 3.14 )
C B A 222
学习好资料欢迎下载
学而思奥数网奥数专题（几何）2010年12月10日答案1、6年级圆与扇形习题答案：
解析：
2、6年级圆与扇形习题答案：
解析：。