按条件平差解算单导线和导线网
导线网平差及精度评定程序设计平差

导线网平差及精度评定程序设计平差问题描述背景:导线网平差及精度评定程序设计平差是在测量和测绘工作中常用的一种技术方法。
它是通过对导线网观测数据进行处理和计算,得出导线网的平差结果,并评定其精度,以确保测量结果的准确性和可靠性。
背景:导线网平差及精度评定程序设计平差是在测量和测绘工作中常用的一种技术方法。
它是通过对导线网观测数据进行处理和计算,得出导线网的平差结果,并评定其精度,以确保测量结果的准确性和可靠性。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
请注意:本文档仅供参考和研究使用,不可用于商业目的或作为法律依据。
建议在实际应用中,根据具体情况和专业要求,进行适当的调整和改进。
请注意:本文档仅供参考和研究使用,不可用于商业目的或作为法律依据。
建议在实际应用中,根据具体情况和专业要求,进行适当的调整和改进。
数字地形测量学知到章节答案智慧树2023年山东科技大学

数字地形测量学知到章节测试答案智慧树2023年最新山东科技大学绪论单元测试1.测绘学的主要分支包括:参考答案:地图学;摄影测量学;海洋测绘学;工程测量学;大地测量学2.地形测量学是一种研究如何将地球表面局部地区的地物、地貌测绘成地形图(包括平面图)的理论、技术和方法。
参考答案:对3.图解法测图,一般包括控制测量和碎部测量两大类。
参考答案:对4.数字测图技术已经取代了传统的图解法测图成为了主要的成图方法。
参考答案:对5.地形测量学是测绘工程专业中重要的课程之一,在专业课程设置里占据着重要的地位,在测绘工程专业教学中起着基础作用,同时也为测绘工程专业的深入学习和研究起到了奠基的作用。
参考答案:对6.电子全站仪、GPS RTK技术等先进测量仪器和技术的广泛应用,促进了地形测量向自动化和数字化方向发展,数字化测图技术应运而生。
参考答案:对7.广义的数字测图包括:利用全站仪或其它测量仪器进行野外数字化测图;利用数字化仪对纸质地形图的数字化;以及利用航摄、遥感像片进行数字化测图等方法。
参考答案:对8.三维激光扫描技术的发展,突破了传统的单点测量方法,具有高效率、高精度的独特优势。
参考答案:对9.倾斜摄影测量广泛使用在三维建模和多样的工程测量中。
参考答案:对10.传统测图方法已经不适合现代测绘,需要舍弃。
参考答案:错第一章测试1.重力的方向是指沿着_________的方向。
参考答案:铅垂线方向2.把一个假想的、与静止的平均海水面重合并向陆地延伸的且包括整个地球的特定重力等位面称为:参考答案:大地水准面3.测量平面直角坐标系的横轴为_________,纵轴为_________。
解析几何中平面直角坐标系的横轴为_________,纵轴为_________。
参考答案:Y轴;X轴;X轴;Y轴4.外业测量的基准面是_________,基准线是_________。
内业计算的基准面是_________,基准线是_________。
地形测量技术设计书

等级
附合路线长度(km)
高程闭合差(m)
最大视距长度(m)
前后视距差(m)
前后视距累积差(m)
黑红面读数之差(mm)
黑红面所测高差之差(mm)
四
等
≤16
≤20?L
00
≤5
≤10
≤3.0
≤5.0
注:L以km为单位
5)电磁波测距三角高程测量的主要技术要求:
3.2高程控制
1)本测区以国家高等级水准点作为高程控制起算点,布设四等水准网,作为首级高程控制,以满足测区高程控制发展之需要。
2)等外水准、测距高程导线,自四等水准联测点起发展不得超过2次。
3)四等水准观测采用DS3以上型号之水准仪,三丝法读数,观测顺序为后-前-前-后,各测段测站为偶数站。作业前须对水准仪和水准尺进行检校,DS1型水准仪视准轴与水准管轴之夹角小于15",DS3型小于20"。
2)平面坐标成果等级点取至0.001m,图根点取至0.01m。
水准联测高程成果取至0.001m,三角高程取至0.01m。
3)所有等级控制点(包括所有用到之起算点)和埋石图根点成果装订成册,并在备注栏中写出该点点位。经四等水准联测之等级点应在成果表备注栏中注明“四等水准”。
5、地形图测绘
随着电子科技之不断发展,地理信息系统(GIS)之不断完善,电子文件地形图已逐渐代替了手工清绘图。且电子文件地形图以坐标方式记录图形要素之几何位置,以编码方式记录图形要素之属性,给设计人员提供了极大之方便。本工程成图时使用“南方cass7.0软件”进行编图、网格注记、图幅整饰,将修改好之地形图使用HP—800绘图仪将地形图打印出来,刻录成光盘提供给用户使用。
导线网平差及精度评定程序设计平差

导线网平差及精度评定程序设计平差引言导线网平差是测量领域中的一项重要工作,它对于保证测量结果的准确性和可靠性具有重要意义。
本文将介绍导线网平差的基本原理和流程,并且设计一个用于导线网平差及精度评定的程序。
程序设计平差流程数据预处理•导入原始测量数据:从测量仪器或文件中导入导线网的原始测量数据。
数据应包括导线长度、角度观测值以及观测仪器的精度等信息。
•数据格式检查:对导入的测量数据进行检查,确保数据的完整性和准确性。
•数据转换:将角度观测值转换为弧度制,便于后续计算。
•建立导线网模型:根据导线的连接关系,建立导线网的拓扑模型。
进行平差计算•确定已知点:根据实际情况,选取导线网中已知点,作为平差计算的基准点。
•建立平差方程:根据导线网模型和已知点的观测值,建立平差方程组。
•进行平差计算:使用最小二乘法或其他适当的方法,求解平差方程组,得到未知点的坐标和精度估计。
•检查计算结果:对平差结果进行检查,确保计算的准确性。
精度评定•计算精度指标:根据计算结果和观测数据的精度,计算导线网的精度指标,如相对误差、中误差等。
•统计分析:对计算结果进行统计分析,得出导线网的整体精度评定。
•生成报告:将计算结果和精度评定结果输出到报告中,方便用户阅读和使用。
程序设计考虑用户界面设计在程序设计过程中,为了方便用户使用,需要设计一个用户友好的界面。
该界面应允许用户导入原始测量数据、选择计算参数、查看计算结果和精度评定结果等。
可以使用图形界面或命令行界面来实现。
程序性能优化导线网平差是一项计算量较大的工作,特别是在处理大规模的导线网时。
为了提高程序的运行效率,可以采用一些优化技术,如矩阵运算优化、并行计算等。
同时,还可以合理选择数据结构和算法,减少计算和存储的开销。
错误处理和异常处理在程序设计中,要考虑到可能出现的数据错误和计算异常情况,为程序添加相应的错误处理和异常处理机制。
当程序发生错误或异常时,应给出合适的提示和错误信息,方便用户及时发现和解决问题。
平差课程设计水准网,导线网解算讲解

《测量平差课程设计》设计报告设计名称:测量平差课程设计学院名称:矿业工程学院专业班级:测绘12-2 学生姓名:雷蕾学号: 2012020782 指导教师:张红华测绘工程教研室2014年8月一.课程设计的目的《测量平差》是一门理论与实践并重的课程,测量平差课程设计是测量数据处理理论学习的一个重要实践环节,是在学生学习了专业基础理论课《误差理论与测量平差基础》课程后进行的一门实践课程,其目的是增强学生对测量平差基础理论的理解,牢固掌握测量平差的基本原理和公式,熟悉测量数据处理的基本原理和方法,灵活准确地应用于解决各类数据处理的实际问题,并能用所学的计算机基础知识,编制简单的计算程序。
二.课程设计题目内容描述和要求1.设计的任务(1)该课的课程设计安排在理论学习结束之后进行的,主要是平面控制网和高程控制网严密平差,时间为一周。
(2)通过课程设计,培养学生运用本课程基本理论知识和技能,分析和解决本课程范围内的实际工程问题的能力,加深对课程理论的理解与应用。
(3)在指导老师的指导下,要求每个学生独立完成本课程设计的全部内容。
2.课程设计要求2.1基本要求:测量平差课程设计要求每一个学生必须遵守课程设计的具体项目的要求,独立完成设计内容,并上交设计报告。
在学习知识、培养能力的过程中,树立严谨、求实、勤奋、进取的良好学风。
课程设计前学生应认真复习教材有关内容和《测量平差》课程设计指导书,务必弄清基本概念和本次课程设计的目的、要求及应注意的事项,以保证保质保量的按时完成设计任务。
2.2具体设计项目内容及要求:2.2.1高程控制网严密平差及精度评定总体思路:现有等级水准网的全部观测数据及网型、起算数据。
要求对该水准网,分别用条件、间接两种方法进行严密平差,并检验。
进行平差模型的正确性水准网的条件平差:①列条件平差值方程、改正数条件方程、法方程;②利用自编计算程序解算基础方程,求出观测值的平差值、待定点的高程平差值;③评定观测值平差值的精度和高程平差值的精度。
【免费下载】导线网平差算例
闭合差计 算与检核
平差
平差报告的 生成和输出
实例 1 符合导线实例
这是一条符合导线的测量数据和简图,A、B、C 和 D 是已知坐标点,2、3 和 4 是
待测的控制点。
原始测量数据如下:
测站点 角度(°′″) 距离(米)
B
A
2
3
4
C
D
导线图如下:
85.30211
254.32322
.04333
272.20202
测站 3 的观测信息
以 4 号点为测站点,以 3 号点为定向点时,照准 C 点的数据输入如下图“测站 4 的观测信息”所示:
测站 4 的观测信息
说明:①数据为空或前面已输入过时可以不输入(对向观测例外) ②在电子表格中输入数据时,所有零值可以省略不输。
以上数据输入完后,点击菜单“文件\另存为”,将输入的数据保存为平差易数据 格式文件(格式内容详见附录 A): [STATION] (测站信息) B,10,8345.870900,5216.602100 A,10,7396.252000,5530.009000 C,10,4817.605000,9341.482000 D,10,4467.524300,8404.762400 2,00 3,00 4,00
导线网平差算例
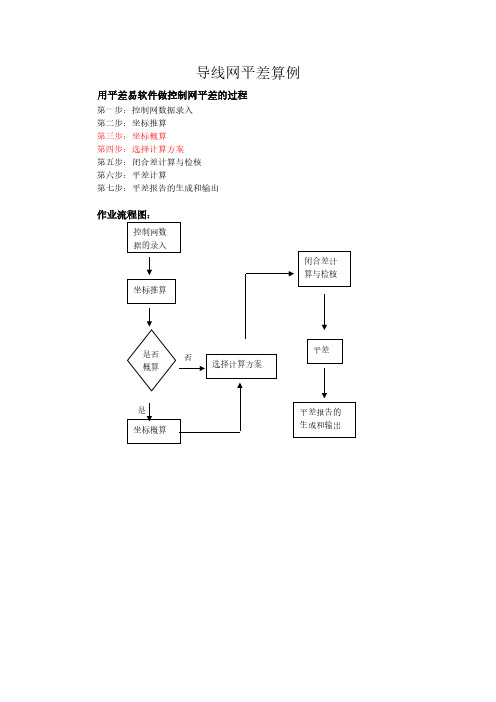
用平差易软件做控制网平差的过程
第一步:控制网数据录入 第二步:坐标推算 第三步:坐标概算 第四步:选择计算方案 第五步:闭合差计算与检核 第六步:平差计算 第七步:平差报告的生成和输出
作业流程图:
控制网数 据的录入
坐标推算
是否 概算
是 坐标概算
否 选择计算方案
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
(整理)导线测量平差教程—计算方案设置

计算方案的设置一、导线类型:1.闭、附合导线(图1)2.无定向导线(图2)3.支导线(图3)4.特殊导线及导线网、高程网(见数据输入一节),该选项适用于所有的导线,但不计算闭合差。
而且该类型不需要填写未知点数目。
当点击表格最后一行时自动添加一行,计算时删除后面的空行。
5.坐标导线。
指使用全站仪直接观测坐标、高程的闭、附合导线。
6.单面单程水准测量记录计算。
指仅进行单面读数且仅进行往测而无返测的水准测量记录计算。
当数据中没有输入“中视”时可以用作五等、等外水准等的记录计算。
当输入了“中视”时可以用作中平测量等的记录计算。
说明:除“单面单程水准测量记录计算”仅用于低等级的水准测量记录计算外,其它类型选项都可以进行平面及高程的平差计算,输入了平面数据则进行平面的平差,输入了高程数据则进行高程的平差,同时输入则同时平差。
如果不需进行平面的平差,仅计算闭、附合高程路线,可以选择类型为“无定向导线”,或者选择类型为“闭附合导线”但表格中第一行及最后一行数据(均为定向点)不必输入,因为高程路线不需定向点。
二、概算1.对方向、边长进行投影改化及边长的高程归化,也可以只选择其中的一项改正。
2.应选择相应的坐标系统,以及Y坐标是否包含500KM。
选择了概算时,Y坐标不应包含带号。
三、等级与限差1.在选择好导线类型后,再选择平面及高程的等级,以便根据《工程测量规范》自动填写限差等设置。
如果填写的值不符合您所使用的规范,则再修改各项值的设置。
比如现行的《公路勘测规范》的三级导线比《工程测量规范》的三级导线要求要低一些。
2.导线测量平差4.2及以前版本没有设置限差,打开4.2及以前版本时请注意重新设置限差。
四、近似平差与严密平差的选择及近似平差的方位角、边长是否反算1.近似平差:程序先分配角度闭合差再分配坐标增量闭合差,即分别平差法。
2.严密平差:按最小二乘法原理平差。
3.《工程测量规范》规定:一级及以上平面控制网的计算,应采用严密平差法,二级及以下平面控制网,可根据需要采用严密或简化方法平差。
导线网条件平差计算

感谢您的观看
汇报人:XX
实例总结和经验教训
实例分析:介绍 具体的导线网条 件平差计算实例, 包括数据来源、 计算过程和结果
分析
总结:对实例分 析的结果进行总 结,提炼出导线 网条件平差计算 的关键技术和方
法
经验教训:分享 在实例分析过程 中遇到的问题和 解决方法,以及 可以改进和优化
的地方
实例应用:探讨 实例分析结果在 实际工程中的应 用,以及如何根 据实际情况调整 和改进计算方法
精度分析和误差处理
精度分析:通过对比实际测量数据和计算结果,评估平差计算的准确性和可靠性。 误差处理:对测量过程中产生的误差进行修正,以提高平差计算的精度。 实例分析:通过具体实例展示精度分析和误差处理在导线网条件平差计算中的应用。 注意事项:强调在进行精度分析和误差处理时应注意的事项,以确保计算结果的准确性。
软件测试和性能评估
测试目的:验证软件是否符合 设计要求和功能需求
测试方法:单元测试、集成测 试、系统测试和验收测试
性能评估指标:处理速度、精 度、可靠性、可扩展性和可维 护性
评估工具:负载测试、压力测 试和性能分析工具
导线网条件平差 计算的未来发展
导线网条件平差计算技术的发展趋势和方向
智能化:随着人 工智能技术的不 断发展,导线网 条件平差计算将 更加智能化,能 够自动识别和解
决各种问题。
自动化:未来导 线网条件平差计 算将更加自动化, 减少人工干预, 提高计算效率和
精度。
精细化:随着测量 技术和数据处理技 术的发展,导线网 条件平差计算将更 加精细化,能够对 各种复杂情况进行
精确处理。
集成化:未来导 线网条件平差计 算将与其他测量 技术进行集成, 形成更加完整的 测量系统,提高 测量精度和效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
n
1
wy = ∑ ∆yi,i+1
i =1
n
i =2
ρ
5.6.1 单导线的平差解算和精度评定
2、 无定向导线和单定向导线的平差解算 、
β
T1
2
β
s
2
n
2
s
1
n
1
Tn
sn
n+1
引入方位角条件未知数T1,Tn,采用附有未 知数的条件平差模型计算。其条件方程如下: 方位角条件:
∑ vβ + δ T − δ T + wT = 0
1
J
n
J+1
每个导线段可列出3个条件:
坐标方位角的条件式:∑ v β + δ TJ − δ TJ +1 + wT
i =1
i
nj
J , J +1
=0
其中: wT
J , J +1
= TJ + ∑ v β − TJ0+1 − n J × 180
0 i =1
i
nj
5.6.2 导线网的平差解算和精度评定
纵坐标条件式: ∑ cos Ti v s − ∑
i
ρ
1
ρ
n
wy = yA + ∑ ∆yi0,i+1 − yc
i =1
n
5.6.1 单导线的平差解算和精度评定
如果只在导线的一端引入方位角未知数 T1,则只 能列出如下两个坐标条件:
0 0 ∑ cosTi vs − ∑ ( yn+1 − yi )vβ − ( yn+1 − y1 )δ T + wx = 0 0 0 0 i =1
,i + 1
+w =0
x A
w
x
= x
+ ∑ ∆x
i=1
n
i ,i + 1
− x
c
根据误差传播率: ∆xi ,i +1 = Si cos Ti
v
代入上式,得:
∆xi ,i +1
= cos T v − ∆y v
0 0 i si i ,i +1 i 2
Ti
v = vβ + vβ + ⋯⋯ + vβ
Ti
i
同理可得,闭合导线的纵横坐标条件为:
∑ cos Ti vs − ∑
0 i =1
i
n
n
1
i =2
ρ
( yn+1 − yi ) + vβ + wx = 0
0 0
i
wx = ∑ ∆xi ,i +1
i =1
n
0 sin Ti vsi − ∑ ( xn+1 − xi0 )vβi + wy = 0 ∑ 0 i =1
i
n
n
1
1
i =1
ρ
i
ρ
1
式中:wx = xA + ∑ ∆xi ,i+1 − xc
i =1
n
sinTi vs − ∑ ( xn+1 − xi )vβ − ( xn0+1 − x10 )δ T + wy = 0 ∑
0 0 0 i =1
i
n
n
1
1
i =1
ρ
i
ρ
1
式中:wy = yA + ∑ ∆yi ,i+1 − yc
ρ
x 0j − x10
δT
1
v y = ∑ sin Ti 0 vs − ∑
j
j −1
j −1
i =1
i
i=2
ρ
j −1
vβ −
i
ρ
δT
1
x j = x j + v x = x A + ∑ ( si0 + vs ) cos(Ti + vT ) 改正后坐标: i =1
0
j i i
y j = y j + v y = y A + ∑ ( si + vs ) sin(Ti + vT )
i =1
i
n
w = T + ∑ β − T − n ×180
T AB i =1 i CD
n+1
0
wβ = ∑ β − (n − 2) ×180
n i =1 i
0
5.6.1 单导线的平差解算和精度评定
纵坐标条件式: ∑ ∆ x i , i + 1 = x C − x
i=1 n n A
∑ v
i=1
∆ xi
0 0
j
j −1
i =1
i
i
5.6.1 单导线的平差解算和精度评定
3、 精度评定 、 平差值函数可表示如下:
F = FY ( L + V ) + FX ( X 0 + δX )
可以证明: QV, X = 0 和 QV,F = 0
QV , X = P −1 AT ( AP−1 AT ) −1[I − CD−1C T ( AP−1 AT ) −1 ]AQAT ( AP−1 AT ) −1 CD−1 = 0
i =1
n
5.6.1 单导线的平差解算和精度评定
上述附有未知数条件式的矩阵形式可表示如下:
AV + CδX + W = 0
按附有未知数的条件平差解法,得法方程如下:
AP A CT
−1
T
C K W + = 0 δX 0 0
K = −( AP −1 AT ) −1 (CδX + W )
由第一式,得: 代入第二式,得:
C T ( AP −1 AT ) −1 CδX + C T ( AP −1 AT ) −1W = 0
5.6.1 单导线的平差解算和精度评定
求解上述法方程,得:
δX = −(C T ( AP −1 AT ) −1 C ) −1 C T ( AP −1 AT ) −1W
i=2
i 1 n
n
wT = T1 + ∑ β i − Tn − ( n − 1) ⋅ 180
0 0 i=2
n
0
5.6.1 单导线的平差解算和精度评定
纵横坐标条件:
0 0 ∑ cosTi vs − ∑ ( yn+1 − yi )vβ − ( yn+1 − y1 )δT − ( yn+1 − yn )δT + wx = 0 0 0 0 0 i =1
= P−1 AT ( AP−1 AT )−1[I − JC ]AP−1 AT [( AP−1 AT )−1 − ( AP−1 AT )−1 JC ]AP−1 = P−1 AT ( AP−1 AT )−1[I − JC ][I − JC ]AP−1 = P−1 AT ( AP−1 AT )−1[I − JC ]AP−1
其中:
JC = CD−1CT ( AP−1 AT )−1
5.6.1 单导线的平差解算和精度评定
V T PV 单位权中误差: σ 0 = ± r 坐标改正数: vx = ∑ cos Ti 0 vs − ∑
j
j −1
j −1
y 0j − yi0
i =1
i
i =2
ρ
x 0j − xi0
vβ −
i
y 0j − y10
2 1 j W环 ∑ k j =1 n j
j
根据测距中误差和估算的测角中误差,确定两者的权比。
5.6.2 导线网的平差解算和精度评定
2. 按附加待定参数的条件分区平差法解算导线网 β β J+2 s β β s 2 s
2
n
1
2
1
n +1
在导线网的每个结 点上,引入一对坐标和 一个方位角未知数,将 导线网分解成通过结点 未知数联系的单导线。
§5.6 按条件平差解算单导线和导线网
5.6.1 单导线的平差解算和精度评定
1、附合导线和闭合导线的条件平差解算 、
n
B TAB β
β
1
s
2
β
n
β
n
D
n
ϕ
1
A
s
2 s2
1
n
s
β
n
n +1
TCD
β
1
1
A(1)
s
C (n+1)
β
2
2
β
s
3
3
方位角条件
s
2
3
∑ vβ + w = 0
i =1
i
n
T
∑ vβ + wβ = 0
0 i =1
i
nj
nj
1
i =1
ρ
Jj
( y J0 +1 − y i0 ) v β
i
−
1
ρ
( y J +1 − y i )δ T j −
0 0
J , J +1
1
ρ
nj i =1
( y J0 +1 − y n0 )δ TJ +1 + δ x J − δ x J +1 + w x
J , J +1
=0
其中: w x
= − D −1C T ( AP −1 AT ) −1W 式中D = C T ( AP −1 AT ) −1 C
进而求得联系数K和改正数V如下:
K = −( AP−1 AT )−1[I − CD−1CT ( AP−1 AT )−1 ]W V = P−1 AT K = −P−1 AT ( AP−1 AT )−1[I − CD−1CT ( AP−1 AT )−1 ]W = −P−1 AT ( AP−1 AT )−1[I − JC ]W
