小波分析结课论文
小波变换论文

《图像处理与分析》结课论文小波变换及其在图像处理与分析中的应用院(系)名称:遥感信息工程学院专业名称:测绘工程学号:学生姓名:指导老师:二○一三年十一月摘要对小波变换的基本概念进行了简要介绍,分析了小波变换在图像压缩、图像去噪以及图像融合等方面的应用,概述了相关算法原理。
以Matlab为平台,进行了基于小波变换的图像融合实验,并分析了实验结果。
关键词:小波变换图像压缩图像去噪图像融合ABSTRACTThe paper give a brief introduction of wavelet transform’s basic conception and analysis the applications of wavelet transform in image compression, image denoising and image fusion、Then it introduces some algorithms about image prosessing、Finally, give a experiment of image fusion based on wavelet transform, which isprogrammed in Matlab platform, and analyze the experimental results、Key words: Wavelet transform Image compression Image denoising Image fusion第1章引言当从时域中观察一个信号时,得到的信息就是信号随着时间的变化,其幅度的起起伏伏。
但就是,如果更进一步想研究起伏速度较快或较慢的部分,就不太容易从时域中信号的波形直接得到所需的信息。
因此,需要将时域中的信号转换到频域中分析。
传统的转换方式就是利用傅立叶变换,然而,傅立叶变换潜在的假设了信号就是平稳信号。
小波分析论文

小波分析理论及其应用胡安兴(武汉工业学院土木工程与建筑学院,交通091,学号090606119)摘要:小波分析的理论与方法是从Fourier分析的思想方法演变而来的。
就象Fourier 分析分为积分Fourier变换和Fourier级数一样,小波分析也分为(积分)小波变换和小波级数两部分,(积分)小波变换的主体是连续小波变换,多尺度小波变换和s-进小波变换;而小波级数的主体部分是关于小波框架的理论。
小波分析理论深刻,应用广泛,并且仍在迅速发展之中。
本文介绍了小波变换的来源及其发展,以及多分辨率分析的问题,小波分析在图像处理中有非常重要的应用。
关键词:小波分析;多分辨率;图像去噪The wavelet analysis theory and its applicationsHU An-xing(Wuhan institute of industrial, civil engineering and architecture institute, traffic civil 091 Student number: 090606119)Abstract:Wavelet analysis theory and method has evolved from the thinking method of Fourier analysis. As Fourier transform and Fourier series is divided into integral Fourier analysis, wavelet analysis is divided into (integral) two parts, the wavelet transform and wavelet series (integral) the body of the wavelet transform is a continuous wavelet transform and multi-scale wavelet transform and s - into the wavelet transform; And the main body of the wavelet series is about wavelet frame theory. Wavelet analysis theory, applications, and are still in rapid development. This paper introduces the source and development of wavelet transform, and multiresolution analysis, wavelet analysis has very important applications in image processing.Key words: Wavelet analysis; multi- resolution ratio; Image denoising1 引言1.1 问题的提出Fourier变换只能告诉我们信号尺度的范围,而无法给出信号的结构以及它蕴含的大小不同尺度的串级过程,即Fourier变换在时空域中没有任何分辨率。
小波分析及其应用
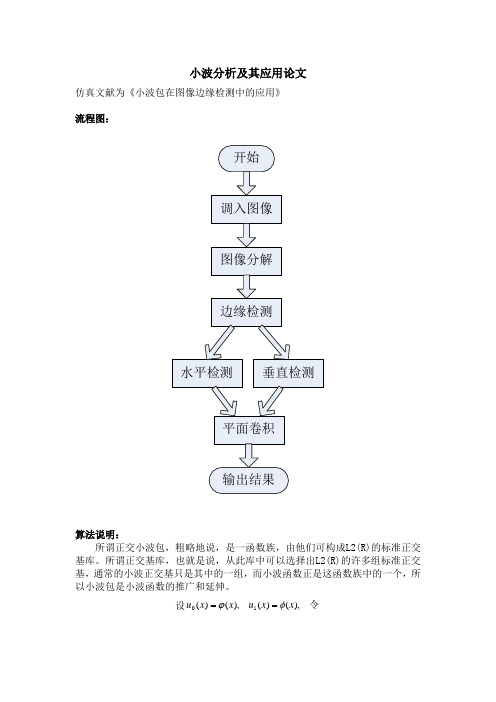
小波分析及其应用论文仿真文献为《小波包在图像边缘检测中的应用》流程图:开始调入图像图像分解边缘检测水平检测垂直检测平面卷积输出结果算法说明:所谓正交小波包,粗略地说,是一函数族,由他们可构成L2(R)的标准正交基库。
所谓正交基库,也就是说,从此库中可以选择出L2(R)的许多组标准正交基,通常的小波正交基只是其中的一组,而小波函数正是这函数族中的一个,所以小波包是小波函数的推广和延伸。
设令),()(),()(10x x u x x u φϕ==)2(2)2(2122k x u g u k x u h u zk n k n zk n k n -=-=∑∑∈+∈其中{}{}k k g h 和为式中的共轭滤波器。
我们称函数族{)(x u n |}+∈Z n 为相对于止交尺度函数)(x ϕ的正交小波包。
小波包对图像分解作多分辨率分解是在小波函数对图像的分解基础上发展起来的,通过水平和垂直滤波,小波包变换将原始图像分为4个子带:水平和垂直方向上的低频子带,水平和垂直方向上的高频子带。
继续对图像的低频子带和高频子带进行分解就可以得到图像的小波包分解结构,如图所示:S1A 1D 2AA 2DA 2AD 2DD 3AAA 3DAA 3ADA 3DDA 3AAD 3DAD 3ADD 3DDD 图像的小波包分解结构示意图由图可见,分解级数越大,也就是选择的小波包尺度越大,小波包系数对应的空间分辨率就越低,利用这一点,可以在不同的空间分辨率上进行分析,实现图像的降噪、图像压缩以及图像增强和图像边缘检测等各种处理工作。
在边缘检测中,常用的一种模板是Sobel 算子。
Sobel 算子有两个,一个是检测水平边缘的;另一个是检测垂直边缘的,与其它算子相比。
Sobel 算子对于像素的位置的影响做了加权,因此效果更好。
由于Sobel 算子是滤波算子的形式,用于提取边缘,可以利用快速卷积函数,简单有效,因此应用广泛。
Sobel 算子是一组方向算子,从不同的方向检测边缘。
《2024年结合小波分析及优化理论的组合预测方法及应用》范文

《结合小波分析及优化理论的组合预测方法及应用》篇一一、引言随着信息技术的飞速发展,预测技术日益显现出其重要价值。
特别是在经济、气象、金融等多个领域,对数据信息的精准预测变得尤为关键。
小波分析作为一种新型的信号处理方法,已在诸多领域展现出强大的性能。
本文将详细介绍一种结合小波分析与优化理论的组合预测方法,探讨其理论基础及其在各领域的应用情况。
二、小波分析理论及其应用小波分析是一种时频局部化分析方法,能够同时提供信号的时间和频率信息。
它通过将信号分解为一系列小波函数的叠加,实现对信号的细致分析。
在预测领域,小波分析能够有效地提取数据中的有用信息,为预测提供准确的数据支持。
三、优化理论及其在预测中的应用优化理论是一种通过数学方法寻找最优解的理论。
在预测领域,优化理论主要用于对预测模型进行优化,以提高预测的准确性和效率。
通过引入优化理论,可以有效地解决预测模型中的参数估计、模型选择等问题。
四、结合小波分析及优化理论的组合预测方法本文提出的组合预测方法,是将小波分析与优化理论相结合,形成一种新的预测方法。
该方法首先利用小波分析对原始数据进行预处理,提取出数据中的有用信息;然后通过优化理论建立预测模型,对提取出的信息进行进一步的处理和优化;最后得出预测结果。
五、组合预测方法的应用1. 经济领域:在股票价格、汇率等金融市场的预测中,组合预测方法能够有效地提取市场信息,提高预测的准确性。
通过优化模型参数,可以更好地反映市场的动态变化,为投资者提供有价值的参考信息。
2. 气象领域:在气象预测中,组合预测方法能够准确预测气候变化趋势。
通过对气候数据进行小波分析,提取出气候变化的周期性和趋势性信息;然后通过优化理论建立预测模型,实现对未来气候的准确预测。
3. 其他领域:除了经济和气象领域外,组合预测方法还可以应用于其他领域,如电力、交通、医疗等。
通过提取各领域的特定信息,建立相应的优化模型,实现对各领域的精准预测。
六、结论本文介绍的组合预测方法,结合了小波分析和优化理论的优势,能够有效地提取数据中的有用信息,提高预测的准确性和效率。
小波分析结课论文

小波分析结课论文基于正交滤波器组的Daubechies 小波设计及Quartus ll 仿真1.非平稳信号的局部变换信号s(t)和其频谱S(w)构成Fourier 变换对,由于Fourier 变换或反变换都属于全局变换,不能告知某种频率分量发生在那些时间内,因此用来不能描述信号的局部统计特性。
对于非平稳信号s(t),应该采用局部变换来描述其随时间变化的统计特性。
并且信号的局部性能需要使用时域和频域是我二维联合表示,才能精确描述。
1.1用内积构造信号变换任何一种信号变换都可以写成该信号与某个选定的核函数之间的内积,因此可以用下面两种基本形式来构造。
信号s(t)的局部变换 = <取信号s(t)的局部,核函数无穷长> 或信号s(t)的局部变换 = <取信号s(t)的全部,核函数局域化>1.2小波变换1.2.1选用小波变换的原因三个信号局部变换的典型例子是短时Fourier 变换、Gabor 变换、小波变换,它们都是时频信号分析的线性变换。
而短时Fourier 变换和Gabor 变换都属于“加窗Fourier 变换”,都以固定的滑动窗对信号进行分析,可以表征信号的局部频率特性。
显然,这种时域固定等宽的滑动窗处理并不是对所有的信号都合适。
因为有较多的自然界信号在低频端应具有很高的频率分辨率,在高频端的频率分辨率可以比较低。
而从不相容原理的角度看,这类信号的高频分量应该具有高的时间分辨率,低频分量应该具有低的时间分辨率。
对这类非平稳信号的线性时频分析,应该在时频平面的不同位置具有不同的分辨率,小波变换就是这样一种多分辨(率)分析方法,其目的是既见森林——信号概貌,又见树木——信号细节,所以,小波分析被称为数学显微镜。
1.2.2连续小波变换的定义及参数含义平方可积分函数s(t)的连续小波变换定义为(,)()*()(),()s ab t b W T a b s t dt s t t aψψ∞-==〈〉⎰, a > 0其中小波变换的基函数()()ab t b t aψ-=是窗函数()t ψ的时间平移b 和尺度压缩a 的结果,乘以因子1/是因为要使变换结果归一化,a 是尺度参数,b 是平移参数。
小波分析小结(小编整理)

小波分析小结(小编整理)第一篇:小波分析小结小波分析的形成小波分析是一门数学分支,是继Fourier变换之后新的时频域分析工具。
小波理论的形成经历了三个发展阶段:Fourier变换阶段:Fourier变换是将信号在整个时间轴上进行积分,它将信号的时域特征和频域特征联系起来,分别进行分析。
设信号f(t),其Fourier变换为:F(ω)=⎰f(t)e-iωtdt-∞∞F(ω)确定了f(t)在整个时间域上的频谱特性。
但Fourier变换不能对信号从时域和频域结合起来分析,它是一种全局变换,在时间域上没有任何分辨率。
例:f(t)=1,(-2<=t<=2),其Fourier变换对应图如下:短时Fourier变换阶段:短时Fourier变换即加窗Fourier变换,其思想是把信号分成许多小的时间间隔,用Fourier分析每个时间间隔,以确定该间隔存在的频率,达到时频局部化目的。
其表达式为:Gf(ω,τ)=〈f(t),g(t-τ)ejωt〉=⎰f(t)g(t-τ)e-jωtdtR式中,g(t)为时限函数,即窗口函数,e-jωt起频限作用,Gf(ω,τ)大致反映了f(t)在τ时、频率为ω的信号成分含量。
由上式,短时Fourier变换能实现一定程度上的时频局部化,但窗口函数确定时,窗口大小和形状固定,所得时频分辨率单一。
小波分析阶段:为了克服上述缺点,小波变换应运而生。
小波变换在研究信号的低频成分时其窗函数在时间窗长度上增加,即在频率宽上减小;在研究信号的高频成分时其窗函数在时间窗长度上减小,而在频率宽上增加。
对信号可以进行概貌和细节上的分析。
小波的定义:∝(ω),若满足设ψ(t)∈L2(R)(为能量有限的空间信号),其Fourier变换为ψ容许条件:|ψ(ω)|2⎰-∞|ω|dω<+∞∞∝∝(0)=∞ψ(t)dt=0,说明ψ(t)具有波动则称ψ(t)为母小波,由容许条件可得:ψ⎰-∞性,在有限区间外恒为0或快速趋近于0.t-12以Marr小波ψ(t)=(1-t)e2为例,如下图:2π2将母小波进行伸缩平移所得小波系列称为子小波,定义式如下:ψb,a(t)=1t-bψ(),a>0aa其中a为伸缩因子,b为平移因子。
小波分析论文

生物医学信号处理论文小波变换分析摘要:小波变换 (wavelet transformation ,WT)是近几年兴起的一种信号处理方法,可用作分析数据压缩和提取有用信息的工具。
在目前的研究中。
db 族小波基在小波中应用最广泛,具有分析近红外光谱这类平滑信号的特性。
其他小波基symmlet 族和coiflet 族等也常被使用。
小波变换在数字图像处理、故障诊断、语音和生物医学信号处理及光谱分析等方面获得了广泛的应用。
关键词:小波变换;研究现状;原理;滤波;应用一、小波理论的发展及研究现状小波分析方法的提出可以追溯到1909年Alfred Haar 提出的小“波”规范正交基。
20世纪70年代,法国地球物理学家Jean Morlet 提出了小波变换的概念,并与法国物理学家Grossman 共同提出连续小波变换的几何体系,其基础是平移和伸缩下的不变性,这使得能将一个信号分解成对空间和尺度(即时间与频率)的独立贡献,同时又不丢失原有信号的信息。
20世纪80年代,法国科学家Y .Meyer 创造性的构造出具有一定衰减性的光滑函数,他用缩放与平移均为2J (j>0的整数)的倍数构造了2L (R)空间的规范正交基,使小波方法得到真正的发展。
1988年Mallat 将计算机视觉领域内的多尺度分析的思想引入到小波分析中,提出了多分辨率分析的概念,用多分辨率分析来定义小波,给出了构造正交小波基的一般方法和与快速傅立叶变换(FFT)相对应的快速小波算法一Mallat 算法,并将这理论用于图像分析和完全重构。
该算法统一了在此之前构造正交小波基的所有方法。
Mallat 将小波理论与信号处理联系起来,开创了小波理论在信号处理中的应用。
小波分析是在傅立叶分析的基础上发展而来的,它优于傅立叶分析的地方是在时间域和频率域同时具有良好的局部化性质。
由于它对高频成分采用逐渐精细的时域或空域取样步长,从而可以聚焦到对象的任意细节。
其局部化格式随频域自动变换,在高频处取窄的时间窗,在低频处取宽的时间窗,适合处理非平稳信号。
《2024年结合小波分析及优化理论的组合预测方法及应用》范文

《结合小波分析及优化理论的组合预测方法及应用》篇一一、引言随着现代科技的发展,预测问题在各个领域中显得尤为重要。
为了更准确地预测各种现象和趋势,研究者们不断探索新的预测方法。
小波分析作为一种有效的信号处理工具,在预测领域具有广泛应用。
同时,优化理论则为组合预测模型提供了强大的理论支持。
本文将结合小波分析和优化理论,探讨一种组合预测方法及其应用。
二、小波分析简介小波分析是一种在时间-频率平面上对信号进行局部分析的方法。
它通过对信号进行多尺度分解,可以有效地提取信号中的有用信息,并对不同频率成分进行针对性处理。
小波分析在信号处理、图像分析、时间序列分析等领域具有广泛应用。
三、优化理论概述优化理论是一种数学方法,旨在寻找最优解或近似最优解的问题。
在预测领域,优化理论为组合预测模型提供了强大的理论支持。
通过优化理论,我们可以选择合适的预测模型参数,使得预测结果的准确度达到最优。
四、组合预测方法本文提出的组合预测方法结合了小波分析和优化理论。
首先,利用小波分析对原始数据进行多尺度分解,提取不同频率成分的信息。
然后,根据优化理论,选择合适的预测模型参数,对不同频率成分进行预测。
最后,将各频率成分的预测结果进行组合,得到最终的预测结果。
五、应用实例以某股票价格预测为例,本文将该方法应用于实际数据中。
首先,利用小波分析对股票价格数据进行多尺度分解,提取不同时间尺度的价格波动信息。
然后,根据优化理论选择合适的股票价格预测模型参数,如线性回归模型、神经网络模型等。
通过这些模型对不同时间尺度的价格波动进行预测。
最后,将各时间尺度的预测结果进行组合,得到最终的股票价格预测结果。
六、实验结果与分析实验结果表明,本文提出的组合预测方法在股票价格预测中取得了较好的效果。
与传统的单一预测方法相比,该方法能够更准确地捕捉价格波动的不同时间尺度信息,提高了预测的准确度。
同时,通过优化理论选择合适的预测模型参数,使得模型能够更好地适应不同数据集的特点,提高了模型的泛化能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小波分析结课论文基于正交滤波器组的Daubechies 小波设计及Quartus ll 仿真1.非平稳信号的局部变换信号s(t)和其频谱S(w)构成Fourier 变换对,由于Fourier 变换或反变换都属于全局变换,不能告知某种频率分量发生在那些时间内,因此用来不能描述信号的局部统计特性。
对于非平稳信号s(t),应该采用局部变换来描述其随时间变化的统计特性。
并且信号的局部性能需要使用时域和频域是我二维联合表示,才能精确描述。
1.1用内积构造信号变换任何一种信号变换都可以写成该信号与某个选定的核函数之间的内积,因此可以用下面两种基本形式来构造。
信号s(t)的局部变换 = <取信号s(t)的局部,核函数无穷长> 或信号s(t)的局部变换 = <取信号s(t)的全部,核函数局域化>1.2小波变换1.2.1选用小波变换的原因三个信号局部变换的典型例子是短时Fourier 变换、Gabor 变换、小波变换,它们都是时频信号分析的线性变换。
而短时Fourier 变换和Gabor 变换都属于“加窗Fourier 变换”,都以固定的滑动窗对信号进行分析,可以表征信号的局部频率特性。
显然,这种时域固定等宽的滑动窗处理并不是对所有的信号都合适。
因为有较多的自然界信号在低频端应具有很高的频率分辨率,在高频端的频率分辨率可以比较低。
而从不相容原理的角度看,这类信号的高频分量应该具有高的时间分辨率,低频分量应该具有低的时间分辨率。
对这类非平稳信号的线性时频分析,应该在时频平面的不同位置具有不同的分辨率,小波变换就是这样一种多分辨(率)分析方法,其目的是既见森林——信号概貌,又见树木——信号细节,所以,小波分析被称为数学显微镜。
1.2.2连续小波变换的定义及参数含义平方可积分函数s(t)的连续小波变换定义为(,)()*()(),()s ab t b W T a b s t dt s t t aψψ∞-==〈〉⎰, a > 0其中小波变换的基函数()()ab t b t aψ-=是窗函数()t ψ的时间平移b 和尺度压缩a 的结果,乘以因子1/是因为要使变换结果归一化,a 是尺度参数,b 是平移参数。
对于一个给定的窗函数()t ψ,若a>1,则基函数相当于将窗函数拉伸,使窗口的时宽增大,窗函数的频率特性压缩,频率带宽变小;若a<1,则相当于将窗函数压缩,使窗口的时宽减小,窗函数的频率特性拉伸,频率带宽变大。
而的作用仅仅是使小波基函数滑动。
从时频网格的划分看,a 大对应于低频端,且频率分辨率高、时间分辨率低;反之,a 小对应于高频端,且频率分辨率低、时间分辨率高。
1.2.3小波应该满足的条件(1)容许条件()0t dt ψ∞-∞=⎰这一条件将使函数()t ψ符合“一小段波”的波形特征,是小波必须具备的最低条件。
(2)归一化条件此条件使小波具有单位能量。
(3) 完全重构条件(或恒等分辨条件)(4) 小波的Fourier 变换满足“稳定性条件”式中0<A ≤B <∞1.2.4对偶小波简介若小波()t ψ满足上述的稳定性条件,则存在一个“对偶小波”~()t ψ,其Fourier 变换~()w ψ由下式给出:*~2()()|(2)|jj w w w ∞=-∞ψψ=ψ∑1.2.5连续小波的性质(易理解但阐述证明繁琐)① 线性② 平移不变性 ③ 伸缩共变性 ④ 自相似性 ⑤冗余性1.2.6离散小波变换及重构(小波逆变换)在使用小波变换重构信号时,需要对小波作离散化处理,采用离散化的小波变换。
这里的离散化都是针对连续的尺度参数a 和平移参数b 的,而不是针对时间变量t 的。
令0j a a =和00j b ka b = ,则有离散小波变换()jk t ψ为()jkt ψ/200()j ja a t kb ψ--=-并且,离散化小波变换000(,)j j f W T a ka b 简记为(,)f W T j k ,并称*(,)()(),jk f jkjkc WT j k f t t dt f ψψ∞-∞===〈〉⎰为离散小波系数,简称小波系数。
实际数值计算时使用的信号重构公式为()()jk jkj k f t cc t ψ∞∞=-∞=-∞=∑∑c 是常数,取c=12小波分析 2.1小波级数表示任何一个平方可积分的实函数2()()f t L R ∈都具有一个小波级数表达式,即~()()jkjk j k f t c t ψ∞∞=-∞=-∞=∑∑式中小波系数为*(,)()(),jk f jkjkc WT j k f t t dt f ψψ∞-∞===〈〉⎰c jk 是平方可求和的序列,即2||jk j k c ∞∞=-∞=-∞<∞∑∑2.2对小波的各种希望从信号重构的精度角度考虑,正交基是信号重构最理想的基函数,所以更希望小波是正交小波。
为了使小波变换成为有用的信号处理工具,小波还须满足三个基本要求:1)小波是一般函数的积木块:小波能作为基函数,对一般函数进行小波级数展开; 2)小波具有时频聚集性:通常要求小波的大部分能量聚集在一个有限的区间内。
理想情况下,在该区间外,小波函数()t ψ的能量应等于零,即小波在频域应该是紧支撑函数。
但由不相容原理知,一个在频域紧支撑的函数,它在时域的支撑区将是无穷的。
因此,小波函数应该在时域是紧支撑的,这样在频域能够快速衰减;3)小波具有快速变换算法:为了使小波函数易于计算机实现,希望小波变换和Faurier 变换一样有快速算法。
在实际应用中,通常希望小波具有以下性质:①紧支撑:如果尺度函数和小波是紧支撑的,则滤波器H 和G 就是有限冲激响应的滤波器,它们在正交快速小波变换时的求和就是有限项的求和。
这显然有利于实现。
如果它们不是紧支撑的,也希望它们是快速衰减的,以使得滤波器H 和G 都可以用FIR ,滤波器合理近似。
②对称性:如果尺度函数和小波是对称的,则滤波器就具有广义的线性相位。
若波器不具有线性相位,则信号通过滤波器后,会发生相位的畸变。
因此,滤波器的线性相位要求在信号处理应用中是非常重要的。
③光滑性:小波的光滑性在压缩应用中起着重要的作用。
令小的系数c jk 为零,再将这些小系数所对应的分量jk jk c ψ从原函数中除去,我们就可以实现原函数的压缩。
如果原函数表示一幅图像,但小波不光滑,则压缩图像的误差就很容易用肉眼看出。
小波越光滑,滤波器的频率局域性就越好。
④正交性:我们知道,在信号的任何一种线性展开或逼近中,正交基是最佳的基函数。
因此,当使用正交的尺度函数时,能够提供最佳的信号逼近。
2.3线性独立基和基小波令()t ψ2()L R ∈,并且()jk t ψ是由()t ψ生成的小波,则{()jk t ψ}是2()L R 的Riesz 基,也等价于{()jk t ψ}是2()L R 的正合框架,还等价于{()jk t ψ}是2()L R 的一个框架,并且是一个线性无关族,即()0jk jkc jk t ψ=∑∑,意味着c jk ≡0,而且Riesz 基界和框架界相同。
至此就得到了基小波(母小波)()t ψ用作小波变换时所必须的三个条件: ①完全重构条件②基小波()t ψ的稳定条件③小波族{()jk t ψ}的线性独立条件,22||{}||jk A c 2||jk jkj k c ψ∞∞=-∞=-∞≤≤∑∑22||{}||jk B c 对于所有平方可求和的序列{c jk }恒成立,其中22||{}||jk c 2||jk j k c ∞∞=-∞=-∞=<∞∑∑,这样其实二维序列{,,}jkj k Z ψ∈是2()L R 内的一个Riesz 基,A 和B 分别是Riesz 基的下界和上界。
小波()t ψ2()L R ∈称为Riesz 小波(Riesz 基称作无条件基,通过Gram-Schmidt 标准正交化Riesz 基可以化成标准正交基),若由它按照/2()2(2)j j jk t t k ψψ=-, j,k ∈Z 生成的离散函数族{()jk t ψ}为Riesz 基。
2.4正交小波与双正交小波根据是否正交,小波可以分为正交小波、半正交小波、非正交小波和双正交小波。
(1)若其生成的离散小波族{()jk t ψ:j,k ∈Z }满足正交条件,()()jkmn j m k n ψψδδ〈〉=-- ,,,,j m k n Z ∀∈则Riesz 小波()t ψ称作正交小波。
(2)若()t ψ及其对偶~()t ψ生成的小波族()jk t ψ和~()jk t ψ是“双正交的”Riesz 基,即~,()()jkmn j m k n ψψδδ〈〉=-- ,,,,j m k n Z ∀∈则Riesz 小波()t ψ称作双正交小波。
上面定义的正交实际上是单个函数自身的正交,而双正交指两个函数之间的正交性。
注意,双正交小波并不涉及()t ψ和()jk t ψ自身的正交性。
正交小波一定是双正交小波,但是双正交小波不一定是正交小波。
2.5多分辨分析,尺度函数、小波函数的双尺度方程多分辨分析又叫多分辨逼近、多尺度分析,多分辩分析的生成元()t φ习惯称为尺度函数。
多分辨分析的主要目的是利用尺度函数构造所需要的小波。
在多分辨分析中,尺度函数()t φ和它的整数时间平移服从”单位分解”式()1,k t k t R φ∞=-∞-=∀∈∑还要满足尺度函数容许条件 (0)()1t dt φ∞-∞Φ==⎰跨尺度的尺度函数()t φ和(2)t φ的双尺度方程(也称伸缩方程或细化方程)为()()(2)k t g k t k φφ∞=-∞=-∑或等价写作()()()2k tg k t k φφ∞=-∞=-∑式中g(k)是生成尺度函数的滤波器G(w)的冲激响应。
()jw kk G w ∞-=-∞=∑可以证明G(w)是一个周期为2π的周期函数,滤波器G(w)是一个低通滤波器。
而基小波()t ψ与尺度函数(2)t φ相关,即满足小波函数的双尺度方程为()()(2)k t h k t k ψφ∞=-∞=-∑式中h(k)是生成小波函数的滤波器H(w)的冲激响应。
()jw kk H w ∞-=-∞=∑可以证明H(w)是一个周期为2π的周期函数,滤波器H(w)是一个高通滤波器。
标准正交尺度函数的构造定理:令V j (其中j ∈Z)是L 2空间的一多分辨逼近,则存在一个标准正交函数0()t V φ∈使得()jk t φ/22(2)j j t k φ=- , k ∈Z 必须是V j 内的一个标准正交基,其中()t φ为多分辨分析的尺度函数。
2.6正交多分辨分析的信号重构高通滤波器H 和低通滤波器G 组成一个滤波器组,使用其共轭滤波器组(G *,H *)对原始信号进行分解,然后用(G ,H )重构信号,即得到正交多分辨分析的信号重构。
