最新北师大版初中七年级数学上册2.7 第2课时有理数乘法的运算律学案
北师大版数学七年级上册2.7《有理数的乘法》(第2课时)说课稿

北师大版数学七年级上册2.7《有理数的乘法》(第2课时)说课稿一. 教材分析《有理数的乘法》是北师大版数学七年级上册第2.7节的内容,本节课的主要内容是有理数的乘法法则,以及如何运用这些法则进行计算。
在教材中,学生已经学习了有理数的加法、减法、乘法和除法,这些知识为本节课的学习打下了基础。
二. 学情分析面对七年级的学生,他们对有理数的加减乘除已经有了一定的了解,但对有理数的乘法法则可能还不是很熟悉。
因此,在教学过程中,我需要引导学生通过观察、思考、讨论,从而发现并掌握有理数的乘法法则。
三. 说教学目标1.知识与技能:让学生掌握有理数的乘法法则,能熟练地进行有理数的乘法计算。
2.过程与方法:通过观察、思考、讨论,培养学生发现问题、分析问题、解决问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队合作意识。
四. 说教学重难点1.教学重点:有理数的乘法法则及其运用。
2.教学难点:理解有理数乘法法则的推导过程,以及如何运用这些法则进行计算。
五.说教学方法与手段在本节课的教学过程中,我将采用问题驱动法、案例教学法和小组合作学习法。
通过提出问题,引导学生思考;通过案例分析,让学生理解并掌握有理数的乘法法则;通过小组合作学习,培养学生的团队合作意识。
六. 说教学过程1.导入:通过复习有理数的加减乘除,引导学生进入本节课的主题——有理数的乘法。
2.新课讲解:讲解有理数的乘法法则,并通过案例进行分析。
3.课堂练习:让学生进行有理数的乘法计算,巩固所学知识。
4.小组讨论:让学生分组讨论,发现并总结有理数乘法法则的推导过程。
5.总结:对本节课的内容进行总结,强调重点知识点。
6.课后作业:布置相关的课后练习,巩固所学知识。
七. 说板书设计板书设计如下:有理数的乘法法则:1.同号相乘,取相同符号,并把绝对值相乘。
2.异号相乘,取相反符号,并把绝对值相乘。
3.任何数乘以0,结果都是0。
八. 说教学评价本节课的教学评价主要从学生的课堂表现、课后作业和小组合作学习三个方面进行。
最新【北师大版】七年级数学上册:2.7.2《有理数乘法的运算律》课时作业(含答案)

最新北师大版数学精品教学资料2.7.2 有理数乘法的运算律1.两个有理数的积是负数,和为零,那么这两个有理数( )A .一个为零,另一个为正数B .一个为零,另一个为负数C .一个为正数,另一个为负数D .互为相反数且都不为零2.若ab >0,则下列结论正确的是( )A .a >0,b >0B .a <0,b <0C .a ,b 同号D .以上答案都不对3.绝对值小于6的所有整数的积是________. 4.判断下列各个乘积的符号: ①(-2)×(-3)×4×(-5)×3;②4×(-2)×(-3.4)×(-6.7)×5×(-9)×3; ③4×7×(-5)×9×(-4.6)×9×13; ④(-2)×0×7×(-4);⑤(-2.1)×(-6)×(-9)×(-6.7)× (-5.8)×(-4.7).其中积为正数的有________,积为负数的有______,另外________的乘积既不是正数也不是负数(只填序号即可).5.计算(-2.5)×0.37×1.25×(-4)×(-8)的值为________. 6.计算:(1)(-4)×(-0.07)×(-25); (2)(47-118+314)×56.7.先阅读提供的材料,再解答相关问题: (1+12)×(1-13)=32×23=1.(1+12)×(1+14)×(1-13)×(1-15)=32×54×23×45=(32×23)×(54×45)=1×1=1.请你求(1+12)×(1+14)×(1+16)×(1-13)×(1-15)×(1-17)的结果.8.若a ,b 互为相反数,c ,d 互为倒数,m 的绝对值是1,求(a +b)cd -2 009m 的值.9.刘亮的妈妈每天早上要送新鲜蔬菜到市场去卖,下面是她一周送出的20筐菜的重量记录表,每筐以25 kg 为标准重量.(2013·台州模拟)计算(-1 00015)×(5-10)的值为( )A .1 000B .1 001C .1 999D .5 001课后作业1.D 两数互为相反数且不为0. 2.C 同号得正. 3.04.②③⑤ ① ④ 积的符号由负因数的个数决定 5.-37 6.解:(1)-7 原式=-4×25×0.07 =-100×0.07=-7;(2)-19 原式=47×56-98×56+314×56=32-63+12 =-19.7.解:原式=32×54×76×23×45×67=1.8.解:2 009或-2 009 ∵a,b 互为相反数,∴a+b =0,∵c,d 互为倒数,∴cd=1, ∵|m|=1,∴m=±1,当m =1时, (a +b)cd -2 009m =0×1-2 009×1 =-2 009;当m =-1时,原式=0×1-2 009×(-1)=2 009.9.解:501.3 kg 25×20+(-0.8×2+0.6×5-0.5×3+4×0.4+2×0.5+4×(-0.3) =500+(-1.6+3-1.5+1.6+1-1.2) =500+1.3 =501.3(kg ). 中考链接D 原式=-(1 000+15)×(-5)=(1 000+15)×5=1 000×5+15×5=5 000+1=5 001,所以选D .。
2.7有理数的乘法(2)学案
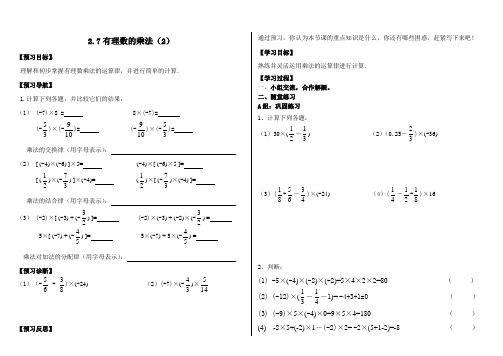
2.7有理数的乘法(2)【预习目标】:理解和初步掌握有理数乘法的运算律,并进行简单的计算. 【预习导航】1.计算下列各题,并比较它们的结果:(1) (-7)×8 = 8×(-7)= (-35)×(-109)= (-109)×(-35)=乘法的交换律(用字母表示): (2) [ (-4)×(-6) ]×5= (-4)×[ (-6)×5 ]= [ (21)×(-37) ]×(-4)= (21)×[ (-37)×(-4) ]= 乘法的结合律(用字母表示):(3) (-2)×[ (-3) + (-23) ]= (-2)×(-3) + (-2)×(-23) = 5×[ (-7) + (-54) ]= 5×(-7) + 5×(-54) =乘法对加法的分配律(用字母表示): 【预习诊断】 (1)(-65 + 83)×(-24) (2)(-7)×(-34)×145【预习反思】通过预习,你认为本节课的重点知识是什么,你还有哪些困惑,赶紧写下来吧! 【学习目标】熟练并灵活运用乘法的运算律进行计算. 【学习过程】一、小组交流,合作解疑。
二、随堂练习 A 组:巩固练习 1、计算下列各题: (1)30×(21-31) (2)(0.25-32)×(-36) (3)(81+65-43)×(-24) (4)(41-21+81)×162、判断:(1) -5×(-4)×(-2)×(-2)=5×4×2×2=80 ( )(2) (-12)×(31-41-1)= -4+3+1=0 ( )(3) (-9)×5×(-4)×0=9×5×4=180 ( ) (4) -2×5+(-2)×1-(-2)×2= -2×(5+1-2)=-8 ( ) B 组:能力提升 1.计算(1)(-2)×(-8)×(-125) (2) 8×(-54)×161(3) (-32)×72×(-43) (4) 0.25×(-3.1)×(-8) 2.计算(1) 53×17 + 53×8 (2)37×7+37×(-3)+37×6(3) 60×73-60×71+60×75 (4) 74×(-245)-(-73)×(-245)C 组:拓展延伸1. 有6张不同数字的卡片:—3,+2,0, —8, 5, +1,如果从中任取3张,(1)使数字的积最小,应如何抽?最小积是多少? (2)使数字的积最大,应如何抽?最大积是多少?2.已知:a 、b 互为相反数,c 、d 互为倒数,x 的绝对值是1,求:3x - [(a +b)+cd]x 的值3.定义一种运算符号△的意义:a △b=ab —1,。
有理数乘法乘法运算律学案教案

有理数乘法乘法运算律学案教案学案教案:有理数乘法运算律一、教学目标1.理解有理数乘法运算律的概念和意义。
2.能够灵活运用有理数乘法运算律解决实际问题。
3.培养学生的逻辑思维和批判性思维能力。
二、教学重点与难点1.有理数乘法运算律的掌握和应用。
2.是理清运算步骤与规律。
三、教学准备1.教学工具:黑板、白板、教学课件等。
2.教学资源:习题、练习题、实例题等。
四、教学过程【导入】1.通过导入问题引出有理数乘法运算律的概念:“对于两个有理数a 和b,它们的积是什么?什么情况下两个有理数的积是正数?什么情况下两个有理数的积是负数?”2.根据学生的回答,引导学生总结有理数乘法运算律的表达方式和规律。
【讲解】1.有理数乘法运算律的概念:对于任意两个有理数a和b,它们的积满足以下运算律:(1)正数乘以正数仍为正数,即a > 0,b > 0时,ab > 0;(2)负数乘以负数仍为正数,即a < 0,b < 0时,ab > 0;(3)正数乘以负数为负数,即a > 0,b < 0时,ab < 0;(4)负数乘以正数为负数,即a < 0,b > 0时,ab < 0;(5)任何数乘以0都等于0,即a×0=0。
2.给出具体的实例进行讲解,帮助学生更好地理解和掌握乘法运算律。
【示范】1.通过示范解题,让学生加深对乘法运算律的理解。
例如:计算(-3/4)×(1/2),请学生按照乘法运算律进行计算,并简化答案。
2.由学生做出的答案进行讲解和订正,帮助学生纠正错误并加深对乘法运算律的印象。
【练习】1.针对乘法运算律进行一些练习题让学生巩固所学知识。
例如:(1)计算12×(-5/6)。
(2)计算-3/5×(-3/4)。
2.让学生分组进行练习,互相订正答案,及时发现和纠正问题。
【拓展】1.引导学生思考乘法运算律在实际应用中的意义和作用,例如:当我们在计算面积、体积、速度等问题时,如何利用乘法运算律简化运算步骤。
北师版七年级数学上册课件(BS) 第二章 有理数及其运算 有理数的乘法 第2课时 有理数的乘法运算律

=4 000×25-5×25(____乘__法__分__配__律_____)
4.(4 分)运用运算律填空:
(1)(-3)×(-6)=-6×___(_-__3_)__;
(2)[(-3)×2]×(-5)=-3×[__2__×(-5)];
1 (3)3
×[(-9)+(-43
)]=31
×__(_-__9_)_+31
数学 七年级上册 北师版
第二章 有理数及其运算
2.7 有理数的乘法
第2课时 有理数的乘法运算律
1.(4 分)算式-54 ×(10-54 +0.05)=-8+1-0.04 这个运算运用了( D ) A.加法结合律 B.乘法交换律
C.乘法结合律 D.乘法分配律
2.(4 分)在算式-57×24+36×24-79×24=(-57+36-79)×24 中,逆用了( D )
15 (3)1916
×(-8)=(20-116
)×(-8)=20×(-8)-116
×(-8)=-160+21
=-
15912
【素养提升】
12.(15 分)计算:(1+21 )×(1-13 )=32 ×32 =1, (1+21 )×(1+14 )×(1-13 )×(1-15 ) =32 ×54 ×32 ×45 =(32 ×23 )×(54 ×45 ) =1×1=1.
8.下列变形不正确的是( C )
A.5×(-6)=(-6)×5 B.(41 -21 )×(-12)=(-12)×(41 -12 ) C.(-16 +13 )×(-4)=(-4)×(-16 )+13 ×4 D.(-25)×(-16)×(-4)=[(-25)×(-4)]×(-16)
9.计算
5 137Βιβλιοθήκη ×_(_-__34__)__.
北师大版七年级数学上册第二章 2. 7有理数的乘法教案

第七节有理数的乘法考点一:有理数的乘法法则1、法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与0相乘,积仍为0。
2、方法导引:(1)几个有理数相乘,先确定积的符号,再把绝对值相乘。
(2)当几个因数中有一个为0时,不用再判断符号,直接得0. 3、总结提升:(1)两个有理数相乘,积的符号是由两个因数的符号确定,同号(++,或--)得正,异号(+-或-+)得负。
(2)0与任何数相乘,积都是0.(3)1乘任何数得原数,-1乘任何数得原数的相反数。
4、题型解析:例1 (1)已知两个数a,b在数轴上对应的点如图所示,下列结论正确的是()A、-a<-bB、a+b>0C、ab<0D、b-a>0(2)一个有理数与它的相反数的积是()A 、正数B 、负数C 、非正数D 、非负数 (3)计算3×(-2)的结果是(4)计算 ①-2×(-5) ②34×(83-) ③-3×0 ④(-312)×(-3)考点二:倒数1、定义:如果两个有理数的乘积为1,那么称其中的一个数是另一个数的倒数,也称这两个有理数互为倒数,如54和45,-7和71-互为倒数。
2、 求法:求带分数的倒数时,先把带分数化成假分数,再求倒数;求小数的倒数时,先把小数化成分数,在求倒数;求整数的倒数时,先把整数看作是分母为1的分数,在求倒数。
3、辨析:(1)0没有倒数。
(2)互为倒数的两个数的符号相同,即正数的倒数是正数,负数的倒数是负数。
(3)若两个数互为倒数,则它们的成绩为1. (4)倒数等于它本身的数是1和-1. 4、题型解析:例2 (1)有理数51-的倒数为( )A 、5B 、51C 、-51 D 、-5 (2)2017的倒数为( ) A 、20171 B 、2017 C 、-2017 D-20171(3)相反数是其本身的是 ,倒数是其本身的是 。
(4)若a,b 互为相反数,c,d 互为倒数,m 的绝对值是3,求:cd m ba -++35的值。
2.7第2课时 有理数的乘法运算律-2020秋北师大版七年级数学上册作业课件

易错点 利用乘法对加法的分配律计算时,易漏乘或弄错符号
7.计算:-48×(12-3-58+56-112).
解:原式=
1 2
×(-48)-3×(-48)-
5 8
×(-48)+
5 6
×(-48)-
1 12
×(-48)
=-24+144+30-40+4
=114.
02 中档题
8
.
计算
11 (12
-76
+
3 4
)
5.运用运算律进行简便运算: (1)(-4)×(-7)×(-25); 解:原式=(-4)×(-25)×(-7) =100×(-7) =-700.
(2)(-10)×13×(-110)×6; 解:原式=(10×110)×(13×6) =2.
(3)12×(112-16+12); 解:原式=12×112-12×16+12×12 =1-2+6 =5.
数学
第二章 有理数及其运算
7 有理数的乘法
第2课时 有理数的乘法运算律
01 基础题
知识点1 有理数的乘法运算律 1.在2×(-7)×5=-7×(2×5)中,运用了( D ) A.乘法交换律 B.乘法结合律 C.乘法对加法的分配律 D.乘法交换律和乘法结合律
2.计算(1-12+13+14)×(-12),运用哪种运算律可避免通分( D ) A.加法交换律 B.加法结合律 C.乘法交换律 D.乘法对加法的分配律
11.学了有理数的运算后,老师给同学们出了一题. 计算:191178×(-9),下面是两位同学的解法: 小方:原式=-31589×9=-3 12831=-17912; 小杨:原式=(19+1178)×(-9)=-19×9-1187×9 =-17912.
最新北师版初中数学七年级上册2.7 第2课时 有理数乘法的运算律导学案

27 有理数的乘法第2课时有理数乘法的运算律(一)创设情景,提出问题在小学我们学过一些乘法的交换律、乘法的结合律以及分配律,谁能给大家介绍一下?问题:小学学习过的有关乘法的运算律,对所有的有理数都还适用吗?通过计算,比较验证同学们的猜想。
做一做:计算下列各题,并比较它们的结果:(1) (-5)×2=-(5×2) =;2×(-5)=-(2×5) =;(2)[2×(-3)]×(-4)=(-6)×(-4)=; 2×[(-3)×(-4)]=2×12=;(3)(-3)×(2+错误!)=(-3)×错误!=; (-3)×2+(-3)×错误!=-6-1=。
让学生进行观察、比较、思考:(1)以上各组题的运算结果有什么特点?(2)各组题的运算形式,与乘法的运算律的结构特征对比,你发现了什么?(3)对于问题,你得到的猜想是什么?(二)合作交流,探索新知探索1完成上述计算(1)、(2),再探索下列两个问题:(1)任意选择两个有理数(至少有一个负数)分别填入下列□和○内,并比较两个运算的结果。
□×○和○×□(2) 任意选择三个有理数(至少有一个负数)分别填入下列□、○和◇内,并比较两个运算的结果。
(□×○)×◇和□×(○×◇)可由多个学生提供实例,从而让学生总结出有理数的乘法满足交换律与结合律。
用文字叙述,并用字母表示。
乘法交换律乘法结合律探索2完成做一做3想一想与小学学过的哪个运算律类似。
请你换一些数试一试,还成立吗?请用用文字叙述,并用字母表示:分配律通过验证,使学生感到分配律在有理数运算中应用的合理性即可。
(三)指导应用,深化理解例2 计算(1) (-12) ×(-37) ×错误!; (2)6× (-10) ×01×错误!; (3) -30×(错误!-错误!+错误!); (4) 499×(-12); (5) 71错误!×(-8)按课本讲解、板书。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.7 有理数的乘法
第2课时有理数乘法的运算律
(一)创设情景,提出问题
在小学我们学过一些乘法的交换律、乘法的结合律以及分配律,谁能给大家介绍一下?
问题:小学学习过的有关乘法的运算律,对所有的有理数都还适用吗?
通过计算,比较验证同学们的猜想。
做一做:计算下列各题,并比较它们的结果:
(1) (-5)×2=-(5×2) =; 2×(-5)=-(2×5) =;
(2)[2×(-3)]×(-4)=(-6)×(-4)=; 2×[(-3)×(-4)]=2×12=;
(3)(-3)×(2+1
3
)=(-3)×
7
3
=; (-3)×2+(-3)×
1
3
=-6
-1=。
让学生进行观察、比较、思考:
(1)以上各组题的运算结果有什么特点?
(2)各组题的运算形式,与乘法的运算律的结构特征对比,你发现了什么?
(3)对于问题,你得到的猜想是什么?
(二)合作交流,探索新知
探索1
完成上述计算(1)、(2),再探索下列两个问题:
(1)任意选择两个有理数(至少有一个负数)分别填入下列□和○内,并比较两个运算的结果。
□×○和○×□
(2) 任意选择三个有理数(至少有一个负数)分别填入下列□、○和◇内,并比较两个运算的结果。
(□×○)×◇和□×(○×◇)
可由多个学生提供实例,从而让学生总结出有理数的乘法满足交换律与结合律。
用文字叙述,并用字母表示。
乘法交换律乘法结合律
探索2
完成做一做3,想一想与小学学过的哪个运算律类似。
请你换一些数试一试,还成立吗?
请用用文字叙述,并用字母表示:分配律
通过验证,使学生感到分配律在有理数运算中应用的合理性即可。
(三)指导应用,深化理解
例2 计算
(1) (-12) ×(-37) ×5
6
; (2)6× (-10) ×0.1×
1
3
; (3) -30
×(1
2
-
2
3
+
4
5
); (4) 4.99×(-12); (5) 71
15
16
×(-8) 按课本讲解、板书。
(组织学生口头回答例题的解答。
应用有理数乘法的运
算律进行运算,可以简便运算,但它仍旧属于有理数的乘法运算,因此应遵循有理数的乘法运算的步骤:确定积的符号;把绝对值相乘。
)
探究活动1:
讲完“有理数的乘法”后,老师在课堂上出了下面一道计算题:7115
16
×(-
8).
不一会儿,不少同学算出了答案。
现在老师把班上同学的解题过程归类写到黑板上。
解法一原式=-1151
16
×(-8)=-
9208
16
=-575
1
2
;
解法二原式=(71+15
16
)×(-8)=71×(-8)+
15
16
×(-8)=-575
1
2
;
解法三原式=(72-
1
16
)×(-8)=72×(-8)-
1
16
×(-8) =-575
1
2
.
对这三种解法,你认为哪种方法最好? ,理由是 。
本题对你有何启发? 。
思维过程:解法二和解法三巧妙地利用了拆分思想,把带分数拆成一个整数与一个真分数的和,在应用分配律,大大简化了计算过程。
例3 某校体育器材室总共有60个篮球。
一天课外活动,有3个班级分别计划借
篮球总数的12 ,13 和14。
请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?(独立完成,再小组交流)
随堂练习:
1.课本中的课内练习第1、2题。
(可先让学生在课本上解答,再请学生板演。
若有错误,请其他同学及时纠正。
)
2.计算:
(1)4×(-15
)×2; (2)(-1.2)×0.75×(-1.25);
(3) 312 ×(-137
); (4)-34 ×715 ×(-23 )×(-514
); (5) (5)-8×(16 -512 +310
)×15; (6)291315
×(-5); (7)4.61×37 -5.39×(-37 )+3×(-37
)。
