第16讲-第十章 刚体的平面运动2
理论力学刚体运动

Ek ( t ) Ek ( t0 ) A外
§6.2 作用在刚体上的力系 一、力系
1、定义:同时作用在一个刚体的一组力称为力系。
2、分类: ①共面力系:所有的力位于同一平面内。 a) 共点力系(汇交力系):所有力的作用线交 于一点的力系。 b) 平行力系:所有力互相平行或反平行。 ②异面力系:力的作用线不在一个平面内。
二、力系等效
1、等效力系的定义 如果在两个力系作用下,刚体的运动相同,则这 两个力系互为等效力系。
2、力系的等效条件:
F1i F2 j
r1i F1i r1 j F1 j
i j
i
j
3、零力系:力系力的矢量和为零,对固定参考点 的力矩和为零的力系。 说明:①所有的零力系都等效 ②任何力系加上零力系后与原力系等效 ③最简单的零力系是一对平衡力组成的力系
2
角动量定理: dL dt
M外
2、平衡条件: Fi 0,
i
且 Mi 0
i
(对任一定点成立)
例 质量为 m ,长为 a 的匀质杆 AB 由系于两端长是 a 的线悬于 O 点,在 B 端挂质量为 m 的重物。求平衡 时杆与水平方向的夹角θ及每根线中的张力 TA 和 TB 。
2、异面力系: 等效于一个单力与一个力偶
z -F3 A F1
F F3
O
x
B F2
y
§6.3 刚体的平衡
刚体运动 平动: 直线平动、曲线平动
转动: 定轴转动、一般转动 平动:运动过程中刚体任一直线的方向保持不变。
转动:刚体上一直线相对参考系的角度发生变化。
O
刚体的一般运动(n=6)
O
理论力学10刚体的平面运动

vB = v A + vBA
a a ? a
VB VBA
大小 ? 方向 a
B VA
v B = v A ctg φ且 v BA
vA = sin φ
v BA = AB ⋅ ω AB v BA vA ∴ω = = l l sin φ
φ VA
ω A x
14
[例2] 图示机构 端以速度 A沿X轴负向运动,AB=l; 例 图示机构A端以速度 端以速度V 轴负向运动, 轴负向运动 求B端的速度? 端的速度? 端的速度 解:1)分析AB;2)分析A,B两点的速度 在AB直线上的投影相等,可以得到: y B
行移动 刚体简单运动 平行移动 定轴转动 定轴转动 刚体复杂运动 刚体的平面运动
平动 合成? 合成? 转动
刚体平面运动的分解 本章分析 平面运动刚体的角速度 平面运动刚体各点的速度 平面运动刚体各点的速度
1
第十章 刚体的平面运动
§10–1 刚体平面运动的概述 §10–2 平面运动分解为平动和转动 · 刚体的平面运动方程 §10–3 平面图形内各点的速度· 速度投影定理 速度瞬心 §10–4 平面图形内各点的加速度 · 加速度瞬心的概念
20
5.几种确定速度瞬心位置的方法 ①已知图形上一点的速度v A 和图形角速度ω, 可以确定速度瞬心的位置.(P点)
AP = vA , AP⊥v A ,且P在v A 顺ω转向绕A点 ω
转90º的方向一侧. ②已知一平面图形在固定面上作无滑动的滚 动, 则图形与固定面的接触点P为速度瞬 心.
21
③已知某瞬间平面图形上A,B两点速度 v A ,v B 的方向,且 v A 不平行 v B 。 过A , B两点分别作速度 v A ,v B的垂线,交点 P即为该瞬间的速度瞬心。 ④ 已知某瞬时图形上A ,B两点速度 v A , v B 大小,且 v A ⊥AB, vB ⊥AB v A − vB (a) v A 与vB 同向, ω = AB v A + vB (b) v A 与vB 反向, ω = AB 注意:交点可能在刚体的外部) (注意:交点转动· 刚体的平面运动方程
小升初六年级数学名校冲刺精编讲义第16讲 平面图形的认识与测量(二)(学生版)

第16讲平面图形的认识与测量(二)知识点一:圆的认识1.在同圆或等圆中,所有的直径都相等,所有的半径都相等。
2.圆是轴对称图形,圆有无数条对称轴,圆的对称轴就是直径所在的直线。
知识点二:圆的周长和面积1.圆的周长(1)圆周率:圆的周长与直径的比值叫作圆周率。
圆周率用希腊字母“π”表示,它是一个无限不循环小数。
经过精密计算:π=3.1415926…在小学数学中,我们常常取圆周率的近似值3.14(2)圆的周长= 圆周率×直径或圆周率×半径×2用字母表示为:C= πd或2πr 2.圆的面积:把一个圆平均分成若干份,剪开后拼成一个近似的平行四边形,如果分的份数越多,拼成的图形越接近长方形,这个近似长方形的长等于圆周长的一半,宽等于圆的半径,由此圆的面积S= πr23.圆环的面积(1)同一个圆心的两个半径不相等的圆,它们之间的部分叫作圆环(2)面积公式: S=πR2-πr2知识点三:组合图形的面积1.求组合图形面积的方法。
(1)分割法:把阴影部分分割成几个基本图形,利用求几个基本图形面积的和求出阴影部分的面积。
(2)添补法:在阴影部分上添补一个基本图形,使其变成另一个基本图形,计算出这个基本图形的面积后减去补上的基本图形的面积,从而求出阴影部分的面积。
考点一:圆的认识和圆周率【例1】(2019•鼓楼区)操作:(1)以O点为圆心,3格长为半径,画一个半圆形.(2)画出半圆形的对称轴.(3)把半圆形向右平移8格.1.(2019秋•花都区期末)下面说法正确的是()A.所有半径都相等,所有直径都相等B.在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关C.大圆的圆周率比小圆的圆周率大2.(2019秋•沧州期末)下面关于圆周率π的说法正确的是()A.π是圆的周长与这个圆的直径的比值B.π是循环小数π=D.π是圆的面积与这个圆的半径的比值C. 3.143.(2019秋•凌源市期末)关于圆的知识,下面说法不正确的是()A.圆心只决定圆的位置,不决定圆的大小B.两端都在圆上的线段叫做直径C.半径相等的两个圆的面积相等D.圆周率是圆周长和这个圆直径的比值4.(2019秋•香坊区期末)下列说法正确的是()A.用圆规画圆时.若圆规两脚间的距离是3cm,则所画圆的直接为3cmB.用4个圆心角都是90︒的扇形,一定可以拼成一个圆C.圆的半径扩大到原来的2倍,周长也扩大到原来的2倍D.小明身高1m,爸爸身高180cm,小明和爸爸身高的比是1:1805.(2019秋•西城区期末)如图所示图形中,对称轴条教最少的是() A.B.C.D.考点二:圆的周长和面积【例2】(2019•天津模拟)计算阴影部分的面积和周长.(单位:厘米)【例3】(2019•番禺区校级模拟)求如图的周长和面积.【例4】(2019秋•古丈县期末)求阴影部分的面积和周长.1.(2019•鄞州区)在一张长12厘米、宽10厘米的彩纸上画一个最大的圆,这个圆的周长是厘米,面积是平方厘米.2.(2019•福田区)已知小圆的半径是2厘米,大圆的半径是3厘米,小圆和大圆周长的比是,面积的比是.3.(2019•长沙)一张半圆形纸片周长是20.56cm,他的半径是cm,面积是2cm.4.(2019秋•中方县期末)把一个直径是5厘米的圆分成若干等份,然后把它剪开,照如图的样子拼起来,拼成的图形的周长比原来圆的周长增加厘米.5.(2019•宿迁)从一个长10分米,宽4分米的长方形木板上锯下一个最大的半圆,半圆的直径是分米,半圆的周长是分米,半圆的面积是平方分米.6.(2019•临川区)如图是三个半圆,求阴影部分的周长.7.(2019•株洲)求图形的周长.8.(2019•中山区)求图中阴影部分的周长.( 取3)9.(2019•玄武区)图中阴影部分的面积是15平方厘米,求环形的面积10.(2019•淮安)如图,长方形的面积和圆的面积相等,已知圆的半径是4厘米,求阴影部分的周长和面积.考点三:组合图形的周长和面积【例5】(2019春•新田县期末)求下列图形的周长或面积【例6】(2019秋•江南区期末)求阴影部分的周长与面积.【例7】(2019•高台县)求图阴影部分的周长和面积.1.(2019•郑州)请求出图中阴影部分的面积(单位:厘米).2.求如图中阴影部分的面积,已知圆的半径为4厘米.3.(1)求图(1)阴影部分的周长. (2)求图(2)阴影部分的面积.(3)如图(3)已知:1S 比2S 多28平方厘米,求BC 长多少厘米?4.求阴影部分的周长与面积:(单位cm )5.(2019秋•黄冈期末)求图中阴影部分的周长和面积.(单位:厘米)6.求图中阴影部分的周长和面积.(单位:厘米)7.求下列图形的周长和面积:(单位:米)8.求下面图形中阴影部分的面积.(单位:)cm (1)长方形面积245cm.(2)(3)(4)9.(2019•厦门)图中圆的周长是12.56cm,圆的面积正好等于长方形的面积,求阴影部分的面积.10.(2019•北京模拟)如图,已知4AOC=;60∠=︒,求阴影部分的面积.OC cm=,2OD cm11.(2019•东莞)求阴影部分的面积、周长.考点四:与圆有关的实际问题【例8】(2019•营山县模拟)将圆平均分成若干个小扇形,剪拼成一个近似的长方形(如图).(1)如果长方形的长是12.56厘米,圆的面积是多少?(2)如果圆的半径是10厘米,阴影部分的面积是多少?【例9】(2019•丹阳市)已知图中阴影部分的面积是220cm,环形的面积是多少平方厘米?【例10】(2019春•武城县期末)一片草地中央有一个边长为8m的正方形羊圈(如图),将一只羊用10m 长的绳子系在羊圈墙外一个角的顶点上,这只羊能吃到的草地面积是多少平方米?1.(2019•娄底模拟)一只环形玉佩的外圆半径为2厘米,比内圆半径多1.5厘米,这只环形玉佩的面积是多少平方厘米?2.(2019•江北区)滨江公园有一个圆形水池,沿着它的外沿修一圈2米宽的草坪,水池的半径是5米,那么草坪的面积是多少平方米?3.(2019•绵阳)一个长方形与一个圆的面积相等,如果长方形的长与圆的直径都是8厘米,那么长方形的宽是多少厘米?(取3.14)4.(2019•石家庄)一个圆形花坛的直径是6m,现在沿花坛的外围铺一条宽1m的石子路,若每平方米石子路面造价80元,建造这条石子路共需多少元?5.(2019秋•海安县期末)在400米的运动场上要举行400米比赛,(起点要前移多少米才恰当?)跑道每道宽1.25米,外一圈起点要比内一圈前移多少米?6.(2019•长汀县模拟)一个圆形羊圈半径6 米,如果要扩建这个羊圈,把它的直径增加2米.(1)扩建后,这个羊圈的周长是多少米?(2)扩建后,这个羊圈的面积增加了多少平方米?7.如图,一只狗用皮带系在1010的正方形狗窝的一角,皮带长为14,在狗窝外面狗能活动的范围的面积是多少?画出示意图并计算.(狗的大小忽略不计,长度单位:分米)小升初专项培优测评卷(十六)平面图形的认识与测量(二)1.(2019秋•望江县期末)如图是光明小学的运动场的示意图,阴影部分为跑道.求跑道的占地面积.2.(2019秋•达州期中)如图是一个花台的平面图,5为圆的半径(单位:)m.求这个花台的周长是多少厘米?3.(2019•郑州)求如图图形阴影部分的面积.4.(2019•石家庄)求如图阴影部分的周长和面积.5.有一个200m的环形跑道(如图所示).(1)东东沿着第二条跑道(由内向外)跑一圈,他跑了多少米?(π取3.14)(2)如果在这个跑道上进行100m赛跑,那么如何确定起跑线的位置呢?(π取3.14)6.(2019•邵阳模拟)某赛车的左、右轮子的距离为2米,因此,当车子转弯时,外侧的轮子比内侧的轮子多走了一段路.赛车跑道如图所示,当赛车车轮行走一圈时,外轮比内轮多走多少米?7.(2019•长沙模拟)如图所示为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多少米?(保留小数点后一位)8.(2019•沈河区)如图,一只羊被一条5米长的绳子拴在木桩上.求羊活动的面积是多少?。
理论力学答案
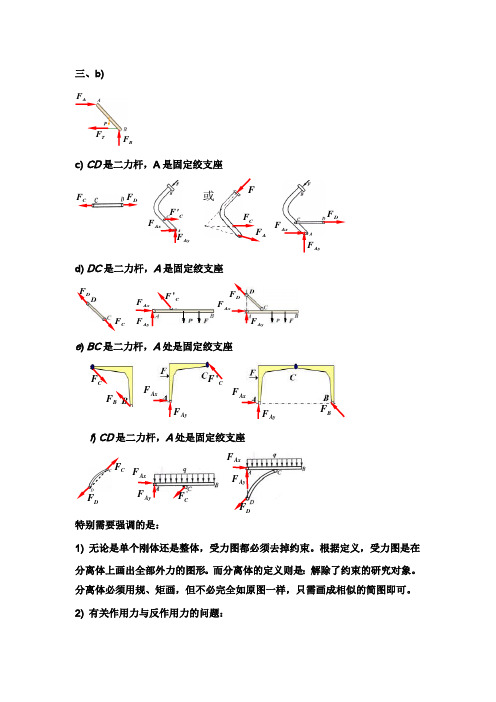
三、b)c) CD 是二力杆,A 是固定绞支座d) DC 是二力杆,A 是固定绞支座e ) BC 是二力杆,A 处是固定绞支座f ) CD 是二力杆,A 处是固定绞支座特别需要强调的是:1) 无论是单个刚体还是整体,受力图都必须去掉约束。
根据定义,受力图是在分离体上画出全部外力的图形。
而分离体的定义则是:解除了约束的研究对象。
分离体必须用规、矩画,但不必完全如原图一样,只需画成相似的简图即可。
2) 有关作用力与反作用力的问题:AyF Ax F 'C F CDF AyF AxF DF CF BFAyF AxF CF 'AyF AxF BF CF 'AyF Ax F DF AyF AxF DF CF AF FCF 或AyF AxF C 'F AyF AxF DF DF CF AF B F TFa ) 习惯上,先找出二力杆,并标示一约束反力(如F D ,将其认为是作用力)。
在另一受力图上的相联点(如D 点),然后根据作用力与反作用力定律确定的约束反力当作反作用力,标示为F'D 。
其中,符号 ' 是为了表示它是F D 的反作用力。
所以,它是有确切含义的。
标注符号时,要注意先后顺序,先确定的约束反力不标注 ' 符号,后确定的约束反力一定要标注符号 ' 。
两者必须成对、反向画。
b ) 为了明确地表示两者的作用力与反作用力关系,两个力的下脚标必须一致,如上述的D 。
不能随手写其它符号,以免产生误解。
下脚标通常用该点的符号表示,不宜象中学物理中那样,标示成数字。
3) 整体受力图一般最后画,整体受力图上的约束反力,应该与各单个刚体上已经画出的约束反力方向一致,以免产生岐义。
一、b ) k 点是光滑面约束,A 是光滑铰链,B 、O 是固定铰支座。
c ) 先确定斜杆(标注为DE )是二力杆,A 是固定绞支座,B 是可动绞支座。
BC 杆带铰,C 铰与AC 杆上C 孔铰接,力F 作用在铰上。
刚体平面运动

第十章刚体的平面运动一、内容提要1、基本概念(1)刚体的平面运动的定义刚体运动时,若其上任一点至某个固定平面的距离保持不变,则称该刚体作平面运动。
(2)刚体的平面运动的简化刚体的平面运动可以简化为平面图形在自身平面内的运动。
(3)刚体平面运动方程为x o'=f1(t) , y o'=f2(t) , ϕ=f3(t) ,(4)刚体平面运动的分解平面图形的运动可以分解为随基点的平动和绕基点的转动。
2、平面图形上各点的速度(1)基点法(速度合成法)V M= V O+V MO(2)速度投影法(V M)MO=(V O)MO(3)速度瞬心法V M=MC∙ω(C点为速度瞬心)3、平面图形上各点的加速度加速度分析主要用基点法(加速度合成法)a M= a O+aτMO+a n MOaτMO =MO∙ε方向垂直于MO,并与ε的转向一致。
a n MO =MO∙ω2 方向由点M指向基点O。
二、基本要求1、熟练掌握平面图形上各点的速度的求解。
2、熟练掌握平面图形上各点的加速度的求解。
三、典型例题例如图所示平面机构,由四杆依次铰接而成。
已知AB=BC=2R,C D=DE=R,AB杆和DE杆分别以匀角速度ω1与ω2绕A、E轴转动。
在图示瞬时,AB与CD铅直,BC与DE水平。
4142 试求该瞬时BC 杆转动的角速度和C 点加速度的大小。
解 AB 杆和DE 杆作定轴转动,BC 杆CD 杆均作平面运动。
(1)求BC 杆的角速度ωBC 因为V B =2R ω1 , V D =R ω2 分别以B 点和D 点为基点,分析C 点速度,有V C = V B + V CB (1)V C = V D + V CD (2) 所以 V B + V CB = V D + V CD (3) 沿BC 方向投影式(3)得V B = V CD则CD 杆的角速度ωCD = V CD /CD=V B /R=2ω1 (逆时针) 沿DC 方向投影式(3)得V CB = V D则BC 杆的角速度ωBC = V CB /BC=V D /2R=0.5ω2 (逆时针)(2)求C 点的加速度a C 因为a B =a B n =2R ω12 ,a D =a D n =R ω22分别以B 点和D 点为基点,分析C 点加速度,有 a C = a B + a CB τ + a CB n (4)a C =a D +a CD τ+a CD n (5)所以 a B + a CB τ + a CB n =a D +a CD τ+a CD n (6) 沿CD 方向投影式(6)得a B n - a CB τ = a CD na CB τ=a B n - a CD n =2R ω12-R(2ω1)2=-2R ω12又将式(4)分别沿x 、y 轴投影式得a Cx =-a CD n =-2R ωBC 2= -0.5R ω22a Cy =-a B n + a CB τ = -2R ω12-2R ω12= - 4R ω12故C 点加速度大小a C =22cy cx a a +=4241642ωω+R43。
刚体运动.ppt

2.平面运动的分解
Y
Y’
⑴概念:
设平面图形相对于静止 坐标系
OXY作平面运动 取S上任一点
O’为基点,并以基点为原点作
动坐标系O’X’Y’
O
A
O’
X’
X
结论:
①绝对运动:S相对于OXY的运动
平面图形的运动(绝对运动)分解为: 随②基相点对的运平动:动O坐’A标+的系绕转O动基’X(’点SY相’的的对转运于动动动)
垂直时滑块B的速度.
VA A
解:⑴⑵基速点度法投.影法:
ω
已V先A知确=RVV定×AB的的A5点速速π/的度度3 速大方度小向:方向O
75°
由=速15度7 c投m影/s 定理:
VA VB
15°
B VBA
再以(V连A 杆) AAB B=作(V为B研) A究B 对象,
选连杆上VB的A=点VA作/ 为co基s15点° 可两以种求方出法B结=点果1的6相3速cm同度/s:
定理中不包含相对速度VBA 所以不能用它来计算AB杆
的角速度。
10.4 速度瞬心
1.瞬心的概念:
L’
如图:已知图形中A点的速度, VCA
C
图形角速度ω.现将半直线L沿
ω转向90°,得半直线L’,在L’
上取一点C,满足VCA = ω ·CA= VA 则:C点的绝对速度:
VC= VCA - VA = 0
2.速度投影定理
(平面图形上任意两 点速度之间的关系)
将关系式 VB = VBA + VA 两端 各量分别投影 在AB连线上 有:
(V ) = (V ) (VBB)AAB B= (VBA )AB + A(VA )AABB
22版:第16讲 考点一 昼夜交替 沿地表水平运动物体的运动方向偏转(步步高)

6.当晨昏线从CD移向EF时,下列叙述正确的是 A.南半球极昼范围增大
√B.太阳直射点向北移动
C.地球公转速度逐渐加快 D.重庆由冬季进入夏季
1 2 3 4 5 6 7 8 9 10 11 12
解析 读图可知,当晨昏线位于CD位置时 是北半球的冬至日,晨昏线位于EF时是北 半球的二分日,晨昏线从CD移向EF时,是 从冬至日到春分日,太阳直射点向北移动, 南半球极昼范围缩小,B对、A错。 地球公转速度在近日点1月初最快,远日点 7月初最慢,因此地球公转速度先加快后减 慢,C错; 重庆由冬季进入春季,D错。选B。
1 2 3 4 5 6 7 8 9 10 11 12
4.飞机从罗马(东三区)起飞的时间是当地时间
A.星期一的18:10
√C.星期日的18:10
B.星期一的12:10 D.星期日的5:10
解析 北京位于东八区,当北京时间为星期一的17:10,正是罗马当地 时间星期一的12:10;飞机从罗马经过18小时飞行到达北京,则在罗马 起飞的时间为星期一12:10减去18小时,即星期日的18:10。
20分,加上6小时,不够24小时,故日期 不变,故选B 根据上题分析可知,图中斜线为 晨线 ,越向北的地方日出时 第2题 间越 早 ,故北半球是夏半年,越向北的地方,白昼越 长 , 故选D 答案 1. B 2._D__
跟踪训练
学以致用 夯基拔高
下图示意晨昏线与纬线的几种位置关系。读图,回答1~2题。
3.确定太阳直射点
纬度的确定
方法 ①直射点的纬度与切点(晨昏线与纬线)的纬度互余 ②直射点的纬度=晨昏线平面与地轴的夹角
①地方时12:00所在经线的经度 经度的确定
第十章刚体的平面运动

理论力学
如图 10-2 所示,刚体运动方式为平面运动,刚体上点 A 的运动轨迹为圆弧,点 B 的运动轨迹为直线,可见刚体上各 点的运动轨迹各不相同。
图 10-2
第10章 刚体的平面运动
理论力学
为了研究刚体的运动情况,将刚体的运动分解为平动和
转动两种基本运动方式,平动部分可任选一点作为基点来研
究。例如 A 点,在基点建立动坐标系 o1x1y1。注意,动坐标系 原点 o1 与刚体上的 A 点是“铰接”关系,即 o1 与 A 点仅仅保 持坐标始终相等,运动轨迹始终相同,但刚体上的 A 点显然 还有与刚体一起旋转的运动,而动坐标系的原点 o1 始终不产 生任何转动,其 x1 轴和 y1 轴的指向始终不变,这样的动坐标 系随 A 点运动时必然只存在平动方式,而且只反映刚体平面 运动中的平动部分,接下来在动坐标系中研究刚体的运动时,
令(υM)O′M、(υO′)O′M、(υMO′)O′M 分别表示 υM、υO′、υMO′ 在 O′M 上的投影,则根据式(10-1)可得:
(υM)O′M=(υO′+υMO′)O′M=(υO′)O′M+(υMO′)O′M
=(υO′)O′M
(10-2)
第10章 刚体的平面运动
理论力学
式(10-2)在推导时,利用了 υMO′始终与 O′M 所具有的 垂直关系,故 υMO′在 O′M 上的投影(υMO′)O′M=0。速度投 影定理的成立主要是由于刚体不可变形的假设而存在的。试 想,如果刚体上两点的速度在其连线上的投影不相等,那么 这两点之间的距离必然发生变化,这与刚体不可变形的假定 相矛盾。
第10章 刚体的平面运动
理论力学
10.2 刚体平面运动时的速度
10.2.1 基点法 根据前面的分析,刚体的任何平面运动都可以分解为两个简
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章
刚体的平面运动
2
运动学/刚体的平面运动§10-4 平面图形内各点的加速度
已知某一瞬时图形S 的ω,ε及其
一点A 的加速度
和图形。
A a 以A 为基点
基点,由基点法合成运动关系:一、基点法
其中:则:
B a a a =n
BA BA A B a a a a ++=τε
τ⋅=AB a BA 2
ω⋅=AB a n
BA r
e a a a a +=BA r a a = A e a a =n
BA
BA a a +=τA
a BA
a n BA
a τBA
a 其中:
即平面图形内任一点的加速度等于基点加速度与该点随图形绕基点转动的切、法向加速度三者矢量和。
二、加速度投影定理将基点法加速度公式
向AB 连线方向投影,有
AB B ][a AB A ][a =n
BA
a −当ω= 0时,a n BA =0
即当平面图形作瞬时平动时,有:
AB B ][a AB
A ][a =当平面图形作瞬时平动时,平面图形上任意两点的加速度在这两点连线上的投影相等。
——加速度投影定理
n
BA
BA A B a a a a ++=τ
τBA
a A
a n
BA
a
ε
加速度投影定理仅当瞬时平动时成立!
运动学/刚体的平面运动
已知:车轮半径为R ,轮心O 点的
速度为,加速度为。
O v O a n
PO
PO
O
P
a a a a ++=τ
用基点法求解大小方向
??
→
⊥OP
由P 指向O
故应先求出车轮ω,ε。
例4沿直线轨道作纯滚动的车轮
试求轮缘上与轨道接触点P 的加速度,
并讨论匀速滚动时加速度瞬心。
分析:O
a ε⋅R 2ω⋅R ?
?
以O 为基点
O
a τPO
a n
PO
a
运动学/刚体的平面运动解:轮O 作平面运动,P 为速度瞬心。
R
v O /=∴ω(
)
因此式在任何瞬时都成立,故有
ωε&=(
)
R v 0&=R a 0=(1)求车轮ω、ε
(2)求轮缘接触点P 的加速度,以O 为基点:
↑
n
PO
PO
O
P
a a a a ++=τ
大小方向
??
→
←
O
a ε
⋅R 2
ω⋅R O
a τPO
a n
PO
a (可以作为公式用)
运动学/刚体的平面运动ετ
⋅=R a PO Q 讨论:1、速度瞬心P 不是加速度瞬心;
2、匀速滚动时,a 0=0,ε=0,
此时轮心O 为瞬时加速度中心,以O 为基点分析,各点加速度与绕O作瞬时定轴转动相同(参见ch7例),而各点速度与绕P 作瞬时定轴转动相同。
O
a τ
PO
a n
PO
a 2
ωR a n PO =作出加速度矢量图如图示。
O a =R
a R O
⋅
=2)(R
v R O ⋅=R v O 2
=
n
PO
P a
a =R v O 2
=)
(↑合成结果为
运动学/刚体的平面运动
例5
已知:O 1A =O 2B ,图示瞬时O 1A //O 2B 。
试问:(a )、(b )两种情况下ω1和ω2,ε1和ε2是否相等?(a )
(b )
解:
因AB 杆作平动,故有
B A v v =)
, (n
B n A B A a a a a ==ττ B A a a =(a ) a A O A ,/11τε=21ωω=B O B a 22/τ
ε=,/1A O 1A v =ωB
O B v 22/=ω2
1εε=运动学/刚体的平面运动
AB 作平面运动,且图示瞬时作瞬时平动,有
(b )(b )
,0=AB ωB
A v v =2
1ωω=,/1A O 1A v =ωB
O B v 22/=ω[]AB
A
a τ
[]AB n
A a +[][]
AB B AB
A a a =瞬时平动有加速度投影定理:
[][]
AB
n
B AB B a a +=τ
即:
n B
a n
A
a τA
a τB
a
ctg ϕωεε2
1122+=可以解得:2
1εε≠ϕεsin 11⋅A O ϕεsin 22⋅=B O ϕωcos 2
11⋅+A O ϕ
ωcos 2
22⋅−B O
ω
运动学/刚体的平面运动已知:滚轮半径R =15cm ,OA 的
转速n =60 r/min ,OA=R 。
求:当α=60º时(OA ⊥AB ),滚
轮的ωB、εB。
要想求出滚轮的ωB、εB,
先要求出v B 、a B 。
解:OA 杆作定轴转动,A B 杆和
轮B 作平面运动。
P 1为其速度瞬心。
例6曲柄滚轮机构
分析:(1) 研究AB 杆
用速度瞬心法求v B ω
P 1
运动学/刚体的平面运动1
/AP v A AB =∴ωAB B BP v ω⋅=1()n
BA
BA
A B a a a a ++=τ
以A 为基点,则B 点加速度为
30/πωn =ω⋅=OA v A 30/60π=π215×=cm/s
30π=)153/(30×=πrad/s 3
2
π=α2
1tg R AP ⋅=R 3=3
21532π
×
×=cm/s
320π=)
(←用基点法求a B
α
αcos /1tg R BP ⋅=R
32=rad/s 2π=ω
P 1
AB
ω运动学/刚体的平面运动
n
BA
BA
A
B
a a a a ++=τ
大小方向
?水平
OA ⋅ω2
由A 指向O ?
AB ⋅ω2AB ⊥AB
由B 指向A
将上式向BA 投影,得
2ω⋅=OA a A 2
AB n BA AB a ω⋅=o 30cos B a 作出加速度矢量图如图所示。
ω
A
a τBA
a n
BA
a B
a 2
)2(15π×=2
2cm/s 60π=2
)3
2(
153π××=2
3
320π=
=n
BA
a 其中:
A
a ω
A a τBA
a n
BA
a B
a 运动学/刚体的平面运动
P 2为其速度瞬心
2/BP v B B =ω2/BP a B B =ε)
(
)
(
o 30cos /n BA B a a =o 30cos B a =n
BA
a 23
/33202π=2
3
40π=2
cm/s 5.131=)
(←(2)研究轮B
P 2
cm/s 320π=B v )
(←15
/320π=rad/s
25.7=15
/5.131=2
rad/s 77.8=
运动学
本次作业:
10 -10,
10 -12,
10 -13,
10 -15。
