随机过程1
合集下载
随机过程(1)
故这一过程称为随机相位正弦波。
6
例3：设X (t) Vcost t , 其中是常数；
V在[0,1]上服从均匀分布,则X (t)是一个随机过程。 对每一固定的t，X (t) Vcost是随机变量V 乘以常 数cost，故也是随机变量,对[0,1]上随机变量取一v值, 就得到相应的一个样本函数x(t) vcost.
P(Y2 2) P(X1 1, X 2 1) P(X1 1)P(X 2 1) q2，
依次类推，当移动n 次时，质点的位置为 Yn n, n 2 , n 4,... (n 4), (n 2), n。
19
若在n 次移动中有m 次质点正向移动，即有m 次Xi 1， 则有n m 次质点作反向移动，即有n m 次Xi 1。
(2) 设Yn是前n次抛掷中出现的最大点数,Yn , n 1也是
一随机过程，它的状态空间仍是1, 2,3, 4,5, 6。
下面分别给出它们的一条样本函数：
xn
6
(1)
5
4
3 2
1
yn
6
xn
5
4
3 2
1
(2)
yn
1 2 3 45 678
n
1 2 3 45 678
n
随机过程的分类： 随机过程可根据参数集T和任一时刻的状态分为四类，
x2
1 x1 1且x2 1
x 13 1
例2：设随机过程X (t) Vcost,t , ，V在[0,1]上均匀分布
求在t
0,
4
,
3 4
,
,
2
时X
(t)的密度函数。
解：对给定的t,若cost 0,记a cost，则X (t) aV的密度函数为：
6
例3：设X (t) Vcost t , 其中是常数；
V在[0,1]上服从均匀分布,则X (t)是一个随机过程。 对每一固定的t，X (t) Vcost是随机变量V 乘以常 数cost，故也是随机变量,对[0,1]上随机变量取一v值, 就得到相应的一个样本函数x(t) vcost.
P(Y2 2) P(X1 1, X 2 1) P(X1 1)P(X 2 1) q2，
依次类推，当移动n 次时，质点的位置为 Yn n, n 2 , n 4,... (n 4), (n 2), n。
19
若在n 次移动中有m 次质点正向移动，即有m 次Xi 1， 则有n m 次质点作反向移动，即有n m 次Xi 1。
(2) 设Yn是前n次抛掷中出现的最大点数,Yn , n 1也是
一随机过程，它的状态空间仍是1, 2,3, 4,5, 6。
下面分别给出它们的一条样本函数：
xn
6
(1)
5
4
3 2
1
yn
6
xn
5
4
3 2
1
(2)
yn
1 2 3 45 678
n
1 2 3 45 678
n
随机过程的分类： 随机过程可根据参数集T和任一时刻的状态分为四类，
x2
1 x1 1且x2 1
x 13 1
例2：设随机过程X (t) Vcost,t , ，V在[0,1]上均匀分布
求在t
0,
4
,
3 4
,
,
2
时X
(t)的密度函数。
解：对给定的t,若cost 0,记a cost，则X (t) aV的密度函数为：
随机过程第一章概率预备知识
随机过程的有限维分布
定义
随机过程的有限维分布是指多个时间点的联合概率分布，描述了随机过程在不同 时间点的相关性。
性质
有限维分布具有时间可加性，即随着时间的推移，联合概率分布可以由单个时间 点的概率分布累加得到。
随机过程的数字特征
定义
随机过程的数字特征是一组统计量， 用于描述随机过程的总体“性格”， 如均值、方差、偏度、峰度等。
状态分类
根据状态之间的转移关系，可以将状态分为 吸收态、周期性状态和遍历状态等。
转移概率矩阵
描述状态之间转移概率的矩阵，其中每个元 素$P_{ij}$表示从状态$i$转移到状态$j$的 概率。
极限定理和不变概率分布
极限定理
描述马尔科夫链状态概率的极限行为，如强大数定律和中心极限定理等。
不变概率分布
随机过程在金融风险管理领域也发挥 了重要作用，如通过蒙特卡洛模拟等 方法评估投资组合的风险。
在物理和工程中的应用
物理模拟
在物理学的许多领域，如粒子物 理学和流体动力学，随机过程用 于模拟自然现象和实验结果的统
计性质。
通信工程
在通信系统中，随机过程用于描 述信号的噪声和干扰，以及信道
容量等性能指标。
对数函数
对于随机变量X，对数函 数f(X)=lnX的期望和方差 分别为E(lnX)=lnE(X)和 Var(lnX)=1/E(X)Var(X)。
Part
03
随机过程的基本概念
随机过程的定义和分类
定义
随机过程是由随机变量构成的数学结 构，每个随机变量对应一个时间点或 位置。
分类
根据不同的特性，随机过程可以分为 离散时间随机过程和连续时间随机过 程，平稳随机过程和非平稳随机过程 等。
随机过程1(1)
4.根据参数集与状态空间离散与否,随机过程可分为
●离散参数,离散状态的随机过程 (例3)
● 离散参数,连续状态的随机过程 (例4)
● 连续参数,离散状态的随机过程 (例1)
● 连续参数,连续状态的随机过程 (例2)
参数集为离散的随机过程也称为随机序列， 或时间序列．
二
随机过程的有限维分布函数族
设X={X(t),t∈T}是S.P.
2 0 2 0
0 h( x ) 1 其它
0 2x 1 其它
2
x0
2 其它
(3)
t
2
时，X (t ) V cos
2
0,
此时X （
2
）是单点分布, 则
F
ห้องสมุดไป่ตู้X(
2
( x ) P{ X (
)
2
) x}
1 x 0 0 x 0
特别注意： 一族随机变量Ｘ(t) 的两个特点：随机性与函数性
随机过程定义
设(Ω,F,P)为一概率空间,T为一参数集,T R,
若对每一 t ∈T,均有定义在(Ω,F,P)上的一个 随机变量X(ω,t),(ω∈Ω)与之对应, 则称X(ω,t)为(Ω,F,P)上的一个随机过程(S.P.) 记X={X(ω,t), ω∈Ω,t∈T},
注意： 设{X(ω,t), ω∈Ω, t∈T}为一S.P.
1. X(ω ,t),实质上为定义在T×Ω上的二元单值函数. 2.对每一个固定的t, X(t)为一随机变量. 随机变量X(t) (t∈T)所有可能取值的集合,称为随机过 程X(ω,t),的状态空间.记为S. S中的元素称为状态. 3.对每一个ω0∈Ω,X(ω0,t)是定义在T上的普通函数. 记为 x(ω0,t), 称为为随机过程的一个样本函数.也称轨 道或实现. 样本函数的图形称为样本曲线．
《随机过程》课后习题解答
6、证函数 f (t ) 解 （1）
（ k 0, 2, n ）
1 为一特征函数，并求它所对应的随机变量的分布。 1 t2
n n i
f (t
i 1 k 1
tk )i k
5
=
i 1 k 1
n
n
i k
1 (ti tk )
2
i 1 k 1
n
n
e jti e jti e jti {1 ( jtk )(1 jtk )} n n e jtk e e i k jti = i 1 k 1 e n(1 jtk ) e
1 n n n j ( ti tk ) l ] i k = [e n i 1 k 1 l 1
（2） （3）
其期望和方差； 证明对具有相同的参数的 b 的 分布，关于参数 p 具有可加性。
解 （1）设 X 服从 ( p , b ) 分布，则
f X (t ) e jtx
0
b p p 1 bx x e dx ( p )
bp ( p)
x
0
p 1 ( jt b ) x
i k
1 M 2
0
ti t k } ） （ M 1max{ i , j n
且 f (t ) 连续 f (0) 1 （2） f (t )
f (t ) 为特征函数
1 1 1 1 1 [ ] 2 2 1 t 1 ( jt ) 2 1 jt 1 jt
3
fZ(k)() t (1 )kk! jk (1 jt)(k1)
E (Z k ) 1 (k ) f Z (0) ( 1) k k ! k j
n
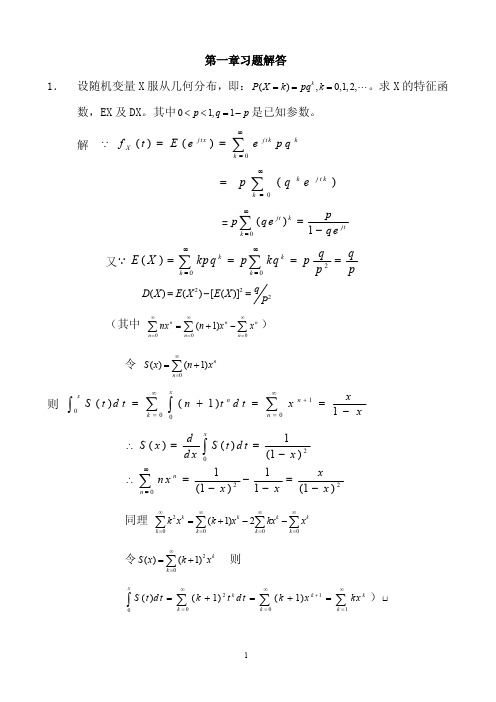
（ k 0, 2, n ）
1 为一特征函数，并求它所对应的随机变量的分布。 1 t2
n n i
f (t
i 1 k 1
tk )i k
5
=
i 1 k 1
n
n
i k
1 (ti tk )
2
i 1 k 1
n
n
e jti e jti e jti {1 ( jtk )(1 jtk )} n n e jtk e e i k jti = i 1 k 1 e n(1 jtk ) e
1 n n n j ( ti tk ) l ] i k = [e n i 1 k 1 l 1
（2） （3）
其期望和方差； 证明对具有相同的参数的 b 的 分布，关于参数 p 具有可加性。
解 （1）设 X 服从 ( p , b ) 分布，则
f X (t ) e jtx
0
b p p 1 bx x e dx ( p )
bp ( p)
x
0
p 1 ( jt b ) x
i k
1 M 2
0
ti t k } ） （ M 1max{ i , j n
且 f (t ) 连续 f (0) 1 （2） f (t )
f (t ) 为特征函数
1 1 1 1 1 [ ] 2 2 1 t 1 ( jt ) 2 1 jt 1 jt
3
fZ(k)() t (1 )kk! jk (1 jt)(k1)
E (Z k ) 1 (k ) f Z (0) ( 1) k k ! k j
n
随机过程-第一章
• 或叙述为 若对每一个时刻t∈T，都有定义在E上 的随机变量X(t，e)，则称一族随机变量
• {X(t， e)，t∈T ，e∈Ω} 为一随机过程。
• 其实际意义就是： 若一物理过程，当时间t（或广义时间）固定，
过程所处的状态是随机的（不确定的），则此
过程就为随机过程。对该过程的一次记录（或
一个观察）就是一个现实，或称作随机过程的
一个样本函数或样本曲线。 • 固定t0，X（t0）是随机变量。 • 固定e0，X（t，e0）是一个现实，是t的函数，记 为 x(t)。
例4：具有随机初位相的简谐波。 X（t）=acos（ω0t+Φ），-∞<t<+∞， 其中a与ω0是正常数， Φ是在[0，2π]上均匀分布的随机变量。 一方面，随机过程X（t）是一族随机变量。 对每个固定t0， X（t0）= acos(ω0t+Φ)是个 随机变量。对（-∞，+∞）上有多少个t， 就对应多少个随机变量。∴对（-∞，+∞） 所有t，X（t）看作一族随机变量。 另一方面，随机过程是一族样本函数（曲线） 对样本空间Ω中每个基本事件e对应一个样本 函数，本例，Φ在Ω=[0，2π] 上任给定一个 相 位φi=e，就对应一个样本曲线，如：书P 4。
例6： 利用抛掷硬币的试验定义一个随机过程。
X（t） { sin π t，出现正面 ，记为记为 ω 0 e ，出现反面, 记 ω 1
t
(t R)
写出X（t）的所有样本函数（现实）
二、随机过程的的分布（有限维分布族） 1、对任意固定的t0∈T，随机过程X(t)的状态 X(t0)是一维随机变量， 其分布函数是P{X(t0)≤x} F(x，t0) 由于t的任意性，称F(x; t) = P{X(t) ≤x } 为随机过程X(t)的一维分布函数。 F(x，t)是与t有关的一维分布函数，在t，x平 面上是X(t)落在区间(X(t) ≤x)上的概率。
• {X(t， e)，t∈T ，e∈Ω} 为一随机过程。
• 其实际意义就是： 若一物理过程，当时间t（或广义时间）固定，
过程所处的状态是随机的（不确定的），则此
过程就为随机过程。对该过程的一次记录（或
一个观察）就是一个现实，或称作随机过程的
一个样本函数或样本曲线。 • 固定t0，X（t0）是随机变量。 • 固定e0，X（t，e0）是一个现实，是t的函数，记 为 x(t)。
例4：具有随机初位相的简谐波。 X（t）=acos（ω0t+Φ），-∞<t<+∞， 其中a与ω0是正常数， Φ是在[0，2π]上均匀分布的随机变量。 一方面，随机过程X（t）是一族随机变量。 对每个固定t0， X（t0）= acos(ω0t+Φ)是个 随机变量。对（-∞，+∞）上有多少个t， 就对应多少个随机变量。∴对（-∞，+∞） 所有t，X（t）看作一族随机变量。 另一方面，随机过程是一族样本函数（曲线） 对样本空间Ω中每个基本事件e对应一个样本 函数，本例，Φ在Ω=[0，2π] 上任给定一个 相 位φi=e，就对应一个样本曲线，如：书P 4。
例6： 利用抛掷硬币的试验定义一个随机过程。
X（t） { sin π t，出现正面 ，记为记为 ω 0 e ，出现反面, 记 ω 1
t
(t R)
写出X（t）的所有样本函数（现实）
二、随机过程的的分布（有限维分布族） 1、对任意固定的t0∈T，随机过程X(t)的状态 X(t0)是一维随机变量， 其分布函数是P{X(t0)≤x} F(x，t0) 由于t的任意性，称F(x; t) = P{X(t) ≤x } 为随机过程X(t)的一维分布函数。 F(x，t)是与t有关的一维分布函数，在t，x平 面上是X(t)落在区间(X(t) ≤x)上的概率。
随机过程-1预备知识
• 概率空间的性质
设(, F,P)为概率空间，则
(4) P()= 0
(5)P(B\A)= P(B) -P(A) , (AB)
(6)
lim n
P(
An
)
P P
n1 n1
An An
, ,
A1 A1
A2 An A2 An
• 显然，这样建立的概率满足三条公理。
17
• 例2 为依次抛掷三枚硬币的试验建立概率模型。 • 解 用“1”表示正面向上，“0”表示反面向上，
样本空间为：
• {(1,1,1),(1,1,0),(1,0,1),(1,0,0),(0,1,1),
(0,1,0),(0,0,1),(0,0,0)}
• 如果上述8种结果出现的可能性相同，根据可 加性和归一性，每个结果的概率为 1/8.
概率实例：
• 例1 给掷一枚硬币的试验建立概率模型。 • 解：掷一枚硬币，有两个可能的结果：正
面和反面。若用 1 表示正面，2 表示反面， 则样本空间为： {1, 2 } • 事件为： {1 , 2 }, {1}, {2 }, • 根据定义和性质，得到
P({1,2 }) 1, P() 0
（2）若AF, 则\AF （对立事件）
（3）若AiF,i=1,2…，则 AiF （可列
并事件）
i 1
称F为-代数，（， F ）为可测空间
例 投掷一次骰子试验，ei表示出现i点， ={e1,e2,e3,e4,e5,e6} F ={，{e1,e2,e3}，{e4,e5,e6}， }
• 定义1.2概率空间：设(,F)为可测空间,映
射P：F R，A|P(A)满足
《随机过程》第一章习题
第一章 随机过程及其分类1、 设随机向量),(Y X 的两个分量相互独立，且均服从标准正态分布)1,0(N 。
（a ） 分别写出随机变量Y X +和Y X -的分布密度（b ） 试问：Y X +与Y X -是否独立？说明理由。
2、 设1X 、2X 、3X 为独立同分布的随机变量，且服从标准正态分布。
令：233211X X X X Y ++=（a ） 试求随机变量Y 的分布密度函数；（b ） 试问有限个独立正态分布随机变量经过非线性变换是否可以服从正态分布？3、 设),0(~2σN X ，对于0>∀b ，试证明正态分布尾概率估计不等式：⎭⎬⎫⎩⎨⎧-⋅≤≥≤⎭⎬⎫⎩⎨⎧-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-222232ex p 21}{2ex p 21σσπσσσπb b b X P b b b 4、 设随机向量()()∑=,~,21μτN X X X ，其中：()()ττμμμ2,1,21==，⎪⎪⎭⎫ ⎝⎛=∑15/45/41，令随机向量()X Y Y Y ⎪⎪⎭⎫ ⎝⎛==3223,21τ。
（a ） 试求随机向量Y 的协方差矩阵、{}12Y Y E 及{}21Y Y E +； （b ） 试问{}122X X E X -与1X 是否独立？证明你的结论。
5、 设}0),({≥t t X 是一个实的均值为零，二阶矩存在的随机过程，其相关函数为t s s t B t X s X E ≤-=),()}()({，且是一个周期为T 的函数，即0),()(≥=+τττB T B ，试求方差函数)]()([T t X t X D +-。
6、 考察两个谐波随机信号)(t X 和)(t Y ，其中：)cos()(),cos()(t B t Y t A t X c c ωφω=+=式中A 和c ω为正的常数；φ是[]ππ,-内均匀分布的随机变量，B 是标准正态分布的随机变量。
（a ） 求)(t X 的均值、方差和相关函数；（b ） 若φ与B 独立，求)(t X 与)(t Y 的互相关函数。
随机信号分析-1 随机过程(1)
X(ξ , t) 是随机过程的一个样本
X(ξ , t) 是一个随机变量 X(ξ , t) 是一个确定值
14
随机过程的定义
随机过程判断举例 例1.1 随机初相正弦波X(t)=A cos(ω0t+Φ )， A和ω0是正常数， Φ服从[0, 2π]上的均匀分布。判断其是否为随机过程. 从定义1的角度考虑： Φ是随机变量，每次观测其取值是随 机的，从而得到不同的样本函数，且该函数是时间函数； 从定义2的角度考虑，固定t时，X(t)是随机变量Φ的函数，也
18
随机过程的概率分布
根据定义2，对随机过程采样，可得多维随机变量。在满足 一定采样间隔要求下，随机过程的统计特性可由该多维随机 变量的统计特性反映；因此可将概率论中对随机变量的概率 统计特性的研究方法推广到随机过程的研究中。 随机过程的一维概率分布 定义3 设{X(t), t ∈T }是随机过程，对任意固定t1∈T 和实数x1 ∈R， 称Fx (x1 ; t1)=P {X(t1) ≤ x1} 为该过程的一维分布函数；若Fx
f X x1 , x2 ,, xn ; t1 , t2 , tn
1
2
n 2
1 ' 1 exp X C X 1 2 2 C
C是协方差矩阵，X=(x1 , x2 , …, xn）
24
随机过程的数字特征
有限维概率密度函数族可完全确定随机过程的全部统计特性， 但有时得到该函数族相当困难，甚至不可能 幸运的是，很多时候只需要掌握随机过程的几个统计值即可； 这些统计值即为随机过程的数字特征，有数学期望、均方值、 方差、相关函数等。 数字特征既能描述随机过程的重要特性，又便于实际测量； 对随机过程的数字特征的计算方法，是先把时间t固定，然 后用随机变量的分析方法来计算。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n1
lin PAn PA.
n
徐
概率空间
A 证：在推论2中
令 Bn An A,则B1 B2 ,
且 Bn An A
n1 n1
Bn= An - A
An
n1
A A
A
lim PBn 0 PAn PA PAn A 0. n
PAn PA (as n )
徐
概率空间
徐
概率空间
第一章 概率论概要
§1.1 概率空间 §1.2 随机变量及其分布 §1.3 随机变量的函数 §1.4 随机变量的数字特征 §1.5 特征函数 §1.6 收敛性与极限定理
徐
概率空间
§1.1 概率空间
一、概率的公理化定义 除了概率的统计定义之外 柯氏公理体系是现代概率论的基石.
徐
概率空间
一一对应.
四、条件分布 定义：设(X,Y)的联合分布函数为F(x, y)，记
徐
概率空间
FY X ( y x) PY y X x
Fx , y Fx , y
lim
,β o
Fx
,
Fx
, ,
, 0
若极限存在，称为在X=x 的条件下,随机变量 X的条件分布函数.
注 需满足对 α 0,β 0,
推论2 (单调性):若 B ，A则
P(A－B)=P(A)－P(B) 且 PA PB,
徐
概率空间
3) 概率的单调性
A1
若 A1 A2 , 且 An ,
i 1
An
则 lim P( An ) 0.
n
证：
An+1
An An An1 An1 An2
Ak
Ak1
ˆ
Bk ,
kn
kn
n 1,2,
称为已知事件A发生的条件下，事件B 发生的
条件概率.
定理：设(Ω,F,P)是概率空间,B∈F,且P(B)>0,则
对 A F, 有P( A B) 对应, 集函数P • B满足三条
公理:
徐
概率空间
1) A F, 0 P( A B) 1;
2) P(Ω B) 1;
3) Ai Fi 1,2, ,且 Ai Aj ,(i j),则
其中B1,B2,…互不相容，由完全可加性有
徐
概率空间
1
P( A1)
P
Bk
k 1
P
Ak
k 1
Ak1
0
收敛级数的余项极限为0,(as n ),即
PAn
PAk
Ak1
0,
(as
n ).
kn
推论1：
若 A1 A2 , 且 An A,则
n1
lin PAn PA.
n
推论2： 若 A1 A2 , 且 An A,则
徐
概率空间
§1.3 随机变量的数字特征
一、数学期望与方差
定义 随机变量X 的分布函数为F(x),若
x dF (x) , 则称 E( X ) ˆ xdF( x).
为随机变量X的数学期望
注 若X是连续型随机变量,则
E(
X
)
xF
(
x)dx
xf
(
x)dx
徐
概率空间
若X是离散型随机变量,则
E( X ) xi P{X xi }
3) lim F ( x, y) 0, lim F ( x, y) 0,
x
y
lim F( x, y) 1;
y
x 徐
概率空间
4) x1 x2 , y1 y2,
F( x2, y2 ) F( x1, y2 ) F( x2, y1) F( x1, y1) 0.
注 1) 此定理的逆成立；
2) 可以推广到任意有限维的情形； 3) 分布函数与概率空间(Ω,F, P)的概率
yk
,
i
1,2,
称为条件分布律.
徐
概率空间
连续型(X, Y),有
FY
X
y
x
PY
y
X
x
y
f x,vdv fX x
称
fY
X y x FY'
X y x
f x, y fX y
为在条件X=x 下, 随机变量Y 的条件密度函数.
徐
概率空间
五、随机向量的独立性 定义：设(X, Y)是二维随机变量,对 ( x, y有) R2
2) 0 F x 1, lim F x 0, lim F x 1;
x
x
3） F(x)是左连续函数, 即对
x R, F x 0 F x.
证3）由于F(x)单调不减，根据单调原理 仅需证,对任意的x∈R, 有
徐
概率空间
lim
F
x
1
F x.
n n
因
X
n1
x
1
n
X
x，
且
X
x 1
X11, , X1,n1 , X2,1, , X2,n2 , , Xk,1, , Xk,nk
若ψi 是ni 元实变实值连续函数,令
Yi φi (Xi1 , , Xi,ni ) i 1,2, , k
有 1) Y1,Y2,…,Yk 必为同一概率空间的随机变量;
2) 若（X11, , X1,n1 , X2,1, , X2,n2 , , Xk,1, , Xk,nk）
思考:
如何准确理解“维”的含义? 如何理解“定义在同一概率空间” ?
徐
概率空间
1. 随机变量概念的理解. X是概率空间(Ω,F, P)上的随机变量,有 1) 对于ω∈Ω，有唯一X(ω)与之对应,
随机变量X
Ω
RX R X
可理解为从 样本空间Ω到
ω
x=X(ω)
实数集Rx的 一个映射.
2) 对x R, 均 有
2)
Ai Ω, Ai Aj .
i 1
完备性 条件.
徐
概率空间
则对任意B∈F 有
1)
PB
P( Ai )P(B Ai );
i 1
2)
P(Aj B)
P(Aj )P(B Aj )
, j 1,2, .
P( Ai )P(B Ai )
i 1
徐
概率空间
§1.2 随机变量及其分布
一、随机变量
定义: 设(Ω,F, P)是概率空间,X(ω)是定义在Ω
PX x,Y y PX xPY y 1
成立,称X与Y相互独立. 注本质上是事件的独立,(X,Y)定义在(Ω,F, P)
上,对 ( x, y)随R机2,事件{X<x}与{Y<y}相互 独立.
1式 FX ( x)FY ( y) F( x, y) 2
对所有(x, y)∈R2成立.
徐
概率空间
定义:(X1,X2,…,Xn)是n 维随机变量,若对任意 （x1,x2,…,xn） Rn , 有
P
Ai
i 1
B
P
i 1
Ai
B
.
条件概率 是概率.
定义:记PB= P(·|B）,则PB 是可测空间(Ω,F) 上的概率,称(Ω,F,PB)是条件概率空间.
徐
概率空间
四、全概率公式与Bayes公式
定理：设 (Ω,F, P)是概率空间,若
1) A i∈F, 且 P(Ai)>0 ，(i=1,2, …);
F(x1, x2, , xn) FX1 (x1)FX2 (x2) FXn (xn).
成立,称随机向量X1, X2 ,…, Xn相互独立. 定理1 若随机变量X1, X2 ,…, Xn相互独立，则
其中任意k（2≤k≤n）个随机变量 Xi1 , X也i2相,互, Xik 独立.
徐
概率空间
定理2 设有n1+n2+…+nk维随机变量
概率空间
序言
随机过程论：研究随机现象演变的统计规律性. 是近代数学的重要组成部分, 特点:
1.应用非常广泛,实际工程背景强; 2.数学基础要求较高; 3.建立随机分析的思维较难. 本课程教学中: 1.立足于基本理论的介绍; 2.力图帮助同学掌握随机分析的基本思想和 基本方法;
徐
概率空间
3.尽量阐述清楚基本概念及相应的工程背景; 4.尝试将各类随机过程与工程问题结合; 5.训练数学表述能力.
Ω {(x, y) : x 0, y 0}
对于样本点( x, y)可Ω定义
身高：X ((x, y)) ˆ x, 体重：Y ((x, y)) ˆ y.
注: 由(X,Y)的分布可确定X, Y 各自的分布,反 之不行. 如“(X,Y)服从二维正态分布”与“X,Y是两个 正态分布随机变量”是完全不同的概念.
定义(概率)：设(Ω,F)是一可测空间，对 AF
定义在F上的实值集函数P(A), 满足
1) 非负性：对 A F, 0 PA 1;
2) 规范性:P(Ω) = 1;
3) 完全可加性,对
Ai F i 1,2, , Ai Aj , i j,
有
P
Ai
PAi
i1 i1
称P是(Ω,F)上的概率(测度),P(A)是事件A
4）多除少补原理
设 Ai F, i 1,2, , n, 有
P
n
Ai
i 1
n
P
i 1
Ai
1ik n
PAi Ak
1n1
P
n
Ai
i 1
.
推论：概率具有次可加性
P
n
Ai
i 1
n
P
i 1
Ai
.
徐
概率空间
三、条件概率
定义：设(Ω,F, P)是概率空间，A, B∈F，