§5.4 理想低通滤波器
低通滤波器设计原理
低通滤波器设计原理低通滤波器是一种常用的信号处理技术，用于从信号中去除高频成分，使得信号中只保留低频成分。
其设计原理基于信号的频率特性和滤波器的特性。
一、低通滤波器的基本原理低通滤波器的基本原理是通过选择合适的频率截止点，使得该频率以下的信号通过滤波器，而高于该频率的信号被滤除或衰减。
这样可以实现去除高频噪声或不必要的信号，保留主要的低频信号。
二、滤波器的频率响应滤波器的频率响应是指滤波器对不同频率信号的响应程度。
低通滤波器的频率响应在截止频率以下保持较高的增益，而在截止频率以上逐渐衰减。
具体来说，低通滤波器的频率响应可以用一个截止频率和一个衰减因子来描述。
三、滤波器的类型根据滤波器的特性，低通滤波器可以分为两类：理想低通滤波器和实际低通滤波器。
理想低通滤波器是指在截止频率以下完全通过信号，而在截止频率以上完全抑制信号的滤波器。
实际低通滤波器是指在截止频率以下有一定的增益，而在截止频率以上有一定的衰减的滤波器。
四、滤波器的设计方法1. 传统方法：传统的低通滤波器设计方法包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。
这些方法通常基于模拟滤波器设计原理，通过选择合适的滤波器阶数和截止频率来实现低通滤波器的设计。
2. FIR滤波器设计：FIR滤波器是一种常用的数字滤波器，其设计方法与传统方法有所不同。
FIR滤波器通过选择合适的滤波器系数来实现低通滤波器的设计。
常用的FIR滤波器设计方法包括窗函数法、最小均方误差法和频率采样法等。
五、滤波器的性能指标低通滤波器的性能指标包括截止频率、衰减因子、通带波动和群延迟等。
截止频率是指滤波器开始衰减的频率，通常用3dB衰减点来定义。
衰减因子是指滤波器在截止频率以上的衰减程度，通常以分贝（dB）为单位来表示。
通带波动是指滤波器在通带范围内的增益波动程度，通常以分贝为单位来表示。
群延迟是指滤波器对不同频率信号的传输延迟，通常以时间为单位来表示。
六、应用领域低通滤波器在各个领域都有广泛的应用。
理想低通滤波器的响应
第五章傅里叶变换应用于通信系统第三讲理想低通滤波器的响应1234理想低通滤波器的冲激响应我们曾经说过，冲激函数是一种很特别的函数。
用冲激函数来激励系统的输入端等价于同时用所有可能频率的相同幅度的正弦波来测试系统，所以输入一个冲激函数就能够确定系统在所有频率的频率响应。
对理想低通滤波器的传输函数进行傅里叶反变换，不难得到其冲激响应，如图5-3-2所示。
图5-3-2 理想低通滤波器的冲激响应分析：1.从响应波形我们可以看出，输出的波形完全不同于冲激信号的波形，产生了很大的失真。
这是因为，理想滤波器是一个限带系统，而冲激信号的频谱带宽是无穷大，自然会造成失真。
在输出波形中，上升和下降的时间（即波形的陡峭程度）与截止频率成反比，截止频率越高，波形越陡峭。
2.虽然带宽的限制造成了波形畸变，但是这个畸变是对称的，即输出波形关于延迟时间对称。
这是因为系统具有线性相移特性的缘故。
系统虽然有振幅畸变，但线性相移特性使得输出波形与输入波形为同一类型的对称形式。
网络的线性相移特性给出了对称的冲激响应和对称的阶跃响应，这在电视和雷达系统中是特别重要的。
3.系统违背了因果律。
输出电压不再是冲激函数，而是在脉冲建立的前后出现起伏的振荡现象，而且这种振荡一直延伸到处。
从响应波形可以看出，冲激响应对应于t的负值也存在，而输入却是在t=0时加入的。
这显然不符合常规，似乎是系统可以预测激励。
实际上，这里所讨论的只是一个理想化的低通滤波器，它的响应特性在物理上是不可实现的。
系统的物理可实现性——佩利-维纳准则虽然理想低通滤波器在实际中是不能实现的，但是我们希望找到一种区分可实现性与不可实现性的标准，这就是佩利-维纳（Paley-Wiener）准则。
物理可实现性在文献中有不同定义方法，这里采用最低限度的定义把物理可实现性系统和不可实现系统区分开来。
我们可以直观地看到，一个物理可实现系统在激励加入之前是不可能有响应输出的，这称为因果条件。
5-2 理想低通滤波器、系统的物理可实现性
§5.2理想低通滤波器、系统的物理可实现性
一、理想低通滤波器 1．理想低通滤波器的频率特性 ① 理想模型 信号：冲激函数、阶跃函数 系统：理想低通、高通、带通、带阻滤波器 ② 理想低通滤波器：矩形幅度、线性相位
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
例2．已知 h(t )
d sin(c t ) [ ] ，求 H ( j) dt t
sin(ct ) u ( c ) u( c ) 解： ct c
sin(c t ) u ( c ) u ( c ) t
H ( j )
1 c c H ( j ) 0 c
c
c
是否满足无 失真条件？
( )
( ) t0
e jt0 c c H ( j ) other 0
t0
作用：使频率低于c的分量无失真的通过，高于c的分量 完全衰减为0；
3.理想低通滤波器的阶跃响应
u(t )
e ① H ( j ) 0
j t0
c c
H ( j )
g (t ) ?
c
E ( j ) ( )
1 j
1 G( j ) H ( j ) E ( j ) [ ( ) ] e jt0 j 1 c 1 jt0 jt 1 g (t ) F [G( j )] c [ ( ) j ]e e d 2 1 1 c cos (t t0 ) 1 c sin (t t0 ) d c c d 2 2 j 2
§5.4 理想低通滤波器
第 4 页
H ( j ) [u( 0 ) u( 0 )] e π Sa(c t ) [u( c ) u( c )] c ωc Sa(c t ) [u( c ) u( c )] π c j t Sac t t 0 [u( c ) u( c )]e
1
3 页
h( t ) H (j )
c
c
c sinc ( t t 0 ) c Sa c t t 0 π c t t 0 π
X
f ( t ) F (j )
f (t t0 ) F (j )e
j t 0
当 c 时， h(t ) ( t t 0 )
系统为全通网络，可以 无失真传输。 2.理想低通滤波器是个物理不可实现的非因果 系统 原因：从h(t)看，t < 0时已有值。
X
二．佩利－维纳准则
物理可实现的网络
第 7 页
时域特性 h( t ) h( t )u( t ) 因果条件 频率特性
§5.4 理想低通滤波器
•理想低通的频率特性 •理想低通的冲激响应
第 1 页
X
一．理想低通的频率特性
1
第 2 页
H (j )
c O
c
H j H ( j ) e c 1 H j c 0
j ( )
c
c O
π
j t 0
0
h( t )
c
π
Sac t t 0
X
第
波形
5 页
(t )
(1)
t
1.失真； 2.物理不可实现的 非因果统
理想低通滤波器
1 4
G(
20
)
1 G(
4
20 ) 2
H ( )
G0 ( j)H ( j) G( j) g(t) c O c X
频谱图示
G( )
A
g(t) cos0t
1 2
[G(
0 )
G(
ห้องสมุดไป่ตู้
0 )]
第 16
页
G1 () g(t) cos 0t
F cos0t
A
2
( )
( )
O m
0
O
0
0
O
0
g0 (t)
t
c O
c
ht
c
π
Sac
t
t0
t
X
第
说明：
7
页
1.理想滤波器的峰值输出比输入δ(t)延迟了t0
2.比较输入输出，可见严重失真；
h(t ) c
π
t 1信号频带无限宽，
而理想低通的通频带(系统频带)有限的 0 ~ c
t0 π
当 经t过理想低通时， 以上c 的频率成分都衰
c
减为0，所以失真。
3.ωC愈高,过零点愈密集,h(t)愈接近于原信号δ(t)
Si(x) x sin y dy 0y
正弦积分函数
X
波形
第
10
f (x) sin x
页
x
Si( y) y sin x dx
0x
g (t )
1 2
1 π
Sic (t
t0 )
X
说明:
第 11
页
1.响应比激励滞后t0
2.输出的前沿是倾斜的,而不是陡直的.阶跃响应上升时 间t1与频带宽度ωc成反比. ωc越大, t1越小,波形越陡 直,失真越小.
理想低通滤波器及其响应
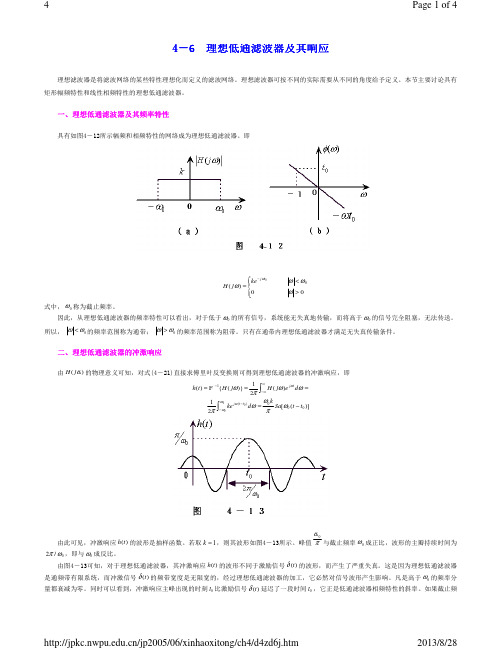
dω =
ω0 k Sa[ω 0 (t − t0 )] π
由此可见，冲激响应 h(t ) 的波形是抽样函数。若取 k = 1 ，则其波形如图4－13所示。峰值 π 与截止频率 ω 0 成正比，波形的主瓣持续时间为
2π / ω 0 ，即与 ω 0 成反比。
ω0
由图4－13可知，对于理想低通滤波器，其冲激响应 h(t ) 的波形不同于激励信号 δ (t ) 的波形，而产生了严重失真。这是因为理想低通滤波器 是通频带有限系统，而冲激信号 δ (t ) 的频带宽度是无限宽的，经过理想低通滤波器的加工，它必然对信号波形产生影响。凡是高于 ω 0 的频率分 量都衰减为零。同时可以看到，冲激响应主峰出现的时刻 t0 比激励信号 δ (t ) 延迟了一段时间 t0 ，它正是低通滤波器相频特性的斜率。如果截止频
四、理想低通滤 理想低通滤波器的矩形脉冲 波器的矩形脉冲响应 脉冲响应
对于图4－17(a)所示的矩形脉冲 f (t ) ，有
f (t ) = U (t ) − U (t − τ )
因此理想低通滤波器对此信号激励产生的响应可直接利用线性时不变性写为
y (t ) =
1
π
{Si[ω 0 (t − t0 )] − Si[ω 0 (t − t0 − τ )]} (4－29)
h(t ) = 0
2频域准则
t<0
H ( jω ) 物理可实现的必要条件是
∫
而且， H ( j 1+ω 2
−∞
dω < ∞
(4－30)
∫
∞
−∞
H ( jω ) dω < ∞ (4－31)
2
式(4－30)也叫做佩利维纳(Paley-Wiener)准则。不满足此准则的幅度函数，其对应系统的冲激响应将是非因果的。 由式(4－30)可以看出， H ( jω ) 可以在某些离散点上为零，但不能在一有限频带内为零，这是因为在 H ( jω ) = 0 的频带内， ln H ( jω ) = ∞ 。
§5.4 理想低通滤波器解析
§5.4 理想低通滤波器
X
主要内容
理想低通的频率特性 理想低通的冲激响应 理想低通的阶跃响应
理想低通对矩形脉冲的响应 重点
难点
理想低通的频率特性
理想低通的阶跃响应
X
一．理想低通的频率特性
H ( )
( )
C O
jt 0 1 e H 0
r (t )
1
Si C (t t 0 )
O r1 t
t
Si C ( t t 0 )
1 1 2
O
t0
t0
t0
2
t
X
讨论
1 时，才有如图示，近似矩形脉冲的响 1． t r 2 C 应。如果 过窄或 C 过小，则响应波形上升与下降时 间连一起完全失去了激励信号的脉冲形象。 2 2. 最小值到最大值的时间 ：t r
令x t t 0
X
正弦积分
sinx Si(y) = dx 0 x 1. 下限为0；
y
sin x 1 x
O
2
3 4
x
2. 奇偶性：奇函数。 3.最大值出现在 x ， 最小值出现在 x 。
Si y
2
O
y
2
X
阶跃响应波形
u t
O
r t
X
二．理想低通的冲激响应
h( t ) H ( )
1 j t h( t ) F H ( ) H ( ) e d 2 1 c j t 0 j t 1 e e d 2 c
1
1 c 1 1 j ( t t 0 ) j t t 0 1 e d e 2 c 2 j t t 0 1 1 1 j C t t0 e e j C t t0 t t 0 2 j c sin c t t 0 c Sa c t t 0 c t t 0
5.4 理想低通滤波器
τ
t
∴r1(t ) =
1
π
{Si[ωC (t − t0 )]
− Si[ωC (t − t0 −τ )]}
1
1 2
O
t 0 t + τ t0 + τ 0 2
t
讨论
1 π <<τ 时，才有如图示，近似矩形脉冲的响 1． t r = 才有如图示， 2 ωC 过小， 应。如果 τ 过窄或 ωC 过小，则响应波形上升与下降时
ωc t sin[ωc (τ -t0 )] g(t) = ∫ h(τ )dτ = ∫ dτ -∞ ω ( − t ) −∞ π c τ 0 1 令 x = ωc (τ −t0 ), 则 dτ = dx ωc 当τ = −∞时， = −∞, 当τ = t 时 x = ωc (t −t0 ) x ,
t
ωc ω (t-t ) sinx 1 g(t ) = ∫ dx x ωc π -∞
c 0
sinx 1 ωc (t −t0 ) sinx = ∫ dx dx + ∫ π -∞ x π 0 x 1
0
sinx 1 ωc (t −t0 ) sinx g(t) = ∫ dx + ∫ dx π -∞ x π 0 x 1 1 ωc (t −t0 ) sinx = + ∫ dx 1 Sinx/x 2 π 0 x y sin x ∫0 x dx = Si( y) 3π π 2π 4π 0 ---- 正弦积分 Si(y) 1
§ 5.4 理想低通滤波器
• 主要内容
•理想低通的频域特性和冲激响应 理想低通的频域特性和冲激响应 •理想低通的阶跃响应 理想低通的阶跃响应 •理想低通对矩形脉冲的响应 理想低通对矩形脉冲的响应
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
主要内容 理想低通的频率特性 理想低通的冲激响应
理想低通的阶跃响应
理想低通对矩形脉冲的响应
重点 理想低通的频率特性
难点 理想低通的阶跃响应
BUPT EE
退出 开始
复习：解调
将已调信号恢复成原来的调制信号的过程。 g t f C ( t ) cos C t
f C (t )
r t
t
1
1 2
C
t0 tr
C
1 1 r t Si C t t 0 2
t
O
退出
r t
几点认识
1 1 2
C
t0 tr
C
t
O
1．上升时间：输出由最小值到最大值所经历的时间， 记作 t r ： 1 C
tr 2 C B
退出
t r 响应波形上升与下降时 间
C
t C 理想低通的截止角频率 C 大 ，r 则小 ， 总之，t r 与 C 成反比
3. 吉伯斯现象 (P281)：具有不连续点（跳变点）的波形 峰起值趋近于跳变值的9%左右，既有9%的上冲。改 变其他的“窗函数”（例如：升余弦类型）有可能消 除上冲。（窗函数：P293-294）
6 页
2．理想低通滤波器是个物理不可实现的非因果系统
原因：从h(t)看，t<0时已有值。
退出
关于物理可实现性§5-5有讨论，我们不要求，但大 家可以看一些近似理想低通滤波器的实例：图5-14所示。
v1 (t )
L
C
R
v2 (t )
L 时，且令 1 其幅频特性与相 当网络满足 R C C LC 频特性如图5-15。 t C 3 2 C 2 sin e C t 其冲激响应如（5-40）式： h( t ) 2 3
1
5 页
C
h(t )
t
c ht Sa c t t 0
t0
c
t
退出
第
几点认识
1．比较输入输出，可见严重失真； t 1信号频带无限宽，
而理想低通的通频带(系统频带)有限的 0 ~ c 当 t 经过理想低通时， c 以上的频率成分都衰 减为0,所以失真。 当时 c ， ( t ) ( t )，系统为全通网络，可以 h 无失真传输。
e1 t
12 页
r (t )
1
Si C (t t 0 )
O r1 t
1
t
Si C ( t t 0 )
1 2
O
t0
t0
t 0
2
退出
t
讨论
1 时，才有如图示，近似矩形脉冲的响 1． t r 2 C 应。如果 过窄或 C 过小，则响应波形上升与下降时 间连一起完全失去了激励信号的脉冲形象。 2 2. 最小值到最大值的时间 t r ：
相乘
理想低通 滤波器
f (t )
H ( )
cos C t
2
G ( )
m
A 4
O
m
A 2
2 C
m 0 m
2 C
退出
一. 理想低通滤波器的频率特性
H ( )
第 3 页
( )
C
C O
C
1 e jt0 H 0
1． 最大值位置： t 0 c
，最小值位置：t 0 c
B
2
fC
B是将角频率折合为频率的滤波器带宽（截止频率）。
2．阶跃响应的上升时间 t r 与网络的截止频率B（带宽） 成反比 B t r
e1 (t ) u(t ) u(t )
响应是从t=0开始，是一个可实现的网络，如图5-16。
退出
三. 理想低通的阶跃响应
激励
1 e( t ) = u( t ) j
1 e j t0 h( t ) H 0
第 8 页
系统
响应
c c
r ( t ) u( t ) h( t )
1 j t 0 (c c ) R e j 1 C 1 j t0 j t 1 r ( t ) F R( ) C ( ) j e e d 2 1 c 1 c e j t t0 e j t t0 d c c j d 令x t t0 2 2 1 2 c sin t t 0 1 1 c t t0 sin x d dx 0 2 2 2 0 x
c c
c 1 H ， c 0 即： t 0
C O
● C 为截止频率， 0 ~ c 称为理想低通滤波器的通频带，简称频带。 ● c在0 ~ c 的低频段内，传输信号无失真.( 只有时移t 0 )
退出
第
二. 理想低通的冲激响应
1
4 页
1 h( t ) H ( ) h( t ) F H ( ) H ( )e j t d 2 1 c j t 0 j t c1 e e d 2 1 c 1 1 j ( t t 0 ) C 1 e d e j t t0 C 2 c 2 j t t 0
退出
第
正弦积分
Si(y) =
9 页
0
y sinx
x
dx
sin x 1 x
1. 下限为0；
O
2
3 4
x
2. 奇偶性：奇函数。
3.最大值出现在 x ， 最小值出现在 x 。
Si y
2
O
y
2
退出
第
阶跃响应波形
u t
C
h(t )
10 页
c
t0
t
O
1 1 j C t t0 e e j C t t0 t t 0 2 j 1
c sin c t t 0 c Sa c t t 0 c t t 0
退出
第
波形
t