矩形和平行四边形
1.3_平行四边形、矩形、菱形、正方形的性质和判定(4)

P
3.已知正方形ABCD中对角线 AB、 CD相交于O. ①若E是AC上的点,过A作AG⊥BE 于G,AG、BD交于F.求证OE=OF.
A F
B D
O E G C
3.已知正方形ABCD中对角线 AB、CD 相交于O. ②若点E在 AC的延长线上,AG⊥EB 交EB的延长线于G,AG的延长线交BD D 的延长线于点F, A OE=OF还成立 O 吗?若成立, 请给予证明, G C 若不成立, B 请说出理由。 F E
O
3 5
4
F
2
B
1
E
C
(1)观察四边形OECF的面积与正 方形ABCD的面积有何关系? (2)如果将正方形A’B’C’D’换成 扇形OB’D’,满足什么条件时上述 的关系还成立吗? A D
O
F
D’
B
E
B’
C
3.如图,正方形ABCD中,E是 对角线BD上一点,过点E作 EF⊥ BC,EG⊥ CD,垂足为F、 G 。求证:AE=FG。
回顾思考
根据图形所具有的性质,在下表相应的空格中打 ”√”
平行四边 形 对边平行且相 等 四边都相等 矩形 菱形 正方形
√
√
√ √
√ √ √
四个角都是直 角
对角线互相平 分 对角线互相垂 直 对角线相等
√
√ √ √ √ √
√ √ √
4.如图,正方形ABCD,AB=4a,M为AB 的中点,ED=3AE。 (1)求ME的长。 (2)求证△EMC为直角三角形。
点拨矫正
如图,已知正方形ABCD,延长 AB到E,作AG⊥EC于G,AG交 BC于F, 求证:AF=CE。 1
2
才艺展示:
1.在正方形ABCD中,O是对角线AC、BD 的交点,过O作 OE⊥OF分别交AB、BC于 E、F,若AE=4,CF=3,则EF长为 . A D
矩形的性质和判定

矩形的性质和判定【知识梳理】一、定义:有一个是直角的平行四边形是矩形。
二、性质:①矩形的四个角都是直角②矩形的对角线相互平分且相等③矩形既是中心对称图形又是轴对称图形,有两条对称轴④矩形的面积S=长×宽三、判定:①有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形;④对角线相等且互相平分的四边形是矩形。
四、矩形与平行四边形的区别与联系:①相同点1、两组对边分别平行2、两组对边分别相等3、两组对角分别相等4、对角线相互平分②区别1、有一个角是直角的平行四边形矩形2、对角线相互平分且相等【例题精讲】考点1 矩形的性质【例1】已知:如图,在矩形ABCD中,BE=CF,求证:AF=DE。
【例2】如图,在矩形ABCD 中,,E F 分别是,BC AD 上的点,且BE DF =。
求证:ABE ∆≌CDF ∆。
【例3】如图,矩形ABCD 的两条对角线相交于点O ,60AOB ∠=︒,2AB =,则矩形的对角线AC 的长是( ) A .2 B .4 C .23 D .43【变式1】下列性质中,矩形具有而平行四边形不一定具有的是( ) A 、对边相等 B 、对角相等 C 、对角线相等 D 、对边平行【变式2】矩形ABCD 的对角线AC 、BD 交于O ,如果ABC ∆的周长比AOB ∆的周长大10cm ,则边AD 的长是 。
【变式3】如图,矩形ABCD 沿AE 折叠,使D 点落在BC 边上的F 点处,如果60BAF ∠=︒,则DAE ∠= 。
FED CBA考点2 矩形的判定【例4】如图,在△ABC 中,AB=AC ,D 为BC 中点,四边形ABDE 是平行四边形。
求证:四边形ADCE 是矩形。
【例5】如图,在平行四边形ABCD 中,E 是CD 的中点,△ABE 是等边三角形,求证:四边形ABCD 是矩形。
ODC BAD EFCAB【变式6】如图11,已知E 是ABCD 中BC 边的中点,连接AE 并延长AE 交DC 的延长线于点F 。
平行四边形菱形矩形正方形的易错点

平行四边形菱形矩形正方形的易错点平行四边形、菱形、矩形、正方形这些几何概念在初中数学中是非常重要的基础知识点。
然而,由于其相似的外观和特性,学生们常常容易混淆它们之间的区别和性质。
在这篇文章中,我们将介绍这些图形的易错点,以帮助学生们更好地理解它们。
首先,我们来看平行四边形。
平行四边形是一个具有两对平行边的四边形。
它的特点是对边平行且长度相等,相邻角的和为180°。
学生们常常容易将平行四边形和其他四边形混淆,例如矩形和菱形。
其次,菱形是一个特殊的平行四边形,具有以下特点:所有边都相等,对角线相互垂直且相等,对角线的交点称为菱心。
很多学生容易错误地认为菱形必定是矩形或正方形,这是一个常见的误解。
接下来,我们谈谈矩形。
矩形是一个具有四个直角的平行四边形,它的特点是所有角都是90°。
同样,学生们常常错把矩形当作正方形,因为它们都具备直角。
最后,我们来讨论正方形。
正方形是一个特殊的矩形,它具有以下特点:所有边相等,所有角都是90°,对角线相等且相互垂直。
尽管正方形的定义相对简单,但学生们在判断平行四边形、矩形和正方形时仍然容易出现困惑。
为了帮助学生们更好地区分这些图形,这里提供一些指导意义。
首先,要注意图形的边长和角度特征。
学生们可以通过测量边长和角度来判断一个图形到底是平行四边形、菱形、矩形还是正方形。
其次,要以图形的特征为准,而不是只凭直觉。
例如,如果一个图形具有所有边和角都相等的特点,那它就是一个正方形,而不是矩形或其他形状。
最后,多加练习和思考。
通过做一些练习题,学生们可以更好地理解和记忆这些图形的特性,避免出现混淆的情况。
总之,平行四边形、菱形、矩形和正方形是初中数学中非常基础的几何图形。
要正确理解和应用它们,学生们需要仔细观察它们的特点,并加以思考和实践。
希望这篇文章能帮助学生们更好地理解这些图形,并避免常见的易错点。
矩形

1 求证: BO = AC 2
证明: 延长BO至D,使OD=BO, 连结AD、DC. ∵AO=OC, BO=OD
A O
D
∴四边形ABCD是平行四边形. B ∵∠ABC=900 ∴ ABCD是矩形 1 1 ∴AC=BD ∴BO= 2 BD= 2 AC
C
定理:直角三角形斜边上的 中线等于斜边的一半。
A
∵∠ABC = ∠DCB = 90° 又∵AB = DC , BC = CB ∴△ABC≌△DCB ∴AC = BD
A
D
B
C
返回
矩形特殊的性质
从角上看:
矩形的四个角都是直角. 从对角线上看: 矩形的两条对角线相等.
矩形的特殊性质
矩形的四个角都是直角
A D
数学语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
A
O D
AB=CD AD=BC AC=BD 1 OA=OC=OB=OD= 1 AC= BD
相等的角:
∠AOB=∠DOC
2
2
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOD=∠BOC
B
C
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有: △OAB △ OBC △OCD △OAD 直角三角形有: Rt△ABC Rt△BCD Rt△CDA Rt△DAB 全等三角形有:
矩形的定义:
有一个角是直角的平行四边形是矩形
什么叫矩形?
定义:有一个角是直角的平行四边形叫矩
形。(rectangle)也叫长方形。
平行四边形
有一个角是直角
A
D
B
C
19[1].2.1矩形的判定
![19[1].2.1矩形的判定](https://img.taocdn.com/s3/m/38527b4e69eae009581bec6d.png)
3、下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形; (2)对角线互相平分且相等的四边形是矩形; (3)有一个角是直角的四边形是矩形; (4)有三个角都相等的四边形是矩形;
(5)有三个角是直角的四边形是矩形; (6)四个角都相等的四边形是矩形;
X
X X
(7)对角线相等,且有一个角是直角的四边形是矩形; X
若已知 ∠DOC=120°,AD=6㎝,则AC=
试一试
A
已知△ABC是Rt△,∠ABC=Rt∠, BD是斜边AC上的中线
B
D
┓
C
1 若BD=3㎝则AC=
6
㎝
2 若∠C=30°,AB=5㎝,则AC= BD= 5 ㎝,∠BDC=
10
㎝,
120°
情景引入
一位很有名望的木工师傅,招收了两名徒弟, 一天,师傅有事外出,两徒弟就自已在家练习用 两块四边形的废料各做了一扇矩形式的门,做完 之后,两人都说对方的门不是矩形,而自已 的是 矩形。
矩形的四个角都是直角; 矩形的对角线相等且平分;
A O D
对角线
直角三角形的性质定理:
B 直角三角形斜边上的中线等于斜边的一半.
在Rt△ABD中,AO是斜边BD的中线 则有:AO= 1 BD
2
试一试
• 四边形ABCD是矩形
D
O
C
1 若已知AB=8㎝,AD=6㎝,
则AC= 10 ㎝ OB=
A
B
5
㎝
2 若已知∠CAB=40°,则∠OCB= 50° ∠OBA= 4 40° ∠AOB= 100° ∠AOD= 80° 12 ㎝
(8)一组对角互补的平行四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
矩形的性质

O B C
D
4、如图,矩形ABCD中,AE平分∠BAD交BC于点E, ED=5cm,EC=3cm,求矩形的周长。 A D 解:∵四边形ABCD是矩形 ∴∠C=∠B=∠BAD=90°,AB=DC
∵DE=5,EC=3 2=DE2-EC2=52-32,即:DC=4 ∴DC C E B ∵AE平分∠BAD 注:解决矩形的有关问 ∴∠BAE=45° 题时,常根据性质转化 ∴AB=BE=4
解:依题意可知: ∠FAE=∠DCA=30 °,AF=AC ∴∠DAC=60 °, ∴∠FAC=90 °,
G
A
∴∠1=45 °, B ∴∠2=∠ACF-∠ACD=15 °
A
在 Rt ABC 中,∠ABC=900 , BO是斜边AC上的中线 O
D
B
1 1 1 OB=OD OB = OA=OC = 2 AC= 2 BD = AC 2
C
推论:直角三角形斜边上的中线等于 斜边的一半。
学有所得
A O B D
直角三角形的性质: 直角三角形斜边上的中线 等于斜边的一半.
C
即兴练一练: 已知一直角三角形两直角边分别为6和8,则其 5 斜边上的中线长为________.
A D
┓
B
C
学海
无涯
2.在 Rt ABC 中,斜边AC上的中线 和高分别是6cm和5cm,则 Rt ABC 的 面积S=( 30cm2 )。
A
D E
B
C
3、如图,矩形AEFG和矩形ADCB的大小、形状完全相同, 把它们拼成如图所示的L型图案,已知∠FAE=30°,分别 求∠1、∠2的度数。
F 1 E H D 2 C
证明二:∵四边形ABCD是矩形 2、矩形的对角线相等 °, AB=CD ∴ ∠ABC=∠DCB=90 2 2 2 2 2 2 AC AB BC , BD CD BC ∴ 注:矩形还含有平行四边形的所有性质 ∴AC=BD
精华总结:平行四边形、矩形、菱形、正方形知识点
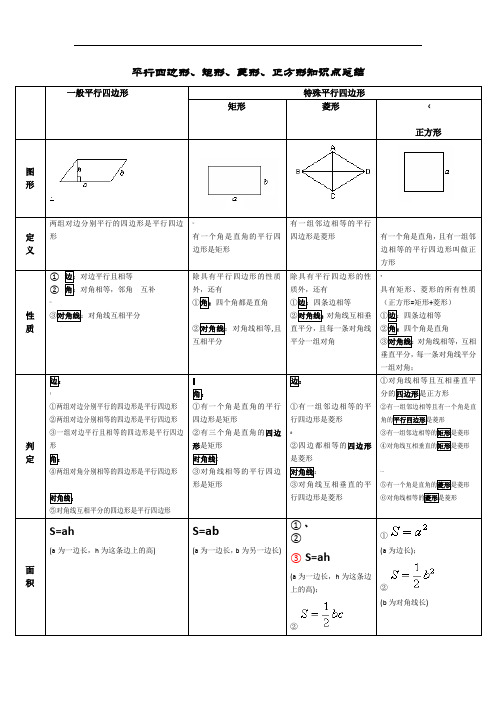
平行四边形、矩形、菱形、正方形知识点总结一般平行四边形特殊平行四边形矩形菱形(正方形图形·定义两组对边分别平行的四边形是平行四边形~有一个角是直角的平行四边形是矩形有一组邻边相等的平行四边形是菱形有一个角是直角,且有一组邻边相等的平行四边形叫做正方形性质①边:对边平行且相等②角:对角相等,邻角互补~③对角线:对角线互相平分除具有平行四边形的性质外,还有①角:四个角都是直角②对角线:对角线相等,且互相平分除具有平行四边形的性质外,还有①边:四条边相等②对角线:对角线互相垂直平分,且每一条对角线平分一组对角*具有矩形、菱形的所有性质(正方形=矩形+菱形)①边:四条边相等②角:四个角是直角③对角线:对角线相等,互相垂直平分,每一条对角线平分一组对角;判定边:!①两组对边分别平行的四边形是平行四边形②两组对边分别相等的四边形是平行四边形③一组对边平行且相等的四边形是平行四边形角:④两组对角分别相等的四边形是平行四边形对角线:⑤对角线互相平分的四边形是平行四边形;角:①有一个角是直角的平行四边形是矩形②有三个角是直角的四边形是矩形对角线:③对角线相等的平行四边形是矩形边:①有一组邻边相等的平行四边形是菱形#②四边都相等的四边形是菱形对角线:③对角线互相垂直的平行四边形是菱形①对角线相等且互相垂直平分的四边形是正方形②有一组邻边相等且有一个角是直角的平行四边形是菱形③有一组邻边相等的矩形是菱形④对角线互相垂直的矩形是菱形…⑤有一个角是直角的菱形是菱形⑥对角线相等的菱形是菱形面积S=ah(a为一边长,h为这条边上的高)S=ab(a为一边长,b为另一边长)①~②③S=ah(a为一边长,h为这条边上的高);②①(a为边长);②(b为对角线长)。
第1节 矩形的性质与判定(一)1

A
1
解析:根据对角线相等的平行四边
形是矩形;矩形的定义. 答案:① ④
D
B
2
C
2.如图,在△ABC中,AB=AC=8,AD是底边上的高,E为 AC的中点,则DE= .
解析: ∵四边形ABCD是矩形. ∴AC=BD,且
OA OC
A O
D
OA OD.
1 OB OD BD. 2
1 AC. 2
B
C
∵∠AOD=120°.
1800 1200 300. ∴∠ODA=∠OAD= 2
你认为例1还可以怎 么去解?
∵∠DAB=90°. ∴BD=2AB=2×2.5=5(cm).
解析:根据直角三角形斜边的中线
等于斜边的一半可得,DE等于AC的 一半,所以DE=4. 答案:4
4.已知:如图,四边形ABCD是由两个全等的正三角形ABD 和BCD组成的,M、N•分别为BC、AD的中点. 求证:四边形BMDN是矩形.
证明:在正三角形ABD和BCD中,M、N•分
别为BC、AD的中点. ∴BN⊥AD,DM⊥BC,∠DBC=60°,
∠BND=∠DMB=90°,∠NBD=30°.
∴∠NBM=90°. ∴四边形BMDN是矩形.
5、已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相 交于点O,∠AOD=120°,AB=2.5cm.求矩形对角线的长. 解:∵四边形ABCD是矩形. ∴AC=BD,且 OA OC AC. 2 1 OB OD BD. 2 ∴OA=OD. ∵∠AOD=120°.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
边
角
对角线 对角线互 相平分
对称性 中心对 称图形
平行四 边形
矩形
对边平行 对角相等 且相等 邻角互补
对边平行 四个角 对角线互相 中心对称图形 且相等 为直角 平分且相等 轴对称图形
O
这是矩形所 特有的性质
A
菱形的性质:
1、菱形的四条边相等
B
E
菱形
O
D
2、菱形的两条对角线互相垂直,
A
O
B
D C
4.四边形ABCD是菱形,O是两条对角线 的交点,AB=5cm,AO=4cm,求两条对角线 AC和BD 的长。
5.菱形的两条对角线的长分别 是6cm和8cm,求菱形的周长 和面积。
6.已知MN∥PQ,同旁内角的平分线AB、 BC和AD、CD分别相交于点B、D. (1)猜想AC和BD间的关系是______; (2)试用理由说明你的猜想.
C
并且每一条对角线平分一组对角。
3、菱形是轴对称图形,对角线所在的直 线是对称轴。 4、菱形的面积=底×高=对角线乘积 的一半
你能归纳矩形的几种判定方法吗?
方法1:
有一个角是直角的平行四边形是矩形。
方法2:
对角线相等的平行四边形是矩形 。
(对角线相等且互相平分的四边形是矩形。)
方法3:
有三个角是直角的四边形是矩形 。
如图,顺次连接矩形ABCD各边中点,得到 四边形EFGH,求证:四边形EFGH是菱形。
E
A
D
F B
G
G
C
作业
• 课本P103 第9题 • P120 第3 、 5题
小结
• 1.三角形中若有边的中点常用中位线试着解 决问题。 • 2.直角三角形中若有斜边的中点常找斜边上 的中线尝试解决问题。 • 3.菱形与矩形的性质与判定要多次画图进行 比较,才能区别开。
四条边都相等 四边形 菱形
平行四边形
填空:
1、矩形两边长是3和4,则矩形的对角线长为 5 ,面积为 12 。 2、Rt ABC中 ,两直角边分别为6和8,则斜边上的中线长为 5 。
3、矩形ABCD中,对角线AC、BD相交于O,∠AOB=600
AC=6,则AB= 3 ,BC= 3 , ∠ACB= 300 。
