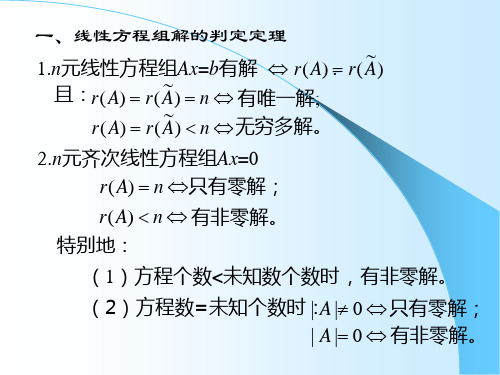
线性方程组解的关系
线性组合与线性相关
五、关于向量组线性相关性的主要结论
1.零向量是线性相关的,一个非零向量是线性无关的。 2.两个向量线性相关的充分条件是对应分量成比例。 3.含有零向量的向量组线性相关。 4.部分组线性相关,则整个向量组组线性相关;
向量组线性无关,则其部分组线性无关。 5. 线性无关向量组的“加长”向量组线性无关;
1 1 1
1 1 1
答案:1. A 1 2 3,| A | t 5 或 A 0 1 2
1 3 t
0 0 t 5
所以,t=5时线性相关,t≠5时线性无关。
2.t取任何值,向量组都线性相关。(4个3维向量)
即4可由1,2,3线性表示,
且表示方式不唯一。
对 A~ 继续施行初等行变换,
A~
1 1 2 2 1 1 2 2
0 2 1
5
0 1
1 2
5 2
1
0
3 2
1 2
0
1
1 2
5 2
0 0 0 0 0 0 0 0 0 0 0 0
最后一个矩阵对应的线性方程组为:
x1
x2
1
2 5
2
3
2 1
2
x3 x3
| A | 0 有非零解。
二、向量组的线性组合
1.线性表示:如果β=k11+k22+···+kss,则称β可由 1,2,···,s 线性表示,或称β是1,2,···,s 的线性组合。 2.β能由1,2,···,s线性表示的含义是线性方程组
x11+x22+···+xss=β
有解,其充要条件是 r(A)=r(A|β)
1,2,···,s,β线性相关 r(1,2,···,s ,β) <s+1 s= r(1,2,···,s)≤ r(1,2,···,s ,β) <s+1
线性方程组解的判定

1 / 3第四节 线性方程组解的判定从本节开始,讨论含有n 个未知量、m 个方程的线性方程组的解.11112211211222221122n n n n m m mn n ma x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ (13—2) 主要问题是要判断出方程组(13-2)何时有解?何时无解?有解时解有多少?如何求出方程组的解。
线性方程组有没有解,以及有怎样的解,完全决定于方程组的系数和常数项。
因此,将线性方程组写成矩阵形式或向量形式,以矩阵或向量作为讨论线性方程组的工具,将带来极大的方便。
方程组(13-2)中各未知量的系数组成的矩阵111212122212n n m m mn a a a a a a A a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦称为方程组(13-2)的系数矩阵.由各系数与常数项组成的矩阵,称为增广矩阵,记作A ,即11121121222212n n m m mn m a a a b a a a b A a a a b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦方程组(13-2)中的未知量组成一个n 行、1列的矩阵(或列向量),记作X ;常数项组成一个m 行、1列的矩阵(或列向量),记作b ,即12n x x X x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,12m b b b b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦由矩阵运算,方程组(13—2)实际上是如下关系111212122212n n m m mn a a a a a a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦12n x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=12m b b b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即 AX=b2 /3 如果令112111m a a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,122222m a a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,…,12n n n mn a a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦则方程组(13-2)的向量形式为1122n n a x a x a x b +++=定理1 (有解判定定理)方程级(13-2)有解的充分必要条件是:秩(A)=秩(A )推论1 线性方程组(13—2)有惟一的充分必要条件是r (A )=r(A )=n 。
线性方程组解的结构(重要知识)

3x5
令自由变量为任意实数
x1 2k1 k2 3k3
x2 x3
k1 4k2 5k3
x2 k1, x4 k2 , x5 k3
x4
k2
x5
k3
2
1
3
说明:
1
0ห้องสมุดไป่ตู้
0
1.基础解系不惟一
x
k1
0 0
k2
4 1
k3
-5 0
2.但所含向量的 个数唯一且等于n-R(A)
1
2
3
2
3 2
,2,
5 2
,3
T
0
通解为:X 2,3,4,5T k3,4,5,6T ,k R
-13-
例6
x
1
x1
x2 x2
x3 x3
x4 0, 3 x4 1,
x1 x2 2 x3 3 x4 1 2.
解
A~
1 1
1 1
1 1
1 3
0 1 1 0 1 1 2 1 0 0 1 2 1 2,
2.如果当非齐次线性方程组Ax 有无穷多解时,
其通解的结构如何?如何写出其向量形式的通解?
-2-
§4.1 线性方程组解的存在性定理
非齐次方程组解的判别定理
对于非齐次方程组 Amn x b(b 0)
(1) 有解 r( A) r( A~) 无解 r( A) r( A~)
(2) 有惟一解 r( A) r( A~) n (3) 有无限多解 r( A) r( A~) n 齐次方程组解的判别定理
(A)AX 0仅有零解,则AX b有唯一解
(B)AX 0有非零解,则AX b有无穷多解 (C)AX b有无穷多解,则AX 0仅有零解
高等代数3.6 线性方程组解的结构

又设 ( l1 , l2 , … , ln ) 是导出组 (1) 的一个解,即
n
aijl j 0 (i 1,2,, s) ,
j 1
显然
n
n
n
aij (k j l j ) aijk j aijl j
j 1
j 1
j 1
bi 0 bi (i 1,2,, s) .
推论 在非齐次线性方程组有解的条件下,解
是唯一的充分必要条件是它的导出组只有零解.
证明 充分性 如果方程组 (9) 有两个不同的
解,那么它的差就是导出组的一个非零解. 因此, 如果导出组只有零解,那么方程组有唯一解.
必要性 如果导出组有非零解,那么这个解 与方程组 (9) 的一个解 (因为它有解) 的和就是 (9) 的另一个解,也就是说,(9) 不止一个解. 因之, 如果方程 (9) 有唯一解,那么它的导出组只有零解.
x3 x3
4 3
, ,
x1 2 bx 2 x3 4 .
讨论方程组的解的情况与参数 a, b 的关系,有解时 求其解.
单击这里开始求解
三、直线平面间的位置关系的判断
平面和直线之间的位置关系是指平面与平面、 平面与直线、直线与直 线之间的位置关系. 由于 平面和直线在直角坐标系下的方程,是三元线性 方程 a1x1 + a2x2 + a3x3 = b 和两个三元线性方程组成 的方程组,因此,讨论它们之间的位置关系 ( 如平 行、重合、相交等 ),可用线性方程组的解的理论 阐明.
方程组 (9) 的解与它的导出组 (1) 的解之间有密 切的关系:
1) 线性方程组 (9) 的两个解的差是它的导出组 (1) 的解.
线性方程组解结构的几何意义

线性方程组解结构的几何意义
线性方程组解可以用几何方法表示,这有助于我们理解它的含义和推断它的结果。
几何意义中所讨论的线性方程组是多变量线性方程组,即不止两个变量。
首先,让我们来了解一下什么是多元线性方程组和什么是解:多变量线性方程组由若干(通常三个或以上)变量组成的一组多项式方程组,它的解是变量的一个有限点的集合,表示为(x,y,z)。
多元线性方程组的解,如下所示:
Ax+By+Cz=D
Ea+Fb+Gc=H
Ix +Jy +Kz=L
以上方程的解是几何意义的另一个概念,它表示一个特定的平面上的一个点集,由多个方程构成,每个方程提供了三个变量(x,y,z)的一个坐标。
这些坐标形成了一个平面上的点集,换句话说,线性方程组解的几何意义,就是一个三维空间中某一特定平面上某个特定点集,这种特定点集表示了线性方程组有多个解的几何意义。
以上给出的线性方程组的解的几何意义可以用图标表示:其中,A,B,C,D,E,F,G,H,I,J,K和L这12个常数分别在三个变量x,y,z上形成了一个解空间,即解的几何意义;而这个解空间中的每一个坐标点(x,y,z)都代表了一个解,也是线性方程组解的几何意义。
综上所述,我们可以发现,线性方程组的解的几何意义是比较清楚的:它是一个三维空间中的特定的平面上的特定的点集,这些点所代表的解就是线性方程组的解。
因此,我们可以用几何的角度更好地理解线性方程组的解的几何意义,从而推断它的结果。
2-3线性方程组有解的判定定理

组 Ax = 0 只有零解 ( 有非零解 )的充分必要 条件是系数行列式
定理 2 n 元非齐次线性方程组 Am×n x = b 有解 的充分必要条件是系数 矩阵 A 的秩等于增广矩 阵 B = ( A, b ) 的秩 .
证 设 A = (α 1 , α 2 , L , α n ), 这里 α 1 , α 2 , L , α n 是 A 的列向量组, 的列向量组,则 Ax = b 可写成 (4) x 1α 1 + x 2α 2 + L + x nα n = b .
5 1 0 − 2 − 1 2 2 1 3 r3 − r2 4 r1 − 2r2 4 0 1 2 0 1 2 3 r2 ÷ ( −3) 3 0 0 0 0 0 0 0 0 即得与原方程组同解的方程组
5 x1 − 2x3 − 3 x4 = 0, 4 x2 + 2x3 + x4 = 0, 3
L 从而方程组( 从而方程组( 2)有解 ⇔ b 可由 α 1 , α 2, , α n L 线性表示 ⇔ R ( A ) = rank (α 1 , α 2, , α n ) = 证毕 rank (α 1 , α 2, , α n, b ) = R ( B ). L
推论
Ax = b有唯一解 ⇔ R(A) = R(B ) = n Ax = b有无穷多解. ⇔ R(A) = R(B ) < n 有无穷多解.
三、线性方程组的求解
例1 求解齐次线性方程组 x1 + 2 x2 + x3 + x4 = 0 2 x1 + x2 − 2 x3 − 2 x4 = 0 . x − x − 4x − 3x = 0 1 2 3 4 解
经典:3-1线性方程组的同解变换

《线性代数》
返回
下页
结束
1.设 A 为 n 阶实矩阵,A T 是 A 的转置矩阵,
则对于线性方程组 (ⅰ)AX =O
(ⅱ) ATAX=O
必有( ). (A) (Ⅱ)的解是(Ⅰ)的解,(Ⅰ)的解也是(Ⅱ)的解; (B) (Ⅱ)的解是(Ⅰ)的解,但(Ⅰ)的解不是(Ⅱ)的解; (C) (Ⅰ)的解不是(Ⅱ)的解,(Ⅱ)的解也不是(Ⅰ)的解; (D) (Ⅰ)的解是(Ⅱ)的解,但(Ⅱ)的解不是(Ⅰ)的解.
0 1 0
-1 -2
0
11022.
(行最简形)
显然, R(A)=R(B)=2, 故方程组有解, 且有
xx31
=x2+x4+12 = 2x4+12
《线性代数》
返回
下页
结束
xx31
=x2+x4+12 = 2x4+12
x1 =1x2 +1x4 +1 2
xxx432
=1x2 = 0x2 = 0x2
+0x4 +2x4 +1x4
称xr+1, ···, xn为上述方程组的自由未知量, 令xr+1=c1, ···,
xn=cn–r, 可得方程组Ax = b的含有n–r个参数的解:
x1
- b11c1
- b c 1 , n - r n - r + d 1
=
xr
x r + 1
- br1c1 -
- b c r , n - r n - r + d r
+1
2
.
所以方程组的通解为:
x1 1 0 1 2
x2 x3 x4
线性方程组的解的性质与判定

线性方程组解的性质与判定在控制系统中的应用,可以用于分析系统的稳定性。 通过线性方程组解的性质与判定,可以确定控制系统的响应时间,优化控制效果。 在控制工程中,线性方程组解的性质与判定可以用于设计控制器,提高系统的性能指标。 在处理复杂控制系统时,线性方程组解的性质与判定能够提供有效的解决方案,简化计算过程。
逻辑回归模型:通过线性方程组解的判定条件,确定最佳分类边界,实现分类任务。
支持向量机:利用线性方程组解的性质与判定,找到支持向量,实现分类和回归任务。
决策树和随机森林:通过线性方程组解的判定条件,确定最佳划分标准,构建决策树和随机 森林模型。
PART FOUR
线性方程组解的性质与判定的研究历史 当前研究的主要方向和重点 近年来的重要研究成果和突破 未来研究展望和挑战
近年来的研究热 点和重点
在各个领域的应 用情况
未来研究的发展 趋势和展望
深入研究线性方程组解的性质与判定的关系,为实际应用提供更准确的数学模型。 探索更高效的算法和计算方法,提高线性方程组求解的效率和精度。 结合人工智能和大数据技术,对大规模线性方程组进行高效求解和优化。 拓展线性方程组解的性质与判定的应用领域,如物理、工程、经济等领域。
汇报人:XX
线性方程组解的 性质与判定可用 于数据清洗,识 别异常值和缺失 值。
在数据分析中, 线性方程组解的 性质与判定可用 于确定数据分布 和趋势。
在机器学习中, 线性方程组解的 性质与判定可用 于特征选择和降 维处理。
在数据预测中, 线性方程组解的 性质与判定可用 于建立预测模型 和优化算法。
线性回归模型:利用线性方程组解的性质与判定,确定最佳拟合直线,提高预测精度。
02
注意事项:在使用系数矩阵判定法时,需要注意 计算秩的正确性和准确性,以避免误判。
