9 强度理论
强度理论
M max ya 80103 N m 135103 m 122.7 MPa 6 4 Iz 8810 m
第9章 强度理论
9-1 强度理论概述
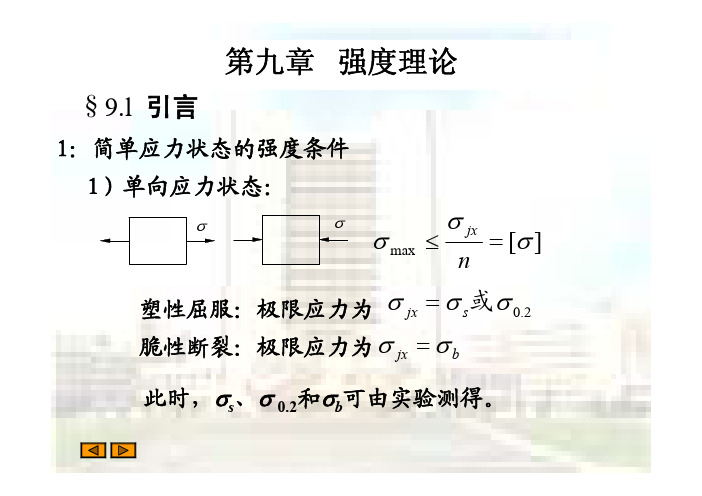
强度条件： max
[ ]
适用于单向应力状态，σmax为拉（压）杆横截面上 的正应力或梁横截面上的最大弯曲正应力。
max [ ]
适用于纯剪切应力状态，τmax为圆轴扭转时横截 面上的最大切应力或梁在横力弯曲时横截面上的 最大弯曲切应力。
[σ]或[τ]是由拉伸（或压缩）试验或纯剪切试验所
且相应的材料多为塑性材料；为避免在校核强度时
需先求主应力值等的麻烦，可直接利用图示应力状
Ⅱ.产生显著塑性变形而丧失工作能力的塑性屈服。
铸铁拉伸时沿试件的横截面断裂
铸铁圆轴扭转时沿与轴线约成 450的螺旋面断裂。 断裂与最大拉应力或最大拉应变有关，是拉应力 或拉应变过大所致。
低碳钢拉伸至屈服时，会出现与轴线约成450 的滑移线。
低碳钢圆轴扭转时沿纵横方向出现滑移线。
屈服或显著塑性变形是切应力过大所致。
2
2 0
3 2 27.7 MP a 2 2
2
由于梁的材料Q235钢为塑性材料，故用第三或第 四强度理论校核a点的强度。
r3 1 3 150.4 MPa 27.7 MPa 178.1 MPa
r4
1 1 2 2 2 3 2 3 1 2 2
材料力学强度理论
材料力学强度理论
材料力学强度理论是材料力学的一个重要分支，它研究材料在外力作用下的强
度和变形特性。
材料的强度是指材料抵抗破坏的能力，而变形特性则是指材料在外力作用下的形变行为。
强度理论的研究对于材料的设计、制备和应用具有重要意义。
首先，强度理论可以帮助我们了解材料的破坏机制。
材料在外力作用下会发生
破坏，而不同的材料在受力时表现出不同的破坏模式，比如拉伸、压缩、剪切等。
强度理论可以通过实验和理论分析，揭示材料在受力时的破坏机制，为材料的设计和选用提供依据。
其次，强度理论可以指导材料的合理使用。
在工程实践中，我们需要根据材料
的强度特性来选择合适的材料，并确定合理的使用条件。
强度理论可以帮助我们评估材料在特定工况下的承载能力，从而保证材料的安全可靠使用。
此外，强度理论还可以为材料的改进和优化提供指导。
通过对材料强度特性的
研究，我们可以发现材料的强度局限性，并提出改进的方案。
比如，可以通过合金化、热处理等手段来提高材料的强度，或者通过结构设计来减小应力集中，提高材料的抗破坏能力。
综上所述，材料力学强度理论是材料科学中的重要内容，它不仅可以帮助我们
了解材料的破坏机制，指导材料的合理使用，还可以为材料的改进和优化提供指导。
在未来的研究和工程实践中，我们需要进一步深入研究强度理论，不断提高材料的强度和可靠性，为社会发展和科技进步做出贡献。
材料力学第9章 强度理论
由于物体在外力作用下所发生的弹性变形既包括 物体的体积改变，也包括物体的形状改变，所以可推 断，弹性体内所积蓄的变形比能也应该分成两部分： 一部分是形状改变比能（畸变能） ，一部分是体积改 变比能 。 在复杂应力状态下，物体形状的改变及所积蓄的 形状改变比能是和三个主应力的差值有关；而物体体 积的改变及所积蓄的体积改变比能是和三个主应力的 代数和有关。
注意：图示应力状态实际上为弯扭组合加载对 应的应力状态，其相当应力如下：
r 3 2 4 2 [ ] 2 2 [ ] r 4 3
可记住，便于组合变形的强度校核。
例1 对于图示各单元体,试分别按第三强度理论及第四强度理论 求相当应力。
120 MPa 140 MPa
r4
1 2 2 2 [(0 120) ( 120 120) ( 120 0) ] 120MPa 2
140 MPa
（2）单元体（b）
σ1 140MPa
σ 2 110MPa
σ3 0
110 MPa
σr 3 σ1 σ 3 140MPa 1 2 2 2 σr 4 [30 110 ( 140) ] 128MPa 2
1u
1u
E
b
E
1 1 1 2 3 E
1u
1u
E
b
E
1 2 3 b
强度条件为： 1 2 3
b
n
[ ]
实验验证： a) 可解释大理石单压时的纵向裂缝； b) 脆性材料在双向拉伸-压缩应力状态下,且压应 力值超过拉应力值时,该理论与实验结果相符合。
σ1 94 .72MPa σ 3 5 .28MPa
工程力学第9章 应力状态与强度理论
27
根据广义胡克定律，有
解 （1）m-m 截面的内力为：
（2）m-m 截面上 K 点的应力为：
28
29
30
9.5 强度理论
9.5.1 强度理论的概念 在第7章中介绍了杆件在基本变形情况下的强度计 算，根据杆件横截面上的最大正应力或最大切应力及相 应的试验结果，建立了如下形式的强度条件：
31
32
33
（2）第二强度理论———最大伸长线应变理论
34
（3）第三强度理论———最大切应力理论
35
（4）第四强度理论———最大形状改变比能理论
36
37
（2）校核正应力强度
（3）校核切应力强度
38
（4）按第三强度理论校核 D 点的强度
39
思考题 9.1 某单元体上的应力情况如图9.18所示，已知 σx=σy。试求该点处垂直于纸面的任意斜截面上的正应力、 切应力及主应力，从而可得出什么结论？
6
9.2.1 方位角与应力分量的正负号约定 取平面单元体位于Oxy平面内，如图9.5（a）所示。 已知x面（外法线平行于x轴的面）上的应力σx及τxy，y 面上的应力σy及τyx。根据切应力互等定理，τxy=τyx。现 在为了确定与z轴平行的任意斜截面上的应力，需要首 先对方位角α以及各应力分量的正负号作如下约定：
10
11
9.2.3 平面应力状态下的主应力 与极值切应力由式（9.1）和式（9.2）可知，当σx， σy和τxy已知时，σα和τα将随α的不同而不同，即随斜截面 方位不同，截面上的应力也不同。因而有可能存在某种 方向面，其上之正应力为极值。设α=α0时，σα取极值。 由
12
13
14
15
16
材料力学第九章强度理论
本章重点
1. 强度理论的概念 2. 四种主要强度理论及其应用 3. 杆件强度的合理设计
§9-1 强度理论
一、强度理论的概念
轴向拉压、弯曲正应力 扭转、弯曲剪应力
m ax [ ]
m ax [ ]
材料破坏的形式主要有两类：
1、脆性断裂（断裂破坏） 2、塑性屈服（剪切破坏）
论没有考虑中间主应力σ2的影响，其带来的最大误 差不超过15％，而在大多数情况下远比此为小。 对三向均匀受拉时，塑性材料也会发生脆性断裂 破坏的事实无法解释。
2、形状改变能密度理论(第四强度理论) （畸变能密度） 假定：复杂应力状态下材料的形状改变能 密度达到单向拉伸时使材料屈服的形状改变 能密度时，材料即会发生屈服。 屈服破坏条件是：
相应地，强度理论也可分为两类： 一类是关于脆性断裂的强度理论； 一类是关于塑性屈服的强度理论。
（一）、关于脆断的强度理论
1、最大拉应力理论（第一强度理论）
假定：无论材料内各点的应力状态如何， 只要有一点的主应力σ1 达到单向拉伸断裂时的 极限应力σu，材料即破坏。 在单向拉伸时，极应变片贴于与母线成45°角的外表面上
1 ,
1
1 E 1
2
0,
3
1 ( 2 3 )
1 E m
m ax
m in
E
d
16
3
0
3
m
d E0
1 6 (1 )
杆件强度设计
关键：如何确定危险截面、危险点的位置 以及危险点的应力状态
材料失效的原因是应力、应变和变形能 等诸因素中的某一因素引起的。 无论是简单或复杂应力状态，引起失效 的因素是相同的。且应具有相同的失效基 准。 利用强度理论可由简单的应力状态的实 验结果，建立复杂应力状态的强度条件。
9_强度理论
3、塑性材料（除三轴拉伸外），宜采用形状改变比能理 论（第四强度理论）和最大剪应力理论（第三强度理论）。
4、三轴压缩状态下，无论是塑性和脆性材料，均采用形状
改变比能理论。
由强度理论可从 σ
推知 τ
3
σ 0.577σ τ 如纯剪时，由第四强度理论得：
二、应用举例 强度准则的统一形式： s r [s ]
强度理论
三、最大切应力理论（第三强度理论）
准则：无论在什么样的应力状态下，材料发生屈
服流动的原因都是单元体内的最大切应力tmax达到某 一共同的极限值tjx。 1.屈服原因：最大切应力tmax（与应力状态无关）； 2.屈服条件：
s1 s 3 s s
3.强度准则： s1 s 3 [s ] 4.应用情况：形式简单，符合实际，广泛应用，偏于安全。
滑移面上所产生的阻碍滑移的内摩擦力却取决于剪切面上 的正应力s的大小。
1. 摩尔理论适用于脆性剪断：
脆性剪断：在某些应力状态下，拉压强度不等的一些材 料也可能发生剪断，例如铸铁的压缩。
2.材料的剪断破坏发生在(tfs)值最大的截面上(这里f为内摩 擦系数)。
①在一定应力状态下，滑移面上为压应力时，滑移阻力增大； 为拉应力时，滑移阻力减小；
[s l ] s1 s [s l ] [s y ] 3
[sl]—拉伸许可应力；[sy]—压缩许可应力。如材料拉压许 用应力相同，则莫尔准则与最大剪应力准则相同。
t
t jx F( s n )
s
极限应力圆
纯剪切
t
拉伸
用单向拉伸、压 缩和纯剪切极限 应力圆作包络线 tjx=F(sn)
压缩
s
D2
形状改变比能理论
（二）塑性屈服理论
1.最大剪应力理论（第三强度理论） 无论材料处于什么应力状态，只要最 大剪应力达到极限值，就发生屈服破坏。 破坏原因：tmax 破坏条件: tmax = to
= s 强度条件: n 适用范围：塑性材料屈服破坏； 一般材料三向
s1 s 3
ss
材料力学
2.形状改变比能理论 (Mises’s Criterion)
第9章 强度理论
材料力学
本章主要内容
§9-1 强度理论的概念
§9-2 四个常用强度理论及其相当应力 §9-3 莫尔强度理论及其相当应力
§9-4 各种强度理论的适用范围及其应用
材料力学
§ 9-1 强度理论的概念
一、建立强度条件的复杂性 复杂应力状态的形式是无穷无尽的，建立 复杂应力状态下的强度条件，采用模拟的方法 几乎是不可能的，即逐一用试验的方法建立强 度条件是行不通的，需要从理论上找出路。
= s 2＋3t 2
材料力学
§9-3 莫尔强度理论 及其相当应力
莫尔强度理论是以各种状态下材料的破坏 试验结果为依据，而不是简单地假设材料地破 坏是由某一个因素达到了极限值而引起地，从 而建立起来的带有一定经验性的强度理论。
材料力学
一、两个概念：
1、极限应力圆：
t
ts
极限应力圆
s s3
O
s
材料力学
二、利用强度理论建立强度条件
（1）对破坏形式分类； （2）同一种形式的破坏，可以认为是由相同的原因造成的； （3）至于破坏的原因是什么，可由观察提出假说，这些假
说称为强度理论；
（4）利用简单拉伸实验建立强度条件。
材料力学
பைடு நூலகம்
§9-2 四个常用强度理论 及其相当应力
四种强度准则
1 3
理论能够很好的解释钢材 等塑性材料的屈服，形式 简单，机械工程中运用得 很广泛。
max
1 ( 1 3 ) u 2
选用单向拉伸实验来确定。
1
1 s max
2 3 0
2 3 0 s 1 ( 1 3 )
r3 1 3
1 r 4 [ (1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ] 2
强度理论的运用
• 温度、静载作用下，通常的脆性材料选用第一、二强 度理论；塑性材料选用第三、四强度理论。 • 破坏形式和应力状态有关，在特殊情况下要作特殊处
1) 最大拉应力是引起脆性断裂的主要因素。 2) 不管材料处于何种应力状态，只要最大拉应力达到 极限值，就会引起脆性断裂。 max u
1 u
无论什么应力状态，上述条件都成立。 选用单向拉伸实验来确定u:
1
1 b u b
2 3 0
2 3 0
选用单向拉伸实验的(uf)u来确定
1
2 3 0
(1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 2 s2
1 [( s ) 2 ( s ) 2 ] (u f ) u 1 6E [( 1 2 )2 ( 2 3 ) 2 ( 3 1 )2 ] [ ] 2 1 (u f ) u [2( s ) 2 ] 这种理论能够很好的解释钢材 6E
§9-10常用的四种强度理论
第一强度理论──最大拉应力理论（17世纪，伽利略） 第二强度理论──最大伸长线应变理论（17世纪，马里奥特）
第三强度理论──最大剪应力理论（1773年，库仑）
材料力学第9章应力分析强度理论
F
n
0
F 0
dA ( xydAcos ) sin ( x dAcos ) cos ( yxdAsin ) cos ( y dAsin ) sin 0
dA ( xydAcos ) cos ( x dAcos ) sin ( yxdAsin ) sin ( y dAsin ) cos 0
2
2 xy
xy
min
y
yx
23
⒉主方向
应力圆：D点顺时针转2α0到A1点
单元体：x轴顺时针转α0到主平面法线
证明：
xy 2 xy AD tg 2 0 CA x y x y 2
24
㈣利用应力圆求剪应力极值 应力圆上最高点、最低点的纵坐标值，为剪 应力的极大、极小值。 证明：
2
?
min
tg 2 0
2 xy
max
yx
x
x y
xy
解出两各极值点α0,α0=90+α0 最大、最小应力即为主应力
max x y x y 2 2 ( ) xy min 2 2
y
σmax、σmin为三个主应力中的两个。
11
讨论： ⑴若代数值σx≥σy，则α0、α0中，绝对值较小者是
σx与σmax之间夹角，且小于45。 ⑵若代数值 σx≤σy ，则α0 、α0 中，绝对值较小者是 σx 与 σmin之间夹角，且小于45。
min
max
yx
x
xy
12
y
㈢τmax、τmin(与z轴平行的任意斜截面上的)
强度理论Word
§10.5 强度理论一、 强度理论的概念强度理论是研究材料在复杂应力条件下强度失效的原因和失效条件的理论。
在前面的章节中，分别介绍了杆件在基本变形时的强度条件，如杆件在轴向拉、压时处于单向应力状态，其强度条件为[]max max N A σσ=≤式中许用应力[σ]是通过拉伸实验得出材料的极限应力再除以安全系数获得的。
圆轴扭转时，材料处于纯剪应力状态状态，其强度条件为[]max max t T W ττ=≤式中许用应力[τ]也是直接通过实验得出材料的极限应力再除以安全系数获得的。
梁横力弯曲时基于最大正应力作用点和基于最大切应力作用点的强度条件也是直接通过实验建立的。
但是，由于工程构件或元件所处的应力状态是多种多样的。
在复杂应力状态下，判断材料失效仅仅通过实验和这些简单应力状态下建立的强度条件是远远不够的。
人们在长期的生产实践中，综合分析材料强度的失效现象，提出了各种不同的假说。
各种假说尽管各有差异，但它们都认为：材料之所以按某种方式失效(屈服或断裂)，是由于应力、应变或应变能密度等诸因素中的某一因素引起的。
按照这种假说，无论单向或复杂应力状态，造成失效的原因是相同的。
所以可将简单应力状态的实验结果，与复杂应力状态的下材料的破坏联系起来，从而建立了强度理论。
二、 材料破坏的两种基本形式综合分析材料破坏现象，可以认为构件由于强度不足将引起两种破坏形式：（1）脆性断裂：材料破坏前无明显的塑性变形，断裂面粗糙，且多发生在最大正应力作用面上，如铸铁受拉和受扭时的破坏，均属于脆性断裂。
（2）塑性屈服（流动）：材料破坏前发生较大的塑性变形，破坏面较光滑，且多发生在最大剪应力作用面上，如低碳钢受拉和受扭时的破坏便属于这类破坏。
三、 工程中常用的几个强度理论1．最大拉应力理论(第一强度理论)该理论认为最大拉应力是引起断裂破坏的主要原因。
即认为不论材料处于简单应力状态还是复杂应力状态，引起材料破坏的原因是它的最大拉应力σ1达到某一极限值，材料就发生断裂。
九章强度理论PPT课件
变能密度达到极限值，就发生屈服破坏。
变形能：构件弹性变形储存的应变能。
应变能密度: 材料单位体积储存的变形能。 分为两部分：体积改变能密度vv 畸变能密度vd
只改变体积
只改变形状
畸变能密度
vd
=
1
6E
s1 -s 2 2 s 2 -s 3 2 s 3 -s1 2
2
2
sx
-s y
2
4t
2 xy
s = s x s y - 1 22
sx
-s y
2
4t
2 xy
s = 0
例题
主应力为
s1＝29.28MPa, s2＝3.72MPa, s3＝0
smax= s1< [st] = 30MPa
结论：满足强度条件。
23 11 10
MPa
例题
P
P=200kN
120 14
s3
强度条件:
s1
sb
n
= s
适用范围: 脆性材料拉、扭； 一般材料三向拉；
铸铁二向拉-拉，拉-压（st＞ sc）
45°
铸铁断口
s3=－t
45°
Kt
s1=t
拉断！
二、最大伸长线应变理论（17世纪末）
无论材料处于什么应力状态，只要最
大伸长线应变达到极限值，材料就发生脆
性断裂。
破坏原因：etmax （最大伸长线应变）
MPa
已知 ： 铸铁构件上 危险点的应力状态。 铸铁拉伸许用应力
[st] =30MPa。
求：试校核该点的 强度。
例题
解：首先根据材料 和应力状态确定失效 形式，选择强度理论。
材料力学第9章 强度理论
第一节 概述 在前面研究杆件基本变形的强度问题时，所用 的强度条件是以杆件横截面上的最大正应力，或最 大切应力为依据的，即
而材料的许用应力［σ］和［τ］是通过拉伸(压 缩)试验和剪切试验，测定出材料破坏时横截面上的 极限应力，然后除以适当的安全因数得到的。
1
解释材料破坏因素的一些假说是否正确，或适 用于什么情况．必须由实践来检验。实际上，也正 是在反复试验与实践的基础上，强度理论才逐步得 到发展并日趋完善。 下面介绍工程中关于各向同 性材料在常温、静载荷条件下几个常用的强度理论。
6
假设单向拉伸直到断裂时，仍可用胡克定律
由广义胡克定律，有
将式(b)、式(c)代入式(a)，该理论的脆性断裂 准则改写为
7
相应的强度条件为 最大伸长线应变理论也称为 第二强度理论。
8
二、关于屈服的强度理论 塑性破坏（plastic failure）一般是对塑性材料 而言的，破坏时，以出现屈服或产生显著的塑性变 形为标志。例如，低碳钢拉伸屈服时，出现与轴线 成45°的滑移线。这类破坏与最大切应力τmax、 畸变能密度有关。
12
于是屈服准则改写为
相应的强度条件为
13
对于梁来说，由于 三、第四强度理论的相当应力为
于是第
关于以上4个强度理论的应用，一般来说，如 铸铁、石料、混凝土、玻璃等脆性材料通常以脆断 方式破坏，宜选用第一和第二强度理论。如低碳钢、 铝、铜等塑性材料通常以屈服的方式失效，宜选用 第三和第四强度理论。
2
第二节 常用的强度理论 一、关于断裂的强度理论 脆性断裂（brittle fracture）一般是对脆性材 料而言，破坏时，材料没有明显的塑性变形，突然 断裂。例如，铸铁拉伸、扭转破坏。这类破坏与σ max（拉）、εmax（拉）有关。
材料力学填空与判断题解总括
F122-题132-题第 2 章 轴向拉伸与压缩二、填空题2-6 承受轴向拉压的杆件，只有在（加力端一定距离外）长度范围内变形才是均匀的。
2-7 根据强度条件][σσ≤可以进行（强度校核、设计截面、确定许可载荷）三方面的强度计算。
2-8 低碳钢材料由于冷作硬化，会使（比例极限）提高，而使（塑性）降低。
2-9 铸铁试件的压缩破坏和（切）应力有关。
2-10 构件由于截面的（形状、尺寸的突变）会发生应力集中现象。
三、选择题2-11 应用拉压正应力公式AN =σ的条件是（ B ）（A ）应力小于比极限；（B ）外力的合力沿杆轴线； （C ）应力小于弹性极限；（D ）应力小于屈服极限。
2-12 图示拉杆的外表面上有一斜线，当拉杆变形时，斜线将（ D ） （A ）平动；（B ）转动；（C ）不动；（D ）平动加转动。
2-13 图示四种材料的应力-应变曲线中，强度最大的是材料（A ），塑性最好的是材料（D ）。
2-14 图示三杆结构，欲使杆3的内力减小，应该（ B ）DC BA ζε（A ）增大杆3的横截面积； （B ）减小杆3的横截面积； （C ）减小杆1的横截面积； （D ）减小杆2的横截面积。
2-15 图示有缺陷的脆性材料拉杆中，应力集中最严重的是杆（ D ）二、填空题3-6 圆杆扭转时，根据（切应力互等定理），其纵向截面上也存在切应力。
3-7 铸铁圆杆发生扭转破坏的破断线如图所示，试画出圆杆所受外力偶的方向。
3-8 画出圆杆扭转时，两种截面的切应力分布图。
3-9 在计算圆柱形密围螺旋弹簧簧丝切应力时,考虑到(剪力引起的切应力及簧丝曲率的影响 ),而加以校正系数。
3-10 开口薄壁杆扭转时，截面上最大切应力发生在(最厚的矩形长边 )处；闭口薄壁杆扭转时,截面上最大切应力发生在( 最小厚度)处.TTF 123题24 F FF FFFF F（A ）（B ） （C ）（D ）第3章 扭转三,选择题3-11阶梯圆轴的最大切应力发生在( D ) (A) 扭矩最大的截面; (B)直径最小的截面; (C) 单位长度扭转角最大的截面; (D)不能确定.3-12 空心圆轴的外径为 D ，内径为 d ，D d /=α。
9. 土体强度理论
b
n j'
o 3' a c
△
n 1'
1 关闭排水阀门，围压下不固结；
2 关闭排水阀门，很快剪切破坏，在施加轴向应力差过程中不排水
十字板剪切试验
1）试验方法
一般适用于测定软粘土的不 排水强度指标；
钻孔到指定的土层，插入十 字形的探头；
通过施加的扭矩计算土的抗 剪强度
2）试验结果
Mmax M1 M 2
M1
பைடு நூலகம்
D/2
2
0
fh
2r rdr
对正常固结黏土 c'≈0
于是
f Ut tanj'
可见 Ut
f
土在固结过程中的总强度
ft 0
天然强度
强度增量
土的天然强度0 ：
一般正常固结黏土 0 ccu p0 tanjcu
ccu、jcu
为固结不
排水剪强
度指标
上覆有效压力
不排水剪切强度
软黏土 超固结土
0 cu S 0 ccu pc tanjcu
4.土的强度和土体破坏关系
（1）土体达到屈服不一定达到破坏 在土体中，局部土体达到强度极限，不一定引起土体的破坏
部分土体达到强度 极限（屈服），地 基并不一定破坏。
塑性区
（2）土体通常是渐进破坏，特殊应力 条件下出现崩塌、断裂
5.土体破坏的判别标准
（1）土体破坏定义：应力-应变过程的最后阶段，这时微小 的应力增量将会引起很大的，或者不可控制的应变增量
土的抗剪强度理论
一、土体破坏与强度理论基本理论
1. 强度公式、破坏准则—莫尔-库仑准则
库仑公式
f = c + tgj
强度理论课件
第三强度理论考虑了等效应力和等效应变的影响，认为当材料受到的等效应力或等效应变超过其等效 应力或等效应变极限时，材料会发生断裂。这种理论适用于各种类型的材料，包括脆性和塑性材料。
第四强度理论
总结词
基于形状改变比能或最大剪切应变能，当材料受到的形状改变比能或剪切应变能超过其形状改变比能极限或剪切 应变能极限时，材料发生断裂。
详细描述
第四强度理论考虑了形状改变比能和剪切应变能的影响，认为当材料受到的形状改变比能或剪切应变能超过其形 状改变比能极限或剪切应变能极限时，材料会发生断裂。这种理论适用于各种类型的材料，包括脆性和塑性材料 。
03
强度理论的计算方法
弹性力学方法
弹性力学是研究弹性物体在外力作用下的应力、应变和位移 的学科。在强度理论中，弹性力学方法通过建立物体的应力应变关系，推导出强度准则，用于评估结构在不同外力作用 下的稳定性。
非线性或复杂环境下的应用还存在局限性。
参数确定困难
02
强度理论中的一些参数，如材料的弹性模量、屈服强度等，在
实际应用中往往难以准确测定。
忽略微观结构影响
03
强度理论通常基于宏观尺度，忽略了材料的微观结构和缺陷对
强度的影响。
强度理论的发展趋势
多尺度分析
随着计算技术的发展，强度理论正朝着多尺度方向发展，以综合考 虑微观、细观和宏观尺度对材料强度的影响。
弹性力学方法基于连续介质力学的基本原理，通过求解微分 方程或积分方程来获得物体的应力分布和位移场，进而分析 结构的强度和稳定性。
有限元方法
有限元方法是数值分析中的一种方法，通过将连续的物体 离散化为有限个小的单元（如三角形、四边形等），然后 对每个单元进行求解，最后将所有单元的解组合起来得到 整个物体的解。
强度理论资料
强度理论在生活中，我们经常会面对各种挑战和压力，而对于这些挑战和压力，不同的人会有不同的应对方式。
有些人可能会崩溃，有些人则能够坚持下去，甚至在面对困难时能更加努力地前行。
为什么会出现这样的差异呢？这就涉及到了强度理论的概念。
强度理论是一种心理学理论，试图解释个体在面对压力和挑战时的应对方式。
根据这一理论，个体的应对方式取决于他们对特定事件的认知评估，以及其应对资源的充足程度。
具体而言，强度理论认为，个体对一个事件产生情绪反应的强度是由两个因素决定的：一是对事件的认知评估，即个体对事件的看法和意义；二是对事件的应对资源，即个体能够动用的资源和技能。
在强度理论中，认知评估被认为是一个重要的因素。
个体对事件的认知评估会影响他们对事件产生情绪反应的方式。
如果一个人对某个事件感到无力和绝望，他可能会产生消极情绪，导致他选择逃避或放弃。
相反，如果一个人对事件持有积极的态度和信念，他可能会更有动力去面对挑战，从而更有可能成功应对困难。
另一个影响个体应对方式的因素是应对资源。
应对资源包括个体的心理、情绪、社会和物质资源，以及他们的应对技能和经验。
当个体拥有足够的应对资源时，他们会更有信心应对挑战，并能够更有效地管理压力。
相反，如果个体的应对资源匮乏，他们可能会感到不知所措，难以有效地处理挑战。
强度理论的一个重要观点是，应对挑战和压力不仅取决于事件本身的性质，还取决于个体对事件的认知评估和应对资源。
因此，培养积极的心态和增强应对资源对于个体有效地面对挑战和压力至关重要。
只有通过提升自身的认知水平、增加应对资源，个体才能更好地应对各种困难和挑战，取得成功。
总的来说，强度理论为我们提供了一种理解个体在应对挑战和压力时的心理过程的框架。
通过认知评估和应对资源的角度，我们可以更好地理解个体在面对困难时的表现，为个体提供更好的支持和帮助。
强度理论的研究不仅有助于我们更好地理解个体的内心世界，也为我们提供了应对挑战和压力的有效途径。
四个强度理论的相当应力表达式
pD ≈ = 90 MPa 4t
( 因为 t «D , 所以 A Dt )
包含直径的纵向截面上的应力
用两个横截面 mm , nn 从圆筒部分 取出
单位长的圆筒研究。
m n
p
m
1
n
由截面法，假想地用 直径平面将取出的单 位长度的圆筒分成两 部分。取下半部分为 研究对象。 包含直径 直径平面
的纵向平
23
11 10
x y
22 2 x yFra bibliotek 2 2 x
29.8MPa 3.72 MPa
(单位 MPa)
1 29.28MPa， 2 3.72MPa， 3 0
1 29.28MPa 30MPa
某结构上危险点处的应力状态如图所示，其中σ＝ 116.7MPa，τ＝46.3MPa。材料为钢，许用应力［σ］＝ 160MPa。试校核此结构是否安全。
1
r3 1 3
rM
c
t
3
在大多数应力状态下,脆性材料将发生脆性断裂.因而应选用 第一强度理论;而在大多数应力状态下,塑性材料将发生屈服和剪 断.故应选用第三强度理论或第四强度理论.但材料的破坏形式不 仅取决于材料的力学行为,而且与所处的应力状态,温度和加载速 度有关.实验表明,塑性材料在一定的条件下低温和三向拉伸,会 表现为脆性断裂.脆性材料在三向受压表现为塑性屈服.
§ 10 - 5 各种强度理论的适用范围及其应用
1、 在三向拉伸应力状态下，会脆断破坏，无论是
脆性或塑性材料，均宜采用最大拉应力理论。 2、对于塑性材料如低C钢，除三轴拉应力状态以外的
复杂应力状态下，都会发生屈服现象，可采用第三、 第四强度理论。
第九章：复杂应力状态及强度理论
杆在周向截面上没有应力。又由切应力互等定理可知， 杆在径向截面上 B 点处应该有与相等的切应力。于是 此单元体各侧面上的应力如图.
第一节：应力状态概念
三、主平面、主应力、应力状态的分类
主单元体：在一般情况下，表示一点处应力状态的应力单元体在其各个表面上同时 存在有正应力和切应力。但是可以证明：在该点处以不同方式截取的各个单元体中， 必有一个特殊的单元体，在这个单元体的侧面上只有正应力而没有切应力。这样的 单元体称为该点处的主应力单元体或主单元体。
sin 2 cos 2
当 450 时， max
当 00 时， max
低碳钢试件扭转破坏是被剪断的，且其抗剪能力低于其抗拉能力。 铸铁试件扭转破坏是被拉断的，且其抗拉能力低于其抗剪能力。
第二节：二向应力状态分析
例 9-3 图示单元体，x =100MPa，x = – 20MPa， y =30MPa。试求：1） =40º的斜截面上的 和 ；2）确定 A 点处的max、max 和它们所在的
由单向应力状态胡克定律可知：主应力 1、 2和 3 单独作用时，分别对 应的纵向线应变为1/E、2/E和 3/E；令横向变形系数 ，则主应力 2 将引起 1 方向相应的线应变为 – 2 /E；其它同理。故 1 由1 的纵向线 应变与 2、3 分别引起的 1 方向相应的横向线应变三项叠加而成。
主应力表示的 广义胡克定律
第三节：三向应力状态分析
第三节：三向应力状态分析
复杂应力状态下一点处的最大应力 1、一点处的最大正应力
设一点处的主应力单元体如图 a 所示，研究证明，当主应力按 1 2 3
排列时，则有
max 1
min 3
第三节：三向应力状态分析
2、一点处的最大切应力
如何理解理论力学中的强度理论？
如何理解理论力学中的强度理论？在理论力学的广袤领域中，强度理论宛如一座坚固的基石，为工程结构的设计和分析提供了关键的指导。
然而，对于许多初学者来说，理解强度理论并非易事。
那么，究竟如何才能真正理解这一重要的概念呢？要理解强度理论，首先得明白它在工程中的重要地位。
强度理论实际上是用来预测材料在复杂应力状态下是否会发生失效的准则。
在实际的工程应用中，材料往往不是只承受单一方向的简单应力，而是处于多种应力同时作用的复杂状态。
比如，机械零件可能同时受到拉伸、压缩、剪切等多种应力的影响。
这时候，强度理论就派上了用场，它能够帮助工程师判断材料在这样的复杂应力环境下是否能够安全可靠地工作。
让我们先来了解一下常见的几种强度理论。
第一个是最大拉应力理论，也称为第一强度理论。
这个理论认为，无论材料处于何种复杂应力状态，只要最大拉应力达到材料在简单拉伸试验中的极限拉应力，材料就会发生断裂。
简单来说，就是把复杂应力状态简化为只考虑最大拉应力的作用。
这个理论对于脆性材料，比如铸铁，在拉伸时的失效预测比较准确。
接下来是最大伸长线应变理论，也就是第二强度理论。
它指出，无论应力状态如何复杂，只要最大伸长线应变达到材料在简单拉伸试验中的极限伸长线应变，材料就会失效。
这个理论适用于脆性材料在受压时的失效分析。
然后是最大切应力理论，又称第三强度理论。
该理论认为，材料的屈服是由最大切应力引起的。
只要最大切应力达到材料在简单拉伸屈服时的最大切应力值，材料就会发生屈服。
对于塑性材料，这个理论在很多情况下能给出较为准确的预测。
最后是形状改变比能理论，即第四强度理论。
它认为，材料的屈服是由形状改变比能引起的。
当形状改变比能达到材料在简单拉伸屈服时的形状改变比能值，材料就会屈服。
这个理论在对塑性材料的屈服预测方面也有较好的表现。
那么，如何在实际中应用这些强度理论呢？以一个简单的例子来说明。
假设我们要设计一个承受多种应力的机械零件，首先需要确定零件所承受的应力状态，通过计算得出各个方向的应力大小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北京林业大学
BEIJING FORESTRY UNIVERSITY
●1997年7月12日，浙江常山县城南开发区一幢5 层住宅楼突然发生中部坍塌，整栋楼内39人中 仅3人幸存
●1994年，青海沟后水库大坝垮塌，淹死下游居 民近300人，失踪几十人 ●1995年12月，四川德阳旌湖开发区一栋7层综 合楼倒塌，造成17人死亡
例1 直径为d=0.1m的铸铁圆杆受力 T=7kNm, P=50kN
[]=40MPa, 用第一强度理论校核强度
T 解：危险点A的应力状态如图 A T
A A
P
P
P 4 50 103 6.37MPa A 0.12
T 16 7000 35.7MPa 3 Wn 0.1
塑性屈服与脆性断裂
北京林业大学
BEIJING FORESTRY UNIVERSITY
POINT LOADS
DISTRIBUTED LOADS
• Hydrostatic Loading
P
• Pressure Vessels • Aerodynamic Wing Loading
P
P(x)
北京林业大学
BEIJING FORESTRY UNIVERSIБайду номын сангаасY
三、关于塑性屈服的强度理论
1、最大剪应力准则（第三强度理论）
强度条件 ：
1 3
s
ns
北京林业大学
BEIJING FORESTRY UNIVERSITY
2、形状改变比能准则（第四强度理论）
强度条件 ：
1 ( 1 2 )2 ( 2 3 )2 ( 3 1 )2 s 2 ns
1
2
( ) 2 2
2
2
6.37 6.37 2 ( ) 35.7 2 39 MPa 32 2 2
1 39 MPa , 2 0, 3 32 MPa 1 安全
例 薄壁圆筒受最大内压时, 测得x=1.8810-4
y=7.3710-4, 用第三强度理论校核其强度
北京林业大学
BEIJING FORESTRY UNIVERSITY
内容提要
研究对象: 受力杆件内危险点处的微立方体 单元。 研究内容: 研究目的: 强度理论的建立和相应的强度条件。 用强度理论校核复杂应力状态的强 度。
北京林业大学
BEIJING FORESTRY UNIVERSITY
一、建立强度理论的基本思想
1 183.1MPa , 2 94.4 MPa , 3 0
1 3 183.1
3
r 3 183.1170 7.70 0 170
所以，此容器不满足第三强度理论, 不安全
北京林业大学
BEIJING FORESTRY UNIVERSITY
BEIJING FORESTRY UNIVERSITY
北京林业大学
BEIJING FORESTRY UNIVERSITY
二、关于脆性断裂的强度理论
1、最大拉应力准则（第一强度理论）
强度条件 ：
1
b
nb
北京林业大学
BEIJING FORESTRY UNIVERSITY
2、最大伸长线应变准则（第二强度理论）
“豆腐渣”工程触目惊心 ●1999年1月4日，长200米的重庆綦江彩虹桥垮塌，死
36人，多人受伤失踪
●1998年8月7日，号称“固若金汤”的九江长江大堤发 生 决堤， 事后调查， 大堤里面根本没有钢筋。 朱总理 怒斥为“王八蛋”工程
●1996年初，投资43亿、我国铁路建设史上规模最大的 北京西客站投入使用后，几乎所有的站台都经过封闭 式返修。天篷玻璃、办公大厅和行包房更是大小毛病 不断
北京林业大学
BEIJING FORESTRY UNIVERSITY
●1996年11月底，总投资 3200万元的 210国道改道工程 完工，仅过了两个月，还未交付使用的西延公路就沿 山段就变成翻浆路，路面凸凹不平、柏油不知去向
●1996年8月初，耗资2000万元的南京长江大桥 路面修补完工，专家称10年内无需大修。只 过了2年，此桥又进行了全面维修 ●1998年10月，沈哈高速公路清阳河大桥出现坍 塌，造成 2人死亡、5人重伤 ●1997年3月25日，福建莆田江口镇新光电子有 限公司一栋职工宿舍楼倒塌，死亡35人、重伤 上百人
北京林业大学
BEIJING FORESTRY UNIVERSITY
四、强度理论的应用
1、选用原则
2、题例
结论：
1）对于中、低强度钢，相应断裂韧度较高，允许临界裂纹长度较长， 因而对中、小型零件不会出现裂纹导致的脆断问题，主要考虑常规 强度问题（应用经典强度理论）。 2）对于高强、超高强钢，如果相应断裂韧度较低，允许临界裂纹 长度很短，除应进行常规强度校核外，必须严格检查与控制内含裂 纹长度，利用 断裂准则进行安全校核，因而对结构材料，高强度不 是追求的唯一目标，还应提高其断裂韧性。
( E = 210GPa, [] = 170MPa, = 0.3 ) 解：由广义虎克定律得
A
y
x
E 2.1 x 2 ( x y ) (1.880.37.37)107 94.4MPa 1 10.32
E 2.1 y 2 ( y x ) (7.370.31.88)107 183.1MPa 1 10.32
强度条件 ：
1 ( 2 3 ) b
nb
北京林业大学
Failure and Damage
BEIJING FORESTRY UNIVERSITY
北京林业大学
Failure and Damage
BEIJING FORESTRY UNIVERSITY
北京林业大学