关于最短路问题的一个简明表格处理法
[管理学]最短路问题
![[管理学]最短路问题](https://img.taocdn.com/s3/m/53ce6a346c175f0e7cd1376c.png)
最短路的子路也是最短路。
思想:将D=(V,A,W)中vs到所有其它顶点的最短
路按其路长从小到大排列为: u0≤ u1 ≤ u2 ≤…≤ un
u0表示vs到自身的长度,相应最短路记为: P0,P1,P2,…,Pn,P1一定只有一条弧。 记X 0 v s , X 0 V \ X 0 , 则
例 用Dijkstra算法求前面例子中从v1到各点的最短路。
v2
6
1 2 6
v5
4 3 10 2
2
v9
6
4
3
v1
1
3
v3
2
v8
v4
10
v6
v7
解:u1=0,u2=6,u3=3,u4=1,u5=u6=u7=u8=u9=+ ,
j=1 (j=2,3,…,9)
X0={v1} ,X0={v2,v3,…,v9}
。设
步骤2 若m+1=n-1,结束。若m+1<n-1,置m=m+1,转步骤1
v2
1
2 5 3 -4
v3
2 3 l(v1)=0, l(vj)=1 (j=2,3,4,5)
v4
u1
(1)
v1
u2 u3
( 2) (1) ( 2) (1)
v5
u 2 w22 1, u 2 w23 3, u5 w54 6, u3 w35 1, u 2 w22 1, u3
uj(m) =
算法步骤:
步骤0 令 l(v1)=0,l(vj)=1(2 j n); m=1,u1(m)=0,uj(m)=w1j (2 j n)。
uk (m) + wkj 步骤1 对于一切2 j n,计算 min 1 k n
最短路问题(整理版)

最短路问题(short-path problem)若网络中的每条边都有一个权值值(长度、成本、时间等),则找出两节点(通常是源节点与结束点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题,我们通常归属为三类:单源最短路径问题(确定起点或确定终点的最短路径问题)、确定起点终点的最短路径问题(两节点之间的最短路径)1、Dijkstra算法:用邻接矩阵a表示带权有向图,d为从v0出发到图上其余各顶点可能达到的最短路径长度值,以v0为起点做一次dijkstra,便可以求出从结点v0到其他结点的最短路径长度代码:procedure dijkstra(v0:longint);//v0为起点做一次dijkstrabegin//a数组是邻接矩阵,a[i,j]表示i到j的距离,无边就为maxlongintfor i:=1 to n do d[i]:=a[v0,i];//初始化d数组(用于记录从v0到结点i的最短路径), fillchar(visit,sizeof(visit),false);//每个结点都未被连接到路径里visit[v0]:=true;//已经连接v0结点for i:=1 to n-1 do//剩下n-1个节点未加入路径里;beginmin:=maxlongint;//初始化minfor j:=1 to n do//找从v0开始到目前为止,哪个结点作为下一个连接起点(*可优化) if (not visit[j]) and (min>d[j]) then//结点k要未被连接进去且最小begin min:=d[j];k:=j;end;visit[k]:=true;//连接进去for j:=1 to n do//刷新数组d,通过k来更新到达未连接进去的节点最小值,if (not visit[j]) and (d[j]>d[k]+a[k,j]) then d[j]:=a[k,j]+d[k];end;writeln(d[n]);//结点v0到结点n的最短路。
管理运筹学 第7章 最短路实例
8
§4 最大流问题
• 最大流问题:给一个带收发点的网络,其每条弧的赋权称之为容量, 在不超过每条弧的容量的前提下,求出从发点到收点的最大流量。 一、最大流的数学模型 例6 某石油公司拥有一个管道网络,使用这个网络可以把石油从采地 运送到一些销售点,这个网络的一部分如下图所示。由于管道的直径 的变化,它的各段管道(vi,vj)的流量cij(容量)也是不一样的。cij的 单位为万加仑/小时。如果使用这个网络系统从采地 v1向销地 v7运送石 油,问每小时能运送多少加仑石油?
2 0 0
2 0 2 1
3 v6 4
3 01
2
v7
3 5
3 1 v4
第五次迭代:选择路为v1 v2 v3 v5 v7 。弧( v2 , v3 )的顺流容 量为2,决定了pf=2,改进的网络流量图如下图:
1 v2 0 5 2 3 0 0 2 3 v5 2 0 0 0
管 理 运 筹 学
15
20
v1 1
3
(a)
图11-12
管 理 运
(b)
筹 学
(c)
5
§3 最小生成树问题
一、求解最小生成树的破圈算法 算法的步骤:
1、在给定的赋权的连通图上任找一个圈。
2、在所找的圈中去掉一个权数最大的边(如果有两条或两条 以上的边都是权数最大的边,则任意去掉其中一条)。
3、如果所余下的图已不包含圈,则计算结束,所余下的图即 为最小生成树,否则返回第1步。
§2 最短路问题
例 设备更新问题。某公司使用一台设备,在每年年初,公司就要 决定是购买新的设备还是继续使用旧设备。如果购置新设备,就要支 付一定的购置费,当然新设备的维修费用就低。如果继续使用旧设备, 可以省去购置费,但维修费用就高了。请设计一个五年之内的更新设 备的计划,使得五年内购置费用和维修费用总的支付费用最小。 已知:设备每年年初的价格表
运筹学最短路问题excel求解

Microsoft Excel 11.0 运算结果报告工作表 [20103848李园园.xls]Sheet1报告的建立: 2003-1-19 6:23:54目标单元格 (最小值)单元格名字初值终值$E$13V7010可变单元格单元格名字初值终值$D$2V2 路径00$D$3V5 路径01$D$4V7 路径00$D$5V5 路径00$D$6V2 路径00$D$7V6 路径00$D$8V3 路径00$D$9V8 路径00$D$10V6 路径01$D$11V8 路径01$D$12V5 路径00$D$13V7 路径00约束单元格名字单元格值公式状态型数值$G$2V1 网络流1$G$2>=$H$2到达限制值0 $G$3V2 网络流0$G$3=$H$3未到限制值0 $G$4V3 网络流0$G$4=$H$4未到限制值0 $G$5V4 网络流0$G$5=$H$5未到限制值0 $G$6V5 网络流0$G$6=$H$6未到限制值0 $G$7V6 网络流0$G$7=$H$7未到限制值0 $G$8V7 网络流0$G$8=$H$8未到限制值0 $D$2V2 路径0$D$2=二进制到达限制值0 $D$3V5 路径1$D$3=二进制到达限制值0 $D$4V7 路径0$D$4=二进制到达限制值0 $D$5V5 路径0$D$5=二进制到达限制值0 $D$6V2 路径0$D$6=二进制到达限制值0 $D$7V6 路径0$D$7=二进制到达限制值0 $D$8V3 路径0$D$8=二进制到达限制值0 $D$9V8 路径0$D$9=二进制到达限制值0 $D$10V6 路径1$D$10=二进制到达限制值0 $D$11V8 路径1$D$11=二进制到达限制值0 $D$12V5 路径0$D$12=二进制到达限制值0 $D$13V7 路径0$D$13=二进制到达限制值0。
excel最短路问题求解模型
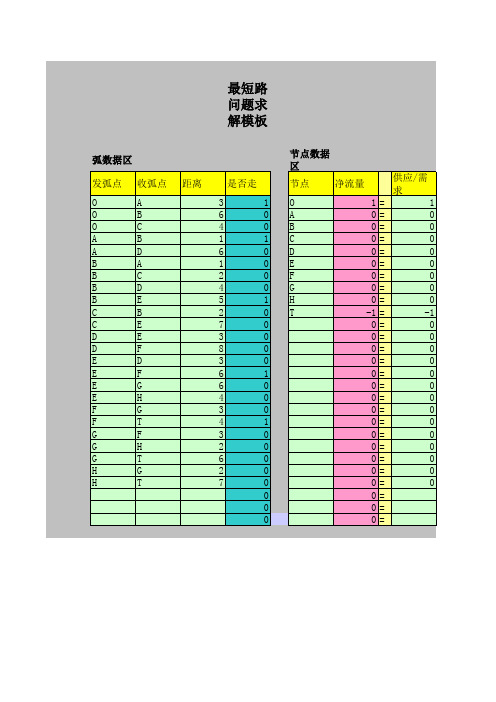
最短路问题求解模板需要对发弧点、收 弧点、距离、节点(节点名称字符随便,但 必须与发弧点和收弧点一致)和供应/需求 栏数据的录入,这里要求供应/需求栏数据 发点为‘1’,收点为“-1”,其余为‘0’。 录完数据,点“工具”→“规划求 解”→“求解”后,在“是否走”栏显示最 优解、“净流量”栏显示相应的约束条件实 际值,最优值显示在N6单元格。 注:使用本模板时,模板中的浅灰色区 域是录入数据的区域;黄色区域是标示区, 尽量不要修改;深浅灰色区域是系统显示最 优解数据的区域,也尽量不要修改;红色区 域中都录有公式,禁止往这些单元格中录入 数据。
最短路问题求解模板
弧数据区 发弧点 O O O A A B B B B C C D D E E E E F F G G G H H 收弧点 A B C B D A C D E B E E F D F G H G T F H T G T 距离 3 6 4 1 6 1 2 4 5 2 7 3 8 3 6 6 4 3 4 3 2 6 2 7 是否走 1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 节点数据区 节点 净流量 O 1 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 T -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 = = = = = = = = = = = = = = = = = = = = = = = = = = = 供应/需求 1 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
最短路问题

最短路问题何谓最短路?最短路问题考虑的是有向网络N=(V,A,W),其中弧(i,j)∈A 对应的权又称为弧长或费用。
对于其中的两个顶点s,t∈V,以s 为起点,t 为终点的有向路称为s-t 有向路,其所经过的所有弧上的权(或弧长、费用)之和称为该有向路的权(或弧长、费用)。
所有s-t 有向路中权最小的一条称为s-t 最短路。
ij w 如何得到最短路?最短路问题的线性规划描述如下:(,)m i ni j i j i j A w x ∈∑ (1):(,):(,)1,,..1,,0,,ij ji j i j A j j i A i s s t x x s i s t ∈∈=⎧⎪t −=−=⎨⎪≠⎩∑∑ (2) 0ij x ≥ (3) 其中决策变量表示弧(i,j)是否位于s-t 路上:当=1时,表示弧(i,j)位于s-t 路上,当=0时,表示弧(i,j)不在s-t 路上。
本来,应当是0-1变量,但由于约束(2)的约束矩阵就是网络的关联矩阵,它是全幺模矩阵,因此0-1变量可以松弛为区间[0,1]中的实数(当用单纯形法求解时,将得到0-1整数解)。
ij x ij x ij x ij x 值得注意的是,我们这里将变量直接松弛为所有非负实数。
实际上,如果可以取0-1以外的整数,则约束条件并不能保证对应于非零的弧所构成的结构(记为P)一定是一条路,因为这一结构可能含有圈。
进一步分析,我们总是假设网络本身不含有负圈,而任何正圈不可能使目标函数最小,因此上面的约束条件(2),(3)可以保证当达到最优解时,P 如果包含圈,该圈一定是零圈,我们从P 中去掉所有的零圈,就可以得到最短路。
ij x ij x ij x 无圈网络与正费用网络一般采用标号设定算法。
Bellman 方程(最短路方程)将约束条件(2)两边同时乘以-1,得到其对偶问题为:m ax()t s u u − (4)..,(,)j i ij s t u u w i j A −≤∀∈ (5)根据互补松弛条件,当x 和u 分别为原问题和对偶问题的最优解时:()0,(,i j j i i j )x u u w i j −−=∀∈A (6) 因此,当某弧(i,j)位于最短路上时,即对应的变量>0时,一定有ij x j i i u u w −=j 。
第三节 最短路问题

作业
195页
习题8
8.4题
( X , X ) { (V1 ,V4 ) ,(V2 ,V4 ) ,(V5 ,V4 ) ,(V5 ,V9 )} 1、 2、K14 K 24 8 K54 5 3 8 K59 1 3 4
3、 (V5 ,V9 ) V9 ( 4 ,
5)
第五轮: V1 (0,0) V2 (2,1) V5 (3,2) V9 (4,5) V7 (7,9) 1、 ( X , X ) { (V1 ,V4 ) ,(V2 ,V4 ) ,(V5 ,V4 ),(V9 ,V6 ),(V9 ,V7 ),(V9 ,V8 )} 2、 K14 K24 K54 8 3、 (V9 ,V7 ) V7 ( 7 ,
V1
(i , i )
V2
5
7
1
V4
6
2 2
V3
1
V5
第三步: 找出第二步中 K ij 最小的那条弧,给它的终 点以标号
(V1 ,V3 ) V3 (2,1)
8
如果有几个 K ij 都取最小值,就同时标号
以后每一轮都重复第二轮的三个步骤, 从而使某个顶点获得标号; 当终点获得标号后,计算结束; 然后逆向追踪获得最短路.
( X , X ) { (V1 ,V4 ) ,(V2 ,V4 ) ,(V5 ,V4 ) ,(V5 ,V9 )} 1、 2、K14 K 24 8 K54 3 5 8 K59 3 1 4
3、 (V5 ,V9 ) V9 ( 4 ,
5)
第三轮: V1 (0,0) V2 (2,1) V5 (3,2)
9)
1)
V4 (8,1) V1 V2 (2,1) V5 (3,2) V9 (4,5) V7 (7,9) V6 (10,9)
最短路(图)

最短路最短路问题(short-path problem):若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点(通常是源节点和阱节点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
单源最短路径包括确定起点的最短路径问题,确定终点的最短路径问题(与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。
在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
)算法可以采用Dijkstra 算法。
Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra 算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法代码1#include <string.h>2#include<algorithm>3using namespace std;45const int maxnum = 100;6const int maxint = 99999999;78int dist[maxnum];9int prev[maxnum];//记录当前点的前一个结点10int c[maxnum][maxnum];11int n,line;1213void dijkstra(int n,int v,int *dist,int *prev,int c[maxnum][maxnum])//v代表源点14{15 bool s[maxnum];//判断是否已存入该点到S中16 for(int i = 1;i <= n;++i)17 {18 dist[i] = c[v][i];19 s[i] = 0;20 if(dist[i] == maxint)//代表当前点与源点没有直接相连21 prev[i] = 0;22 else23 prev[i] = v;//代表当前点的前一个节点是v,即源点24 }25 dist[v] = 0;//源点到源点的距离初始化为026 s[v] = 1;//源点已被遍历过,标记为12728 for(int i = 2;i <= n;++i)29 {30 int tmp = maxint;31 int u = v;32 for(int j = 1;j <= n;++j)33 {34 if((!s[j]) && dist[j] <tmp)//该点没有被遍历到并且源点到j点的距离小于记录的距离35 {36u = j;//记录下这一点37tmp = dist[j];//记录下这一点到源点的距离38 }39 }40 //找到距离最短的点退出循环41 s[u] = 1;//标记该点已经遍历过4243 for(int j = 1;j <= n;++j)44 {45 if((!s[j]) && c[u][j] <maxint)//j没有被遍历过并且从u到j还有这条路径46 {47 int newdist = dist[u] + c[u][j];//新的距离是从源点到u的距离加上从u到的距离48 if(newdist <dist[j])//如果新的距离比原来到j的距离要短49 {50 dist[j] = newdist;//则更新dist数组51 prev[j] = u;//标记j的前一个节点是u52 }53 }54 }55 }56}5758void searchpath(int *prev,int v,int u)//查找从v到u的最短路径59{60 int que[maxnum];//保存路径61 int tot = 1;62 que[tot] = u;//把终点存入路径数组63 tot++;64 int tmp = prev[u];65 while(tmp != v)66 {67 que[tot] = tmp;68 tot++;69tmp = prev[tmp];70 }71 que[tot] = v;72 for(int i = tot;i >= 1;--i)73 {74 if(i != 1)75 printf("%d->",que[i]);76 else77 printf("%d\n",que[i]);78 }79}808182int main()83{84 scanf("%d",&n);//输入结点数85 scanf("%d",&line);//输入路径数目86 int p,q,len;87 for(int i = 1;i <= n;++i)//初始化存储数组88 {89 for(int j = 1;j <= n;++j)90 {91 c[i][j] = maxint;92 }93 }94 for(int i = 1;i <= line;++i)//往存储数组里存放路径95 {96 scanf("%d%d%d",&p,&q,&len);97 if(len <c[p][q])//如果两个点之间有多条路,取路径较短的那一条98 c[p][q] = len;99 c[q][p] = len;//该语句根据实际情况写,用于无向路径中100 }101 for(int i = 1;i <= n;++i)//初始化标记数组102 dist[i] = maxint;//该数组记录从起点到该点的最短路径长度103104105 dijkstra(n,1,dist,prev,c);106 printf("从源点到最后一个顶点的最短路径长度为:%d\n",dist[n]);107 printf("从源点到最后一个顶点的路径为:");108 searchpath(prev,1,n);109}全局最短路求图中所有的最短路径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 引言
最短 路问题 是运 筹学中 的一 个重 要研究 对象 , 它在工程 技术、 企业 管理、 工农业 生产以及军事等 方 面有着 广泛的应用。关于最短路 问题的求解方法 也 很多 , 但它们都有一 些不令人满意的地 方 , 如有的 方 法 简捷 明 了 , 但适 用范 围 狭窄 , 有 的 方法 适用 范 围 广 , 但缺乏直观性和 易操作性 , 从 而解决一般的最 短 路问题对于普通人来说是较辛苦的。为此 , 作者通过 研究 , 得 到了一种 适用 范围广 泛、 直观 性强、 操作 简 便的处 理最短路问题的方 法。下 面将通过处理具 体 问题来介绍此法。
5
→○ L → , 其长度为 a1 ) 。 下 面 列表计 算 f k ( i ) , 当 计算 出 f 4 ( i ) 或 尚未 计 算 到 f 4 ( i ) 但出 现了 ( 2. 2) 中的现 象即终止计 算。有 关 结果将 展现于 表中〈 对于在 计算过 程中无 须知 道 的数 据和本 来就没 有的数 据 , 在 下表 相应位 置我 们 以“ - ” 表示 , 若某 f k ( i ) 的结果 被填为 “ - ” , 则表 示 当 步数不 超过 K 时 , 从第 i 城 沿公 路无法 到达 第 5 城〉 。 Cij S 5 2 25 25 25 25 T ! ∀
第 11 卷第 2 期 达县师范高等专科学校学报( 自然科学版) 2001 年 6 月 Vol. 11 No. 2 Journal of Daxian Teachers Coll ege ( Natural Science Edition) Jun. 2001
关于最短路问题的一个简明表格处理法
图 中有向边 ( Ui , U j ) 上的 一数据 C i j 为该边的 长 度。 求结 点 U 1 到 其它各 结点的 最短 有向路 径及 其 长度。 解 以 f k ( i ) 表从 U 1 到 Ui 的步数 不超过 K 的 所 有通路中最短路径 的长度。令 U ( i ) = { j U j 到 Ui 存在有向边 } , 则有迭代公式如下
f k + 1 ( i ) = min { C j i + f k ( j ) }
j ∈U ( i ) j ≠i
k 为正整数 , i ∈ { 2,
f k ( 1) = 0 3, 4, 5, 6} 约定 若 f 1 ( i ) = a , 则记 f 1 ( i ) = a 1 i ∈ { 2, 3, 4, 5, 6} , 若 f k ( i ) = C j ′ ) = a ( k 为不小于 2 的 i + f k -1 ( j ′ 整数 ) , 则记 f k ( i ) = aj ′ i ∈ { 2, 3, 4, 5, 6} ( 它表示从 U 1 到 U i 的步 数不超过 K 的所有通路 中最短路 径的长 度为 a 且该路径的最后一步为从 Uj ′ 到 U i ( 简记为 U i ← Uj ′ ) > , 其它 有关约定参见问题 I 。 下 面列表 计算 f k ( i ) , 当计 算出 f 5 ( i ) 或尚 未计 算到 f 5 ( i ) 但 对其 正整数 n 出 现了 f n+ 1 ( i ) = f n ( i ) , 有关结果将展现于 i ∈ { 2, 3, 4, 5, 6} 时即终止计算。 表中 Ci j Vi U2 U3 U4 U5 U6 f 1( j ) f 2( j ) f 3( j ) f 4( j ) Uj U1 3 2 5 0 0 0 0 U2 U3 2 1 7 31 21 31 21 31 21 31 21 ( 表Ⅱ ) U4 5 51 33 33 33 U5 5 3 1 U6 102, 4 84 84
陈熙德
( 四川省畜牧兽医学院 基础部 , 重庆 荣昌 402460)
【 摘 要】 给出了求解短路问题的一类迭代公式和具 体求解时的一种简明的表格处理方法。 【 关键词】 最短路径 ; 迭代公式 ; 表格方法 [ 中图分类号 ] O 22 [ 文献标识码 ] A [ 文章编号 ] 1008- 4886( 2001) 02- 0005- 02 i 城 和第 j 城间 的 边表 这两 城 间的 最短 直 通公 路 , ( 若某两 城间无 边 , 则 表该两 城间无 直通公 路 ) 无向 i ,○ j ] 上的 数据 C i j 表第 i 城与第 j 城 间最 边[ ○ 短直通公路的长度 ( i , j ∈ { 1, 2, 3, 4, 5} ) 。 求第 1, 2, 3, 4 城分别到 第 5 城的最短 公路路径 及其长度。 解 设 f k ( i ) 表从第 i 城到达第 5 城的步 数不超 过 K 的 所有通路 ( 沿公路 ) 中最短路径的长度。U( i ) i ○ j = { j 结点 ○ 与间有边 } , 则有迭代公式如下 f k + 1 ( i ) = min { C ij + f k ( j ) } j ∈U ( i ) j ≠i K 为正整数 , i ∈ f k ( 5) = 0 { 1, 2, 3, 4} 由题设和上式易知 ( 2. 1) f 4 ( i ) 必为第 i 城到 第 5 城 的最短 公路 路径 的长度 ( 因为 只有 5 个城且最 短路 径中不 含回 路 ) i ∈ { 1, 2, 3, 4} 。 ( 2. 2) 若对 某 正整 数 K , 出 现了 f k + 1 ( i ) = f k ( i ) , i ∈ { 1, 2, 3, 4} , 则必 有 f k ( i ) = f 4 ( i ) , 从而 f k ( i ) 必为第 i 城到第 5 城的最短公路路径的长度。 符号约定 若 f 1 ( i ) = a , 则记 f 1 ( i ) = a 5 , i 1, 2, 3, 4, 若 f k+ 1 ( i ) = C in + f k ( n ) = a < k 为正整数且 k ≥ 1> 则记 f k+ 1 ( i ) = a n , i = 1, 2, 3, 4 ( 它表 f ( k+ 1) ( i ) = a 且表 示从第 i 城 到第 5 城步数不超过 k+ 1 的最 短公 路路 径的第 1 步 为从第 i 城到第 n 城 〈 简 记为 i ○ i 表第 i 个城市 ( i = 1, 2, 3, 4, 5) , 第 图中 结点 ○ n 〉 →○ 。易 知 , 若 f k ( i ) = a j 1 , f k - 1 ( j 1 ) = aj22 , …… , f k - L ( j L ) = a 5 L + 1 , 则从第 i 城到第 5 城的步数不 i →○ j 1 →○ j 2 →…… 超过 K 的最短公 路路径为 ○
注 表中 f 2 ( 6) = 102, 4 表示 f 2 ( 6) = 102 或 f 2 ( 6) = 10 4 由表Ⅱ知 U1 到 U 2 的最 短路 径为 U 2 ← U 1 其长 度为 f 3 ( 2) = 3 。 U1 到 U 3 的最 短路 径为 U 3 ← U 1 其长 度为 f 3 ( 3) = 2 。 U1 到 U 4 的最短路径为 U 4 ← U3 ←U 1 其长度为 f 3 ( 4) = 3 U1 到 U5 无通路。 U1 到 U 6 的最短 路径为 U6 ← U4 ← U 3 ← U 1 其长 度为 f 3 ( 6) = 8 上面 , 我们通 过两 类问 题介绍 了求 解最短 路问 题的简 明表格 处理方 法 , 虽 然我们 所讨 论的问 题中 边上的 权均为 正数 , 但这种 方法对 边上 带负权 的图 仍然成立 , 限于篇幅 , 此处不再举例。
A N ote of W idth on the Limited Convex Body
Yang L u Xu Dan
Abstract : A g eomet ry inequality on the w idt h and vo lume o f the limited convex body is obtained as its application, t he w idth of sphere is m aximal in co nvex bodies that have so me vo lume Key words: lim ited co nvex body; widty ; g emoet ry inequality
A Simple Chart M ethod to Find the M inim um Pat h
Chen Xide
Abstract : T his paper offer s some it erat ive fo rmulae and a sim ple cha rt met ho d t o find the minimum path . Key words: minimum path; iterat ive fo rm ulae; char t method
5 2 2 1 5 7 1 1 5 5 1 3 f 1( j ) 75 55 35 0 f 2( j ) 63 44 35 0 3 4 5 f 3( j ) 5 4 3 0 f 4( j ) 53 44 35 0 ( 表Ⅰ ) 说明 : A 、 f 1 ( j ) 之值直接根据所给图填出。 B、 对每个正整数 K , f ( 5) 之值为 0。 对不小 于 2 的正 整数 K , f ( j ) < j ∈ k { 1, 2, C、 j 所在 行的数据与下半 表 3, 4} > 之值 为上半表中 ○ j 中 f k- 1 ( j ) 所 在行 的 对 应 数据 之 和 的 最小 值 ( 若 ○ 所 在行的 各元与 f k- 1 ( j ) 所在行 的每 组对应 元中 均 至少有一元为“ - ” , 则 f k ( j ) 的结果填为“ - ” )。 由表Ⅰ知 第 1 城到 第 5 城的最短公路路 径为 → 其 长 度为 f 3 ( 1) = 2 第 2 城到 第 5 城的最短公路路 径为 → → → 其长度为 f 3 ( 2) = 5 第 3 城到 第 5 城的最短公路路 径为 → → 其长度为 f 3 ( 3) = 4 第 4 城到 第 5 城的最短公路路 径为 → 其 长 度为 f 3 ( 4) = 3 问题Ⅱ 有一网络图如下
