第5章 无源网络综合(一端口综合)

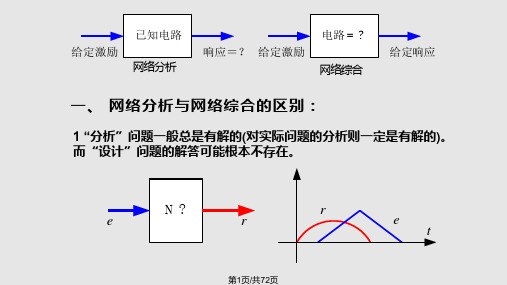
第五章 无源网络综合§5.1 网络分析与网络综合网络分析网络综合（a ） (b)图5.1 网络分析与网络综合网络综合：研究科学的数学的设计方法。

网络分析与网络综合的区别：1 “分析”问题一般总是有解的(对实际问题的分析则一定是有解的)。

而“设计”问题的解答可能根本不存在。

-V 5.0+图5.2 网络综合解答不存在情况一W 5.21.05.0W 125.0412L 2max==<=⨯=PP(a) (b)图5.3 网络综合解答不存在情况二2“分析”问题一般具有唯一解，而“设计”问题通常有几个等效的解。

-+-V 4+V 4+---V4+(a) (b) (c)图5.4 网络综合存在多解情况3“分析”的方法较少，“综合”的方法较多。

网络综合的主要步骤：(1) 按照给定的要求确定一个和实现的逼近函数。

(2) 寻找一个具有上述逼近函数的电路。

§5.2 网络的有源性和无源性输入一端口网络N 的功率()()()p t v t i t =从任何初始时刻0t 到t ，该网络的总能量0()()()()d tt W t W t v i τττ=+⎰式中0()W t 为在初始时刻0t 时该一端口储存的能量。

若对所有0t 以及所有时间0t t ≥，有()0,(),()W t v t i t ≥∀ （1）则此一端口N 为无源的。

如果一端口不是无源的，达就是有源的。

就是说，当且仅当对某个激励和某一初始值0t 以及某一时间0t t ≥，有()0W t <，则此一端口就是有源的。

换句话说，如果一个一端口是有源的，就一定能找到某一激励以及至少某一时间t ，式（1）对这个一端口不能成立。

在以上有关无源性的定义中必须计及初始储存能量0()W t 。

例如，对时不变的线性电容，设它的电容值为C ，则有0()00()22200()()()()()111()()()()222tv t t v t W t W t v i d W t C vdvW t Cv t Cv t Cv t τττ=+=+=+-=⎰⎰式中2001()()2W t Cv t =。

所以0C >时，电容元件为无源的，而当0C <时（线性负电容），则为有源的。

但是，如不计及式中的初始能量项，则22011()()()22W t Cv t Cv t =-()W t 为从0t 到t 输入网络的能量。

这样即使0C >，()W t 在某些时间将小于零。

事实上充电的电容有可能向外释放储存的能量，但是计及初始能量，它不可能释放多余原先储存的能量。

为了考虑这种情况，引入了有关“无损性”的概念。

设一端口的所有(),()v t i t 从0t →∞为“平方可积”，即有：2(),tt v t dt <∞⎰2()tt i t dt <∞⎰如果对任何初始时间0t ，下式成立0()()()()d 0tt W t W t v i τττ=+=⎰式中0()W t 为在初始时刻0t 时该一端口储存的能量，则称此一端口为无损网络。

以上关于()v t 和()i t 平方可积的条件，也即()()()()0v v i i ∞=-∞=∞=-∞=就是说，一端口在t =∞和t =-∞时均为松弛的。

假设一端口在t =-∞时无任何存储能量，则无源性可按下式定义()()()d 0tW t v i τττ-∞=≥⎰(),(),v t i t t ∀≥-∞ （2）以上关于有源性的定义可以推广到N 端口。

如果全部端口的电压电流允许信号对是真实的，且对所有t ，输入端口的总能量为非负的，则此N 端口为无源的，即对全部t ≥-∞，有()()()d 0tT W t v i τττ-∞=≥⎰这里设t =-∞时，()0,()0-∞=-∞=v i 。

如果对某些信号对，且对某些t >-∞，有()()()d 0tT W t v i τττ-∞=<⎰则此N 为有源的。

如果对所有平方可积有限值允许信号对，有()()()d 0tT W t v i τττ-∞==⎰则称此N 端口为无损的。

一个无损的N 端口将最终把输入端口的能量全部返回。

线性（正）电阻元件、电容元件、电感元件均为无源元件。

例如，对二端电阻，按式（2）有2()()()d ()t tW t v i Ri d τττττ-∞-∞==⎰⎰可见，只要0R >，对所有t ，()W t 总是非负的。

同理，对于非零的()v t 和()i t ，()W t 将是t 的单调非递减正值函数，因此当t =∞时，()W t 不可能是零值，所以线性电阻是无源的、非无损的。

线性负电阻、负电感、负电容是有源元件。

对于理想变压器，有112200v i n i n v ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦按式（1－25）1122()[()()()()]d 0tW t v i v i τττττ-∞=+=⎰所以理想变压器是无源的且是无损的。

练习：讨论回转器和负阻抗变换器的有源性和无源性。

回转器：112200v i r v r i -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，负阻抗变换器：112200v i k i k v ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦§5.3归一化和去归一化归一化定义：用一些合适的系数(常数)按比例换算所有电量，而不改变电路性质。

例如，用50作为电阻的换算系数(归一化常数)，则Ω75=R (实际值)变成Ω515075./==N R (归一化值)。

归一化值、实际值、归一化常数之间的关系)()()(0s Z s Z s Z N =，)()()(0s Y s Y s Y N =，0R R R N =，0L L L N =，0C CC N = 0T T T N =，0f f f N =，0ωωω=N ，0s s s N = 对实际值适用的物理关系，对归一化值网络应保持不变，因此得)()(s Y s Z 1=)()(s Y s Z N N 1=)()(s Z s 001=:Y R s Z =)(N N R s Z =)()(s Z 00=:R :L sL s Z =)(N N L s s Z =)(N )(s Z L 000=:C sCs Z 1=)(N N N C s s Z 1=)()(s Z C 0001=:f T f 1=NN T f 1=01T f =:ωfπω2=N N f πω2=00f =ωωσj s +=:s NN N j s ωσ+=000ωσ==s 实际值归一化值化常数共七个关系式。

综上得知，只有两个独立的归一化常数，若选择多于两个，则有可能破坏电量之间的关系。

通常选择0Z 和0f 。

此时000000000000000111Z Y f s f T f Z C f Z L Z R /,,/),/(,/,=======ω 【例】图5.5(a)所示电路归一化电压转移函数为2212++==N N NN N N s s ss U s U s H )()()( 中心角频率为2。

(1) 如要求中心频率为10kHz ，求网络函数。

(2) 如固定Ω1=R ，求L ，C 。

(3) 如固定C=0.1µF,求R ，L 。

2(a) (b)图5.5 归一化例题图【解】：(1) 频率归一化常数为4400010442942102⨯=⨯===.πωs f将0s ss N =代入已知的)(N s H 得： 94242002012109479.3104429.4104429.42)()()(⨯+⨯+⨯=++==s s ss s s s s s s U s U s H (2) 0000000011f Z C f Z L Z R R R N =====，，/ 508220.==L L L N µH ， 254110.==C C C N µF(3)mH5332539112105332539112539112110250101000300000000760.../....===⨯======⨯=⨯==---N N N L L L R R R f Z L Z R C f Z C C C ，＝，，，Ω§3.4正实函数1 定义 设)(s F 是复变量j s σω=+的函数，如果 (1) 当0]Im[=s 时，0)](Im[=s F ；(2) 当0]Re[≥s 时，0)](Re[≥s F 。

则称)(s F 为正实函数，简称PR 函数。

正实函数的映射关系如图5.6所示。

)](s F 图5.6正实函数的映射关系s 平面F(s)平面2 正实函数的性质(1) F (s )的全部极点位于s 平面的闭左半平面，F (s)在s 的右半平面是解析的。

证明思路：设F (s )在s 的右半平面存在极点，级数展开，F (s )变号，与正实函数矛盾，假设不成立。

(2)位于ωj 轴上的极点是一阶的，且其留数为正实数。

(包括0和±∞) (3) 正实函数的倒数仍为正实函数(对正实函数的零点也做了规定)。

(4) 设)()()(s D s N s a s a s b s b s F ll n n k k m m =++++= 。

则1≤-||n m ，1≤-||l k 。

因为n m n m s s a b s F -∞→=)(lim ， lk lk s s a b s F -→=)(l i m 0在∞→s 和0=s 处为一阶极点(零点)。

3 布隆定理(Otto Brune 1931年提出)(s I 1)(/)(s Y s Z 1=)(s I k kkk+-)(s U k（a ） (b)图5.7 布隆定理的证明对图5.7(b)， ∑≠=+++=bkj j j kj k k k k k s I sM s I sC sL R s U 2)()()1()(定理：当且仅当Z(s)是s 的正实函数时，阻抗函数Z(s)使用集中参数的RLCM 元件(非负值)才是可实现的。

必要性的证明：(充分性留在后续各节))]()(1)([|)(|1)(])()()1[(|)(|1)()()(|)(|1)()(|)(|1)()()()()()()(0002122212k k 211121111111s sM s V ss F s I s I s I sM s I sC sL R s I s I s U s I s I s U s I s I s I s I s U s I s U s Z k b k b kj j j kj k k k k b k ++=+++=====∙=≠==****∑∑∑由特勒根定理 (5.1)其中∑∑∑∑∑∑∑∑==≠=∙==≠=∙==≥=≥+=+=≥=≥=bk k k bk bk j j k j kj bk bk bkj j k j kj k k bk k kbk k k s I L T s I s I M T s I s I M s I L s M s I C s V s I R s F 220220222202202200|)(|0)()()()(|)(|)(0|)(|1)(0|)(|)(由式(5.1) 得(1) 当0=]Im [s 时，0=)](Im[s Z 。